Introduction

The focus of this paper is on addressing the following question: what is the lowest-depth quantum circuit that can generate computationally pseudorandom quantum states, i.e., quantum states that cannot be distinguished from Haar random by an adversary limited to polynomial resources? For us this question was motivated by two conjectures concerning scrambling by quantum circuit models of black hole dynamics that have emerged in the context of decades-old efforts of reconciling general relativity with quantum mechanics. The first, due to Susskind and collaborators, is that black holes are the fastest scramblers in nature with a scrambling time \({\tau }_{sc} \sim \log n\), where n is the number of degrees of freedom of the system1, a conjecture supported by holography-based calculations2,3,4. The second conjecture is that black holes must be also thorough scramblers of information5,6,7. In a nutshell, the idea is that black holes are also efficient generators of (computational) pseudorandomness: that they scramble information efficiently (i.e., in polynomial time) but that unscrambling (decoding) that information requires superpolynomial (in n) effort. While convincing arguments have been advanced for each of these conjectures, the question of whether one can achieve both “speed” and “thoroughness” at the same time—namely whether a quantum circuit of \(\log n\) depth (corresponding to a “computational time” scaling as \(\log n\)) can create pseudorandom states indistinguishable from Haar random for an adversary with polynomial resources—has, to our knowledge, not been discussed explicitly in the black hole literature.

Irrespective of whether or not satisfying both “speed” and “thoroughness” conditions is critical to understanding the quantum mechanics of black holes, the question of the level of scrambling by \(\log n\)-depth circuits is conceptually and practically important to a number of areas of quantum information. In particular, the issue has been discussed in the context of t-designs. In their comprehensive studies, Harrow and Mehraban8 conjectured that complete-graph-structured \(\log n\)-depth random circuits display the property of anti-concentration, namely that the probability that two different realizations of the circuit lead to identical outcomes is exponentially small in n, and at most a constant multiple of the value obtained by averaging over the Haar measure. They also conjectured that \(\log n\)-depth long-range circuits are sufficient for reaching 2-designs. While the anti-concentration conjecture was recently proved for a few circuit connectivities, anti-concentration is not sufficient for proving 2-design9,10. In particular, we show below that \(\log n\)-depth long-range 2-qubit circuits lead to polynomial (rather than superpolynomial) decay of a 4-point out-of-time-order correlator, and therefore these shallow circuits cannot produce 2-designs. We note that being a 2-design is a stronger (statistical) condition than computational indistinguishability based on measurements of 2-time/4-operator correlations. The notion of t-design refers to “statistical indistinguishability” from Haar-random, which is determined using the distance between probability distributions or the difference between the correlations they produce. By contrast, the discussions of pseudorandomness and all arguments of this paper are limited to “computational indistinguishability”, a more physical notion referring to adversaries who are limited to a polynomial number of measurements. Building computational pseudorandom Boolean functions with \(\log n\)-depth (NC1) circuits, a closely related classical version of the question we ask of quantum circuits, has been addressed by the cryptography community11,12,13. These classical constructions, however, involve pre-processing and non-trivial storage considerations that are not obviously amenable to low-depth quantum implementations.

Our own interest in information scrambling and the issues raised in this paper stem from our work on n-input/n-output reversible-circuit-based classical block ciphers and, in particular, on the question of what is the fastest, lowest-depth block cipher that is secure to attacks by polynomially-limited adversaries. In ref. 14 we proposed a cipher design that is capable of scrambling information with only \({{{\mathcal{O}}}}(\log n)\) layers of gates, on a par with the conjectured fastest scrambling time by black holes, but, we argued, to cryptographic level: the special \(\log n\)-depth cipher produces a permutation which is computationally indistinguishable from pseudorandom to an adversary with polynomial resources. [We stress that the \({{{\mathcal{O}}}}(\log n)\)-depth cipher design in ref. 14 meets necessary conditions for indistinguishability from a pseudorandom permutation. These conditions are based on quantitative measures of chaos and irreversibility in quantum systems (such as out-of-time-order correlators and string entropies). We do not establish sufficiency of these measures as this would be equivalent to proving that P ≠ NP.] It is also worth noting that these ciphers are NC1 reversible circuits, implemented without the need for preprocessing or additional storage11,12,13.

At first sight, classical ciphers seem only distantly related to the problem of information scrambling by quantum circuits. However, our progress in designing fast classical ciphers was based on a mapping of reversible classical computations into the space of Pauli strings. Within the framework of strings, the notions of irreversibility and chaos and their quantitative measure in terms of string entropies and out-of-time-order correlators (OTOCs) used in studies of quantum scrambling translate naturally to the problem of scrambling by reversible classical circuits. It is the string space picture that allows us to use the intuition gained from the study of one problem to the study of the other.

In particular, in the context of random reversible classical circuits, the repeated forward and backward propagation that defines OTOCs involving a polynomial number of string operators naturally describes arbitrary polynomial measurements carried out by an adversary on inputs and/or outputs of the circuits. Security to such attacks—referred to as differential attacks in cryptoanalysis—requires that all OTOCs describing correlations between results of such alternating measurements vanish faster than any polynomial (and ideally exponentially) in the number of bits acted on by the circuit. However, as discussed in ref. 14 for unstructured classical random circuits of universal reversible gates and as explained in the body of the paper for 2-qubit-gate-based random quantum circuits, the typical OTOC vanishes exponentially with “computational time”—the number of layers of gates applied. (The same exponential decay of the OTOC with time is the generic behavior expected for scrambling of information and the approach to chaos in quantum systems described by unitary Hamiltonian evolution4.) As a result, generic circuits of \(\log n\) depth lead to polynomial decays of the OTOCs, and thus are not secure to polynomial attacks (in the classical case) and do not generate computationally pseudorandom quantum states (in the quantum case).

The first message of this paper is that generic random quantum circuits of 2-qubit gates like those used as simple models of black hole dynamics cannot produce computationally pseudorandom quantum states while at the same time saturating the \(\log n\) lower bound on the scrambling time purported to qualify black holes as the fastest scramblers in nature. The root of the problem is the presence of polynomial tails of the stay-probabilities for low-weight Pauli strings, illustrated schematically in Fig. 1. In turn, for generic \(\log n\)-depth random circuits, these tails translate into a polynomial decay of OTOCs with n. Using the intuition gained from the study of shallow classical ciphers in ref. 14, we argue that ensuring a superpolynomial decay of OTOCs in \(\log n\)-depth quantum circuits requires employing special “inflationary gates” that eliminate the stay-probability of weight-1 strings and accelerate the spreading of string operators (see the inset of Fig. 1).

Fig. 1: Evolution of weight-1 Pauli strings.
figure 1

An effective 2-qubit reversible gate obtained by averaging uniformly over 2-qubit gates in U(4) leads to equal transition amplitudes among the 15 (=42 − 1) non-trivial weight-1 and weight-2 string states, including a finite stay probability, pw=1 < 1, for weight-1 strings (i.e., a finite amplitude for the transition from a weight-1 to another weight-1 string state). Applying \(\log n\) layers of 2-qubit gates leads to a polynomial tail \({({p}_{w = 1})}^{\log n}={n}^{-\log (1/{p}_{w = 1})}\) in the stay probability of weight-1 strings that, in turn, translates into polynomial tails in OTOCs. Exponential decay of OTOCs in \(\log n\) depth quantum circuits requires the use of special “inflationary” gates that map all weight-1 strings into weight-2 strings, thus eliminating the stay probability for weight-1 strings, as depicted schematically in the inset.

Full size image

Our second message is that, while inflationary gates do not exist as 2-qubit gates in U(4), they can be realized as 2-qudit gates with local Hilbert space dimension d ≥ 3 and d prime, or as 3-qubit gates. Circuits built from these gate sets would implement cryptographic level scrambling at the \(\log n\) “speed limit”, performance one might like to ascribe to a supreme “superscrambling” black hole.

Finally, we note that, while saturating the \(\log n\) scrambling time lower bound may not be critical for resolving black hole paradoxes, reaching computationally pseudorandom permutations at the \(\log n\) “speed limit” for scrambling was crucial in our own work on classical ciphers. As discussed in a recent paper15, ciphers of \(\log n\)-depth enable Encrypted Operator Computing (EOC), a gate-based polynomial complexity approach to secure computation on encrypted data that offers an alternative to Fully Homomorphic Encryption. For larger-depth circuits (and even for circuits of \({\log }^{2}n\) depth), the implementation of the EOC scheme would become superpolynomial in n and thus computationally intractable.

Results

Our contributions

The principal conclusions of this paper are that:

  • Due to polynomial tails in the stay-probability for weight-1 Pauli strings, 2-qubit-gate-based random quantum circuits of depth \({{{\mathcal{O}}}}(\log n)\) cannot produce pseudorandom states.

  • Reaching pseudorandom quantum states with \({{{\mathcal{O}}}}(\log n)\)-depth circuits becomes possible if one employs circuits comprised of special universal 3-qubit gates or 2-qudit gates with local Hilbert space dimension d ≥ 3 and d prime. These gates, which we refer to as “inflationary quantum gates”, or IQ gates, both expand and proliferate Pauli strings.

These conclusions are built on the intuition gained from our work in ref. 14 on classical ciphers based on reversible circuits of \(\log n\) depth, which we translate to the problem of information scrambling by quantum circuits. The polynomial tails in the probability distribution of weight-1 strings also occur in random reversible classical circuits and it is the elimination of these tails that required the structured design of our \(\log n\)-depth classical cipher. This design involves a permutation \(\hat{P}\) expressed as a 3-stage circuit \(\hat{P}={\hat{L}}_{r}\ \hat{N}\ {\hat{L}}_{l}\), with each stage represented by tree-structured reversible classical circuits built out of 3-bit permutations (gates), which enable universal classical computing. (The wiring of tree-structured circuits is described in the “Tree-structured circuits” discussion in the “Methods” section.) The bookends \({\hat{L}}_{l,r}\) are comprised of \({\log }_{2}n\) layers of special (classical) linear inflationary gates, that flip at least two output bits upon flipping a single input. The implementation of inflationary gates in string space eliminates the stay probability of weight-1 strings and accelerates the spreading of their effect across the n bitlines of the circuit. These inflationary stages flank a reversible circuit \(\hat{N}\), comprised of \({\log }_{3}n\) layers of (classical) nonlinear gates that maximize production of (Pauli)-string entropy. As argued in ref. 14, the 3-stage circuit realizes a \(\log n\)-depth cipher that satisfies the necessary (and we conjecture sufficient) conditions for pseudorandomness. [We note that the tree structure mimics a system of infinite dimension and, when combined with the inflationary property of the gates, ensures that the weight of the strings grows exponentially with the depth or number of layers of gates.]

The interplay between inflation and proliferation of strings leads to a double exponential decay of OTOCs as a function of the computational time, i.e., the number of layers of gates. For our shallow \(\log n\)-depth cipher this double exponential behavior, which implies an infinite Lyapunov exponent, translates into an exponential decay of OTOCs with n. We note that, in classical circuits, inflation and proliferation of strings are implemented by different families of gates and thus, as described above, fast and thorough scrambling requires a structured 3-stage cipher. In this paper we exploit the interplay of inflation and proliferation of strings in the context of quantum circuits. Unlike the case of classical circuits, in the quantum case one can build IQ gates that incorporate both string inflation and string proliferation. As a result, fast and thorough quantum scrambling can be realized with unstructured single-stage random quantum circuits comprised of IQ gates.

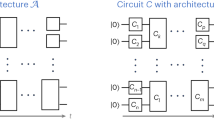
Generating pseudorandom quantum states with \(\log n\)-depth circuits

In this section we first argue that \(\log n\)-depth random quantum circuits built by sampling uniformly over 2-qubit gates in U(4) cannot produce pseudorandomness. We then give an example, schematically depicted in Fig. 2, of how to construct a pseudorandom state by employing a quantum circuit comprising a layer of Hadamard gates followed by the \(\log n\)-depth 3-stage classical cipher of ref. 14. Given that the classical cipher produces a pseudorandom permutation, an assumption tested via the Strict Avalanche Criterion (SAC) for pseudorandomness of classical ciphers16,17,18, we show that the resulting quantum state satisfies the pseudorandomness condition expressed in Eq. (1) below.

Fig. 2: The circuit architecture that generates the pseudorandom quantum state with depth \({{{\mathcal{O}}}}(\log n)\).
figure 2

This construction uses the three-stage (computationally) pseudorandom permutation of ref. 14, which is built out of three circuits, \({\hat{L}}_{l/r}\) and \(\hat{N}\), comprised of linear inflationary gates and nonlinear proliferation gates, respectively. Each block contains \({{{\mathcal{O}}}}(n\,\log n)\) three-qubit gates organized into a tree structure of \({{{\mathcal{O}}}}(\log n)\) layers (see the “Tree-structured circuits” discussion in the “Methods” section).

Full size image

We proceed by relating quantum expectation values of string operators to OTOCs, an identity which turns out to be useful in establishing the results of this section. We consider a quantum state \(\left\vert \psi \right\rangle\) on the Hilbert space of n qubits that is obtained through the evolution via a unitary transformation \(\hat{U}\) applied to an initial product state \(\left\vert {\psi }_{0}\right\rangle\): \(\left\vert \psi \right\rangle =\hat{U}\,\left\vert {\psi }_{0}\right\rangle\). If the state \(\left\vert \psi \right\rangle\) is pseudorandom, then the expectation values of (non-trivial) Pauli string operators must vanish faster than any polynomially bounded function η(n) of the number of qubits, n:

$$| \left\langle \psi \right\vert \ {\hat{{{{\mathcal{S}}}}}}_{\alpha }\ \left\vert \psi \right\rangle {| }^{2}\, < \,\eta (n)\ ,$$
(1)

where a Pauli string:

$${\hat{{{{\mathcal{S}}}}}}_{\alpha }=\mathop{\prod}\limits_{j\in {\alpha }^{{{{\rm{x}}}}}}\ {\hat{\sigma }}_{j}^{{{{\rm{x}}}}}\ \mathop{\prod}\limits_{k\in {\alpha }^{{{{\rm{z}}}}}}\ {\hat{\sigma }}_{k}^{{{{\rm{z}}}}}\ ,$$
(2)

is labeled by the set α = (αx, αz) of qubit indices present in the string. By adding a phase \({i}^{{\alpha }^{{{{\rm{x}}}}}\cdot {\alpha }^{{{{\rm{z}}}}}}\) to \({\hat{{{{\mathcal{S}}}}}}_{\alpha }\)—picking up an i each time both a \({\hat{\sigma }}_{j}^{{{{\rm{x}}}}}\) and \({\hat{\sigma }}_{j}^{{{{\rm{z}}}}}\) appear at the same j, or basically deploying the \({\hat{\sigma }}^{{{{\rm{y}}}}}\) s as well—would make the string operator Hermitian. Here we prefer the definition Eq. (2) for the applications we consider, and work explicitly with both \({\hat{{{{\mathcal{S}}}}}}_{\alpha }^{\ }\) and \({\hat{{{{\mathcal{S}}}}}}_{\alpha }^{{\dagger} }\) when needed. (When convenient, we also use the equivalent notation \({\alpha }_{i}^{{{{\rm{x,z}}}}}=1\leftrightarrow i\in {\alpha }^{{{{\rm{x,z}}}}}\) and \({\alpha }_{i}^{{{{\rm{x,z}}}}}=0\leftrightarrow i\notin {\alpha }^{{{{\rm{x,z}}}}}\), as for example in the definition of the dot product a ⋅ b ≡ ∑iaibi.)

We next move the unitary transformation onto the string operators to rewrite the left hand side of Eq. (1) in terms of “time”-evolved Pauli strings, \({\hat{{{{\mathcal{S}}}}}}_{\alpha }(\tau )\equiv {\hat{U}}^{{\dagger} }\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }\ \hat{U}\), and \({\hat{{{{\mathcal{S}}}}}}_{\alpha }(-\tau )\equiv \hat{U}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }\ {\hat{U}}^{{\dagger} }\) (\({\hat{{{{\mathcal{S}}}}}}_{\alpha }(0)\equiv {\hat{{{{\mathcal{S}}}}}}_{\alpha }\)). Without loss of generality, we consider an initial product state in the computational basis, \(\left\vert {\psi }_{0}\right\rangle =\left\vert x\right\rangle\), where x is an n-bit binary vector. We can then write:

$$\begin{array}{lll}{\left\vert \left\langle x\right\vert {\hat{{{{\mathcal{S}}}}}}_{\alpha }(\tau )\left\vert x\right\rangle \right\vert }^{2}&=&{{{\rm{tr}}}}\,\left[{\hat{{{{\mathcal{P}}}}}}_{x}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }^{{\dagger} }(\tau )\ {\hat{{{{\mathcal{P}}}}}}_{x}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }(\tau )\right]\\ &=&\frac{1}{{4}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}},{\beta }^{{\prime} {{{\rm{z}}}}}}\ {(-1)}^{({\beta }^{{{{\rm{z}}}}}\oplus {\beta }^{{\prime} {{{\rm{z}}}}})\cdot x}\ {{{\rm{tr}}}}\,\left[{\hat{{{{\mathcal{S}}}}}}_{{\beta }^{{{{\rm{z}}}}}}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }^{{\dagger} }(\tau )\ {\hat{{{{\mathcal{S}}}}}}_{{\beta }^{{\prime} {{{\rm{z}}}}}}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }(\tau )\right]\ ,\end{array}$$
(3)

where \({\hat{{{{\mathcal{P}}}}}}_{x}\) is the projector onto the state \(\left\vert x\right\rangle\), expressed in terms of Pauli strings as:

$${\hat{{{{\mathcal{P}}}}}}_{x}=\mathop{\prod}\limits_{i}\left[\frac{1+{(-1)}^{{x}_{i}}{\sigma }_{i}^{z}}{2}\right]=\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}{(-1)}^{{\beta }^{{{{\rm{z}}}}}\cdot x}\ {\hat{{{{\mathcal{S}}}}}}_{{\beta }^{{{{\rm{z}}}}}}\ .$$
(4)

If the correlator in Eq. (3) decays superpolynomially in n for all initial states \(\left\vert x\right\rangle\), then the superpolynomial decay carries over to the average over all initial states. Thus, averaging Eq. (3) over x, and using \({\sum }_{x}{(-1)}^{({\beta }^{{{{\rm{z}}}}}\oplus {\beta }^{{\prime} {{{\rm{z}}}}})\cdot x}={2}^{n}\,{\delta }_{{\beta }^{{{{\rm{z}}}}},{\beta }^{{\prime} {{{\rm{z}}}}}}\), yields:

$$\begin{array}{l}{Q}_{\alpha }(\tau )\equiv \,\frac{1}{{2}^{n}}\,\mathop{\sum}\limits_{x}\ {\left\vert \left\langle x\right\vert {\hat{{{{\mathcal{S}}}}}}_{\alpha }(\tau )\left\vert x\right\rangle \right\vert }^{2}\\ \qquad\quad=\,\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}\ \left\{\frac{1}{{2}^{n}}\ {{{\rm{tr}}}}\,\left[{\hat{{{{\mathcal{S}}}}}}_{{\beta }^{{{{\rm{z}}}}}}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }^{{\dagger} }(\tau )\ {\hat{{{{\mathcal{S}}}}}}_{{\beta }^{{{{\rm{z}}}}}}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }(\tau )\right]\right\}\\ \qquad\quad=\,\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}\ \left\{\frac{1}{{2}^{n}}\ {{{\rm{tr}}}}\,\left[{\hat{{{{\mathcal{S}}}}}}_{{\beta }^{{{{\rm{z}}}}}}^{{\dagger} }(-\tau )\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }^{{\dagger} }\ {\hat{{{{\mathcal{S}}}}}}_{{\beta }^{{{{\rm{z}}}}}}(-\tau )\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }\right]\right\}\ ,\end{array}$$
(5)

where we shifted the time-dependence from τ to −τ by using the cyclic property of the trace and the fact that the z-string operator \({\hat{{{{\mathcal{S}}}}}}_{{\beta }^{{{{\rm{z}}}}}}\) is Hermitian. Notice that the expression within parentheses in Eq. (5) represents an OTOC of Pauli string operators.

Equation (5) can be translated into a more intuitive form by writing the τ-dependent string, \(U\,{\hat{{{{\mathcal{S}}}}}}_{\alpha }\,{U}^{{\dagger} }={\sum }_{\beta }\ {A}_{\alpha \beta }(-\tau )\ {\hat{{{{\mathcal{S}}}}}}_{\beta }\) in terms of string amplitudes, Aαβ(−τ), and then expressing Qα(τ) as:

$$\begin{array}{ll}{Q}_{\alpha }(\tau )=\,\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}\ \mathop{\sum}\limits_{\gamma ,{\gamma }^{{\prime} }}\ {A}_{\gamma {\beta }^{{{{\rm{z}}}}}}^{* }(-\tau )\ {A}_{{\gamma }^{{\prime} }{\beta }^{{{{\rm{z}}}}}}(-\tau )\ \left\{\frac{1}{{2}^{n}}\ {{{\rm{tr}}}}\,\left[{\hat{{{{\mathcal{S}}}}}}_{\gamma }^{{\dagger} }\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }^{{\dagger} }\ {\hat{{{{\mathcal{S}}}}}}_{{\gamma }^{{\prime} }}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }\right]\right\}\\ \qquad\quad=\,\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}\ \mathop{\sum}\limits_{\gamma ,{\gamma }^{{\prime} }}{A}_{\gamma {\beta }^{{{{\rm{z}}}}}}^{* }(-\tau )\ {A}_{{\gamma }^{{\prime} }{\beta }^{{{{\rm{z}}}}}}(-\tau )\ {\delta }_{\gamma ,{\gamma }^{{\prime} }}\ {(-1)}^{{\alpha }^{{{{\rm{x}}}}}\cdot {\gamma }^{{{{\rm{z}}}}}}\ {(-1)}^{{\alpha }^{{{{\rm{z}}}}}\cdot {\gamma }^{{{{\rm{x}}}}}}\\ \qquad\quad=\,\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}\ \mathop{\sum}\limits_{\gamma }\ | {A}_{\gamma {\beta }^{{{{\rm{z}}}}}}(-\tau ){| }^{2}\ \ {(-1)}^{{\alpha }^{{{{\rm{x}}}}}\cdot {\gamma }^{{{{\rm{z}}}}}}\ {(-1)}^{{\alpha }^{{{{\rm{z}}}}}\cdot {\gamma }^{{{{\rm{x}}}}}}\ .\end{array}$$
(6)

For simplicity we consider a local z-string, \({\hat{{{{\mathcal{S}}}}}}_{\alpha }={\hat{\sigma }}_{i}^{{{{\rm{z}}}}}\) (i.e., \({\alpha }^{{{{\rm{x}}}}}=0,{\alpha }_{j}^{{{{\rm{z}}}}}={\delta }_{ij}\)), in which case, \({Q}_{{\hat{\sigma }}_{i}^{{{{\rm{z}}}}}}(\tau )\equiv \frac{1}{{2}^{n}}\,{\sum }_{x}| \left\langle x\right\vert \ {\hat{\sigma }}_{i}^{{{{\rm{z}}}}}(\tau )\ \left\vert x\right\rangle {| }^{2}\) is given by:

$$\begin{array}{ll}{Q}_{{\hat{\sigma }}_{i}^{{{{\rm{z}}}}}}(\tau )\,=\,\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}\bigg[\mathop{\sum}\limits_{\gamma | {\hat{\sigma }}_{i}^{{{{\rm{x}}}}}\notin {\hat{{{{\mathcal{S}}}}}}_{\gamma }}\ | {A}_{\gamma {\beta }^{{{{\rm{z}}}}}}(-\tau ){| }^{2}-\mathop{\sum}\limits_{\gamma | {\hat{\sigma }}_{i}^{{{{\rm{x}}}}}\in {\hat{{{{\mathcal{S}}}}}}_{\gamma }}\ | {A}_{\gamma {\beta }^{{{{\rm{z}}}}}}(-\tau ){| }^{2}\bigg]\\ \qquad\quad\,=\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}\ \big[({p}_{i;{\mathbb{1}}}(-\tau ;{\beta }^{{{{\rm{z}}}}})+{p}_{i;z}(-\tau ;{\beta }^{{{{\rm{z}}}}}))-({p}_{i;x}(-\tau ;{\beta }^{{{{\rm{z}}}}})+{p}_{i;y}(-\tau ;{\beta }^{{{{\rm{z}}}}}))\big]\ ,\end{array}$$
(7)

where \({p}_{i;{\mathbb{1}}}(-\tau ;{\beta }^{{{{\rm{z}}}}}),{p}_{i;z}(-\tau ;{\beta }^{{{{\rm{z}}}}}),{p}_{i;x}\left(-\tau ;{\beta }^{{{{\rm{z}}}}}\right.\) and pi;y(−τ; βz) are the probabilities that, at position i (and computational time −τ), the Pauli string contains, respectively, an identity, a \({\hat{\sigma }}^{{{{\rm{z}}}}}\), a \({\hat{\sigma }}^{{{{\rm{x}}}}}\), or the product \({\hat{\sigma }}^{{{{\rm{x}}}}}{\hat{\sigma }}^{{{{\rm{z}}}}}\). [Throughout we keep track of the initial non-trivial string state βz defining the transition amplitudes \({A}_{\gamma {\beta }^{{{{\rm{z}}}}}}(-\tau )\) in Eq. (7).]

Unstructured random quantum circuits

We will now make use of Eq. (7) to address the following question: can a \(\log n\)-depth random quantum circuit built from 2-qubit gates (2-local) in U(4) representing the unitary operator \(\hat{U}\) in \(\left\vert \psi \right\rangle =\hat{U}\,\left\vert {\psi }_{0}\right\rangle\) lead to pseudorandom states for which \({Q}_{{\hat{\sigma }}_{i}^{{{{\rm{z}}}}}}\) satisfies the pseudorandomness condition in Eq. (1)? We answer this question by considering the average string weight, which is obtained by averaging Eq. (7) uniformly over circuits and over the axis of quantization, whereby we can write \(\overline{{p}_{i;x}(-\tau ;{\beta }^{{{{\rm{z}}}}})}=\overline{{p}_{i;y}(-\tau ;{\beta }^{{{{\rm{z}}}}})}=\overline{{p}_{i;z}(-\tau ;{\beta }^{{{{\rm{z}}}}})}=\frac{1}{3}\rho (-\tau ;{\beta }^{{{{\rm{z}}}}})\), where ρ(−τ; βz) is the string density. As a result:

$$\begin{array}{rc}\overline{{Q}_{{\hat{\sigma }}^{{{{\rm{z}}}}}}(\tau )}&=\frac{1}{{2}^{n}}\mathop{\sum}\limits_{{\beta }^{{{{\rm{z}}}}}}\ \left[1-\frac{4}{3}\ \rho (-\tau ;{\beta }^{{{{\rm{z}}}}})\right]\ .\end{array}$$
(8)

The averaging in Eq. (8) is carried out over random 2-qubit-gate-based universal circuits in which case the superpolynomial bound on \({Q}_{{\hat{\sigma }}_{i}^{{{{\rm{z}}}}}}(\tau )\) for a given random circuit remains valid for the average \(\overline{{Q}_{{\hat{\sigma }}^{{{{\rm{z}}}}}}(\tau )}\). Here we assume that \({Q}_{{\hat{\sigma }}_{i}^{{{{\rm{z}}}}}}(\tau )\) obtained for a typical random circuit coincides with the average over circuits, \(\overline{{Q}_{{\hat{\sigma }}^{{{{\rm{z}}}}}}(\tau )}\). [Note that considering the average quantity eliminates the pathological behavior of individual atypical circuits—such as for example one comprised of only identity gates—because their contribution are only included in the average with vanishingly small probability.] Moreover, the average of the string density over circuits depends on the initial condition, βz, but is independent of the site index i. Also, note that we kept the subscript \({\hat{\sigma }}^{{{{\rm{z}}}}}\) on \({Q}_{{\hat{\sigma }}^{{{{\rm{z}}}}}}(\tau )\) as a reminder of the initial \({\hat{\sigma }}^{{{{\rm{z}}}}}\)-string expectation value in Eq. (7). Parametrizing the τ dependence in terms of the number of layers of gates ℓ (the depth) of the circuit describing the unitary transformation \(\hat{U}\) that generated the evolution of string amplitudes up to time −τ, we can define:

$$\begin{array}{r}\epsilon (\ell ;{\beta }^{{{{\rm{z}}}}})\equiv 1-\frac{4}{3}\rho (\ell ;{\beta }^{{{{\rm{z}}}}})\ ,\end{array}$$
(9)

to write \(\overline{{Q}_{{\hat{\sigma }}^{{{{\rm{z}}}}}}(\tau )}=\frac{1}{{2}^{n}}{\sum }_{{\beta }^{{{{\rm{z}}}}}}\epsilon (\ell ;{\beta }^{{{{\rm{z}}}}})\). A lower bound on the function η(n) in Eq. (1) is determined by how fast ρ(ℓ; βz) reaches its asymptotic value of 3/4 starting from an initial condition associated with the arbitrary (non-trivial) initial string state βz.

The equation describing the evolution of the average string weight ρ(ℓ; βz) can be derived by following all 15(=4 × 4 − 1) non-trivial two-site strings through the unitary evolution with consecutive layers of effective (average) gates which connect with equal amplitude each of these states to themselves and to each other. Here we shall make a mean-field approximation, which is equivalent to the assumption that the densities at different positions along the string are uncorrelated. It then follows that, since the identity string does not scatter into a non-trivial string, a configuration involving identity operators on both sites, which occurs with probability (1 − ρ)2, cannot contribute a Pauli operator on a given site. Otherwise, with probability 1 − (1 − ρ)2, non-trivial 1-site and 2-site string states scatter into a configuration with a Pauli operator on a given site with transition probability 12/15 = 4/5, accounting for the fact that only 12 (3 weight-1 strings and 9 weight-2 strings) out of the 15 non-trivial string states feature a Pauli operator on that site. Therefore:

$$\begin{array}{l}\rho (\ell +1;{\beta }^{{{{\rm{z}}}}})={\left(1-\rho (\ell ;{\beta }^{{{{\rm{z}}}}})\right)}^{2}\times 0\\ \qquad\qquad\qquad+\,[1-{\left(1-\rho (\ell ;{\beta }^{{{{\rm{z}}}}})\right)}^{2}]\times \frac{4}{5} \equiv \frac{4}{5}\ \rho (\ell ;{\beta }^{{{{\rm{z}}}}})\ (2-\rho (\ell ;{\beta }^{{{{\rm{z}}}}}))\ .\end{array}$$
(10)

As expected, ρ(ℓ → ∞; βz) = 3/4 is a fixed point. Writing Eq. (10) in terms of ϵ(ℓ; βz) defined in Eq. (9), we obtain:

$$\begin{array}{rc}\epsilon (\ell +1;{\beta }^{{{{\rm{z}}}}})=&\frac{2}{5}\ \epsilon (\ell ;{\beta }^{{{{\rm{z}}}}})+\frac{3}{5}\ {(\epsilon (\ell ;{\beta }^{{{{\rm{z}}}}}))}^{2}\ .\end{array}$$
(11)

This equation must be solved with initial condition ϵ(0; βz) = 1 − (4/3) ρ(0; βz). Asymptotically, ϵ(ℓ; βz) tends to zero exponentially in ℓ as ~(2/5)ℓ, for any initial string state βz.

We note that incorporating two-site correlations beyond mean-field can alter the coefficients in Eq. (11) by terms of order 1/n but cannot change the fixed point density, ρ(ℓ → ∞; βz) = 3/4. In particular, these 1/n corrections can modify the coefficient of the linear term in Eq. (11) but cannot eliminate it all together, thus preserving the exponential decay of OTOCs with ℓ. For \(\ell \sim {{{\mathcal{O}}}}(\log n)\), \(\overline{{Q}_{{\hat{\sigma }}^{{{{\rm{z}}}}}}}\) in Eq. (8) can only decay as a power law in n, violating the assumption that η(n) in Eq. (1) is superpolynomially small in n, as pseudorandomness requires. We conclude that evolution via a \(\log n\)-depth circuit built from universal 2-qubit gates drawn uniformly from unitaries in U(4) is incapable of reaching a pseudorandom state. [It is interesting to note that the number of layers required to reach the equilibrium string weight ρ = 3/4 (1 − ϵ) starting from an initial value \(\rho (0;{\beta }^{{{{\rm{z}}}}}={\hat{\sigma }}_{i}^{{{{\rm{z}}}}}) \sim 1/n\) that emerges from the differential equation derived from the mean-field recursion in Eq. (10) corresponds to a circuit of size \(S=\frac{5}{6}\,n\left[\ln n+\ln (1/\epsilon )\right]\). This is precisely the expression for the lower bound on circuit size required for anti-concentration derived in ref. 10 for 2-qubit gates on a complete graph and conjectured earlier by Harrow and Mehraban8.]

In the next section we use the \({{{\mathcal{O}}}}(\log n)\)-depth structured classical reversible circuits discussed in ref. 14 to build a pseudorandom quantum state, i.e., a quantum state for which the bound in Eq. (1) is satisfied.

Structured random quantum circuits

Let us start with a product state \({\left\vert 0\right\rangle }^{\otimes n}\) in the computational basis, and apply a non-trivial string βx of Pauli \({\hat{\sigma }}^{{{{\rm{x}}}}}\) operators that flips the initial state to \(\left\vert {\beta }^{{{{\rm{x}}}}}\right\rangle\). By applying Hadamard gates to this state we then obtain:

$${H}^{\otimes n}\ \left\vert {\beta }^{{{{\rm{x}}}}}\right\rangle =\frac{1}{\sqrt{{2}^{n}}}\mathop{\sum}\limits_{x}\ {(-1)}^{{\beta }^{{{{\rm{x}}}}}\cdot x}\ \left\vert x\right\rangle \ .$$
(12)

Finally, evolving the resulting state with a classical reversible permutation circuit \(\hat{P}\), \(\hat{P}\,\left\vert x\right\rangle =\left\vert P(x)\right\rangle\), leads to:

$$\begin{array}{ll}\left\vert {\psi }_{{\beta }^{{{{\rm{x}}}}}}\right\rangle =\frac{1}{\sqrt{{2}^{n}}}\mathop{\sum}\limits_{x}\ {(-1)}^{{\beta }^{{{{\rm{x}}}}}\cdot x}\ \left\vert P(x)\right\rangle \\ \qquad\quad=\frac{1}{\sqrt{{2}^{n}}}\mathop{\sum}\limits_{x}\ {(-1)}^{{\beta }^{{{{\rm{x}}}}}\cdot {P}^{-1}(x)}\ \left\vert x\right\rangle \ .\end{array}$$
(13)

A general reversible classical circuit \(\hat{P}\) can be built from 3-bit gates in S8, which generate all permutations on the space of n bits within the alternating group \({A}_{{2}^{n}}\) (all even permutations in the group \({S}_{{2}^{n}}\)).

References 19,20 show that a state of the form in Eq. (13), with the phase given by a pseudorandom function, is a pseudorandom state. Here we will use pseudorandom permutations that, for large n, cannot be distinguished from pseudorandom functions. More precisely, we will deploy 3-stage \(\log n\)-depth circuits discussed in ref. 14, where it was argued that such circuits generate permutations satisfying the necessary (and conjectured to also be sufficient) conditions for pseudorandomness. The resulting quantum circuit architecture that generates the pseudorandom quantum states considered in this section is shown in Fig. 2.

To illustrate the importance of the 3-stage structure to the generation of pseudorandomness, we consider the expectation value of a Pauli string operator in the state \(\vert {\psi }_{{\beta }^{{{{\rm{x}}}}}}\rangle\) of Eq. (13). We proceed by applying \({\hat{{{{\mathcal{S}}}}}}_{\alpha }\) to this state:

$$\begin{array}{ll}{\hat{{{{\mathcal{S}}}}}}_{\alpha }\ \left\vert {\psi }_{{\beta }^{{{{\rm{x}}}}}}\right\rangle =\frac{1}{\sqrt{{2}^{n}}}\mathop{\sum}\limits_{x}\ {(-1)}^{{\beta }^{{{{\rm{x}}}}}\cdot {P}^{-1}(x)}\ {\hat{{{{\mathcal{S}}}}}}_{\alpha }\left\vert x\right\rangle \\ \qquad\qquad=\frac{1}{\sqrt{{2}^{n}}}\mathop{\sum}\limits_{x}\ {(-1)}^{{\beta }^{{{{\rm{x}}}}}\cdot {P}^{-1}(x)}\ {(-1)}^{{\alpha }^{{{{\rm{z}}}}}\cdot x}\left\vert x\oplus {\alpha }^{{{{\rm{x}}}}}\right\rangle \\ \qquad\qquad={(-1)}^{{\alpha }^{{{{\rm{z}}}}}\cdot {\alpha }^{{{{\rm{x}}}}}}\frac{1}{\sqrt{{2}^{n}}}\mathop{\sum}\limits_{x}\ {(-1)}^{{\beta }^{{{{\rm{x}}}}}\cdot {P}^{-1}(x\oplus {\alpha }^{{{{\rm{x}}}}})}\ {(-1)}^{{\alpha }^{{{{\rm{z}}}}}\cdot x}\left\vert x\right\rangle \ ,\end{array}$$
(14)

which, in turn, leads to the following expression for the expectation value of the string operator \({\hat{{{{\mathcal{S}}}}}}_{\alpha }\):

$$\begin{array}{rc}\left\langle {\psi }_{{\beta }^{{{{\rm{x}}}}}}\right\vert \ {\hat{{{{\mathcal{S}}}}}}_{\alpha }\ \left\vert {\psi }_{{\beta }^{{{{\rm{x}}}}}}\right\rangle &={(-1)}^{{\alpha }^{{{{\rm{z}}}}}\cdot {\alpha }^{{{{\rm{x}}}}}}\frac{1}{{2}^{n}}\mathop{\sum }\limits_{x}\ {(-1)}^{{\beta }^{{{{\rm{x}}}}}\cdot [{P}^{-1}(x)\oplus {P}^{-1}(x\oplus {\alpha }^{{{{\rm{x}}}}})]}\ {(-1)}^{{\alpha }^{{{{\rm{z}}}}}\cdot x}\ .\end{array}$$
(15)

We note that for αz = 0, \({\alpha }_{k}^{{{{\rm{x}}}}}={\delta }_{k,i}\) (i.e., \({\hat{{{{\mathcal{S}}}}}}_{\alpha }={\hat{\sigma }}_{i}^{{{{\rm{x}}}}}\)), and \({\beta }_{l}^{{{{\rm{x}}}}}={\delta }_{l,j}\) (i.e., flipping only the jth qubit of the initial state) this expectation value is expressed as the OTOC representing the SAC14, a simple test of security for a classical block cipher:

$$\begin{array}{rc}{Q}_{ij}^{{{{\rm{SAC}}}}}&\equiv \frac{1}{{2}^{n}}\mathop{\sum}\limits_{x}\ {(-1)}^{[{P}_{j}^{-1}(x)\oplus {P}_{j}^{-1}(x\oplus {c}_{i})]}\ \ ,\end{array}$$
(16)

where the qubit-wise XOR operation for two n-qubit strings x ⊕ ci flips the ith qubit of x (i.e., ci = 2i).

In ref. 14 we presented a calculation of the evolution of the SAC OTOC Eq. (16) through the application of consecutive layers of the structured cipher. To summarize the results of that calculation, we first introduce \({\hat{P}}^{-1}(\ell )\), the partial circuit comprised of the first ℓ layers of the circuit \({\hat{P}}^{-1}\), with \({\hat{P}}^{-1}(0)\equiv {\mathbb{1}}\) and \({\hat{P}}^{-1}({\ell }_{f})\equiv {\hat{P}}^{-1}\) and define the expectation value of the string operator in Eq. (16) after ℓ layers of the permutation P−1 are applied as:

$${Q}_{ij}^{{{{\rm{SAC}}}}}(\ell )=\frac{1}{{2}^{n}}\mathop{\sum}\limits_{x}\ {(-1)}^{[{P}_{j}^{-1}(x,\ell )\oplus {P}_{j}^{-1}(x\oplus {c}_{i},\ell )]}\ .$$
(17)

As in the mean-field calculation above we will focus on averages over circuits, \(s(\ell )=\overline{{Q}_{ij}^{{{{\rm{SAC}}}}}(\ell )}\) and \(q(\ell )=\overline{{[{Q}_{ij}^{{{{\rm{SAC}}}}}(\ell )]}^{2}}\). Since gates defining individual layers are chosen independently we can easily derive recursion relations relating s(ℓ + 1) and q(ℓ + 1) to s(ℓ) and q(ℓ), which depend on the specific gate set chosen. As shown in ref. 14 and summarized in the “SAC OTOC” discussion of the “Methods” section, evolution through ℓ layers of linear inflationary gates, leads to:

$$s(\ell +1)=\frac{2}{3}\,{[s(\ell )]}^{2}+\frac{1}{3}\,{[s(\ell )]}^{3}\ ,$$
(18a)
$$q(\ell +1)=\frac{2}{3}\,{[q(\ell )]}^{2}+\frac{1}{3}\,{[q(\ell )]}^{3}\ ;$$
(18b)

and evolution through ℓ layers of supernonlinear gates, which maximize string entropy productionǹ14, leads to:

$$s(\ell +1)=\frac{3}{7}\,s(\ell )+\frac{3}{7}\,{[s(\ell )]}^{2}+\frac{1}{7}\,{[s(\ell )]}^{3}\ ,$$
(19a)
$$\begin{array}{ll}q(\ell +1)=\frac{3}{28}\,\left({[s(\ell )]}^{2}+{[s(\ell )]}^{3}\right)\\ \qquad\qquad\,\,\,+\,\frac{3}{28}\,q(\ell )\,\left(1+2\,s(\ell )+2\,{[s(\ell )]}^{2}\right)\\ \qquad\qquad\,\,\,+\,\frac{3}{28}\,{[q(\ell )]}^{2}\,\left(1+s(\ell )\right)+\frac{1}{28}\,{[q(\ell )]}^{3}\ .\end{array}$$
(19b)

We note that the recursion relations in Eqs. (18a), (18b), (19a), and (19b) are exact for tree-structured circuits of depth \(\ell \le {\log }_{3}n\).

We note that if the circuit contained only supernonlinear gates, the analysis of the decay of the OTOC (and of the expectation value of the string operator) could be carried out by linearizing Eqs. (19b) for small s and q:

$$s(\ell +1)=\frac{3}{7}\,s(\ell )+\cdots \ ,$$
(20a)
$$q(\ell +1)=\frac{3}{28}\,q(\ell )+\cdots \ .$$
(20b)

In this case, it is inescapable that q(ℓ) can only decay exponentially with depth ℓ: q(ℓ) ~ e−λℓ, with \(\lambda =\ln (28/3)\). One can interpret the coefficient of the linear term in the expansion of the recursion relation as a Lyapunov exponent, λ. The exponential decay of q(ℓ) with a finite Lyapunov exponent λ implies that circuits of \(\log n\) depth can only lead to polynomial decay of the SAC OTOC. It is important to stress that the same linear leading behavior in s and q of the recursion relations occurs for random circuits of universal gates. Eliminating the linear terms requires fine tuning—this is precisely what makes the linear inflationary gates both special and necessary for ensuring that the SAC OTOC decays exponentially with n for depth \(\log n\) structured circuits.

Indeed, the recursions for s and q in the case of inflationary gates start with quadratic leading terms. [Note that q = 1 is a fixed point of the recursion Eq. (18b), and thus nonlinear gates are needed to reduce the value of q below 1 before the system can evolve toward the q = 0 fixed point.] To lowest order in q, the recursion Eq. (18b), which is activated following the action of the layers of supernonlinear gates, reads:

$$q(\ell +1)=\frac{2}{3}\,{[q(\ell )]}^{2}+\cdots \ ,$$
(21)

the asymptotic solution of which is a double exponential in ℓ, \(q(\ell ) \sim \frac{3}{2}{\left[\frac{2}{3}q(0)\right]}^{{2}^{\ell }}\). This behavior, which corresponds to an infinite Lyapunov exponent, is non-universal but essential in ensuring the exponential decay with n of the SAC OTOC and, equivalently, in proving the superpolynomial bound of Eq. (1) for expectation values of string operators in the quantum state \(\left\vert {\psi }_{{\beta }^{{{{\rm{x}}}}}}\right\rangle\) in Eq. (13).

We note that there are 144 3-bit inflationary gates among the 8! gates 3-bit gates in S814. One can then ask whether inflationary gates are also present among the 2-qubit U(4) gates that generate universal quantum computation, in which case one could imagine constructing pseudorandom quantum states by employing such 2-qubit gates. Below we show that there are no 2-qubit inflationary gates, but that 2-qudit inflationary gates do exist for d ≥ 3 and d prime.

Absence of two-qubit inflationary gates

The main message of this section is that there are no inflationary 2-qubit gates in U(4), i.e., that there are no U(4) gates which eliminate the stay probability of weight-1 strings. We prove this statement first for 2-qubit Clifford gates, and then for general unitary gates in U(4).

Clifford gates

We argue by contradiction: suppose that a two-qubit Clifford gate UCl maps both Pauli operators \({\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\) and \({\hat{\sigma }}_{1}^{{{{\rm{z}}}}}\) on site 1 to Pauli strings of weight two with a footprint on both site 1 and site 2:

$$\begin{array}{rc}{U}_{{{{\rm{Cl}}}}}^{{\dagger} }\ {\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\ {U}_{{{{\rm{Cl}}}}}&={\hat{\sigma }}_{1}^{\alpha }\ {\hat{\sigma }}_{2}^{\beta }\ ,\\ {U}_{{{{\rm{Cl}}}}}^{{\dagger} }\ {\hat{\sigma }}_{1}^{{{{\rm{z}}}}}\ {U}_{{{{\rm{Cl}}}}}&={\hat{\sigma }}_{1}^{\mu }\ {\hat{\sigma }}_{2}^{\nu }\ .\end{array}$$
(22)

Since the anticommutation relation is preserved under gate conjugation, \(\{{\hat{\sigma }}_{1}^{\alpha }{\hat{\sigma }}_{2}^{\beta },{\hat{\sigma }}_{1}^{\mu }{\hat{\sigma }}_{2}^{\nu }\}=0\), the operator content of the two Pauli strings must be identical on one site, i.e., one must have either α = μ, β ≠ ν or β = ν, α ≠ μ. By considering the transformation of the commutator it immediately follows that UCl maps \({\hat{\sigma }}_{1}^{{{{\rm{y}}}}}\) to a single-site Pauli operator, thus contradicting the initial assumption that UCl maps all weight-1 strings to weight-2 strings.

U(4) unitaries

We start with a special case which we then use to establish the general result. Again, we argue by contradiction: we assume that a 2-qubit unitary maps \({\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\) into a single weight-2 Pauli string, \(\hat{{{{\mathcal{S}}}}}\), and maps \({\hat{\sigma }}_{1}^{{{{\rm{z}}}}}\) to a superposition of weight-2 Pauli strings:

$$\begin{array}{ll}{U}^{{\dagger} }\ {\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\ U\,=\,\hat{{{{\mathcal{S}}}}}\\ {U}^{{\dagger} }\ {\hat{\sigma }}_{1}^{{{{\rm{z}}}}}\ U\,=\,\mathop{\sum}\limits_{\mu }\ {b}_{\mu }^{c}\ {\hat{{{{\mathcal{S}}}}}}_{c}^{\mu }+\mathop{\sum}\limits_{\nu }\ {b}_{\nu }^{a}\ {\hat{{{{\mathcal{S}}}}}}_{a}^{\nu },\end{array}$$
(23)

where, in the second equation, the \({b}_{\mu }^{c}\) and \({b}_{\nu }^{a}\) are string amplitudes, associated separately with Pauli strings that commute or anticommute with \(\hat{{{{\mathcal{S}}}}}\): \([\hat{{{{\mathcal{S}}}}},{\hat{{{{\mathcal{S}}}}}}_{c}^{\mu }]=0\) and \(\{\hat{{{{\mathcal{S}}}}},{\hat{{{{\mathcal{S}}}}}}_{a}^{\nu }\}=0\). Again, the conjugated Pauli operators must satisfy: \(\{{U}^{{\dagger} }\,{\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\,U\,,\,{U}^{{\dagger} }\,{\hat{\sigma }}_{1}^{{{{\rm{z}}}}}\,U\}=0\). This condition is automatically satisfied by \({\hat{{{{\mathcal{S}}}}}}_{a}^{\nu }\), whereas for \({\hat{{{{\mathcal{S}}}}}}_{c}^{\mu }\) it requires:

$$2\,\mathop{\sum}\limits_{\mu }\,{b}_{\mu }^{c}\,\hat{{{{\mathcal{S}}}}}\,{\hat{{{{\mathcal{S}}}}}}_{c}^{\mu }=0.$$
(24)

We next consider the evolution of \({\hat{\sigma }}_{1}^{{{{\rm{y}}}}}\):

$${U}^{{\dagger} }\,{\hat{\sigma }}_{1}^{{{{\rm{y}}}}}\,U\propto \mathop{\sum}\limits_{\mu }\,{b}_{\mu }^{c}\,\hat{{{{\mathcal{S}}}}}\,{\hat{{{{\mathcal{S}}}}}}_{c}^{\mu }+\mathop{\sum}\limits_{\nu }\,{b}_{\nu }^{a}\,\hat{{{{\mathcal{S}}}}}\,{\hat{{{{\mathcal{S}}}}}}_{a}^{\nu }.$$
(25)

Notice that the summation in the second term of Eq. (25) must involve operators of weight 1 for the same reason as explained above: the operator content of \(\hat{{{{\mathcal{S}}}}}\) and \({\hat{{{{\mathcal{S}}}}}}_{a}^{\nu }\) must be identical on one site in order for these operators to anticommute, whereas the first term must vanish according to Eq. (24). Hence, we reach a contradiction, namely that the inflationary condition of Eqs. (23) cannot be satisfied for all Pauli operators (weight-1 Pauli strings).

Finally, we consider the general case in which the unitary transformation evolves \({\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\) into a superposition of weight-2 strings: \({U}^{{\dagger} }\,{\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\,U={\sum }_{\alpha \beta }\,{M}_{\alpha \beta }\ {\hat{\sigma }}_{1}^{\alpha }\,{\hat{\sigma }}_{2}^{\beta }\), where M is a 3 × 3 real matrix. One can perform a singular value decomposition, M = A Λ B⊤, which amounts to a basis rotation of the single-site Pauli operators: \({\hat{\tilde{\sigma }}}_{1}^{\beta }={\sum }_{\alpha }\,{\hat{\sigma }}_{1}^{\alpha }\ {A}_{\alpha \beta }\), \({\hat{\tilde{\sigma }}}_{2}^{\beta }={\sum }_{\alpha }\,{\hat{\sigma }}_{2}^{\alpha }\ {B}_{\alpha \beta }\). In the new basis, the Pauli strings are diagonal:

$${U}^{{\dagger} }\ {\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\ U={\lambda }_{x}\ {\hat{\tilde{\sigma }}}_{1}^{{{{\rm{x}}}}}\,{\hat{\tilde{\sigma }}}_{2}^{{{{\rm{x}}}}}+{\lambda }_{y}\ {\hat{\tilde{\sigma }}}_{1}^{{{{\rm{y}}}}}\,{\hat{\tilde{\sigma }}}_{2}^{{{{\rm{y}}}}}+{\lambda }_{z}\ {\hat{\tilde{\sigma }}}_{1}^{{{{\rm{z}}}}}\,{\hat{\tilde{\sigma }}}_{2}^{{{{\rm{z}}}}}\ .$$
(26)

However, since the right hand side of Eq. (26) must square to the identity, two of the λ’s must be zero while the other one must be equal to unity. Thus, we have reduced the general case to the special case where \({\hat{\sigma }}_{1}^{{{{\rm{x}}}}}\) evolves into a single weight-2 string, as in Eq. (23). Thus, we proved the main assertion of this section, namely that if one restricts oneself to 2-qubit unitary gates, there will always be a finite stay probability for weight-1 strings. As already discussed, in turn, this prevents one from reaching pseudorandom quantum states with \(\log n\)-depth circuits.

Existence of two-qudit inflationary gates for q ≥ 3

An important conclusion of this paper, which suggests a circuit design for realizing fast and thorough quantum scramblers, is that it is always possible to construct inflationary 2-qudit Clifford unitaries which transform all single-site generalized Pauli operators (weight-1 generalized Pauli strings) into weight-2 generalized Pauli strings. The proof of this result is given in the “Two-qudit inflationary Clifford gates” discussion of the “Methods” section for a subset of unitaries in U(q2) for which the local Hilbert-space dimension d ≥ 3 and d prime.

Padding such a 2-qudit Clifford gate with 1-qudit rotations at inputs and outputs, as depicted in Fig. 3, leads to special inflationary quantum (IQ) gates, to which we already referred in the introduction and in the “Our contributions” section above. Because of their inflationary property, the 2-qudit Clifford gates discussed in this section are necessarily entangling. These 2-qudit Clifford gates also form a finite group, which includes the identity gate, and therefore one can write single qudit unitaries as products of IQ gates. As demonstrated in ref. 21, an entangling 2-qudit gate and arbitrary single qudit rotations are the two ingredients required for the universality of a gate set. Therefore, the 2-qudit IQ gates in Fig. 3 form a universal set for quantum computation.

Fig. 3: Inflationary quantum (IQ) gates.
figure 3

a 2-qudit IQ gates obtained by padding Clifford qudit inflationary gates (see the “Two-qudit inflationary Clifford gates” section of “Methods”) that transform weight-1 strings into weight-2 strings gates with 1-qudit rotations at inputs and outputs; b 3-qubit IQ gates obtained by adopting the 144 3-bit classical (linear) inflationary gates that transform weight-1 strings into weight-2 strings (see ref. 14) to qubits, and padding the resulting 3-qubit gates with 1-qubit rotations at inputs and outputs. Employing random circuits of 3-qubit or 2-qudit IQ gates will eliminate the stay probability of weight-1 Pauli strings, as depicted in the inset to Fig. 1, while, at the same time proliferating operator strings and generating string entropy.

Full size image

IQ gates can also be realized by padding the 144 classical inflationary gates of ref. 14 (shown in Fig. 7) with 1-qubit rotations at inputs and outputs, as depicted in Fig. 3b. We note that the 144 classical inflationary gates generate all classical linear 3-bit gates and, in particular, the identity gate and 2-bit CNOTs across any of the 3 bitlines, [The inflationary gates associated to the two permutations 0 3 5 6 7 4 2 1 and 1 4 6 3 2 7 5 0 suffice to generate the group of all 1344 permutations associated to classical linear 3-bit gates, i.e., gates g such that g(x ⊕ y) = g(x) ⊕ g(y) ⊕ c, for a constant c.] One can then write both single qubit unitaries and entangling CNOTs as products of IQ gates and thus, the 3-qubit IQ gates in Fig. 3b also form a universal set for quantum computation.

As discussed in the “Our contributions” section above and in more detail in ref. 14, reaching cryptographic-level scrambling with \(\log n\)-depth classical reversible circuits required a 3-stage structure that separated linear classical gates responsible for string inflation from nonlinear classical gates responsible for string proliferation and entropy production.

What makes these 2-qudit and 3-qubit IQ gates special is that they generate both “diffusion” and “confusion” in the sense of Shannon22, i.e., IQ gates posses the ability to simultaneously (1) eliminate stay-probabilities for weight-1 strings and accelerate the inflation of strings; and (2) proliferate the number of strings and generate string entropy. We thus expect that single-stage random quantum circuits comprised of IQ gates can scramble both at the speed limit (i.e., in \(\log n\)-depth) and to cryptographic level.

Discussion

As we detailed in this paper, scrambling rapidly (i.e., with \(\log n\)-depth) and thoroughly (i.e., to cryptographic precision), via quantum circuits, is a tall order. More precisely, this paper makes two specific complementary points, namely: (1) that generic 2-qubit-gate quantum circuits cannot scramble information to cryptographic precision within a computational time scaling as \(\log n\); and (2) that fast scrambling to cryptographic precision can be realized with a special set of universal inflationary quantum (IQ) gates. These special IQ gates can simultaneously expand individual Pauli strings as well as proliferate their number, the latter leading to string entropy production.

IQ gates should play a key role in a number of areas in quantum information in which fast scrambling is desirable. (We note that the special properties of IQ gates will affect the behavior of circuits in any architecture, beyond the tree-structured circuits of long-ranged gates on which we concentrated in this paper.) For example, in the case of one-dimensional “brickwall” circuits of 2-qudit IQ gates, the front associated with operator spreading will propagate deterministically without dispersion, at the Lieb-Robinson speed limit. This behavior is due to the fact that at the front (i.e., at the edges of the Pauli strings at the light cone boundary) an IQ gate always acts on a fresh site with vanishing string weight (i.e., an up to then untouched site just outside the front), so that the inflationary property ensures that the evolved string will always acquire weight at that site after evolution by the gate. By contrast, as described in ref. 23, evolution by generic qudit circuits, would lead to a stochastic evolution of the front, with an average velocity below the maximum attainable value, and with a front-width that spreads diffusively. A cartoon of the difference between these cases is shown in Fig. 4. More generally, IQ gates would lead to faster, deterministic front propagation in any spatial dimension D. The speed up is most dramatic when D → ∞ as in the case of our tree-structured circuits, for which IQ gates are essential for reaching cryptographic-level scrambling with minimal \(\log n\)-depth circuits.

Fig. 4: Operator front profile evolution.
figure 4

Illustration of the profile of the right operator front ρR(x, t) (i.e., total weight of Pauli strings with right endpoint at x) under random unitary circuit and IQ circuit evolution. IQ circuits lead to a larger butterfly velocity and an absence of operator front broadening compared to random unitary circuits.

Full size image

Furthermore, we expect that the rapid scrambling property of IQ gates provides an additional ingredient that should lead to stronger bounds on t-designs. For example, a circuit of IQ gates may validate the conjecture of Harrow and Mehraban8 that one can build 2-designs with \(\log n\)-depth circuits.

IQ gates may also be useful in designing novel quantum advantage experiments, since they accelerate the expansion and proliferation of Pauli strings. We note, however, that inflation of strings are counter-acted by depolarizing noise, which removes contributions from high weight strings. This mechanism of suppression of large strings has been explored in refs. 24,25 to design efficient classical algorithms for sampling from the output distribution of a noisy random quantum circuit.

Finally, while employing random circuits of IQ gates should enable the construction of cryptographic level fast quantum scramblers—quantum “superscramblers”—we do not expect that unitary evolution via a time-independent Hamiltonian of interacting qudits or qubits can scramble to such a level in a time \({{{\mathcal{O}}}}(\log n)\), even if non-local couplings are employed.

Methods

Tree-structured circuits

Here we present the wiring of tree-structured circuits that both accelerate the scrambling and allowed us to obtain analytically the recursion relations (18a,18b,19a,19b, 20a, 20b, 21), the detailed derivation of which we present below.] Tree-structure circuits connect qubits or, more generally, qudits in a hierarchy of scales, and mimic systems in D → ∞ spatial dimensions.

We consider first a tree-structured circuit in which pairs of qudit indices acted by 2-qudit gates are arranged in a hierarchical (tree) structure. Let us consider the case when the number of qudits, n, is a power of 2, n = 2q. Each level in the tree hierarchy comprises of a layer with n/2 2-qudit gates. We proceed by forming pairs indices for each layer ℓ of gates, selected as follows:

$$\begin{array}{ll}\ell =1:&(0,1)\ (2,3)\ (4,5)\ (6,7)\ldots \\ \ell =2:&(0,2)\ (1,3)\ (4,6)\ (5,7)\ldots \\ \ell =3:&(0,4)\ (1,5)\ (2,6)\ (3,7)\ldots \\ \ell =4:&(0,8)\ (1,9)\ (2,10)\ (4,11)\ldots \\ \ldots \,&\end{array}$$
(27)

More precisely, each of the n/2 = 2q−1 pairs in layer ℓ are indexed by (i, j), which we write in base 2 as:

$$\begin{array}{rc}i=&{z}_{0}+2\ {z}_{1}+{2}^{2}\ {z}_{2}+\cdots +{2}^{\ell -1}\times \underline{0}+\ldots \ {2}^{q-1}\ {z}_{q-1}\\ j=&{z}_{0}+2\ {z}_{1}+{2}^{2}\ {z}_{2}+\cdots +{2}^{\ell -1}\times \underline{1}+\ldots \ {2}^{q-1}\ {z}_{q-1}\ ,\end{array}$$
(28)

where za = 0, 1, for a = 0, …, q − 1. Notice that at layer ℓ the members of the pairs, (i, j), are numbers that only differ in the (ℓ − 1)-th bit, while the other q − 1 bits za, a ≠ ℓ − 1, enumerate the 2q−1 = n/2 pairs. (If more than q layers are needed, we recycle in layer ℓ > q the pairs of layer \(\ell \,\,\,{{\mathrm{mod}}}\,\,q\)).

Once the pairs of indices, (i, j), are selected for each layer, we can generate other similar binary trees by mapping (i, j) onto \(\left(\pi (i),\pi (j)\right)\), via a (randomly chosen) permutation π of the n indices. A schematic of the hierarchical tree-structure presented above is shown in Fig. 5 below.

Fig. 5: Hierarchical tree-structured circuit consisting of two-qudit unitary gates.
figure 5

Each unitary gate is represented as a solid line with square endpoints, which indicate the two qudits on which the gate acts. Each layer contains n/2 gates acting on different non-overlapping pairs of qudits. Circuits consisting of three-qubit gates that form a ternary tree structure, like the circuits \({\hat{L}}_{l/r}\) and \(\hat{N}\) shown in Fig. 2, can be constructed in a similar fashion.

Full size image

The construction can be generalized to trees of other degrees, for example the ternary tree introduced in ref. 14, which we borrow to provide an additional example. Consider the case when n is a power of 3, n = 3q. In the ternary case, we proceed by forming groups of triplets of indices for each layer, selected as follows:

$$\begin{array}{l}\ell =1:\,(0,1,2)\,(3,4,5)\,(6,7,8)\ldots \\ \ell =2:\,(0,3,6)\,(1,4,7)\,(2,5,8)\ldots \\ \ell =3:\,(0,9,18)\,(1,10,19)\,(2,11,20)\ldots \\ \ell =4:\,(0,27,54)\,(1,28,55)\,(2,29,56)\ldots \\ \ldots \,\,\end{array}$$
(29)

More precisely, each of the n/3 = 3q−1 triplets in layer ℓ are indexed by (i, j, k), which we write in base 3 as:

$$\begin{array}{rc}i=&{z}_{0}+3\ {z}_{1}+{3}^{2}\ {z}_{2}+\cdots +{3}^{\ell -1}\times \underline{0}+\ldots \ {3}^{q-1}\ {z}_{q-1}\\ j=&{z}_{0}+3\ {z}_{1}+{3}^{2}\ {z}_{2}+\cdots +{3}^{\ell -1}\times \underline{1}+\ldots \ {3}^{q-1}\ {z}_{q-1}\\ k=&{z}_{0}+3\ {z}_{1}+{3}^{2}\ {z}_{2}+\cdots +{3}^{\ell -1}\times \underline{2}+\ldots \ {3}^{q-1}\ {z}_{q-1}\ ,\end{array}$$
(30)

where za = 0, 1, 2, for a = 0, …, q − 1. Notice that at layer ℓ the members of the triplets, (i, j, k), are numbers that only differ in the (ℓ − 1)-th trit, while the other q − 1 trits za, a ≠ ℓ − 1, enumerate the 3q−1 = n/3 triplets. (Again, if more than q layers are needed, we recycle in layer ℓ > q the triplets of layer \(\ell \,\,\,{{\mathrm{mod}}}\,\,q\).)

Once the triplets of indices, (i, j, k), are selected for each layer, we can map them onto groups of three indices \(\left(\pi (i),\pi (j),\pi (k)\right)\), via a (randomly chosen) permutation π of the n indices.

The construction above can be generalized for trees of degree k, in which case k-tuples of indices can be selected for k-qudit gates to act on.

Two-qudit inflationary Clifford gates

In this section we prove:

Theorem 1 There exist 2-qudit inflationary Clifford gates, for local Hilbert space dimension d ≥ 3 and d prime, that expand all weight-1generalized Pauli strings into weight-2generalized Pauli strings.

We start with a brief review of the higher dimensional Pauli group and its symplectic representation. Pauli matrices have a natural generalization in higher dimensions. Define the generalized Pauli matrices for qudits with local Hilbert-space dimension d (hereafter assumed to be a prime number) as:

$$Z=\mathop{\sum }\limits_{j=0}^{d-1}{\omega }^{j}\left\vert j\right\rangle \left\langle j\right\vert ,\quad X=\mathop{\sum }\limits_{j=0}^{d-1}\left\vert j\right\rangle \left\langle j+1\right\vert ,$$
(31)

where ω = ei2π/d is the primitive d-th root of unity. The above Pauli operators satisfy the following relations:

$${Z}^{d}={X}^{d}=1,\quad XZ=\omega ZX.$$
(32)

It is easy to check that the above matrices reduce to the familiar Pauli matrices for qubits upon taking d = 2.

A Pauli string is an element of the Pauli group \({{{{\mathcal{P}}}}}_{n}\) acting on n qudits:

$${Z}_{1}^{{u}_{1}}{X}_{1}^{{v}_{1}}\otimes {Z}_{2}^{{u}_{2}}{X}_{2}^{{v}_{2}}\otimes \cdots \otimes {Z}_{n}^{{u}_{n}}{X}_{n}^{{v}_{n}},$$
(33)

where we have ignored a possible phase factor. The above Pauli string admits the following symplectic representation as a vector in \({{\mathbb{Z}}}_{d}^{\otimes 2n}\):

$$g=({u}_{1},{u}_{2},\ldots ,{u}_{n}\,| \,{v}_{1},{v}_{2},\ldots ,{v}_{n}),$$
(34)

where ui, vi ∈ [0, d − 1]. For d prime, the integers in \({{\mathbb{Z}}}_{d}\) form a finite field (or Galois field) \({{\mathbb{F}}}_{d}\), such that the multiplicative inverse exists for each element. Since we are interested in the process where a single-site Pauli operator evolves into a weight-two Pauli string, we focus on n = 2. As a concrete example, Pauli-Z and −X operators acting on site 1 are represented as vectors:

$${Z}_{1}:\to {g}_{1}=(1,0\,| \,0,0)\quad {X}_{1}:\to {g}_{2}=(0,0\,| \,1,0).$$
(35)

In the vector representation, products of two Pauli strings correspond to the addition of the two vectors: g1 + g2 (mod d).

The commutation relation between two Pauli strings in the symplectic representation can be conveniently computed from the following matrix:

$${{{\Lambda }}}_{4\times 4}=\left(\begin{array}{rc}{0}_{2\times 2}&{{\mathbb{1}}}_{2\times 2}\\ -{{\mathbb{1}}}_{2\times 2}&{0}_{2\times 2}\end{array}\right),$$
(36)

namely,

$${{{{\mathcal{S}}}}}_{1}{{{{\mathcal{S}}}}}_{2}={\omega }^{r}{{{{\mathcal{S}}}}}_{2}{{{{\mathcal{S}}}}}_{1}\,\leftrightarrow \,{g}_{1}{{\Lambda }}{g}_{2}^{T}=r\,({{{\rm{mod}}}}\,d),$$
(37)

where g1 and g2 are vectors representing \({{{{\mathcal{S}}}}}_{1}\) and \({{{{\mathcal{S}}}}}_{2}\), respectively.

Proof of Theorem 1: To prove Theorem 1, we need the following lemmas.

Lemma 1 If under a Clifford gate UCl, single-site Pauli operators Z1 and X1 evolve to weight-2 strings of the form:

$${Z}_{1}:\to {g}_{1}=({a}_{1},{b}_{1},0,0)\quad {X}_{1}:\to {g}_{2}=(0,0,{\tilde{a}}_{1},{\tilde{b}}_{1})\ ,$$
(38)

with \({a}_{1},{b}_{1},{\tilde{a}}_{1},{\tilde{b}}_{1}=1,2,\ldots ,d-1\), then all single-site Pauli operators of the form \({Z}_{1}^{{u}_{1}}{X}_{1}^{{v}_{1}}\) will evolve to weight-2 strings under UCl.

Proof

First, we note that both g1 and g2 are weight-2 strings, as is evident from their vector representations. Then, consider all other single-site Pauli operators of the form \({Z}_{1}^{{u}_{1}}{X}_{1}^{{v}_{1}}\) with u1 ≠ 0 and v1 ≠ 0. Under UCl, such an operator evolves into:

$${Z}_{1}^{{u}_{1}}{X}_{1}^{{v}_{1}}:\to g={u}_{1}\,{g}_{1}+{v}_{1}\,{g}_{2}({{{\rm{mod}}}}\,d).$$
(39)

However, due to properties of the finite field, all elements of g must be nonzero. Hence, we conclude that all single-site Pauli operators evolve to weight-2 strings under UCl. ■

In the above lemma, we assume that the Pauli operators Z and X on site 1 evolve to strings of the form g1 and g2 under a two-qudit Clifford gate. At this point, it is unclear whether the specific form of g1 and g2 can be achieved. The answer is affirmative for d ≥ 3, as is shown in Lemma 2 below.

Lemma 2 The form of g1 and g2 in Lemma 1 can always be achieved via evolution under a Clifford gate UCl for d ≥ 3, while it is not possible for d = 2.

Proof

The only constraint on the time-evolved Pauli strings g1 and g2 is that they must preserve the commutation relation XZ = ωZX of the original Pauli operators. Using the symplectic representation, this amounts to the following linear equation:

$${g}_{1}\,{{\Lambda }}\,{g}_{2}^{T}=1({{{\rm{mod}}}}\,d),$$
(40)

or, explicitly,

$${a}_{1}\,{\tilde{a}}_{1}+{b}_{1}\,{\tilde{b}}_{1}=1({{{\rm{mod}}}}\,d).$$
(41)

For d ≥ 3, one can take \({a}_{1}{\tilde{a}}_{1} > 1\) and \({b}_{1}{\tilde{b}}_{1} > 1\). Due to properties of the finite field, there always exist pairs of integers (x, y) in \({{\mathbb{F}}}_{d}\), such that \(x+y=1\,({{{\rm{mod}}}}\,d)\). We can then take \({a}_{1}{\tilde{a}}_{1}=x\,({{{\rm{mod}}}}\,d)\), and \({b}_{1}{\tilde{b}}_{1}=y\,({{{\rm{mod}}}}\,d)\). Again, using properties of the finite field, it is always possible to find non-zero \({a}_{1},\,{\tilde{a}}_{1}\), b1 and \({\tilde{b}}_{1}\) that satisfy these two equations. Thus, non-zero solutions of Eq. (41) always exist.

On the other hand, for d = 2, Eq. (41) can only be satisfied when \(({a}_{1}{\tilde{a}}_{1},{b}_{1}{\tilde{b}}_{1})=(1,0)\) or (0, 1). Either case implies that one of the four numbers \({a}_{1},{b}_{1},{\tilde{a}}_{1},{\tilde{b}}_{1}\) must be zero, which contradicts our assumption in Lemma 1. In other words, one of the strings g1 and g2 must have weight 1. Therefore, the particular form of g1 and g2 in Lemma 1 cannot be achieved for d = 2. ■

Combining the results of Lemma 1 and 2, we have shown that for d ≥ 3, it is always possible to choose two-qudit Clifford gates such that all single-site Pauli operators supported on site 1 evolve to weight-2 strings. To complete the proof of Theorem 1, we need to show that the same Clifford gate is also able to evolve all single-site Pauli operators on site 2 to weight-2 strings.

We show that this is possible by explicitly finding a set of solutions. We assume that the single-site Pauli operators Z1, X1, Z2 and X2 evolve into weight-2 Pauli strings of the following form under UCl:

$$\begin{array}{rcl}&&{Z}_{1}:\to {g}_{1}=(1,1,0,0)\quad {X}_{1}:\to {g}_{2}=(0,0,{\tilde{a}}_{1},{\tilde{b}}_{1})\\ &&{Z}_{2}:\to {g}_{3}=({a}_{2},{b}_{2},0,0)\quad {X}_{2}:\to {g}_{4}=(0,0,{\tilde{a}}_{2},{\tilde{b}}_{2}).\\ \end{array}$$
(42)

Essentially, we have assumed that both Z1, X1 and Z2, X2 evolve into the form of Lemma 1, and further take a1 = b1 = 1. We demand that the resulting Pauli strings preserve the original commutation relations, which translates into the following set of linear equations:

$${\tilde{a}}_{1}+{\tilde{b}}_{1}=1({g}_{1}\,{{\Lambda }}\,{g}_{2}^{T}=1)$$
(43)
$${a}_{2}\,{\tilde{a}}_{2}+{b}_{2}\,{\tilde{b}}_{2}=1({g}_{3}\,{{\Lambda }}\,{g}_{4}^{T}=1)$$
(44)
$${\tilde{a}}_{2}+{\tilde{b}}_{2}=0({g}_{1}\,{{\Lambda }}\,{g}_{4}^{T}=0)$$
(45)
$${a}_{2}\,{\tilde{a}}_{1}+{b}_{2}\,{\tilde{b}}_{1}=0({g}_{2}\,{{\Lambda }}\,{g}_{3}^{T}=0),$$
(46)

where the equality mod d is implicit. Notice that with the above parametrization, the commutation relations \({g}_{1}\,{{\Lambda }}\,{g}_{3}^{T}=0\) and \({g}_{2}\,{{\Lambda }}\,{g}_{4}^{T}=0\) are automatically guaranteed.

Our procedure for finding a particular solution to the above set of equations goes as follows.

  1. (1)

    We start by solving Eq. (43). Due to properties of the finite field, a solution to Eq. (43) always exists.

  2. (2)

    Next, we solve Eq. (45) by taking \(({\tilde{a}}_{2},{\tilde{b}}_{2})=(1,d-1)\).

  3. (3)

    Finally, we find a unique solution (a2, b2) by solving Eqs. (44) and (46).

Of course, the solution is not unique, and we specialize to a particular one in the above procedure, which suffices to complete the proof of Theorem 1. ■

Examples

Below, we give two concrete examples of the construction, for d = 3 and d = 5.

\(\underline{d=3}\): For simplicity, we take Eq. (43) with \({\tilde{a}}_{1}={\tilde{b}}_{1}\), which is always possible since the solution to \(2x=1\,({{{\rm{mod}}}}\,d)\) always exits for finite fields. We find \({\tilde{a}}_{1}={\tilde{b}}_{1}=2\). Next, in step 2, we take \(({\tilde{a}}_{2},{\tilde{b}}_{2})=(1,2)\). Finally, solving the remaining two equations yields (a2, b2) = (2, 1). We thus have:

$$\begin{array}{rcl}{Z}_{1}:\to {g}_{1}&=&(1,1,0,0)\quad {X}_{1}:\to {g}_{2}=(0,0,2,2)\\ {Z}_{2}:\to {g}_{3}&=&(2,1,0,0)\quad {X}_{2}:\to {g}_{4}=(0,0,1,2).\end{array}$$

\(\underline{d=5}\): Again, we solve Eq. (43) with \({\tilde{a}}_{1}={\tilde{b}}_{1}\) and find \({\tilde{a}}_{1}={\tilde{b}}_{1}=3\). Then, we solve Eq. (45) by taking \(({\tilde{a}}_{2},{\tilde{b}}_{2})=(1,4)\). Finally, solving the remaining two equations yields (a2, b2) = (3, 2). We thus have:

$$\begin{array}{rcl}{Z}_{1}:\to {g}_{1}&=&(1,1,0,0) \quad {X}_{1}:\to {g}_{2}=(0,0,3,3)\\ {Z}_{2}:\to {g}_{3}&=&(3,2,0,0)\quad {X}_{2}:\to {g}_{4}=(0,0,1,4).\end{array}$$

SAC OTOC recursion relations for the three-stage cipher

For the reader’s convenience, we reproduce the calculation presented in ref. 14 of the square of the SAC OTOC, \({q}^{ij}\equiv {\left({C}_{{{{\rm{SAC}}}}}^{ij}\right)}^{2}\), as a function of the number of applied layers of gates ℓ of the tree-structured reversible circuit of 3-bit permutations described in Sec. 7.1 of that reference. We use the mean-field assumption (which was checked numerically in ref. 14) that the system self-averages, implying that qij = q, independent of i and j. The independence of i and j can be traced back to the fact that the three bit lines entering the gate g of layer ℓ + 1 originate from independent branches of the tree circuit emerging from layer ℓ (see Fig. 6). As long as \(\ell \le {\log }_{3}n\), gates in subsequent layers always bring in fresh bits and, upon averaging over gates, bitlines i and j remain uncorrelated.]

Fig. 6: The hierarchical structure of the circuit connectivity.
figure 6

The tree connectivity illustrates the arguments used in the derivation of a recursion relation for the probability pi that a bit flips upon flipping a number of inputs.

Full size image

We proceed recursively, layer-by-layer, relating q(ℓ + 1) to q(ℓ). The calculation is set up in bit space in terms of probabilities pi(ℓ) that after applying the ℓ-th layer bit i does not flip. In the hierarchical tree construction, the no-flip probability for a given output bit i (at level ℓ + 1) is determined by the outputs, at bitlines i0, i1, i2 coming from separate branches of the tree (at level ℓ) and by the 3-bit gate g in layer ℓ + 1 that takes those three bitlines as inputs and connects to bit i as one of its outputs.

The specific action of the gate g determines the fraction of inputs for which the output i does not flip when x → x ⊕ c, with \(x\equiv {x}_{{i}_{0}}+2\ {x}_{{i}_{1}}+{2}^{2}\,{x}_{{i}_{2}}\) and c ≡ c0 + 2 c1 + 22 c2 encoding which ones of the three bits are flipped (c0,1,2 = 0 for an unflipped input or 1 for a flipped one). This fraction is expressed as \({C}_{{c}_{0}{c}_{1}{c}_{2}}^{{g}_{i}}\equiv {C}_{c}^{{g}_{i}}=\left({f}_{c}^{{g}_{i}}+1\right)/2\), with:

$${f}_{c}^{{g}_{i}}=\frac{1}{{2}^{3}}\mathop{\sum }\limits_{x=0}^{7}{(-1)}^{{g}_{i}(x)\oplus {g}_{i}(x\oplus c)}\ .$$
(47)

The recursion for the no-flip probabilities can then be written as:

$$\begin{array}{lll}{p}_{i}(\ell +1)&=&h\left({p}_{{i}_{0}}(\ell ),{p}_{{i}_{1}}(\ell ),{p}_{{i}_{2}}(\ell );\{{C}_{c}^{{g}_{i}}\}\right)\\ &=&{p}_{{i}_{0}}(\ell )\,{p}_{{i}_{1}}(\ell )\,{p}_{{i}_{2}}(\ell )\ {C}_{000}^{{g}_{i}}+(1-{p}_{{i}_{0}}(\ell ))\,{p}_{{i}_{1}}(\ell )\,{p}_{{i}_{2}}(\ell )\ {C}_{100}^{{g}_{i}}+\cdots \\ && +\, (1-{p}_{{i}_{0}}(\ell ))\,(1-{p}_{{i}_{1}}(\ell ))\,(1-{p}_{{i}_{2}}(\ell ))\ {C}_{111}^{{g}_{i}}\ .\end{array}$$
(48)

We now proceed to consider ensembles of circuits, and analyze the evolution of the probability distribution, P(pi; ℓ), of the pi, as function of ℓ. The recursion relation for P(pi; ℓ), obtained by using Eq. (48), reads:

$$\begin{array}{rc}P({p}_{i};\ell +1)&=\mathop{\sum}\limits_{g\in {S}_{8}}\int\,{dp}_{{i}_{0}}\,d{p}_{{i}_{1}}\,d{p}_{{i}_{2}}\ P({p}_{{i}_{0}};\ell )\ P({p}_{{i}_{1}};\ell )\ P({p}_{{i}_{2}};\ell )\ {{{{\mathcal{P}}}}}_{{{{\rm{set}}}}}(g)\ \delta \left[{p}_{i}-h\left({p}_{{i}_{0}},{p}_{{i}_{1}},{p}_{{i}_{2}};\{{C}_{c}^{{g}_{i}}\}\right)\right]\ ,\end{array}$$
(49)

where the gates g are drawn from a probability distribution \({{{{\mathcal{P}}}}}_{{{{\rm{set}}}}}(g)\) that depends on the specific set of gates employed, and which we assume to be independent of the bitline index i. The initial condition is determined by the fraction f of bits that are flipped on input:

$$P(p;\ell =0)=f\ \delta (p)+(1-f)\ \delta (p-1)\ .$$
(50)

[We note that the assumption of independence of the bitline index cannot be justified unless f is intensive, which only occurs through the action of sufficient number of layers of inflationary gates.]

The evolution of the distribution and the vanishing of the SAC can be obtained by considering the average and moments of p. It is useful to change variables to si(ℓ + 1) ≡ 2 pi(ℓ + 1) − 1, for which the recursion Eq. (48) reads:

$$\begin{array}{r}{s}_{i}(\ell +1)={\widetilde{C}}_{100}^{{g}_{i}}\ {s}_{{i}_{0}}(\ell )+{\widetilde{C}}_{010}^{{g}_{i}}\ {s}_{{i}_{1}}(\ell )+{\widetilde{C}}_{001}^{{g}_{i}}\ {s}_{{i}_{2}}(\ell )+\cdots +{\widetilde{C}}_{111}^{{g}_{i}}\ {s}_{{i}_{0}}(\ell )\ {s}_{{i}_{1}}(\ell )\ {s}_{{i}_{2}}(\ell )\ ,\end{array}$$
(51)

with:

$$\begin{array}{r}{\widetilde{C}}_{a}^{{g}_{i}}\equiv \frac{1}{{2}^{3}}\mathop{\sum }\limits_{c=0}^{7}{(-1)}^{a\cdot c}\ {C}_{c}^{{g}_{i}}\ ,\end{array}$$
(52)

where a ⋅ c ≡ a0 c0 + a1 c1 + a2 c2.

We are now in position to derive the evolution of the moments \(\overline{{s}^{q}(\ell )}\). (Even if the distributions for the si are identical, independent of i, we keep some of the explicit indices for bookkeeping of contractions.) The average:

$$\begin{array}{rc}\overline{s(\ell +1)}&=\mathop{\sum }\limits_{a=1}^{7}\overline{{\widetilde{C}}_{a}^{{g}_{i}}}\ \overline{{[{s}_{{i}_{0}}(\ell )]}^{{a}_{0}}}\,\overline{{[{s}_{{i}_{1}}(\ell )]}^{{a}_{1}}}\,\overline{{[{s}_{{i}_{2}}(\ell )]}^{{a}_{2}}}\\ &=\mathop{\sum }\limits_{a=1}^{7}\overline{{\widetilde{C}}_{a}^{{g}_{i}}}\ {\left[\overline{s(\ell )}\right]}^{{a}_{0}+{a}_{1}+{a}_{2}}\,\ .\end{array}$$
(53)

Similarly, we compute the second moment:

$$\overline{{s}^{2}(\ell +1)}=\mathop{\sum }\limits_{a,b=1}^{7}\overline{{\widetilde{C}}_{a}^{{g}_{i}}\ {\widetilde{C}}_{b}^{{g}_{i}}}\ \overline{{[{s}_{{i}_{0}}(\ell )]}^{{a}_{0}+{b}_{0}}}\,\overline{{[{s}_{{i}_{1}}(\ell )]}^{{a}_{1}+{b}_{1}}}\,\overline{{[{s}_{{i}_{2}}(\ell )]}^{{a}_{2}+{b}_{2}}}\ .$$
(54)

The recursion relations relating \(\overline{s}(\ell +1)\) to \(\overline{s}(\ell )\) depend on the gate set used for layer ℓ through the coefficients \(\overline{{\widetilde{C}}_{a}^{{g}_{i}}}\), which we present explicitly below for the cases of inflationary and super-nonlinear gates. For notational simplicity, we define the variables \(s(\ell )\equiv \overline{s(\ell )}\) and \(q(\ell )\equiv \overline{{s}^{2}(\ell )}\).

Inflationary layers

Upon computing the averages \(\overline{{\widetilde{C}}_{a}^{{g}_{i}}}\) and \(\overline{{\widetilde{C}}_{a}^{{g}_{i}}\ {\widetilde{C}}_{b}^{{g}_{i}}}\) over the 144 inflationary gates (see Fig. 7), the recursion relations read:

$$s(\ell +1)=\frac{2}{3}\,{[s(\ell )]}^{2}+\frac{1}{3}\,{[s(\ell )]}^{3}\ ,$$
(55a)
$$q(\ell +1)=\frac{2}{3}\,{[q(\ell )]}^{2}+\frac{1}{3}\,{[q(\ell )]}^{3}\ .$$
(55b)

The recursion relations of Eqs. (55a) and (55b) display two special features: the first and second moments decouple; and more importantly, the coefficient of the linear term in q(ℓ) in the equation for the second moment vanishes.

Fig. 7: Inflationary 3-bit gates expressed in terms of CNOTs (from ref. 14).
figure 7

By permuting bitlines and control polarities, one obtains 24 distinct inflationary gates from topology A, 24 from B, 48 from C, and 48 from D, for a total of 144.

Full size image

Note that the bimodal initial condition Eq. (50), where p only takes values p = 0, 1, implies that an initial q = 1 cannot evolve under Eq. (55b), which displays fixed points at q = 0, 1 (and a non-physical one at q = −3). However, with the deployment of nonlinear gates q drops below 1, following which inflationary gates significantly accelerate the decay of q(ℓ) with ℓ due to the absence of the linear term in q(ℓ) in Eq. (55b).

Super nonlinear layers

Using averages \(\overline{{\widetilde{C}}_{a}^{{g}_{i}}}\) and \(\overline{{\widetilde{C}}_{a}^{{g}_{i}}\ {\widetilde{C}}_{b}^{{g}_{i}}}\) computed over the 10,752 super-nonlinear gates, leads to the recursion relations characterizing evolution via super nonlinear gates, namely:

$$s(\ell +1)=\frac{3}{7}\,s(\ell )+\frac{3}{7}\,{[s(\ell )]}^{2}+\frac{1}{7}\,{[s(\ell )]}^{3}$$
(56a)

and

$$\begin{array}{ll}q(\ell +1)=\frac{3}{28}\,\left({[s(\ell )]}^{2}+{[s(\ell )]}^{3}\right)+\frac{3}{28}\,q(\ell )\,\left(1+2\,s(\ell )+2\,{[s(\ell )]}^{2}\right)\\ \qquad\qquad\quad+\,\frac{3}{28}\,{[q(\ell )]}^{2}\,\left(1+s(\ell )\right)+\frac{1}{28}\,{[q(\ell )]}^{3}\ .\end{array}$$
(56b)

By contrast to the case of inflationary gates, the recursion relations for q(ℓ + 1) in Eqs. (56a) and (56b) depend on both s(ℓ) and q(ℓ), and contain a term linear in q(ℓ). Eqs. (55a), (55b), (56a), and (56b) are the starting point for the discussion of the decay of the SAC OTOC with ℓ.