Introduction

Fault-tolerant quantum computers offer profound computational speed-ups across diverse applications, but are challenging to build. However, even in the near term without full error correction, quantum computers have the potential to offer improvements over classical computing approaches in run time scaling1 and energy consumption for certain tasks2. There is a rich and diverse array of schemes for realising quantum computation, each formally equivalent in computational power3,4,5, with important differences with regards to practical realisations. In the gate-based approach, a quantum algorithm is expressed as a quantum circuit consisting of a series of quantum logic gates. Typically, such gates are applied to a stationary array of qubits (for example through electromagnetic waves or optical pulses), relying on the delivery of a complex series of accurate, quasi-simultaneous control pulses to each qubit. This can lead to practical challenges ranging from cross-talk in the control pulses between nearby qubits6,7 to increased demands on digital-to-analogue converters (DACs) particularly when fully integrating control systems with a cryogenic quantum chip.

To mitigate the practical challenges associated with high-density control electronics, global qubit control schemes have been explored8,9,10. However, these approaches require a precision in the position and homogeneity of qubit structures, as well as the control pulses, to a degree that is technically challenging with available technology. Alternatively, local addressing can be used to bring qubits into resonance with globally applied control fields to create an effective local control11,12. However, this approach still requires fast run-time control for the addressing13. A second strategy is to accept the cost of a much lower effective qubit density in exchange for mitigating effects such as cross-talk—in such a distributed model of quantum computing14 qubits, or small qubit registers, are well-separated and interfaced by a common entangling (typically photonic) mode. While such hybrid matter/photon systems have been successfully realised in several platforms15,16,17, high gate speeds compatible with the demands of NISQ algorithms18 may be difficult to achieve.

A further consideration when designing NISQ hardware architectures is that NISQ algorithms based on (e.g.) variational approaches18,19 require multiple repetitions of the same quantum circuit—or simple variations thereof—to be performed. In turn this requires identical, or similar, sequences of local control fields to be repetitively applied to the qubits, presenting an opportunity for more efficient hardware implementations. In this Article, we propose a quantum computing architecture for implementing quantum circuits in which all runtime control is applied globally, and local quantum operations such as 1-qubit (1Q) and 2-qubit (2Q) gates are ‘programmed’ into the array in advance. This is achieved by shuttling qubit states through a grid of gated structures which have been electronically configured to realise specific gates.

In such an approach, each layer of gates in the original quantum circuit corresponds to a one-dimensional array of structures, such that the scheme is more demanding in terms of physical resources on a chip for confining qubits. However, when applying multiple repetitions of the same circuit by pipelining—i.e. running distinct, staggered layers of qubits through the array simultaneously—the physical resource efficiency becomes broadly equivalent to more conventional approaches, combined with potential practical benefits.

Below, we introduce the concept of a qubit pipeline in more detail in “Qubit pipeline”, before focusing on a potential implementation for the silicon metal-oxide-semiconductor (SiMOS) electron spin qubit platform in “Implementation with silicon quantum dots”. We then estimate the expected improvement in run time for an example algorithm in “Application as bespoke hardware for a NISQ eigensolver”. In particular, in “Shuttling”, we outline a scheme for synchronous shuttling, and in “Initialization, readout and pre-configuration”, we discuss initialisation, readout, and parallelised pre-configuration, mostly outlining established methods. In “Z-rotation gates with Stark-shifted g-factors–Transversal rotation gates”, we show how to realise an universal gate set for the pipeline in the silicon electron spin platform including: single-qubit Z-rotations using local, voltage-controllable g-factor Stark shifts, globally-applied \(\sqrt{X}\) operations enabled by B1-drive frequency binning and 2Q SWAP-rotation gates using the native interaction of nearest neighbour exchange. Each of the above gate implementations is designed to accommodate natural variations, such as random g-factor differences, across the QDs while enabling synchronized operation and thus fixed gate times.

Results

Qubit pipeline

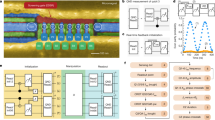
For solid-state quantum processors the qubit array may consist of a two-dimensional lattice with nearest-neighbour couplings (see Fig. 1a). The qubit pipeline approach replaces the two-dimensional lattice of stationary qubits with an N × D grid (see Fig. 1b), such that N qubits are arranged in a one-dimensional array and propagate through the grid to perform a quantum circuit of depth D. Each column therefore represents a single ‘time step’ of quantum logic gates in the corresponding quantum circuit while each row of structures forms a ‘pipe’ of computational length D along which a qubit travels. Multiple qubits can simultaneously travel through each pipe, at different stages, in order to more efficiently use the physical resource.

Fig. 1: The qubit pipeline.
figure 1

a In a typical N-qubit solid state quantum processor, qubits reside at fixed spatial locations (e.g. on a \(\sqrt{N}\times \sqrt{N}\) grid) with nearest-neighbour connectivity. b The qubit pipeline is a weaved grid in which N qubits are shuttled through D locations where fixed single- (1Q) or two-qubit (2Q) logic gates are implemented. Vertical lines indicate 2Q couplers, while horizontal lines indicate shuttling couplers. At runtime, qubits are initialized at one end, synchronously shuttled through the pipeline, and read out on the opposite end. c An example quantum circuit diagram, where an algorithm is decomposed into alternating steps of 1Q and 2Q gates. d–f The qubit pipeline contains physical locations which have been configured to implement 1Q (circles) and 2Q (connected circles) gates. Different qubit arrays (first (χ0, χ1, . . . ), then (ψ0, ψ1, . . . ), (φ0, φ1, . . . )) can be piped sequentially through the structures, each representing one execution of the configured quantum circuit.

Full size image

Run-time operation begins by initializing a one-dimensional array of N qubit states on the input edge. This initialised array is synchronously pushed through D structures that have been preconfigured to perform the single- and two-qubit gates in the desired quantum circuit. Qubit states are read out on the opposite output edge. Between initialization and readout, operations on the qubit array alternate between synchronous one- and two-qubit gate steps and shuttling steps. Figure 1c–f illustrate the equivalence between an example quantum circuit (Fig. 1c) and time-evolution on the qubit pipeline (Fig. 1d–f). In this way, local qubit control of the typical qubit grid is replaced by a combination of global control (at least, with widely shared control lines) to push the qubit states from start to finish, combined with quasi-statically tuneable elements within the larger number of physical structures used to define the quantum circuit prior to running it.

We assume that while the parameters of the quantum logic gates can be tuned in-situ (e.g. electrically), the type of gate performed in each cell of the array is defined when fabricating the quantum processor. Indeed, though more generally reconfigurable implementations may be possible (see e.g. Supplementary Note 1) and offer potential efficiencies, a suitably chosen pattern of gates is sufficient for universal quantum computation, subject only to the constraints of the qubit number and circuit depth. Assuming the quantum processor is restricted to a two-dimensional topology, the pipeline approach presented here is limited to a linear qubit array. Many quantum algorithms can be mapped onto such a linear array without significant loss of efficiency, such as the variational quantum eigensolver for the Fermi-Hubbard model, a promising task that could be implemented on NISQ hardware18,19,20 There is no guarantee that mapping the two-dimensional Fermi-Hubbard model to a connected two-dimensional qubit lattice offers an overall advantage over a one-dimensional qubit array21. This is intuitively related to the non-local nature of fermions, which has to be encoded in the simulation of fermionic charge degrees of freedom. Attempts to reconcile this intrinsic non-locality with the two-dimensional-lattice qubit layout would lead to encoding schemes that offer a better circuit depth scaling, but at a cost of almost doubling the numbers of qubits21,22, thus not necessarily reducing the overall circuit size. This complication is absent in the simpler one-dimensional qubit array, which instead requires additional Fermionic SWAP operations to represent the original connectivity.

Conventional approaches to operate an N qubit processor with tuneable nearest neighbour couplings demand at least \({{{\mathcal{O}}}}(N)\) fast signal generators for single-qubit control, for qubit-qubit couplings, and for state readout. In contrast, the pipeline scheme presented here may require a constant (even just one) number of fast pulse generators, utilized for shuttling the qubit states through the grid in a manner analogous to a charge-coupled device. For example, three waveforms biasing columns \(d\,{{{\rm{mod}}}}\,3=0,d\,{{{\rm{mod}}}}\,3=1\), and \(d\,{{{\rm{mod}}}}\,3=2\), create a local potential minimum for a qubit which can then be driven forward through the array23. Implementing such a shuttling scheme, synchronicity is achieved if gate steps take an equal amount of time for all qubits. For example, for logic gates expressed as \(\exp (-i\omega \tau \sigma )\) for some single- or two-qubit operator σ, we fix a common τ but select ω to control the amount of rotation and thus distinguish the logic operations. The gate speed ω is varied using parameters such as dc gate voltages and magnetic field amplitudes at the preconfiguration stage. In principle, different columns of gates (e.g. all single-qubit gates, or all two-qubit gates) could have different durations, at the cost of a more complex shuttling pulse sequence. The three-column approach to shuttling represents the maximum density with which different sets of qubits can be pipelined through the circuit.

Due to the statistical nature of measurement in quantum mechanics, several types of quantum algorithms, such as those that yield an expectation value following some quantum circuit24,25, must be run a large number of times to obtain a meaningful result. Such algorithms are well-suited to the pipeline approach as multiple, independent qubit arrays can be pushed through the pipeline simultaneously, enabling multiple circuit runs in parallel. The maximum density of independent logical instances of a quantum circuit which can be pipelined through the structure is determined by the physical constraints of ensuring forward shuttling and avoiding unwanted interactions between qubits. Furthermore, if the duration of either the initialisation or readout stage is greater than that of the 1Q/2Q gates, this density must be further reduced. Exploiting such pipelining, the algorithm runtime is proportional to (D + Nr)τ instead of DNrτ, providing a significant speedup for circuits with large number of repetitions Nr, or large depths. Here, τ is the timescale of the longest operation: a qubit gate, readout, or initialization. Table 1 summarises these main differences between a qubit lattice and the qubit pipeline.

Table 1 Comparison between the quantum lattice and the pipeline processors
Full size table

Implementation with silicon quantum dots

We now analyse a hardware implementation well-suited to the qubit pipeline paradigm, i.e. qubits based on single electron spins trapped in silicon-based QDs. Silicon spin qubits can achieve high density due to their small footprint of \({{{\mathcal{O}}}}(50\times 50\,{{{{\rm{nm}}}}}^{2})\), and can leverage the state-of-the-art nanoscale complementary metal-oxide-semiconductor (CMOS) manufacturing technology used in microprocessors7,26,27,28. Quasi-CMOS-compatible electron spin qubits can be patterned as gated planar MOS devices29,30,31, confining electrons at the Si-SiO2 interface below the gates, or using Si/SiGe heterostructures31,32. Typical values for single- and two-qubit gate fidelities measured so far in such systems include 99.96% and 99.48% in SiMOS33,34 and 99.9% and 99.5% in Si/SiGe32,35,36. Coherent spin shuttling has been demonstrated at a transfer fidelity of 99.97% for spin eigenstates, and 98% for spin-superposition states37,38, while SWAP gates have also be shown to transport arbitrary qubit states with fidelity up to 84%39. In addition, silicon on insulator (SOI) nanowire and fin field-effect transistors (nwFET and finFET) devices40,41,42 have been used to confine spin qubits within etched silicon structures, and have been proposed for sparsely-connected two-dimensional qubit architectures43. These devices typically show a large electrostatic gate control of the QDs (larger so-called lever arms α) which is advantageous for reflectometry readout techniques, or spin-photon coupling44,45.

To realise the qubit pipeline, we propose a sparse two-dimensional quantum dot(QD) array, which we refer to as a nanogrid (see Fig. 2a). The nanogrid is a weaved grid of silicon ‘channels’ in which QDs can be formed (e.g. etched silicon in the case of nwFET and finFET approaches, or through confining depletion gates in the case of planar MOS). Metal gates (green and orange shapes) for forming QDs are placed along and over the exposed Si to form locally one-dimensional QD arrays, which make 90-degree angles at T-junctions to join neighbouring pipes. Such weaving is required for entangling all the qubits from different pipes. Extra control from a second gate layer aids tuning all QDs to nominally identical setpoints despite variability in e.g. charging energies46,47. The metal gates are routed with vias. The overall architecture can be realised in a variety of silicon QD platforms, including planar MOS, SOI, and finFETs, with cross-sections illustrated in Fig. 2b–d. In addition, a similar layout can be used in a Si/SiGe architecture or indeed other types of electron or hole semiconductor spin qubits.

Fig. 2: Silicon quantum dot pipeline unit cell.
figure 2

a Unit cell of a qubit pipeline, realised as a weaved grid of silicon channels (dark grey grid) which may be defined by etching or electrostatically by depletion gates (not shown). Overlapping metal gates (coloured rectangles) are used to confine, shuttle and manipulate electron spin qubits within the channels. Connectivity for five-stage shuttling is shown as coloured lines where all sites mod 5 (for example, those controlling two subsequent 2Q sites) are connected to the same ac voltage source. All barrier gates receive individual dc biases. b–d Side views of different gate stacks which could be used in this implementation, including (b) planar MOS, (c) SOI nanowire, and (d) finFET. Quantum dots (magenta blobs) are confined using etched silicon or confinement gates (light yellow). e Sketch of the shuttling pulse sequence (relative pulse durations not to scale). Voltages Vin (Vout) are those at which single (zero) electron occupancy of the QD becomes the ground state. Single- and two-qubit gates are separated by short shuttling steps—in general, the number of shuttling steps depends on the exact gate layout, and depend on e.g. footprints required for routing. f Structures for local electron reservoirs (R), for spin readout (with an auxiliary state φ), and hence for preconfiguration of quantum states ψ. The operation of these structures, which can be placed along pipes between d + 1 and d + 2 (see a), is discussed further in the text.

Full size image

Shuttling

In the qubit pipeline, we shuttle electrons between different columns d where logical 1Q and 2Q gate operations are performed. Electrons can be shuttled from one QD to another by inverting the biasing between gates, i.e. by pulsing over the inter-dot charge transition with DQD charge occupancies (1, 0) → (0, 1)48,49,50. This scheme is also referred to as bucket-brigade shuttling.

The shuttling time τs is determined by the inter-site tunnel coupling frequency tij/h (typically 1 − 20 GHz in two-layer QD arrays using barrier gates49) and the electron temperature, which affects charge relaxation rates. Each barrier gate receives an individual dc bias to tune each tunnel coupling individually. The present architecture does not correct for charge shuttling errors, akin to erasure errors. These would propagate into the final state of each run. Additionally, a charge stuck at a site as a result of a shuttling error might also affect the subsequent run. As such, it relies on charge shuttling fidelity to remain well below one error per run. Charge shuttling errors are expected to be minimized when the pulsing rate is slow compared to the inter-dot tunnel coupling37,51, where non-adiabatic Landau-Zener (LZ) transitions are minimal. At tunnel coupling tij/h = 20 GHz, the ramp can be performed adiabatically (PLZ < 10−4) with shuttling times of 9.1 ns or more (see Supplementary Note 2). Electron charges and spins have been demonstrated to shuttle reliably over these timescales37,51, so we take 10 ns as the range of target shuttling times τs. The exact shuttling time should be determined to avoid LZ transitions to excited states, such as valley-orbit states. The systematic Z-phases arising from g-factor differences between sites can be accounted for as part of single-qubit control, as discussed in “Z-rotation gates with Stark-shifted g-factors”.

The pulse sequence depicted in Fig. 2e can realise the shuttling and logic gate dynamics modulation. To this end, each plunger gate is routed to an ac + dc voltage combining circuit. The ac nodes from gates from a single column, and mod 5 steps, are combined at interconnect level with a power splitter, whereas each gate receives an individual dc bias. Bias tees at gate nodes enable applying dc biases from individual dc sources. See Supplementary Note 2 for footprint estimates. As there are signals with three different periods, we could employ e.g. phase modulation or partially digital signal processing to generate the five shuttling biases, and hence shuttling biases for the entire pipeline with only three voltage pulse generators. We can fill the pipeline up to every fifth physical gate column of QDs single electrons, which we refer to as maximal filling.

Initialization, readout and pre-configuration

Initialisation and readout is analogous to a shift register for single-electron spins, where electrons are moved through a pipe and electron reservoirs are located at the input and output ends of the array. Preconfiguration of the unit cells can be done locally, utilizing initialization and readout nodes like the one depicted in Fig. 2f. Logical ground states \(\vert {\downarrow }_{q}\rangle\) are initialised using spin-dependent reservoir-to-dot tunnelling52. The fidelity is typically determined by the relative magnitude of the spin Zeeman energy splitting and kBT where T is the temperature of the electron reservoirs and kB is Boltzmann’s constant. For example, at B0 = 1 T, \({{{\mathcal{F}}}}\ge 0.9999\) at T ≲ 73 mK. The initialization time is determined by the reservoir-to-dot tunnelling time 1/ΓψR, which can be controlled with a barrier gate, and can reach tens of GHz53. At higher electron reservoir temperatures, required fidelities could be obtained using real-time monitoring of the qubit through a negative-result measurement at the expense of longer initialization times54.

For readout, we employ the so-called Elzerman readout, where we detect spin states using the reverse of the spin-dependent tunnelling described above, detected by a capacitively-coupled charge sensor, such as a single-electron box55,56, at site φ (see Fig. 2(f)). This method is estimated to yield a spin readout fidelity \({{{\mathcal{F}}}}\ge 0.993\) in ≤4 μs53, while advances in resonant readout techniques could help increase \({{{\mathcal{F}}}}\ge 0.9999\) in 50 ns57.

We highlight Elzerman readout over Pauli spin blockade or parity readout58 since (i) we operate the pipeline at relatively high B0 fields, B0 ≈ 1 T, see “Z-rotation gates with Stark-shifted g-factors”, (ii) it is not compromised by low valley-orbit splitting53,55,59 and (iii) the readout pulsing protocol is simpler since it does not require the state preparation of the ancilla spin60, making it more amenable to the shift registry operation of the pipeline. Nevertheless, initialization and readout could be performed using Pauli spin blockade or parity projections with an ancilla spin of known orientation (via g-factor calibration in the preconfiguration stage) using the structure in Fig. 2f e.g. using a pulsing protocol similar to that in ref. 60. In the case of singlet-triplet or parity readout, the temperature of operation of the pipeline could be raised up to 0.5 K while retaining 99.9% fidelity58,61. We consider realistic estimates of processor run-time operating temperatures to be largely outside the scope of this work, but we briefly return to power consumption in the context of transversal qubit control in “Transversal rotation gates”.

Z-rotation gates with Stark-shifted g-factors

The electron spin g-factor g*, which defines the Larmor frequency ω0 = g*μBB0/ℏ (where μB is the Bohr magneton and B0 the applied dc magnetic field) can be shifted using electric fields from gate voltages. In SiMOS heterostructures the dominant Stark shift is understood to arise from wavefunction displacement with respect to the Si/SiO2 interface62. Linear or quasi-linear shifts δgq(V) with ∂g/∂Ez(V) = ± (1–5) × 10−3 (MV/m)−1 have been reported for QDs in planar MOS devices30,63,64 with an in-plane magnetic field and Ez applied perpendicular to the interface. The sign of the shift depends on the valley state of the electron62,63. The roughness of the Si/SiO2 interface also introduces some random contribution Gq to the effective g-factor, which can be larger than the tuneability, \({G}_{q}=\pm {{{\mathcal{O}}}}(1{0}^{-3}...1{0}^{-2})\)64. Hence, the g-factor of a spin at some site q can be considered as a combination of these shifts on some intrinsic value, gSi, such that \({g}_{q}^{* }={g}_{{{{\rm{Si}}}}}+{G}_{q}+\delta {g}_{q}(V)\). In the following, we assume gSi = 2.0.

We use the gate-voltage controllable g-factor Stark shift to perform relative single-qubit \(Z({\varphi }_{q})={e}^{-i{\varphi }_{q}{\sigma }_{z}/2}\) gates by synchronously shuttling the qubit onto a QD structure (see columns d + 1 and d + 3 in Fig. 2a) with predetermined dc gate voltages. Spins encoding the qubit state remain at the same site for a fixed time τ1Q to acquire some phase (relative to a spin with g = gSi) before synchronously shuttling forward. The gate Z(φq) is achieved by selecting a suitable g-factor shift

$$\begin{array}{rc}\delta {g}_{q}(V)&=\frac{{\varphi }_{q}-2\pi {r}_{q}}{{\mu }_{B}{B}_{0}{\tau }_{1Q}{\hslash }^{-1}}.\end{array}$$
(1)

Here, \({r}_{q}\in \left[0,1\right)\) is selected from GqμBB0τ1Qℏ−1 ≔ 2π(nq + rq), for \({n}_{q}\in {\mathbb{Z}}\). Since we only require phase matching up to 2π, the site-to-site randomness Gq only contributes via 2πrq, which remains in the same order of magnitude for any Gq. As a result, the randomness does not affect the required tuneability to attain a rotation angle over a target gate time. Similarly, systematic phase shifts arising from the other QDs involved in shuttling can be accounted for as an effective contribution to Gq and corrected in the same way. The order of magnitude of δgq(V) required to generate a π phase shift at varying τ1Q and B0 is plotted in Fig. 3a, where we take Gq = 0 for simplicity. Tunabilities of at least δg ≈ ± 3.6 × 10−5 and δg ≈ ± 3.6 × 10−4 are required at B0 = 1 T for τ1Q = 1 μs and τ1Q = 0.1 μs, respectively.

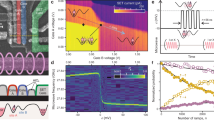
Fig. 3: Z-rotation gate using Stark shifts.
figure 3

a Order of magnitude of Stark shift δgq, with respect to the bulk value gSi ≈ 2.0, as a function of external magnetic field B0 and single-qubit gate time τ1Q, required for the π-rotation gate Z(π). b Gate layout realisation of the g-factor tuning scheme with shuttling through quantum dots under gates q − 1, to q, and to q + 1. The voltage Vq is used to tune the g-factor at site q, while the voltage Vμ is used to compensate for the change in the electrochemical potential due to the g-factor tuning. c, d Overlaid stability diagrams of the (q − 1, q, q + 1) triple quantum dot at the start and end (blue lines), and at the middle (red lines) of the shuttling sequence, illustrate the requirement for electrochemical potential compensation. Using a waveform as shown in Fig. 2e, shuttling proceeds from the charge configuration (nq+1 nq nq−1) = (001) (blue circle marker) to (010) (red star marker), and to (100) (blue triangle marker). c In the perfectly compensated case with g-factor tuning, the (010) region opens up during the shuttling sequence. d In the non-compensated case, adjusting Vq to tune the g-factor at q causes the (010) region to shift away from the ground state charge configurations. e Electric field gradients evaluated along the cut shown as a grey dotted line in (d). Electric field gradients due to Vq are denoted as blue, and those due to Vμ as orange traces. f Estimated fidelity of Z(π) as a function of variance in actual gate duration and voltage noise affecting δg, with fixed σG = 10−3gSi, B0 = 1 T, and τ1Q = 1 μs. (see main text).

Full size image

To realise such Stark shifts, we propose to employ the plunger gate as the g-factor tuning gate, and a neighbouring gate as a μ-compensating gate (gate labelled with μ in Fig. 3b). This additional compensating gate is required to ensure the electrochemical potentials (see Supplementary Note 3), and hence QD electron occupancies remain correct under the applied electric field for g-factor tuning, as illustrated in the triple QD stability diagrams shown in Fig. 3c, d. In planar MOS, the plunger gate contributes dominantly to Ez, while the μ-compensating gate electric field mostly to Ex, at site q, having negligible effect on the g-factor. In etched silicon devices, due to two facets of Si/SiO2 interface (Fig. 2f), we expect both split gates to contribute to the Stark shift, but as long as the effects of the two gates to the g-factor Stark shift and the electrochemical potential shift are asymmetric, the pair of gates allows to compensate for the shift in the electrochemical potential.

Analytical estimates for the E-field derivatives ∂Ez/∂Vj and ∂Ex/∂Vj due to the plunger and μ-compensating voltages Vq and Vμ, as a function of longitudinal position x, close to the MOS interface, are plotted in Fig. 3e, with simulation details given in Supplementary Note 3. The estimated values of the Ez-gradient at site q, together with a conservative figure of ∂g/∂Ez = ± 1 × 10−3 (MV/m)−1 suggest a required voltage shift dVq = 615 V × δgq. For example, a target Stark shift δgπ = ± 3.6 × 10−5, would require the dc bias on the gate to be shifted dVq = ± 22 mV. The corresponding change in μq can be compensated with the μ-compensating gate, by setting the voltage dVμ ≈ − αqq/αqμdVq, where αij is the lever arm between QD at site i and gate j (see Supplementary Note 3).

We evaluate the sensitivity of this Z(φq) gate to noise using the so-called process fidelity65 between an ideal and a noisy unitary gate, for the case of τ1Q = 1.0 μs and B0 = 1.0 T. We sample a value for Gq from a normal distribution with width σG set to 10−3gSi, and use it to find δgq (Eq. (1)) to hit φq = π for an ideal gate. For the noisy gate, we consider shuttling time errors of magnitude δτ that lead to gate time errors, and fluctuations in the gate voltage, δVq, which lead to impacts in the g-factor according to δgq = δVq/615 V. For example, shuttling time error is thus assumed to change the gate time from τ1Q to τ1Q + δτ. These noise contributions δτ and δVq are also sampled from normal distributions with varying widths of στ and σV, respectively.

In Fig. 3(f), we plot the resulting Z(π) fidelities, averaged over 1000 samples at each pair of noise levels. We find that the noise sources for the gate time and g-tuning errors add up independently. Noise levels of στ ≲ 0.08 ns, i.e. ~ 10−2τs for the target shuttling time of τs = 10 ns, and σV ≲ 100 μV are required to achieve \({{{\mathcal{F}}}}[Z({\varphi }_{q})]\ge 0.9999\). Charge noise acts equivalently to gate voltage fluctuations. Based on state-of-the art charge noise spectral densities in industrial SiMOS devices42,66,67, we would expect voltage fluctuations of σV ≈ 30. . . 90 μV over a bandwidth of 1 Hz − 1 GHz, which is sufficient for our fidelity requirements, whereas there is less experimental data available on timing errors in shuttling.

Two-qubit gate family with gate-voltage-tuneable exchange

To perform two-qubit operations, qubits are shuttled to neighbouring sites that connect adjacent pipes, in order to introduce an exchange interaction whose strength, Jij, can be estimated by

$$\begin{array}{rc}{J}_{ij}\,\approx \,\frac{2{t}_{ij}^{2}\Delta K}{\left[{(\Delta K)}^{2}-\epsilon {(t)}^{2}\right]}.\end{array}$$
(2)

Here, ϵ(t) is the detuning of the single-particle level spacings proportional to chemical potentials and ΔK is the difference between the on-site and inter-site charging energies. Jij can thus be in-situ modulated by the detuning using the plunger gates, or the tunnel coupling using the barrier gates. Both knobs can modulate the exchange strength over several order of magnitude. We choose to use module the tunnel coupling to allow us to operate in the centre of the (1, 1) charge configuration, where charge noise is minimised68,69.

In the logic basis \(\{\vert {\uparrow }_{i}\,{\uparrow }_{j}\rangle ,\vert {\uparrow }_{i}\,{\downarrow }_{j}\rangle ,\vert {\downarrow }_{i}\,{\uparrow }_{j}\rangle ,\vert {\downarrow }_{i}\,{\downarrow }_{j}\rangle \}\), the interaction between two exchange-coupled spins with a Zeeman energy difference ΔEZ (see Supplementary Note 4) generates time-evolution which is analogous to the single-qubit semiclassical Rabi dynamics in the mz = 0 subspace, while the decoupled mz = ± 1 subspaces merely acquire phases according to their Larmor frequencies. In this analogy, within the mz = 0 subspace, Δij ≈ ΔEZ corresponds to the qubit-drive detuning, Jij to the transversal coupling strength, and \({\Omega }_{ij}=\sqrt{{\Delta }_{ij}^{2}+{J}_{ij}^{2}}/h\) to the Rabi frequency.

This time evolution is our native two-qubit operation. To classify the resulting operations, we may represent the unitary operation with two angle variables, as

$$\begin{array}{rcl}{U}_{{{{\rm{Nat}}}}}(\epsilon ,\varphi ,\chi )&\hat{=}&{e}^{i\varphi \cos (\chi )}\\ &\times &\left(\begin{array}{cccc}{e}^{-i{\varphi }_{Z}-i\alpha (\varphi ,\chi )}&0&0&0\\ 0&\left[\cos (\varphi )+i\sin (\chi )\sin (\varphi )\right]&-i\cos (\chi )\sin (\varphi )&0\\ 0&-i\cos (\chi )\sin (\varphi )&\left[\cos (\varphi )-i\sin (\chi )\sin (\varphi )\right]&0\\ 0&0&0&{e}^{i{\varphi }_{Z}-i\alpha (\varphi ,\chi )}\end{array}\right).\end{array}$$
(3)

Using this parameterization (also see Supplementary Note 4), we observe that dynamics in the mz = 0 subspace is analogous to the single-qubit dynamics under the semiclassical Rabi Hamiltonian. This analogue is illustrated using a Bloch sphere in Fig. 4a. Here, the angle φ = Ωijτ2Q is set by the gate time τ2Q and the frequency Ωij, the Rabi frequency analogue. The angle \(\chi =\arctan (x)\) is set by the ratio x = Δij/Jij. Here, Δij is the detuning-analogue, and Jij the transversal coupling analogue. The angle χ is the analogue of the angle complementary to the single-qubit effective magnetic field polar angle arccos (Δij/Ωij) via arccos \(({\Delta }_{ij}/{\Omega }_{ij})={{{\rm{arccot}}}}(x)\). We also have φZ = (EZ + ΔEZ)φ/Ωij, and \(\alpha (\varphi ,\chi )=\varphi \cos (\chi )\). When x → 0, coinciding with negligible Zeeman energy differences, the native operation (3) reduces to the SWAP-rotation with the rotation angle given by φ (viewed from the frame from which EZ = 0). But even in the presence of ΔEZ, the native operation (3) can be used to realise several familiar two-qubit operations. Figure 4b–e illustrates some circuit identities obtained from it.

Fig. 4: Two-qubit gate family from nearest-neighbour exchange.
figure 4

a Bloch sphere two-qubit dynamics on the mz = 0 subspace under nearest-neighbour exchange. The mz = 0 states rotate around an axis defined by the relative magnitudes of exchange strength and Zeeman energy difference. b–e Circuit identities for the unitary time evolution UNNE(ϵ, φ, χ) Eq. (3), describing nearest-neighbour exchange in the presence of Zeeman energy differences. Multiples of 2πn are left out of the rotation angles for simplicity. b, c Choice of rotation angle φ = π + 2πn realises the phase gates (b) CPhase and (c) Ising ZZ-rotation gate. d Choice of φ = π/2 + 2πn realises a gate close to the Givens rotation, where the rotation angle χ depends on the ratio ΔEZ/Jij. e The SWAP-rotation gate can be constructed from the native unitary gate with φ = π/2 + 2πn and χ = π/4, as two such native operations separated by single-qubit Z-rotation gates. The phases of the mz = ± 1 components are fixed by subsequent application of another phase gate and single-qubit Z-rotations. f Bloch sphere representation of the SWAP-rotation identity of (e). g–i Fidelities for the native gates with (g) ϕ = π + 2πn, realising the Ising ZZ-rotation gate, and (h) ϕ = π/2 + 2πn, realising the Givens(χ) SWAP operation, which, for χ = π/4 is used in the composition of SWAP(θ) (see e), and (i) the composite SWAP(θ) rotation gate as a function of rotation angles and tunnel coupling variance \({\sigma }_{{t}_{ij}}/{t}_{ij}\).

Full size image

One way to engineer desired gates starts by considering interaction times that correspond to particular numbers of completed rotations with respect to the single-qubit analogue of the Rabi frequency. In doing so, are left to fix χ to define the operation. Since we largely do not control the Zeeman energy difference, we choose the polar angle analogue with Jij. By choosing φ = π + 2πn, we realise the diagonal two-qubit phase gates70, as

$$\begin{array}{rcl}&&Z({\varphi }_{11})\otimes Z({\varphi }_{11}){e}^{-i\alpha -i\varphi }{U}_{{{{\rm{Nat}}}}}(\epsilon =0,\varphi =\pi +2\pi n,\chi )\\ &&={{{\rm{CPhase}}}}\left[-2\alpha (\varphi =\pi +2\pi n,\chi )\right].\end{array}$$
(4)

where we have defined φ11 = − φZ − α(φ, χ), and

$$\begin{array}{rcl}&&Z(-{\varphi }_{Z})\otimes Z(-{\varphi }_{Z}){U}_{{{{\rm{Nat}}}}}(\epsilon ,\varphi =\pi +2\pi n,\chi )\\ &&={{{\rm{Ising}}}}\left[\alpha (\varphi =\pi +2\pi n,\chi )+\pi \right].\end{array}$$
(5)

The circuits are visualised in Fig. 4b, c. See Supplementary Note 5 for their matrix representations. These gates are maximally entangling (for certain rotation angles), but e.g. the SWAP gate, or any non-diagonal gate using just phase gates and single-qubit Z-rotations is not possible. In general, a larger set of gates allows more efficient decompositions for algorithms. For example, the variational eigensolvers for the Fermi-Hubbard model natively decompose into SWAP-rotations and single-qubit Z-rotations, so we show how to construct the SWAP-rotation from the native operation.

By instead choosing φ = π/2 + 2πn, we obtain a gate close to the so-called Givens rotation (see Supplementary Note 5), as

$$\begin{array}{rcl}&&Z({\varphi }_{11}+\pi /2)\otimes Z({\varphi }_{11}+\pi /2){e}^{-i\alpha +i\varphi }\\ &&\times {U}_{{{{\rm{Nat}}}}}(\epsilon ,\varphi =\pi /2+2\pi n,\chi )\\ &&={{{\rm{CPhase}}}}\left[-2\alpha (\pi /2+2\pi n,\chi )+\pi \right]{{{\rm{Givens}}}}(\chi ){{{\rm{SWAP}}}}.\end{array}$$
(6)

The circuit identity is illustrated in Fig. 4d. The angle of the Givens rotation is controllable with the polar angle analogue, although not all rotation angles are attainable equally easily. In particular, rotation angles of 0 and π/2 would require negligible Zeeman energy difference or exchange strength, respectively. However, these cases are not interesting, since in the absence of Zeeman energy differences, we may employ a SWAP-rotation gate, and in the absence of an interaction the operation is non-entangling.

The rotation angle χ = ± π/4 corresponds to the case where the (absolute value of the) Zeeman energy difference is equal to the exchange strength. Here, the mz = 0 matrix elements simplify to \(| {U}_{{{{\rm{Nat}}}}}{(\epsilon ,\pi /2,\pi /4)}_{ij}| =1/\sqrt{2}\). The native operation UNat(ϵ, π/2, π/4) thus acts as a controlled Hadamard operation for the mz = 0 subspace. The operation can be used to convert single-qubit Z(θ)-rotations into SWAP-rotations, as

$$\begin{array}{rcl}{{{\rm{SWAP}}}}(\theta )&=&-{e}^{-i\theta \pm i\pi }\,Z\left(-2{\varphi }_{Z}\right)\otimes Z\left(-2{\varphi }_{Z}\right){{{\rm{Ising}}}}\left[-\theta -2\alpha -2\varphi \right]\\ &\times &{U}_{{{{\rm{Nat}}}}}\left(\epsilon ,\frac{\pi }{2},\pm \frac{\pi }{4}\right)\,Z(\pm \theta )\otimes Z(\mp \theta )\,{U}_{{{{\rm{Nat}}}}}\left(\epsilon ,\frac{\pi }{2},\pm \frac{\pi }{4}\right).\end{array}$$
(7)

The circuit is illustrated in Fig. 4e. We have written the circuit identity using the Ising gate for clarity, but in realising it using Eq. (5), we may absorb the Z-rotations into the final step, reducing physical gates from 6 to 5. It provides an exact method to perform SWAP-rotation operations, including the non-entangling SWAP gate, in the presence of Zeeman energy differences See e.g. refs. 71,72 for prior, related works discussing the non-entangling SWAP gate in the mz = 0 subspace. The fidelity of this operation does not depend on the magnitude of ΔEZ (as long as an equally large exchange strength is attainable), which means that the gate decomposition can be used with e.g. micromagnets, with which \(\Delta {E}_{Z}={{{\mathcal{O}}}}(1-10\,{{{\rm{GHz}}}})\)39.

The \(\sqrt{{{{\rm{SWAP}}}}}\) operation obtained using identity (7) is visualised on the mz = 0 Bloch sphere as a trajectory for the initial state \(\left\vert \downarrow \uparrow \right\rangle\) in Fig. 4f. The strategy for choosing parameters for the φ = π/2 + 2πn operation is as follows (also see Supplementary Note 6 for further details). Knowing ΔEZ, we set Jij = ∣ΔEZ∣. We are required to set the gate time, as \(\tau =(\pi /2+2\pi n)/(\sqrt{2}{J}_{ij})\). The gate time is limited by a minimum set by ΔEZ, and a resolution \(2\pi n/(\sqrt{2}{J}_{ij})\), but we may use g-factor tuneability at QD j for fine-tuning τ (after which Jij is recalculated). Smaller g-factor tuneability then requires a longer gate time to minimise gate time errors.

For example, setting the target gate time and rotation angle, as τ = 1 μs, and χ = π/4, respectively, and assuming ΔK = 1 meV, σG = 10−3gSi, B0 = 1 T yields the desired Givens-like gate with x = ± 1, and with average exchange strength, number of rotations, and average timing errors of Jij ≈ 32 MHz, n ≈ 45, and δτ2Q ≈ 0.1 ns. For the phase gates, the protocol is similar, but x is solved from the desired rotation angle. We note that typically, the two-qubit gates impose an independent restriction to the g-factor tuneability to ensure that fidelities are not limited by gate timing errors, which we find to be higher than the requirements for single-qubit gates. For example, in the above, we require ~δg ≥ ± 1 × 10−4 (corresponding to dVq ≤ ± 61 mV).

The process fidelities of the native Ising(α + π), Givens(χ)SWAP, and composite SWAP(θ) operations are shown in Fig. 4(g)–(i), as a function of rotation angle and relative variance in tunnel coupling noise, \({\sigma }_{{t}_{ij}}/{t}_{ij}\). They are evaluated using the exact perturbative Hamiltonian (Supplementary Note 4), at ϵ = 0. We average over N = 1000 random g-factor pairs. For the Givens-like gate, we determine the sign of χ from the sign of the g-factor difference. All gates enable fidelities \({{{\mathcal{F}}}}\ge 0.9999\) for sufficiently low noise in the tunnel coupling. For example, charge noise in the barrier gate voltage propagates to noise in the tunnel coupling. The dependence of both rotation angles on tunnel coupling is reflected in the fidelities: angles that require higher tij are more sensitive to tunnel coupling noise. However, since the rotation angles of the SWAP-rotation gate (7) arise from single-qubit Z-rotations, it’s fidelity is approximately independent of rotation angles, and expected to be limited by the fidelity of the Givens(χ)SWAP operation.

Transversal rotation gates

A gate set enabling universal quantum computing requires another single-qubit gate besides the Z(φq) gate and a maximally entangling two-qubit gate73. To this end, we propose to realise a globally applied \(\sqrt{X}={{{\bf{I}}}}(1+i)/2+{\sigma }_{x}(1-i)/2\). The gate composes into a single-qubit rotation gate e.g. via the identity \(Y({\varphi }_{q}):= \sqrt{X}Z({\varphi }_{q}){\sqrt{X}}^{{\dagger} }\).

In the nanogrid, a \(\sqrt{X}\) gate can be applied globally by providing a small B1 perpendicular to B0 from large resonant structures, such as a dielectric 3D cavity resonator74, or a superconducting resonator based on a coplanar waveguide patterned e.g. over the metal gate layers75, with a resonance frequency coinciding with the average qubit frequency fSi ≈ 28 GHz, and a quality factor Q ≈ 100 to cover a bandwidth of 280 MHz corresponding to Gq ≤ ± 10−2 (>5σG, assuming σG = 10−3gSi). Global control allows avoiding issues related to crosstalk and impedance matching, which would be a challenge with partially or fully local broadband structures76.

The global X-control together with pipelining provides an extra limitation for the circuit compilation and density of pipelining. Since all qubits on the pipeline undergo the \(\sqrt{X}\) pulses, the algorithms must be compiled with periodic X-control. A simple example code block for the pipelined, global-X-controlled compilation is given by

$$\begin{array}{r}\left[Z({\theta }_{1}),X(\pi /2),Z({\theta }_{2}),Z({\theta }_{3}),{X}^{{\dagger} }(\pi /2),{{{\rm{Native}}}}({\theta }_{4})\right]\times D/6,\end{array}$$
(8)

where Native(θ4) is a native two-qubit gate of the system, as discussed in “Two-qubit gate family with gate-voltage-tuneable exchange”. This code block allows pipelining at a filling density of one in every three (logical) columns. The code block (8) maps to an equal density of single-qubit Z-rotation gates, Y-rotation gates, and native two-qubit interactions. Due to the variations in g-factor discussed above, driving all spins with a single drive tone is challenging. We instead opt for multitone driving and frequency binning77, which is discussed in Supplementary Note 8. We show that reaching a crosstalk-limited fidelity \({{{\mathcal{F}}}}\ge 0.9999\) for a qubit distribution with Gq ≤ ± 10−2 is feasible with 112 drive tones and a bin width νbin/(2π) ≥ 5 MHz.

Application as bespoke hardware for a NISQ eigensolver

We summarise the proposed qubit control protocols for operating the silicon spin qubit pipeline from “Implementation with silicon quantum dots” in Table 2. The requirements of synchronous shuttling, lack of local runtime control, and qubit frequency variability leads to protocols where we fix gate times and adjust qubit frequencies with dc voltage tuneable parameters, namely the g-factor (qubit frequency) and the exchange strength. Each of these protocols are feasible up to fidelities \({{{\mathcal{F}}}}\ge 0.9999\) in the presence of noise, in the realistic scenario where qubit frequency variabilities are larger than the frequency tuneability.

Table 2 Qubit control protocols on the pipeline
Full size table

We now exemplify how these elements propagate into solving a quantum computing problem in the NISQ era. Here, we focus on the variational eigensolver for the Fermi-Hubbard model, where the resources required to run the algorithm on a set of physical qubits have been estimated in18, and where the task is to estimate the ground state of a 5 × 5 Fermi-Hubbard Hamiltonian. See supplementary Note 9 for details of this algorithm. At the low level, the algorithm breaks down into SWAP-, and single-qubit Z-rotation gates for the so-called (simulated) state initialisation and (simulated) state evolution stages, while the bit-string (physical qubit) initialisation and readout stages also require qubit-selective qubit-flip X(π) and basis-change X(π/2) operations. We assume that we are not limited by initialisation or readout times. That is, we assume that the initialization and readout times are as fast as the clockspeed of 1 μs. The single-qubit gate times, and the two-qubit gate time errors are upper limited by the qubit frequency tuneability. While the tuneability has not been studied on a large number of devices, based on the literature, we expect the processor clockspeeds no slower than 1 MHz (at B0 = 1 T). This means that to run an algorithm of depth 10000, for example, we require qubit \({T}_{2}^{* }\ge 10\) ms.

We summarise the estimated pipelined run-time, and contributions to the run-time, of the Fermi-Hubbard variational eigensolver in Table 3, using the resource estimates from18. There are several layers at the high level. The algorithm requires a number of iterations. Each iteration consists of a number of runs, which is equal to the number of circuit configurations multiplied by runs per configuration. The number of circuit configurations, in turn, is determined by the number of parameters, number of measured observables, and the number of noise levels, which is part of an error mitigation protocol78. The number of runs per configuration is determined by the number of runs for one parameter, to measure one set of commuting observables, and the extra sampling cost for error mitigation. For each parameter-observable-set-specific run, we may then evaluate the circuit run time.

Table 3 NISQ Fermi-Hubbard eigensolver run-time on the pipeline
Full size table

Two types of classical parallelisation are possible. As discussed in “Qubit pipeline”, pipelining allows to perform Nr number of repetitions for a circuit of depth D in time (D + Nr)τ. For example, at maximal filling, this runtime scaling is (D + 2Nr)τ. For single-qubit and two-qubit gate depths of D1Q and D2Q, the run-time for Nr repetitions on the nanogrid pipeline (Fig. 2a) with three physical shuttling steps between gates is then (D1Q + 2Nr)(τ1Q + 3τs) + (D2Q + 2Nr)(τ2S + 3τs). For D1Q = 1174 and D2Q = 219618, and the gate time estimates for Z-rotation and SWAP-rotation gates from Table 2, we find that pipelining reduces the run-time per circuit configuration from 25.5 min (assuming τ1Q = 1 μs) to 1.74 s, i.e. by roughly a factor of 880.

We may also run e.g. different circuit configurations on different physical pipeline processors in parallel. To estimate the footprint of the pipeline processor, we expect the width of a single pipe to be ~340 nm, with a same-layer gate pitch of 100 nm. Likewise, we expect the length of a single-qubit or two-qubit gate step to be ~190 nm. Then, for N = 25 qubits, and a circuit depth of D = D1 + D2 = 1174 + 2196 = 3370 quantum logic gates, we estimate the footprint of a single pipeline qubit processor to be 8.5 μm × 640.3 μm.

Discussion

We have analysed a qubit pipeline architecture for realizing gate based quantum computation in the NISQ era. The architecture minimizes run-time local control resources, utilizing instead global run-time, and local pre-configuration control. This is made possible by a combination of an increased qubit grid layout size, and by synchronized operation, where steps of qubit state shuttling and quantum logic gates alternate.

Having described the architectural paradigm, we focused on a physical implementation case-study in the SiMOS electron spin qubit platform. Here, we laid out qubit control protocols under the pipeline- and platform-specific restrictions, demonstrating each theoretically with NISQ-high fidelities while remaining robust against qubit frequency variabilities characteristic for the platform. Our main focus has been to address this frequency variability, while we may improve robustness against noise with bespoke control methods in the future. Most of the elements are possible to implement with present-day technology without further advances, but we expect more microwave engineering efforts to designing and testing switchable, dense transmission lines or resonators, and their ability to support a finite frequency bin. We then assessed the performance of this architecture for a NISQ variational eigensolver task. In the future, it may be possible to decrease the number of required gates per run by more directly utilising the native two-qubit gate family that arises from nearest neighbour exchange in the presence of Zeeman energy differences. The silicon spin qubit platform is well-suited to the pipeline approach, but the concept may also be implemented in other architectures, such as with trapped ions, or with superconducting qubits by replacing shuttling with SWAPs.

Indeed it would be an interesting topic of further work to explore an implementation based on SWAPs. There, the qubit grid remains fully occupied and stationary, and useful quantum information is transferred forward through the array (while states carrying no quantum information propagate in reverse). As before, the horizontal density of quantum information in the array can be adjusted as required (e.g. to accommodate initialisation and measurement times) by introducing buffer states which do not participate in the calculation. Back-propagating states or buffer states do not interfere with the calculation due to the non-entangling nature of the SWAP gate.