Introduction

Variational Quantum Algorithms (VQAs) are emerging as a promising solution to achieve quantum advantage on the currently available Noisy Intermediate-Scale Quantum (NISQ) devices1. These algorithms have been employed for solving a wide range of tasks in different frameworks2 from the estimate of the ground state of a given Hamiltonian3,4,5, solving all those problems that undergo the name of variational quantum eigensolver6,7,8, for simulating the dynamics of quantum systems9,10, to quantum error correction problems11,12. They consist in hybrid classical-quantum algorithms where a classical optimizer is used to minimize a cost function, representative of the solution of the addressed problem, that is efficiently estimated through the quantum system.

Recently, VQAs have been introduced in the context of quantum metrology and sensing considered one of the pillars of current quantum technologies13,14. The quest for enhanced measurement sensitivities has driven to exploit probe states with quantum correlations in order to go beyond the classical limits. To this end, the optimization of the probe state and the measurement settings are crucial to retrieve such enhanced estimation performances13,15. Several approaches have been proposed for the optimization of the figures of merit able to certify the quantum estimation performances, such as the Quantum Fisher Information (QFI)16,17, of probe states in nuclear magnetic resonance systems18,19,20 and of trapped atomic arrays21,22 also considering noisy conditions23 which make the optimization task even harder. However, up to now, the experimental realizations that make use of variational algorithms in the sensing field are still limited to the single-parameter regime.

The next challenge is to apply these methods to the multiparameter regime24,25, where the number of parameters upon which the probe evolution and thus the optimization task depends increases. In such a framework, finding the optimal settings becomes indeed particularly hard and resource expensive. For this reason, several machine learning-based procedures have already been demonstrated as really practical in this scenario26,27. Therefore, the true potential of VQAs can be valued when applied to multiparameter estimation problems allowing to efficiently explore and optimize complex, high-dimensional parameter spaces. Variational approaches can provide some advantages in certain scenarios with respect to machine-learning optimization and in particular to reinforcement learning. Indeed, the capability of a direct optimization on the actual device renders variational methods robust against noise, while reinforcement learning optimization can deviate from accurately learning control policies when exploring a complex and too large parameter space. Conversely, the use of variational approaches requires some level of knowledge of the system model, which is not required in other machine learning methods. In a multiparameter framework the simultaneous estimation of the parameters, feasible by exploiting a quantum probe, can be favorable with respect to a separable estimation strategy28,29,30, also in a distributed sensing scenario31. However, finding the optimal settings assuring the sensor best performances is harder in this framework, where in general the saturation of the ultimate precision bound, i.e., the quantum Cramér-Rao bound (QCRB), is also not guaranteed32. Moreover, when including noise linked to actual experimental conditions, standard approaches can make the required high-dimensional optimization task impossible. Very recently, two theoretical proposals of using VQA in a multiparameter framework have been developed for magnetic field sensing33,34, but their general application on an actual multiparameter sensor is still lacking.

In this work, we devise and implement a VQA to optimize the operation of a quantum optical multiphase sensor. We extended previous theoretical works33, developed using the qubit formalism, to the photonic case devising a methodology tailored for the domain of quantum optics. Such a procedure allows us to retrieve the gradient of the experimental quantum photonic circuit depending on the Fock state at the input. The gradient evaluation of the response function of the noisy quantum circuit is crucial to determine its actual estimation performances. This is obtained by applying either the standard parameter-shift rule or the generalized one35,36 depending on the probe state used, allowing to retrieve the Fisher information matrix (FIM) from the experimental measurements as a function of the variational parameters, depending on the number of photons in the optical modes. In a consecutive step, a gradient-free learning algorithm updates the parameters in order to optimize the FIM, thus improving the estimation performances. Since the FIM is derived directly from the measured data, all the experimental imperfections will automatically be incorporated into the optimization procedure that thus become inherently resilient to noise.

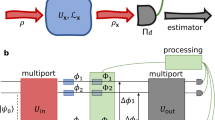
The device we exploit is an integrated programmable interferometer37,38 that can achieve quantum-enhanced performances in the simultaneous estimation of three independent optical phases when injected by two-photon quantum states as demonstrated in39. Thanks to the integrated photonic chip reconfigurability40, it is possible to tune both the probe preparation and the measurement settings. Notably, the algorithm training and the cost function evaluation are performed directly on the noisy experimental quantum circuit. Therefore, we do not require, at any step of the optimization procedure, the knowledge of the sensor response function, which can remain unknown to its users.

Results

Variational quantum metrology

One of the most investigated multiparameter problems is the estimate of a vector of p phases \(\overrightarrow{\phi }=({\phi }_{1},\ldots ,{\phi }_{p})\) embedded into a multi-arm interferometer41. The process is investigated by means of a photonic probe prepared in the initial state ρ0 and evolving according to the unitary transformation:

$$\begin{array}{l}{U}_{\overrightarrow{\phi }}={e}^{i\mathop{\sum }\nolimits_{m = 1}^{p}{G}_{m}{\phi }_{m}}\\ {G}_{m}={n}_{m}\end{array}$$
(1)

where ϕm is the phase shift occurring in the mode m and Gm is the generator of the phase shift transformation, resulting to be the photon number operator of the relative interferometer mode. After the evolution through the studied system, the probe state becomes \({\rho }_{\overrightarrow{\phi }}={U}_{\overrightarrow{\phi }}{\rho }_{0}{U}_{\overrightarrow{\phi }}^{{\dagger} }\). The choice of the probe state plays a crucial role since it determines the ultimate estimation precision achievable. The second important role is determined in the measurement stage, indeed depending on the implemented positive-operator-valued measure (POVM) Πx, it is possible to extract a different amount of information (defined as the classical Fisher information) about the investigated parameters that will be lower or equal to the QFI.

In the multiparameter scenario, these quantities become matrices and the inequality can be generalized considering their diagonal elements:

$$\,{{\mbox{Tr}}}\,[\,{{\mbox{Cov}}}\,(\overrightarrow{\phi })]\ge \frac{\,{{\mbox{Tr}}}\,[{F}_{C}^{-1}(\overrightarrow{\phi })]}{M}\ge \frac{\,{{\mbox{Tr}}}\,\left[{F}_{Q}^{-1}\left({\rho }_{\scriptstyle\overrightarrow{\phi }}\right)\right]}{M}.$$
(2)

Here, the first inequality corresponds to the Cramér-Rao bound (CRB), where \(\,{{\mbox{Cov}}}\,(\overrightarrow{\phi })\) is the covariance matrix representing the sensitivity of the estimate, and M represents the number of repetitions of the experiment, while the elements of the FIM are:

$${F}_{C}{(\overrightarrow{\phi })}_{ij}=\mathop{\sum}\limits_{x}\frac{1}{P(x| \overrightarrow{\phi })}\left(\frac{\partial P(x| \overrightarrow{\phi })}{\partial {\phi }_{i}}\frac{\partial P(x| \overrightarrow{\phi })}{\partial {\phi }_{j}}\right).$$
(3)

Where \(P(x| \overrightarrow{\phi })=\,{{\mbox{Tr}}}\,\{{\Pi }_{x}{\rho }_{\overrightarrow{\phi }}\}\) represents the conditional measurement probability relative to the output x. From a practical point of view, to optimize the sensor operation, it is necessary to take into account noise and consider only the possible set of available measurements. Therefore, it is useful to develop a procedure that maximizes the classical Fisher information, finding the optimal settings to reduce the error on the estimate of the vector of parameters \(\overrightarrow{\phi }\). According to Eq. (3), this requires knowing the dynamic of the sensor in order to retrieve the measurement outcome probabilities \(P(x| \overrightarrow{\phi })\) as well as their derivatives. Both these tasks are non-trivial since they require to have full knowledge of the sensor operation in a noisy environment. Moreover, it can be hard to find the analytical solution for the optimization of the probe state and the measurement settings considering environmental imperfections in practical applications.

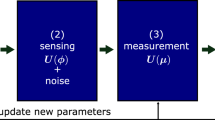
In particular, we minimize the trace of the inverse of the FIM, chosen as the problem cost function, by optimizing the measurement settings. With this approach, we evaluate the FIM directly with the quantum circuit using the measured data to sample the probability distributions \(P(x| \overrightarrow{\phi })\) in Eq. (3) and, by means of the standard and generalized parameter-shift rules35,36, we compute their partial derivatives with respect to the parameters ϕi. To perform the minimization procedure we adopted instead a different approach. In order to reduce the number of required experimental points, we implement the function minimization using the Nelder-Mead algorithm42, which results to be one of the most employed and best-performing gradient-free algorithms. The scheme of the complete algorithm we have implemented is shown in Fig. 1.

Fig. 1: Scheme of the implemented variational algorithm.
figure 1

The four-mode integrated interferometer is injected either with single or two-photon probe states. A first layer of internal phase shifters is used to set the vector of phases \(\overrightarrow{\phi }\) consisting of the parameters of interest. A second layer of phase shifters can instead be used to perform the optimization by shifting the measurement point of \(\overrightarrow{\theta }\). Depending on the selected probe state and the set \(\overrightarrow{\phi }\), the FIM is computed by the quantum circuit through a generalization of the parameter-shift rule. The FIM is then used to compute the cost function of a learning algorithm that optimizes the variational parameter \(\overrightarrow{\theta }\), enhancing the sensor estimation performances.

Full size image

Gradient of the photonic circuit

We use the parameter-shift rule35,36 to extract the analytic gradient, directly from the experimental data, necessary for the computation of the FIM, as can be seen from Eq. (3). We require gradient computation to evaluate the cost function of the problem consisting of the trace of the inverse of the FIM. Gradient evaluation can be particularly challenging on noisy hardware, thus motivating the application of this rule for quantum machine learning43. The majority of the optimization procedures indeed require knowledge of the gradient of the cost function. For instance, the most common and powerful optimization algorithm to train machine learning models and neural networks is gradient descent44, which uses the gradient of the cost function to determine the model parameter values. Most of the currently adopted variational quantum algorithms relied either on gradient-free methods or on numerical differentiation, resulting to be highly inefficient or even ineffective. To retrieve the numerical derivative it is indeed necessary to evaluate the function of interest in an infinitesimal shifted point. However, for NISQ devices, the most common scenario corresponds to situations where noise fluctuations are larger than the difference between the function in the original and the shifted point, making it unfeasible to use the finite difference approximation. Moreover, from a practical point of view, numerical differentiation would require having high levels of control of the quantum circuit, allowing one to discriminate among the two settings that differ by an infinitesimal quantity. The parameter-shift rule solves these issues by obtaining the analytic gradient from the evaluation of the quantum circuit in shifted points of macroscopic size. This reduces the sensitivity to control errors and noise as we show in Supplementary Note 1.

Here, we extend a generalization of the parameter-shift rule (see Methods) to the photonic case by applying the parameter-shift rule to Fock states, retrieving the partial derivatives of the output probabilities with respect to the parameters under study. To our knowledge, no photonic implementation has been realized before obtaining the gradient of the system outcome probabilities allowing its use in a variational framework. In particular, we show that the number of points in which is necessary to evaluate the quantum photonic circuit, in this case, depends on the photon number of the input state.

Considering our quantum system described by Eq. (1), the generator of the implemented unitary transformation is the photon number operator, therefore, it will depend on the number of photons in the probe state. More specifically, given a probe with k photons, the spectrum of the phase shift generator along the mode m is:

$$spec({G}_{m})=\{0,1,2,\ldots ,k\}.$$
(4)

We perform the multiparameter estimation of the vector of phases \(\overrightarrow{\phi }\) using two kinds of probe states: we study the 4-mode interferometer behavior when it is probed with single-photon states and then by exploiting entangled two-photon probes that allow to a achieve superior measurement precision. When the interferometer is injected with single-photon states the Eq. (4) provides spec(Gm) = {0, 1}. Thus, the partial derivatives of the output probability distribution with respect to the three parameters under study, necessary to compute the FIM in Eq. (3), can be obtained by applying the simple parameter-shift rule of Eq. (8) with \(r=\frac{1}{2}\) (see Methods). This allowed us to reconstruct directly from the experimental data the FIM considering the measured outcomes when the device internal phases are set to ϕ1, ϕ2 and ϕ3 for the reconstruction of the conditional probabilities \(P(x| \overrightarrow{\phi })\). On the contrary, the measurement performed shifting the phases by a factor \(\pm \frac{\pi }{2}\) allows to obtain their derivatives \({\partial }_{{\phi }_{i}}P(x| \overrightarrow{\phi })\), also required to reconstruct the FIM [see Eq. (3)]. More specifically, the partial derivative with respect to the phase ϕi of the outcome probability is obtained by:

$${\partial }_{{\phi }_{i}}P\left(x| \overrightarrow{\phi }\right)=\frac{1}{2}\left[P\left(x| \overrightarrow{\phi }+{\overrightarrow{\Delta }}^{(i)}\right)-P\left(x| \overrightarrow{\phi }-{\overrightarrow{\Delta }}^{(i)}\right)\right],$$
(5)

where i = 1, 2, 3, and \({\overrightarrow{\Delta }}^{(i)}\) is a vector with components \({({\overrightarrow{\Delta }}^{(i)})}_{j}=\frac{\pi }{2}{\delta }_{ij}\), and δij is the Kronecker’s delta.

The situation changes when we inject into the interferometer two-indistinguishable photons. In this case Eq. (4) gives spec{Gm} = {0, 1, 2}, resulting in a generator with more than two distinct eigenvalues. This requires the adoption of a modified and more general parameter-shift rule valid for generators with a larger spectrum. The extension of the rule can be achieved through various methodologies as detailed in Supplementary Note 2. We thus prove that the four-term rule [Eq. (9)] can be applied to our system, and we compute the required parameters in order to retrieve the partial derivatives of interest, proving that we obtain the analytic partial derivatives of the measurement outcomes probabilities of the photonic circuit injected with two-photon states:

$$\begin{array}{l}{\partial }_{{\phi }_{i}}P(x| \overrightarrow{\phi })=\left[P(x| \overrightarrow{\phi }+\frac{\pi }{4}{\overrightarrow{\Delta }}^{(i)})-P(x| \overrightarrow{\phi }-\frac{\pi }{4}{\overrightarrow{\Delta }}^{(i)})\right]\\\qquad\qquad\quad+-\frac{\sqrt{2}-1}{2}\left[P(x| \overrightarrow{\phi }+\frac{\pi }{2}{\overrightarrow{\Delta }}^{(i)})-P(x| \overrightarrow{\phi }-\frac{\pi }{2}{\overrightarrow{\Delta }}^{(i)})\right].\end{array}$$
(6)

Once having retrieved the analytic gradient of the system’s response function, it is possible to compute the FIM and optimize the measurement settings to saturate the CRB. Once having retrieved the cost function, its optimization is instead obtained through a gradient-free minimization method.

From a practical point of view, it is fundamental to study how the estimate of \(P(x| \overrightarrow{\phi })\), also referred to as the likelihood function of the system, its partial derivatives, and, as a consequence, the CRB is affected by measurement statistics. We report in Fig. 2 such a value applying the parameter-shift rule to Monte Carlo simulated data for systems of increasing dimensionality. More specifically, in Fig. 2a, we report the retrieved CRB of the estimate of a phase shift ϕ in a non-perfect (visibility lower than one) two-mode interferometer when the measurement is performed at its most informative point, i.e., \(\frac{\pi }{2}-\phi\). The robustness of values reconstructed by the parameter-shift rule depends on the number of events N used to sample the probability distributions. In Fig. 2b, we did the same study on the four-arm interferometer when seeded with two-photon states. The increased complexity of the system and of the structure of the probability distributions requires, as expected, a larger number of events to correctly reconstruct the FIM. Moreover, in the latter case the presence of a lot of divergences in the FIM (see Supplementary Note 1 for more details) can affect the reconstruction performed by the variational algorithm for a few number of events. Indeed, considering the average over different reconstructions, the situations when the algorithm ends up in a divergence prevail.

Fig. 2: Numerical simulations addressing the protocol robustness to finite statistics and noise.
figure 2

Plots in panels a, b show how the reliability of the quantum circuit in reconstructing the Fisher information depends on the measurement statistics. a Inverse of the Fisher information reconstructed by applying the parameter shift rule to a two-mode interferometer with fringe visibility v = 0.8. The orange points represent the average results over 30 different repetitions with a selected random phase ϕ ∈ [0, π] with the relative standard deviation also reported as the blu triangles. b The same study is done for the four-mode interferometer injected with two-photon states considering the ideal scenario. In this case, the Fisher information is a 3 × 3 matrix. In both panels, on the x-axis is reported the number of events used to reconstruct the probabilities needed to obtain the Fisher; the dot-dashed lines refer to the respective QCRB. c Error on the estimate of ϕ in a two-mode interferometer for different levels of noise. Blue points refer to a strategy where the measurement is not shifted while in red the same estimate is done in the shifted point optimized by the learning algorithm which minimize the inverse of the Fisher. All the results are averaged over 15 phase values each repeated 20 times. The estimates are performed using a number of probes equal to 5000. The importance of using the optimized strategy emerges in particular when the level of noise in the system increases. Error bars refer to the standard deviation over the different repetitions.

Full size image

The importance of shifting the measurement based on the noise level affecting the probe evolution is demonstrated in Fig. 2c for a simulated two-mode system. The error on the estimate of the phase shift is compared when measurements are not shifted and when the parameter-shift rule is applied to compute optimal measurement settings. We perform such a study for different levels of visibility of interference fringes, which is the main source of noise in the system. In the ideal scenario, the Fisher Information does not depend on the value of the parameter under study, therefore there is no gain from the application of the optimization procedure. As soon as a non-ideal value of the visibility is taken into account it becomes evident that, in order to saturate the CRB, it is necessary to optimize the measurement settings even in this simple scenario. Importantly, we demonstrate here that our procedure, outlined in Fig. 1, allows the saturation of the CRB for any value of V, where the usefulness of the variational algorithm becomes evident.

Experimental results

We start by reconstructing experimentally the FIM of our device for each vector of phases \(\overrightarrow{\phi }\) investigated. In the experiment, we need to find a balance between the number of events necessary to correctly reconstruct the desired quantities and the overall acquisition time, therefore we fix the number of events for each phase point of this step to 5000. This number of data is used to reconstruct all the probabilities and their derivatives needed to compute the FIM. Once the FIM is obtained, we minimize the trace of its inverse, which serves as the cost function for the problem. This optimization enhances the quality of the estimation, ultimately leading to the saturability of the CRB, in the limit of large resources. Since the figure of merit optimized is reconstructed at each step of the algorithm from the experimental results, it is important to choose an algorithm that converges with a minimal number of function evaluations. To mitigate the impact of experimental errors due to finite measurement statistics, we perform the optimization by exploiting a gradient-free algorithm in this second stage. Specifically, the Nelder-Mead algorithm has proven to be particularly effective for our purposes, as it does not rely on the analytic form of the function being minimized. We have also tested other gradient-free optimization algorithms, such as COBYLA, and their performance comparison is provided in Supplementary Note 3.

As described in the Methods section and in ref. 39, we use the first layer of internal phase shifters to set the three optical phase shifts \(\overrightarrow{\phi }\), which represents the parameters of interest with respect to the phase of the fourth arm taken as a reference (Fig. 3a). The second layer of phase shifters is used instead to shift the measurement, thus setting the phases \(\overrightarrow{\theta }\). Consequently, the overall evolution imparts a vector of phase shifts \(\overrightarrow{\phi }+\overrightarrow{\theta }\) to the initial probe. We fix the starting point of the implemented optimization algorithm to \(\overrightarrow{\theta }=\{\frac{\pi }{2},\frac{\pi }{2},\frac{\pi }{2}\}\) and the number of optimization steps to mfev = 20. This choice is justified by looking at Fig. 3b, c where the cost function for a certain vector \(\overrightarrow{\phi }\) is reported as a function of the algorithm’s optimization steps and the related choice of the vector of parameters \(\overrightarrow{\theta }\). Further details can be found in Supplementary Note 4.

Fig. 3: Integrated photonic circuit and experimental optimization.
figure 3

a Sketch of the integrated photonic device and possible selection of different input probe states. The tuned phase shifts \(\overrightarrow{\phi }\), corresponding to the triplet of phases to estimate, and \(\overrightarrow{\theta }\), allowing to shift the measurement settings, are highlighted. b Experimental value of the cost function during the optimization strategy for the configuration \(\overline{s}6\) as a function of the optimization steps. c The Nelder-Mead algorithm minimizes the cost function by changing the variational parameters \(\overrightarrow{\theta }\), here we report the values set during the optimization procedure for a certain phases triplet.

Full size image

To demonstrate the effectiveness of the optimization algorithm in finding the measurement settings \(\overrightarrow{\theta }\), we compare the estimation performances obtained through the variational approach with those obtained when \(\overrightarrow{\theta }\) is set to the null vector or is chosen randomly. We demonstrate the validity of the variational approach independently of the selected phases \(\overrightarrow{\phi }\) and of the input probe state, by examining the performances achieved with two-photon probes states and with single-photon states. We quantify the performances of the estimation strategy by looking at the quadratic loss i.e. \({(\overrightarrow{\phi }-{\overrightarrow{\phi }}_{true})}^{T}(\overrightarrow{\phi }-{\overrightarrow{\phi }}_{true})\), where \({\overrightarrow{\phi }}_{true}\) represents the true set values of the phases. We investigate this for a scenario where the interferometer is seeded with M = 50 probes. For each vector of investigated phases, randomly chosen in the whole periodicity interval, i.e., ϕi ∈ [ − π, π], we repeat the procedure 30 times reporting in Fig. 4a, b the averaged results and the corresponding standard deviations. The 10 different phase configurations selected for two-photon probes (s1…s10) and the six different ones chosen when the system is instead seeded with single-photon probes (\(\overline{s}1\ldots \overline{s}6\)) have been selected randomly by applying different voltages to the three phase shifters of the first-layer on the internal arms of the integrated device and are reported in the in Tables 1 and 2.

Fig. 4: Experimental estimation performances.
figure 4

Comparison of the estimation performances obtained without adjusting the measurement settings (blu points), shifting them randomly (green dashed line), and setting them to the values retrieved with the developed variational strategy (red points). The results are compared with the QCRB (black dot-dashed line) obtained considering the injected probes in the 4-mode interferometer. The reported experimental results are the average over 30 different repetitions of the estimate for each phase vector with the relative standard deviation. a Experimental quadratic loss obtained using two-photon probes for the estimate of 10 different phase configurations reported on the x-axis. For the optimization procedure, the FIM is reconstructed by applying the generalized parameter-shift rule. The inset reports the distributions of the experimental performances achieved on the last set, i.e., configuration s10 when repeating the estimation procedure 100 times. b Experimental quadratic loss obtained by injecting single-photon probes in the 4-mode interferometer for the estimate of 6 different vector of phases reported on the x-axis. Here, the measurement settings are retrieved by reconstructing the FIM with the standard parameter-shift rule. c Averaged experimental reconstructed posterior distributions of the estimate of the configuration \(\overline{s}1\) for different phase noise values, i.e., phn = (0, 0.02, 0.04, 0.06, 0.08, 0.1, 0.2, 0.3) achieved with null controls, the dark blue curves represents the results without noise while the lighter the ones with the higher value of noise. d–f Comparison of the reconstructed posteriors for the estimate of ϕ1 with variational selected controls (red curves) and null controls (blu curves).

Full size image
Table 1 Set of phase configurations investigated with two-photon probes
Full size table
Table 2 Set of phase configurations investigated with single-photon probes
Full size table

The validity of the variational approach in identifying the optimal measurement strategy emerges also from what it is reported in the inset of Fig. 4a, where the distribution of results obtained by shifting the measurement to the values computed by the variational algorithm is compared to those achieved by randomly selecting the measurement settings. In the former case, the variability of the results is solely attributed to experimental fluctuations, resulting in a Gaussian distribution. Instead, when the measurement is randomly chosen, the distribution of achieved results reflects the influence of measurement selection on the estimation procedure, leading to a significantly wider spread.

When the interferometer is seeded by two indistinguishable photons, the FIM is computed at every step of the optimization algorithm by applying, as explained above, the generalized parameter-shift rule. We apply the same procedure also seeding the interferometer with single-photon states (Fig. 4b), demonstrating that in this case, the standard parameter-shift rule is instead sufficient to reconstruct the FIM and thus retrieving the optimal measurement settings allowing the saturation of the QCRB. It is important to note that the QCRB reported in the plots refers to the bound relative to the ideal device corresponding to a QCRB of 2.5/M for the two-photon inputs and a QCRB of 6/M for single-photon inputs. Therefore, the observed discrepancies are related to the fact that the actual phase sensor has a higher bound due to experimental imperfections, that in general can also depend on the specific vector of phases under investigation.

Finally, we have experimentally tested the resilience of the developed variational approach to different sources of noise. Specifically, we have examined the performances when introducing additional phase noise phn in the single-photon probe estimates and when reducing the indistinguishability among the two-photon probes. In Fig. 4c we report the experimental posterior probabilities, reconstructed with the Bayesian estimate14,39, obtained for different noise strengths on the estimate of one vector of phases without adjusting the measurement settings. The reconstructed posteriors are obtained by averaging the results obtained over 30 different repetitions of the experiment, performed by seeding the system with M = 500 single-photon probes. As expected, the performance of the estimation process deteriorates with increasing phase noise, resulting in a dual effect. On one hand, the height of the posterior distribution decreases, and on the other, its mean value results shifted with respect to the true value of the phase. Conversely, if we perform the estimate with the variational approach under noisy conditions, there is still a significant advantage, even with high levels of noise as shown in Fig. 4d–f (see also Supplementary Note 4).

Another investigated scenario consists in studying the effectiveness of the variational algorithm when reducing the degree of indistinguishability of the two-photon probes. In this situation, the estimation precision deteriorates losing the quantum-enhanced performances achieved using entangled probes. As a consequence, the ultimate precision bound increases. For the ideal device, the QCRB obtained when injecting into the system M indistinguishable photon pairs is 2.5/M, while it becomes 3/M for completely distinguishable photons. It follows that the estimation performances will get worse when increasing the level of distinguishability. In these conditions, it is interesting to study how the estimation performances decay and compare the results that can be achieved when the measurements are optimized through the variational approach in this noisy scenario. In Fig. 5 we show how the level of indistinguishability can be tuned through a delay line, monitoring the bunching and anti-bunching effects at the outputs of the chip (Fig. 5a), while in Fig. 5b, c we report the achieved performances in terms of quadratic loss and variances, respectively, for the estimate of a vector of phases. Notably, even though a slight reduction of the performances is observed, the enhancement achieved with the variational strategy, with respect to the non-shifted measurements scenario, becomes even more pronounced when the two photons become completely distinguishable.

Fig. 5: Experimental results as a function of degree of two-photon indistinguishability.
figure 5

a Normalized coincidences events among different output modes registered when changing the respective arrival time of the two photons. This is changed by moving a translation stage in one of the photon paths, allowing to adjust the degree of indistinguishability of the two photons. The magenta points refer to events with both photons in the first output while orange points to events with one photon on the first and one on the second output. Error bars are obtained considering the Poissonian statistics of the measurement counts. b, c Study of the estimation performances in terms of quadratic loss and variances, respectively, obtained when degrading the indistinguishability of the two photons. The blu points are the results obtained without shifting the measurement while the red points are the ones achieved with the variational strategy. The results are the avereges of the estimate with M = 200 two-photon probes of one vector of phases repeated 30 times and error bars refer to the relative standard deviations.

Full size image

Discussion

In this work, we have implemented a variational approach to optimize a multiparameter quantum phase sensor operating in a noisy environment. Rather than relying on classical computations to determine the optimal measurement settings, a procedure that can be particularly hard, especially in the multiparameter framework, our method exploits directly the quantum circuit to reconstruct a meaningful cost function successively fed into a classical optimization algorithm.

We demonstrated the validity of our method by experimentally reconstructing the FIM and optimizing the measurement settings for a multiphase sensor probed with single-photon and entangled two-photon probe states. This approach allows us to overcome the limitations of traditional methods and our experimental results showed significant improvements in estimation accuracy and noise robustness compared to cases where the measurement settings were not optimized or chosen randomly. The variational approach is resilient to noise and can effectively explore and optimize the high-dimensional multi-parameter spaces, making it a promising tool for practical applications in quantum sensing and quantum information processing with photonic circuits.

Here, we extended and validate experimentally the procedure presented in ref. 33 to the photonic case, developing a method that, depending on the selected probe state, and thus on the number of photons in the optical modes, retrieves the circuit gradient directly from the measurement outcomes. Such a method can benefit in general quantum photonic protocols requiring gradient evaluation.

In conclusion, the obtained results pave the way for the implementation of variational techniques in the challenging multiparameter framework and set the stage for enhancing both quantum sensing capabilities and for future advancements in quantum information processing with photonic circuits.

Methods

Standard and generalized parameter-shift rule

The parameter-shift rule, as demonstrated in35,36,45,46, provides a method to obtain the partial derivatives of quantum expectation values with respect to a circuit parameter x directly by using the quantum hardware as follows:

$${\partial }_{x}\langle A\rangle =r\left[\langle A\rangle \left(x+\frac{\pi }{4r}\right)-\langle A\rangle \left(x-\frac{\pi }{4r}\right)\right],$$
(7)

where 〈A〉 = 〈0∣U†(x)AU(x)∣0〉, with U(x) representing the evolution obtained applying the overall set of gates that make up the quantum circuit, and \(r=\frac{1}{2}\). The validity of such a rule has been first demonstrated for gates with generators with two unique eigenvalues such as single-qubit rotations, linear combinations of Pauli operators, and for Gaussian gates in the continuous variable regime36. This has also been extended to unitary evolution of the form U(ϕ)[ρ] = eiϕGρe−iϕG depending on a single parameter ϕ and on the generator G, whose spectrum has at most two distinct eigenvalues: spec(G) = {λ1, λ2}, obtaining:

$${\partial }_{\phi }U(\phi )[\rho ]=r\left[U\left(\phi +\frac{\pi }{4r}\right)[\rho ]-U\left(\phi -\frac{\pi }{4r}\right)[\rho ]\right],$$
(8)

with \(r=\frac{| {\lambda }_{1}-{\lambda }_{2}| }{2}\). Although the rule has initially been derived to retrieve the gradient of quantum unitary evolutions, it has been recently extended to evolutions affected by noise, proving its validity also after the application of dephasing and depolarizing channels33,45 and for multi-qubit quantum evolution using stochastic methods46. Then, this method has been generalized to generators with a larger spectrum. In this case, it is possible to extend the rule either by exploiting a polynomial expansion of the unitary transformation47, or using trigonometric functions48, or through spectral decomposition of the generator49. In particular, for a generator whose spectrum has three distinct but equidistant eigenvalues in ref. 50 has been demonstrated that the gradient evaluation requires four evaluations of Uρ(ϕ) at different points:

$$\begin{array}{ll}{\partial }_{\phi }U(\phi )[\rho ]&={r}_{1}\left[U(\phi +{x}_{1})[\rho ]-U(\phi -{x}_{1})[\rho ]\right]+\\ &-{r}_{2}\left[U(\phi +{x}_{2})[\rho ]-U(\phi -{x}_{2})[\rho ]\right].\end{array}$$
(9)

The generalization to generators with more eigenvalues can be retrieved instead following47,48,49 (see Supplementary Note 2 for the details).

Photon source

The single- and two-photon probe states employed are generated by a non-collinear spontaneous parametric down-conversion source of Type I. In particular, photon pairs at 808 nm are emitted by the source, which are then coupled into single-mode fibers. For the study with single-photon states one photon is directly detected by a single-photon avalanche photodiode, acting as a trigger, while the other is injected into the integrated circuit. For the two-photon probes scenario both the photons are injected into the chip after being made indistinguishable in polarization and time of arrival degrees of freedom through wave plates and a delay line. To properly address all the possible outcome configurations, in this scenario, we use 4 fiber beam splitters for each of the outcomes of the circuit in turn connected to 8 single-photon avalanche photodiode detectors.

Integrated photonic device

The integrated circuit consists of two sequentially arranged sections, each made up of four directional couplers set up in a dual-layer arrangement and a three-dimensional waveguide intersection. The different optical phases are obtained by applying voltages on microheaters that allow setting specific phase shifts in the desired optical modes. The interferometric area between the two sections consists of four straight waveguide segments, the optical phases of which \(\overrightarrow{\phi }+\overrightarrow{\theta }\) can be adjusted using eight thermal phase shifters. The total length of the device is 3.6 cm. All thermal shifters were created using femtosecond laser micromachining and include laser-etched isolation trenches around each microheater40. Lastly, two four-channel single-mode fiber arrays have been glued at the input and output facets of the interferometer, with average total insertion losses (from the connector of the input fiber to the connectors of the output fiber array) of 2.5 dB (insertion loss of the bare device before pigtailing of 1.5 dB).