Introduction

Calculating the ground-state energy of a molecular Hamiltonian is an important but hard task in computational chemistry1. For strongly correlated systems, exact classical approaches quickly become infeasible as system sizes exceed 100 spin-orbitals. Other, approximate, methods often lack accuracy1,2,3,4,5. This makes quantum computers an attractive alternative. A potential route to quantum-chemistry simulations relies on the quantum-phase-estimation algorithm (QPEA)1,6. However, the QPEA requires executing millions of gates on error-corrected hardware7. Realizing such hardware requires significant resource overheads and gate-error probabilities below a minimal threshold8. For example, the surface code9,10, requires thousands of physical qubits to implement a single logical qubit at a gate-error probability of 10−4 11. In view of these requirements, the QPEA is not yet feasible.

To reduce the qubit number and gate-error requirements, the variational quantum eigensolver (VQE) was proposed12. The VQE is a hybrid quantum-classical algorithm that uses a classical optimizer and a parameterized quantum circuit, the ‘ansatz’, to estimate ground-state energies. Combined with significant hardware developments13, VQEs have facilitated successful demonstrations of quantum computational chemistry for small systems12,14,15,16,17,18. These demonstrations have been aided by VQE algorithms’ abilities to correct for certain errors15,19,20. Despite these achievements, there are still significant hurdles to overcome for VQEs to become useful. First, the short, gate-efficient ansätze used in small-scale experimental demonstrations12,14,15,16,17,18 face optimization difficulties for larger systems. This is related to the emergence of barren plateaus (vanishing gradients), which are more likely when the ansatz is unrelated to the Hamiltonian21,22. Current research, for example on growing the ansatz circuit iteratively (the ADAPT-VQE algorithm23) is aimed at avoiding or mitigating the issue of barren plateaus21. Another significant hurdle comes from gate-error rates in hardware. Although current noisy intermediate-scale quantum devices24,25,26 have sufficiently many qubits to run VQEs for molecules with more than 100 spin-orbitals13, their gate-error rates are too high.

At present, efforts to ameliorate the gate-error issue aim to either reduce ansatz circuit depths23,27,28,29,30 or implement elaborate error-mitigation schemes31,32,33. However, VQEs are often benchmarked in the absence of gate errors, with circuit depths and CNOT counts used as proxies of their noise resilience30. It has been argued that the maximum viable circuit depth for a VQE ansatz circuit is given by the reciprocal of gate-error probability 1/p1. More rigorously, given a gate-error probability p, the maximum VQE circuit depth which cannot be simulated classically scales as \({{{\mathcal{O}}}}({p}^{-1})\)34,35. A research question, which remains under-explored, is to quantify the gate-error probabilities that VQEs can tolerate. Specifically, considering the analogy of a surface code, which has a well-defined fault-tolerance threshold11, we aim to find the maximally allowed gate-error probability, below which a certain VQE estimates a certain molecule’s energies within chemical accuracy. Quantifying the maximally allowed gate-error probability allows the noise resilience of leading VQEs to be ranked, and provides useful goals for the hardware community.

In this article, we numerically quantify under how high gate-error probabilities VQEs can operate successfully. More specifically, using density-matrix simulations, we simulate the ground-state search of leading, gate-based VQEs for a range of molecules. In the presence of depolarizing noise, we show that: (i) Even the best performing VQEs require gate error probabilities pc on the order of 10−6 to 10−4 (without error mitigation) in order to predict molecular ground-state energies within chemical accuracy of 1.6 × 10−3 Hartree. This is significantly below the fault-tolerance threshold of the surface code11. For small systems, error mitigation can be employed such that the required pc values can be improved to 10−4 to 10−2. (ii) ADAPT-VQEs tend to tolerate higher gate-error probabilities than VQEs that use fixed ansätze, such as UCCSD and k-UpCCGSD. (iii) ADAPT-VQEs tolerate higher gate-error probabilities when circuits are synthesized from gate-efficient27,28,29,36, rather than physically-motivated23, elements. We support these claims by estimating, in the presence of depolarizing noise, the scaling relation between the maximally tolerable gate-error probability pc and the number NII of noisy (two-qubit) gates. Our results indicate that \({p}_{c}\mathop{\propto }\limits_{ \sim }{N}_{{{{\rm{II}}}}}^{-1}\) for any gate-based VQE. (iv) We find that the maximally allowed gate-error probability, pc, decreases with system size, with and without error mitigation. This shows that larger molecules would likely require even lower gate-errors. We conclude that substantial quantum advantage in VQE-based quantum chemistry is unlikely, unless gate-errors are significantly reduced, or error-corrected hardware is realized, or error-mitigation protocols are improved and made scalable.

Results

ADAPT-VQEs

In this work, we investigate several classes of VQE algorithms. Our study prioritizes VQEs with short ansatz circuits, as these are expected to be more noise resilient29,30. Specifically, we consider ADAPT-VQEs, which have comparatively short ansatz circuits23,29 and the ability to mitigate rough parameter landscapes21. We further consider UCCSD37 and k-UpCCGSD38 as prototypes of fixed ansatz VQEs – the latter for its comparatively shallow ansatz circuits30. Before we outline the results of our noise-resilience investigation, we describe the workings of the (ADAPT-)VQE.

The main idea of VQEs is to use shallow ansatz circuits, defined by a set of parameters θ, to generate entangled trial states ρ(θ). A classical optimizer is then used to vary θ and minimize the energy-expectation value of H. Provided that the ansatz is sufficiently expressive, the Rayleigh-Ritz variational principle,

$$E({{{\boldsymbol{\theta }}}})={{{\rm{Tr}}}}\left[H\rho ({{{\boldsymbol{\theta }}}})\right]\ge {{{{\mathcal{E}}}}}_{0},$$
(1)

allows \(\mathop{\min }\nolimits_{{{{\boldsymbol{\theta }}}}}(E({{{\boldsymbol{\theta }}}}))\) to approach the molecular ground-state energy \({{{{\mathcal{E}}}}}_{0}\)1. ADAPT-VQEs use a classical optimizer in two ways23: to conduct the Rayleigh-Ritz minimization with respect to a parameterized quantum state; and to iteratively construct the ansatz that generates the parameterized state itself. A quantum computer is used to calculate the energy-expectation value of the parameterized state.

Consider the state generated by the ansatz Un:

$${\rho }_{n}({\theta }_{1},\ldots ,{\theta }_{n})={U}_{n}({\theta }_{1},\ldots ,{\theta }_{n}){\rho }_{0}\,{U}_{n}^{{\dagger} }({\theta }_{1},\ldots ,{\theta }_{n}).$$
(2)

\({\rho }_{n}({\theta }_{1},\ldots ,{\theta }_{n})\) is parameterized by n parameters. In ADAPT-VQE, the classical optimizer and the quantum computer work to find a minimum-energy expectation value:

$${E}_{n}\equiv \mathop{\min }\limits_{{\theta }_{1},\ldots ,{\theta }_{n}}{{{\rm{Tr}}}}\left[H{\rho }_{n}({\theta }_{1},\ldots ,{\theta }_{n})\right].$$
(3)

An ADAPT-VQE iteratively adds parameterized elements to its ansatz to construct ρn(θ1, …, θn) such that E1 > … > En and En approaches \({{{{\mathcal{E}}}}}_{0}\).

The iterative ansatz construction proceeds as follows. First, the ADAPT-VQE algorithm initializes a state ρ0, usually the Hartree-Fock state2. Then, the algorithm generates a sequence of trial states by successively adding elements of the form

$$\begin{array}{r}{A}_{\alpha }(\theta )={e}^{\theta {T}_{\alpha }},\end{array}$$
(4)

picked from a finite pool \({{{\mathcal{P}}}}\) of operators (see below). Here, Tα, for \(\alpha \in [1,\ldots ,| {{{\mathcal{P}}}}| ]\), are anti-Hermitian operators. Thus, the unitary ansatz grows as

$${U}_{0}={\mathbb{I}},$$
(5)
$${U}_{n}({\theta }_{1},\ldots ,{\theta }_{n})={A}_{n}({\theta }_{n}){U}_{n-1}({\theta }_{1},\ldots ,{\theta }_{n-1}).$$
(6)

The ansatz element \({A}_{n}({\theta }_{n})\in {{{\mathcal{P}}}}\) is typically picked to yield the steepest energy gradient. For each value of α, a quantum computer evaluates the energy expectation value after adding Aα(θn) in the nth step:

$${E}_{n,\alpha }({\theta }_{n})\equiv {{{\rm{Tr}}}}\left[H{A}_{\alpha }({\theta }_{n}){\rho }_{n-1}{A}_{\alpha }^{{\dagger} }({\theta }_{n})\right].$$
(7)

The ADAPT-VQE algorithm then picks the element \({A}_{n}\equiv {A}_{\alpha = {\alpha }_{n}}\) with

$$\begin{array}{l}{\alpha }_{n}\,=\,\mathop{{{{\rm{argmax}}}}}\limits_{\alpha :{A}_{\alpha }\in {{{\mathcal{P}}}}}\,\left\vert {\left.\frac{\partial {E}_{n,\alpha }({\theta }_{n})}{\partial {\theta }_{n}}\right\vert }_{{\theta }_{n} = 0}\right\vert \\ \qquad=\,\mathop{{{{\rm{argmax}}}}}\limits_{\alpha :{A}_{\alpha }\in {{{\mathcal{P}}}}}\,\left\vert {{{\rm{Tr}}}}\left\{\left[H,{T}_{\alpha }\right]{\rho }_{n-1}\right\}\right\vert .\end{array}$$
(8)

Alternatively, one may define a sub-pool \({{{\mathcal{S}}}}\subset {{{\mathcal{P}}}}\) of operators with the largest gradients and let the algorithm pick the element with the largest energy difference:

$${\alpha }_{n}=\mathop{{{{\rm{argmin}}}}}\limits_{\alpha :{A}_{\alpha }\in {{{\mathcal{S}}}}}\,\left[\mathop{\min}\limits_{{\theta }_{n}}{E}_{n,\alpha }({\theta }_{n})\right].$$
(9)

After choosing the nth ansatz element An(θn), a classical computer optimizes and updates the parameters θ1, …, θn to minimize the energy expectation value En in Eq. (3). Provided that En − En−1 > ϵ, for some energy precision ϵ, the iterative algorithm continues. When En − En−1 ≤ ϵ the algorithm halts at some final length n = N, and outputs EN ≡ En as the estimate of \({{{{\mathcal{E}}}}}_{0}\).

In this work, we focus on the three main types of ADAPT-VQEs: fermionic-ADAPT-VQE, QEB-ADAPT-VQE and qubit-ADAPT-VQE. (Efficient gate-representations for their relevant ansatz elements can be found in refs. 28,29). These algorithms differ in their ansatz-element pools \({{{\mathcal{P}}}}\).

First, we consider the fermionic-ADAPT-VQE23. As the name suggests, this algorithm uses a pool of operators that closely simulate the physics of fermionic excitations. The pool is formed from

$${T}_{ik}={a}_{i}^{{\dagger} }{a}_{k}-{a}_{k}^{{\dagger} }{a}_{i},\quad {{{\rm{and}}}}$$
(10)
$${T}_{ijkl}={a}_{i}^{{\dagger} }{a}_{j}^{{\dagger} }{a}_{k}{a}_{l}-{a}_{k}^{{\dagger} }{a}_{l}^{{\dagger} }{a}_{i}{a}_{j}.$$
(11)

Here, \({a}_{i}^{{\dagger} }\) and ai are fermionic creation and annihilation operators acting on the ith orbital. Throughout this work, we represent these operators using the Jordan-Wigner transformation39, where

$${a}_{i}^{{\dagger} }\mapsto \frac{1}{2}\left({X}_{i}-{{{\rm{i}}}}{Y}_{i}\right)\mathop{\prod }\limits_{r=0}^{i-1}{Z}_{r},\quad {{{\rm{and}}}}$$
(12)
$${a}_{i}\mapsto \frac{1}{2}\left({X}_{i}+{{{\rm{i}}}}{Y}_{i}\right)\mathop{\prod }\limits_{r=0}^{i-1}{Z}_{r}.$$
(13)

Xi, Yi, Zi are the Pauli operators acting on the ith qubit. The fermionic-ADAPT-VQE leads to shallower and more gate efficient circuits than UCCSD23. Further, choosing fermionic excitations along the gradient of minimum energy produces H-tailored circuits, which can potentially avoid barren plateaus21.

Second, we consider the QEB-ADAPT-VQE29,36. This algorithm uses a pool of operators that nearly (up to a ± sign) simulate the physics of fermionic excitations. The pool is formed from

$${T}_{ik}={Q}_{i}^{{\dagger} }{Q}_{k}-{Q}_{k}^{{\dagger} }{Q}_{i},\quad {{{\rm{and}}}}$$
(14)
$${T}_{ijkl}={Q}_{i}^{{\dagger} }{Q}_{j}^{{\dagger} }{Q}_{k}{Q}_{l}-{Q}_{k}^{{\dagger} }{Q}_{l}^{{\dagger} }{Q}_{i}{Q}_{j},$$
(15)

where

$$\begin{array}{r}{Q}_{i}^{{\dagger} }:=\frac{1}{2}\left({X}_{i}-{{{\rm{i}}}}{Y}_{i}\right)\,\,{{\mbox{and}}}\,\,{Q}_{i}:=\frac{1}{2}\left({X}_{i}+{{{\rm{i}}}}{Y}_{i}\right).\end{array}$$
(16)

\({Q}_{i}^{{\dagger} }\) and Qi are known as qubit creation and annihilation operators, respectively. Due to the CNOT efficiency of its pool, the QEB-ADAPT-VQE can find ground-state and excited-state energies with fewer CNOT gates than the fermionic-ADAPT-VQE28,29,36.

Finally, we consider the qubit-ADAPT-VQE27. This algorithm uses a pool of gate-efficient elements without physical motivation. The pool is formed from segments of Pauli-operator strings:

$${T}_{ij}=i{\sigma }_{i}{\sigma }_{j},\quad {{{\rm{and}}}}$$
(17)
$${T}_{ijkl}=i{\sigma }_{i}{\sigma }_{j}{\sigma }_{k}{\sigma }_{l},$$
(18)

where σi denotes Pauli operators Xi, Yi, Zi acting on the ith qubit. In previous works, this pool has been found to generate the most shallow and CNOT efficient circuits for ADAPT-VQEs27. In our simulations, we use a pool formed from XY-Pauli strings of length two and four with an odd number of Y’s. It is possible to use reduced pools27, but at the expense of reduced circuit efficiency of the final ansatz29.

Typically, the fermionic-ADAPT-VQE and the qubit-ADAPT-VQE use the gradient-based decision rule expressed in Eq. 8. On the other hand, the original QEB-ADAPT-VQE uses the energy-based decision rule, shown in Eq. 9. These algorithms are summarized in a flow-chart summary in Fig. 1, and in the pseudocode of Supplementary Note 1.

Fig. 1: Flowchart describing the ADAPT-VQE algorithm.
figure 1

At each iteration, an ansatz element is chosen according to one of the two decision rules defined in green below the chart. This element is appended to the ansatz, the parameters are optimized, and the energy expectation value is estimated. The algorithm halts when the change in energy between iterations is below a given threshold.

Full size image

To demonstrate the benefits of iteratively-grown ansätze, we compare them to a typical fixed-ansatz-VQE method: the UCCSD-VQE17,37. In Supplementary Note 4, we extend this comparison to the k-UpCCGSD algorithm38. Owing to its linear scaling of circuit depth with qubit number, this algorithm was recently put forward as the leading fixed-ansatz VQE30. We simulate the workings of the fixed-ansatz methods using the aforementioned fermionic and QEB elements.

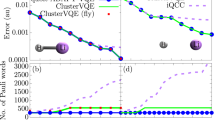
Given the breadth of work on VQEs30, it is not possible to perform an exhaustive analysis of all existing algorithms. Nevertheless, the analytical results in Sec. II E, and the low circuit depths provided by ADAPT-VQE30, suggest that our results provide a lower bound on the requirements for gate-based VQE algorithms to operate successfully. However, there exist algorithms that differ greatly from typical VQEs, and could deserve future attention. We discuss some of these, and the reasons for our exclusion of them, below. We will not consider iterative qubit coupled cluster (iQCC)40 and ClusterVQE41 algorithms. We do not anticipate these algorithms to be feasible options to study strongly correlated systems, whose simulation using quantum algorithms provides the most benefit over classical algorithms. We also omit the DISCO-VQE42. Due to its large jumps in Hilbert space during the discrete optimizations of the ansatz, we expect DISCO-VQE to lack tolerance to barren plateaus. These problems may be overcome in future improvements of these VQE algorithms. We leave the design of improved algorithms, and the noise-evaluation of them, to future articles. Finally, we omit the ctrl-VQE algorithm43. Although highly interesting, this Hamiltonian algorithm operates with device-tailored pulses, rather than quantum gates, and thus lies outside the scope of this work.

Density-matrix simulations

To investigate the effect of noise on gate-based VQE, we constructed a VQE-tailored density-matrix simulator, expanding the state-vector circuit simulator of ref. 29. We represent molecular orbitals in the Slater type orbital-3 Gaussians (STO-3G) spin-orbital basis set44, with the option of frozen orbitals. The openfermion-Psi4 package45,46 is used to generate the second-quantized Hamiltonian and to perform the Jordan-Wigner transformation39. Ansatz parameters are optimized using Nelder-Mead47 or gradient-descent-based (BFGS)48 methods in SciPy49.

We note that, due to the wide array of quantum-computing platforms and their contrasting qubit-control implementations, no noise model can be simultaneously realistic and platform-agnostic. In this work, we model noise by applying single-qubit depolarizing noise to the target qubit i after the application of each two-qubit CNOT gate. Our noise channel can be represented by

$${{{\mathcal{D}}}}(i,p)\left[\rho \right]:=\left(1-p\right)\rho +\frac{p}{3}\mathop{\sum}\limits_{{\sigma }_{i}}{\sigma }_{i}\rho {\sigma }_{i},$$
(19)

where p ∈ [0, 1] is the gate-error probability.

In real devices, noise from two-qubit gates completely dominates the noise from single-qubit gates25,50,51,52. Thus, we ignore the latter. Additionally, we exclude state preparation and measurement errors, which are often lower in magnitude than the accumulated two-qubit gate errors50, and can be mitigated efficiently in experiments53,54,55,56,57,58. (We note that ADAPT-VQE algorithms have high measurement requirements, such that measurement errors may prevent the algorithm from reaching the global minimum energy. This topic requires further investigation). Depolarizing noise is commonly used to represent local and Markovian gate errors when assessing both NISQ59,60,61 and quantum-error-correction11,62,63,64 algorithms. More realistic models can include thermal-relaxation noise (dephasing and amplitude damping)65 and device-specific gate errors derived from gate-set-tomography data66. When T1 ≈ T2 thermal relaxation noise can be approximated using our depolarizing noise model62. This is a reasonable model for superconducting hardware50. On the other hand, when T2 ≪ T1 dephasing noise dominates and our depolarizing noise model is less accurate. This is common in trapped-ion devices51,52 and spin qubits67 and has recently been investigated in ref. 68. Moreover, existing VQE algorithms require unrealistically low error rates to give chemically accurate energies. Any attempt to scale down the error rates in realistic noise models to these low levels must be theoretically-justified. This is challenging for a complex, multi-parameter model. Hence, we exclude noise models based on gate-set tomography. Finally, we do not consider coherent errors, since their effect can be suppressed by randomized compiling69 and dynamical decoupling70,71. Randomized compiling72 can also be used to convert coherent errors to stochastic errors. Additionally, VQE algorithms are somewhat resilient to coherent errors12,73. Thus, in this work we focus on incoherent errors. Note that, if VQE algorithms were studied with a coherent noise model, their perceived performance may be greater.

When simulating the smallest molecules (H2 and H4) we apply our noise channel [Eq. (19)] after each application of a CNOT gate. This gate-by-gate method is computationally expensive. To facilitate feasible simulations of molecules larger than H4, we approximate each noisy ansatz element by a corresponding noiseless ansatz evolution and a noise-inducing evolution. The noise-inducing evolution corresponds to depolarizing noise applied to each qubit in accordance with the number of times that qubit was a CNOT target in the ansatz element. We observe that this lower-bounds the effect of noise. For example, for H4, applying noise after each CNOT with gate-error probability \(p={p}^{{\prime} }\), gives approximately the same energy accuracy as applying total noise after each element with \(p\approx 1.3{p}^{{\prime} }\). Consequently, our simulations of larger molecules should not be compared directly with those for H2 and H4. A detailed illustration of our noise approximation is given in Supplementary Note 3.

Energy accuracy is the key metric of VQE performance. It is defined as

$$\begin{array}{r}\Delta E(p,n):={E}_{n}(p)-{E}_{{{{\rm{FCI}}}}}.\end{array}$$
(20)

Here, En(p) is the VQE-calculated energy with gate-error probability p in the nth iteration and EFCI is the energy given by the full-configuration-interaction5 calculation of the true ground-state energy \({{{{\mathcal{E}}}}}_{0}\). A key objective of our study is to find the maximally allowed gate-error probability pc for which ΔE(p, n) < 1.6 milli-Hartree.

Classical optimizers are used to tune θ1, …, θn. The parameters are optimized until the gradient norm, \(\left\vert {\nabla }_{\boldsymbol{\theta }}E\right\vert \le {\epsilon }_{O}\), for some precision ϵO. In our simulations of H2 we calculate converged values of En(p) using our density-matrix simulator. To keep larger-molecule simulations tractable, we estimate ΔE as follows. We first grow the ansatz circuit \({{{{\mathcal{C}}}}}_{n}\) in noiseless, unitary simulations until the nth iteration, for which the energy accuracy ΔE(0, n) first drops below a cut-off energy precision ϵt: ΔE(0, n) < ϵt. Then, we approximate ΔE(p, n) by simulating the implementation of \({{{{\mathcal{C}}}}}_{n}\) with noise on our density-matrix simulator. Thus, ΔE(p, n) may depend on the iteration n. As demonstrated in Supplementary Note 2, ansatz growth and optimization in the presence of noise have little effect on the noise probability required for chemical accuracy.

Comparison between ADAPT-VQEs with noise

In this section, we benchmark the noise resilience of ADAPT-VQEs using our density-matrix simulator. We study H2, H4, LiH, HF and BeH2. Our simulations were conducted using a parameter optimization cut-off of \(\left\vert {\nabla }_{\boldsymbol{\theta }}E\right\vert \le {\epsilon }_{O}=1{0}^{-6}\) Hartree and ansatz growth cut-off of En − En−1 ≤ ϵ = 10−12 Hartree. In our simulations of the larger molecules, we used an ansatz-truncation cut-off of ΔE(0, n) < ϵt = 10−4 Hartree. Below, we use ΔE(p) = ΔE(p, nfinal) to refer to the energy accuracy at the final ansatz length n = nfinal. Because of the significant skepticism towards error-mitigation strategies35,74,75, we omit such strategies from the analyses presented in this section and investigate error mitigation separately in Sec. II F.

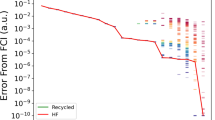
The inset of Fig. 2a shows how ΔE(p) varies with p for H2. The values of p ∈ [0, 0.02] include the well-known surface-code fault-tolerance threshold8,11 as well as the gate-error probability of currently available quantum hardware25,50,51,52. All tested VQE algorithms require extremely small gate-error probabilities if they are to improve on the Hartree-Fock energy approximation, even for the simple H2 molecule. The region of chemical accuracy is too small to show in the inset. In real implementations of ADAPT-VQE algorithms, energies exceeding the Hartree-Fock approximation would not be achieved, since, in this case, adding elements to the ansatz does not improve the initial energy accuracy. Here, we add noise to a noiselessly-grown ansatz such that these energies are shown. These observations motivated us to reduce significantly the range of p used in the rest of this study.

Fig. 2: Energy accuracy as a function of gate-error probability.
figure 2

Plotted for H2 (a), H4 (at 1 Å (b) and 3 Å (c) interatomic separation), LiH (d), HF (e) and BeH2 (f). Ansätze using fermionic, qubit, and Pauli string elements are plotted in red, blue and green, respectively. All curves labeled as “fixed” VQE ansätze use the UCCSD ansatz17,37. Energy accuracies lower than chemical accuracy are highlighted by the yellow region. The purple line in the H2 inset is the energy calculated using the Hartree-Fock2 state. Extrapolated noise-susceptibility calculations are shown in black for the fermionic-ADAPT-VQE (d), the QEB-ADAPT-VQE (e) and the qubit-ADAPT-VQE (f).

Full size image

The rest of Fig. 2 shows our calculations of ΔE(p) as a function of p for all considered molecules. The region of chemical accuracy is highlighted by yellow shading. We emphasize six general trends supported by our data. First, the maximally allowed gate-error probabilities pc for computing ground-state energies within chemical accuracy are extremely small. For all molecules investigated in this study, the value of pc is on the order of 10−6 to 10−4 (see Table 1 for details). These values are significantly below the fault-tolerance thresholds of leading error-correction protocols. Second, our simulations of H2 and H4 (1 Å) suggest that ADAPT-VQEs outperform fixed ansatz methods. For a given pool of ansatz elements, the corresponding ADAPT-VQE algorithm leads to better energy accuracies than the corresponding fixed ansatz VQE algorithm. Third, the efficient representation of fermionic excitations28 improves the performance of the fermionic-ADAPT-VQE significantly. This representation reduces CNOT depth, but its scaling of CNOT depth with molecule size is still worse than the scaling of QEB and Pauli string elements. The second and third observations support the claim29 that the CNOT count is a useful estimator of VQE’s noise vulnerability. Fourth, the more gate-efficient (Pauli string and QEB) pools outperform the most physically-motivated (fermionic) pool. The fermionic-ADAPT-VQE is consistently outperformed by either the qubit-ADAPT-VQE or the QEB-ADAPT-VQE. Fifth, sometimes the QEB-ADAPT-VQE outperforms the qubit-ADAPT-VQE and vice versa. For H2, H4 (1 Å) and BeH2, the qubit-ADAPT-VQE outperforms the QEB-ADAPT-VQE. On the other hand, for HF, the QEB-ADAPT-VQE (energy-based decision rule) outperforms the qubit-ADAPT-VQE. For LiH, the QEB-ADAPT-VQE and the qubit-ADAPT-VQE perform similarly. Notably, for H4 (3 Å), the qubit-ADAPT-VQE fails to add more than two elements to the ansatz. Hence, it never surpasses chemical accuracy. This gives some indication that the qubit-ADAPT-VQE is worse than the QEB-APAPT-VQE at simulating strongly correlated molecules. Sixth, different decision rules for QEB-ADAPT-VQEs yield different performances. For HF, LiH and BeH2, the energy-reduction decision rule gives a better energy accuracy than the maximum-gradient rule. Conversely, for H4 (1 Å and 3 Å) the gradient-based decision rule performs better. A study of the optimal decision rules for various molecular-energy landscapes is left for the future.

Table 1 Maximum gate-error probabilities pc [ × 10−5] for which chemical accuracy is achieved.
Full size table

We close this subsection with a comment on benchmarks of fixed-ansatz VQEs. Both UCCSD and k-UpCCGSD ansätze have been investigated with numerical simulations. However, their energy accuracies significantly worse than those obtained using ADAPT-VQEs. In particular, the energy accuracies for the k-UpCCGSD algorithm do not fit the scale of Fig. 2. Hence, these results are presented separately, in Supplementary Note 4.

Optimal truncation of iteratively-grown ansätze with noise

In the above analyses of ADAPT-VQEs for larger molecules, we truncated noiselessly-grown ansätze in the nth iteration when an energy precision of ϵt was reached. Thus, we established a performance hierarchy between different VQEs. However, deeper circuits are generally more vulnerable to noise, and fixing n in noiseless simulations could generate artificially deep circuits. Therefore, to showcase the full benefit of ADAPT-VQEs in the presence of noise, one must vary the truncation length. This would happen automatically for an ansatz grown with noise, as any truncation criterion would be met with shorter ansätze. Here, we simulate this to conduct an alternative, more exact and more computationally expensive, comparison between ADAPT-VQEs. We optimize energy accuracy with respect to ansatz length:

$$\begin{array}{r}\Delta E(p,{n}_{{{{\rm{opt}}}}})\equiv \mathop{\min }\limits_{n}\left\{\Delta E(p,n)\right\}.\end{array}$$
(21)

Below, we present numerical results for H4 (1 Å), H4 (3 Å) and LiH in the left, middle and right columns of Fig. 3, respectively. The color plots show ADAPT-VQE simulations of ΔE(p, n) as a function of n and p. The top row of Fig. 3 shows the optimized ΔE(p, nopt) as a function of p. Additional color plots for the VQE methods not shown in Fig. 3 are provided in Supplementary Note 5.

Fig. 3: Color plots representing the energy accuracy (from FCI) at different gate-error probabilities and ansatz lengths.
figure 3

Plotted for three different molecules: H4 (at 1 Å (a) and 3 Å (b) interatomic separation) and LiH (c). Three iterative-growth methods are included: the fermionic-ADAPT-VQE with efficient elements, the QEB-ADAPT-VQE with the energy decision rule and the qubit-ADAPT-VQE (the plots for the remaining two methods are given in Supplementary Note 2). The yellow lines on the color plot highlight the ansatz lengths that minimize the energy accuracies for each gate-error probability. The top-column figures are extracted from the color plots by plotting the energy accuracy along these curves.

Full size image

The data in Fig. 3 warrant four comments. First, in the absence of noise (p = 0), the energy accuracy decreases monotonically as the ansatz length (n) increases, eventually surpassing chemical accuracy. This is expected from the nature of the ADAPT-VQE methods. The exception is the qubit-ADAPT-VQE simulation of H4 (3 Å), which simply fails after n = 2 and does not achieve chemical accuracy. Second, at small but finite values of p, ΔE(p, n) initially decreases with larger n. However, after an optimal length nopt(p), the improvement from appending additional ansatz elements is outweighed by the detrimental increase of noise. At this point, ΔE(p, n) starts to increase with n. Thus, the ideal ansatz truncation happens at n = nopt(p). The nopt(p) values are shown as yellow lines on the color plots of Fig. 3. These curves show nopt(p) decreasing monotonically as p increases. Third, plots of ΔE(p, nopt) as a function of p (top Fig. 3), show the same relative performance between the fermionic-ADAPT-VQE, the QEB-ADAPT-VQE and the qubit-ADAPT-VQE as in Fig. 2. Fourth, the values for pc increase when the ansätze are truncated at an optimal value of n, as compared to the arbitrary truncation used when producing Fig. 2. The values of pc are presented in Table 1 and Fig. 6. After this optimal-truncation analysis, our overall conclusion remains unchanged: Even for the best-performing ADAPT-VQEs, the maximally allowed gate-error probability is on the order 10−6 to 10−4 Hartree.

Analytical noise-susceptibility analysis

To analytically support our numerical results, we study the linear response of energy accuracy ΔE(p) to noisy perturbations of the unitary ansatz circuits. Then, we use our results to show that pc is roughly inversely proportional to the number NII of noisy (two-qubit) gates.

Noise susceptibility

From Fig. 2 we see that \(\Delta E(p)\approx {\chi }^{{\prime} }p\), for some constant \({\chi }^{{\prime} }\). Inspired by this observation, we define the noise-susceptibility parameter:

$$\begin{array}{r}\chi ={\left.\frac{\partial \Delta E(p)}{\partial p}\right\vert }_{p = 0}.\end{array}$$
(22)

Now, we show that χ ∝ NII (details are given in Supplementary Note 6). If p = 0, an ansatz circuit \({{{\mathcal{C}}}}\) can be expressed as a product of R unitary gates: U = GR ⋯ G1. We use \({{{{\mathcal{R}}}}}_{{{{\rm{CX}}}}}\) to denote the set of indices for which Gr is a noisy (CNOT) gate, and we use ir to denote the qubit which noise acts on. Further, we define a perturbed version of the target unitary U as

$$\begin{array}{rc}{U}_{{{{\rm{p}}}}}(\sigma ,r,{i}_{r})&={G}_{R}\cdots {G}_{r+1}{\sigma }_{{i}_{r}}{G}_{r}\cdots {G}_{1},\end{array}$$
(23)

where the Pauli gate σ acts on qubit ir after the rth gate. The corresponding energy expectation values are

$${E}_{U}={{{\rm{Tr}}}}\left[HU{\rho }_{0}{U}^{{\dagger} }\right],$$
(24a)
$${E}_{{U}_{{{{\rm{p}}}}}}(\sigma ,r,{i}_{r})={{{\rm{Tr}}}}\left[H{U}_{{{{\rm{p}}}}}(\sigma ,r,{i}_{r}){\rho }_{0}{U}_{{{{\rm{p}}}}}^{{\dagger} }(\sigma ,r,{i}_{r})\right].$$
(24b)

Usually, EU is close to \({{{{\mathcal{E}}}}}_{0}\). Thus, we interpret \({E}_{{U}_{{{{\rm{p}}}}}}(\sigma ,r,{i}_{r})\) as a noise-induced excitation. We call \({E}_{{U}_{{{{\rm{p}}}}}}(\sigma ,r,{i}_{r})-{E}_{U}\) the noise-induced fluctuation. The average noise-induced fluctuation of the ansatz is

$$\begin{array}{r}\delta E\equiv \frac{1}{{N}_{{{{\rm{II}}}}}}\mathop{\sum}\limits_{r\in {{{{\mathcal{R}}}}}_{{{{\rm{CX}}}}}}\frac{1}{3}\mathop{\sum}\limits_{\sigma \in \{X,Y,Z\}}\left[{E}_{{U}_{{{{\rm{p}}}}}}(\sigma ,r,{i}_{r})-{E}_{U}\right],\end{array}$$
(25)

In Supplementary Note 6, we show that

$$\begin{array}{r}\chi =\delta E\times {N}_{{{{\rm{II}}}}}.\end{array}$$
(26)

Below, we analyze this expression for the noise-susceptibility parameter.

Simplified computations

The energy expectation values underlying χ can be simulated with unitary operations on a state vector. Such simulations are significantly simpler to perform than density-matrix simulations. Thus, we can more easily estimate the energy accuracy for small values of p:

$$\begin{array}{r}\Delta E(p)\approx \chi p.\end{array}$$
(27)

To test our method we compare Eq. (27) (black dotted lines) with some curves in Fig. 2. Eq. (27) estimates the simulated data remarkably well. Next, we use our method to estimate pc for molecules too large to study with our density-matrix simulator. The estimates of pc for H20 and \({{{{\rm{NH}}}}}_{2}^{-}\) are listed in the final two columns of Table 1. We stress that Eq. (27) is an excellent predictor of ΔE(p) for the gate-error probabilities p ∈ [0, pc] which allow for chemically-accurate simulations.

Scaling

The energy fluctuations are bounded by the spectral range of H: \(\delta E\le {{{{\mathcal{E}}}}}_{\max }-{{{{\mathcal{E}}}}}_{0}\). Thus, Eq. (26) suggests that noise susceptibility grows linearly with NII, as δE is constant. Figure 4 supports this claim. The curves indicate that \(\chi \mathop{\propto }\limits_{ \sim }{N}_{{{{\rm{II}}}}}\) and \(\delta E\approx {{{\mathcal{O}}}}(1)\), for a variety of molecules, ADAPT-VQE algorithms and circuit depths. Combining these observations with Eq. (27), we estimate that

$$\begin{array}{r}{p}_{{{{\rm{c}}}}}\approx \frac{\Delta {E}_{C}}{\delta E}\times \frac{1}{{N}_{{{{\rm{II}}}}}}\mathop{\propto }\limits_{ \sim }\frac{1}{{N}_{{{{\rm{II}}}}}}.\end{array}$$
(28)

where ΔEC = 1.6 × 10−3 Hartree (chemical accuracy). This result is supported by recent results in condensed matter systems76. The inverse proportionality between pc and NII suggests that gate-error probabilities will have to reach extremely small values for useful chemistry calculations with VQE algorithms to be viable. Alternatively, we require improved VQE algorithms with shallower circuits and fewer noisy (two-qubit) gates.

Fig. 4: Numerical noise susceptibility scaling.
figure 4

Noise susceptibility (top) and average energy fluctuation (bottom) as functions of the number NII of CNOT gates for all molecules and algorithms reported in Sec. II C, at all circuit depths.

Full size image

Quantum error mitigation

In the absence of error-corrected hardware, several strategies to mitigate the effect of noise have been suggested31,32,33,77. Quantum error mitigation is a family of strategies which generally rely on knowledge of a circuit, noise model, or both to generate a set of modified circuits. Sampling from these circuits can generate a better estimate of the noiseless circuit’s output77. While these strategies have been demonstrated in simple VQE implementations14,78,79, they suffer, in general, from exponential scaling of sample requirements with qubit number35,74,75, potentially preventing their viability in useful NISQ VQE implementations. Indeed, leading reviews on quantum computational chemistry1, state that ‘it seems unlikely that error-mitigation methods alone would enable more than a small multiplicative increase in the circuit depth.’ This unfavorable scaling has also been observed experimentally, where it has prevented the use of all but the most simple mitigation strategies26.

The main goal of this work is to assess the required error rates for useful VQE implementations of molecules with more than 100 spin-orbitals. Due to the uncertainty around their scalability, as well as the unclear performance in the presence of time-dependent noise (particularly two-level-system defects80 which drift in frequency), a study of this type should not include quantum error mitigation in its current form. Despite this, we believe it is relevant to extend our study to ascertain the maximally allowed gate-error probability pc to calculate molecular energies within chemical accuracy for an error-mitigation protocol with polynomial sampling overhead. To partially address this question, we repeat our numerical simulations using linear zero-noise extrapolation31,32 with a noise multiplication factor of 3. Despite being biased and heuristic81, we choose linear zero-noise extrapolation for its modest sampling overhead and numerical stability, which proved useful in recent large-scale demonstrations of error mitigation26.

The results for H2, H4 and LiH are depicted in Fig. 5. Compared to their counterparts in Fig. 3(a), we note the following: (i) The maximally allowed error probability increases by one or two orders of magnitude. This demonstrates the utility of error mitigation to make VQE more viable, especially for smaller molecules. (ii) The resulting energy error displays a roughly parabolic behavior. This is expected from the series expansion of the depolarizing noise and indicates that further improvement (at an increased sampling overhead) may be possible by using higher-order extrapolations. (iii) We note that while all VQE algorithms display an increased noise resilience from error mitigation, their relative pc-ranking does not change. This suggests that a VQE algorithm with higher noise resilience in the absence of error mitigation would remain more noise resilient when error mitigation is applied. Finally, we put the improved gate-error probabilities pc into context by plotting them as crosses in Fig. 6. Given the sharp decrease of pc with the problem size N, in the presence and absence of error mitigation, it is unlikely that error mitigation will improve pc sufficiently for useful system sizes, N > 100. Ultimately, it remains an open question whether the unfavorable scaling of error mitigation prevents its use in realistic quantum-chemistry applications.

Fig. 5: Plot representing the energy error (from FCI) using different noise probabilities and VQE algorithms.
figure 5

Plotted for H2 (a), H4 (at 1 Å) (b), LiH (c), and BeH2 (d), using linear zero-noise extrapolation31,32. Energy accuracies lower than chemical accuracy are highlighted by the yellow region. The crosses represent the intercepts of the curves with this region.

Full size image
Fig. 6: Plot representing the noise probability required to reach chemical accuracy, pc, for different ansätze and molecule sizes (number of orbitals).
figure 6

For molecules with the same number of orbitals, the mean probability is taken. The crosses and circles represent the noise probabilities required to reach chemical accuracy with and without error mitigation, respectively. The data without error mitigation is taken from Table 1, and the data with error mitigation is taken from the crosses in Fig. 5. Additionally, a recent state-of-the-art two-qubit gate-error rate with superconducting qubits is shown in purple93.

Full size image

Discussion

Any quantum algorithm aimed at near-term NISQ devices must be designed to tolerate some level of noise. In this work, we numerically quantify the maximally allowed depolarizing gate-error probabilities, pc, required by leading gate-based VQEs to achieve chemically accurate energy estimates. Based on numerical simulations, we reach five conclusions. First, even the best-performing VQE algorithms require gate-error probabilities between 10−6 and 10−4, for the small molecules we assess. Such errors are at least an order of magnitude below state-of-the-art experiments25,50 and the surface-code threshold8,11. If error mitigation is viable, the pc values can be improved to 10−4 to 10−2 with linear zero-noise extrapolation. Second, larger molecules tend to require longer ansatz-circuits and thus, lower gate-error probabilities, see Fig. 6. This is the case both with and without error mitigation. Third, in the presence of noise, ADAPT-VQEs can tolerate approximately an order of magnitude greater gate-errors pc than equivalent fixed-ansatz VQEs, including those with the shortest ansatz circuits30,38. Fourth, the more gate-efficient the ADAPT-VQE ansatz pool, the more noise resilient the algorithm. From a noise-resilience perspective, qubit excitations and Pauli-string excitations outperform fermionic excitations. Fifth, the maximum gate-error probability allowed to reach chemical accuracy is roughly inversely proportional to the number of CNOT gates: \({p}_{{{{\rm{c}}}}}\mathop{\propto }\limits_{ \sim }{N}_{{{{\rm{II}}}}}^{-1}\). We now conclude this work with a couple of comments.

In this work, we quantify the maximally allowed gate-error probability of ADAPT-VQEs, UCCSD VQE and the leading fixed-ansatz VQE, k-UpCCGSD38. The latter is chosen as due to its favorable circuit depth scaling with molecule size30. This ignores plenty of other VQE algorithms which would benefit from similar studies in the future, as discussed in the main text40,41,42,43,82,83,84,85,86,87.

As opposed to a fault-tolerance threshold in error correction, the maximally allowed gate-error probability pc crucially depends on the size of the input problem, see Fig. 6. More specifically, pc tends to shrink as the number of spin orbitals N increases. A key question for future research is to elucidate how fast pc decreases with N. Our numerical data in Fig. 6 suggests an exponential scaling, both with and without error mitigation. Meanwhile, assuming VQEs achieve molecular ground-state energies with polynomially shallow circuits (NII = poly(N)), Eq. (28) suggests a polynomial scaling. Having analytical expressions of the decrease of pc with the number of spin orbitals N, would inform us whether quantum advantage is at all feasible for input problems beyond 100 spin orbitals.

While this study is entirely focused on gate-errors, other sources of noise may also be relevant. These include errors from state preparation and measurement as well as statistical noise due to sampling of expectation values from a limited number of shots. As mentioned when justifying the noise model, errors due to state preparation and measurement tend to be smaller than the accumulated gate errors, and there are widely-implemented methods to compensate for them53,54,55,56,57,58. However, in principle, measurement errors may lead to sub-optimal parameter values or operator choices during ansatz growth of ADAPT-VQE, which may prevent the algorithm from reaching the global minimum energy. A detailed analysis of such effects is left for future work.

While it is possible to sample any expectation value with ϵ accuracy in polynomially few shots1,30, the scaling prefactor may lead to prohibitively large run-times30,88,89,90. This issue is particularly acute for ADAPT-VQE algorithms, where each growth step requires shots for both parameter optimization and element selection. In this case, the number of necessary gradient measurements for each ansatz growth step is greater than that for VQE parameter optimization, by a factor which scales linearly in the number of qubits91. Holistic studies of VQE run-times30,88,89,90 provide predictions which vary greatly depending on the estimation methodology. The estimated run-times are often intractable without significant parallelization. The number of necessary measurements for parameter optimization can potentially be reduced via alternate groupings of Pauli operators83,84,85, or tensor contraction of the Hamiltonian (such as by double factorization86,87,92). Despite this progress, run-time scaling remains a significant obstacle to overcome before ADAPT-VQEs can perform useful computations on real hardware. A balance must be found between run-time and the acceptable level of statistical noise. This is complicated by the combination of gate errors, measurement errors and statistical errors, which may affect VQEs adversely in a non-trivial way. We leave this as an open problem for the community as, in this work, we focus on the noise resilience of ADAPT-VQEs.

This work numerically investigated the maximally allowed gate-error probability pc required to achieve chemically accurate predictions as a core metric of VQE performance. Similar to a fault-tolerance threshold in error correction, pc should provide a transparent metric to compare the noise resilience of VQEs as well as provide useful guidance for the experimental community. Having demonstrated that pc is between 10−4 and 10−6 for very small molecules (and worse for larger molecules), we conclude that quantum advantage in VQE-based quantum chemistry requires: (i) Substantially improved error mitigation, (ii) error correction, and/or (iii) significantly improved hardware in which gate errors are reduced by orders of magnitude.