Abstract
Entanglements serve as a resource for any quantum information system and are deterministically generated or swapped by a joint measurement called complete Bell state measurement (BSM). The determinism arises from a quantum nondemolition measurement of two coupled qubits with the help of readout ancilla, which inevitably requires extra physical qubits. We here demonstrate a deterministic and complete BSM with only a nitrogen atom in a nitrogen-vacancy (NV) center in diamond as a quantum memory without relying on any carbon isotopes, which are the extra qubits, by exploiting electron‒nitrogen (14N) double qutrits at a zero magnetic field. The degenerate logical qubits within the subspace of qutrits on the electron and nitrogen spins are holonomically controlled by arbitrarily polarized microwave and radiofrequency pulses via zero-field-split states as the ancilla, thus enabling the complete BSM deterministically. Since the system works under an isotope-free and field-free environment, the demonstration paves the way to realize high-fidelity quantum repeaters for long-haul quantum networks and quantum interfaces for large-scale distributed quantum computers.
Similar content being viewed by others
Introduction
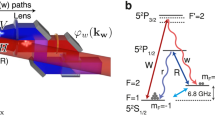
The development of large-scale distributed quantum computers requires quantum networks1,2,3 based on remote entanglement to connect the computers4,5,6,7,8,9,10. This necessitates the use of quantum repeaters11,12,13,14,15 or quantum interfaces16 that can perform, with high fidelity, a deterministic and complete Bell state measurement (BSM)17,18,19,20. The BSM is important not only for extending the distance of photon transmission21 and for routing photons over the networks but also for interfacing the quantum state between photons and qubits in quantum computers16,22,23,24,25. A complete BSM allows us to project any two-qubit states into one of the four Bell states deterministically, which typically requires quantum nondemolition measurement known as single-shot measurement26,27,28,29,30,31. Due to the possibility of quantum manipulation with communicating photons32,33,34,35,36,37, as well as the rich coherence time of solid-state spins36,38,39,40,41,42,43,44, which is over a minute for a nuclear spin44, nitrogen-vacancy (NV) centers in diamond45,46,47 are of interest as core devices for quantum repeaters with quantum memories (Fig. 1a). A negatively charged NV center, in particular, has electron and nitrogen (14N) nuclear spin composite systems and also accompanies numerous carbon isotopes with a nuclear spin. The measurement-based entanglement combined with a single-shot measurement was previously demonstrated by utilizing a nitrogen nuclear spin and the nearby carbon isotope spins as the Bell states and utilizing an electron spin as the readout ancilla17. Subsequently, unconditional quantum teleportation between distant NV centers has been demonstrated based on a high-fidelity (89% measured) deterministic BSM18 that reads out the Bell states composed of electron and nitrogen nuclear spins, respectively. In both of those studies, the BSM was achieved by utilizing the entanglement of electron spins with the nitrogen and carbon isotope spins. However, the underlying interactions between an electron spin and other nuclear spins were also an unavoidable factor for the readout infidelity. The composite system of the NV center is formed by spin-1 triplets of a nitrogen-14 nuclear spin and an electron spin so that the required three states (two states for qubit basis and one for the readout ancilla) can be inherently provided in the single spins, eliminating the need to use additional ancilla qubits for the readout. The spins, at a zero magnetic field, provide V- and Λ-shaped three-level qutrits with degenerate \({m}_{s}=\pm 1\) qubits and an energy-split \({m}_{s}=0\) ancillary state component owing to the zero-field splitting of \({D}_{0}/2\pi =2.88\) GHz for the electron (Fig. 1b) and the nuclear quadrupole splitting of \(Q/2\pi =4.95\) MHz for the nitrogen (Fig. 1c). The coupled-system Hamiltonian is given as
where \({S}_{z}\) and \({I}_{z}\) are the \(z\) component of the spin-1 operator of the electron spin and the nitrogen nuclear spin, respectively, and \(A/2\pi =2.17{\rm{MHz}}\) is the hyperfine coupling between the two spins. The energy-level diagram of the system is shown in Fig. 1d. The Bell states are composed of inherently degenerate qubits, which we call geometric spin qubits20,31,35,37,48,49,50,51,52,53,54,55, according to the computational basis states \(|\pm 1{\rangle }_{{\rm{e}}}\) for the electron and \(|\pm 1{\rangle }_{{\rm{N}}}\) for the nitrogen (dashed area in Fig. 1d). These states are operated by the universal holonomic quantum gate with polarized microwave (MW) and radiofrequency (RF) pulses via the ancilla states \(|0{\rangle }_{{\rm{e}}}\) and \(|0{\rangle }_{{\rm{N}}}\)54. The geometric spin qubits \(|\pm 1{\rangle }_{{\rm{e}}}\) on an electron and \(|\pm 1{\rangle }_{{\rm{N}}}\) on a nitrogen atom are analogous to the polarization qubits on photons showing a geometric nature and have been demonstrated in terms of geometrically entangled emission35 and absorption37 of a photon. In this paper, we propose and experimentally demonstrate a novel scheme for the deterministic and complete BSM at a zero magnetic field with only a single quantum memory on a nitrogen atom in an NV center in diamond, without relying on any carbon isotopes, by exploiting the electron‒nitrogen double qutrits at a zero magnetic field.
The schematic in a shows the diamond device where electron and nitrogen (14N) nuclear spins are manipulated by a crossed-wire antenna54. b, c show an energy diagram of the V- and Λ-shaped three-level qutrit systems of the individual electron (e) and nitrogen nuclear (N) spins at a zero magnetic field. \({D}_{0}\) and \(Q\) are the zero-field splitting of the electron and the nuclear quadrupole splitting of the nitrogen, respectively. d The energy diagram of the double-qutrit joint states coupled with hyperfine interaction \(A\). The four Bell states \({\left|{\Psi }^{\pm }\right\rangle }_{{\rm{e}},{\rm{N}}}\) and \({\left|{\Phi }^{\pm }\right\rangle }_{{\rm{e}},{\rm{N}}}\) on the logical qubits are based on the \({\left|\pm 1,\pm 1\right\rangle }_{{\rm{e}},{\rm{N}}}\) computational bases (dashed area), and the \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) and \({\left|\pm \mathrm{1,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) states serve as readout ancilla (shadowed area).
Results
The double qutrits-based complete Bell state measurement
The NV electron and nitrogen nuclear spins are individually manipulated with arbitrarily polarized MW and RF pulses created by two orthogonal wires54 as shown in Fig. 1a. Here, the MW pulses are generated with the GRadient Ascent Pulse Engineering (GRAPE) algorithm, which enables high-fidelity operations of geometric spin qubits54,56. The MW (RF) pulses drive the unitary operations on the electron (nitrogen nuclear) spins in the Rabi frequency on the order of MHz (kHz). Figure 2a illustrates the quantum circuit for the complete BSM consisting of a disentanglement, which transforms the four Bell states into four eigenstates, and four sequential measurements of the four eigenstates. The Bell states defined as
a The quantum circuit utilizing the two-qubit joint states. After the entanglement generation, the BSM is achieved via the disentanglement operation consisting of CNOT (Controlled NOT) and Hadamard gates followed by a single-shot measurement. b–d The procedure for measuring the \({\left|+1,+1\right\rangle }_{{\rm{e}},{\rm{N}}}\) state. First, (b) each computational basis is selectively transformed to the \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) state by applying GRAPE (GRadient Ascent Pulse Engineering algorithm)-optimized microwave (MW) and radiofrequency (RF) pulses. Next, (c) the population is read out by irradiating a red laser pulse. Finally, (d) the probabilistic transition states of \({\left|\pm \mathrm{1,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) are initialized to the \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) state by irradiating a GRAPE-optimized MW pulse.
are transformed as \({\left|{\Phi }^{+}\right\rangle }_{{\rm{e}},{\rm{N}}}\,\to \,{\left|+1,+\right\rangle }_{{\rm{e}},{\rm{N}}}\to \,{\left|+1,+1\right\rangle }_{{\rm{e}},{\rm{N}}}\), \({\left|{\Phi }^{-}\right\rangle }_{{\rm{e}},{\rm{N}}}\,\to \,{\left|+1,-\right\rangle }_{{\rm{e}},{\rm{N}}}\to \,{\left|+1,-1\right\rangle }_{{\rm{e}},{\rm{N}}}\), \({\left|{\Psi }^{+}\right\rangle }_{{\rm{e}},{\rm{N}}}\to \,{\left|-1,+\right\rangle }_{{\rm{e}},{\rm{N}}}\,\to \,{\left|-1,+1\right\rangle }_{{\rm{e}},{\rm{N}}}\), and \({\left|{\Psi }^{-}\right\rangle }_{{\rm{e}},{\rm{N}}}\to {\left|-1,-\right\rangle }_{{\rm{e}},{\rm{N}}}\,\to \,{\left|-1,-1\right\rangle }_{{\rm{e}},{\rm{N}}}\) by applying an MW pulse for the Controlled NOT (CNOT) gate and RF pulses for the Hadamard gate as depicted in Fig. 2b, where \({\left|\pm \right\rangle }_{{\rm{e}}({\rm{N}})}=\frac{1}{\sqrt{2}}({\left|+1\right\rangle }_{{\rm{e}}\left({\rm{N}}\right)}\pm {\left|-1\right\rangle }_{{\rm{e}}({\rm{N}})})\). It should be noted that the direct transition between \({\left|\pm 1\right\rangle }_{{\rm{e}}({\rm{N}})}\,\) states is not permitted, so the geometric nature is also utilized for the realization of the Hadamard gate55. Moreover, since the Hadamard gate for the nitrogen qubit uses a geometric phase in \(|0{\rangle }_{{\rm{e}}}\) subspace induced by the RF pulse54, the electron qubit states \(|\pm 1{\rangle }_{{\rm{e}}}\) are sequentially transferred to \(|0{\rangle }_{{\rm{e}}}\) to apply the geometric phase and then back to the original states. Finally, each of the resulting eigenstates (computational bases) \({\left|\pm 1,\pm 1\right\rangle }_{{\rm{e}},{\rm{N}}}\) can be measured with quantum nondemolition readout by using an extra subspace in the three-level systems (Fig. 2b–d). The details of the measurement are discussed later.
Quantum state tomography
We initially evaluate the process of disentanglement by quantum state tomography (QST) of the four prepared Bell states, the states after the CNOT gate, and the states after the Hadamard gate. As shown in Fig. 3a, QST consists of a transfer of the arbitrary state \({\left|{\psi }_{{\rm{e}}},{\psi }_{{\rm{N}}}\right\rangle }_{{\rm{e}},{\rm{N}}}\) into the \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) state and the repetitive readout of the nuclear spin state via electron spin. Initially, the GRAPE-optimized MW pulse transforms the \({\left|{\psi }_{{\rm{e}}}\right\rangle }_{{\rm{e}}}\) state, which is selected by the polarization of the MW, into the \({\left|0\right\rangle }_{{\rm{e}}}\) state regardless of the nuclear spin state. Next, the RF pulse transforms the \({\left|{\psi }_{{\rm{N}}}\right\rangle }_{{\rm{N}}}\) state, which is also selected by the polarization of the RF, into the \({\left|0\right\rangle }_{{\rm{N}}}\) state conditioned on the electron spin state of \({\left|0\right\rangle }_{{\rm{e}}}\). As a result, the population of the target state is stored in \({\left|0\right\rangle }_{{\rm{N}}}\) and the others remain in \({\left|\pm 1\right\rangle }_{{\rm{N}}}\), allowing repetitive readout of the target state via the nuclear spin. The sub-sequence of the readout repeated 30 times consists of the initialization of the electron spin, the mapping of the nuclear spin state into the electron spin state, and the readout of the electron spin. The initialization is performed by spin pumping into the \({\left|0\right\rangle }_{{\rm{e}}}\) state by \({\left|\pm 1\right\rangle }_{{\rm{e}}}\)-selective excitation to the \({E}_{\mathrm{1,2}}\) excited state. The mapping is performed by the GRAPE-optimized MW pulse to flip the \({\left|0\right\rangle }_{{\rm{e}}}\) state into the \({\left|\pm 1\right\rangle }_{{\rm{e}}}\) state conditioned on the nuclear spin state of \({\left|0\right\rangle }_{{\rm{N}}}\). The readout is performed by counting the photons of phonon sideband emission during \({\left|0\right\rangle }_{{\rm{e}}}\)-selective excitation to the \({E}_{y}\) excited state. Figure 3b–d shows the reconstructed density matrices of the \({\left|{\Psi }^{\pm }\right\rangle }_{{\rm{e}},{\rm{N}}}\) and \({\left|{\Phi }^{\pm }\right\rangle }_{{\rm{e}},{\rm{N}}}\) states after entanglement generation, the \({\left|\pm 1,\pm \right\rangle }_{{\rm{e}},{\rm{N}}}\) states after the CNOT gate operation, and the \({\left|\pm 1,\pm 1\right\rangle }_{{\rm{e}},{\rm{N}}}\) states after the Hadamard gate operation, respectively (fidelities are shown in the figures). The obtained fidelities exceed 90% on average for all three stages: the prepared Bell states, the states after the CNOT gate, and the states even after the Hadamard gate.
a The pulse sequence of QST. An arbitrary state is mapped to the \({\left|0\right\rangle }_{{\rm{N}}}\) state and repeatedly read out by \({E}_{y}\) resonant red laser (100 nW). The real part of the QST b after Bell state generation, c after the CNOT gate, and d after the Hadamard gate. The basis labeled \(\pm 1,\pm 1\) for each state corresponds to the \({\left|\pm 1,\pm 1\right\rangle }_{{\rm{e}},{\rm{N}}}\) state, respectively. Note that the RF-pulse polarizations for the final state (d) are optimized, slightly increasing the fidelity compared with the others (b, c). For each state, the obtained fidelity \(F\) exceeds 90%.
The measurements of our device
We now demonstrate the complete BSM, which enables deterministic discrimination of all four Bell states with only one set of measurements. Figure 4a illustrates the pulse sequence for the BSM. The measurements are carried out in the order of \({\left|{\Phi }^{+}\right\rangle }_{{\rm{e}},{\rm{N}}}\), \({\left|{\Psi }^{+}\right\rangle }_{{\rm{e}},{\rm{N}}}\), \({\left|{\Psi }^{-}\right\rangle }_{{\rm{e}},{\rm{N}}}\), and \({\left|{\Phi }^{-}\right\rangle }_{{\rm{e}},{\rm{N}}}\) by selecting the MW-pulse frequency and RF-pulse polarization (R or L) to transfer them into the corresponding computational bases \({\left|\pm 1,\pm 1\right\rangle }_{{\rm{e}},{\rm{N}}}\), which are then selectively transformed again into the readout state \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) by the polarized MW and RF pulses. The \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) state is repeatedly measured in the ancillary space {\({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}},{\left|\pm \mathrm{1,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\)}. In contrast to the case of QST, initialization by \({E}_{\mathrm{1,2}}\) excitation is no longer available since it disrupts the state awaiting the next measurement. Instead of using \({E}_{\mathrm{1,2}}\) lasers, we use the GRAPE-optimized MW pulses to transform a part of the \({\left|\pm 1,0\right\rangle }_{{\rm{e}},{\rm{N}}}\) states relaxed by the \({E}_{y}\) excitation during the measurement of \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\) (here, the \({\left|+,0\right\rangle }_{{\rm{e}},{\rm{N}}}\) state) back into the \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\), allowing for repetitive measurements of all the computational bases \({\left|\pm 1,\pm 1\right\rangle }_{{\rm{e}},{\rm{N}}}\) through the readout state \({\left|\mathrm{0,0}\right\rangle }_{{\rm{e}},{\rm{N}}}\). Photon counts are accumulated by repeating the sub-sequences 25 times in a similar way as for the QST. The Bell states are discriminated by the conditions as
where \(\{{n}_{1},{n}_{2},{n}_{3},{n}_{4}\}\) are the photon counts for the successive measurements in the \({\left|{\Phi }^{+}\right\rangle }_{{\rm{e}},{\rm{N}}}\), \({\left|{\Psi }^{+}\right\rangle }_{{\rm{e}},{\rm{N}}}\), \({\left|{\Psi }^{-}\right\rangle }_{{\rm{e}},{\rm{N}}}\), and \({\left|{\Phi }^{-}\right\rangle }_{{\rm{e}},{\rm{N}}}\) bases and \({n}_{{\rm{c}}}\) is the threshold of the photon counts, which is set to \({n}_{{\rm{c}}}=1\) in this demonstration. Figure 4b shows the probability distributions of the accumulated photon counts. The distribution clearly changes from a dark state (0.3 on average) to a bright state (1.8 on average) when the prepared Bell state corresponds to the measurement state, indicating that the Bell states are well discriminated by Eq. (3). It should be noted that the distribution is kept bright for the following measurements after the correspondence, since the population of the measured state remains in the readout ancilla. The final measurement in \({\left|{\Phi }^{-}\right\rangle }_{{\rm{e}},{\rm{N}}}\) is confirmed to be bright as \({n}_{4}\ge {n}_{{\rm{c}}}\), although it should be determined by three measurements. All four Bell states are thus equivalently discriminated deterministically. Figure 4c shows the probability distributions of the measurement outcome after the thresholding discrimination. Note that the discriminated Bell states (red bars) correspond to the prepared Bell states with a fidelity of \({F}_{{\rm{BSM}}}=\) 68% on average.
a The pulse sequences of the single-shot measurements (the \({\left|{\Phi }^{+}\right\rangle }_{{\rm{e}},{\rm{N}}}\) measurement is described only as an example). The BSM consists of selective transformation from the prepared Bell state into the readout state \({\left|0,0\right\rangle }_{{\rm{e}},{\rm{N}}}\) through the computational basis \({\left|\pm 1,\pm 1\right\rangle }_{{\rm{e}},{\rm{N}}}\) by corresponding GRAPE-shaped MW and polarized square-shaped RF π-pulses followed by a repetitive single-shot measurement by \({E}_{y}\) laser pulses for the measurement of\(\,{\left|0,0\right\rangle }_{{\rm{e}},{\rm{N}}}\) and GRAPE-based MW π-pulses for the initialization (instead of \({E}_{\mathrm{1,2}}\) lasers), respectively. The pulse sequences for the other measurements are the same as those for \({\left|{\Phi }^{+}\right\rangle }_{{\rm{e}},{\rm{N}}}\) (shown in the shadowed area) except for the GRAPE waveform (targeting the upper or lower level) and the RF polarization (R or L) depending on the prepared Bell state. b The probability distribution of the accumulated photon counts for the BSM. Magenta (blue) bars indicate that the obtained photon counts exceed (fall below) a threshold. c Probability distributions of the Bell states after the thresholding discrimination. The red bars indicate that the discriminated state corresponds to the prepared Bell state.
Discussion
In our scheme, the BSM is achieved by utilizing the repetitive single-shot measurement in \({\left|0\right\rangle }_{{\rm{N}}}\) readout ancilla at a zero magnetic field, whereas the conventional BSMs rely on the electron spin18. In our device, the low extraction efficiency of photons emitted from bulk diamond makes it difficult to determine the all-prepared state using an electron-spin readout (see Supplementary Note 1). Moreover, it is numerically demonstrated that the enhanced fidelity in our scheme by introducing a solid immersion lens (SIL) is still larger than that in the conventional readout18 (see Supplementary Note 2), indicating the significance and potential of the qutrit nature with the readout ancilla.
The demonstrated scheme also plays a complementary role to the conventional scheme. A recent report57 showed that quantum repeaters can be realized by performing the BSM only at intermediate nodes of communicating photons. On the other hand, it has been proposed that NV centers can also serve as interface devices for communicating photons58 with other qubits, such as superconducting qubits59, which play a key role in distributed quantum computers60,61,62. In considering such schemes, the realization of the high-fidelity BSM without relying on other spins and/or magnetic fields is also useful for a wide range of applications in quantum technologies.
In summary, a deterministic and complete BSM has been demonstrated at a zero magnetic field with only a single quantum memory by fully exploiting the inherent qutrit nature of electron and nitrogen spins in an NV center. The double qutrit systems enabled nondestructive joint-state measurements without relying on additional carbon isotopes or high photon extraction efficiency from an electron, owing to the long memory time of the nitrogen nuclear spin. The present demonstration paves the way for realizing high-fidelity quantum repeaters for long-haul quantum networks and quantum interfaces for large-scale distributed quantum computers with minimal physical resources.
Methods
Diamond device and optical set up
We use a single naturally occurring NV center in a high-purity-type IIa chemical vapor deposition-grown diamond with a <100> crystalline orientation produced by Element Six. All measurements are performed below 5 K to allow coherent control of the electron orbital, and the sample is placed under an applied magnetic field with three-dimensional coils to suppress the geomagnetic field. Phonon sideband photons from an NV center are emitted and detected by the following optical setup. The system consists of a confocal microscope similar to those used in previous studies; it has a green-laser path (515 nm in wavelength) for nonresonant excitation and initialization of the charge state of an NV center and the electron spin as well as two red-laser paths (637 nm in wavelength) for the resonant excitation, initialization, and readout of the electron spin. In addition, the path for detecting the emitted photons is filtered by a dichroic mirror to exclude the green and red lasers, and the photons are focused on the avalanche photodiode (APD), selectively detected as the phonon sideband.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The code used for generating data of this study are available from the corresponding author upon reasonable request.
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).
Awschalom, D. et al. Development of Quantum Interconnects (QuICs) for next-generation information technologies. PRX Quantum 2, 017002 (2021).
Ladd, T. D. et al. Quantum computers. Nature 464, 45 (2010).
Gottesman, D. & Chuang, I. L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402, 390 (1999).
Leung, D. W. Quantum computation by measurements. Int. J. Quantum Inf. 02, 33 (2004).
Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).
Raussendorf, R. & Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98, 190504 (2007).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493 (1995).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932 (1998).
Childress, L., Taylor, J. M., Sørensen, A. S. & Lukin, M. D. Fault-tolerant quantum communication based on solid-state photon emitters. Phys. Rev. Lett. 96, 070504 (2006).
Jiang, L. et al. Quantum repeater with encoding. Phys. Rev. A 79, 032325 (2009).
Delteil, A., Sun, Z., Fält, S. & Imamoğlu, A. Realization of a cascaded quantum system: heralded absorption of a single photon qubit by a single-electron charged quantum dot. Phys. Rev. Lett. 118, 177401 (2017).
Ruf, M., Wan, N. H., Choi, H., Englund, D. & Hanson, R. Quantum networks based on color centers in diamond. J. Appl. Phys. 130, 070901 (2021).
Kurizki, G. et al. Quantum technologies with hybrid systems. Proc. Natl Acad. Sci. 112, 3866–3873 (2015).
Pfaff, W. et al. Demonstration of entanglement-by-measurement of solid-state qubits. Nat. Phys. 9, 29 (2013).
Pfaff, W. et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 345, 532 (2014).
Welte, S. et al. A nondestructive Bell-state measurement on two distant atomic qubits. Nat. Photon. 15, 504 (2021).
Reyes, R. et al. Complete Bell state measurement of diamond nuclear spins under a complete spatial symmetry at zero magnetic field. Appl. Phys. Lett. Appl. Phys. Lett. 120, 194002 (2022).
Liu, X. et al. Heralded entanglement distribution between two absorptive quantum memories. Nature 594, 41 (2021).
Schuster, D. I. et al. High-cooperativity coupling of electron-spin ensembles to superconducting cavities. Phys. Rev. Lett. 105, 140501 (2010).
Kubo, Y. et al. Strong coupling of a spin ensemble to a superconducting resonator. Phys. Rev. Lett. 105, 140502 (2010).
Zhu, X. et al. Coherent coupling of a superconducting flux qubit to an electron spin ensemble in diamond. Nature 478, 221–224 (2011).
Leent, T. et al. Entangling single atoms over 33 km telecom fibre. Nature 607, 69 (2022).
Neumann, P. et al. Single-shot readout of a single nuclear spin. Science 329, 542 (2010).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574 (2011).
Dréau, A., Spinicelli, P., Maze, J. R., Roch, J.-F. & Jacques, V. Single-shot readout of multiple nuclear spin qubits in diamond under ambient conditions. Phys. Rev. Lett. 110, 060502 (2013).
Waldherr, G. et al. Quantum error correction in a solid-state hybrid spin register. Nature 506, 204 (2014).
Zhang, Q. et al. High-fidelity single-shot readout of single electron spin in diamond with spin-to-charge conversion. Nat. Commun. 12, 1529 (2021).
Nakazato, T. et al. Quantum error correction of spin quantum memories in diamond under a zero magnetic field. Commun. Phys. 5, 102 (2022).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–734 (2010).
Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86 (2013).
Vasconcelos, R. et al. Scalable spin–photon entanglement by time-to-polarization conversion. npj Quantum Inf. 6, 9 (2020).
Sekiguchi, Y. et al. Geometric entanglement of a photon and spin qubits in diamond. Commun. Phys. 4, 264 (2021).
Yang, S. et al. High-fidelity transfer and storage of photon states in a single nuclear spin. Nat. Photonics 10, 507–511 (2016).
Tsurumoto, K., Kuroiwa, R., Kano, H., Sekiguchi, Y. & Kosaka, H. Quantum teleportation-based state transfer of photon polarization into a carbon spin in diamond. Commun. Phys. 2, 74 (2019).
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8, 383–387 (2009).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283 (2012).
Bar-Gill, N., Pham, L. M., Jarmola, A., Budker, D. & Walsworth, R. L. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 4, 1743 (2013).
Herbschleb, E. D. et al. Ultra-long coherence times amongst room-temperature solid-state spins. Nat. Commun. 10, 3766 (2019).
Bradley, C. E. et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Nguyen, C. T. et al. An integrated nanophotonic quantum register based on silicon-vacancy spins in diamond. Phys. Rev. B 100, 165428 (2019).
Bartling, H. P. et al. Entanglement of spin-pair qubits with intrinsic dephasing times exceeding a minute. Phys. Rev. X 12, 011048 (2022).
Maze, J. R. et al. Properties of nitrogen-vacancy centers in diamond: the group theoretic approach. N. J. Phys. 13, 025025 (2011).
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Gali, Á. Ab initio theory of the nitrogen-vacancy center in diamond. Nanophotonics 8, 1907–1943 (2019).
Kosaka, H. et al. Coherent transfer of light polarization to electron spins in a semiconductor. Phys. Rev. Lett. 100, 096602 (2008).
Kosaka, H. et al. Spin state tomography of optically injected electrons in a semiconductor. Nature 457, 702 (2009).
Kosaka, H. & Niikura, N. Entangled absorption of a single photon with a single spin in diamond. Phys. Rev. Lett. 114, 053603 (2015).
Sekiguchi, Y. et al. Geometric spin echo under zero field. Nat. Commun. 7, 11668 (2016).
Sekiguchi, Y., Niikura, N., Kuroiwa, R., Kano, H. & Kosaka, H. Optical holonomic single quantum gates with a geometric spin under a zero field. Nat. Photonics 11, 309 (2017).
Ishida, N. et al. Universal holonomic single quantum gates over a geometric spin with phase-modulated polarized light. Opt. Lett. 43, 2380 (2018).
Nagata, K., Kuramitani, K., Sekiguchi, Y. & Kosaka, H. Universal holonomic quantum gates over geometric spin qubits with polarised microwaves. Nat. Commun. 9, 3227 (2018).
Sekiguchi, Y., Komura, Y. & Kosaka, H. Dynamical decoupling of a geometric qubit. Phys. Rev. Appl. 12, 051001 (2019).
Khaneja, N., Reiss, T., Kehlet, C., Schulte-Herbrüggen, T. & Glaser, S. J. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. J. Magn. Reson. 172, 296 (2005).
Pompili, M. et al. Realization of a multinode quantum network of remote solid-state qubits. Science 372, 259 (2021).
Blinov, B. B., Moehring, D. L., Duan, L. M. & Monroe, C. Observation of entanglement between a single trapped atom and a single photon. Nature 428, 153 (2004).
Kurokawa, H., Yamamoto, M., Sekiguchi, Y. & Kosaka, H. Remote entanglement of superconducting qubits via solid-state spin quantum memories. Phys. Rev. Appl. 18, 064039 (2022).
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500 (2014).
Córcoles, A. D. et al. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6, 6979 (2015).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66 (2015).
Acknowledgements
We thank H. Kato, T. Makino, T. Teraji, Y. Matsuzaki, K. Nemoto, N. Mizuochi, F. Jelezko, and J. Wrachtrup for their discussions and help with the experiment. This work was supported by Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (grant numbers 20H05661 and 20K2044120); by the Japan Science and Technology Agency (JST) CREST (grant number JPMJCR1773); and by the JST Moonshot R&D (grant number JPMJMS2062). We also acknowledge the assistance of the Ministry of Internal Affairs and Communications (MIC) under the initiative Research and Development for Construction of a Global Quantum Cryptography Network (grant number JPMI00316).
Author information
Authors and Affiliations
Contributions
A.K., K.W., K.M., and Y.S. carried out the experiment and the simulation. A.K., K.W., and K.M. analyzed the data. A.K., Y.S., and H.K. designed the work and wrote the manuscript. H.K. supervised the project. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kamimaki, A., Wakamatsu, K., Mikata, K. et al. Deterministic Bell state measurement with a single quantum memory. npj Quantum Inf 9, 101 (2023). https://doi.org/10.1038/s41534-023-00771-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-023-00771-z