Introduction

One of the great promises of quantum technology is the development of quantum networks, which will allow global distribution of entanglement for tasks such as distributed quantum computing1,2, distributed quantum sensing3,4 and quantum-secure communication5,6,7,8,9,10. To leverage the full potential of quantum networks we require protocols that draw an efficiency advantage from genuine multi-partite entanglement as opposed to strictly pair-wise correlations such as Bell states. Multi-user entanglement such as Greenberger-Horne-Zeilinger (GHZ) states have already found application in quantum conference key agreement11,12,13,14, quantum secret sharing15,16,17 and quantum communication complexity problems18,19.

In quantum conference key agreement (QCKA), N users aim to establish a common and identical secret key for group-wide encryption. Using standard two-party QKD schemes, this can be achieved by generating a set of N-1 pair-wise keys either via prepare-and-send schemes or via shared entangled Bell pairs20,21. The set of keys can then be used to algorithmically generate the conference key by performing a bit-wise XOR operation on the individual keys—we will refer to this as the ‘2QKD’ approach. If the participating users are part of a network as depicted in Fig. 1, a more resource-efficient protocol called ‘NQKD’ leverages multi-partite entanglement to obtain conference key bits directly from GHZ states supplied to all participating users. NQKD can outperform the 2QKD scheme by consuming up to N − 1 times fewer network resources in constrained quantum networks11,22. QCKA was recently demonstrated in a four-user NQKD scenario where a four-photon GHZ state was transmitted over up to 50 km of telecom fibre14. However, a direct comparison showing the experimental resource advantage over the 2QKD approach in a quantum network has not yet been achieved.

Fig. 1: Conceptual illustration of a multi-node quantum network.
figure 1

Physical qubits are represented by nodes (circles), while edges (lines) represent pair-wise interactions that entangle the qubits within the wider network. Here, we define a network consisting of six users represented by nodes within the rounded rectangle. Within this network, four of the users may wish to perform quantum protocols such as conference key agreement. The traditional method involves distributing Bell pairs among the participants first, followed by post-processing steps to extract keys in a pairwise fashion before arriving at the final conference key as shown by the right path in blue. An alternative approach is to obtain a GHZ state and employ a multi-party quantum conference key agreement protocol to extract the key directly, as represented in the left red path.

Full size image

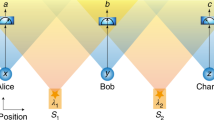
In this work we consider the scenario of multi-user conference key agreement in a small-scale quantum network, as illustrated in Fig. 1. The network comprises six users: Alice and three Bobs distil a secure conference key, while two non-participants, Charlie and Debbie, facilitate the operation of the network. This scenario, wherein participants of a protocol are indirectly connected via other non-participating users, is expected to naturally occur in future multi-node quantum networks that generate large-scale entanglement in the background. In order to efficiently distribute entanglement resources to requesting parties, we will use so-called network coding techniques23,24,25 which involve local operations, quantum measurements and classical communication to alter the network connectivity. Using this network we implement the two QCKA approaches, i.e., NQKD and 2QKD, to demonstrate the resource advantage when using the multi-partite-entanglement-enabled protocol.

For the NQKD approach we consider the N-BB84 protocol12 that was implemented in ref. 14. In each protocol round, an N-partite GHZ state is distributed among N users. Each user performs a measurement on their respective qubit according to a pre-agreed sequence of two possible measurements. In type-1 rounds each user measures their qubit in the Pauli Z-basis, exploiting the perfect Z-correlations for generation of the raw key; type-2 rounds correspond to jointly measuring in the Pauli X-basis and are used for parameter estimation. Security is established by evaluating the phase error rate (QX) from the type-2 rounds and determining the quantum bit error rate (QBER) from a random subset of publicly disclosed type-1 outcomes. We can assess the performance of the N-BB84 protocol, in the limit of an infinite number of rounds, by determining these two parameters and calculating the asymptotic key rate (AKR)12,14. The AKR establishes the fractional secret key bit extracted for each copy of the resource state and is defined as,

$${{{\rm{AKR}}}}=1-H({{{\rm{QBER}}}})-H({Q}_{{{{\rm{X}}}}}),$$
(1)

where \(H(x)\doteq {-}x{\log }_{2}(x)-(1-x){\log }_{2}(1-x)\) is the binary entropy function. The explicit evaluation of QBER and QX is detailed in the Methods.

In the case of 2QKD, users initially obtain sets of Bell states, rather than a GHZ state, from which they run pairwise BB84 protocols whose AKR is also given by the expression in (1). However, unlike in the NQKD approach, the 2QKD method involves obtaining N − 1 unique, pairwise keys spanning the N-user group first. This is followed by a classical step, e.g., applying the bit-wise XOR, to transform the individual keys into the final conference key11. As we will show in our experiment, depending on the underlying topology of the quantum network, this leads to the 2QKD approach requiring up to N − 1 times more network resource states than NQKD.

Results

Network preparation and operation

Quantum networking studies usually assume a basic universal building block, for example the ‘ring’ network from which larger networks can be constructed. A common feature of these building blocks is that they allow arbitrary pairs of nodes to share Bell pairs via network coding routines, which distill sub-graphs from a network via local measurements and the discarding of non-participating network nodes. The six-node quantum network we implement, Fig. 2a, shares several features with the universal ring network, allowing us to directly compare GHZ-based QCKA and the Bell-pair-based 2QKD. We experimentally constructed the 6-photon network via a linear optics setup consisting of telecom-wavelength photon-pair sources and polarisation optics, see Methods for details.

Fig. 2: Experimentally generating and manipulating the six-photon graph state.
figure 2

a On the left is the linear optical circuit for generating the target graph state on the right. Three photon-pair sources are represented as black boxes with each horizontal line representing a labelled optical mode containing one photon. Two sources produce Bell states, \(\left\vert {\Phi }^{+}\right\rangle\), while the third generates a biseparable state with each photon in \(\left\vert +\right\rangle\). The two-qubit fusion gates are denoted by two squares on the modes they act upon connected by a vertical line. Single-qubit operations, i.e., Hadamard and Pauli-Z gates are shown as squares with letters \({\mathbb{H}}\) and Z respectively. b The set of graph transformations for obtaining the four-qubit GHZ state, in modes {1, 2, 5, 6}, are depicted in the red path. This corresponds to local operations consisting of single-qubit gates \({{{\rm{N}}}}\doteq \sqrt{-i{{{\rm{X}}}}}\) and \({{{\rm{T}}}}\doteq \sqrt{i{{{\rm{Z}}}}}\), where X and Z are again Pauli gates, followed by quantum measurements on non-participatory qubits {3, 4} in the Z basis. The remaining qubits can be measured in the joint-Z or-X basis allowing us to evaluate the key rate performance for the NQKD method. c Local graph operations for obtaining Bell pairs between nodes {1, 2} and {5, 6} (top) and a Bell pair between nodes {5, 6} (bottom) which are needed for the 2QKD approach.

Full size image

We now outline the method of manipulating the 6-node graph state23 via local complementation (LC)23,24,25. The LC operations on the six-photon graph results in a four-party GHZ state in modes {1, 2, 5, 6}, corresponding to four users, e.g., Alice, Bob-1, Bob-2 and Bob-3, implementing NQKD is shown in Fig. 2b. Conventionally, Alice denotes the party who co-ordinates the error correction and privacy amplification steps after the raw key is established11,12,14. We also include LC operations mapped to sets of single-qubit gates25 in the circuit. Nodes 3 and 4 represent users Charlie and Debbie, who do not participate in the QCKA key generation. They measure their qubits in the Z basis then announce their outcomes, which allows the qubits to be coherently removed from the graph. The remaining four qubits are transformed into the star graph which is locally equivalent to the four-party GHZ state23 required for the NQKD protocol. We then construct measurement sequences consistent with type-1 and type-2 rounds, i.e., Z⊗4 and X⊗4 respectively, of the NQKD protocol.

The method for allocating Bell pairs in the network, for the 2QKD protocol, is shown in Fig. 2c. To generate a conference key among the four users, at least three pairwise keys are required. There are two sets of network transformations for obtaining three individual Bell pairs among the same group of four users that participated in the NQKD protocol. The top of Fig. 2c shows how to obtain Bell pairs between nodes {1, 2} and {5, 6} respectively from a single copy of the network resource state. The bottom panel shows how a single Bell pair is established between modes {2, 5}. We similarly construct the measurement sequences corresponding to type-1 and type-2 rounds for each Bell pair, see Methods for details.

Evaluating protocol performance

The outcomes of type-1 and type-2 rounds are used to calculate the noise parameters QBER and QX which are then used to evaluate the AKR using the expression in (1). This expression corresponds to the asymptotic conference key rate for the NQKD approach and we denote it as AKRN. For the 2QKD approach, we use Eq. (1) to compute the pairwise AKR of each BB84 protocol, denoted \(\{{r}_{{{{{\rm{AB}}}}}_{1}},{r}_{{{{{\rm{B}}}}}_{2}{{{{\rm{B}}}}}_{3}},{r}_{{{{{\rm{AB}}}}}_{2}}\}\); the resulting asymptotic conference key rate is then obtained using the expression,

$${{{{\rm{AKR}}}}}_{2}=\left[{r}^{-1}_{{{{{\rm{AB}}}}}_{2}}+\max \left\{{r}^{-1}_{{{{{\rm{AB}}}}}_{1}},{r}^{-1}_{{{{{\rm{B}}}}}_{2}{{{{\rm{B}}}}}_{3}}\right\}\right]^{-1}.$$
(2)

In the ideal case where the AKR of each Bell pair is unity, we obtain \({{{{\rm{AKR}}}}}_{2}^{{{{\rm{ideal}}}}}=1/2\) while for the NQKD case with an ideal four-party GHZ state we can attain \({{{{\rm{AKR}}}}}_{{{{\rm{N}}}}}^{{{{\rm{ideal}}}}}=1\). The expected ratio of the key rate advantage in favour of NQKD is therefore \({{{{\rm{AKR}}}}}_{{{{\rm{N}}}}}^{{{{\rm{ideal}}}}}:{{{{\rm{AKR}}}}}_{2}^{{{{\rm{ideal}}}}}=2\). This advantage originates from the ability to use a single copy of the network resource state to produce one secure bit of the conference key via NQKD, whereas in 2QKD each secure bit requires two copies of the network resource state.

We compare the experimental results of type-1 and type-2 measurements for both approaches in Fig. 3. We set the pump power to each source to obtain an average six-photon detection rate of ~0.0141 Hz for all measurements. This optical pumping regime was chosen to limit multi-photon events while still ensuring sufficient detection rates to collect statistics for each protocol, for details on the effect of optical pump parameters see Supplementary Methods. From the data in Fig. 3 we calculate QBER and QX, for each resource state. We then evaluate the asymptotic conference key rate for NQKD, AKRN = 0.093(22) and for 2QKD, AKR2 = 0.044(15). We arrive at the experimentally measured ratio of the two approaches to be \({{{{\rm{AKR}}}}}_{{{{\rm{N}}}}}^{\exp }:{{{{\rm{AKR}}}}}_{2}^{\exp }=2.13(6)\). The uncertainties reported here are taken as one standard deviation from the average of samples via a Monte Carlo simulation which assumes Poissonian counting statistics.

Fig. 3: Experimentally measured populations of the different resource states for NQKD.
figure 3

a Populations of the three Bell pairs used for 2QKD. b Populations of the four-party GHZ state for NQKD. The type-1 rounds are shown in the top set of measurements, while type-2 rounds are shown in the bottom set. These outcomes are extracted from complete measurements in the six-photon state space, wherein post-selection of the non-participatory nodes has taken place. The theoretically expected populations are included as transparent bars. All measurements are recorded for the same integration time (300 s) at a fixed optical pump power (75 mW) and error bars are shown for one standard deviation assuming Poissonian statistics. We collected 4801 rounds of data, which in total took ~400 h, accumulating 20272 six-fold counts.

Full size image

In practice, only a limited number of rounds can be performed and this necessitates accounting for finite-key effects in the conference key rate14. We perform a finite-key analysis for both NQKD and 2QKD by using the measured noise parameters for each resource state, see Table 1, and by simulating the finite-key effects for a range of total rounds, Ltot, where each round corresponds to a successful distribution of the shared resource state. The finite key rate expression for the NQKD approach is explicitly defined in ref. 12,14, while its calculation for 2QKD presents some notable differences. In the 2QKD approach, the first step is to obtain three separate pair-wise keys, whose length is given by the finite-key rate formula of the BB84 protocol (it can be recovered from the NQKD finite-key rate by setting the number of parties to two). The second step employs the established keys to distribute the final conference key via a one-time pad. As a result, the conference key length cannot exceed the shortest pair-wise key among the three established ones. Moreover, for a given security parameter associated to the conference key, ϵtot, each bipartite key must be processed with a more stringent security parameter in order to recover ϵtot through composability, which reduces the overall key rate. Furthermore, in 2QKD the total number of network resource states is subdivided among the three pairwise protocols, implying that each protocol can only rely on a smaller set of data, thereby increasing the weight of the statistical corrections in the key rate. By these arguments, we expect the NQKD approach to retain its advantage over 2QKD in the finite-key regime. Figure 4 reports the conference key rates with finite-key effects of both NQKD and 2QKD, where the total security parameter is fixed to: ϵtot = 10−8. We observe that the advantage of the NQKD protocol over the 2QKD counterpart increases significantly in the finite-key regime. Remarkably, the minimal number of resource states required to distil a non-zero conference key is reduced by nearly one order of magnitude with NQKD.

Table 1 Noise terms measured for each of the states in the QCKA protocol.
Full size table
Fig. 4: Conference key rate, with finite-key effects, as a function of the number of successful network usages (Ltot).
figure 4

The performance for the NQKD protocol is shown by the solid line, while the 2QKD protocol is given by the dashed line. Both assume a fixed total security parameter, ϵtot = 10−8.

Full size image

Discussion

We have shown that, once genuine quantum networks capable of providing multi-node entanglement in the background become available, NQKD conclusively outperforms 2QKD in terms of key rate per network use. The NQKD advantage is at best N − 1. Many graphs however will allow for a Bell state multi-cast11,24, where more than one Bell pair can be distilled in a single network use between participating users. The graph we chose for our network demonstration allows precisely this, reducing the maximal theoretical NQKD advantage over 2QKD from three-fold to two-fold, thus providing the fairest possible comparison between the two QCKA protocols. In the Supplementary Discussion we investigate the option to multi-cast in the ring network.

Conversely, in a scenario with direct transmission of GHZ states over multiple quantum channels connecting Alice to the Bobs (as in14), NQKD is unlikely to achieve higher absolute rates than what is possible via 2QKD with state-of-the-art systems. GHZ state generation is currently probabilistic and slow, but will eventually catch up because deterministic multi-photon sources are on the development path for optical quantum computation. Even then, NQKD requires N photons to be detected simultaneously, which exponentiates the known rate-distance limit26,27 in individual quantum channels. In 2QKD, N − 1 photons can be transmitted and detected asynchronously, and the rate loss is therefore merely additive. This comparison becomes more complex once repeater nodes are incorporated into networks, as multi-hops and routing configurations need to be considered28,29,30. Indeed, when allowing for storage of quantum states at repeater nodes the transmission of GHZ states instead of Bell pairs can improve transmission distances, storage times and robustness to noise31,32,33.

As one of the first multi-user quantum communication protocols with a network advantage, QCKA is now a very active research area. Protocols have been developed for measurement-device independent scenarios30,34 and implementations with weak coherent states that might outperform N-photon GHZ state transmission35,36. Loss-resilient encoding of GHZ states for QCKA using error correction methods have also been proposed37. Studies of QCKA have raised fundamental questions about the type of entanglement that is useful in multi-user quantum communication. It has been shown that genuine multi-partite entanglement is not strictly required for QCKA38. Nonetheless, obtaining a non-zero conference key could be used as a witness for entanglement in a network38,39.

It will be important to explore other network protocols that gain an advantage from multi-partite entanglement. One example is QCKA-based anonymous conference key agreement which generates a conference key while hiding the identities of the participants40,41,42,43, theoretically achieving a significant advantage when using both GHZ states and Bell pairs41 compared to using Bell pairs alone44. Quantum secret sharing45 also gains a network advantage from GHZ states. Going beyond communication protocols, it has been shown that distributed sensing can benefit from multi-partite entanglement shared between measurement nodes46. A key question for these protocols is whether the required multi-party sub-graphs can be obtained from a network efficiently. For networks based on graph states this has been answered in the affirmative24 however generalisations to other resource states is an ongoing challenge47.

Methods

Parameter estimation

In the N-BB84 protocol QBER is defined as the largest pair-wise error rate observed from the type-1 rounds, i.e., when all users measure jointly in the Z basis. For convenience we adopt a general labelling of a group of N users following the set, {A, B1, B2, . . . , BN−1}. Thus for an N-GHZ state, errors in the Z basis occur when there is a non-zero probability that one of the Bobs obtains an outcome that differs from Alice. Explicitly, the QBER is defined as:

$${{{\rm{QBER}}}}\,\doteq \mathop{\max }\limits_{i\in \{1,2,\ldots ,({{{\rm{N}}}}-1)\}}{Q}_{{{{{\rm{AB}}}}}_{i}},$$
(3)

where \({Q}_{{{{{\rm{AB}}}}}_{i}}=\Pr ({{{{\rm{Z}}}}}_{{{{\rm{A}}}}}\,\ne \,{{{{\rm{Z}}}}}_{{{{{\rm{B}}}}}_{i}})=(1-\langle {{{{\rm{Z}}}}}_{{{{\rm{A}}}}}{{{{\rm{Z}}}}}_{{{{{\rm{B}}}}}_{i}}\rangle )/2\). When evaluating the pair-wise error rates for different i, the role of Alice does not have to be assigned to a specific user. Rather, we can permute the role of Alice within the set of users, by updating the indices of each user. We find different maximum pair-wise error rates (QBER) depending on the permutation, due to noise being distributed unevenly among each of the six qubits of the resource state. By iterating through all permutations, we select the role of Alice based on yielding the lowest QBER, optimising the conference key rate.

Phase error for a N-GHZ state can be estimated from X basis measurements. This is calculated by determining the deviation in measurement outcome from the expected correlations. This is expressed as,

$${Q}_{{{{\rm{X}}}}}=(1-\langle {{{{\rm{X}}}}}^{\otimes {{{\rm{N}}}}}\rangle )/2.$$
(4)

Both QBER and QX are zero in the absence of error and noise, indicating that there is no deviation from the expected behaviour of the GHZ state.

For Bell states, both QBER and QX can be evaluated using the same expressions as above. However, since there are only two users sharing a Bell state we skip the step of permuting the role of Alice in the group.

Experimental layout

Photon pair sources

To produce the six-photon graph state we use three photon-pair sources which are optically pumped by a 1.3 picosecond Ti-Sapph laser that has a nominal repetition rate of 80 MHz. All three are type-II parametric down-conversion (PDC) sources based on domain-engineered aperiodically-poled KTP (aKTP) crystals that are optimally phase-matched for spectrally pure photon pairs at 1550 nm. We can therefore achieve two-photon interference visibilities of up to 98.6 ± 1.1%. For more details on the design of the crystals, please see ref. 48. High spectral purity is achieved without needing narrow-band filters which improves collection efficiency and increases the overall detection rate. Each aKTP crystal is embedded in a polarisation-based Sagnac interferometer which can be optically pumped bidirectionally to produce polarisation-entangled photon pairs49,

$${\left\vert {\Psi }^{-}\right\rangle }_{a,b}=\frac{{\left\vert {\mathsf{hv}}\right\rangle }_{a,b}-{\left\vert {\mathsf{vh}}\right\rangle }_{a,b}}{\sqrt{2}},$$

where \(\left\vert {\mathsf{h}}\right\rangle\) and \(\left\vert {\mathsf{v}}\right\rangle\) correspond to horizontal and vertical polarisation states respectively, and subscripts denote optical modes. We remark that the \(\left\vert {\Psi }^{-}\right\rangle\) Bell state can be transformed into the \(\left\vert {\Phi }^{+}\right\rangle\) Bell state via a local operation using polarisation optics. Both Sagnac interferometers produced Bell states with purities of 0.9783(5) and 0.9706(3). Last, we can configure one of the sources to produce separable states by optically pumping the Sagnac loop in one direction, thus generating the state \(\left\vert ++\right\rangle \doteq \left\vert {\mathsf{dd}}\right\rangle\), where \(\left\vert {\mathsf{d}}\right\rangle \doteq (\left\vert {\mathsf{h}}\right\rangle +\left\vert {\mathsf{v}}\right\rangle )/\sqrt{2}\) is the diagonal polarisation state.

The linear optical circuit responsible for producing the six-photon graph state consists of three fusion gates50 along with single-qubit gates on the respective modes, shown in Fig. 2. The linear optical fusion gate is probabilistic, with a success rate of 1/2, however successful operation is heralded by the detection of one photon in each output of the gate. The overall success probability of all three fusion gates is 1/8. See Supplementary Methods for further experimental detail. After the network of fusion gates and upon detecting one photon in each of the six numbered modes, the joint quantum state of the system is given by,

$$\begin{array}{lll}{\left\vert \Psi \right\rangle }_{{{{\rm{initial}}}}}\,=\,\left(\left\vert {\mathsf{hhhhhh}}\right\rangle -\left\vert {\mathsf{hhhhvv}}\right\rangle -\left\vert {\mathsf{hhvvhh}}\right\rangle \right.\\ \qquad\qquad\quad-\left\vert {\mathsf{hhvvvv}}\right\rangle -\left\vert {\mathsf{vvhhhh}}\right\rangle +\left\vert {\mathsf{vvhhvv}}\right\rangle \\ \qquad\qquad\quad-\left.\left\vert {\mathsf{vvvvhh}}\right\rangle -\left\vert {\mathsf{vvvvvv}}\right\rangle \right)/\sqrt{8}.\end{array}$$
(5)

We remark that this state is equivalent to the six-photon graph state discussed in the main body of work, subject to a set of local rotations,

$$({\mathbb{H}}\otimes {{{\rm{Z}}}}\otimes {\mathbb{H}}\otimes {{{\rm{Z}}}}\otimes {\mathbb{H}}\otimes {{{\rm{Z}}}}){\left\vert \Psi \right\rangle }_{{{{\rm{initial}}}}}={\left\vert {\mathsf{G}}\right\rangle }_{{{{\rm{target}}}}}$$

where the target state is a graph state, \({\left\vert {\mathsf{G}}\right\rangle }_{{{{\rm{target}}}}}\) and \({\mathbb{H}}\) is the Hadamard gate.

After the fusion gates, the photons go to tomography stages which consist of a HWP, QWP and a PBS, after which photons are coupled into single mode fibres.

Graph state formalism

We use the graph state formalism to represent the transformations of the resource state used to distribute the GHZ state and Bell pairs between the four users. As the resource state is capable of distilling a GHZ state and sets of Bell pairs, this enables direct comparison of QCKA based on NQKD and 2QKD without changing the structure of the linear optical circuit. The general form of a graph state G = (V, E) reads:

$$\left\vert {\mathsf{G}}\right\rangle =\mathop{\prod}\limits_{(i,j)\in E}{{\mathsf{CZ}}}_{ij}{\left\vert +\right\rangle }^{\otimes | V| }.$$
(6)

where CZi,j is the two-qubit controlled-Z gate acting on modes {i, j}, E is the list of edges connecting two vertices and ∣V∣ is the number of vertices of the graph. Using this notation, we define our target graph state as,

$${\left\vert {\mathsf{G}}\right\rangle }_{{{{\rm{target}}}}}=({{\mathsf{CZ}}}_{1,2}\otimes {{\mathsf{CZ}}}_{2,4}\otimes {{\mathsf{CZ}}}_{3,4}\otimes {{\mathsf{CZ}}}_{4,6}\otimes {{\mathsf{CZ}}}_{5,6}){\left\vert +\right\rangle }^{\otimes 6},$$
(7)

For more details on this construction and the graph state formalism see Supplementary Methods.

One specific transformation within the graph state formalism is called local complementation (LC). An LC operation itself is comprised of two different unitaries. On a vertex designated as the target, the operation \({{{\rm{T}}}}=\sqrt{-i{{{{\rm{X}}}}}_{t}}\) is applied where,

$${{{\rm{T}}}}=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}&-\frac{i}{\sqrt{2}}\\ -\frac{i}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{array}\right)$$

whilst each vertex neighbouring the target, the operation \({{{\rm{N}}}}=\sqrt{i{{{{\rm{Z}}}}}_{n}}\) is applied where,

$${{{\rm{N}}}}=\left(\begin{array}{cc}{e}^{\frac{i\pi }{4}}&0\\ 0&-i{e}^{\frac{i\pi }{4}}\end{array}\right).$$

Measurement sequences

After the fusion gates, each photon is sent to a tomography stage consisting of a set of controllable HWP and QWP then onto a PBS with both output ports fibre coupled. From the initial target graph \({\left\vert {\mathsf{G}}\right\rangle }_{{{{\rm{target}}}}}\) LC operations are used, transforming the initial graph into alternative graphs within the same entanglement class (or graph state orbit), whereby different combinations of Bell states or a single GHZ state can be obtained25. This is illustrated in Fig. 2 in the main text.

We assign Alice, Bob-1, Charlie, Debbie, Bob-2 and Bob-3, to qubit numbers 1, 2, 3, 4, 5 and 6 respectively. To evaluate the AKR for a comparison between QCKA techniques, we need to calculate QZ (or QBER) and QX for each state that plays a part in the QCKA protocol. All single-qubit operations applied to the initial graph such that network users obtain the correct state and perform the correct measurements are encoded onto the measurement settings, including the LC operations. Obtaining a GHZ shared between Alice and the Bobs in the four-photon state space, to carry out QCKA with a multi-partite resource, Charlie and Debbie are required to make projections in the Z basis. So for each round of measurements, whilst Charlie and Debbie should always measure in the Z basis, Alice and the Bobs measurements are made based on whether they want to complete a type-1 round or type-2 round of the protocol. For example, to measure the observable 〈Z1Z2Z5Z6〉 of the GHZ state to evaluate the QBER, all users must measure the observable 〈Z1Z2X3X4Z5Z6〉, where the required single-qubit operations leave the default measurement settings unchanged for Alice and the Bobs, but rotate Charlie and Debbie’s measurement settings. To measure the observable 〈X1X2X5X6〉 of the GHZ state to obtain QX, all network users must measure the observable 〈X1Y2X3X4X5Y6〉, where now single-qubit operations encoded onto the measurement settings correspond to rotations of measurements into a different basis. When Alice and the Bobs wish to partake in QCKA with bi-partite resources, the measurement procedure suitably follows that of the GHZ state, except now the observables are for Bell states, and alternate single-qubit operations—based on required rotations applied to the initial graph—are encoded onto these settings. Full blueprints containing the operations applied to each qubit within each measurement set are presented in Fig. 2. The measured 〈Z⊗N〉 and 〈X⊗N〉 observables, where N is the qubit number, of the three Bell states and the GHZ state used in this protocol are presented in Fig. 3.