Introduction

Using controllable quantum systems, quantum simulation provides a powerful approach to study many-body physics, which might be challenging for a classical computer1,2. In analog quantum simulation, specific model Hamiltonians can be directly realized by engineering the platform Hamiltonians such that dynamics of real quantum systems can be studied in a controllable manner, such as in trapped ions3,4,5, atoms in optical lattices6,7,8,9, superconducting qubits10,11,12, and nuclear spins13,14. Particularly, superconducting quantum simulation can explore a wide regime from localization to weak and strong thermalization in non-equilibrium quantum many-body systems15,16,17,18,19,20,21,22,23.

On the other hand, the 1D Aubry-André-Harper (AAH) model24,25, as a workhorse for studying localization and topological states, has attracted much attention both theoretically and experimentally16,26,27,28,29,30,31,32,33,34,35,36. The original AAH model can be derived from a 2D quantum Hall system with nearest-neighbor hopping. When considering the next-nearest-neighbor hopping, one can deduce a generalization of the AAH model with both on-site and off-diagonal quasi-periodic modulations37,38. The generalized AAH (GAAH) model shows different and interesting localization and topological properties, for instance, the critical phase featured by multifractal wave functions and the topological adiabatic pumping39,40,41,42,43,44. With the development of experimental technologies, the GAAH model has been realized in photonic crystals with on-site or off-diagonal modulation31, and cold atoms systems in momentum space45, which observes the dynamics only at the single-particle level (or the mean-field level). With flexible control and precise measurement of superconducting processor, the GAAH model may be simulated analogously, given off-diagonal quasi-periodic modulations can be implemented precisely.

In our experiment, taking advantage of recently developed tunable coupling architecture46,47, we simulate the GAAH model for a wide variety of parameters on a superconducting processor . By adjusting both qubits and couplers, we experimentally observe the dynamics of the extended, localized, and critical phase in the GAAH model, and investigate the phase transition from the perspective of non-equilibrium many-body dynamics. We observe that in the critical phase, the spin can propagate over a range intermediate between that of the extended phase and of the localized phase, for both initial single- and multi-excitation states. In addition, we quantify how fast the initial states spread over the Hilbert space for different phases by experimentally measuring the time evolution of participation entropies, and characterize the transitions between the extended, localized, and critical phase by calculating averaged late-time participation entropies.

Results

Model and set-up

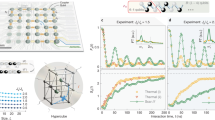
Our quantum processor consists of a chain array of L = 10 transmon superconducting qubits, and 9 tunable couplers with each placed between every two nearest-neighbor qubits, which enable an accurate control of couplings (see Fig. 1a and Supplementary Note 1 for details). The effective Hamiltonian of the qubits system reads

$$\frac{\hat{H}}{\hslash }=\mathop{\sum }\limits_{j=1}^{9}{J}_{j,j+1}({\hat{\sigma }}_{j}^{+}{\hat{\sigma }}_{j+1}^{-}+{\hat{\sigma }}_{j}^{-}{\hat{\sigma }}_{j+1}^{+})+\mathop{\sum }\limits_{j=1}^{10}{h}_{j}{\hat{\sigma }}_{j}^{+}{\hat{\sigma }}_{j}^{-},$$
(1)

where \({\hat{\sigma }}_{j}^{+}({\hat{\sigma }}_{j}^{-})\) is the raising (lowering) operator, hj is the tunable local potential, and Jj,j+1 is the nearest-neighbor coupling strength.

Fig. 1: Experimental setup.
figure 1

a Circuit diagram of the superconducting processor, consisting of ten transmon qubits, Q1–Q10, and nine couplers C1–C9, each of which is placed between every two nearest-neighbor qubits. b Schematic representation of the GAAH model with both the on-site and off-diagonal quasi-periodic modulations. The darkness of the double-headed arrows above the qubits indicates the variation of nearest-neighbor coupling strength Ji,i+1, and the sinusoidal curve below the qubits shows the on-site potential hj with modulation amplitude V. c Phase diagram of the GAAH model, divided into extended (E), localized (L), and critical (C) phases. The heatmap shows the inverse participation ratio (IPR) averaged over all eigenstates and 100 configurations of δ for system size L = 1000. d Experimental pulse sequences for observing localization properties of the GAAH model.

Full size image

In our superconducting processor with tunable couplers, the coupling Jj,j+1 contains two part: (i) direct coupling between nearest-neighbor qubits \({J}_{j,j+1}^{0}\) and (ii) superexchange interaction via the coupler in between \({J}_{j,j+1}^{SE}\propto 1/{{{\Delta }}}_{j,j+1}\) with Δj,j+1 denoting frequency detuning between the j-th coupler and the two nearest-neighbor qubits (see Methods and Supplementary Note 1 for details). Therefore, we can individually adjust the coupling by controlling the frequency of the corresponding coupler with the fast flux bias. In our processor, it allows a range of Jj,j+1/(2π) from − 30 to + 4.8 MHz. In addition, by applying the fast Z pulse on each qubit, the local potential can also be arbitrarily tuned relative to reference frequency ~ 4.36 GHz.

In the experiments, as depicted in Fig. 1b, we take a quasi-periodic modulation \({J}_{j,j+1}=\lambda \left(1+\mu \cos \left[2\pi \left(j+1/2\right)\alpha +\delta \right]\right)\) and \({h}_{j}=\lambda V\cos (2\pi j\alpha +\delta )\), where μ and V indicate the off-diagonal and on-site modulation amplitudes, respectively. We manipulate μ and V by applying the fast voltages to the corresponding Z control lines of the coupler and qubit respectively, and we choose λ/(2π) = 4 MHz throughout the work. Besides, \(\alpha =(\sqrt{5}-1)/2\) is the irrational frequency which takes the same value for on-site and off-diagonal modulations, and \(\delta \in \left[-\pi ,\pi \right)\) is an arbitrary global phase offset.

For different parameters μ and V, localization property of the eigenstates of Hamiltonian (1) can be characterized by the inverse participation ratio (IPR)48,49,50,51,52,53. In Fig. 1c, we plot the single-particle localization phase diagram of Hamiltonian (1). The heatmap shows the negative logarithm of eigenstate’s IPR \(={\sum }_{i}{\left\vert {\psi }_{n,i}\right\vert }^{4}\), where ψn,i = 〈ψn∣i〉 is the wave function coefficient of the eigenstate \(\left\vert {\psi }_{n}\right\rangle\) on site i. Since mobility edges are absent in our model42, (i) for V < 2, μ < 1, all bulk eigenstates are extended, denoted as the extended phase, where the IPR vanishes and its negative logarithm is close to \(\log L\); (ii) for \(V > 2\max (1,\mu )\), all bulk eigenstates are localized with the IPR close to one and its negative logarithm close to zero, denoted as the localized phase; (iii) in the rest (\(\mu > \max (1,V/2)\)), the eigenstates are critical with intermediate IPRs, denoted as the critical phase.

Observation of spin transport in the GAAH model

First, we show that the GAAH model can be simulated with our superconducting qubits in a tunable coupling architecture. The experimental scheme is that three phases of the GAAH model manifest distinguishing localization properties by measuring the on-site population of spins for specific initial states. We initially excite the leftmost qubit Q1, i.e., the system is initialized as \(\left\vert \psi (0)\right\rangle =\left\vert 1000000000\right\rangle\), where \(\left\vert 0\right\rangle\) (\(\left\vert 1\right\rangle\)) denotes the ground (excited) state of a qubit. Then we apply the fast Z pulse on each qubit and coupler, and the system will evolve under the Hamiltonian (1). We measure the on-site population of each qubit \({P}_{j}(t)=\langle \psi (t)\vert {\hat{\sigma }}_{j}^{+}{\hat{\sigma }}_{j}^{-}\vert \psi (t)\rangle\) from t = 0 to 500 ns. For each time point, we perform 5000 repeated single-shot measurements.

The experimental results for the three phases are plotted in the left panel of Fig. 2a–c, with a comparison of numerical simulations in the right panel of Fig. 2a–c (see Supplementary Note 2 for details of numerical simulations). In the extended phase, the spin excitation spreads ballistically from an initially excited qubit to its neighboring qubits and reflects at the boundary. The spin serving as the carrier of the information propagates as light travels in spacetime, referred to as lightcone-like propagation21, and it is still visible when weak off-diagonal and on-site quasi-periodic disorder exists, as shown in Fig. 2a. As the opposite, for sufficiently large on-site disorder V, the spin is fully localized, and only initially excited qubits have the population close to one at any time (Fig. 2c). In the critical region (Fig. 2b), the spin transport is not completely blocked, but instead, the spin tends to oscillate around adjacent sites of the initially excited qubit. The propagation range in this phase is intermediate between the two aforementioned phases, leading to a non-zero probability of finding spin excitations even on the right half of the spin chain.

Fig. 2: Spin transport.
figure 2

The time evolutions of qubit-resolved on-site population Pj(t) for the system initialized in (a–c)\(\left\vert \psi (0)\right\rangle =\left\vert 1000000000\right\rangle\), and (d–f)\(\left\vert \psi (0)\right\rangle =\left\vert 1010101010\right\rangle\), in (a, d) the extended phases with μ = 0.5 and V = 0.5; b, e the critical phases with μ = 2.0 and V = 0.5; c, f the localized phases with μ = 0.5 and V = 4.0. The left panel of each figure shows experimental data, and the right panel shows numerical simulation. Experimental data are averaged over 5 different choices of δ, while numerical results are averaged over 50 choices of δ with decoherence taken into account.

Full size image

With the capability of precise simultaneous control and readout, we can also prepare initial product states to probe the half-filled sector. The experimental sequences are shown in Fig. 1d. Here, we focus on an initial Néel state \(\left\vert \psi (0)\right\rangle =\left\vert 1010101010\right\rangle\). The experimental and numerical results are plotted in Fig. 2d–f. As shown in Fig. 2d, in the extended region, the mean population oscillates around 0.5 at long times for all ten qubits with a small fluctuation, showing a pattern of oscillation between odd and even sites back and forth. In Fig. 2e, the population for all qubits is also close to 0.5 in the critical region, but exhibits a certain degree of dependence on the initial configuration. The population for the initially excited qubits tends to stay above 0.5, while that for the qubits initialized in \(\left\vert 0\right\rangle\) tends to stay below 0.5. Figure 2f shows the spin transport is completely blocked in the localized region, and the population stays close to one for the initially excited qubits, and close to zero for the qubits initialized in \(\left\vert 0\right\rangle\).

Dynamical signature of localization via participation entropies

As stated above, localization properties can be quantified by the IPR and the associated participation entropy. Here, we define the q-th order dynamical participation entropy19,52 as

$${S}_{q}^{{{{\rm{PE}}}}}(t)=\frac{1}{1-q}\log \mathop{\sum }\limits_{i}^{{{{\mathcal{N}}}}}{p}_{i}{(t)}^{q},$$
(2)

where \({{{\mathcal{N}}}}\) is the dimension of Hilbert space, and pi(t) = ∣〈ψ(t)∣i〉∣2 with the computational basis \(\{\left\vert i\right\rangle \}\). Considering the U(1) symmetry, the dimension of the half-filled sector is \({{{\mathcal{N}}}}=(\begin{array}{l}10\\ 5\end{array})=252\). Here, we focus on the second-order participation entropy, i.e., \({S}_{2}^{{{{\rm{PE}}}}}(t)=-\log \mathop{\sum }\limits_{i}^{{{{\mathcal{N}}}}}{p}_{i}{(t)}^{2}\), which is related to IPR by taking the negative logarithm. In the Supplementary Note 3, we also display the results of first-order participation entropy.

The dynamical participation entropy is a characterization quantifying how fast \(\left\vert \psi (t)\right\rangle\) spreads over the Hilbert space19,54. Initial product states, with probability one as a Fock state, diffuse in Fock space as the system evolves, and the wave functions have more and more non-zero probabilities in the computational (Fock) basis, which results in the increase of the participating entropy with time. Here we select 2 × M = 10 initial states which is far from equilibrium, taking the form \(\left\vert {\psi }_{i}(0)\right\rangle ={\left\vert 10\right\rangle }^{\otimes (M+1-i)}\bigotimes {\left\vert 01\right\rangle }^{\otimes (i-1)}\), and \(\left\vert {\psi }_{M+i}(0)\right\rangle =\hat{G}\left\vert {\psi }_{i}(0)\right\rangle\) with a global spin-flip operator \(\hat{G}=\mathop{\prod }\limits_{j=1}^{L}{\hat{\sigma }}_{j}^{x}\), for i = 1, …, M. The experimental data shown in Fig. 3 are averaged over these 10 initial states, and the measured multi-qubit probabilities pi(t) are post-selected within the half-filled sector due to the U(1) symmetry.

Fig. 3: Time evolution of participation entropy.
figure 3

a The dynamics of participation entropy for the system quenched into the three phases. The yellow, red, and purple points are experimental data for the extended (μ = 0.5, V = 1.0), critical (μ = 2.0, V = 1.0), and localized (μ = 0.5, V = 4.0) phases, respectively. The dynamics of participation entropy with (b) fixed μ = 0.5 and varying V = 1 to 4, and (c) fixed V = 1 and varying μ = 0.5 to 2. Lines with the same color as points are numerical simulation under the same parameters with decoherence taken into account. Error bars represent the standard deviation.

Full size image

Figure 3a displays the time evolution of participation entropy for the system quenched into the three phases. After a fast initial relaxation, the participation entropy oscillates around some certain value, which varies in different phases. For both small μ and V, the system lies in the extended phase, where the late-time participation entropy keeps at a high value with a small oscillation. For small μ and sufficiently large V, the participation entropy oscillates around a much smaller value. For sufficiently large \(\mu \,>\, \max (1,V/2)\), the late-time participation entropy in the critical phase oscillates around a plateau intermediate between the values observed in the extended and localized phases. This behavior is similar to that near the critical line (V = 2 for small μ), as can be seen from the data for V = 2 in Fig. 3b for comparison.

Figure 3b, c shows the time evolution of participation entropy with increasing V for fixed μ = 0.5, and increasing μ for fixed V = 1, respectively. As shown in Fig. 3b, with the increase of V, the growth of participation entropy is suppressed significantly, reflecting a transition from the extended region to the localized region. In contrast, in Fig. 3c, as μ increases to approach the theoretical transition point μc = 1.0, the growth of participation entropy slows down compared to the extended phase. However, as μ continues to increase, the curve of time evolution of participation entropy rises slightly again. The late-time participation entropy in the critical phase reflect a multifractal behavior, and the multifractal analysis can be found in the Supplementary Note 4.

In addition, the averaged participation entropy at long times can be used as an experimentally accessible characterization of phase transition. Here, we experimentally measure the averaged late-time participation entropies \(\overline{{S}_{2}^{{{{\rm{PE}}}}}}\) along three paths I, II, and III in the μ−V plane (see Fig. 4a), corresponding to extended to localized transition, extended to critical transition, and localized to critical transition, respectively. Averages are taken over a time window from 350 to 450 ns (see the gray area in Fig. 3a), and among the 10 initial states as defined before. In Fig. 4a, we also display the numerical results of the averaged late-time participation entropy calculated using Hamiltonian (1) for the whole μ−V plane (0 ≤ V ≤ 4, 0 ≤ μ ≤ 2) as a reference, which exhibits a similar phase diagram to IPR averaged over eigenstates in Fig. 1c. Because the time window is far less than the averaged \(\overline{{T}_{1}}\sim22.3\mu\) s, we ignore the effect of decoherence in the simulation here (see Supplementary Note 2 for details). The numerical simulation and experimental results are consistent well with each other.

Fig. 4: Averaged late-time participation entropy.
figure 4

a Averaged late-time participation entropy \(\overline{{S}_{2}^{{{{\rm{PE}}}}}}\) as a function of μ and V. The stripes I, II and III show the experimentally measured averaged late-time participation entropy, and the underlying phase diagram shows the numerically calculated averaged late-time participation entropy using the Hamiltonian (1). The white dashed line shows theoretical phase boundaries as a guide to eye. Comparisons between experimental data and numerical simulation along (b) the path I with fixed μ = 0.5, (c) II with fixed V = 1, and (d) III with fixed V = 3. Points with statistical error bars are experimental data, and solid lines are numerical simulation using the Hamiltonian (1). Dashed lines exhibit the numerically calculated averaged late-time participation entropy rescaled as \(\widetilde{\overline{{S}_{2}^{{{{\rm{PE}}}}}}}(L)=\frac{\log {{{{\mathcal{N}}}}}_{10}}{\log {{{{\mathcal{N}}}}}_{L}}\cdot \overline{{S}_{2}^{{{{\rm{PE}}}}}}(L)\) for larger system sizes. Error bars represent the standard deviation.

Full size image

Comparisons of the specific experimental data with numerical simulation of the three paths I, II and III are plotted in Fig. 4b, c and d, respectively. Different from the path I, where \(\overline{{S}_{2}^{{{{\rm{PE}}}}}}\) decreases monotonically as μ increases, for the path II, \(\overline{{S}_{2}^{{{{\rm{PE}}}}}}\) first decreases to the minimum around the theoretical transition point μc = 1.0, and then increases slightly but keeps almost unchanged for increasing μ in the critical phase. Note that both the experimentally measured and numerically calculated minimum \(\overline{{S}_{2}^{{{{\rm{PE}}}}}}\) are reached at μ = 1.25 instead of μc = 1.0 for L = 10, which we attribute to finite size effects. To see this, we also display the numerically calculated averaged late participation entropies for larger system sizes L = 14, 18, 22, rescaled as \(\widetilde{\overline{{S}_{2}^{{{{\rm{PE}}}}}}}(L)=\frac{\log {{{{\mathcal{N}}}}}_{10}}{\log {{{{\mathcal{N}}}}}_{L}}\cdot \overline{{S}_{2}^{{{{\rm{PE}}}}}}(L)\), with \({{{{\mathcal{N}}}}}_{L}=(\begin{array}{l}L\\ L/2\end{array})\) for a direct comparison to the experimental system size L = 10. In the systems with L = 14, 18, 22, the minimum \(\overline{{S}_{2}^{{{{\rm{PE}}}}}}\) are reached at μc = 1.0. For the path III, i.e., the localized to critical transition, \(\overline{{S}_{2}^{{{{\rm{PE}}}}}}\) decreases slightly for increasing μ ≤ 1, and then increases and finally reaches a intermediate value featuring a multifractal behavior, as μ increases across the transition point \({\mu }_{c}^{{\prime} }=1.5\) for fixed V = 3. The slope at the transition point \({\mu }_{c}^{{\prime} }=1.5\) increases with system size, which will diverge in the thermodynamic limit as a signature of the localized to critical transition.

In summary, different from the Anderson model which would be localized at any non-zero random disorder in on-site potential or in hopping coupling (see Supplementary Note 5 for details), a critical region emerges in the GAAH model due to the combined effect of deterministic quasi-periodic on-site potential and hopping coupling, which exhibit different dynamical behavior from that in the extended and the localized phases.

Just like the critical line (V = 2 for small μ) exhibiting intermediate behavior, the critical phase (\(\mu \,> \,\max (1,V/2)\)) also exhibits properties that are in between the other two phases. Therefore, the critical phase shares some similarities with the extended phase, such as its delocalized nature; and it also resembles the localized phase in some respects, for example, only a small fraction of the Fock space which is actively involved54,55, leading to oscillations of the participation entropy similar to that in the localized phase, and stronger than that in the extended phase for the same system size and the same number of different choices of δ. A more detailed discussion from the perspective of Fock space can be found in Supplementary Note 6.

Discussion

In this work, we implement a simulation of the GAAH model for a wide range of parameters. The capability of individual control and multi-qubit simultaneous readout of our superconducting processor allows for observation of multi-qubit spin transport and measurement of participation entropies revealing different dynamical behaviors in three distinct phases and phase transitions of the model.

Our work extends the current state of quantum simulations by introducing simultaneous tunable coupling and qubit frequency control, which, for example, enables engineering more types of Hamiltonians exhibiting different topological properties, and measuring quantities like Loschmidt echo and OTOCs which needs coherently reverse time evolution by changing the sign of Hamiltonians. In addition, we note that the GAAH model with many-body interactions hosts a similar phase diagram, where a novel many-body critical phase which is delocalized but nonthermal emerges due to interaction effects44. The phase transitions between the ergodic phase, the many-body localized phase, and the many-body critical phase deserve further experimental exploration by probing many-body dynamics.

Methods

Adjustment of the hopping coupling

As mentioned in the main text, the coupling Jj,j+1 contains two part: (i) direct coupling between nearest-neighbor qubits \({J}_{j,j+1}^{0}\) and (ii) superexchange interaction via the coupler in between \({J}_{j,j+1}^{SE}={J}_{j}^{0}{J}_{j+1}^{0}/{{{\Delta }}}_{j,j+1}\). Therefore, the effective coupling strength can be described by refs. 46,47:

$${J}_{j,j+1}={J}_{j,j+1}^{0}+{J}_{j,j+1}^{SE},$$
(3)

where \({J}_{j,j+1}^{0}\) is the direct coupling between Qj and Qj+1, \({J}_{j}^{0}\) is the direct coupling between Qj and Cj, and \({{{\Delta }}}_{j,j+1}=2/\left[1/\left({\omega }_{{Q}_{j}}-{\omega }_{{C}_{j}}\right)+1/\left({\omega }_{{Q}_{j+1}}-{\omega }_{{C}_{j}}\right)\right]\) denotes frequency detuning between the j-th coupler and the two nearest-neighbor qubits. The effective coupling Jj,j+1 can be tuned by applying fast flux bias to the Z control lines of the couplers and measured precisely by the joint probility as a function of qubit-qubit swapping time (see Supplementary Note 1 for details). In principle, the coupling can be adjusted arbitrarily according to Eq. (3). However, limited by the microwave frequency band of measurement devices (from 4 to 7 GHz) and the undesired ZZ interaction between a coupler and its two nearest-neighbor qubits, the applicable adjustable range of coupling is −30.0 to 4.8 MHz, and we used only −15.0 to 3.8 MHz in our experiments. To realized the target coupling distribution, we firstly estimated all the Z pulse amplitudes of the couplers by Eq. (3) and checked each coupling of two nearest-neighbor qubits by the time-dependent swap experiment at the resonant frequency around 4.36 GHz. If the checked coupling strength is not close to the target, we will fine-tune the Z pulse of the corresponding coupler (within the tolerance 0.1 MHz). For each off-diagonal modulation amplitude μ, we calibrated all the coupling strengths and fixed this configuration for the on-site potential calibrations.

Calibration of the on-site potential

The on-site potentials satisfying Eq. (1) was realized by performing two specific vacuum Rabi oscillation experiments on the target qubit. In order to mitigate the AC Stark effect between qubits when simultaneously biased the frequencies, we designed two staggered frequency distributions (±80 MHz away from the reference frequency) of non-target qubits. The Z pulse amplitude corresponding to the target on-site potential of each qubit was determined by the average of the results from these two experiments under different configurations (see more details in Supplementary Note 1).

Measurement of spin transport and participation entropies

In the experiments of spin transport, we prepared the single-particle and half-filled excited states as the initial states and then manipulated all the qubits and couplers to their operating points corresponding to the GAAH model. By varying the evolution time from 0 to 500 ns, for each choice of the global phase offset δ, we simultaneously measured the on-site populations of all the qubits by 5000 repeated single-shot measurements for each time point. The readout correction was implemented by using the single-qubit readout fidelity matrix. For the experiments of measuring the participation entropies, all 210 probabilities of single-shot measurements were performed and the readout errors were corrected via the direct product of single-qubit readout fidelity matrices. To calculate the participation entropies, considering the U(1) symmetry of the GAAH model, we post-selected the states that conserve the total excitations17,19.