Critical parametric quantum sensing

Abstract

Critical quantum systems are a promising resource for quantum metrology applications, due to the diverging susceptibility developed in proximity of phase transitions. Here, we assess the metrological power of parametric Kerr resonators undergoing driven-dissipative phase transitions. We fully characterize the quantum Fisher information for frequency estimation, and the Helstrom bound for frequency discrimination. By going beyond the asymptotic regime, we show that the Heisenberg precision can be achieved with experimentally reachable parameters. We design protocols that exploit the critical behavior of nonlinear resonators to enhance the precision of quantum magnetometers and the fidelity of superconducting qubit readout.

Introduction

Criticality is a compelling resource, commonly used in classical sensing devices such as transition-edge detectors and bolometers¹. However, these devices do not follow optimal sensing strategies from the quantum mechanical point of view. A promising approach to quantum sensing exploits quantum fluctuations in the proximity of the criticality to improve the measurement precision. Despite a critical slowing down at the phase transition, theoretical analyses of many-body systems^{2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17} show that critical quantum sensors can achieve the optimal scaling of precision¹⁸, both in the number of probes and in the measurement time^8,17. Furthermore, it has been shown¹⁹ that finite-component phase transitions^{20,21,22,23,24}—where the thermodynamic limit is replaced by a scaling of the system parameters^{25,26,27,28,29}—can also be applied in sensing protocols. Surprisingly, quantum criticalities are versatile sensing resources that do not require the complexity of many-body system, as demonstrated by efficient dynamical protocols³⁰, the inclusion of quantum-control methods³¹ or ancillary probes³², the design of multiparameter estimation protocols³³ and of a critical quantum-thermometer³⁴, and by first experimental implementations³⁵.

Finite-component critical sensors have hitherto been designed for light–matter interacting models where the atomic levels introduce a nonlinearity³⁶. Despite their high experimental relevance in quantum optics and information^{37,38,39,40,41,42,43,44,45,46,47}, driven resonators with nonlinear photon-photon interactions have so far been overlooked for applications in critical quantum metrology. These systems display a broad and exotic variety of critical phenomena, and their nontrivial dynamics and steady states depend on both the system and bath parameters^26,48,49.

Here, we introduce the critical parametric quantum sensor, a measurement apparatus based on the second-order driven-dissipative phase transition of a parametric nonlinear (Kerr) resonator. We apply tools of quantum parameter estimation, quantum hypothesis testing, and non-linear quantum optics to characterize the potential of this instrument for finite-component critical sensing. Our treatment uses the analytical solutions of the driven-dissipative Kerr resonator model^50,51,52, together with exact numerical calculations to: (i) Evaluate the quantum Fisher information (QFI) for frequency estimation, analyzing its scaling in the thermodynamic limit of small–but finite–Kerr nonlinearity. We provide the parameter set maximizing the QFI, and show that homodyne detection virtually saturates the optimal precision bound. Importantly, the whole analysis considers the role of dissipation in these driven transitions. This allows us to design a highly-sensitive magnetometer, that can be built with state-of-the-art circuit QED technology. (ii) Compute the optimal and homodyne-based error probabilities in distinguishing the normal and the symmetry-broken phases. We apply this result to the dispersive qubit readout task in circuit-QED. Our approach goes beyond the semi-classical approximation^53,54, and allows one to recognize the set of parameters minimizing the average error probability. We find that the optimal working point lies in proximity of the critical point, in a region where semi-classical or Gaussian approximation can not be applied.

Results and discussion

Kerr resonator model

Our starting point is the Kerr-resonator model, whose Hamiltonian is

$${\hat{H}}_{{{{\rm{Kerr}}}}}/\hslash =\omega {\hat{a}}^{{\dagger} }\hat{a}+\frac{\epsilon }{2}({\hat{a}}^{{\dagger} 2}+{\hat{a}}^{2})+\chi {\hat{a}{}^{{\dagger} }}^{2}{\hat{a}}^{2}.$$

(1)

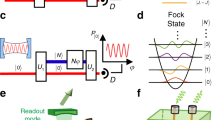
This ${{\mathbb{Z}}}_{2}$-symmetric model can be realized in various photonic platforms. In particular, we consider the case of a circuit-QED implementation, where a resonator at frequency ω_r is coupled with a superconducting quantum interference device (SQUID) element^53,55. If the resonator is pumped at a frequency ω_p ≃ 2ω_r, then Eq. (1) describes effectively the system, by interpreting ω = ω_r − ω_p/2 as the pump-resonator detuning, ϵ as the effective pump-power, and χas the SQUID-induced nonlinearity. We consider the system embedded in a Markovian thermal bath at zero temperature, described by the Lindblad dissipation superoperator ${{{{\mathcal{L}}}}}_{D}[\cdot ]=\hslash {{\Gamma }}[2\hat{a}\cdot {\hat{a}}^{{\dagger} }-\{{\hat{a}}^{{\dagger} }\hat{a},\cdot \}]$, where Γ ≥ 0 is loss rate induced by the system-bath coupling. Such a dissipator leaves the model ${{\mathbb{Z}}}_{2}$ invariant (see the Supplemental Material). With no loss of generality, we take ϵ positive. For χ = 0, the model is Gaussian and its phenomenology can be easily explained. In the absence of noise, for Γ = 0, the model has a ground state only for ϵ < ∣ω∣. This is a squeezed vacuum state with squeezing approaching infinity in the ϵ/∣ω∣ → 1 limit. When the bath is turned on, for Γ > 0, the diverging point is shifted. In this case, the steady-state is a squeezed thermal-state and exists only for $\epsilon < \sqrt{{\omega }^{2}+{{{\Gamma }}}^{2}}\equiv {\epsilon }_{c}$, with purity approaching zero when ϵ/ϵ_c → 1. The effect of the nonlinearity χ > 0 is to regularize the model for all parameter values, thus erasing the divergences. In the scaling limit χ → 0 a second-order dissipative phase transition (DPT) emerges, associated with the spontaneous breaking of the ${{\mathbb{Z}}}_{2}$-symmetry of the model²⁶ (see the Supplemental Material). The steady-state is still Gaussian for ϵ < ϵ_c. Beyond the critical point, for ϵ > ϵ_c, the steady-state is double-degenerate, and it is given by a statistical mixture of two equiprobable displaced squeezed thermal-states²⁷, see Fig. 1. Since χ can be made small in a circuit QED implementation, we can exploit the presence of this DPT for both quantum parameter estimation and discrimination. On the one hand, we can use the large susceptibility of the steady state in the proximity of the critical point, in order to get a good estimation of ω. In turn, as the resonator frequency has a steep dependence on the external magnetic field threading the SQUID loop, the DPT can be applied in the design of a critical magnetometer. On the other hand, the presence of the DPT allows one to faithfully discriminate between two discrete values of ω, each corresponding to a different phase, in a single-shot measurement.

Fig. 1: Wigner function of the system steady-state.

This has been obtained with numerical simulations of the full quantum model (colormap) and half-height contours (dashed blue circles) of the corresponding analytical solutions obtained under semi-classical approximation (see “Methods”). The four sub plots are obtained taking ω = 1Γ, χ = 0.04Γ and for increasing values of the pump strength ϵ. The figure shows the transition from the normal (a) to the symmetry-broken [(c) and (d)] phases, taking place around the semiclassical prediction $\epsilon ={\epsilon }_{c}=\sqrt{{\omega }^{2}+{{{\Gamma }}}^{2}}$ (b). The system is highly susceptible in the proximity of the criticality, and so it can be exploited in high-sensitivity magnetometry. Moreover, the system shows two highly distinguishable phases, corresponding to a vacuum-like (a) and displaced state (d), a feature that can be exploited in high-fidelity qubit readout.

Quantum parameter estimation

Given an observable $\hat{O}$, we can define the signal-to-noise ratio (SNR) for estimating the parameter ω as

$${S}_{\omega }[\hat{O}]=\frac{| {\partial }_{\omega }{\langle \hat{O}\rangle }_{\omega }{| }^{2}}{{{\Delta }}{\hat{O}}_{\omega }^{2}},$$

(2)

where ${{\Delta }}{\hat{O}}_{\omega }^{2}={\langle {\hat{O}}^{2}\rangle }_{\omega }-{\langle \hat{O}\rangle }_{\omega }^{2}$, and the expectation values are computed in the steady-state manifold. This standard definition of SNR is useful for parameter estimation protocols because it is directly related to the mean-square error of the estimator⁵⁶. The corresponding precision over M measurements is ${{\Delta }}{\omega }^{2}\simeq {[M{S}_{\omega }]}^{-1}$. In this paper, we consider the SNR for three important measurements: homodyne, heterodyne, and the quantum–mechanical optimal given by the QFI. Homodyne detection consists in projecting on the rotated quadrature operator ${\hat{x}}_{\varphi }=\cos (\varphi )\hat{x}+\sin (\varphi )\hat{p}$. Due to the ${{\mathbb{Z}}}_{2}$-symmetry of the system, we consider the observable ${\hat{x}}_{\varphi }^{2}$, and define the homodyne SNR as ${S}_{\omega }^{{{{\rm{Hom}}}}}=\mathop{\max }\nolimits_{\varphi }{S}_{\omega }[{\hat{x}}_{\varphi }^{2}]$. Heterodyne detection corresponds to a noisy measurement of the conjugate quadratures, with outcomes X and P. We consider the SNR for the outcome X² + P², which can be written as ${S}_{\omega }^{{{{\rm{Het}}}}}=| {\partial }_{\omega }{\langle \hat{a}{\hat{a}}^{{\dagger} }\rangle }_{\omega }{| }^{2}/[{\langle {\hat{a}}^{2}{\hat{a}}^{{\dagger} 2}\rangle }_{\omega }-{\langle \hat{a}{\hat{a}}^{{\dagger} }\rangle }_{\omega }^{2}]$, see “Methods”. Finally, if we maximize the SNR in Eq. (2) among all the observables, we obtain the QFI: ${I}_{\omega }=\mathop{\max }\nolimits_{\hat{O}}{S}_{\omega }[\hat{O}]$. This can be expressed as⁵⁷

$${I}_{\omega }=\mathop{\lim }\limits_{d\omega \to 0}\frac{8}{d{\omega }^{2}}\left[1-\sqrt{F({\rho }_{\omega },{\rho }_{\omega -d\omega })}\right],$$

(3)

where $F({\rho }_{\omega },{\rho }_{{\omega }^{{\prime} }})={[{{\mbox{Tr}}}(\sqrt{{\rho }_{\omega }\sqrt{{\rho }_{{\omega }^{{\prime} }}}{\rho }_{\omega }})]}^{2}$ is the fidelity between the steady-states ρ_ω and ${\rho }_{{\omega }^{{\prime} }}$.

The normal phase (χ → 0)

To begin with, we consider the case χ → 0, which provides us with a good approximation of the steady-state when we are far enough from the DPT. The model in Eq. (1) with χ = 0 has a steady-state solution only for ϵ < ϵ_c, corresponding to the normal phase. Using the analytical formula for Gaussian states⁵⁸, we compute the QFI with respect to the parameter ω, in the steady-states manifold:

$$\begin{array}{r}{I}_{\omega }(\epsilon \,<\, {\epsilon }_{c})\mathop{\longrightarrow }\limits^{\chi \to 0}\frac{1}{2{\epsilon }_{c}^{2}-{\epsilon }^{2}}\left[2N+\frac{8{\omega }^{2}}{{\epsilon }^{2}}{N}^{2}\right],\end{array}$$

(4)

where $N={\epsilon }^{2}/[2({\epsilon }_{c}^{2}-{\epsilon }^{2})]$ is the number of photons [see Fig. 2a]. We have two possible diverging scaling for ϵ/ϵ_c → 1. For ω ≠ 0 we retrieve the Heisenberg scaling I_ω = O(N²), while for ω = 0 one has I_ω = O(N). Notice that here we focused on the scaling with respect to the number of photons, which is the most relevant figure for the relevant regime of parameters. However, even if the Gaussian model presents a critical slowing down, the Heisenberg scaling can in principle be achieved also with respect to time^17,19. We notice also that the divergence rate I_ω/N² is maximal at ω = Γ. In the following, we focus at this point, where the QFI is maximal for low-enough χ.

Fig. 2: Metrological performance of the critical parametric quantum sensor.

(a) QFI for the estimation of ω as a function of ϵ, computed for ω/Γ = 1 and various values of χ/Γ. In the Gaussian case (χ → 0), the QFI diverges at $\epsilon =\sqrt{{\omega }^{2}+{{{\Gamma }}}^{2}}$. For finite values of χ, the QFI has a maximum. In the inset, we show that ${{{{\mathcal{S}}}}}_{\omega }=\mathop{\max }\nolimits_{\epsilon }{S}_{\omega }^{{{{\rm{Hom}}}}} \sim c{({{\Gamma }}\chi )}^{-1}$, with c ≃ 0.55. Since $N={{\Theta }}(\sqrt{{\chi }^{-1}})$, the Heisenberg scaling is reached already for χ/Γ ≲ 10⁻². (b) SNR for the homodyne (${S}_{\omega }^{{{{\rm{Hom}}}}}$) and heterodyne detection (${S}_{\omega }^{{{{\rm{Het}}}}}$) at ω/Γ = 1 and χ/Γ = 0.04. Homodyne detection virtually saturates the QFI.

The symmetry-broken phase (χ → 0)

The model is invariant under the transformation $\hat{a}\to -\hat{a}$, resulting in a ${{\mathbb{Z}}}_{2}$-symmetry. In the χ → 0 limit, and for ϵ > ϵ_c, such a symmetry is broken resulting in a second-order DPT. The symmetry-broken solutions are well-approximated by Gaussian states that can be obtained by displacing the field $\hat{a}\to \hat{a}+\alpha$, with $\alpha \in {\mathbb{C}}$²⁹. For nonzero χ, the steady state is well-approximated by a statistical mixture of two Gaussian states⁵⁰. Indeed, a Gaussian approximation leads to $\rho =\frac{1}{2}[D(\alpha ){\rho }_{+}D(\alpha )+D(-\alpha ){\rho }_{-}D(-\alpha )]$. Here, ρ_± are the steady-states for ${H}_{\pm }={\omega }^{{\prime} }{\hat{a}}^{{\dagger} }\hat{a}+\frac{1}{2}({\epsilon }^{{\prime} }{\hat{a}}^{{\dagger} 2}+{{\epsilon }^{{\prime} }}^{* }{\hat{a}}^{2})+O(\sqrt{\chi })$ and dissipator ${{{{\mathcal{L}}}}}_{D}$, where ${\omega }^{{\prime} }=2\sqrt{{\epsilon }^{2}-{{{\Gamma }}}^{2}}-\omega$ and $| {\epsilon }^{{\prime} }| ={\epsilon }_{c}$. Namely, α is the solution of ωα + ϵα^* + 2χ∣α∣²α − iΓα = 0, see “Methods”. By setting α = ∣α∣e^iϕ, we find the two solutions, holding for ϵ > ϵ_c:

$$| \alpha {| }^{2}=\frac{\sqrt{{\epsilon }^{2}-{{{\Gamma }}}^{2}}-\omega }{2\chi },\quad \phi =\frac{\arcsin \left({{\Gamma }}/\epsilon \right)\pm \pi }{2}.$$

(5)

Notice that the Hamiltonians H_± are the same at the zeroth order in χ. Therefore, ρ₊ ≃ ρ₋ and the steady-state solutions consist in a mixture of two identical squeezed-thermal states displaced in opposite directions⁵⁰. The QFI shows a divergence at ϵ → ϵ_c, as seen in the normal phase. This confirms that in the proximity of the transition the QFI diverges for χ → 0. Instead, for sufficiently large ϵ, the QFI value is solely determined by the response of α to the ω’s changes. Using Eq. (5), one can easily see that I_ω = Θ(ϵ⁻¹) for ϵ ≫ 1.

The full model (finite χ)

We are now ready to show our results beyond the Gaussian approximation. Hereafter, the observables for the QFI are obtained through the analytical solutions in refs. ^50,51,52, while the steady-state density matrix are obtained solving the equation $-i[{\hat{H}}_{{{{\rm{Kerr}}}}},{\rho }_{{{{\rm{ss}}}}}]+{{{{\mathcal{L}}}}}_{D}[{\rho }_{{{{\rm{ss}}}}}]=0$ via sparse LU decomposition⁵⁹. We then compute the QFI using Eq. (3). The effect of the Kerr term is to regularize the model, eliminating the divergences that appear in the Gaussian approximation. As expected, the QFI increases with ϵ up to a maximum point, then it starts to decrease. The maximum is reached for ϵ = ϵ_c in the χ → 0 limit. Let us consider the quantity ${{{{\mathcal{S}}}}}_{\omega }=\mathop{\max }\nolimits_{\epsilon }{S}_{\omega }^{{{{\rm{Hom}}}}}$, and focus on the ω = Γ point. With a numerical fit, we find that ${{{{\mathcal{S}}}}}_{\omega }\simeq c{(\chi {{\Gamma }})}^{-1}$ for χ/Γ ≲ 10⁻², where c ≃ 0.55 (see Fig. 2a). Since $N={{\Theta }}(\sqrt{{\chi }^{-1}})$ holds, the Heisenberg scaling is reached already for χ/Γ ≲ 10⁻². In Fig. 2b, we show that homodyne detection virtually saturates the QFI already for χ/Γ = 0.04. In fact, one can easily see that homodyne detection is optimal in the χ → 0 limit, see Methods.

Magnetometry

We now consider an application of our results for the quantum estimation of magnetic flux. Let us consider a SQUID coupled with a λ/4 resonator. A magnetometer can be designed by coupling the magnetic field to the SQUID loop. The effective Hamiltonian is given in Eq. (1). Here, the resonator frequency ω_r depends on the external magnetic flux as ${\omega }_{r}({{\Phi }})\simeq {\omega }_{\lambda /4}/[1+{\gamma }_{0}/| \cos ({{\Phi }})| ]$, where ω_λ/4 is the bare resonant frequency in the absence of the SQUID, Φ = πΦ_ext/Φ₀ is the applied magnetic flux Φ_ext in unit of the flux quantum Φ₀, and γ₀ is the ratio of SQUID inductance at zero external magnetic flux and the geometric inductance of the resonator. For π/4 ≲ Φ < π/2, where the pump-induced non-linearity is small, the non-linearity depends on the magnetic field as $\chi ({{\Phi }})\simeq {\chi }_{0}{\omega }_{\lambda /4}{\gamma }_{0}^{3}/| {\cos }^{3}({{\Phi }})|$, where χ₀ = πZ₀e²/(2ℏ) is a constant dependent on the resonator characteristic impedance Z₀ (see the Supplemental Material). Assuming a typical value Z₀ ≃ 50Ω⁵⁵, we have χ₀ ≃ 0.02. It is convenient to work at the point Φ ≃ π/4, where χ is minimized. We can also assume χ to be independent on Φ, by working in the limit ${\chi }_{0}{\gamma }_{0}^{2}\ll 1$, which ensures the condition $\left\vert \frac{\partial \chi }{\partial {{\Phi }}}\right\vert \ll \left\vert \frac{\partial \omega }{\partial {{\Phi }}}\right\vert$ to hold. The protocol consists in: (i) Apply a constant magnetic flux bias Φ ≃ π/4 to the SQUID. (ii) Apply a pump at frequency ω_p ≃ 2[ω_r(π/4) − Γ]. This allows to work at ω ≃ Γ, where the QFI is maximal. (iii) Perform homodyne detection of the output signal.

From the input-output theory, we have that the resonator output mode is ${\hat{a}}_{{{{\rm{out}}}}}=\sqrt{2{{\Gamma }}}\,\hat{a}-{\hat{a}}_{{{{\rm{in}}}}}$, where ${\hat{a}}_{{{{\rm{in}}}}}$ is the input mode assumed to be in the vacuum⁶⁰. By applying the right temporal filter at the output mode, one can retrieve the same statistics of the intracavity mode^61,62. With this premise, the SNR for the output mode is the same as the one derived for the intracavity mode. A change of Φ by δΦ induces the shift $\omega \to \omega +\frac{\partial {\omega }_{r}}{\partial {{\Phi }}}\delta {{\Phi }}$. Therefore, the uncertainty over M independent measurements is ${{\Delta }}{{{\Phi }}}_{| {{\Phi }}\simeq \pi /4}\simeq {\left[\sqrt{{{{{\mathcal{S}}}}}_{\omega }M}\left\vert {\frac{\partial {\omega }_{r}}{\partial {{\Phi }}}}_{| {{\Phi }}\simeq \pi /4}\right\vert \right]}^{-1}$. Let us consider the regime χ/Γ ≲ 10⁻², where ${{{{\mathcal{S}}}}}_{\omega }\simeq c{({{\Gamma }}\chi )}^{-1}$, see Fig. 2a. Let us assume an independent measurement every 2π/Γ, and a measurement time of half a second, i.e., M = Γ Hz⁻¹/(4π). The magnetometer sensitivity becomes

$$\frac{{{\Delta }}{{\Phi }}}{\sqrt{{{{\rm{Hz}}}}}}\lesssim 0.8{\left(\frac{{\gamma }_{0}}{{\omega }_{\lambda /4}}\right)}^{1/2}$$

(6)

for γ₀ ≲ 10⁻², see “Methods”. Best sensitivity values reported in the literature are of the order of 4.5 × 10⁻⁷$\sqrt{{{{\mbox{Hz}}}}^{-1}}$⁶³. Our protocol improves this value by one order of magnitude if we set ω_λ/4 ≃ 2π × 10 GHz, and γ₀ ≃ 10⁻⁴. The sensitivity can be greatly enhanced by engineering more sophisticated circuit schemes using SQUID arrays or other Josephson-junction configurations, high-impedance metamaterials and large circuits lengths.

Dispersive qubit readout

We now discuss an application of the Kerr resonator for superconducting-qubit readout. By dipersively coupling a qubit to the resonator Hamiltonian in Eq. (1), the Hamiltonian becomes

$${\hat{H}}_{{{{\rm{disp}}}}}/\hslash ={\hat{H}}_{{{{\rm{Kerr}}}}}/\hslash +({\omega }_{r}+{{\Delta }})\left\vert e\right\rangle \left\langle e\right\vert +\delta \omega \left\vert e\right\rangle \left\langle e\right\vert {\hat{a}}^{{\dagger} }\hat{a}.$$

(7)

Here, δω = g²/Δ is a frequency-shift that depends on the qubit-resonator coupling g and the qubit-to-resonator detuning Δ⁶⁴. When the qubit is in its excited state $\left\vert e\right\rangle$, a frequency-shift is induced onto the resonator. The Hamiltonian ${\hat{H}}_{{{{\rm{disp}}}}}$ can be derived by applying perturbation theory to the full qubit-resonator Hamiltonian, for g/Δ ≪ 1. The dispersive approximation holds as long as g²N/(4Δ²) ≡ η ≪ 1, where N is the number of photons in the resonator. Notice that a small η also minimizes the disturbance induced to the qubit by the readout scheme (see the Supplemental Material). In the following, we show how the presence of a DPT leads to two highly distinguishable quantum states, that can be used to perform high-fidelity qubit readout. A similar setup, with an unoptimized set of parameters, has been experimentally investigated in ref. ⁵⁴. Here, the authors map the qubit discrimination problem to distinguish between the vacuum and a classical state of ~200 photons, where the dispersive approximation is clearly not valid anymore. As a result, the qubit significantly suffers from additional dissipation processes mediated by the readout resonator. Therefore, one must reduce the number of photons, bringing the system closer to the critical point, where the semiclassical approximation does not hold, and quantum fluctuations shall unavoidably be taken into account. In the following, we conduct this performance analysis in a systematic way using the full quantum model, identifying the set of parameters that maximizes the readout fidelity, while still respecting the dispersive approximation.

Generally speaking, the method consists in discriminating between two density matrices, i.e., ρ_g and ρ_e, corresponding to the steady-states when the qubit is in the state $\left\vert e\right\rangle$ or $\left\vert g\right\rangle$ respectively. We limit ourselves to the case of discrimination via a single measurement of the mode $\hat{a}$ (single-shot readout). The average error probability is bounded by ${P}_{{{{\rm{err}}}}}\le {P}_{{{{\rm{err}}}}}^{{{{\rm{opt}}}}}$, also known as the Helstrom bound⁵⁷, where ${P}_{{{{\rm{err}}}}}^{{{{\rm{opt}}}}}=\frac{1}{2}\left[1-\frac{1}{2}\parallel {\rho }_{e}-{\rho }_{g}{\parallel }_{1}\right]$ and $\parallel \sigma {\parallel }_{1}=\,{{\mbox{Tr}}}\,\,\sqrt{{\sigma }^{{\dagger} }\sigma }$ is the trace norm (the qubit readout fidelity can be defined as F = 1 − P_err). The optimal error probability ${P}_{{{{\rm{err}}}}}^{{{{\rm{opt}}}}}$ is in principle achievable by measuring in the eigenbasis of ρ_e − ρ_g. In Fig. 3a, we show a map of the ${P}_{{{{\rm{err}}}}}^{{{{\rm{opt}}}}}$ values with respect to the frequency-shift δω and the pump strength ϵ, for χ = 0.08Γ. For a given value of η, the graph shows the presence of a sweet spot where the error probability is minimized. The value ${P}_{{{{\rm{err}}}}}^{{{{\rm{opt}}}}}$ is always attainable, and gives us a bound on what error probabilities can be in principle reached. However, the measurement can be complicated to implement, so we consider also a practical strategy based on homodyne detection. Let us define the probability density functions P_g,e(x) = ∫W_g,e(x, p)dp, where W_g,e(x, p) are the Wigner functions of the resonator steady-state in the case of qubit in the $\left\vert g\right\rangle$ or $\left\vert e\right\rangle$ states. We declare that the state of the qubit is $\left\vert g\right\rangle$ if our measurement outcome belongs to {x∣P_g(x) > P_e(x)} and $\left\vert e\right\rangle$ otherwise. The error probability for this discrimination strategy is

$${P}_{{{{\rm{err}}}}}=\frac{1}{2}\int\mathop{\min }\limits_{x}\{{P}_{g}(x),{P}_{e}(x)\}{\rm{d}}x.$$

(8)

This procedure can be further optimized by considering a rotated homodyne measurement. Notice that we have used the Wigner function as a tool to find the best threshold value distinguishing between the two qubit states, given a single homodyne measurement. Indeed, our strategy does not rely on the reconstruction of the resonator Wigner function. In Fig. 3b, we show that the homodyne strategy, although not saturating the optimal strategy, achieves error probability values of the order of 10⁻³. Notice, however, that the position of the minimum of the error probability with the homodyne strategy coincides with that of ${P}_{{{{\rm{err}}}}}^{{{{\rm{opt}}}}}$. In the Supplemental Material, we show that for η = 10⁻² there is no backaction on the qubit states (see the Supplemental Material). Experimentally achievable values attaining the optimal value for η = 10⁻² are: Γ ≃ 2π × 1 MHz, χ/Γ ≃ 0.08, g/Γ ≃ 10², ω_r/Γ ≃ 8 × 10³, ω_q/Γ ≃ 6 × 10³. In this case, the resonator has at most N ≃ 30 photons at the steady-state.

Fig. 3: Qubit detection performance with a critical parametric quantum sensor.

(a) Error probability map with respect to δω/Γ = g²/(ΓΔ) and ϵ/Γ, for ω = 0 and χ/Γ = 0.08. The dashed lines represent different values of the dispersive parameter η = Nδω²/(4g²), where $N=\max \{{N}_{\left\vert g\right\rangle },{N}_{\left\vert e\right\rangle }\}$ and we have fixed g/Γ = 10² to be in the strong—but not ultrastrong—coupling regime. For η = 10⁻², we can reach error probability values as low as 10⁻⁴ with the optimal measurement. (b) Error probability for homodyne detection at the optimal points and optimal angle φ for different values of η. The inset shows the separation in time of $\langle {\hat{x}}_{\varphi }^{2}\rangle$ for the normal and symmetry-broken phases. The steady-state value is reached at Γt ≃ 10.

Methods

The Gaussian approximation for χ → 0

Here, we find the Gaussian approximation for χ → 0, for both the regimes ϵ < ϵ_c (normal phase) and ϵ > ϵ_c (symmetry-breaking phase).

The normal phase (ϵ < ϵ _c)

For ϵ < ϵ_c, we set χ = 0 and look for the steady-state solutions. It is convenient to rewrite the master equation as Fokker–Planck equation, in the Wigner function formalism:

$$\frac{\partial W}{\partial t}(x,p)=-(\omega -\epsilon )p\frac{\partial W}{\partial x}+(\omega +\epsilon )x\frac{\partial W}{\partial p}+{{\Gamma }}\left[2W+\mathop{\sum }\limits_{i=1}^{2}{x}_{i}{\partial }_{i}W+\frac{1}{2}\mathop{\sum }\limits_{i=1}^{2}{\partial }_{i}^{2}W\right],$$

(9)

where we defined $\hat{a}=(\hat{x}+i\hat{p})/\sqrt{2}$. Since this equation is quadratic in x and p, it can be solved by a Gaussian ansatz

$$W=\frac{1}{\pi \sqrt{\det \sigma }}\exp \left\{-\frac{1}{4}\mathop{\sum}\limits_{i,j}{r}_{i}{({\sigma }^{-1})}_{ij}{r}_{j}\right\},$$

(10)

where r = (x, p) and the Wigner function is normalized to one. The covariance matrix σ is defined as ${\sigma }_{ij}=\langle \{{\hat{r}}_{i},{\hat{r}}_{j}\}\rangle -2\langle {\hat{r}}_{i}\rangle \langle {\hat{r}}_{j}\rangle$. From (9) we get the linear system of equations

$${\partial }_{t}\sigma =B\sigma +\sigma {B}^{T}-2{{\Gamma }}(\sigma -{\sigma }^{L})\,$$

(11)

where ${\sigma }^{L}={{\mathbb{I}}}_{2}$ and $B=\left[\begin{array}{cc}0&(\omega -\epsilon )\\ -(\omega +\epsilon )&0\end{array}\right]$. We find the steady state by solving ∂_tσ_ss = 0. The solution is

$${\sigma }_{{{{\rm{ss}}}}}=\frac{1}{{\epsilon }_{c}^{2}-{\epsilon }^{2}}\left[\begin{array}{cc}{\epsilon }_{c}^{2}-\omega \epsilon &-{{\Gamma }}\epsilon \\ -{{\Gamma }}\epsilon &{\epsilon }_{c}^{2}+\omega \epsilon \end{array}\right],$$

(12)

which corresponds to a physical state only for ${\epsilon }^{2} \,<\, {\omega }^{2}+{{{\Gamma }}}^{2}\equiv {\epsilon }_{c}^{2}$. This sets the critical value in the χ → 0 limit. In this limit, the number of photons is

$$N(\chi \to 0)=\frac{{({\sigma }_{{{{\rm{ss}}}}})}_{11}+{({\sigma }_{{{{\rm{ss}}}}})}_{22}-2}{4}=\frac{{\epsilon }^{2}}{2({\epsilon }_{c}^{2}-{\epsilon }^{2})},$$

(13)

which diverges for ϵ → ϵ_c.

The symmetry-broken phase (ϵ > ϵ _c)

Let us derive an effective quadratic Hamiltonian for ϵ > ϵ_c. We follow the approach developed in ref. ²⁹. The idea is that for small χ, the model is well approximated by a double-well potential, and that the low-energy physics can be described with a quadratic expansion around each minimum. In order to center the reference frame on one of the two minima, let us apply a displacement operation such that ${U}^{{\dagger} }\hat{a}U=\hat{a}+\alpha$. We obtain an effective Hamiltonian

$${\hat{H}}_{\alpha }={\hat{H}}^{(1)}+{\hat{H}}^{(2)}+{\hat{H}}^{(3/4)}+\,{{\mbox{const.}}}\,,$$

(14)

where

$${\hat{H}}^{(1)}=(\omega \alpha +\epsilon {\alpha }^{* }+2\chi | \alpha {| }^{2}\alpha -i{{\Gamma }}){\hat{a}}^{{\dagger} }+\,{{\mbox{H.c.}}}\,$$

(15)

$${\hat{H}}^{(2)}=(\omega +4\chi | \alpha {| }^{2}){\hat{a}}^{{\dagger} }\hat{a}+\left(\frac{\epsilon }{2}+\chi {\alpha }^{2}\right){\hat{{a}^{{\dagger} }}}^{2}+\left(\frac{\epsilon }{2}+\chi {{\alpha }^{* }}^{2}\right){\hat{a}}^{2},$$

(16)

$${\hat{H}}^{(3/4)}=\chi ({\hat{a}}^{{\dagger} }{\hat{a}}^{{\dagger} }\hat{a}\hat{a}+2\alpha {\hat{{a}^{{\dagger} }}}^{2}\hat{a}+2{\alpha }^{* }{\hat{a}}^{{\dagger} }{\hat{a}}^{2}).$$

(17)

The dissipator ${{{{\mathcal{L}}}}}_{D}$, instead, is left unchanged. The quadratic part of the displaced Hamiltonian (14) is well-defined, i.e., it has normal modes with positive frequency and is bounded from below. Accordingly, far from the critical point the steady state will have bounded quantum fluctuations, and the norm of the creation/annihilation operators on the steady state will be bounded. In the limit of small χ, and of large α, higher-order terms are negligible and the model is well-approximated by a Gaussian approximation which includes only terms quadratic in ${\hat{a}}^{{\dagger} }$ and $\hat{a}$ [see the solutions below in Eq. (18)]. Of course this approximation will break in a small region for $\epsilon \to {\epsilon }_{c}^{+}$, and the size of the critical region is proportional to χ (the smaller the nonlinearity, the more reliable the Gaussian approximation even as the critical point is approached).

The linear equation defining the equilibrium points is found by imposing ${\hat{H}}^{(1)}=0$, i.e., ωα + ϵα^* + 2χ∣α∣²α − iΓα = 0. Setting α = ∣α∣e^iϕ we find two solutions for ϵ > ϵ_c:

$${\left\vert \alpha \right\vert }^{2}=\frac{\sqrt{{\epsilon }^{2}-{{{\Gamma }}}^{2}}-\omega }{2\chi }$$

(18)

$$\phi =\frac{1}{2}\arcsin \left({{\Gamma }}/\epsilon \right)\pm \pi /2.$$

(19)

We find the effective Hamiltonians in the symmetry-broken phase by plugging the solution into Eq. (14). We get

$${H}_{\pm }={\omega }^{{\prime} }{a}^{{\dagger} }a+\frac{1}{2}({\epsilon }^{{\prime} }{{a}^{{\dagger} }}^{2}+{{\epsilon }^{{\prime} }}^{* }{a}^{2})+O(\sqrt{\chi }),$$

(20)

with

$${\omega }^{{\prime} }=2\sqrt{{\epsilon }^{2}-{{{\Gamma }}}^{2}}-\omega$$

(21)

$${\epsilon }^{{\prime} }={\epsilon }_{c}{\rm{e}}^{{\rm{i}}\theta }$$

(22)

$$\theta =-2\arctan \left[\frac{{{\Gamma }}\left(\sqrt{{\epsilon }^{2}-{{{\Gamma }}}^{2}}-\omega \right)}{\epsilon {\epsilon }_{c}+\omega \sqrt{{\epsilon }^{2}-{{{\Gamma }}}^{2}}+{{{\Gamma }}}^{2}}\right].$$

(23)

Notice that the Hamiltonians H_± are the same for χ → 0. Therefore, in this limit the two solutions are degenerate. Increasing the pump power ϵ corresponds to an effective growth of the pump-resonator detuning, since ${\omega }^{{\prime} } \sim \epsilon$ for large ϵ. Instead, the effective squeezing parameter ${\epsilon }^{{\prime} }$ remains constant in modulus, while its argument changes until reaching the value ${\theta }_{\epsilon /{\epsilon }_{c}\gg 1}=-2\arctan \sqrt{({\epsilon }_{c}-\omega )/({\epsilon }_{c}+\omega )}$. Therefore, the effect of increasing the pump is to displace the state to the new equilibrium points, and to rotate and reduce the squeezing of each of the resulting states.

Quantum parameter estimation

Here, we derive the quantum parameter estimation results for the full model.

Signal-to-noise ratio (SNR)

The SNR induced by the observable $\hat{O}$ in the task of estimating the parameter ω is defined as

$${S}_{\omega }[\hat{O}]=\frac{{[{\partial }_{\omega }{\langle \hat{O}\rangle }_{\omega }]}^{2}}{{{\Delta }}{\hat{O}}_{\omega }^{2}},$$

(24)

where ${{\Delta }}{\hat{O}}_{\omega }^{2}={\langle {\hat{O}}^{2}\rangle }_{\omega }-{\langle \hat{O}\rangle }_{\omega }^{2}$ and the index ω indicates the expectation value computed on the steady-state ρ_ω. The SNR computed in ω = ω₀ should be interpreted as the precision achievable for estimating the parameter ω when its value is close to ω₀, through the relation ${{\Delta }}{\omega }_{| \omega \simeq {\omega }_{0}}^{2}\simeq {[M\times {S}_{{\omega }_{0}}]}^{-1}$, where M ≫ 1 is the number of measurements. Generally speaking, if an experimentalist is able measure the expectation value of a class of observables $\{O(\overrightarrow{r})\}$, with $\overrightarrow{r}=({r}_{1},\ldots ,{r}_{K})$, they would like to maximize the SNR with respect to $\overrightarrow{r}$ in order to obtain a better precision rate (call ${\overrightarrow{r}}_{\max }$ the maximizing set of parameters). This in principle requires the preknowledge of ω₀. If this knowledge is not provided, then they can implement a two-step adaptive protocol, where first they measure the expectation value of $A\in \{O(\overrightarrow{r})\}$ such that the function f(ω) = 〈A〉_ω is invertible in the range of values where ω belongs, obtaining a first order estimation of ω, i.e., ω₀. Then they find ${\overrightarrow{r}}_{\max }$ and measure $O({\overrightarrow{r}}_{\max })$.

We are particularly interested in the following SNRs.

• Homodyne detection: This is defined by the POVM ${{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}}={\{\left\vert {x}_{\varphi }\right\rangle \left\langle {x}_{\varphi }\right\vert \}}_{{x}_{\varphi }\in {\mathbb{R}}}$, where $\left\vert {x}_{\varphi }\right\rangle$ is an eigenstate of the rotated quadrature

  $$\hat{x}(\varphi )=\cos (\varphi )\hat{x}+\sin (\varphi )\hat{p}=\frac{1}{\sqrt{2}}[\hat{a}{\rm{e}}^{-{\rm{i}}\varphi }+{\hat{a}}^{{\dagger} }{\rm{e}}^{{\rm{i}}\varphi }].$$

  (25)

  We consider this SNR ${S}_{\omega }[{\hat{x}}_{\varphi }^{2}]$ to evaluate the perfomance of homodyne detection for finite χ. This will be clear in the following, when we will evaluate the classical Fisher information. We also consider the best phase choice, i.e.,

  $${S}_{\omega }^{{{{\rm{Hom}}}}}\equiv \mathop{\max }\limits_{\varphi }{S}_{\omega }[{\hat{x}}_{\varphi }^{2}].$$

  (26)

• Heterodyne detection: This is defined by the POVM ${{{{\mathcal{X}}}}}^{{{{\rm{Het}}}}}={\left\{\frac{1}{\pi }\left\vert \gamma \right\rangle \left\langle \gamma \right\vert \right\}}_{\gamma \in {\mathbb{C}}}$, where $\left\vert \gamma \right\rangle$ is a coherent state. The heterodyne measurement can be modeled as the signal $\hat{a}$ entering in a beamsplitter with a thermal mode $\hat{h}$ as the other input, obtaining the two modes ${\hat{b}}_{\pm }=[\hat{a}\pm {\hat{h}}^{{\dagger} }]/\sqrt{2}$. The quadratures ${\hat{X}}_{+}=[{\hat{b}}_{+}+{\hat{b}}_{+}^{{\dagger} }]/\sqrt{2}$ and ${\hat{P}}_{-}=-i[{\hat{b}}_{-}-{\hat{b}}_{-}^{{\dagger} }]/\sqrt{2}$ are finally measured. This is equivalent to measure the complex envelope operator

  $$\hat{S}\equiv {\hat{X}}_{+}+i{\hat{P}}_{-}=\hat{a}+{\hat{h}}^{{\dagger} }.$$

  (27)

  Indeed, from the measurement outcomes one can estimate the moments of $\hat{S}$, and then invert Eq. (27) to obtain an estimation of the moments of $\hat{a}$. In the quantum-limited case, when $\hat{h}$ is a vacuum mode, the moments of $\hat{S}$ can be easily computed as $\langle {\hat{S}}^{{\dagger} m}{\hat{S}}^{n}\rangle =\langle {\hat{a}}^{n}{\hat{a}}^{{\dagger} m}\rangle$, since $[\hat{S},{\hat{S}}^{{\dagger} }]=0$^65,66. The SNR for the observable ${\hat{O}}_{{{{\rm{Het}}}}}={\hat{X}}_{+}^{2}+{\hat{P}}_{-}^{2}={\hat{S}}^{{\dagger} }\hat{S}$ is then

  $$\begin{array}{r}{S}_{\omega }[{\hat{O}}_{{{{\rm{Het}}}}}]=\frac{{[{\partial }_{\omega }{\langle \hat{a}{\hat{a}}^{{\dagger} }\rangle }_{\omega }]}^{2}}{{\langle {\hat{a}}^{2}{\hat{a}}^{{\dagger} 2}\rangle }_{\omega }-{\langle \hat{a}{\hat{a}}^{{\dagger} }\rangle }_{\omega }^{2}}\equiv {S}_{\omega }^{{{{\rm{Het}}}}}.\end{array}$$

  (28)

• Classical Fisher information (FI): Let us focus on the homodyne POVM ${{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}}={\{\left\vert {x}_{\varphi }\right\rangle \left\langle {x}_{\varphi }\right\vert \}}_{{x}_{\varphi }\in {\mathbb{R}}}$. The estimation precision is given by the FI, which is defined as the SNR maximized over the observables which are diagonal in ${\{\left\vert {x}_{\varphi }\right\rangle \left\langle {x}_{\varphi }\right\vert \}}_{{x}_{\varphi }\in {\mathbb{R}}}$, i.e., ${F}_{\omega }({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})=\mathop{\max }\nolimits_{\hat{O={\sum }_{{x}_{\varphi }}}p({x}_{\varphi })\left\vert {x}_{\varphi }\right\rangle \left\langle {x}_{\varphi }\right\vert }{S}_{\omega }[\hat{O}]$. This can be generally expressed as⁶⁷

  $${F}_{\omega }({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})={\int}_{{\mathbb{R}}}dx\,p({x}_{\varphi }| \omega )\,{\left\{{\partial }_{\omega }\left[\ln p({x}_{\varphi }| \omega )\right]\right\}}^{2},$$

  (29)

  where $p({x}_{\varphi }| \omega )=\left\langle {x}_{\varphi }\right\vert {\rho }_{\omega }\left\vert {x}_{\varphi }\right\rangle$ is the probability density function of the outcome.

• Quantum Fisher information (QFI): Generally speaking, the QFI provides the precision for the optimal unbiased estimator allowed by quantum mechanics. This is indeed defined as ${I}_{\omega }=\mathop{\max }\limits_{\hat{O}}{S}_{\omega }[\hat{O}]$, that can be generally expressed as⁵⁷

  $${I}_{\omega }=\mathop{\lim }\limits_{d\omega \to 0}\frac{8}{d{\omega }^{2}}\left[1-\sqrt{F({\rho }_{\omega },{\rho }_{\omega -d\omega })}\right],$$

  (30)

  where $F({\rho }_{\omega },{\rho }_{\omega -d\omega })={\left({{\mbox{Tr}}}\sqrt{{\rho }_{\omega }\sqrt{{\rho }_{\omega -d\omega }}{\rho }_{\omega }}\right)}^{2}$ is the fidelity between the two density matrices ρ_ω and ρ_ω−dω, and ρ_ω (ρ_ω−dω) is the steady-state of the model with pump-resonator detuning ω (ω − dω). This expression can be easily evaluated numerically by considering a dω smaller and smaller, and by doing a convergence check. In the paper, this procedure has been used to compute the QFI in the steady-state manifold for the χ > 0 case. Indeed, Eq. (30) has been evaluated numerically by letting the system evolve to the steady-state for two values of ω close to each other.

Quantum parameter estimation for χ → 0 (Normal phase)

Here, we derive the formulas for the QFI and the FI for the Gaussian model. We show that homodyne detection saturates the QFI for χ → 0.

QFI for the Gaussian model

The QFI for the Gaussian model can be analytically calculated using the covariance matrix formalism⁵⁸, using the solutions of Eq. (12):

$${I}_{\omega }=\frac{1}{2(1+{\mu }^{2})}\,{{\mbox{Tr}}}\,\left[{\left({\sigma }^{-1}{\partial }_{\omega }\sigma \right)}^{2}\right]\,+\,\frac{2{({\partial }_{\omega }\mu )}^{2}}{1-{\mu }^{4}},$$

(31)

where $\mu ={(\det \sigma )}^{-1/2}$ is the purity of the quantum state, and we have used that the displacements are zero for all parameter values. The solution has been computed using a symbolic computation software, obtaining

$$\begin{array}{r}{I}_{\omega }=\frac{{\epsilon }^{2}}{2{\epsilon }_{c}^{2}-{\epsilon }^{2}}\left[\frac{1}{{\epsilon }_{c}^{2}-{\epsilon }^{2}}+\frac{2{\omega }^{2}}{{({\epsilon }_{c}^{2}-{\epsilon }^{2})}^{2}}\right].\end{array}$$

(32)

This expression can be cast as in Eq. (4) using the relation $N={\epsilon }^{2}/[2({\epsilon }_{c}^{2}-{\epsilon }^{2})]$. We recall that the quantum Fisher information provides an upper bound to the achievable SNR as defined in Eq. (2), which can be saturated when the optimal measurement is implemented.

FI for the Gaussian model

Let us focus on the homodyne POVM ${{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}}={\{\left\vert {x}_{\varphi }\right\rangle \left\langle {x}_{\varphi }\right\vert \}}_{{x}_{\varphi }\in {\mathbb{R}}}$. One can easily see that in the Gaussian approximation ${F}_{\omega }({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})={\left[{\partial }_{\omega }{s}_{\omega }(\varphi )\right]}^{2}/(2{s}_{\omega }{(\varphi )}^{2})={S}_{\omega }[{\hat{x}}_{\varphi }^{2}]$, where ${s}_{\omega }(\varphi )={\cos }^{2}(\varphi )\,{({\sigma }_{ss})}_{11}+{\sin }^{2}(\varphi )\,{({\sigma }_{ss})}_{22}-\sin (2\varphi )\,{({\sigma }_{ss})}_{12}$⁵. This can be expanded as

$${F}_{\omega }({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})=\frac{{\epsilon }^{2}{\left[({{{\Gamma }}}^{2}-{\omega }^{2}-{\epsilon }^{2})\cos (2\varphi )+2\omega \epsilon +2\omega {{\Gamma }}\sin (2\varphi )\right]}^{2}}{2{({\epsilon }_{c}^{2}-{\epsilon }^{2})}^{2}{[{\epsilon }_{c}^{2}-\epsilon (\omega \cos (2\varphi )-{{\Gamma }}\sin (2\varphi ))]}^{2}}.$$

(33)

• For ω = 0, we have that

  $${F}_{\omega = 0}({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})=\frac{{\epsilon }^{2}{\cos }^{2}(2\varphi )}{2{[{\epsilon }_{c}^{2}+{\epsilon }_{c}\epsilon \sin (2\varphi )]}^{2}}.$$

  (34)

  This is maximal for $\sin (2\varphi )=-\epsilon /{\epsilon }_{c}$, for which we obtain ${F}_{\omega = 0}({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})={\epsilon }^{2}/[2{\epsilon }_{c}^{2}({\epsilon }_{c}^{2}-{\epsilon }^{2})]$. Since ${F}_{\omega = 0}({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})/{I}_{\omega = 0}\to 1/2$ for ϵ/ϵ_c → 1, we have that homodyne does not saturate the QFI when ω = 0. However the FI and the QFI share the same diverging scaling, i.e., ${F}_{\omega = 0}({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})=O{({\epsilon }_{c}-\epsilon )}^{-1}$ for ε → ε_c.

• For ω ≠ 0, the FI scales differently with respect to ϵ_c − ϵ. We exemplify the calculation for ω = Γ, that is the point where the QFI shows the maximal divergence rate. Here, we have that

  $${F}_{\omega = {{\Gamma }}}({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})=\frac{{\epsilon }^{2}{[{\epsilon }_{c}^{2}\sin (2\varphi )-{\epsilon }^{2}\cos (2\varphi )+\sqrt{2}{\epsilon }_{c}\epsilon ]}^{2}}{{\epsilon }_{c}^{2}{({\epsilon }_{c}^{2}-{\epsilon }^{2})}^{2}{[\sqrt{2}{\epsilon }_{c}-\epsilon (\cos (2\varphi )-\sin (2\varphi ))]}^{2}}.$$

  (35)

  In the ϵ/ϵ_c → 1 limit, we have that ${F}_{\omega = {{\Gamma }}}({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}}) \sim {\epsilon }_{c}^{2}/{({\epsilon }_{c}^{2}-{\epsilon }^{2})}^{2}$ for any φ. This means that ${F}_{\omega = {{\Gamma }}}({{{{\mathcal{X}}}}}_{\varphi }^{{{{\rm{Hom}}}}})/{I}_{\omega = {{\Gamma }}}\to 1$, and homodyne detection saturates the QFI for any φ,

Quantum parameter estimation for χ > 0

Let us evaluate the QFI scaling in two regimes: (i) ϵ/ϵ_c ≫ 1, and (ii) ϵ close to the criticality.

• ϵ/ϵ_c ≫ 1. In this regime, we have seen that the Wigner function becomes a mixture of two equiprobable coherent states, symmetrically displaced with respect to the center. These states are uniquely determined by ∣α(ω)∣², as the phase ϕ in Eq. (19) does not depend on ω. Therefore, for symmetry reasons, the optimal observable is the photon-number operator. This gives rise to the optimal SNR scaling

  $${I}_{\omega } \sim {S}_{\omega }[\hat{N}]=\frac{{\left\vert {\partial }_{\omega }({\left\vert \alpha \right\vert }^{2})\right\vert }^{2}}{{\left\vert \alpha \right\vert }^{2}}=\frac{1}{2\chi \left[\sqrt{{\epsilon }^{2}-{{{\Gamma }}}^{2}}-\omega \right]} \sim \frac{1}{2\chi \epsilon }.$$

  (36)

• ϵclose to the criticality. In this case, we have analyzed numerically the scaling of ${{{{\mathcal{S}}}}}_{\omega }=\mathop{\max }\nolimits_{\epsilon }{S}_{\omega }^{{{{\rm{Hom}}}}}$, computed in ω = Γ, where the QFI is maximal for low-enough χ. We find that ${{{{\mathcal{S}}}}}_{\omega }(\omega ={{\Gamma }}) \sim c{(\chi {{\Gamma }})}^{-1}$ for χ/Γ ≲ 0.01, where c ≃ 0.55. In addition, since in the same regime we have that $N={{\Theta }}(\sqrt{{\chi }^{-1}})$, that the Heisenberg scaling is reached. Let us focus on ${{{{\mathcal{I}}}}}_{\omega }=\mathop{\max }\nolimits_{\epsilon }{I}_{\omega }$. On the one hand, we always have that ${{{{\mathcal{I}}}}}_{\omega }(\omega ={{\Gamma }})\ge {{{{\mathcal{S}}}}}_{\omega }(\omega ={{\Gamma }})$. On the other hand, in practice homodyne detection already saturates the QFI for χ/Γ = 0.04, meaning that one should expect ${{{{\mathcal{I}}}}}_{\omega }(\omega ={{\Gamma }})\simeq {{{{\mathcal{S}}}}}_{\omega }(\omega ={{\Gamma }})$ already in this regime, since homodyne performs optimally for χ → 0.

The magnetometer sensitivity

Here, we derive the sensitivity of the magnetometer in Eq. (6). We have that

$${{\Delta }}{{{\Phi }}}_{| {{\Phi }}\simeq \pi /4}\simeq {\left[\sqrt{{{{{\mathcal{S}}}}}_{\omega }(\omega \simeq {{\Gamma }})M}\left\vert {\frac{\partial {\omega }_{r}}{\partial {{\Phi }}}}_{| {{\Phi }}\simeq \pi /4}\right\vert \right]}^{-1},$$

(37)

where ${{{{\mathcal{S}}}}}_{\omega }(\omega ={{\Gamma }})\simeq c{(\chi {{\Gamma }})}^{-1}$ for χ/Γ ≲ 0.01, M = ΓHz⁻¹/(4π), and ${\omega }_{r}({{\Phi }})\simeq {\omega }_{\lambda /4}/[1+{\gamma }_{0}/| \cos ({{\Phi }})| ]$. In the 0 ≤ Φ ≤ π/2 regime, we have that

$$\frac{\partial {\omega }_{r}}{\partial {{\Phi }}}\simeq -\frac{{\gamma }_{0}{\omega }_{\lambda /4}\sin ({{\Phi }})}{{({\gamma }_{0}+\cos ({{\Phi }}))}^{2}}.$$

(38)

It follows that

$$\frac{{{\Delta }}{{{\Phi }}}_{| {{\Phi }}\simeq \pi /4}}{\sqrt{{{{\rm{Hz}}}}}}\simeq \sqrt{\frac{\pi }{2c}}\frac{{(2{\gamma }_{0}+\sqrt{2})}^{2}}{{\gamma }_{0}}\frac{\sqrt{\chi ({{\Phi }}\simeq \pi /4)}}{{\omega }_{\lambda /4}}.$$

(39)

We now use that $\chi ({{\Phi }})\simeq {\chi }_{0}{\omega }_{\lambda /4}{\gamma }_{0}^{3}/| {\cos }^{3}({{\Phi }})|$ to obtain

$$\frac{{{\Delta }}{{{\Phi }}}_{| {{\Phi }} = \pi /4}}{\sqrt{{{{\rm{Hz}}}}}}\simeq {2}^{1/4}\sqrt{\frac{{\chi }_{0}}{4{\pi }^{3}c}}{(2{\gamma }_{0}+\sqrt{2})}^{2}\sqrt{\frac{{\gamma }_{0}}{{\omega }_{\lambda /4}}}$$

(40)

$$\simeq 0.39{(2{\gamma }_{0}+\sqrt{2})}^{2}\sqrt{\frac{{\gamma }_{0}}{{\omega }_{\lambda /4}}},$$

(41)

where we have used that χ₀ = 2π³Z₀e²/ℏ ≃ 0.02 for Z₀ ≃ 50Ω, and c ≃ 0.55. This means that

$$\frac{{{\Delta }}{{{\Phi }}}_{| {{\Phi }} = \pi /4}}{\sqrt{{{{\rm{Hz}}}}}}\lesssim 0.8\sqrt{\frac{{\gamma }_{0}}{{\omega }_{\lambda /4}}},$$

(42)

for γ₀ ≲ 10⁻², which is Eq. (6).

Finally, let us see how χ changes with respect to small changes of Φ. In the 0 ≤ Φ ≤ π/2 regime, we have that

$$\frac{\partial \chi }{\partial {{\Phi }}}\simeq 3{\chi }_{0}{\omega }_{\lambda /4}{\gamma }_{0}^{3}\frac{\sin ({{\Phi }})}{{\cos }^{4}({{\Phi }})}.$$

(43)

At Φ = π/4, the condition $\left\vert \frac{\partial \chi }{\partial {{\Phi }}}\right\vert \ll \left\vert \frac{\partial \omega }{\partial {{\Phi }}}\right\vert$ is equivalent to $6{\chi }_{0}{\gamma }_{0}^{2}\ll 1$.

Dispersive qubit readout

Dispersive Hamiltonian

Consider a qubit-resonator system, with Hamiltonian

$${\hat{H}}_{{{{\rm{qr}}}}}={\hat{H}}_{{{{\rm{JC}}}}}+\frac{\hslash \epsilon }{2}({\hat{a}}^{2}+{\hat{a}}^{{\dagger} 2})+\hslash \chi {\hat{a}}^{{\dagger} 2}{\hat{a}}^{2},$$

(44)

where ${\hat{H}}_{{{{\rm{JC}}}}}/\hslash ={\omega }_{r}{\hat{a}}^{{\dagger} }\hat{a}+{\omega }_{q}\left\vert e\right\rangle \left\langle e\right\vert +g({\sigma }^{-}{\hat{a}}^{{\dagger} }+{\sigma }^{+}\hat{a})$ is the Jaynes-Cumming Hamiltonian with qubit-resonator coupling g and qubit-frequency ω_q. Dispersive-readout protocols assume the qubit-resonator coupling to be in the linear dispersive regime, where an effective Hamiltonian is found applying the unitary transformation $U=\exp \{(g/2{{\Delta }})[{\sigma }^{+}\hat{a}-{\sigma }^{-}{\hat{a}}^{{\dagger} }]\}$, where Δ = ∣ω_q − ω_r∣ is the qubit-resonator detuning, and applying perturbation theory with respect to g/Δ. One then finds the effective Hamiltonian

$${\hat{H}}_{{{{\rm{disp}}}}}/\hslash ={\omega }_{q}\left\vert e\right\rangle \left\langle e\right\vert +(\omega +\delta \omega \left\vert e\right\rangle \left\langle e\right\vert ){\hat{a}}^{{\dagger} }\hat{a}+\frac{\epsilon }{2}({\hat{a}}^{{{\dagger} }^{2}}+{\hat{a}}^{2})+\chi {\hat{a}{}^{{\dagger} }}^{2}{\hat{a}}^{2},$$

(45)

that can be cast as in Eq. (7). Here, δω = g²/Δ is a qubit-state dependent frequency-shift, that depends on the qubit-resonator coupling g and the qubit-resonator detuning Δ⁶⁴. The dispersive approximation holds as long as g²N/(4Δ²) ≡ η ≪ 1, where N is the number of photons in the resonator.

Optimal parameter choice

For each sample, the state of the resonator collapse either on ρ_e or ρ_g. Discriminating between these two states gives us the measurement result. Fixing a value of χ/Γ, one can draw a (δω, ϵ)-dependent map of the optimal error probability for discriminating ρ_e and ρ_g, i.e., ${P}_{{{{\rm{err}}}}}^{{{{\rm{opt}}}}}=\left[1-\parallel {\rho }_{e}-{\rho }_{g}\parallel /2\right]/2$. Since ϵ is monotone with respect to N, for each value of (δω, ϵ, η), one can find a value of g and Δ satisfying the conditions δω = g²/Δ and η = g²N/(4Δ²). However, since g/Γ cannot be too large, otherwise we go to the ultrastrong regime where the counter-rotating terms appear, we have fixed g/Γ = 10², and choose ω_r and ω_q such that $g/\min \{{\omega }_{q},{\omega }_{r}\}\ll 1$. We have then drawn the lines for η equals to 10⁻² and 0.5 × 10⁻², see Fig. 3a.