Abstract
We propose a scheme for scalable and robust quantum computing on two-dimensional arrays of qubits with fixed longitudinal coupling. This opens the possibility for bypassing the device complexity associated with tunable couplers required in conventional quantum computing hardware. Our approach is based on driving a subarray of qubits such that the total multi-qubit Hamiltonian can be decomposed into a sum of commuting few-qubit blocks, and efficient optimisation of the unitary evolution within each block. The driving pulses are optimised to implement a target gate on the driven qubits, and at the same time identity gates on the neighbouring undriven qubits, cancelling any unwanted evolution due to the constant qubit-qubit interaction. We show that it is possible to realise a universal set of quantum gates with high fidelity on the basis blocks, and by shifting the driving pattern one can realise an arbitrary quantum circuit on the array. Allowing for imperfect Hamiltonian characterisation, we use robust optimal control to obtain fidelities around 99.99% despite 1% uncertainty in the qubit-qubit and drive-qubit couplings, and a detuning uncertainty at 0.1% of the qubit-qubit coupling strength. This robust feature is crucial for scaling up as parameter uncertainty is significant in large devices.
Similar content being viewed by others
Introduction
Great progress has been achieved recently in various physical platforms for quantum computing, most notably is the 54-qubit programmable superconducting processor1. High-fidelity two-qubit gates were also demonstrated for trapped ions2, neutral atoms in optical tweezers3, and spin qubits in silicon4,5 and GaAs6. These experimental implementations are based on tunable coupling between qubits where the interaction is switched on only when two qubit gates are needed. In solid-state quantum computers, tunable couplers typically involve more circuit elements and require their own external control for tuning the interaction1,4,7, leading to overheads in fabrication and wiring. For solving real-world problems, a quantum computer needs a large number of qubits8, and the complexity of tunable couplers adds to the technological difficulties in scaling up the device. In contrast, fixed couplers do not require the extra components for controlling the interaction, resulting in a substantial simplification of the hardware architecture and hence a significant advantage for scaling up.
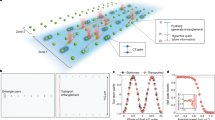
An important requirement for quantum computing with fixed coupling is the ability to cancel the unwanted evolution due to the fixed interaction on qubits where no gate is needed. In NMR quantum computing, where the qubits have fixed longitudinal couplings, this is achieved by applying a series of cleverly designed refocusing pulses9,10. For large arrays of qubits these series become increasingly complex, which is a bottleneck for scaling up10. In this paper, we describe a simple method for quantum computing on qubit arrays with fixed coupling without refocusing pulses. Instead, we rely on a key observation that, by driving a specific subarray, one can implement any gate on the driven qubits, and at the same time implement an identity operator on all undriven qubits, effectively cancelling the unwanted evolution on these undriven qubits. Any arbitrary quantum circuit can then be implemented by changing the driven subarray between the time steps. An overview of the driving pattern and the implementation of gates is given in Fig. 1, with more technical details provided later. Our method can be scaled up to an arbitrarily large array in a straightforward manner, opening an alternative pathway for a simplified quantum computer hardware architecture based entirely on fixed coupling.
a An example of implementing quantum gates on an array of qubits with fixed couplings. In any given step only a subarray can be driven. This subarray can be chosen to satisfy specific requirements so that the array’s Hamiltonian can be decomposed into commuting few-qubit blocks. Each drive can implement a gate on the driven qubit, and through its combination with the fixed qubit-qubit couplings also implements an identity operator on the neighbouring undriven qubits. In the next step, a different subarray is driven for implementing gates on a different set of qubits. Here C-X on two adjacent qubits denotes the CNOT gate and/the identity gate. b Illustration of a quantum circuit in our scheme. The key feature is that any idle interval between gates is filled with an identity gate for preventing unwanted evolution due to the fixed couplings.
In principle, designing the subarray could be difficult. This is because simulating a constantly interacting system of qubits is in general not possible due to the exponential wall: the cost in memory and time increases exponentially with the number of qubits. Thus, one cannot predict the unitary gate implemented by a driving pulse. In our method this problem is avoided, because the driven subarray can be chosen such that the total Hamiltonian of the system can be decomposed into a sum of commuting blocks of only a few qubits. Each block has a low dimensional Hilbert space, and thus its unitary evolution can be simulated and optimised efficiently. This decomposition exists when the qubit-qubit coupling term is longitudinal, i.e., diagonal in the computational basis, for example, the ZZ interaction.
An appealing feature of our method is the robustness of the gates against uncertainty in all the physical parameters of the array. By using robust optimal control we find pulses for realising gates with fidelities around 99.99% despite a 1% uncertainty in all the qubit-qubit and drive-qubit couplings, and a detuning uncertainty at 0.1% of the qubit-qubit coupling strength. This robustness of the fidelity against uncertainties is crucial for an architecture with entirely fixed couplers because it is not possible to isolate a qubit or qubit pair for a precise measurement of the parameter values, and hence there is always a significant residual uncertainty even after device characterisation.
This paper is organised as follows: In “Results” section we describe the key details of our method, including the driving pattern to make the Hamiltonian decomposable, the application of a universal set of gates, and the implementation of an arbitrary circuit. Next, we show how to use optimal control to make the gates robust against parameter uncertainty in the Hamiltonian. Finally, we discuss potential physical realisations and provide details of our optimisation algorithm in Methods.
Results
The system’s Hamiltonian
We first describe our method for implementing an arbitrary quantum circuit on qubit arrays with fixed longitudinal coupling. We consider a system of qubits coupled by fixed nearest-neighbour longitudinal interaction, i.e., an interaction that commutes with the bare qubit’s Hamiltonian. For simplicity we choose the ZZ interaction, which has been realised experimentally for superconducting qubits11,12. When a subset of qubits is driven by external fields, the system’s Hamiltonian is
where νj is the frequency of the drive on the j-th qubit, \({E}_{j}^{x}(t)\) and \({E}_{j}^{y}(t)\) the two quadratures of the field, dj the j-th qubit’s dipole matrix element, and \({{{\mathcal{L}}}}\) the driven subset. Typically, the qubit’s transition energy, ωj, is much larger than the interaction, Jjk, and hence \(\left\vert 0,0,...,0\right\rangle\) is the ground state of the undriven Hamiltonian and can be initialised by cooling.
In the frame rotating with the qubits’ frequencies, described by the unitary transformation \({U}_{0}(t)={e}^{i{\sum }_{j}\frac{{\omega }_{j}}{2}{\sigma }_{j}^{z}t}\), the Hamiltonian is
where
Here, \({{{\Omega }}}_{j}^{x,y}(t)\equiv {d}_{j}{E}_{j}^{x,y}(t)\) is the Rabi frequency and δj ≡ νj − ωj is the detuning.
Decomposition into commuting blocks
Computing the unitary evolution of a many-body Hamiltonian like H(t) is in general intractable due to the exponential complexity of the wave function, unless one can decompose the Hamiltonian into a sum of commuting few-qubit blocks, i.e., H(t) = ∑lHl(t), where all the Hl(t) are mutually commuting. The unitary evolution after a time duration T is then U(T) = ∏lUl(T) where \({U}_{l}(T)={{{\mathcal{T}}}}{e}^{-i\int\nolimits_{0}^{T}d{t}^{{\prime} }{H}_{l}({t}^{{\prime} })}\) and \({{{\mathcal{T}}}}\) is the time-ordering operator. Ul(T) can be efficiently computed since it involves only a few qubits. The Ul(T) factors are also mutually commuting and can be seen as parallel gates applied on separate qubit blocks.
We find that the simplest geometry that allows the decomposition of H(t) into few-qubit commuting blocks is a honeycomb array of qubits with nearest-neighbour ZZ coupling, as shown in Fig. 2. We consider an alternating driving pattern where only the subarray coloured in yellow in Fig. 2a is driven, then \(H(t)={\sum }_{j\in {{{\mathcal{L}}}}}{H}_{j}(t)\) where \({{{\mathcal{L}}}}\) is the driven subarray and
where NBj is the set of the three nearest neighbours of qubit j. Each of the block Hamiltonians, Hj, has only four qubits and they commute with each other. This can be seen in a more transparent way by the graphical representation in Fig. 2a. Each link in the graph represents a ZZ coupling term; a yellow vertex represents a single qubit driving term, and a cyan vertex represents an undriven qubit. All the ZZ terms commute with each other. A yellow vertex does not commute with only the three links connected to it, because σx and σy do not commute with σz. Thus, the total Hamiltonian can be expressed as a sum of commuting four-qubit blocks enclosed by the dash circles in Fig. 2a. Note that each block has only one driven qubit in the centre. The qubits at the intersection of two neighbouring blocks must not be driven for the commutativity to hold. We will show below that it is possible to implement a single qubit gate on the driven qubit without changing the state of the undriven qubits at the end of the gate, despite the permanent ZZ interaction in the block.
a An arbitrarily large 2D array of coupled qubits in a honeycomb array. Each link represents a ZZ coupling term. A yellow (cyan) vertex represents a driven (undriven) qubit. The total Hamiltonian can be decomposed into a sum of identical four-qubit blocks that commute with each other (enclosed in the dashed circles). An undriven qubit is shared by three neighbouring blocks. b The pattern of driving for implementing a two-qubit gate, resulting in a central row of identical six-qubit blocks (enclosed by the dashed rectangles). The rest of the array can be decomposed into the four-qubit blocks as in a.
The driving pattern needs to be modified slightly for implementing two-qubit gates. In a conventional device with tunable couplers the qubit-qubit interaction is turned on only when a two-qubit entangling gate is applied. In our case, the ZZ coupling is always on, and in general it entangles all the qubits at all times. However, we find that it is still possible to implement a specific two-qubit entanging gate, for example, the CNOT gate, between two targeted qubits by driving both. Turning on the drives on two neighbouring qubits results in the pattern of Fig. 2b where the central row is built from identical six-qubit blocks. The rest of the array can be driven in the alternating pattern as before. The reader may wonder why the six-qubit blocks are required for the entire central row when only one two-qubit gate is needed. This is necessary for applying the identity operators on all undriven qubits for cancelling the actions of the fixed ZZ coupling, which requires that any undriven qubit must have at least one neighbouring driven qubit (more details below). If a link, \({J}_{jk}{\sigma }_{j}^{z}{\sigma }_{k}^{z}\), is not connected to any driven qubit, then it commutes with all other terms in the Hamiltonian, and its contribution to the total unitary evolution is simply the factor \({e}^{-i{J}_{jk}{\sigma }_{j}^{z}{\sigma }_{k}^{z}T}\), which cannot be cancelled due to the absence of control.
Applying gates using optimal control
We now describe how to apply targeted gates on the driven qubits while at the same time apply the identity operators on the neighbouring undriven qubits. Note that the four and six qubit blocks in Fig. 2a, b have the form of a star graph where only a central subset of qubits is driven, as depicted in Fig. 3a. Our method lies in the key numerical finding that, for such a star graph, it is possible to use optimal control algorithm to find pulse shapes, \({{{\Omega }}}_{j}^{x,y}(t)\) where j ∈ driven subset, to implement a unitary operation of the type \({U}_{{{{\mathcal{C}}}}}\otimes {I}_{{{{\mathcal{B}}}}}\), where \({U}_{{{{\mathcal{C}}}}}\) is a unitary acting on the driven subset, and \({I}_{{{{\mathcal{B}}}}}\) the identity matrix acting on the undriven subset at the boundary. The net effect is that the gate \({U}_{{{{\mathcal{C}}}}}\) is applied to the driven subset while the rest remains unchanged. If the driven subset has one (two) qubit, then \({U}_{{{{\mathcal{C}}}}}\) is a single qubit (two-qubit) gate.
a A star graph with undriven qubits on the boundary and a driven subset of one or more qubits in the centre. Each undriven qubit must be connected to at least one driven qubit. By utilising optimal control on the driven subset it is possible to apply a unitary of the form \({U}_{{{{\mathcal{C}}}}}\otimes {I}_{{{{\mathcal{B}}}}}\) where \({U}_{{{{\mathcal{C}}}}}\) is a target unitary on the central driven subset, and \({I}_{{{{\mathcal{B}}}}}\equiv I\otimes I\otimes \cdots \otimes I\) is the identity in the Hilbert space of the undriven qubits on the boundary (see text). b Examples of applying a Hamadard gate on the four-qubit block and CNOT (CX) gate on the six-qubit block of Fig. 2. In both cases the identity operators are applied on all undriven qubits.
Obviously the qubits on the boundary are acted on by the ZZ interactions, and hence their states are changed during the pulse, but by choosing the right pulse shape one can use the combined effect of the central driving term and the ZZ connectors to ensure that the identity operators are applied at the end of the pulse, removing the ZZ interactions in a stroboscopic fashion. This can be partly understood by looking at the Baker-Campbell-Hausdorff (BCH) formula. For the four-qubit block with the Hamiltonian of Eq. (3), for example, the unitary evolution in a small time step is
where the last step follows from the BCH formula13. Here \({H}_{j}^{d}(t)\equiv (1/2)[{{{\Omega }}}_{j}(t){\sigma }_{j}^{x}+{{{\Omega }}}_{j}^{{\prime} }(t){\sigma }_{j}^{y}]\) is the driving term, \({H}_{j}^{int}\equiv {\sum }_{k\in {{{\mathrm{NB}}}}_{j}}{J}_{jk}{\sigma }_{j}^{z}{\sigma }_{k}^{z}\) the ZZ interaction terms, and \([{H}_{j}^{d}(t),{H}_{j}^{int}]\) the commutator of the two. While the first term is responsible for applying a gate on the driven qubit, the second is the unwanted evolution due to the ZZ interaction. Since \([{H}_{j}^{d}(t),{H}_{j}^{int}]={\sum }_{k\in {{{\mathrm{NB}}}}_{j}}i{J}_{jk}\left[{{{\Omega }}}_{j}(t){\sigma }_{j}^{x}-{{{\Omega }}}_{j}^{{\prime} }(t){\sigma }_{j}^{y}\right]{\sigma }_{k}^{z}\), it follows that the third exponential term of Eq. (4) allows partial control of the undriven qubits, labelled by k, through shaping \({{{\Omega }}}_{j}^{x,y}(t)\); and we find that this is sufficient for undoing the evolution due to the ZZ interaction.
Using optimal control we are able to obtain pulses for realising the unitary operator \({U}_{{{{\mathcal{C}}}}}\otimes {I}_{{{{\mathcal{B}}}}}\) with maximum fidelity, F = 1, up to numerical precision, where \({U}_{{{{\mathcal{C}}}}}\) is the Hadamard, π/8 and the direct identity gate on the single driven qubit of the four-qubit block. Here, we use “direct identity gate” to refer to an identity gate applied on a driven qubit to differentiate it from the identity operators applied on the undriven qubits. These results are demonstrated later in Table 1. The same results are achieved where \({U}_{{{{\mathcal{C}}}}}\) is the CNOT gate and the direct two-qubit identity gate, I ⊗ I, on the two driven qubits of the six-qubit block of Fig. 3b. Note that in all cases the identity operators are applied on the undriven qubits. These one and two qubit gates form a universal set, i.e., a set from which any muti-qubit unitary can be approximated with arbitrary precision, allowing the implementation of an arbitrary quantum circuit14. More details of the optimal control algorithm and pulse shapes are given later when we discuss the robustness of these gates against parameter uncertainty in the Hamiltonian.
Implementing quantum circuits
An implementation of quantum computation on the array is illustrated in Fig. 1 where the driven subarray is varied from one step to the next to apply the target gate on the right qubits. As can be seen in Fig. 1 the identity operators are applied on the undriven qubits at all steps. Note that the commuting blocks are not fixed, but may vary constantly during the execution of a quantum circuit, depending on where the gates are applied and whether they are single or two-qubit gates.
We show in Fig. 4a simple example of how the driven/undriven subarrays and the blocks are varied during the implementation of a simple quantum circuit. Consider the following sequence of gates on two qubits, denoted by A and B: a two-qubit gate on A and B, followed by a single qubit gate on A, and then a single qubit gate on B. Note how the driven/undriven subarrays and the blocks are changed at each step. In step 1 both qubits, A and B, are driven in a six-qubit block, in step 2 only qubit A is driven in a four-qubit block and qubit B now becomes an undriven qubit, and in step 3 qubit B is driven and qubit A undriven. At each step gates can also be implemented in parallel on the driven qubits other than A and B. This parallel processing helps reduce the number of steps in a computation. If there is no gate on a driven qubit at a given step one simply applies the direct identity gate to keep its state unchanged. Following this example it is straightforward to derive the driving pattern for an arbitrary quantum circuit.
In our method, the undriven subarray is crucial for the Hamiltonian decomposition into commuting blocks, but this means that there are always qubits that have no gate at a given step, leading to an overhead in the number of steps compared with conventional quantum computation with tunable couplers. The exact amount of this overhead depends on the gate configuration of a circuit, and also on the topology of the array. However, as shown in Fig. 2, when building the array from four-qubit, or six-qubit, blocks, or a combination of them, the number of undriven qubits is less than half of the total. In addition, the best case scenario for conventional quantum computation is when parallel gates are applied to all qubits at the same time step; hence, the overhead is at worst a factor of 2, which does not change the computational complexity order of an algorithm.
Now we discuss readout for the qubit array which takes a finite duration. At the end of the computation the drives are turned off and the system evolves according to the background Hamiltonian \({H}_{0}={\sum }_{j,k}{J}_{j,k}{\sigma }_{j}^{z}{\sigma }_{k}^{z}\). The final wavefunction can be expanded in the computational basis, \(\left\vert {\psi }_{f}\right\rangle \,=\,{\sum }_{{j}_{1},...,{j}_{N} = 0,1}{c}_{{j}_{1},...,{j}_{N}}\left\vert {j}_{1},...,{j}_{N}\right\rangle\). Since H0 consists of exclusively σz terms, \(\left\vert {j}_{1},...,{j}_{N}\right\rangle\) is an eigenstate of H0 and the evolution under H0 introduces only addition phases in the coefficients \({c}_{{j}_{1},...,{j}_{N}}\). These phases can be neglected if the qubits are read out in the Z basis at the end of a computation.
For quantum error correction, however, one must measure the qubits in the middle of a computation, and it is important to cancel the accumulated phases due to the fixed ZZ couplings during the measurement process. We find that this is possible if the qubit is measured by coupling to an external quantum system, for example, a resonator in the case of superconducting qubits, and that the coupling Hamiltonian commutes with the ZZ qubit-qubit interaction, for example σzVe, where Ve is an operator acting on the external quantum system alone. We first consider the simplest case of two ZZ-coupled qubits where the second qubit is coupled to the external system. As \({\sigma }_{1}^{z}{\sigma }_{2}^{z}\) commutes with \({\sigma }_{2}^{z}{V}_{e}\), we can use the same method as for applying the direct identity gates for the star graph of Fig. 3. Again, we drive only the 1st qubit, so the Hamiltonian of the whole system,
is a sum of two commuting terms: \({H}_{12}(t)\equiv {{{\Omega }}}_{1}(t){\sigma }_{1}^{x}+{{{\Omega }}}_{1}^{{\prime} }(t){\sigma }_{1}^{y}+{J}_{12}{\sigma }_{1}^{z}{\sigma }_{2}^{z}\) and \({H}_{2e}(t)\equiv {J}_{2e}(t){\sigma }_{2}^{z}{V}_{e}+{H}_{e}(t)\), where He(t) is the Hamiltonian of the external system. The measurement is done through the coupling H2e(t) and local operations (LOs) acting on the external system alone, for example a homodyne detection of the resonator mode. These LOs do not share support with H12(t), and H12(t) commutes with H2e(t), thus, the action of H12(t) on the system is simply \({U}_{12}(T)={{{\mathcal{T}}}}{e}^{-i\int\nolimits_{0}^{T}{H}_{12}({t}^{{\prime} })d{t}^{{\prime} }}\) where T is the pulse duration. One now uses optimal control to apply the identity gate, U12(T) ≡ I ⊗ I, thus cancelling the effect of the ZZ interaction during the measurement process. Any change in the system’s state is now due to the effect of the measurement alone, and our scheme is now equivalent to a measurement on non-interacting qubits. A formal description of this measurement process is given in Supplementary Information.
Extending this result to the honeycomb array of Fig. 2, the effect of all the ZZ terms can be cancelled by driving the three neighbouring qubits of the measured qubit to apply the identity gates. For superconducting qubits, this measurement procedure can be realised with the non-demolition readout of ref. 15, which utilises a longitudinal coupling between the qubit and a resonator, Jzzσz(a + a†), where a is the annihilating operator of the resonator mode. The reader can refer to ref. 16 for a review of longitudinal readouts for superconducting qubits.
Robustness against parameter uncertainty
We now describe the optimal control algorithm for maximising the fidelity of the unitary \({{{\mathcal{{U}}}_{C}}}\otimes {{{\mathcal{{I}}}_{B}}}\) and how to make this unitary robust against parameter uncertainty in the Hamiltonian. We divide the pulse duration, T, into M time bins of interval Δt. In each time bin the field amplitudes are kept constant. The set of the Rabi frequencies form the control vector, \({{{\boldsymbol{c}}}}=\{{{{\Omega }}}_{jn}^{\mu }:1\le n\le M;\mu =x,y;j\in {{{\mathcal{C}}}}\}\), where \({{{\mathcal{C}}}}\) is the driven subset. The unitary evolution \({U}_{{{{\mathcal{G}}}}}(T)\) of the star graph \({{{\mathcal{G}}}}\) is then a function of c. Each qubit-qubit coupling, Jjk, and detuning, δj, is allowed to vary independently in the uncertainty intervals \([\bar{J}-{{\Delta }}J/2,\bar{J}+{{\Delta }}J/2]\), and \([\bar{\delta }-{{\Delta }}\delta /2,\bar{\delta }+{{\Delta }}\delta /2]\), respectively. The uncertainty in the Rabi frequencies can be caused by that in the dipole-matrix elements, or a slow drift in the drive leading to changes in the field amplitudes from one experiment to the next. This can be modelled by replacing \({{{\Omega }}}_{j}^{x,y}(t)\) in \({H}_{{{{\mathcal{G}}}}}\) by \({\alpha }_{j}{{{\Omega }}}_{j}^{x,y}(t)\) where αj is a dimensionless parameter that varies in the interval [1 − Δα/2, 1 + Δα/2]. Now the unitary \({U}_{{{{\mathcal{G}}}}}(T)\) also depends on Jjk, αj, and δj. The qubit-qubit coupling and dipole-matrix element of a qubit usually cannot be measured with high precision, and they can change substantially due to experimental drift. In contrast, we find that it is possible to determine the frequency of every qubit in the array with precise spectroscopic measurement. In the array the resonant frequency of each qubit is shifted due to the ZZ interactions, but there exists a procedure of one and two-photon absorption measurements that can be combined to cancel these shifts and obtain the bare qubit frequency, ωj (see Supplementary Information). Thus, we assume that the driving fields are tuned to resonance, \(\bar{\delta }=0\), with residual detuning uncertainties much smaller than the average qubit-qubit interaction, \({{\Delta }}{\delta }_{j}/\bar{J}=0.1 \%\), which is typical for superconducting qubits (For superconducting qubits with ~10 kHz frequency drift17 and ~ 10 MHz coupling12, Δδ/J ~ 0.1%). This small detuning uncertainty should be achievable in most physical realisations of qubits owing to the high accuracy of spectroscopic measurements.
Denote the set of these uncertain parameters as v, then the robust optimal control problem can be defined as a max-min optimisation problem: We find an optimal control that maximises the minimum fidelity over v,
where \({{{\mathcal{V}}}}\) is the hypercube containing the possible values of v, and F(c, v) the gate fidelity based on the trace distance
where D is the dimension of the Hilbert space of \({{{\mathcal{G}}}}\), \({I}_{{{{\mathcal{B}}}}}\) the identity matrix of the subset of undriven qubits on the boundary, and \({U}_{{{{\mathcal{C}}}}}\) the target unitary that we want to apply on the central driven subset.
Finding the minimum of a high dimensional fidelity function is in general intractable, and one usually chooses a grid of points, vi, in \({{{\mathcal{V}}}}\), and optimise the minimum fidelity in this set. However, having a dense grid is not possible when there are many uncertain variables. For example, the 6-qubit block in Fig. 2b has 9 uncertain parameters, five Js, two αs, and two δs. A grid with 10 points in each parameter has a billion points in total, and one has to compute a billion fidelities at every step of the optimisation. We use a two-step optimisation process to reduce the computational cost. We first maximise the fidelity at the centre of the hypercube, making the fidelity function concave in the hypercube \({{{\mathcal{V}}}}\), which means that its minimum over v lies at one of the extreme points, i.e., one of the corners of the hypercube. Next, we maximise the fidelity at the extreme points. We find that this two-step process is sufficient to make the fidelity high in the entire hypercube. At the end of the optimisation, we obtain the fidelity distribution in the hypercube by calculating the fidelities at a large number of points generated uniformly at random, and we simply take the smallest value in this set, including the values at the extreme points, as our worst-case fidelity. More details and justifications can be found in Methods.
Optimising only the extreme points drastically reduces the number of points where F(c, v) has to be computed during the optimisation. There are \({2}^{{n}_{u}}\) extreme points in a hypercube of nu uncertain parameters. For the 6-qubit block we need to compute 29 ≡ 512 values of F(c, vi) for any given c. Using the symmetry of the problem we find that some extreme points always give the same fidelity, and thus the number of extreme points can be further reduced (see Methods). Gradient-based algorithms are used for all optimisations in this work.
For the four-qubit block of Fig. 2a, we derive optimal pulses to realise \({U}_{{{{\mathcal{C}}}}}\otimes {I}_{{{{\mathcal{B}}}}}\) where \({U}_{{{{\mathcal{C}}}}}\) is the Hadamard, π/814, and the single-qubit identity gate. And for the six-qubit block of Fig. 2b we want \({U}_{{{{\mathcal{C}}}}}\) to be the CNOT and the two-qubit identity gate. These gates form a universal set; and we recall that the identity gates are necessary for keeping the state of all qubits in a block unchanged when there is no gate on these qubits at any step in the circuit.
In Table 1 we show the robust fidelities obtained for the universal set and the identity gates at increasing levels of uncertainty. The gate duration is \(T=2\pi /\bar{J}\), divided into 100 time bins. For 1% uncertainty the fidelity is higher than 99.99% for both the single qubit and two-qubit gates. Even if the uncertainty is as high as 5% four-nine fidelities are still achieved for the single qubit gates, and above 99.94% for the two-qubit gates. This can be improved by increasing the number of initial guesses, relaxing the constraints, or raising the number of control variables. The optimal pulse shape for the Hadamard gate is shown in Fig. 5, and the pulse shapes for the other gates are given in Supplementary Information. We choose \(T=2\pi /\bar{J}\) for all gates but this exact value is not essential. The same order of magnitude is achieved for the fidelities when T is changed by 10%. In order to see the effectiveness of robust optimal control we also calculate the fidelities with non-robust optimal control: We first neglect all the uncertainties and optimise the fidelity for the ideal case where \({J}_{j}=\bar{J}\), αj = 1 and δj = 0 for all j, then we use the obtained optimal control, cideal, to calculate the minimum fidelity in the hypercube, \({{{\mathcal{F}}}}=\mathop{\min }\limits_{v\in {{{\mathcal{V}}}}}F({{{{\boldsymbol{c}}}}}_{{{\mathrm{ideal}}}},{{{\boldsymbol{v}}}})\). The results are shown in the parentheses of Table 1. robust optimisation improves the fidelities by two to three nines when the uncertanties are significantly large (1% and 5%).
Optimal pulse for the Hadamard gate at 1% uncertainty in Table 1. The gate duration is \(T=2\pi /\bar{J}\).
Discussion
A promising physical realisation of our model is the superconducting flux and transmon qubits. A direct ZZ interaction between flux qubits can be realised by coupling the qubits inductively, as demonstrated in quantum annealers11,18. There is another interesting scheme based on the inductive longitudinal coupling of the flux qubits with a common bus resonator15,16,19, which can be scaled up to 2D arrays20. A cross-Kerr ZZ interaction was utilised for implementing a CZ gate between two transmon qubits12. More recently, a universal set of gates, including the CNOT, was realised with always-on ZZ interaction on a two-transmon device, where pulse-shaping is used for cancelling the effect of the ZZ interaction on the single-qubit gates21. Thus, the feasibility of our proposal were partially demonstrated in experiments. While flux qubits are very good two-level systems and hence our results are immediately applicable, for transmons, leakage to higher excited states must be addressed in the optimal control algorithm22. This leakage can be suppressed at all time by including the leakage population as a penalty in the fidelity cost function23. Alternatively, one can optimise the pulse to allow the system to explore the leakage levels, but bring it back into the computational subspace at the end23,24. Other than superconducting qubits, the ZZ coupling is also the natural interaction in nuclear magnetic resonance quantum computers9, for which sophisticated pulse shaping is available25, making it a good test bed for our model.
Our approach relies on the ZZ qubit-qubit interaction for the total Hamiltonian to be decomposed into a sum of commuting blocks. However, in experimental realisations, especially with superconducting qubits, the interaction normally has both XX and ZZ components. The XX components can be suppressed by a large detuning between the qubit’s transition frequencies, i.e., ∣ω2 − ω1∣ ≫ Jxx where Jxx is the strength of the XX component. To see this consider a two-qubit Hamiltonian
In the frame rotating with the qubit frequencies, described by the unitary operator \({U}_{0}={e}^{i(\frac{{\omega }_{1}}{2}{\sigma }_{1}^{z}+\frac{{\omega }_{2}}{2}{\sigma }_{2}^{z})t}\), this becomes
where we have neglected the anti-rotating terms. When ∣ω2 − ω1∣ ≫ JXX the XX term is fast oscillating and hence can be neglected. A large detuning is indeed used in the experiment of ref. 12 to suppress the effect of the XX component. Note that the ZZ term does not change in the rotating frame, i.e., its effect is independent of the qubit detuning. For our honeycomb array of Fig. 2, one can detune one subarray from the other such that any two neighbouring qubits have large detuning.
The pulse duration, T, is also limited by the coherence time, T2, of the qubits. The decoherence rate of a block of \({N}^{{\prime} }\) qubits is enhanced by a factor of approximately \({N}^{{\prime} }\) in the worst case, giving rise to a lifetime of \({T}_{2}^{{\prime} }={T}_{2}/{N}^{{\prime} }\). The fidelity of a multi-qubit unitary on the block is then bounded by \(F\le 1-T/{T}_{2}^{{\prime} }=1-{N}^{{\prime} }T/{T}_{2}\). Therefore, to achieve a fidelity F for the four-qubit and six-qubit blocks in Table 1, the pulse duration needs to be shorter than \({T}_{2}(1-F)/{N}^{{\prime} }\) where \({N}^{{\prime} }=4\) and 6, respectively. In our simulation \(T=2\pi /\bar{J}\approx 40\)ns when \(\bar{J}\approx 2\pi \times 30\) MHz, which is typical for superconducting qubits12. A fidelity of 99.9% is then possible with T2 ~ 100 μs.
Although a honeycomb array is the focus of this paper, the qubits can be arranged in any physical shape that has the same connectivity, for example a square array with each qubit connected to only three nearest neighbours. Moreover, there exist driving patterns that satisfy the conditions of commutitativity and robust control for other geometries such as square arrays and one-dimensional chains (see Supplementary Information). One can also envisage a hybrid architecture where large clusters of fixed couplers are connected with tunable couplers, keeping the number of required tunable couplers low. Such a modular structure can help ease the technological difficulties in scaling up quantum computers.
To conclude, we find that it is feasible to implement quantum computing with accurate operations on 2D qubit arrays with exclusively fixed couplers. The quantum gates are robust against significant uncertainty in the qubit’s frequency, qubit-qubit, and drive-qubit coupling caused by imperfect characterisation and/or slowly fluctuating fields. Our proposal shows that scalability can be accelerated with simplified architecture based on fixed longitudinal coupling, motivating further development of this coupling in various physical platforms.
Methods
Calculating fidelity and gradient
We first describe how the fidelity and its gradients are calculated with the midpoint rule. The time duration is divided into M equal time bins with t0 = 0 and tM = T. The field amplitudes are kept constant during each time bin. The Hamiltonian of a star graph, \({{{\mathcal{G}}}}\), at the midpoint of the n − th interval from tn−1 to tn is
where αj is the dimensionless factor introduced to model the uncertainty in the Rabi frequencies, \({{{\mathcal{C}}}}\) the driven subset at the centre of the graph, Jjk ≠ 0 only for nearest neighbours, and
where \({{{\Omega }}}_{jn}^{x,y}\) are the Rabi frequencies of the driving field on the j-th driven qubit during the interval from tn−1 to tn. They are the elements of the \(2M{N}_{{{{\mathcal{C}}}}}\times 1\) control vector, c, where \({N}_{{{{\mathcal{C}}}}}\) is the number of qubits in the driven subset. The unitary evolution from tn−1 to tn, \({U}_{n}={e}^{-i{H}_{{{{\mathcal{G}}}},n}{{\Delta }}t}+O({{\Delta }}{t}^{3})\), is computed with the expm function in Matlab. For an efficient calculation of the fidelity and the gradients we compute and store all the Un, and then obtain the forward and backward unitary propagation operators26,27, defined by
using the recursive relations \({U}_{n}^{f}={U}_{n}{U}_{n-1}^{f}\) and \({U}_{n+1}^{b}={U}_{n+2}^{b}{U}_{n+1}\). Then the fidelity is
where \({N}_{{{{\mathcal{G}}}}}\) is the number of qubits in the star graph.
For computing the gradients, we note that
where
The derivative of \({U}_{n}\equiv {e}^{-i{H}_{{{{\mathcal{G}}}},n}{{\Delta }}t}\) with respect to \({{{\Omega }}}_{jn}^{\mu }\) is26
where \(\left[{H}_{{{{\mathcal{G}}}},n},{K}_{j,n}^{\mu }\right]\) is a commutator. It follows that the derivative of \({U}_{M}^{f}\equiv {U}_{n+1}^{b}{U}_{n}{U}_{n-1}^{f}\) is
and from this it is straight forward to compute the gradient of the fidelity. The most computationally expensive part of the calculation is the matrix exponentiation for obtaining Un, which is done M times. This matrix exponentiation can be sped up by using the Krylov subspace method on sparse matrices.
Robust optimisation
To make the fidelity robust against uncertainty we use a two-step optimisation method:
Step 1: We fist optimise the fidelity at the centre of the hypercube, i.e, F(c, v0) where v0 is the centre of \({{{\mathcal{V}}}}\). Starting from a random control, c0, we use gradient ascent to find c1 such that F(c1, v0) is extremely close to 1 (see the 2nd row of Table. 1 for example). Now v0 is essentially a global maximum of F(c1, v), as a function of v, in the hypercube, hence its 1st derivatives with respect to v are zeros and the Hessian matrix of the 2nd derivatives are negative semidefinite. Since the uncertain region is typically small, \(F({{{{\boldsymbol{c}}}}}_{1},{{{\boldsymbol{v}}}})\approx 1+{({{{\boldsymbol{v}}}}-{{{{\boldsymbol{v}}}}}_{0})}^{T}{{{\mathcal{M}}}}({{{{\boldsymbol{c}}}}}_{1},{{{{\boldsymbol{v}}}}}_{0})({{{\boldsymbol{v}}}}-{{{{\boldsymbol{v}}}}}_{0})\) where \({{{\mathcal{M}}}}({{{{\boldsymbol{c}}}}}_{1},{{{{\boldsymbol{v}}}}}_{0})\) is the Hessian matrix, which follows from Taylor expansion up to 2nd order around v0. As \({{{\mathcal{M}}}}({{{{\boldsymbol{c}}}}}_{1},{{{{\boldsymbol{v}}}}}_{0})\) is negative semidefinite, this approximate function is a concave quadratic function and thus has its minimum at one of the extreme points of the hypercube (it is a multidimensional analogue of an inverted parabola). We verify that the exact fidelity function indeed has its minimum at one of the extreme points by calculating the fidelity at 106 points generated uniformly at random in the hypercube. This number of sampling points is large enough such that adding more points leads to no noticeable change in the shape, the mean value, and the standard deviation of the sampled distribution.
Step 2: Starting with c1 as the initial control, we now optimise the fidelity F(c, v) at the extreme points, \({{{{\boldsymbol{v}}}}}_{i}^{\,{{\mathrm{ex}}}\,}\), of \({{{\mathcal{V}}}}\) using gradient ascent, obtaining an optimal control coptm. At the end of this step there is no guarantee that F(coptm, v) is still concave, i.e, its minimum over v may no longer remains at one of the extreme points. However, we find that after this step the fidelity is very high in the entire hypercube. To verify this we again calculate a fidelity distribution of 106 points generated uniformly at random, and we take the smallest value in this set, including the values at the extreme points, as the worst-case fidelity. For most cases of Table. 1 the minimum fidelity does remain at one of the extreme points after step 2, except for the \(\pi /8\otimes {I}_{{{{\mathcal{B}}}}}\) and \(I\otimes {I}_{{{{\mathcal{B}}}}}\) gates at 5% uncertainty, where the minimum of the sampled distribution is lower than the extreme point minimum, but the difference is less than 10−5.
The optimisation problems in Table 1 is highly symmetric. Interchanging the boundary qubits of the four-qubit block does not change the fidelity, and neither does interchanging the top two, or the bottom two, of the six-qubit block. Therefore, many extreme points have the same fidelity, and we utilise this symmetry to reduce the number of extreme points in our calculation from 32 to 16 for the four-qubit block, and from 512 to 288 for the six-qubit block.
Figure 6 shows the fidelity distributions in the uncertain region at the end of steps 1 and 2 for the Hadamard gate in Table. 1 at 5% uncertainty. Although the fidelity at the centre is 1, the distribution after step 1 has a long tail in the 98–99% range, showing the inadequacy of non-robust optimisation. After the extreme-point optimisation of step 2, the entire distribution is squeezed up to a very narrow range between 99.999% and 1, showing the effectiveness of our two-step optimisation algorithm.
Fidelity distribution in the hypercube for the Hadamard gate at 5% uncertainty in the control amplitude and the coupling (last row of Table 1). a Distribution after the centre optimisation of step 1 (see text). b Distribution after the extreme-point optimisation of step 2. The three lines indicate, from left to right, the minimum fidelity at the extreme points, the fidelity at one standard deviation below the average fidelity, and the average fidelity.
We use two gradient ascent methods to optimise the fidelity at the extreme points. The first is based on sequential convex programming28. We start with initial control c1 and u0 for the control vector and the upper limit (trust region) of the step, respectively. Then, a step ∣δc∣ < u0 is found to maximise \(\mathop{\min }\limits_{i}{\nabla }_{{{{\boldsymbol{c}}}}}F({{{\boldsymbol{c}}}},{{{{\boldsymbol{v}}}}}_{i}^{\,{{\mathrm{ex}}}\,})\cdot \delta {{{\boldsymbol{c}}}}\), i.e., to maximise the minimum first-order increment. This ensures all the fidelities at the extreme points are increased. The above optimisation problem can be solved by using the YALMIP toolbox and SPDT3 package in Matlab. If a step can be found such that \(\mathop{\min }\limits_{i}{\nabla }_{{{{\boldsymbol{c}}}}}F({{{\boldsymbol{c}}}},{{{{\boldsymbol{v}}}}}_{i}^{\,{{\mathrm{ex}}}\,})\cdot \delta {{{\boldsymbol{c}}}}\) is positive then we increase the upper bound u0 by 1.15, otherwise we decrease it by 2. We chose these factors as they give the fastest convergence in our numerical tests. The procedure is repeated until either the maximum iteration is reached or the step’s upper bound drops below a small tolerance.
The second approach is to simply maximise the average fidelity at the extreme points, \(\bar{{{{\mathcal{F}}}}}({{{\boldsymbol{c}}}})=\mathop{\sum }\nolimits_{i = 1}^{{n}_{{{\mathrm{ex}}}}}F({{{\boldsymbol{c}}}},{{{{\boldsymbol{v}}}}}_{i}^{\,{{\mathrm{ex}}}})/{n}_{{{\mathrm{ex}}}},\) where nex is the total number of extreme points, using a quasi-Newton method. Obviously this does not guarantee that the worst-case fidelity is increased, as the mean can be increased without increasing the minimum value in the set. However, we found that in our calculations the worst-case fidelity is always improved substantially when we maximise the average fidelity. We optimise \(\bar{{{{\mathcal{F}}}}}({{{\boldsymbol{c}}}})\) using the interior-point method implemented in Matlab’s fmincon function, where the Hessian is computed from the gradients with the BFGS approximation. In our tests the first algorithm is more sensitive on the initial guesses of the control parameters. For the two-qubit gates in Table 1 the computation is expensive so it is not practical to run the optimisation with too many initial guesses. We find that for the same running time the second algorithm gives higher fidelities, and the results in Table 1 are obtained with it. The number of function and gradient evaluations in each optimisation is around 5000 for the four-qubit block and 10000 for the six-qubit block.
Data availability
The simulation data and computer code for this work are available without restriction29.
References
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Ballance, C., Harty, T., Linke, N., Sepiol, M. & Lucas, D. HigH-fidelity Quantum Logic Gates Using Trapped-ion Hyperfine Qubits. Phys. Rev. Lett. 117, 060504 (2016).
Levine, H. et al. ParallEl Implementation Of High-fidelity Multiqubit Gates With Neutral Atoms. Phys. Rev. Lett. 123, 170503 (2019).
He, Y. et al. A two-qubit gate between phosphorus donor electrons in silicon. Nature 571, 371–375 (2019).
Huang, W. et al. Fidelity benchmarks for two-qubit gates in silicon. Nature https://www.nature.com/articles/s41586-019-1197-0 (2019).
Nichol, J. M. et al. High-fidelity entangling gate for double-quantum-dot spin qubits. npj Quant. Inform. https://www.nature.com/articles/s41534-016-0003-1 (2017).
Chen, Y. et al. Qubit architecture with high coherence and fast tunable coupling. Phys. Rev. Lett. 113, 220502 (2014).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Vandersypen, L. M. K. et al. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887 (2001).
Tsunoda, T., Bhole, G., Jones, S. A., Jones, J. A. & Leek, P. J. Efficient Hamiltonian programming in qubit arrays with nearest-neighbor couplings. Phys. Rev. A 102, 032405 (2020).
Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).
Collodo, M. C. et al. Implementation of conditional phase gates based on tunable zz interactions. Phys. Rev. Lett. 125, 240502 (2020).
Wilcox, R. M. Exponential operators and parameter differentiation in quantum physics. J. Math. Phys. 8, 962–982 (1967).
Nielsen, M. A. & Chuang, I. L.Quantum Computation and Quantum Information. Vol. 1 (Cambridge University Press, 2000).
Didier, N., Bourassa, J. & Blais, A. Fast quantum nondemolition readout by parametric modulation of longitudinal qubit-oscillator interaction. Phys. Rev. Lett. 115, 203601 (2015).
Blais, A., Grimsmo, A. L., Girvin, S. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).
Schlör, S. et al. Correlating decoherence in transmon qubits: low frequency noise by single fluctuators. Phys. Rev. Lett. 123, 190502 (2019).
Tennant, D. M. et al. Demonstration of long-range correlations via susceptibility measurements in a one-dimensional superconducting Josephson spin chain. npj Quant. Inf. 8, 1–9 (2022).
Billangeon, P.-M., Tsai, J. S. & Nakamura, Y. Circuit-QED-based scalable architectures for quantum information processing with superconducting qubits. Phys. Rev. B 91, 094517 (2015).
Richer, S. & DiVincenzo, D. Circuit design implementing longitudinal coupling: a scalable scheme for superconducting qubits. Phys. Rev. B 93, 134501 (2016).
Long, J. et al. A universal quantum gate set for transmon qubits with strong ZZ interactions. http://arxiv.org/abs/2103.12305. Preprint at arXiv:2103.12305 [quant-ph] (2021).
Motzoi, F., Gambetta, J. M., Rebentrost, P. & Wilhelm, F. K. Simple pulses for elimination of leakage in weakly nonlinear qubits. Phys. Rev. Lett. 103, 110501 (2009).
Ashhab, S. et al. Speed limits for two-qubit gates with weakly anharmonic qubits. Phys. Rev. A 105, 042614 (2022).
Allen, J. L., Kosut, R. & Ginossar, E. Minimal time robust two qubit gates in circuit QED. http://arxiv.org/abs/1902.08056. Preprint at arXiv.1902.08056 (2019).
Yang, X.-D. et al. Assessing three closed-loop learning algorithms by searching for high-quality quantum control pulses. Phys. Rev. A 102, 062605 (2020).
de Fouquieres, P., Schirmer, S., Glaser, S. & Kuprov, I. Second order gradient ascent pulse engineering. J. Magn. Reson. 212, 412–417 (2011).
Motzoi, F., Gambetta, J. M., Merkel, S. T. & Wilhelm, F. K. Optimal control methods for rapidly time-varying Hamiltonians. Phys. Rev. A 84, 022307 (2011).
Allen, J. L., Kosut, R., Joo, J., Leek, P. & Ginossar, E. Optimal control of two qubits via a single cavity drive in circuit quantum electrodynamics. Phys. Rev. A 95, 042325 (2017).
Le, N. H. Code and data for N Le et al. “Scalable and robust quantum computing on qubit arrays with fixed coupling” Zenodo https://doi.org/10.5281/zenodo.7154729 (2022).
Acknowledgements
This work is supported by the UK Hub in Quantum Computing and Simulation, part of the UK National Quantum Technologies Programme with funding from UKRI EPSRC grant EP/T001062/1, and the EPSRC strategic equipment grant no. EP/L02263X/1.
Author information
Authors and Affiliations
Contributions
N.H.L. and E.G. developed the method for quantum computation. N.H.L. and M.C. worked on the optimisation algorithms. N.H.L. and E.G. wrote the paper. E.G. and N.H.L. designed the project. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Le, N.H., Cykiert, M. & Ginossar, E. Scalable and robust quantum computing on qubit arrays with fixed coupling. npj Quantum Inf 9, 1 (2023). https://doi.org/10.1038/s41534-022-00668-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00668-3
This article is cited by
-
Archives of Quantum Computing: Research Progress and Challenges
Archives of Computational Methods in Engineering (2024)