Detection of molecular transitions with nitrogen-vacancy centers and electron-spin labels

Abstract

We present a protocol that detects molecular conformational changes with two nitroxide electron-spin labels and a nitrogen-vacancy (NV) center in diamond. More specifically, we demonstrate that the NV can detect energy shifts induced by the coupling between electron-spin labels. The protocol relies on the judicious application of microwave and radiofrequency pulses in a range of parameters that ensures stable nitroxide resonances. Furthermore, we demonstrate that our scheme is optimized by using nitroxides with distinct nitrogen isotopes. We develop a simple theoretical model that we combine with Bayesian inference techniques to demonstrate that our method enables the detection of conformational changes in ambient conditions including strong NV dephasing rates as a consequence of the diamond surface proximity and nitroxide thermalization mechanisms. Finally, we counter-intuitively show that with our method the small residual effect of random molecular tumbling becomes a resource that can be exploited to extract inter-label distances.

Introduction

A precise knowledge of molecular structure and dynamics would shed new light on the mechanisms by which, e.g., proteins interact with their environment¹. This finds important applications in distinct fields such as biochemistry and biology, since macromolecular conformational changes underlie numerous biological processes. In this regard, different techniques have been proposed to study molecular structure and dynamics^2,3,4. In particular, methods based on nuclear magnetic resonance (NMR)^5,6 and on electron-spin resonance (ESR)^7,8 stand out as they are central to investigate a wide variety of molecules, with ESR being more sensitive due to the much larger gyromagnetic ratio of electrons⁹. One commonly used ESR method is the Double Electron-Electron Resonance (DEER) in which synchronized and/or delayed pulses are delivered to, e.g., estimate average distances among free radicals in molecular ensembles¹⁰. However, traditional ESR based on inductive detection with macroscopic coils requires macroscopic samples with a high chemical purity to produce a detectable response. This rules out ESR investigations of static and dynamic properties of individual molecules.

Detectors based on NV centers in diamond^11,12 are promising candidates to overcome the limitations of inductive detection. Indeed, such detectors enable ESR and NMR detection of molecular samples down to the micron- and nanoscale and even down to the level of single molecules. The potential of NV centers in diamond originates from a number of appealing properties and early demonstrations. They can be initialized and read out using laser light in the visible spectrum, thereby removing thermal fluctuations from the measurement process^13,14,15. Moreover, NV hyperfine states can be manipulated with microwave radiation in such a way that the NV couples coherently to nearby nuclear and electron spins while at the same time being decoupled from environmental fluctuations^{16,17,18,19,20}. These concepts have enabled shallowly implanted NV centers to detect electron spins²¹ and even nuclear spins ^22,23 above the diamond surface with single-spin sensitivity. Detection protocols have also been developed allowing for nanoscale NMR^24,25,26,27 and ESR detection^28,29,30 with spectral resolution approaching that of macroscopic ESR and NMR based on inductive detection. Fluctuating electron spins of biological samples^31,32,33,34 and small groups of statistically polarized nuclear spins in a target protein³⁵ have been detected. Finally and particularly relevant to the present work, an NV center has also been used to detect a single nitroxide electron-spin label³⁶ attached to a protein. The use of nitroxide spin labels is particularly attractive because it enables the study of non-paramagnetic molecules³⁷. In particular, ref. ³⁸ reported the detection of an effective inter-label coupling in molecular ensembles using advanced multi-frequency spectroscopy techniques. Attaching several nitroxides to a single target protein could enable the study of its internal dynamics at room temperature with an NV center. However, this approach is challenging because spin labels have resonance frequencies and interaction strengths that strongly depend on their orientation with respect to the external magnetic field³⁹. Therefore, the identification of these parameters is complicated by the unavoidable molecular motion and environmental noise affecting the NV and the electron-spin labels.

In this work, we show how even a simple pulse sequence applied to a single pair of electron-spin labels and a shallow NV [see Fig. 1(a)] can detect single-molecule conformational transitions at room temperature. Our carefully engineered DEER sequence asymmetrically delivers microwave (radiofrequency) pulses to electron spins of the NV center (nitroxide spin labels) to resolve small energy shifts in the NV spectrum owing to the coupling between labels. Crucially, we find an energy-transition branch of the labels that presents an excellent robustness against unavoidable tumbling motion in ambient conditions. In addition, we show that this branch is especially robust when each nitroxide label contains a distinct nitrogen isotope. Finally, we develop a simple but accurate model which enables us to estimate not only the coupling but also the distance between labels using Bayesian inference. In particular, we counter-intuitively show that the small residual effect of tumbling, instead of being detrimental, enables the extraction of the distance between labels.

Fig. 1: System schematics and employed sequence.

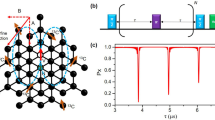
a A protein with two attached labels is near a diamond surface that contains a shallow NV. b Nitroxide molecule including the electron spin (yellow). The principal axes are shown in red, while the laboratory frame is shown in black. The azimuth θ (the angle between the z principal axis and the z laboratory axis) determines the energy-transition branches of the label. c MW and RF driving scheme. This includes initialization and read out with laser and microwave pulses, two free evolution stages of duration τ_free, 2N + 1 MW π-pulses on the NV, and a simultaneous RF π-pulse on the labels.

Results

The system

The Hamiltonian of the NV, the two nitroxide electron-spin labels, and the microwave (MW) and radiofrequency (RF) driving fields reads

$$\begin{array}{ll}H=&\frac{1}{2}\left({\mathbb{I}}+{\sigma }^{z}\right)\left({{{{\bf{a}}}}}_{1}\cdot {{{{\bf{J}}}}}_{1}+{{{{\bf{a}}}}}_{2}\cdot {{{{\bf{J}}}}}_{2}\right)\\ &+\,{H}_{{n}_{1}}+{H}_{{n}_{2}}+{g}_{12}\left[{J}_{1}^{z}{J}_{2}^{z}-\frac{1}{4}\left({J}_{1}^{+}{J}_{2}^{-}+{J}_{1}^{-}{J}_{2}^{+}\right)\right]\\ &+\,\frac{{{{\Omega }}}_{{{{\rm{MW}}}}}}{2}{\sigma }^{x}+2{{{\Omega }}}_{{{{\rm{RF}}}}}\left({J}_{1}^{x}+{J}_{2}^{x}\right)\cos ({\omega }_{{{{\rm{RF}}}}}t).\end{array}$$

(1)

Here, σ^z is the Pauli z operator for the NV two-level system and J_i are spin-1/2 operators for each label (i = 1, 2). The Hamiltonian of the ith nitroxide label is ${H}_{{n}_{i}}$ and the coupling of each label to the NV is mediated by the vectors a_i. Moreover, ${J}_{i}^{\pm }={J}_{i}^{x}\pm i{J}_{i}^{y}$ are electron-spin ladder operators and g₁₂ is the coupling constant between labels. The last line in Eq. (1) describes a MW field resonant with the NV, leading to the term $\frac{{{{\Omega }}}_{{{{\rm{MW}}}}}}{2}{\sigma }^{x}$ in a suitable interaction picture. In addition, an RF field of frequency ω_RF and Rabi frequency Ω_RF excites the electronic resonances of the nitroxide labels. Equation (1) is derived in the Supplementary Note 1 and a sketch of the system is presented in Fig. 1(a).

The term ${H}_{{n}_{i}}$ models each nitroxide label as^39,40

$${H}_{{n}_{i}}={\mu }_{{{{\rm{B}}}}}{B}^{z}\hat{{{{\rm{z}}}}}\cdot {{\mathbb{G}}}_{i}\cdot {{{{\bf{J}}}}}_{i}+{\gamma }_{{{{\rm{N}}}}}{B}^{z}{I}_{i}^{z}+{{{{\bf{I}}}}}_{i}\cdot {{\mathbb{Q}}}_{i}\cdot {{{{\bf{I}}}}}_{i}+{{{{\bf{J}}}}}_{i}\cdot {{\mathbb{A}}}_{i}\cdot {{{{\bf{I}}}}}_{i},$$

(2)

where μ_B is the Bohr magneton, B^z is a magnetic field applied along the z axis, γ_N is the nuclear gyromagnetic ratio equal to 2π × 3.077 kHz mT⁻¹ for ¹⁴N and to 2π × − 4.316 kHz mT⁻¹ for ¹⁵N, I_i is the nuclear spin operator for the ith nitroxide label, and ${{\mathbb{G}}}_{i}$, ${{\mathbb{Q}}}_{i}$, and ${{\mathbb{A}}}_{i}$ are respectively the Landé, quadrupolar, and electron-nucleus interaction tensors⁴⁰. We note that I_i is a spin-1 (spin-1/2) operator when describing a ¹⁴N (¹⁵N) nuclear spin. The components of the ${{\mathbb{G}}}_{i}$, ${{\mathbb{Q}}}_{i}$, and ${{\mathbb{A}}}_{i}$ tensors in a general reference frame depend on the frame’s relative orientation with respect to the principal axes of the nitroxide [see Fig. 1(b)]. In the principal frame, ${{\mathbb{G}}}_{i}$, ${{\mathbb{Q}}}_{i}$, and ${{\mathbb{A}}}_{i}$ are diagonal⁴⁰. In particular, the Landé tensor in the principal frame is ${{\mathbb{G}}}_{i}^{(P)}={{{\rm{diag}}}}\left({G}^{x},{G}^{y},{G}^{z}\right)$, with G^x ≈ G^y ≈ 2.007 ≡ G^⊥ and G^z ≈ 2.002 ≡ G^∥. The quadrupolar tensor for ¹⁴N is ${{\mathbb{Q}}}_{i}^{(P)}={{{\rm{diag}}}}\left({Q}^{x},{Q}^{y},{Q}^{z}\right)$, with Q^x ≈ 2π × 1.26 MHz, Q^y ≈ 2π × 0.53 MHz, and Q^z ≈ 2π × − 1.79 MHz. The quadrupolar tensor vanishes for ¹⁵N. Finally, the tensor that mediates electron-nucleus interactions in each nitroxide is ${{\mathbb{A}}}_{i}^{(P)}={{{\rm{diag}}}}\left({A}^{x},{A}^{y},{A}^{z}\right)$, where A^x ≈ A^y ≈ 2π × 14.7 MHz ≡ A^⊥ and A^z ≈ 2π × 101.4 MHz ≡ A^∥ for ¹⁴N, while A^x ≈ A^y ≈ 2π × 27MHz ≡ A^⊥ and A^z ≈ 2π × 141 MHz ≡ A^∥ for ¹⁵N⁴⁰.

We obtain approximate nitroxide transition frequencies via a perturbative treatment of the nuclear degrees of freedom in Eq. (2), see Supplementary Note 2. For a nitroxide hosting ¹⁴N, we find

$${H}_{{n}_{i}}\approx \left[{E}_{1}^{i}\left\vert \widetilde{1}\right\rangle {\left\langle \widetilde{1}\right\vert }_{i}+{E}_{0}^{i}\left\vert \widetilde{0}\right\rangle {\left\langle \widetilde{0}\right\vert }_{i}+{E}_{-1}^{i}\left\vert -\widetilde{1}\right\rangle {\left\langle -\widetilde{1}\right\vert }_{i}\right]{J}_{i}^{z}.$$

(3)

The three energy-transition branches exhibit transition energies given by ${E}_{1,-1}^{i}={\mu }_{{{{\rm{B}}}}}{B}^{z}G({\theta }_{i})\pm \frac{1}{\sqrt{2}}\sqrt{\left[{({A}^{\parallel })}^{2}-{({A}^{\perp })}^{2}\right]\cos (2{\theta }_{i})+{({A}^{\perp })}^{2}+{({A}^{\parallel })}^{2}}$ and ${E}_{0}^{i}={\mu }_{{{{\rm{B}}}}}{B}^{z}G({\theta }_{i})+\frac{1}{2{\mu }_{{{{\rm{B}}}}}{B}^{z}G({\theta }_{i})}\frac{2{({A}^{\perp }{A}^{\parallel })}^{2}+\left[{({A}^{\perp })}^{4}-{({A}^{\perp }{A}^{\parallel })}^{2}\right]{\sin }^{2}({\theta }_{i})}{{({A}^{\perp })}^{2}{\sin }^{2}({\theta }_{i})+{({A}^{\parallel })}^{2}{\cos }^{2}({\theta }_{i})}$. Here, θ_i is the azimuth angle between the applied magnetic field and the principal z axis of the nitroxide [see Fig. 1(b)], $G({\theta }_{i})=\frac{1}{2}[({G}^{\parallel }-{G}^{\perp })\cos (2{\theta }_{i})+{G}^{\perp }+{G}^{\parallel }]$, and ${\left\vert \widetilde{1}\right\rangle }_{i}$, ${\left\vert \widetilde{0}\right\rangle }_{i}$, and ${\left\vert -\widetilde{1}\right\rangle }_{i}$ are the states of the ith nitroxide nucleus dressed by the hyperfine interaction with the nitroxide electron, see Supplementary Note 2. Similarly, for a nitroxide hosting ¹⁵N, we find

$${H}_{{n}_{i}}\approx \left[{E}_{1/2}^{i}\vert \widetilde{1/2}\rangle {\langle \widetilde{1/2}\vert }_{i}+{E}_{-1/2}^{i}\vert -\widetilde{1/2}\rangle {\langle -\widetilde{1/2}\vert }_{i}\right]{J}_{i}^{z}.$$

(4)

There are now two energy-transition branches with transition energies given by ${E}_{1/2,-1/2}^{i}={\mu }_{{{{\rm{B}}}}}{B}^{z}G({\theta }_{i})\pm \frac{1}{2\sqrt{2}}\sqrt{{({A}^{\perp })}^{2}+{({A}^{\parallel })}^{2}+\left[{({A}^{\parallel })}^{2}-{({A}^{\perp })}^{2}\right]\cos (2{\theta }_{i})}$. Figure 2a compares the energy-transition branches in Eqs. (3) and (4) (dashed lines) with numerical diagonalization of Eq. (2) (solid lines). Note that since we will target the ${E}_{0}^{i}$ branch for label detection, we have further developed its functional form to include second-order corrections in the electron-nitrogen coupling, see Supplementary Note 2. Figure 2(a) focuses on a single nitroxide (the index i = 1 is removed for clarity) and shows that our expression for E₀ is in excellent agreement with numerical diagonalization.

Fig. 2: Energy branches of the spin labels and associated spectra.

a Energy-transition branches of an electron spin label at B^z = 30 mT for ¹⁴N (¹⁵N). Solid black (gray) lines show the transition energies as a function of the azimuth θ obtained via numerical diagonalization of Eq. (2). Dashed black (gray) lines correspond to E_1,0,−1 in Eq. (3) [E_1/2,−1/2 in Eq. (4)]. The vertical line highlights the case θ_i = 30°, with red dots indicating the transition energies relevant in the following plots. b NV spectrum ${\langle {\sigma }^{x}\rangle }_{{{{\rm{NV}}}}}$ as a function of the RF frequency applied near ${E}_{0}^{1}$. The spectrum was obtained by unitary propagation of Eq. (1) with ${H}_{{n}_{i}}$ given by Eq. (2) (black line) and by ${E}_{0}^{i}{J}_{i}^{z}$ (gray circles). The first nitroxide has azimuth θ₁ = 30° while the second nitroxide has azimuth θ₂ = 91.7°. The splitting of the peaks is induced by the inter-label coupling g₁₂ ≈ 2π × 1 MHz. The positions of the resonances are indicated by the dashed red lines. In (c, d), shaded areas show the average NV spectra ${\overline{\langle {\sigma }^{x}\rangle }}_{{{{\rm{NV}}}}}$ in the presence of tumbling of the first (near-resonant) nitroxide. Tumbling was mimicked by averaging over a random azimuth following a Gaussian distribution centered at the equilibrium value θ_1,eq = 30°. The orientation of the other nitroxide was kept fixed for simplicity. The standard deviation was chosen to be σ_θ = 6.25°. In (c), we observe that tumbling leads to a loss of contrast and to signal broadening near ${E}_{0}^{1}$. Nevertheless, the spectrum still shows two clearly separated peaks. For comparison, the case without tumbling in (b) is superimposed (black line). d Average NV spectrum ${\overline{\langle {\sigma }^{x}\rangle }}_{{{{\rm{NV}}}}}$ near ${E}_{1}^{1}$. Here, the energy splitting cannot be resolved due to nitroxide tumbling. Also note that tumbling severely reduces contrast. For that reason, the spectrum in the absence of tumbling has much higher contrast and is not shown.

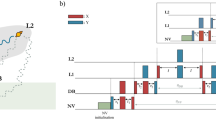
The inter-label coupling leads to an additional splitting ∝ g₁₂ of the energy-transition branches in Eqs. (3), (4). This term typically simplifies as ${g}_{12}\left[{J}_{1}^{z}{J}_{2}^{z}-\frac{1}{4}\left({J}_{1}^{+}{J}_{2}^{-}+{J}_{1}^{-}{J}_{2}^{+}\right)\right]\longrightarrow {g}_{12}{J}_{1}^{z}{J}_{2}^{z}$, since labels with different orientations have different resonance frequencies, thus eliminating the flip-flop contribution. Note that while this simplification is frequently (but not always) valid when using two ¹⁴N, it is guaranteed to be valid when using nitroxides hosting different nitrogen isotopes since E₀ (for ¹⁴N) differs from E_1/2,−1/2 (for ¹⁵N) for any value of the azimuth [see Fig. 2(a)]. For ¹⁴N, the available resonances of, e.g., the first label are then determined by the modified nitroxide Hamiltonian $H^{\prime}_{{n}_{1}}={H}_{{n}_{1}}+{g}_{12}{J}_{1}^{z}{J}_{2}^{z}$

$$\begin{array}{lll}H^{\prime}_{{n}_{1}}&=&\left[{E}_{1}^{1}\vert \widetilde{1}\rangle {\langle \widetilde{1}\vert }_{1}+{E}_{0}^{1}\vert \widetilde{0}\rangle {\langle \widetilde{0}\vert }_{1}+{E}_{-1}^{1}\vert -\widetilde{1}\rangle {\langle -\widetilde{1}\vert }_{1}\right]{J}_{1}^{z}+{g}_{12}{J}_{1}^{z}{J}_{2}^{z}\\ &=&\mathop{\sum}\limits_{q=1,0,-1}\left[\left({E}_{q}^{1}+\frac{{g}_{12}}{2}\right)\left\vert \widetilde{q}e\right\rangle \left\langle \widetilde{q}e\right\vert +\left({E}_{q}^{1}-\frac{{g}_{12}}{2}\right)\left\vert \widetilde{q}g\right\rangle \left\langle \widetilde{q}g\right\vert \right]{J}_{1}^{z}.\end{array}$$

(5)

That is, any energy-transition branch ${E}_{q}^{1}$ (corresponding to the $\left\vert \widetilde{q}\right\rangle$ nuclear state of the first nitroxide) splits as

$${E}_{q}^{1}\longrightarrow \left({E}_{q}^{1}+\frac{{g}_{12}}{2},{E}_{q}^{1}-\frac{{g}_{12}}{2}\right)$$

(6)

depending on the electronic state $\left\vert e\right\rangle$, $\left\vert g\right\rangle$ of the second nitroxide. Supplementary Note 2 includes a complete energy diagram of an electron spin in a nitroxide.

The protocol

Our DEER protocol simultaneously delivers MW and RF pulses to detect energy shifts in the NV spectrum due to inter-label coupling. The sequence contains two free-evolution stages of duration τ_free separated by a driving stage [see Fig. 1(c)]. The NV is prepared in the + 1 eigenstate of σ^x and the nitroxides are assumed to be in a fully thermalized state. During free evolution, the NV accumulates a phase due to the term ${\sigma }^{z}\left({{{{\bf{a}}}}}_{1}\cdot {{{{\bf{J}}}}}_{1}+{{{{\bf{a}}}}}_{2}\cdot {{{{\bf{J}}}}}_{2}\right)$ in Eq. (1). This term can be approximated as ${\sigma }^{z}\left({a}_{1}^{z}{J}_{1}^{z}+{a}_{2}^{z}{J}_{2}^{z}\right)$ in the rotating-wave approximation (RWA) since the ${J}_{i}^{x,y}$ contributions are suppressed by the large electronic precession frequencies of the nitroxides. Indeed, the energies ${E}_{1,0,-1}^{i}$ reach several hundreds of MHz even for moderate values of B^z (we use B^z = 30 mT in our simulations). By contrast, the NV-label coupling takes values of hundreds of kHz for typical NV-label distances of several nanometers. During MW/RF irradiation, the NV undergoes an overall flip σ^z → − σ^z via 2N + 1 contiguous π-pulses arising from the same continuous MW drive. At the same time, a single weaker RF π-pulse on the labels induces ${J}_{i}^{z}\to -{J}_{i}^{z}$ if it is near-resonant with an electronic transition (i.e., with ${E}_{1,0,-1}^{i}$ for ¹⁴N or with ${E}_{1/2,-1/2}^{i}$ for ¹⁵N). The simultaneous flipping of the NV and spin label ensures a constructive and coherent accumulation of the NV phase during free evolution. Meanwhile, the use of 2N + 1π-pulses on the NV ensures that the Rabi frequencies of the two drives are well separated, which effectively averages out spurious NV-label interactions during irradiation. Consequently, scanning the RF frequency near nitroxide transitions yields clean resonance peaks in the NV response. As long as Ω_RF < g₁₂, the resonance peaks are split by g₁₂. Figure 2(b) shows the NV spectrum (the expectation value of σ^x) associated with the transitions $\left\vert 0g\right\rangle \left\vert g\right\rangle \leftrightarrow \left\vert 0e\right\rangle \left\vert g\right\rangle$ and $\left\vert 0g\right\rangle \left\vert e\right\rangle \leftrightarrow \left\vert 0e\right\rangle \left\vert e\right\rangle$. The resonances are split by ~ g₁₂ as expected. The solid black line in Fig. 2(b) was obtained by numerically propagating Eq. (1) with ${H}_{{n}_{i}}$ given by Eq. (2), while gray circles were obtained assuming the simplified ${H}_{{n}_{i}}$ in Eq. (3). The two spectra are in excellent agreement. Simulations in Fig. 2(b) assume B^z = 30 mT, which is in the range of values that ensure the stability of the ${E}_{0}^{i}$ energy-transition branch discussed below, see Supplementary Note 2. Moreover, the parameters of the pulse sequence are τ_free = 1.3 μs, Ω_RF = 2π × 250 kHz, and Ω_MW = 31 × Ω_RF, for a total sequence time of 4.6 μs. In addition, the labels are separated from the NV by the distances d₁ ≈ 6.9 nm and d₂ ≈ 7.3 nm, leading to ${{{{\bf{a}}}}}_{1}\approx 2\pi \,\times \left(128,-132,-223\right)$ kHz and ${{{{\bf{a}}}}}_{2}\approx 2\pi \,\times \left(-22,-16,-264\right)$ kHz, while the distance between labels is d₁₂ ≈ 3.297 nm.

The expressions for the energy-transition branches in Eqs. (3) and (4) reveal a dependence on the azimuth angle, i.e., ${E}_{q}^{i}\equiv {E}_{q}^{i}({\theta }_{i})$. Consequently, unavoidable protein motion during the irradiation stage leads to a distortion in the spectrum and to a difficult interpretation of the signal. However, it is important to note the distinct nature of the ${E}_{0}^{i}$ branch, which shows a much weaker dependence on θ_i than ${E}_{1,-1}^{i}$. This makes the ${E}_{0}^{i}$ branch particularly well suited for robust detection of the energy splitting [see Fig. 2(c, d)]. To maximize the robustness, we chose the magnetic field to be large enough to energetically suppress the effect of the anisotropic hyperfine interaction, but small enough that the anisotropy of the Landé tensor does not become significant, see Supplementary Note 2.

Numerical simulations

We now illustrate our method in realistic ambient conditions including decoherence leading to NV dephasing with decoherence time T₂ = 20 μs (for a 4 nm NV depth³⁶), electron-spin label relaxation with T₁ = 4 μs³⁶, and molecular tumbling. The dissipative model used in this section is described in the Supplementary Note 3 and captures the main decoherence mechanisms identified in ref. ³⁶. Note that for the specific protocol considered here, decoherence mainly manifests as a reduced line contrast and not as an increased linewidth. This is because we keep the sequence duration fixed and sweep ω_RF to find the resonances, as opposed to varying the sequence length at fixed ω_RF to observe an echo signal. The molecular tumbling is modelled as a random rigid rotation of both nitroxides around an axis parallel to the laboratory x axis, see Supplementary Note 3. Our simulations use a rotation angle δ that is Gaussian-distributed with standard deviation σ_δ = 6.25°. This is somewhat smaller but comparable to the fluctuations observed in ref. ³⁶. Note that immobilizing proteins in more rigid matrices^41,42 or attaching them to the diamond surface³⁵ through multiple rigid covalent bonds could further reduce tumbling. The resulting tumbling-averaged spectra ${\overline{\langle {\sigma }^{x}\rangle }}_{{{{\rm{NV}}}}}$ are shown in Fig. 3. In Fig. 3(a, b, c), the parameters τ_free, Ω_MW, Ω_RF, and a_i are the same as in Fig. 2. In Fig. 3(a), the labels are separated by d₁₂ ≈ 3.297 nm and the inter-label coupling is g₁₂ ≈ 2π × 1 MHz. When the frequency of the RF field is set close to ${E}_{0}^{1}$, we clearly identify two resonance peaks in spite of tumbling. We have verified that the two resonances are still visible even if we choose σ_δ to be four times larger. Since ${g}_{12}\propto {d}_{12}^{-3}$, a change in the relative position of the labels significantly modifies the observed spectrum. This is shown in Fig. 3(b) where the second label was displaced such that d₁₂ ≈ 4.03 nm, leading to the disappearance of the splitting. This change in the spectrum certifies a change in the relative position between labels and, by extension, a conformational change in the host molecule.

Fig. 3: Simulated spectra and Bayesian inference of the inter-label distance.

a Simulated average NV spectrum ${\overline{\langle {\sigma }^{x}\rangle }}_{{{{\rm{NV}}}}}$. Two resonance peaks due to g₁₂ are observed. b Similar to (a) but with lower g₁₂. c Simulated average spectrum ${\overline{\langle {\sigma }^{x}\rangle }}_{{{{\rm{NV}}}}}$ for overlapping label resonances with two ¹⁴N isotopes (blue shaded area) and with distinct ¹⁴N and ¹⁵N isotopes (gray shaded area). d Marginal distribution L(d₁₂∣X) of the inter-label distance for simulated data acquisition using the spectrum shown in (a). The true value of the distance and its posterior expectation, 3.297 nm and 3.54(25) nm, are indicated with vertical lines. The error is the standard deviation of the marginal posterior.

So far, all simulations were performed for nitroxides hosting ¹⁴N and having distinct transition energies. If both nitroxides have similar transition energies (e.g., due to similar azimuths), the spectra of the two nitroxides overlap and the inter-label flip-flop terms cannot be neglected. This complicates the interpretation of the spectrum. As shown in Fig. 3(c), this problem is avoided by using distinct ¹⁴N and ¹⁵N isotopes in each nitroxide. In this case, the E₀ branch of the ¹⁴N nitroxide never overlaps with the branches of the ¹⁵N nitroxide and flip-flop terms can be safely neglected. As a result, the interpretation of the spectrum is much simpler. We emphasize that the purpose of using such orthogonal labels is not merely to resolve their distinct spectral signatures⁴³: rather, it is to simplify the form of the inter-label interaction itself for all label orientations.

Bayesian inference

Finally, we show how to infer the inter-label distance d₁₂ under realistic ambient conditions. We first simulate the experimental acquisition of ${\overline{\langle {\sigma }^{x}\rangle }}_{{{{\rm{NV}}}}}$. The simulated dataset has the form X = {X₁, …, X_M}, where X_j is an experimental estimate of the probability of measuring σ^x = + 1 after N_m measurements at RF frequency ω_RF,j. Second, we use a simplified model to efficiently extract information from X. The model captures the relevant features of the tumbling-averaged spectrum $\overline{{{{\mathcal{S}}}}}({\omega }_{{{{\rm{RF}}}}})$. More precisely, we derive the approximate expression ${{{\mathcal{S}}}}({\omega }_{{{{\rm{RF}}}}},\theta ,\beta )={{{{\mathcal{S}}}}}_{0}-{\sum }_{s = +,-}{{{{\mathcal{C}}}}}_{s}{\left[\frac{{{{\Omega }}}_{{{{\rm{RF}}}}}}{{{{\Omega }}}_{s}({\omega }_{{{{\rm{RF}}}}},\theta ,\beta )}\right]}^{2}{\sin }^{2}\left[\frac{\pi }{2}\frac{{{{\Omega }}}_{s}({\omega }_{{{{\rm{RF}}}}},\theta ,\beta )}{{{{\Omega }}}_{{{{\rm{RF}}}}}}\right]$ for a specific nitroxide azimuth θ and a specific angle β between the magnetic field and the line joining the nitroxides. Here, ${{{\Omega }}}_{\pm }^{2}({\omega }_{{{{\rm{RF}}}}},\theta ,\beta )={{{\Omega }}}_{{{{\rm{RF}}}}}^{2}+{\left[{\omega }_{{{{\rm{RF}}}}}-{E}_{0}(\theta )\pm {g}_{12}(\beta )/2\right]}^{2}$ and ${{{{\mathcal{S}}}}}_{0}$ and ${{{{\mathcal{C}}}}}_{\pm }$ are parameters that adjust the baseline and contrast, respectively (see Supplementary Note 3). Moreover, E₀(θ) is the ¹⁴N energy-transition branch, while ${g}_{12}(\beta )\propto {d}_{12}^{-3}(1-3{\cos }^{2}\beta )$ is the inter-label coupling. Both θ and β depend on the tumbling angle δ. Averaging ${{{\mathcal{S}}}}[{\omega }_{{{{\rm{RF}}}}},\theta (\delta ),\beta (\delta )]$ over a Gaussian distribution for δ gives the tumbling-averaged spectrum $\overline{{{{\mathcal{S}}}}}({\omega }_{{{{\rm{RF}}}}})$. Assuming that the baseline ${{{{\mathcal{S}}}}}_{0}$ is known, our model contains eight free parameters denoted by V. These include d₁₂ and the unknown standard deviation σ_δ of the tumbling. It must be emphasized that the light tumbling dependence of the E₀ branch enables the determination of the inter-label distance. Indeed, a simple measurement of the line splitting ${g}_{12}\propto {d}_{12}^{-3}(1-3{\cos }^{2}\beta )$ cannot give independent access to the distance d₁₂ and the angle β. This is because β is unknown a priori. However, light tumbling fluctuations allow the NV to probe different geometric configurations of the nitroxides. This results in a small distortion of the line shape that yields information beyond that contained in the splitting g₁₂. This in turn enables the independent extraction of the distance d₁₂ and of the angle β. With the help of our model, we can therefore obtain the posterior probability of the parameters V using Markov Chain Monte Carlo sampling⁴⁴. Assuming a uniform prior for V, the posterior probability for V is $L({{{\bf{V}}}}| {{{\bf{X}}}})={\prod }_{j = 1,M}{{{{\rm{e}}}}}^{-{[{X}_{j}-(\overline{{{{\mathcal{S}}}}}({\omega }_{{{{\rm{RF}}}},j})+1)/2]}^{2}/2{\sigma }_{m}^{2}}/\sqrt{2\pi {\sigma }_{m}^{2}}$. Here, the noise variance ${\sigma }_{m}^{2}\approx \left(1-{\overline{\langle {\sigma }^{x}\rangle }}_{{{{\rm{NV}}}}}^{2}\right)/4{N}_{m}$ is assumed to be approximately constant and known. In Fig. 3(d) we show the resulting marginal L(d₁₂∣X) of d₁₂ for a dataset X simulated from the spectrum shown in Fig. 3(a). Here, X was obtained by taking N_m = 2 × 10⁴ ideal measurements for each of M = 25 frequencies ranging from ω_RF/2π = 839–843 MHz (we estimate that the same accuracy is achieved with N_m ≈ 5 × 10⁵ for imperfect NV detection efficiency⁴⁵). The expectation of the marginal posterior is d₁₂ = 3.54(25) nm, close to the real value 3.297 nm [see Fig. 3(d)].

Discussion

Our results open many interesting avenues for future investigation. In particular, it would be of great interest to extend our scheme to molecules with more than two attached spin labels. This would yield a stronger NV response, leading to a more detailed observation of conformational changes as well as to an enhancement in the range of inter-label distances to be estimated. The scheme could also be improved through the use of multiple NVs to better triangulate the label positions. In addition, our analytical understanding of the NV response could enable fast Bayesian inference of molecular dynamical properties. Our results pave the way for the observation of conformational dynamics of individual proteins using tools from magnetic resonance.