Introduction

Quantum information processing based on continuous-variable (CV) resources1,2,3,4,5 represents an interesting alternative to a more common discrete-variable (DV) approach based on photons6,7,8 or other particles9,10,11. In particular, non-Gaussian states represented by the superposition or entanglement of a finite number of coherent states are useful resources in various protocols in both approaches12. The interest in these states has been fueled by various schemes for sensing13,14, computing15,16,17,18, and communication19,20 with promising merits in scalability and fault-tolerance21,22,23. There have been significant efforts into the generation of the superposition of coherent states (SCSs) and entangled coherent states (ECSs), both in the optical24,25,26,27,28, microwave29,30,31,32,33,34,35, and phononic domains36,37,38. Moreover, simple CV quantum processing tasks have been carried out on optical fields39,40, while more advanced processing has been demonstrated in the microwave regimes including quantum error correction41,42.

A formidable challenge associated with the faithful processing, transmission, and storage of SCSs lies in the inevitable decoherence by bosonic loss. Even a weak bosonic loss can still reduce the usefulness of the large excitation SCS states. While non-Gaussian43,44 or correlated45 noise sources can be circumvented for any type of encoding in bosonic modes by means of simple Gaussian transformations, the stationary bosonic loss—the dominant decoherence source in most bosonic systems - is non-trivial to correct for. To overcome the effect of loss in quantum information processing, one could use the protocol of entanglement distillation of resources46 in combination with deterministic teleportation, or more advanced quantum error correction coding schemes in which errors are corrected by encoding quantum information into special bosonic codes such as Gottesman–Kitaev–Preskill (GKP) states41,42,47,48,49,50,51,52,53,54,55, binomial states50,56,57 or SCSs58,59,60. However, those “ultimate” approaches require challenging large resources to universal loss correction.

Bosonic losses can be also partially but deterministically compensated for by transforming the encoded quantum state with a special symmetry into a state that is more robust against losses. For example, by conditionally de-amplifying a coherent state46,61,62,63, or unconditionally squeezing their superposition states64,65,66,67 prior to a lossy bosonic channel, the coherence or non-classicality can survive for a longer time. In these two protective schemes enabled by pre-processing, the quantum information has resided entirely in a bosonic quantum state. However, Gaussian squeezing is challenging on bosonic hybrid systems, such as mechanical systems68,69 and superconducting circuits70,71.

Loss (or amplitude damping) on qubit states can be corrected or re-amplified with smaller resources than on CV states spanning infinite high-dimensional Hilbert spaces, due to the former’s low-dimensional Hilbert space. A feasible example of such a lossless qubit is found in hyperfine qubits in the manifold of two ground states in trapped ion systems, which are extremely long-lived due to the lacking mechanism for relaxation due to the absence of a level with a lower energy72,73,74. In these systems, indeed qubit dephasing is the main noise mechanism. Superconducting qubits are also under extensive technical development to have extended coherence time75,76.

In this article, we propose the next step in a deterministic hybrid protection strategy for SCSs and ECSs, or a qubit bypass strategy, where the quantum information of these states does not reside fully in the lossy bosonic mode - as in previous schemes - but is substantially converted into a lossless two-level system. The quantum information is by large protected from bosonic loss by such a hybrid strategy, albeit being traded for phase decoherence of the two-level system. Our protection scheme is enabled by a strong coherent coupling—the Rabi coupling—which can be implemented in superconducting systems, ion systems, or photonic or molecular crystal systems77,78,79,80,81,82,83,84,85,86,87 where the bosonic mode is represented by a microwave, a phononic, or even an optical field. This bypass strategy is more economical than a full conversion of large CV states to many qubits and back. Our approach uses only a minimal number of low-loss qubits sufficient to perform efficient protection of the given class of CV states under boson loss. In this scheme, the number of used two-level systems and Rabi couplings is kept at a minimum, while the coupling strength is dictated by the amplitudes of the coherent states of the SCSs and ECSs. Our approach is therefore complementary to an approach where the available number of Rabi gates and ancillas are unlimited which in principle would allow for a complete transfer of the information from the bosonic mode to the two-level systems88. We analyze our protocol using different measures (i.e., fidelity, coherence in phase space, and entanglement), with respect to the simple protection scheme of pre-squeezing64. We find that the robustness to losses is significantly increased in all these measures, remarkably for large-amplitude SCSs. Our strategy can be extended to states with higher complexity, e.g., with more coherent state components or modes, thereby indicating that further extensions of the method to general CV states might be viable.

Results

Qubit bypass protocol

Our qubit bypass protocol is based on the quantum Rabi model77,78. This model incorporates a CV-DV hybrid non-Gaussian interaction, where an electromagnetic field or mechanical oscillator strongly couples to a two-level system, e.g., an atom. The unitary evolution operator associated with the coupling in the model is written as \(\exp [{{{\rm{i}}}}\tau {\hat{\sigma }}_{\theta }{\hat{X}}_{{{\Phi }}}]\) with strength τ (the strength of the Hamiltonian is combined with the duration time), where a Pauli operator \({\hat{\sigma }}_{\theta }\) with θ = {x, y, z} acts on the two-level system, and the generalized quadrature operator \({\hat{X}}_{{{\Phi }}}=\frac{\hat{a}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}{{\Phi }}}+{\hat{a}}^{{\dagger} }{{{{\rm{e}}}}}^{{{{\rm{i}}}}{{\Phi }}}}{\sqrt{2}}\) with arbitrary angle Φ governs the field. The rotating-wave approximation is not valid within this model, and the unitary operator contains both rotating and counter-rotating terms. Strong Rabi coupling has been achieved experimentally in cavity QED systems such as trapped ions82 or superconducting systems89,90 among many other systems. It can be used to create diverse classes of non-Gaussian effects such as nonlinear phase gates91,92, which are essential in CV quantum information processing3. The use of weak Rabi coupling for a longer time is vulnerable to large noises, and the free evolution effects are actively canceled by external drives77.

The unitary Rabi gate executes a controlled displacement operation, where the conjugate generalized momentum, \({\hat{P}}_{{{\Phi }}}={\hat{X}}_{{{\Phi }}+\frac{{{{\rm{\pi }}}}}{2}}\), of an oscillator is displaced depending on the state of an ancillary qubit encoded in \({\hat{\sigma }}_{\theta }\)-eigenstates. Here, we will drop the subscript for Φ = 0 below for these operators. The Rabi gate is particularly suitable for the generation of SCSs77,78. These controlled displacement operations have been used in numerous experiments to generate superpositions of two and four coherent states (for example, as in ref. 93). In the current work, we will reverse the generation process by mapping the SCSs onto a two-level ancilla, or more precisely, partially converting the complex coefficients of SCSs onto the complex coefficients of a qubit, addressing the possibility to manipulate the SCSs by Rabi gates.

Two coherent state superposition

Throughout the paper, we will refer the superposition of n coherent states as n-SCSs. We start with the simplest SCSs, namely the arbitrary superposition of two coherent states (2-SCS) of opposite amplitudes, \(\left|{\psi }_{0}\right\rangle =N(\mu \left|\alpha \right\rangle +\nu \left|-\alpha \right\rangle )\). We describe here the case of pure states, but the protocol works on the mixed states that might have been affected by noises in an equivalent way. The normalization factor is given by \({N}^{-2}=| \mu {| }^{2}+| \nu {| }^{2}+({\mu }^{* }\nu +\mu {\nu }^{* }){{{{\rm{e}}}}}^{-2{\alpha }^{2}}\) but will be omitted below for simplicity in the description. While the unknown complex coefficients of the superposition \(\mu ,\nu \in {\mathbb{C}}\) are carrying encoded information, the amplitude \(\alpha \in {\mathbb{R}}\) is typically assumed to be known. We focus primarily on nearly orthogonal coherence states with large α ≫ 2 when this state can be considered as a qubit of basis \(\left|\pm \alpha \right\rangle\).

Before going to the details of our protocol, let us first consider the decoherence of an unprotected 2-SCS undergoing bosonic loss channel Γη. Any density matrix ρ under Γη evolves as \({{{\Gamma }}}_{\eta }[\rho ]=\mathop{\sum }\nolimits_{l = 0}^{\infty }\frac{{\left(1-\eta \right)}^{l}}{l!}{\eta }^{\hat{n}/2}{\hat{a}}^{l}\rho {\hat{a}}^{{\dagger} l}{\eta }^{\hat{n}/2}\) with the loss parameter \(\eta ={{{{\rm{e}}}}}^{-\gamma t}\in \left(0,1\right]\) and γt is the dimensionless damping parameter, equivalent to Kraus operator notation in ref. 94. This is equivalent to the solution of the Lindblad equation \({\partial }_{t}\rho =L\rho {L}^{{\dagger} }-\frac{1}{2}\{{L}^{{\dagger} }L\rho \}\) with a Lindblad operator with \(L=\sqrt{\gamma }\hat{a}\). 2-SCS evolves by this loss simply as

$$\begin{array}{ll}{{{\Gamma }}}_{\eta }[\left|{\psi }_{0}\right\rangle\left\langle {\psi }_{0}\right|]\,\,\,=&{\left|\mu\right|}^{2}\left|\sqrt{\eta }\alpha \right\rangle \left\langle\sqrt{\eta }\alpha \right|+{\left|\nu \right|}^{2}\left|-\sqrt{\eta}\alpha \right\rangle \left\langle -\sqrt{\eta }\alpha \right|\\&+\,\mu{\nu }^{* }{{{{\rm{e}}}}}^{-2{\alpha }^{2}(1-\eta )}\left|\sqrt{\eta}\alpha \right\rangle\ \left\langle -\sqrt{\eta }\alpha \right|\\&+\,{\mu}^{* }\nu {{{{\rm{e}}}}}^{-2{\alpha }^{2}(1-\eta )}\left|-\sqrt{\eta}\alpha \right\rangle \left\langle \sqrt{\eta }\alpha\right|.\end{array}$$
(1)

The off-diagonal elements carrying the quantum coherence in this nearly orthogonal coherent state basis, are rapidly decreasing for a large α by the factor \({{{{\rm{e}}}}}^{-2{\alpha }^{2}(1-\eta )}\). This rapid decoherence can be avoided if α is effectively reduced, e.g., by mapping the information onto a two-level system, which will be the virtual effect of our protocol on the coherent states in the oscillator.

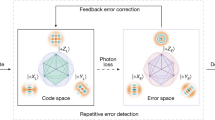
Our bypass protocol illustrated in Fig. 1a consists of a set of two Rabi gates \({\hat{U}}_{{{{\rm{T}}}}}={\hat{U}}_{{{{\rm{D}}}}}{\hat{U}}_{{{{\rm{R}}}}}\) applied before the lossy channel, effectively reducing the coherent amplitudes in two steps. The first weak unitary Rabi gate, \({\hat{U}}_{{{{\rm{R}}}}}=\exp [{{{\rm{i}}}}\epsilon {\hat{\sigma }}_{{{{\rm{x}}}}}\hat{X}]\) with \(\epsilon ={{{\rm{\pi }}}}/4\sqrt{2}\alpha\), rotates the initial ancillary qubit state \(\left|g\right\rangle\) controlled by the amplitudes in the coherent states to have an entangled state while only weakly disturbing the coherent states as:

$$\begin{array}{ll}&\exp [{{{\rm{i}}}}\epsilon {\hat{\sigma}}_{{{{\rm{x}}}}}\hat{X}]\left|g\right\rangle (\mu \left|\alpha \right\rangle +\nu \left|-\alpha \right\rangle )=\mu \hat{D}[\alpha ]\exp [{{{\rm{i}}}}\epsilon {\hat{\sigma}}_{{{{\rm{x}}}}}(\hat{X}+\sqrt{2}\alpha )]\left|g\right\rangle \left|0\right\rangle \\&+\,\nu \hat{D}[-\alpha ]\exp \left[{{{\rm{i}}}}\epsilon {\hat{\sigma}}_{{{{\rm{x}}}}}(\hat{X}-\sqrt{2}\alpha )\right]\left|g\right\rangle \left|0\right\rangle =\frac{{{{\rm{i}}}}}{2}\left\{\mu \hat{D}[\alpha ]\left(\left|{-}_{{{{\rm{i}}}}}\right\rangle \left|{\frac{{{{\rm{i}}}}\epsilon}{\sqrt{2}}}_{+}\right\rangle -\,{{{\rm{i}}}}\left|{+}_{{{{\rm{i}}}}}\right\rangle \left|{\frac{{{{\rm{i}}}}\epsilon}{\sqrt{2}}}_{-}\right\rangle \right)\right.\\&\,\,-\,\nu \hat{D}[-\alpha ]\left(\left|{+}_{{{{\rm{i}}}}}\right\rangle \left|{\frac{{{{\rm{i}}}}\epsilon}{\sqrt{2}}}_{+}\right\rangle +{{{\rm{i}}}}\left|{-}_{{{{\rm{i}}}}}\right\rangle \left|{\frac{{{{\rm{i}}}}\epsilon}{\sqrt{2}}}_{-}\right\rangle \right)\left.\right\} \mathop{\longrightarrow}\limits^{\alpha \gg 2}{{{\rm{i}}}}\left(\mu \left|{-}_{{{{\rm{i}}}}}\right\rangle \left|\alpha \right\rangle -\nu \left|{+}_{{{{\rm{i}}}}}\right\rangle \left|-\alpha \right\rangle \right),\end{array}$$
(2)

where an ordering relation \(\hat{D}[\alpha ]\hat{X}\hat{D}[-\alpha ]=\hat{X}+\sqrt{2}\alpha\) was used on the first equality. The approximation used on the last line is \(\left|\beta +{{{\rm{i}}}}\varepsilon \right\rangle \approx \exp [{{{\rm{i}}}}\beta \varepsilon ]\left|\beta \right\rangle\), for ε ≪ 1. Here, the unnormalized coherent superposition states are denoted as \(\left|{\delta }_{\pm }\right\rangle =\left|\delta \right\rangle \pm \left|-\delta \right\rangle\) and the qubit states \(\left|{\pm }_{{{{\rm{i}}}}}\right\rangle\) denote the eigenstates of \({\hat{\sigma }}_{{{{\rm{y}}}}}\) with eigenvalues ±1. In the limit of a large amplitude α ≫ 289,95, the odd superpositions states vanish \(\left|{\frac{{{{\rm{i}}}}\epsilon }{\sqrt{2}}}_{-}\right\rangle \to 0\) and the even superpositions approach the vacuum \(\left|{\frac{{{{\rm{i}}}}\epsilon }{\sqrt{2}}}_{+}\right\rangle \to \left|0\right\rangle\). In total, eq. (2) can be interpreted as an entangling process of the 2-SCS and the qubit ancilla.

Fig. 1: Bypass protocol.
figure 1

a Schematic of the protection protocol for a superposition of two coherent states in a bosonic mode (thick), exploiting a single qubit bypass (thin). The oscillator and the ancillary qubit interact by a unitary coupling \({\hat{U}}_{{{{\rm{T}}}}}\) made of two Rabi gates, i.e., controlled qubit rotation \({\hat{U}}_{{{{\rm{R}}}}}=\exp [{{{\rm{i}}}}\epsilon {\hat{\sigma }}_{{{{\rm{x}}}}}\hat{X}]={\hat{R}}_{{{{\rm{x}}}}}[2\epsilon \hat{X}]\) where qubit rotation is denoted as \({\hat{R}}_{{{{\rm{x}}}}}[\vartheta ]=\exp [{{{\rm{i}}}}\vartheta {\hat{\sigma }}_{{{{\rm{x}}}}}/2]\), and controlled displacement \({\hat{U}}_{{{{\rm{D}}}}}=\exp [-{{{\rm{i}}}}\sqrt{2}\alpha {\hat{\sigma }}_{{{{\rm{y}}}}}\hat{P}]=\hat{D}[{{{\rm{i}}}}\alpha {\hat{\sigma }}_{{{{\rm{y}}}}}]\). This bosonic channel undergoes linear damping in a lossy channel, whereas a lossless qubit channel degrades only by a phase damping; the bosonic damping and phase damping are represented with trace-preserving maps Γη and Γp, respectively. The qubit bypass is intrinsically protected against the amplitude damping by the qubit encoding to two ground states. After \({\hat{U}}_{{{{\rm{T}}}}}\), the quantum information is transferred to the qubit substantially, but keeping the CV channel is still beneficial. After decoherence by the error channels, the input state is restored by the inverse unitary process \({\hat{U}}_{{{{\rm{T}}}}}^{{\dagger} }\). An extension of the protocol exploiting two bypass qubits b to a single-mode superposition of four coherent states, and c to bipartite entangled states where the protocol is applied locally on each mode.

Full size image

The second Rabi gate \({\hat{U}}_{{{{\rm{D}}}}}=\exp [-i\sqrt{2}\alpha {\hat{\sigma }}_{{{{\rm{y}}}}}\hat{P}]=\hat{D}[i\alpha {\hat{\sigma }}_{{{{\rm{y}}}}}]\) acts as a controlled displacement, i.e., the ancilla qubit encoded in \(\left|{\pm }_{{{{\rm{i}}}}}\right\rangle\) from (2) as the control and oscillator as the target, which transfers the information to the qubit ancilla, at which stage the reduction of the amplitude actually takes place. Applying \({\hat{U}}_{{{{\rm{D}}}}}\) on (2), we obtain the state which will undergo the noise channels:

$$\begin{array}{ll}&\exp \left[-{{{\rm{i}}}}\sqrt{2}\alpha {\hat{\sigma }}_{{{{\rm{y}}}}}\hat{P}\right]\exp [{{{\rm{i}}}}\epsilon {\hat{\sigma }}_{{{{\rm{x}}}}}\hat{X}]\left|g\right\rangle (\mu \left|\alpha \right\rangle +\nu \left|-\alpha \right\rangle )\\& ={{{\rm{i}}}}\mu \left(\left|{-}_{{{{\rm{i}}}}}\right\rangle \frac{\left|{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle +\left|-{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle }{2}+\left|{+}_{{{{\rm{i}}}}}\right\rangle \frac{{e}^{-{{{\rm{i}}}}{{{\rm{\pi }}}}/4}\left|2\alpha +{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle -{{{{\rm{e}}}}}^{{{{\rm{i}}}}{{{\rm{\pi }}}}/4}\left|2\alpha -{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle }{2{{{\rm{i}}}}}\right)\\& -\,{{{\rm{i}}}}\nu \left(\left|{+}_{{{{\rm{i}}}}}\right\rangle \frac{\left|{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle +\left|-{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle }{2}-\left|{-}_{{{{\rm{i}}}}}\right\rangle \frac{{e}^{{{{\rm{i}}}}{{{\rm{\pi }}}}/4}\left|-2\alpha +{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle -{e}^{-{{{\rm{i}}}}{{{\rm{\pi }}}}/4}\left|-2\alpha -{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle }{2{{{\rm{i}}}}}\right)\\ &\mathop{\longrightarrow }\limits^{\alpha \gg 2}{{{\rm{i}}}}\left(\mu \left|{-}_{{{{\rm{i}}}}}\right\rangle -\nu \left|{+}_{{{{\rm{i}}}}}\right\rangle \right)\left|0\right\rangle .\end{array}$$
(3)

This state contains an even superposition of coherent states \(\left|\pm {{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle\) close to a vacuum state and erroneous states \(\left|\pm 2\alpha \pm {{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle\) far from the phase space origin. We note that only the erroneous terms are affected heavily by loss due to their large amplitudes while the terms with small amplitudes are less affected by loss, and it can be still advantageous to keep the bosonic channel. For a finite α, the information is still shared between the oscillator and the qubit as is evidenced from the entangled form, and we can still exploit the information transferred to the erroneous terms to help maintaining high fidelity when the loss is weak. This equation shows that the information of the input states at with a large α are nearly transferred onto the qubit states, and thus can have enhanced robustness to the boson loss in the oscillator.

We consider qubit ancilla to be lossless without amplitude damping while the effect of qubit loss is considered in Supplementary Sec. VIII, but sensitive to small phase damping9,10 as the main threat to robustness. We model the phase damping as \({{{\Gamma }}}_{p}[\rho ]=(1-\frac{p}{2})\rho +\frac{p}{2}{\hat{\sigma }}_{{{{\rm{z}}}}}\rho {\hat{\sigma }}_{{{{\rm{z}}}}}\) for any state ρ with dephasing parameter p. This channel is an identity channel at p = 0, and the maximal dephasing channel at p = 1. The same dephasing channels act independently on all physical qubit ancillas involved through the paper. Note that it is also possible to correct this dephasing error actively by transferring the information into multiple ancillas for conventional DV error correction methods96,97, or by a hybrid qubit protection scheme using the Rabi type of interactions as in the Supplementary Sec. IV. In the following section, we show that after the error channels Γη and Γp, the original state is substantially restored by the inverse operations \({\hat{U}}_{{{{\rm{T}}}}}^{{\dagger} }\). We also note that in principle, the entire protocol can be achieved by dispersive interaction and displacement which transforms a dispersive coupling into a synthetic Rabi coupling98,99 in traveling-wave microwave/optical platforms for future experiments extending the scheme in ref. 28. We note that our scheme has a similarity and can be replaced with a conversion based on dispersive couplings22,42. However, our bypass scheme has an advantage in terms of fidelity due to the approximate nature and fragility of noises of the dispersive interactions, especially in a large α limit.

Four coherent state superposition

This methodology can be scaled up to cases of more coherent state components in the superposition, e.g., to 4-SCS \({\mu }_{1}\left|\alpha \right\rangle +{\mu }_{2}\left|{\alpha }^{* }\right\rangle +{\mu }_{3}\left|-\alpha \right\rangle +{\mu }_{4}\left|-{\alpha }^{* }\right\rangle\) for \(\alpha ={\alpha }_{r}+{{{\rm{i}}}}{\alpha }_{{{{\rm{i}}}}}\in {\mathbb{C}}\)100. This class of states are of particular interest recently, due to its ability for high precise sensing13 and a fault-tolerant encoding it42. Gaussian operations such as squeezing cannot protect such states at all, as the broken symmetry in phase space by squeezing leads to more severe decoherence. Therefore, these states can be an advanced testbed for the extension of the bypass strategy to general SCSs. We note that a single qubit will not be sufficient for the bypass due to the existence of 4 unknown coefficients μj’s, and we need to extend the circuit to two ancilla qubits for the minimal complexity. Similarly, as in the 2-SCSs, we demonstrate the protocol for pure states, while it can work equivalently for mixed states.

To protect a general 4-SCS with our hybrid bypass scheme, two ancillas with indices \(j=1^{\prime} ,2^{\prime}\) couple respectively to the quadrature variables X and P of an oscillator by four Rabi gates forming \({\hat{U}}_{{T}_{X,P}}\) as depicted in Fig. 1b. The two quadratures are independently coupled to each of the ancillas similarly to the two-step protocol for 2-SCSs by the operations \({\hat{U}}_{{{{\rm{R}}}}}^{(1^{\prime} )}=\exp [{{{\rm{i}}}}{\epsilon }_{r}{\hat{\sigma }}_{{{{\rm{x}}}}}^{(1^{\prime} )}\hat{X}]\) and \({\hat{U}}_{{{{\rm{R}}}}}^{(2^{\prime} )}=\exp [{{{\rm{i}}}}{\epsilon }_{{{{\rm{i}}}}}{\hat{\sigma }}_{{{{\rm{x}}}}}^{(2^{\prime} )}\hat{P}]\) with a single Pauli operator acting on \(j^{\prime}\)-th qubit ancilla \({\hat{\sigma }}_{{{{\rm{x}}}}}^{(j^{\prime} )}\), approximated in the large-amplitude limit αr,i ≫ 2 as:

$$\begin{array}{l}{\hat{U}}_{{{{\rm{R}}}}}^{(2^{\prime} )}{\hat{U}}_{{{{\rm{R}}}}}^{(1^{\prime} )}{\left|g\right\rangle }_{1^{\prime} }{\left|g\right\rangle }_{2^{\prime} }\left|{\alpha }_{r}+{{{\rm{i}}}}{\alpha }_{{{{\rm{i}}}}}\right\rangle \approx \exp [{{{\rm{i}}}}{\epsilon }_{{{{\rm{i}}}}}{\hat{\sigma }}_{{{{\rm{x}}}}}^{(2^{\prime} )}\hat{P}]{\left|{{{\rm{sgn}}}}{[{\alpha }_{r}]}_{{{{\rm{i}}}}}\right\rangle }_{1^{\prime} }\\{\left|g\right\rangle }_{2^{\prime} }\left|{\alpha }_{r}+{{{\rm{i}}}}{\alpha }_{{{{\rm{i}}}}}\right\rangle \approx {\left|{{{\rm{sgn}}}}{[{\alpha }_{r}]}_{{{{\rm{i}}}}}\right\rangle }_{1^{\prime} }{\left|{{{\rm{sgn}}}}{[{\alpha }_{{{{\rm{i}}}}}]}_{{{{\rm{i}}}}}\right\rangle }_{2^{\prime} }\left|{\alpha }_{r}+{{{\rm{i}}}}{\alpha }_{{{{\rm{i}}}}}\right\rangle .\end{array}$$
(4)

Here, \({{{\rm{sgn}}}}[x]\) denotes the sign of the argument x. Coupling strengths are set respectively as \({\epsilon }_{r,i}={{{\rm{\pi }}}}/4\sqrt{2}{\alpha }_{r,i}\). The coherent peaks are then shifted toward the phase space origin by the controlled displacement \({\hat{U}}_{{{{\rm{D}}}}}^{(1)}=\exp [{{{\rm{i}}}}\sqrt{2}{\alpha }_{r}{\hat{\sigma }}_{{{{\rm{y}}}}}^{(1^{\prime} )}\hat{P}]\) and \({\hat{U}}_{{{{\rm{D}}}}}^{(2)}=\exp [-{{{\rm{i}}}}\sqrt{2}{\alpha }_{{{{\rm{i}}}}}{\hat{\sigma }}_{{{{\rm{y}}}}}^{(2^{\prime} )}\hat{X}]\) by the ancillary states before the erroneous channels as

$$\begin{array}{l}{\hat{U}}_{{{{\rm{D}}}}}^{(2)}{\hat{U}}_{{{{\rm{D}}}}}^{(1)}{\left|{{{\rm{sgn}}}}{[{\alpha }_{r}]}_{{{{\rm{i}}}}}\right\rangle }_{1^{\prime} }{\left|{{{\rm{sgn}}}}{[{\alpha }_{{{{\rm{i}}}}}]}_{{{{\rm{i}}}}}\right\rangle }_{2^{\prime} }\left|{\alpha }_{r}+{{{\rm{i}}}}{\alpha }_{{{{\rm{i}}}}}\right\rangle \approx {\hat{U}}_{{{{\rm{D}}}}}^{(2)}{\left|{{{\rm{sgn}}}}{[{\alpha }_{r}]}_{{{{\rm{i}}}}}\right\rangle }_{1^{\prime} }\\{\left|{{{\rm{sgn}}}}{[{\alpha }_{{{{\rm{i}}}}}]}_{{{{\rm{i}}}}}\right\rangle }_{2^{\prime} }\left|{{{\rm{i}}}}{\alpha }_{{{{\rm{i}}}}}\right\rangle \approx {\left|{{{\rm{sgn}}}}{[{\alpha }_{r}]}_{{{{\rm{i}}}}}\right\rangle }_{1^{\prime} }{\left|{{{\rm{sgn}}}}{[{\alpha }_{{{{\rm{i}}}}}]}_{{{{\rm{i}}}}}\right\rangle }_{2^{\prime} }\left|0\right\rangle .\end{array}$$
(5)

After the error channels, the original state can be substantially restored by the inverse operations \({\hat{U}}_{{T}_{X,P}}^{{\dagger} }\). This example demonstrates that complex n-SCSs can be protected by the qubit bypass in similar ways; for other examples see Supplementary Information VII.

Two-mode entangled coherent states

Our scheme can be extended to multi-mode ECSs in a straightforward way, for the simplest example to the two-mode state \(\left|{{{{\rm{ECS}}}}}^{\pm }\right\rangle ={N}_{\pm }({\left|\alpha \right\rangle }_{1}{\left|\alpha \right\rangle }_{2}\pm {\left|-\alpha \right\rangle }_{1}{\left|-\alpha \right\rangle }_{2})\) with oscillator indices J = 1, 2 with a normalization factor \({N}_{\pm }={(2\pm 2{e}^{-4{\alpha }^{2}})}^{-1/2}\). Without any protective scheme, the two-mode ECS will decohere at approximately double decay rate of single-mode superposition states as

$$\begin{array}{l}{{{\Gamma }}}_{\eta }^{(2)}[{{{\Gamma }}}_{\eta }^{(1)}[\left|{{{{\rm{ECS}}}}}^{\pm }\right\rangle \left\langle {{{{\rm{ECS}}}}}^{\pm }\right|]]={N}_{\pm }^{2}\left({\left|\alpha ^{\prime} \right\rangle }_{1}\left\langle \alpha ^{\prime} \right|\otimes {\left|\alpha ^{\prime} \right\rangle }_{2}\left\langle \alpha ^{\prime} \right|+{\left|-\alpha ^{\prime} \right\rangle }_{1}\right.\\ \left\langle -\alpha ^{\prime} \right|\otimes {\left|-\alpha ^{\prime} \right\rangle }_{2}\left\langle -\alpha ^{\prime} \right|\pm {{{{\rm{e}}}}}^{-4{\alpha }^{2}(1-\eta )}{\left|\alpha ^{\prime} \right\rangle }_{1}\left\langle -\alpha ^{\prime} \right|\otimes {\left|\alpha ^{\prime} \right\rangle }_{2}\\\left.\left\langle -\alpha ^{\prime} \right|\pm {{{{\rm{e}}}}}^{-4{\alpha }^{2}(1-\eta )}{\left|-\alpha ^{\prime} \right\rangle }_{1}\left\langle \alpha ^{\prime} \right|\otimes {\left|-\alpha ^{\prime} \right\rangle }_{2}\left\langle \alpha ^{\prime} \right|\right),\end{array}$$
(6)

where \(\alpha ^{\prime} =\sqrt{\eta }\alpha\). For this state, our scheme utilizes two local bypasses of ancillary modes \(1^{\prime} ,2^{\prime}\) acting on both CV modes. The state \(\left|{{{{\rm{ECS}}}}}^{\pm }\right\rangle\) then evolves by \({\hat{U}}_{{{{{\rm{T}}}}}_{1}}{\hat{U}}_{{{{{\rm{T}}}}}_{2}}\) to a loss-robust state

$${\hat{U}}_{{{{{\rm{T}}}}}_{1}}{\hat{U}}_{{{{{\rm{T}}}}}_{2}}\left|{{{{\rm{ECS}}}}}^{\pm }\right\rangle ={{{\rm{i}}}}{\left|{\phi }_{+}\right\rangle }_{1,1^{\prime} }{\left|{\phi }_{+}\right\rangle }_{2,2^{\prime} }\mp {{{\rm{i}}}}{\left|{\phi }_{-}\right\rangle }_{1,1^{\prime} }{\left|{\phi }_{-}\right\rangle }_{2,2^{\prime} }$$
(7)

where \(\left|{\phi }_{+}\right\rangle =\left|{-}_{{{{\rm{i}}}}}\right\rangle \frac{\left|{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle +\left|-{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle }{2}+\left|{+}_{{{{\rm{i}}}}}\right\rangle \frac{{e}^{-{{{\rm{i}}}}{{{\rm{\pi }}}}/4}\left|2\alpha +{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle -{e}^{{{{\rm{i}}}}{{{\rm{\pi }}}}/4}\left|2\alpha -{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle }{2{{{\rm{i}}}}}\) and \(\left|{\phi }_{-}\right\rangle =\left|{+}_{{{{\rm{i}}}}}\right\rangle \frac{\left|{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle +\left|-{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle }{2}-\left|{-}_{{{{\rm{i}}}}}\right\rangle \frac{{e}^{{{{\rm{i}}}}{{{\rm{\pi }}}}/4}\left|-2\alpha +{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle -{{{{\rm{e}}}}}^{-{{{\rm{i}}}}{{{\rm{\pi }}}}/4}\left|-2\alpha -{{{\rm{i}}}}\epsilon /\sqrt{2}\right\rangle }{2{{{\rm{i}}}}}\). For an n-mode ECSs, we can similarly apply local schemes to all n modes to transform into more loss-robust states. These examples explain well the logical steps to be applied to any specific superposition of finite number of coherent states in different modes. Again, the effect of qubit loss in the protection of these states was analyzed in Supplementary Sec. VIII.

Single-mode superposition states

As a measure of performance of the protocol, we can first look at fidelity101,102. Fidelity is defined as \(F({\rho }_{{{{\rm{in}}}}},{\rho }_{{{{\rm{out}}}}})={{{\rm{tr}}}}{(\sqrt{\sqrt{{\rho }_{{{{\rm{in}}}}}}{\rho }_{{{{\rm{out}}}}}\sqrt{{\rho }_{{{{\rm{in}}}}}}})}^{2}\) between input ρin and output ρout. For large α ≫ 2, the superpositions of coherent states represent a qubit space that is well characterized by fidelity. The average performance of the schemes on 2-SCSs \(\mu \left|\alpha \right\rangle +\nu \left|-\alpha \right\rangle\) with a fixed α but arbitrary μ and ν over the “Bloch sphere" of coherent states can be measured by the channel fidelity94. It is defined as the fidelity between an input virtual entangled state \({2}^{-1/2}(\left|{{{\bf{0}}}}\right\rangle \left|\alpha \right\rangle +\left|{{{\bf{1}}}}\right\rangle \left|-\alpha \right\rangle )\) and the output state after the noise channels, where \(\{\left|{{{\bf{0}}}}\right\rangle ,\left|{{{\bf{1}}}}\right\rangle \}\) are fictitious qubit basis. We note that in contrast to a conventional qubit, the statistical weight of states represented in the channel fidelity is not homogeneous over all coefficients μ, ν. For example, the weight of balanced superposition states \(\left|\alpha \right\rangle \pm \left|-\alpha \right\rangle\) has the extrema values, but this inhomogeneity is negligible for α ≳ 2. Compared to the original definition of channel fidelity which calculates from a state \({2}^{-1/2}(\left|{{{\bf{0}}}}\right\rangle \left|+\right\rangle +\left|{{{\bf{1}}}}\right\rangle \left|-\right\rangle )\) where \(\left|\pm \right\rangle ={N}_{\pm }(\left|\alpha \right\rangle \pm \left|-\alpha \right\rangle )\), the difference between the two methods is very small, less than 10−9 in this regime.

We compared the strategy of Gaussian squeezing strategy prior to transmission through the lossy channel64,67 as a benchmark. The optimization of the Gaussian strategy was with respect to the average photon number in the CV modes at each α. The optimal squeezing parameter ropt for the initial state \(\mu \left|\alpha \right\rangle +\nu \left|-\alpha \right\rangle\) is given as

$$\begin{array}{l}{r}_{{{{\rm{opt}}}}}=\frac{1}{4}\left(\log \left[\frac{4{{{{\rm{e}}}}}^{2{\alpha }^{2}}{\alpha }^{2}{\mu }^{* }}{{{{{\rm{e}}}}}^{2{\alpha }^{2}}{\mu }^{* }+\nu {\left({\mu }^{* }\right)}^{2}+{\mu }^{2}\nu }+1\right]\right.\\\qquad\;\;\left.-\,\log \left[1-\frac{4{\alpha }^{2}\nu \left({\left({\mu }^{* }\right)}^{2}+{\mu }^{2}\right)}{{{{{\rm{e}}}}}^{2{\alpha }^{2}}{\mu }^{* }+\nu {\left({\mu }^{* }\right)}^{2}+{\mu }^{2}\nu }\right]\right).\end{array}$$
(8)

In Fig. 2, we show the effectiveness of our strategy quantified by the channel fidelity for general 2-SCSs of various amplitudes against bosonic loss (fidelity for individual states are calculated in Supplementary Sec. I. This is well evidenced by the decay rate γ of the fidelity model Fc(η) = Fc(1)e−γ(1−η), where a larger γ represents a faster decay. Fig. 2a clearly shows the qualitative difference of our qubit bypass strategy showing decreased γ approximately described as 0.65 − 0.025α1.2. In contrast, the γs for no protection and Gaussian squeezing protection are described by increasing trends respectively as 0.17 + α1.92 and 0.29 + 0.96α. In Fig. 2b, we can see that the channel fidelity of the bypass scheme significantly surpasses the Gaussian strategy for a mild level of dephasing for a large amplitude α ≫ 2, and loss is not critically detrimental to our scheme. At complete lossy case η = 0 for p = 0 corresponding to the complete blockage of the oscillator, the channel fidelity of our scheme can be approximately given in the large α limit as

$${F}_{{{{\rm{c}}}}}\approx \frac{{{{{\rm{e}}}}}^{-\frac{3{{{{\rm{\pi }}}}}^{2}}{64{\alpha }^{2}}}+{{{{\rm{e}}}}}^{-\frac{{{{{\rm{\pi }}}}}^{2}}{64{\alpha }^{2}}}}{2}.$$
(9)

We can see in Supplementary Fig. 1a, b that keeping the oscillator is still beneficial even though it carries little information.

Fig. 2: Performance of bypass protection protocol in Fig. 1a for a superposition of two coherent states in a bosonic mode compared to the Gaussian strategy under various dephasings.
figure 2

a The logarithmic decay rate \(\log \gamma\) of channel fidelity is modeled as Fc(η) = Fc(1)e−γ(1−η) for various cases. The curves for different p's are overlapped. b Channel fidelity vs. loss parameter for α = 6. This result shows the qualitative difference between bypass and Gaussian strategies.

Full size image

The negative part of the Wigner functions can serve as a quantitative measure of the non-classical features, highly sensitive to both losses and noises103,104. The equal-weight 2-SCSs \(\left|\alpha \right\rangle +{{{{\rm{e}}}}}^{{{{\rm{i}}}}\phi }\left|-\alpha \right\rangle\) have interference fringes around the origin of the phase space. In Fig. 3a, these interference fringes along P-axis in phase space are shown for various ϕ under various levels of loss and dephasing. We note that the negativity of all interference fringes are preserved, not only in the largest one. The bypass scheme protects the interference fringes even under a large dephasing, especially for a large α ≫ 2. Although the input state \(\left|\alpha \right\rangle +{{{\rm{i}}}}\left|-\alpha \right\rangle\) is not fully protected in terms of fidelity under dephasing, the interference fringes are not critically destroyed, although not immune. Mathematically, the value of the Wigner function at the phase space origin is proportional to the average value of the parity operator as \(W(0,0)=\frac{2}{{{{\rm{\pi }}}}}\langle \rho {(-1)}^{\hat{n}}\rangle\). The bypass scheme protects the interference fringes even under a large dephasing, especially for a large α ≫ 2. The deepest negative peak of the initial state \(\left|\alpha \right\rangle -\left|-\alpha \right\rangle\) is located at the phase space origin, and its first-order approximation for our protocol vs. the loss parameter 1 − η and the dephasing parameter p scales approximately in the large α limit as

$$W(0,0)\approx -\frac{2-4{{{{\rm{e}}}}}^{-2{\alpha }^{2}}}{{{{\rm{\pi }}}}}+(1-\eta )\frac{2{{{{\rm{e}}}}}^{-2{\alpha }^{2}}{\alpha }^{2}}{{{{\rm{\pi }}}}}+p\frac{1-{{{{\rm{e}}}}}^{-\frac{{{{{\rm{\pi }}}}}^{2}}{8{\alpha }^{2}}}}{2{{{\rm{\pi }}}}}.$$
(10)

Here the effect of loss and dephasing evidenced in the second and third terms is weakening for a large α, therefore remaining nearly constant for all α, η and p. This is because the state \(\left|\alpha \right\rangle -\left|-\alpha \right\rangle\) is mapped onto the oscillator ground state (Eq. (3)), which is unaffected by both boson loss and dephasing. Fig. 3b shows that our scheme protects this negative peak better than the Gaussian squeezing protection, especially at large α, whose negative peak at the origin is described approximately by \(-\frac{2}{{{{\rm{\pi }}}}}+0.61(1-\eta ){\alpha }^{1.60}\). In comparison, without any protection, the negative peak at the origin scales as \(\frac{2{{{{\rm{e}}}}}^{2{\alpha }^{2}(1-\eta )}-2{{{{\rm{e}}}}}^{2{\alpha }^{2}\eta }}{{{{\rm{\pi }}}}\left({{{{\rm{e}}}}}^{2{\alpha }^{2}}-1\right)}\), which is influenced more harshly than the others.

Fig. 3: Protection of negative peaks of Wigner functions of superposition of two coherent states as in Fig. 1b.
figure 3

a, b Interference fringes in cross-section of the Wigner function for \(\left|\alpha \right\rangle +{{{{\rm{e}}}}}^{{{{\rm{i}}}}\phi }\left|-\alpha \right\rangle\) at α = 6 with ϕ = π/2, π under 1 − η = 0.01 of loss and p = 0, 0.05, 0.1 of dephasing. The interference fringes for complete lossy channel η = 0 and under various p's are overlapped largely with the initial curve. c The depths of the negative peak located at phase space origin vs. loss parameter 1 − η at α = 6 for the initial state \(\left|\alpha \right\rangle -\left|-\alpha \right\rangle\) (curves with p > 0 are overlapped), d and the logarithm of slopes of the curves in c vs. α.

Full size image

In Supplementary Sec. II, we calculated the Wigner functions and channel fidelity of the 4 SCSs for a special encoding as in22,42 under various levels of loss and dephasing. Similarly, as for 2-SCSs, we can also protect the negative peaks of 4 SCSs with an increased fidelity in large α limit against loss under a modest level of dephasing on the ancilla.

Two-mode entangled states

Entangled coherent states12,105 were engineered experimentally from trapped ions106,107 and superconducting circuits35,108. We briefly note that in terms of fidelity, similar tendencies, e.g., enhancement at large α beyond Gaussian strategies, can be obtained as single-mode states. An important question is whether a non-local property such as entanglement of these states can also be protected by the local bypass schemes as in Fig. 1c, which cannot be simply predicted by the fidelity. For our protocol, intuitively we expect this to be the case, as we transfer the entanglement from the bosonic modes to the ancillas, thus bypassing losses. As a measure of entanglement which can characterize the bipartite states ρ, we choose logarithmic negativity \({N}_{{{{\rm{L}}}}}[\rho ]=\log | | {\rho }^{{{{\rm{PT}}}}}| |\) with partial transposition PT and the trace norm ∣∣ ⋅ ∣∣, which operationally is connected to the upper bound on the distillable entanglement109. The even superposition state \(\left|{{{{\rm{ECS}}}}}^{+}\right\rangle\) has 0 logarithmic negativity at small α as it is close to the vacuum and thus has no entanglement. On the other hand, the odd superposition state \(\left|{{{{\rm{ECS}}}}}^{-}\right\rangle\) possesses a value \(\ln 2\) at all α.

At each α, the squeezing parameters for Gaussian strategies were optimized to minimize the average photon number before the lossy channel. The Gaussian squeezing protection can be applied on both modes, with the optimal squeezing parameter with respect to the average photon number is given as

$$\begin{array}{l}{r}_{{{{\rm{opt}}}}}=\frac{1}{4}\left(\log \left[2{\alpha }^{2}+2{\alpha }^{2}\coth \left(2{\alpha }^{2}\right)+1\right]\right.\\\qquad\;\;\;\left.-\,\log \left[-2{\alpha }^{2}+2{\alpha }^{2}\coth \left(2{\alpha }^{2}\right)+1\right]\right).\end{array}$$
(11)

In addition, we optimized the Gaussian protection numerically at each α as well.

The scaling of the logarithmic negativity vs. α and η can be described by a fitted function \(\log 2-(1-\eta )f[\alpha ]\) when the dephasing is absent. The loss effect functions are approximately given as f[α] = 1.59α2 + 0.12α + 0.59 for no protection, \(f[\alpha ]=-0.26+1.34\alpha -0.70\log \alpha\) for Gaussian squeezing protection, and \(f[\alpha ]=0.44-0.22\log \alpha\) for bypass protocol. In Fig. 4, the curves for the logarithmic negativities of \(\left|{{{{\rm{ECS}}}}}^{-}\right\rangle\) after various noise channels were drawn numerically. We notice again that the entanglement of the bipartite states suffers a weaker effect by qubit bypass protocol than the Gaussian strategies, with enhanced performance in large α limit under a moderate qubit dephasing.

Fig. 4: Protection of entangled coherent states \(\left|{{{{\rm{ECS}}}}}_{-}\right\rangle\) in Fig. 1c quantified by numerically calculated logarithmic negativities.
figure 4

a vs. α for 1 − η = 0.01 and b vs. 1 − η for α = 3.

Full size image

Additionally, the negative Wigner function of the projected state by a local detection shows a sensitive witness of the entanglement. If the bipartite state becomes factorizable in coherent basis due to decoherence as \({\left|\alpha \right\rangle }_{1}\left\langle \alpha \right|\otimes {\left|\alpha \right\rangle }_{2}\left\langle \alpha \right|+{\left|-\alpha \right\rangle }_{1}\left\langle -\alpha \right|\otimes {\left|-\alpha \right\rangle }_{2}\left\langle -\alpha \right|\), no measurement in mode 1 can create a negative peak in the phase space of mode 2. In contrast, ECSs allow measurement-induced preparation of coherent superposition states which possess negative Wigner function. As the simplest examples, we can consider homodyne measurements \({\left|P\right\rangle }_{1}\left\langle P\right|\) or \({\left|X\right\rangle }_{1}\left\langle X\right|\) with X = 0 or P = 0, or a projection on vacuum state \({\left|0\right\rangle }_{1}\left\langle 0\right|\). For an ideal entangled state \(\left|{{{{\rm{ECS}}}}}^{\pm }\right\rangle\), all projections will prepare superposition states \({\left|\alpha \right\rangle }_{2}\pm {\left|-\alpha \right\rangle }_{2}\).

In Fig. 5, we compared how the deepest negative peak of the Wigner function behaves for different α and η. Without protection, the formula for the largest negative peak depth is given as \({w}_{0}=\frac{2\left({{{{\rm{e}}}}}^{-4{\alpha }^{2}(\eta -1)}-{{{{\rm{e}}}}}^{2{\alpha }^{2}\eta }\right)}{{{{\rm{\pi }}}}\left({{{{\rm{e}}}}}^{-2{\alpha }^{2}(\eta -2)}-1\right)}\), and by squeezing protection approximately as \({({w}_{0})}^{{{{{\rm{e}}}}}^{-0.18}}\). The approximate formula for the qubit bypass scheme is given as \(-\frac{2\exp [-\left(1.46{\alpha }^{2}-7.14\alpha +11.0\right)(1-\eta )]}{{{{\rm{\pi }}}}}\). We can see that our protocol is clearly superior to the Gaussian squeezing strategies in protecting the locally induced negativity of of Wigner functions in all parameter regions of αs and ηs. Interestingly, the squeezing is not highly effective in protecting the negative interference fringes here.

Fig. 5: Protection in Fig. 1c of the Wigner function negative peak depths at the phase space origin of \(\left|{{{{\rm{ECS}}}}}^{-}\right\rangle\) after a projective vacuum measurement on one mode.
figure 5

a vs. loss parameter 1 − η at α = 6 (curves for p > 0 are overlapped), b the logarithm of the slope of the curves in a. The curves for the protection by squeezing were calculated numerically. The dephasing noise does not affect the depth of the negative peaks, as is evidenced by the overlap of the curves.

Full size image

Notably, for a large α, this Wigner function negative peak of the local projected state is impacted by loss even though the entanglement itself is preserved by our protection. This discrepancy is caused by the effect of loss on local projection in the control mode. It might limit some applicability of the protected states to non-local tasks in multi-modes, and further evaluation of the loss tolerance of conditional states may be needed. We speculate that certain non-local protocols may enhance the protection of non-local aspects.

Discussion

In this work, we proposed a deterministic bypass protocol utilizing Rabi couplings to lossless qubit ancillas under a low level of dephasing, to mitigate decoherence by stable loss on the unknown single-mode and two-mode superposition of coherent states with a various number of components. Our method depends on the experimental realization of the Rabi couplings: high strengths of the coupling, and the existence of counter-rotating terms in the Hamiltonians. The generation of high strength gate can be in principle assisted by inline squeezings (see Supplementary Sec. V). This protocol can be implemented in various cavity QED systems which support the precise control of Rabi couplings77,78,79,80,81,82,99,110. The adjustment of the proposal to moving platforms is still possible. Optical experiments to achieve Rabi interactions by using stationary atoms coupled dispersively to a cavity have been already proposed99 and the first experimental tests towards this future are recently presented28. Still, the high spontaneous decay rate needs to be improved by a better qubit for applications in the future. In such setups, light can be potentially transmitted directly through a lossy channel, while states of stationary qubit systems, instead of directly traveling with the oscillator, can be teleported using the DV type of the teleportation scheme111. We analyzed the performance by various measures in comparison to optimal Gaussian strategies and confirmed the superiority of our protocol.

Our protocol possesses the following characteristics: (i) it utilizes a minimal number of resources in contrast to ultimate but challenging quantum error correction schemes, (ii) the performance improves for larger α in contrast to existing protocols optimal in the opposite regime, and (iii) CV channel plays non-negligible role except for a very large α ≳ 10, and (iv) it can be combined with conventional error correction schemes on qubits41,42,47,48,49,50,51,52,53,54,55,56,58,59 or a Gaussian protection scheme on CV states64,65,66,67. Our work implies that robust qubit channels can be exploited for future extension of the method to various classes of CV quantum non-Gaussian or non-local resources.