Environment-assisted bosonic quantum communications

Abstract

We consider a quantum relay that is used by two parties to perform several continuous-variable protocols of quantum communication, from entanglement distribution (swapping and distillation) to quantum teleportation, and quantum key distribution. The theory of these protocols is suitably extended to a non-Markovian model of decoherence characterized by correlated Gaussian noise in the bosonic environment. In the worst-case scenario where bipartite entanglement is completely lost at the relay, we show that the various protocols can be reactivated by the assistance of classical (separable) correlations in the environment. In fact, above a critical amount, these correlations are able to guarantee the distribution of a weaker form of entanglement (quadripartite), which can be localized by the relay into a stronger form (bipartite) that is exploitable by the parties. Our findings are confirmed by a proof-of-principle experiment where we show, for the first time, that memory effects in the environment can drastically enhance the performance of a quantum relay, well beyond the single-repeater bound for quantum and private communications.

Introduction

The concept of a relay is at the basis of network information theory¹. Indeed the simplest network topology is composed by three nodes: two end-users, Alice and Bob, plus a third party, the relay, which assists their communication. This scenario is inherited by quantum information theory^{2,3,4,5,6,7,8,9,10,11,12,13}, where the mediation of a quantum relay can be found in a series of fundamental protocols. By sending quantum systems to a middle relay, Alice and Bob may perform entanglement swapping^14,15,16,17, entanglement distillation¹⁸, quantum teleportation^19,20,21 and quantum key distribution (QKD)^{22,23,24,25,26,27}.

Quantum relays are crucial elements for quantum network architectures at any scale, from short-range implementations on quantum chips to long-distance quantum communication. In all cases, their working mechanism has been studied assuming Markovian decoherence models, where the errors are independent and identically distributed (iid). Removing this iid approximation is one of the goals of modern quantum information theory.

In a quantum chip (e.g., photonic^28,29 or superconducting³⁰), quantum relays can distribute entanglement among registers and teleport quantum gates. Miniaturizing this architecture, correlated errors may come from unwanted interactions between quantum systems. A common bath may be introduced by a variety of imperfections, e.g., due to diffraction or slow electronics. It is important to realize that non-Markovian dynamics³¹ will become increasingly important as the size of quantum chips further shrinks.

At long distances (in free-space or fibre), quantum relays intervene to assist quantum communication, entanglement and key distribution. Here, noise correlations and memory effects may naturally arise when optical modes are employed in high-speed communications³², or propagate through atmospheric turbulence^33,34,35 and diffraction-limited linear systems. Most importantly, correlated errors must be considered in relay-based QKD, where an eavesdropper (Eve) may jointly attack the two links with the relay (random permutations and de Finetti arguments^36,37 cannot remove these residual correlations). Eve can manipulate the relay itself as assumed in measurement-device independent QKD^22,23,24. Furthermore, Alice’s and Bob’s setups may also be subject to correlated side-channel attacks.

For all these reasons, we generalize the study of quantum relays to non-Markovian conditions, developing the theory for continuous-variable (CV) systems¹⁰ (qubits are discussed in the Supplementary Material). We consider an environment whose Gaussian noise may be correlated between the two links. Our model is formulated as a spatial non-Markovian model, where spatially separated bosonic modes are subject to correlated errors, but could also be connected to a time-like model where the parties use the same channel at different times. In this scenario, while the relay always performs the same measurement, the parties may implement different protocols (swapping, distillation, teleportation, or QKD) all based, directly or indirectly, on the exploitation of bipartite entanglement.

We find a surprising behaviour in conditions of extreme decoherence. We consider entanglement-breaking links^38,39, so that no protocol can work under Markovian conditions. We then induce non-Markovian effects by progressively increasing the noise correlations in the environment while keeping their nature separable (so that there is no external reservoir of entanglement). While these correlations are not able to re-establish bipartite entanglement (or tripartite entanglement) we find that a critical amount reactivates quadripartite entanglement, between the setups and the modes transmitted. In other words, by increasing the separable correlations above a ‘reactivation threshold’ we can retrieve the otherwise lost quadripartite entanglement (it is in this sense that we talk of ‘reactivated’ entanglement below). The measurement of the relay can then localize this multipartite entanglement into a bipartite form, shared by the two remote parties and exploitable for the various protocols.

As a matter of fact, we find that all the quantum protocols can be reactivated. In particular, their reactivation occurs in a progressive fashion, so that increasing the environmental correlations first reactivates entanglement swapping and teleportation, then entanglement distillation and finally QKD. Our theory is confirmed by a proof-of-principle experiment which shows the reactivation of the most nested protocol, i.e., the QKD protocol. In particular, we show that the key rate of this environmental-assisted protocol outperforms the single-repeater upper-bound for private communication⁴⁰, i.e., the maximum secret-key rate that is achievable in the presence of memoryless links.

Results

General scenario

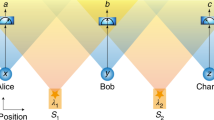
As depicted in Fig. 1, we consider two parties, Alice and Bob, whose devices are connected to a quantum relay, Charlie, with the aim of implementing a CV protocol (swapping, distillation, teleportation or QKD). The connection is established by sending two modes, A and B, through a joint quantum channel ${{\mathcal{E}}}_{AB}$, whose outputs ${A}^{\prime}$ and ${B}^{\prime}$ are subject to a CV Bell detection⁴¹. This means that modes ${A}^{\prime}$ and ${B}^{\prime}$ are mixed at a balanced beam splitter and then homodyned, one in the position quadrature ${\hat{q}}_{-}=({\hat{q}}_{{A}^{\prime}}-{\hat{q}}_{{B}^{\prime}})/\sqrt{2}$ and the other in the momentum quadrature ${\hat{p}}_{+}=({\hat{p}}_{{A}^{\prime}}+{\hat{p}}_{{B}^{\prime}})/\sqrt{2}$. The classical outcomes q₋ and p₊ can be combined into a complex variable γ: = q₋ + ip₊, which is broadcast to Alice and Bob through a classical public channel.

Fig. 1: Quantum relay.

Alice and Bob connect their devices (red boxes) to a quantum relay, Charlie, for implementing a CV protocol. On the received modes, Charlie always performs a CV Bell detection whose outcome γ is broadcast. Separable Gaussian environment. The travelling modes are subject to a joint Gaussian channel ${{\mathcal{E}}}_{AB}$. This is realized by two beam splitters with tranmissivity τ which mix A and B with two ancillary modes, E₁ and E₂, respectively. These ancillas inject thermal noise with variance ω and belong to a correlated (but separable) Gaussian state ${\rho }_{{E}_{1}{E}_{2}}$. Entanglement breaking. For ω > ω_EB(τ), bipartite (and tripartite) entanglement cannot survive at the relay. In particular, ${A}^{\prime}$ is disentangled from Alice’s device, and ${B}^{\prime}$ is disentangled from Bob’s, no matter if the environment is correlated or not. Non-Markovian reactivation. Above a critical amount of separable correlations, quadripartite entanglement is reactivated between Alice’s and Bob’s devices and the transmitted modes, ${A}^{\prime}$ and ${B}^{\prime}$. Bell detection can localize this multipartite resource into a bipartite form and reactivate all the protocols.

The joint quantum channel ${{\mathcal{E}}}_{AB}$ corresponds to an environment with correlated Gaussian noise. This is modelled by two beam splitters (with transmissivity 0 < τ < 1) mixing modes A and B with two ancillary modes, E₁ and E₂, respectively (see Fig. 1). These ancillas are taken in a zero-mean Gaussian state¹⁰${\rho }_{{E}_{1}{E}_{2}}$ with covariance matrix (CM) in the symmetric normal form

$${{\bf{V}}}_{{E}_{1}{E}_{2}}(\omega ,g,{g}^{\prime})=\left(\begin{array}{ll}\omega {\bf{I}}&{\bf{G}}\\ {\bf{G}}&\omega {\bf{I}}\end{array}\right),\,\begin{array}{l}{\bf{I}}:={\rm{diag}}(1,1),\\ {\bf{G}}:={\rm{diag}}(g,{g}^{\prime}).\end{array}$$

Here ω ≥ 1 is the variance of local thermal noise, while the block G accounts for noise correlations.

For G = 0 we retrieve the standard Markovian case, based on two independent lossy channels^15,16,17. For G ≠ 0, the lossy channels become correlated and the local dynamics cannot reproduce the global non-Markovian evolution of the system. Such a separation becomes more evident by increasing the correlation parameters, g and ${g}^{\prime}$, whose values are bounded by the bona fide conditions ∣g∣ < ω, $| {g}^{\prime}| \,<\,\omega$, and $\omega \left|g+{g}^{\prime}\right|\le {\omega }^{2}+g{g}^{\prime}-1$ (refs. ^42,43). In particular, we consider the realistic case of separable environments (${\rho }_{{E}_{1}{E}_{2}}$ separable), identified by the additional constraint $\omega \left|g-{g}^{\prime}\right|\le {\omega }^{2}-g{g}^{\prime}-1$ (ref. ⁴³). The amount of separable correlations can be quantified by the quantum mutual information $I(g,{g}^{\prime})$.

To analyse entanglement breaking, assume the asymptotic infinite-energy scenario where Alice’s (Bob’s) device has a remote mode a (b) which is maximally entangled with A (B). We then study the separability properties of the global system composed by a, b, ${A}^{\prime}$ and ${B}^{\prime}$. In the Markovian case (G = 0), all forms of entanglement (bipartite, tripartite⁴⁴, and quadripartite⁴⁵) are absent for ω > ω_EB(τ): = (1 + τ)/(1 − τ), so that no protocol can work. In the non-Markovian case (G ≠ 0) the presence of separable correlations does not restore bipartite or tripartite entanglement when ω > ω_EB(τ). However, a sufficient amount of these correlations is able to reactivate 1 × 3 quadripartite entanglement⁴⁵, in particular, between mode a and the set of modes $b{A}^{\prime}{B}^{\prime}$. See Fig. 2.

Fig. 2: Non-Markovian reactivation of 1 × 3 quadripartite entanglement.

Assuming maximally entangled states for the parties and entanglement-breaking conditions (here τ = 0.9 and ω = 1.02 × ω_EB = 19.38), we show how quadripartite entanglement is reactivated by increasing the separable correlations of the environment (bits of quantum mutual information, which are constant over the concentric contour lines). Inside the grey region there is no quadripartite entanglement with respect to any 1 × 3 grouping of the four modes $ab{A}^{\prime}{B}^{\prime}$. Outside the grey region all the possible 1 × 3 groupings are entangled. The external black region is excluded, as it corresponds to entangled or unphysical environments.

Once quadripartite entanglement is available, the Bell detection on modes ${A}^{\prime}$ and ${B}^{\prime}$ can localize it into a bipartite form for modes a and b. For this reason, entanglement swapping and the other protocols can be reactivated by sufficiently-strong separable correlations. In the following, we discuss these results in detail for each specific protocol, starting from the basic scheme of entanglement swapping. For each protocol, we first generalize the theory to non-Markovian decoherence, showing how the various performances are connected. Then, we analyse the protocols under entanglement-breaking conditions.

Entanglement swapping

The standard source of Gaussian entanglement is the two-mode squeezed vacuum (TMSV) state, which is a realistic finite-energy version of the ideal EPR state¹⁰. More precisely, this is a two-mode Gaussian state with zero mean value and CM

$${\bf{V}}(\mu )=\left(\begin{array}{ll}\mu {\bf{I}}&\sqrt{{\mu }^{2}-1}{\bf{Z}}\\ \sqrt{{\mu }^{2}-1}{\bf{Z}}&\mu {\bf{I}}\end{array}\right),\,{\bf{Z}}:={\rm{diag}}(1,-1),$$

where the variance μ ≥ 1 quantifies its entanglement. Indeed the log-negativity^46,47,48 is strictly increasing in μ: It is zero for μ = 1 and tends to infinity for large μ.

Suppose that Alice and Bob have two identical TMSV states, ρ_aA(μ) describing Alice’s modes a and A, and ρ_bB(μ) describing Bob’s modes b and B, as in Fig. 3(i). They keep a and b, while sending A and B to Charlie through the joint channel ${{\mathcal{E}}}_{AB}$ of the Gaussian environment. After the broadcast of the outcome γ, the remote modes a and b are projected into a conditional Gaussian state ρ_ab∣γ, with mean value x = x(γ) and conditional CM V_ab∣γ. In the Supplementary Material, we compute

$${{\bf{V}}}_{ab| \gamma }=\left(\begin{array}{ll}{\bf{A}}&{\bf{C}}\\ {{\bf{C}}}^{\mathrm T}&{\bf{B}}\end{array}\right),$$

(1)

where the 2 × 2 blocks are given by

$${\bf{A}}={\bf{B}}={\rm{diag}}\left[\mu -\frac{{\mu }^{2}-1}{2(\mu +\kappa )},\mu -\frac{{\mu }^{2}-1}{2(\mu +{\kappa }^{\prime})}\right],$$

(2)

$${\bf{C}}={\rm{diag}}\left[\frac{{\mu }^{2}-1}{2(\mu +\kappa )},-\frac{{\mu }^{2}-1}{2(\mu +{\kappa }^{\prime})}\right],$$

(3)

and the κ’s contain all the environmental parameters

$$\kappa :=({\tau }^{-1}-1)(\omega -g),\,{\kappa }^{\prime}:=({\tau }^{-1}-1)(\omega +{g}^{\prime}).$$

(4)

Fig. 3: Relay-based quantum protocols in a correlated Gaussian environment.

i Entanglement swapping. Alice and Bob possess two TMSV states with variance μ. Modes A and B are sent through the joint channel ${{\mathcal{E}}}_{AB}$ and received by Charlie. After the outcome γ is broadcast, the remote modes, a and b, are projected into a conditional state ρ_ab∣γ. ii Quantum teleportation. Alice’s coherent state $\left|\nu \right\rangle$ is teleported into Bob’s state ρ_out(ν), after the communication of γ and the action of a conditional quantum operation ${{\mathcal{Q}}}_{\gamma }$. iii Entanglement/key distillation. In the limit of many uses of the relay, Alice performs a quantum instrument on her modes a, communicating a classical variable k to Bob, who performs a conditional quantum operation on his modes b. This is a non-Gaussian quantum repeater where entanglement swapping is followed by optimal one-way distillation. iv Practical QKD. Alice and Bob prepare Gaussian-modulated coherent states to be sent to Charlie. The communication of the outcome γ creates remote classical correlations which are used to extract a secret key. Here the role of Charlie could be played by Eve, so that the relay becomes an MDI-QKD node.

From V_ab∣γ we compute the log-negativity ${\mathcal{N}}=\max \{0,-{\log}_{2}\varepsilon \}$ of the swapped state, in terms of the smallest partially transposed symplectic eigenvalue ε¹⁰. In the Supplementary Material, we derive

$$\varepsilon ={\left[\frac{(1+\mu \kappa )(1+\mu {\kappa }^{\prime})}{(\mu +\kappa )(\mu +{\kappa }^{\prime})}\right]}^{1/2}.$$

(5)

For any input entanglement (μ > 1), swapping is successful (ε < 1) whenever the environment has enough correlations to satisfy the condition $\kappa {\kappa }^{\prime}\,<\,1$. The actual amount of swapped entanglement ${\mathcal{N}}$ increases in μ, reaching its asymptotic optimum for large μ, where

$$\varepsilon \simeq {\varepsilon }_{\text{opt}}:=\sqrt{\kappa {\kappa }^{\prime}}.$$

Quantum teleportation

As depicted in Fig. 3(ii), we consider Charlie acting as a teleporter of a coherent state $\left|\nu \right\rangle$ from Alice to Bob. Alice’s state and part of Bob’s TMSV state are transmitted to Charlie through the joint channel ${{\mathcal{E}}}_{AB}$. After detection, the outcome γ is communicated to Bob, who performs a conditional quantum operation² ${{\mathcal{Q}}}_{\gamma }$ on mode b to retrieve the teleported state ${\rho }_{\text{out}}(\nu )\simeq \left|\nu \right\rangle \left\langle \nu \right|$. In the Supplementary Material, we find a formula for the teleportation fidelity $F=F(\mu ,\kappa ,{\kappa }^{\prime})$, which becomes asymptotically optimal for large μ, where

$$F\simeq {F}_{\text{opt}}:={\left[(1+\kappa )(1+{\kappa }^{\prime})\right]}^{-1/2}\le {(1+{\varepsilon }_{\text{opt}})}^{-1}.$$

(6)

Thus, there is a direct connection between the asymptotic protocols of teleportation and swapping: If swapping fails (ε_opt ≥ 1), teleportation is classical (F_opt ≤ 1/2 (ref. ¹⁰)). We retrieve the relation ${F}_{\text{opt}}={(1+{\varepsilon }_{\text{opt}})}^{-1}$ in environments with antisymmetric correlations $g+{g}^{\prime}=0$.

Entanglement distillation

Entanglement distillation can be operated on top of entanglement swapping as depicted in Fig. 3(iii). After the parties have run the swapping protocol many times and stored their remote modes in quantum memories, they can perform a one-way entanglement distillation protocol on the whole set of swapped states ρ_ab∣γ. This consists of Alice locally applying an optimal quantum instrument⁴⁹${\mathcal{A}}$ on her modes a, whose quantum outcome α is a distilled system while the classical outcome k is communicated. Upon receipt of k, Bob performs a conditional quantum operation ${{\mathcal{B}}}_{k}$ transforming his modes b into a distilled system $\mathbf{\beta}$.

The process can be designed in such a way that the distilled systems are collapsed into entanglement bits (ebits), i.e., Bell state pairs². The optimal distillation rate (ebits per relay use) is lower-bounded⁴⁹ by the coherent information ${I}_{{\mathcal{C}}}$^50,51 computed on the single copy state ρ_ab∣γ. In the Supplementary Material, we find a closed expression ${I}_{{\mathcal{C}}}={I}_{{\mathcal{C}}}(\mu ,\kappa ,{\kappa }^{\prime})$ which is maximized for large μ, where ${I}_{{\mathcal{C}}}\simeq -{\log}_{2}(e{\varepsilon }_{\text{opt}})$. Asymptotically, entanglement can be distilled for ε_opt < e⁻¹ ≃ 0.367.

Secret-key distillation

The scheme of Fig. 3(iii) can be modified into a key distillation protocol, where Charlie (or Eve²²) distributes secret correlations to Alice and Bob, while the environment is the effect of a Gaussian attack. Alice’s quantum instrument is here a measurement with classical outputs α (the secret key) and k (data for Bob). Bob’s operation is a measurement conditioned on k, which provides the classical output β (key estimate). This is an ideal key-distribution protocol⁵² whose rate is lower-bounded by the coherent information, i.e., K ≥ $I_{\mathcal{C}}$ (see Supplementary Material).

Practical QKD

The previous key-distribution protocol can be simplified by removing quantum memories and using single-mode measurements, in particular, heterodyne detections. This is equivalent to a run-by-run preparation of coherent states, $\left|\alpha \right\rangle$ on Alice’s mode A, and $\left|\beta \right\rangle$ on Bob’s mode B, whose amplitudes are Gaussianly modulated with variance μ − 1. As shown in Fig. 3(iv), these states are transmitted to Charlie (or Eve²²) who measures and broadcasts γ ≃ α − β^*.

Assuming ideal reconciliation¹⁰, the secret key rate $R=R(\mu ,\kappa ,{\kappa }^{\prime})$ increases in μ. Modulation variances μ ≳ 50 are experimentally achievable and well approximate the asymptotic limit for μ ≫ 1, where the key rate is optimal and satisfies (see Supplementary Material)

$${R}_{\text{opt}}\,\gtrsim \,{\log}_{2}\left(\frac{{F}_{\text{opt}}}{{e}^{2}{\varepsilon }_{\text{opt}}}\right)+h(1+2{\varepsilon }_{\text{opt}}),$$

(7)

with $h(x):=\frac{x+1}{2}{\log}_{2}\frac{x+1}{2}-\frac{x-1}{2}{\log}_{2}\frac{x-1}{2}$. Using Eq. (6), we see that the right-hand side of Eq. (7) can be positive only for ε_opt ≲ 0.192. Thus the practical QKD protocol is the most difficult to reactivate: Its reactivation implies that of entanglement/key distillation and that of entanglement swapping. This is true not only asymptotically but also at finite μ as we show below.

Reactivation from entanglement breaking

Once the theory of the previous protocols has been extended to non-Markovian decoherence, we can study their reactivation from entanglement-breaking conditions. Consider an environment with transmissivity τ and entanglement-breaking thermal noise ω > ω_EB(τ), so that no protocol can work for G = 0. By increasing the separable correlations in the environment, not only can quadripartite entanglement be reactivated but, above a certain threshold, it can also be localized into a bipartite form by the relay’s Bell detection. Once entanglement swapping is reactivated, all other protocols can progressively be reactivated. As shown in Fig. 4, there are regions of the correlation plane where entanglement can be swapped (${\mathcal{N}}\,>\,0$), teleportation is quantum (F > 1/2), entanglement and keys can be distilled (${I}_{{\mathcal{C}}}$, K > 0), and practical QKD can be performed (R > 0). This occurs both for large and experimentally achievable values of μ.

Fig. 4: Non-Markovian reactivation of quantum protocols from entanglement-breaking (here τ = 0.9 and ω = 1.02 × ω_EB = 19.38).

Each point of the correlation plane corresponds to a Gaussian environment with separable correlations. In the left panel we consider the optimal scenario of large μ (asymptotic protocols). Once quadripartite 1 × 3 entanglement has been reactivated (outside the grey ring), we have the progressive reactivation of entanglement swapping (${\mathcal{N}}\,>\,0$, yellow region), quantum teleportation of coherent states (F > 1/2, green region), entanglement/key distillation (${I}_{{\mathcal{C}}}$, K > 0, blue region) and practical QKD (R > 0, red region). The right panel refers to a realistic scenario with experimentally achievable values of μ. We consider μ ≃ 6.5 (refs. ^54,55) as input entanglement for the entanglement-based protocols, and μ ≃ 50 as modulation for the practical QKD protocol. The reactivation phenomenon persists and can be explored with current technology. Apart from teleportation, the other thresholds undergo small modifications.

Note that the reactivation is asymmetric in the plane only because of the specific Bell detection adopted, which generates correlations of the type g > 0 and ${g}^{\prime}\,<\,0$. Using another Bell detection (projecting onto ${\hat{q}}_{+}$ and ${\hat{p}}_{-}$), the performances would be inverted with respect to the origin of the plane. Furthermore, the entanglement localization (i.e., the reactivation of entanglement swapping) is triggered for correlations higher than those required for restoring quadripartite entanglement, suggesting that there might exist a better quantum measurement for this task. The performances of the various protocols improve by increasing the separable correlations of the environment, with the fastest reactivation being achieved along the diagonal $g+{g}^{\prime}=0$, where swapping and teleportation are first recovered, then entanglement/key distillation and practical QKD, which is the most nested region.

Correlated additive noise

The phenomenon can also be found in other types of non-Markovian Gaussian environments. Consider the limit for τ → 1 and ω → + ∞, while keeping constant n := (1 − τ)ω, c := g(ω − 1)⁻¹ and ${c}^{\prime}:={g}^{\prime}{(\omega -1)}^{-1}$. This is an asymptotic environment which adds correlated classical noise to modes A and B, so that their quadratures undergo the transformations

$$\left({\hat{q}}_{A},{\hat{p}}_{A},{\hat{q}}_{B},{\hat{p}}_{B}\right)\to \left({\hat{q}}_{A},{\hat{p}}_{A},{\hat{q}}_{B},{\hat{p}}_{B}\right)+({\xi }_{1},{\xi }_{2},{\xi }_{3},{\xi }_{4}).$$

Here the ξ_i’s are zero-mean Gaussian variables whose covariances $\left\langle {\xi }_{i}{\xi }_{j}\right\rangle$ are specified by the classical CM

$${\bf{V}}\left(n,c,{c}^{\prime}\right)=n\left(\begin{array}{cc}{\bf{I}}&{\rm{diag}}(c,{c}^{\prime})\\ {\rm{diag}}(c,{c}^{\prime})&{\bf{I}}\end{array}\right),$$

(8)

where n ≥ 0 is the variance of the additive noise, and $-1\le c,{c}^{\prime}\le 1$ quantify the classical correlations. The entanglement-breaking condition becomes n > 2.

To show non-Markovian effects, we consider the protocol which is the most difficult to reactivate, the practical QKD protocol. We can specify its key rate $R(\mu ,n,c,{c}^{\prime})$ for $c={c}^{\prime}=1$ and assume a realistic modulation μ ≃ 52. We then plot R as a function of the additive noise n in Fig. 5. As we can see, the rate decreases in n but remains positive in the region 2 < n ≤ 4 where the links with the relay become entanglement-breaking. As we show below, this behaviour persists in the presence of loss, as typically introduced by experimental imperfections.

Fig. 5: Plot the secret-key rate R (bits per relay use) as a function of the additive noise n.

The solid black curve is the theoretical rate computed for a correlated additive environment ($c={c}^{\prime}=1$) and realistic signal modulation (μ ≃ 52). This rate is positive after entanglement breaking (n > 2) and beats the single-repeater bound⁴⁰ (based on memoryless links). Points are experimental data: blue circles refer to ideal reconciliation and purple squares to achievable reconcilation efficiency (≃0.97). Error bars on the x-axis are smaller than the point size. Due to loss at the untrusted relay, the experimental key rate is slightly below the theoretical curve (associated with the correlated side-channel attack).

Recall that, for an additive Gaussian channel with added noise n, the secret-key capacity (and any other two-way assisted quantum capacity) is upper-bounded by

$${{\Phi }}(n):=\frac{(n/2)-1}{{\rm{ln}}2}-{\log}_{2}(n/2),$$

(9)

for n ≤ 2 and zero otherwise. The bound Φ(n) in Eq. (9) has been proven in ref. ⁵³ [see Eq. (29)] and here reported in our different vacuum units. In the presence of a relay/repeater, where each link is described by an independent bosonic Gaussian channel, ref. ⁴⁰ established that the secret-key capacity assisted by the repeater K_1−rep is upper-bounded by the minimum secret-key capacity of the links. In the present setting, we therefore have the single-repeater bound K_1−rep ≤ Φ(n). As we show in Fig. 5, the presence of classical (separable) correlations in the Gaussian environment lead to the violation of the bound Φ(n) when n ≳ 0.369 (for the theoretical curve) and n ≳ 0.4 (for the experimental results).

Experimental results

Our theoretical results are confirmed by a proof-of-principle experiment, whose setup is schematically depicted in Fig. 6. We consider Alice and Bob generating Gaussianly modulated coherent states by means of independent electro-optical modulators, applied to a common local oscillator. Simultaneously, the modulators are subject to a side-channel attack: Additional electrical inputs are introduced by Eve, whose effect is to generate additional and unknown phase-space displacements. In particular, Eve’s electrical inputs are correlated so that the resulting optical displacements introduce a correlated additive Gaussian environment described by Eq. (8) with c ≃ 1 and ${c}^{\prime}\simeq 1$. The optical modes then reach the midway relay, where they are mixed at a balanced beam splitter and the output ports photo-detected. Although the measurement is highly efficient, it introduces a small loss (≃2%) which is assumed to be exploited by Eve in the worst-case scenario.

Fig. 6: Experimental setup.

Alice and Bob receive 1064 nm light from the same laser source (local oscillator). At both stations, the incoming beams are Gaussianly modulated in phase and amplitude using electro-optical modulators driven by uncorrelated signal generators. In addition, the phase and amplitude modulators for Alice and Bob have correlated inputs respectively, such that a noisy modulation identical for both Alice and Bob is added to the phase and amplitude signals (side-channel attack). The magnitudes of the correlated noise modulations are progressively increased (from n = 0 to 4), and kept symmetrical between the quadratures, while the signal modulations are kept constant at the same level in both quadratures for Alice and Bob (μ ≃ 52). At the untrusted relay, the modes are mixed at a balanced beam splitter and the output ports photo-detected, with an overall efficiency of ≃98%. Photocurrents are then processed to realize a CV Bell measurement. See Supplementary Material for details.

From the point of view of Alice and Bob, the side-channel attack and the additional (small) loss at the relay are jointly perceived as a global coherent Gaussian attack of the optical modes. Analysing the statistics of the shared classical data and assuming that Eve controls the entire environmental purification compatible with this data, the two parties may compute the experimental secret-key rate (see details in the Supplementary Material). As we can see from Fig. 5, the experimental points are slightly below the theoretical curve associated with the correlated additive environment, reflecting the fact that the additional loss at the relay tends to degrade the performance of the protocol. The experimental rate is able to beat the single-repeater bound for additive-noise Gaussian links⁴⁰ and remains positive after the entanglement-breaking threshold, so that the non-Markovian reactivation of QKD is experimentally confirmed.

Discussion

We have theoretically and experimentally demonstrated that the most important protocols operated by quantum relays can work in conditions of extreme decoherence thanks to the presence of non-Markovian memory effects in the environment. Assuming high Gaussian noise in the links, we have considered a regime where any form of entanglement (bipartite, tripartite, or quadripartite) is broken under Markovian memoryless conditions. By allowing for a suitable amount of correlations in the environment, we have proven that we can reactivate the distribution of 1 × 3 quadripartite entanglement, and this resource can successfully be localized into a bipartite form exploitable by Alice and Bob. As a result, all the basic protocols for quantum and private communication can be progressively reactivated by the action of the relay.

Surprisingly, this reactivation is possible without the need of any injection of entanglement from the environment, but just because of the presence of weaker classical correlations (described by a separable state for the environment). In particular, we have shown that these correlations lead to the violation of the single-repeater bound for quantum and private communications.

Our results might open new perspectives for all quantum systems where correlated errors and memory effects are typical forms of decoherence. This may involve both short-distance implementations (e.g., chip-based) and long-distance ones, as is the case of relay-based QKD. Non-Markovian memory effects should therefore be regarded as a potential physical resource to be exploited in various settings of quantum communication.

Methods

Theoretical and experimental methods are given in the Supplementary Material. Theoretical methods contain details about the following points: (i) Study of the Gaussian environment with correlated thermal noise, including a full analysis of its correlations. (ii) Study of the various forms of entanglement available before the Bell detection of the relay. (iii) Study of the entanglement swapping protocol, i.e., the computation of the CM V_ab∣γ in Eq. (1) and the derivation of the eigenvalue ε in Eq. (5). (iv) Generalization of the teleportation protocol with details on Bob’s quantum operation ${{\mathcal{Q}}}_{\gamma }$ and the analytical formula for the fidelity $F(\mu ,\kappa ,{\kappa }^{\prime})$. (v) Details of the distillation protocol with the analytical formula of ${I}_{{\mathcal{C}}}(\mu ,\kappa ,{\kappa }^{\prime})$. (vi) Details of the ideal key-distillation protocol, discussion on MDI-security, and proof of the lower-bound $K\ge {I}_{{\mathcal{C}}}$. (vii) Derivation of the general secret-key rate $R(\xi ,\mu ,\kappa ,{\kappa }^{\prime})$ of the practical QKD protocol, assuming arbitrary reconciliation efficiency ξ and modulation variance μ. (viii) Explicit derivation of the optimal rate R_opt and the proof of the tight lower bound in Eq. (7). (ix) Derivation of the correlated additive environment as a limit of the correlated thermal one. (x) Study of entanglement swapping and practical QKD in the correlated additive environment, providing the formula of the secret-key rate $R(\xi ,\mu ,n,c,{c}^{\prime})$.