Zero uncertainty states in the presence of quantum memory

Abstract

The uncertainty principle imposes a fundamental limit on predicting the measurement outcomes of incompatible observables even if complete classical information of the system state is known. The situation is different if one can build a quantum memory entangled with the system. Zero uncertainty states (in contrast with minimum uncertainty states) are peculiar quantum states that can eliminate uncertainties of incompatible von Neumann observables once assisted by suitable measurements on the memory. Here we determine all zero uncertainty states of any given set of nondegenerate observables and determine the minimum entanglement required. It turns out all zero uncertainty states are maximally entangled in a generic case, and vice versa, even if these observables are only weakly incompatible. Our work establishes a simple and precise connection between zero uncertainty and maximum entanglement, which is of interest to foundational studies and practical applications, including quantum certification and verification.

Introduction

The uncertainty principle represents a key distinction between quantum mechanics and classical mechanics and is still a focus of current research^1,2,3,4. It imposes a fundamental limit on our ability to predict the measurement outcomes of incompatible observables, such as position and momentum^5,6. However, uncertainty relations have to be modified in the presence of a quantum memory because entanglement between the memory and system can reduce the uncertainty^{7,8,9,10,11,12}. Besides foundational significance, this simple fact is of interest to diverse applications, including entanglement detection^8,9,10 and quantum cryptography^8,11,13. Nevertheless, several fundamental questions are still left open. Notably, what quantum states of the system and memory can minimize or even eliminate the uncertainty completely? How much entanglement is required to achieve this goal?

In this paper we are interested in those quantum states that can eliminate the uncertainty completely, which are referred to as zero uncertainty states (ZUSs) henceforth. In contrast with the familiar minimum uncertainty states and intelligent states studied in the literature^14,15,16, our definition of ZUSs does not rely on a specific uncertainty measure, but has a clear operational interpretation. In particular, we determine all ZUSs with respect to any given set of nondegenerate observables on a finite-dimensional Hilbert space coupled with a quantum memory. We also determine the minimum entanglement required to construct any ZUS. It turns out all ZUSs are determined by a simple graph constructed from transition probabilities between eigenbases of the relevant observables. Moreover, all ZUSs are maximally entangled states (MESs), and vice versa, whenever this graph is connected. Notably, this is the case for a generic set of two or more observables, even if these observables are only weakly incompatible. Nevertheless, ZUSs and MESs are not necessarily pure states.

Our study establishes a simple and precise connection between zero uncertainty and maximum entanglement, which is independent of specific uncertainty and entanglement measures. Moreover, our approach applies to arbitrary sets of nondegenerate observables, in sharp contrast with most previous approaches, which are restricted to two observables or complementary observables. This work may shed light on the foundational studies of uncertainty relations, quantum entanglement, and quantum steering^{7,17,18,19,20}. Meanwhile, it is of direct interest to many tasks in quantum information processing, including remote state preparation^21,22 and semi-device-independent quantum certification and verification^{18,23,24,25,26}.

Results

Maximally entangled states

To establish our main results, first we need to better understand MESs. A bipartite state ρ on the Hilbert space ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ of dimension d_A × d_B is a MES if we can create every state on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ from ρ by local operations and classical communication (LOCC)²⁷. This definition is independent of any specific entanglement measure and is thus quite appealing to the current study. When d_A≤ d_B, the state $\left|{{\Phi }}\right\rangle :=\mathop{\sum }\nolimits_{j = 0}^{{d}_{{\rm{A}}}-1}\left|jj\right\rangle /\sqrt{{d}_{{\rm{A}}}}$ is a canonical example, where ${\{\left|j\right\rangle \}}_{j = 0}^{{d}_{{\rm{A}}}-1}$ and ${\{\left|j\right\rangle \}}_{j = 0}^{{d}_{{\rm{B}}}-1}$ are the computational bases of ${{\mathcal{H}}}_{{\rm{A}}}$ and ${{\mathcal{H}}}_{{\rm{B}}}$, respectively. A MES is not necessarily pure, as clarified in the following lemma, essentially proved in ref. ²⁸; see the Supplementary Information for an independent proof.

Lemma 1 Let ρ be a bipartite state on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ with d_A≤ d_B. Then the following statements are equivalent.

• 1. ρ is a MES.

• 2. $H{({\rm{A}}| {\rm{B}})}_{\rho }=-{\mathrm{log}\,}_{2}{d}_{{\rm{A}}}$.

• 3. ${E}_{{\rm{R}}}(\rho )={\mathrm{log}\,}_{2}{d}_{{\rm{A}}}$.

• 4. ${E}_{{\rm{F}}}(\rho )={\mathrm{log}\,}_{2}{d}_{{\rm{A}}}$.

• 5. ρ has a spectral decomposition $\rho ={\sum }_{s}{\lambda }_{s}\left|{{{\Psi }}}_{s}\right\rangle \left\langle {{{\Psi }}}_{s}\right|$ such that all $\left|{{{\Psi }}}_{s}\right\rangle$ are MESs, and ${\mathrm{tr}}_{{\rm{A}}}(\left|{{{\Psi }}}_{s}\right\rangle \left\langle {{{\Psi }}}_{s}\right|)$ have mutually orthogonal supports.

Here H(A∣B)_ρ = S(ρ) − S(ρ_B) is the conditional entropy of A given B, where S(ρ) and S(ρ_B) are the von Neumann entropies of ρ and ${\rho }_{{\rm{B}}}:={\mathrm{tr}}_{{\rm{A}}}(\rho )$, respectively. E_R(ρ) and E_F(ρ) are the relative entropy of entanglement and entanglement of formation²⁷. By Lemma 1, all MESs on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ are pure when d_A≤ d_B < 2d_A²⁸. In general, each MES is a convex mixture of pure MESs whose local supports for Bob are mutually orthogonal. Given a MES ρ on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ with d_A≤ d_B, let ${{\mathcal{H}}}_{{\rm{B}}^{\prime} }$ be the support of ρ_B. Then ${{\mathcal{H}}}_{{\rm{B}}^{\prime} }$ has a decomposition ${{\mathcal{H}}}_{{\rm{B}}^{\prime} }={{\mathcal{H}}}_{{{\rm{B}}}_{1}}\otimes {{\mathcal{H}}}_{{{\rm{B}}}_{2}}$ with $\dim ({{\mathcal{H}}}_{{{\rm{B}}}_{1}})={d}_{{\rm{A}}}$ such that $\rho =\left|{{\Phi }}^{\prime} \right\rangle \left\langle {{\Phi }}^{\prime} \right|\otimes \tau$, where $\left|{{\Phi }}^{\prime} \right\rangle$ is a pure MES in ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{{\rm{B}}}_{1}}$, and τ is a full-rank density operator on ${{\mathcal{H}}}_{{{\rm{B}}}_{2}}$. So all MESs on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ are equivalent under local operations of Bob.

Corollary 1 All MESs on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ with d_A≤ d_B can be turned into each other by local operations on ${{\mathcal{H}}}_{{\rm{B}}}$. When d_A≤ d_B < 2d_A, all MESs are pure and can be turned into each other by unitary transformations on ${{\mathcal{H}}}_{{\rm{B}}}$.

Zero uncertainty states

Consider the uncertainty game in which Alice can measure m nondegenerate von Neumann observables ${\mathscr{O}}={\{{O}_{x}\}}_{x = 1}^{m}$ on ${{\mathcal{H}}}_{{\rm{A}}}$ with uniform probabilities (generalization to nonuniform probabilities is straightforward), and Bob is asked to predict the measurement outcome given the specific observable chosen by Alice⁸. Let ${{\mathcal{B}}}_{x}={\{\left|{\psi }_{xk}\right\rangle \}}_{k}$ be an orthonormal eigenbasis of O_x and ${\mathscr{B}}={\{{{\mathcal{B}}}_{x}\}}_{x = 1}^{m}$. Then predicting the outcome of O_x amounts to predicting the outcome of the projective measurement on the basis ${{\mathcal{B}}}_{x}$. When these observables are incompatible (do not commute with each other), in general Bob cannot predict the measurement outcome with certainty even if he knows the complete classical description of the system state as characterized by the density matrix ρ_A. In the case of two observables for example, the uncertainties of the measurement outcomes satisfy the Maassen-Uffink inequality²⁹,

$$H({O}_{1})+H({O}_{2})\ge {\mathrm{log}\,}_{2}({c}^{-1}),$$

(1)

where H(O₁) and H(O₂) are the Shannon entropies of the measurement outcomes of O₁ and O₂, respectively, and $c=\mathop{\max }\nolimits_{j,k}| \left\langle {\psi }_{1j}| {\psi }_{2k}\right\rangle {| }^{2}$.

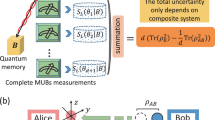
The situation is different if Bob holds a quantum memory with Hilbert space ${{\mathcal{H}}}_{{\rm{B}}}$ and can create an entangled state ρ on the joint system ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$, as illustrated in Fig. 1. Suppose Alice chooses the basis ${{\mathcal{B}}}_{x}$ (observable O_x), then Bob can perform a generalized measurement characterized by a positive operator-valued measure (POVM) ${\{{{{\Pi }}}_{xk}\}}_{k}$ on his subsystem ${{\mathcal{H}}}_{{\rm{B}}}$, where Π_xk corresponds to guessing the outcome k given the measurement basis ${{\mathcal{B}}}_{x}$ of Alice. The average success guessing probability reads ∑_xp_x/m with

$${p}_{x}=\sum _{k}{\mathrm{tr}}\,[\rho (\left|{\psi }_{xk}\right\rangle \left\langle {\psi }_{xk}\right|\otimes \Pi_{xk})]=\sum _{k}{\mathrm{tr}}\,({\rho }_{xk}\Pi_{xk}),$$

(2)

where ${\rho }_{xk}=\left\langle {\psi }_{xk}\right|\rho \left|{\psi }_{xk}\right\rangle$ are subnormalized reduced states of Bob. Note that p_x is also the probability that the POVM ${\{{{{\Pi }}}_{xk}\}}_{k}$ can successfully distinguish the ensemble of states

$${\mathscr{S}}(\rho ,{{\mathcal{B}}}_{x})=\{\left\langle \psi \right|\rho \left|\psi \right\rangle \ :\ \left|\psi \right\rangle \in {{\mathcal{B}}}_{x}\}.$$

(3)

The maximum of the average guessing probability over all POVMs can be determined by semidefinite programming, and this maximum is determined by the state ρ and the basis set ${\mathscr{B}}$ (or the observable set ${\mathscr{O}}$) of Alice.

Fig. 1: Connection between zero uncertainty and maximum entanglement in the uncertainty game.

By performing suitable measurements (depending on the observables of Alice) on his quantum memory, Bob can better predict the measurement outcomes of Alice. When the set of observables of Alice is irreducible, Bob can predict these measurement outcomes with certainty iff his quantum memory is maximally entangled with Alice.

Given a set of observables ${\mathscr{O}}={\{{O}_{x}\}}_{x = 1}^{m}$ or bases ${\mathscr{B}}={\{{{\mathcal{B}}}_{x}\}}_{x = 1}^{m}$ for Alice, a joint state ρ of Alice and Bob is a ZUS if Bob can predict the measurement outcome of Alice with certainty by a suitable measurement depending on the choice of Alice. Given a ZUS, the guessing probability p_x for each measurement of Alice can attain the maximum 1, and the conditional entropy H(O_x∣B) is 0. In contrast with minimum uncertainty states and intelligent states^14,15,16, ZUSs not only minimize the uncertainty, but also eliminate the uncertainty completely. Moreover, here the definition is independent of any specific uncertainty measure.

To appreciate the significance of entanglement to constructing a ZUS, consider an example with two observables, in which case the uncertainty relation in Eq. (1) is modified as follows⁸,

$$H({O}_{1}| {\rm{B}})+H({O}_{2}| {\rm{B}})\ge {\mathrm{log}}_{2}({c}^{-1})+H{({\rm{A}}| {\rm{B}})}_{\rho }.$$

(4)

Here the conditional entropy H(A∣B)_ρ manifests the impact of entanglement in reducing the uncertainty. Interestingly, a variant of Eq. (4) may be interpreted as uncertainty-reality complementarity, which builds on an intimate connection between uncertainty (or rather certainty) and reality^7,30,31,32.

By Eq. (4), any ZUS ρ must satisfy the inequalities

$${E}_{{\rm{F}}}(\rho )\ge {E}_{{\rm{R}}}(\rho )\ge -H{({\rm{A}}| {\rm{B}})}_{\rho }\ge {\mathrm{log}}_{2}({c}^{-1}),$$

(5)

where the second one is derived in ref. ³³ (cf. ref. ³⁴). Suppose O₁ and O₂ are complementary, so that ${{\mathcal{B}}}_{1}$ and ${{\mathcal{B}}}_{2}$ are mutually unbiased, which means $| \left\langle {\psi }_{1j}| {\psi }_{2k}\right\rangle {| }^{2}=1/{d}_{{\rm{A}}}$ for all j, k³⁵. Then we have c = 1/d_A and

$${E}_{{\rm{F}}}(\rho )={E}_{{\rm{R}}}(\rho )=-H{({\rm{A}}| {\rm{B}})}_{\rho }={\mathrm{log}\,}_{2}{d}_{{\rm{A}}},$$

(6)

which implies that d_B≥ d_A and ρ is a MES by Lemma 1, in which case ρ is indeed a ZUS. Unfortunately, this reasoning does not work in general. To address this problem, we need a completely different line of thinking.

Key observations about ZUSs

Bob can predict the measurement outcome on the basis ${{\mathcal{B}}}_{x}$ with certainty iff the ensemble ${\mathscr{S}}(\rho ,{{\mathcal{B}}}_{x})$ defined in Eq. (3) is perfectly distinguishable, that is, all states in ${\mathscr{S}}(\rho ,{{\mathcal{B}}}_{x})$ have mutually orthogonal supports. The state ρ is a ZUS with respect to ${\mathscr{B}}={\{{{\mathcal{B}}}_{x}\}}_{x = 1}^{m}$ iff each ensemble ${\mathscr{S}}(\rho ,{{\mathcal{B}}}_{x})$ is perfectly distinguishable. The following three propositions are simple corollaries of these observations.

Proposition 1 Suppose ρ is a ZUS, then any state supported in the support of ρ is a ZUS.

Proposition 2 Suppose ρ₁ and ρ₂ are two ZUSs on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$. If ${\mathrm{tr}\,}_{{\rm{A}}}({\rho }_{1})$ and ${\mathrm{tr}\,}_{{\rm{A}}}({\rho }_{2})$ have orthogonal supports, then any convex mixture of ρ₁ and ρ₂ is a ZUS.

Proposition 3 Suppose ρ is bipartite state on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ and Λ is a completely positive and trace-preserving (CPTP) map (quantum channel) from system B to system $\tilde{{\rm{B}}}$. Then ρ is a ZUS if (1 $\otimes$ Λ)(ρ) is.

Here Propositions 1 and 2 are tied to the fact that mixture of quantum states can only reduce distinguishability unless the reduced states of Bob have orthogonal supports. Proposition 3 follows from the simple fact that quantum operations cannot enhance distinguishability. Two states ρ₁ and ρ₂ on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ are equivalent if they can be turned into each other by local operations on ${{\mathcal{H}}}_{{\rm{B}}}$. In that case, ρ₁ is a ZUS with respect to ${\mathscr{B}}$ iff ρ₂ is. Under these local operations, ZUSs divide into equivalent classes.

Transition graphs

To determine ZUSs with respect to a given basis set ${\mathscr{B}}={\{{{\mathcal{B}}}_{x}\}}_{x = 1}^{m}$ in ${{\mathcal{H}}}_{{\rm{A}}}$, we first need to pinpoint a key property of the basis set. The transition graph $G({\mathscr{B}})$ of ${\mathscr{B}}$ is an m-partite graph with md_A vertices which are in one-to-one correspondence with the basis states (identical states in different bases correspond to different vertices). Two different vertices are adjacent iff the corresponding states are not orthogonal, that is, the transition probability between the two states is nonzero. The graph $G({\mathscr{B}})$ encodes the incompatibility structure of the basis set ${\mathscr{B}}$, which is crucial to studying ZUSs and quantum verification, as we shall see later.

The basis set ${\mathscr{B}}$ is irreducible if the transition graph $G({\mathscr{B}})$ is connected, in which case the projectors onto basis states generate the whole operator algebra on ${{\mathcal{H}}}_{{\rm{A}}}$. Any basis set composed of m ≥ 2 mutually unbiased bases (or generic random bases) is irreducible since the transition graph is a complete m-partite graph, as illustrated in Fig. 2.

Fig. 2: Transition graph of three mutually unbiased bases for a qubit, which corresponds to the eigenbases of the three Pauli matrices.

Two vertices of the same color are associated with the two states in the same basis. This transition graph is connected, so the corresponding basis set is irreducible.

The basis set ${\mathscr{B}}$ is reducible if the transition graph $G({\mathscr{B}})$ is not connected. In this case, the basis set may be seen as a direct sum of basis sets defined on smaller subspaces. Suppose $G({\mathscr{B}})$ has g connected components G₁, G₂, …, G_g, then each component G_a is also an m-partite graph in which all parties have the same number of vertices. Let ${{\mathcal{B}}}_{x}^{a}$ be the subset of ${{\mathcal{B}}}_{x}$ that corresponds to the vertices in the component G_a. The component subspace${{\mathcal{H}}}_{{\rm{A}},a}$ associated with component a is the subspace of ${{\mathcal{H}}}_{{\rm{A}}}$ spanned by all $\left|\psi \right\rangle \in {{\mathcal{B}}}_{x}^{a}$, with component projector and component rank given by

$${P}_{a}={P}_{a}({\mathscr{B}})=\sum _{\left|\psi \right\rangle \in {{\mathcal{B}}}_{x}^{a}}\left|\psi \right\rangle \left\langle \psi \right|,\quad {r}_{a}=\mathrm{tr}\,({P}_{a}).$$

(7)

These definitions are independent of the choice of the basis index x. Denote by ${\mathscr{P}}({\mathscr{B}}):={\{{P}_{a}({\mathscr{B}})\}}_{a = 1}^{g}$ the set of component projectors, which are mutually orthogonal. In this way, ${{\mathcal{H}}}_{{\rm{A}}}$ decomposes into a direct sum of component subspaces ${{\mathcal{H}}}_{{\rm{A}},a}$. In addition, ${{\mathcal{B}}}_{x}^{a}$ for x = 1, 2, …, m can be regarded as bases in ${{\mathcal{H}}}_{{\rm{A}},a}$, and the basis set ${{\mathscr{B}}}^{a}:={\{{{\mathcal{B}}}_{x}^{a}\}}_{x = 1}^{m}$ is irreducible for ${{\mathcal{H}}}_{{\rm{A}},a}$.

Connect ZUSs with MESs

Now we are ready to present our main results on ZUSs and MESs as illustrated in Fig. 1. First, we clarify when Bob can predict the outcome of one projective measurement of Alice. The following lemma proved in the Supplementary Information is a stepping stone to understanding ZUSs in the presence of a quantum memory.

Lemma 2 Suppose $\rho =\left|{{\Psi }}\right\rangle \left\langle {{\Psi }}\right|$ is a bipartite pure state on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ and ${\mathcal{B}}$ is an orthonormal basis for ${{\mathcal{H}}}_{{\rm{A}}}$. Then the ensemble ${\mathscr{S}}(\rho ,{\mathcal{B}})$ is perfectly distinguishable iff ${\mathcal{B}}$ is an eigenbasis of ${\rho }_{{\rm{A}}}={\mathrm{tr}\,}_{{\rm{B}}}(\rho )$.

Note that Bob can predict the measurement outcome of Alice on the basis ${\mathcal{B}}$ with certainty iff the ensemble ${\mathscr{S}}(\rho ,{\mathcal{B}})$ defined in Eq. (3) is perfectly distinguishable. By Lemma 2, this is the case iff ρ_A is diagonal with respect to the basis ${\mathcal{B}}$. Therefore, the pure state ρ is a ZUS with respect to a basis set ${\mathscr{B}}$ iff ρ_A is diagonal with respect to each basis in ${\mathscr{B}}$. When ${\mathscr{B}}$ is irreducible, it turns out only MESs can satisfy this condition. Based on this observation we can derive the following theorem as proved in the Supplementary Information.

Theorem 1 Suppose ${\mathscr{B}}$ is an irreducible basis set in ${{\mathcal{H}}}_{{\rm{A}}}$. Then a bipartite (pure or mixed) state ρ on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ is a ZUS with respect to ${\mathscr{B}}$ iff d_B ≥ d_A and ρ is a MES.

By Theorem 1 and Lemma 1, each ZUS with respect to ${\mathscr{B}}$ is a tensor product of a pure MES and an ancillary state. In addition, to attain zero uncertainty, the measurements of Bob on the support of ρ_B are uniquely determined by the counterpart of Alice, as shown in Supplementary note E. All ZUSs with respect to ${\mathscr{B}}$ can be turned into each other by local operations on ${{\mathcal{H}}}_{{\rm{B}}}$ and thus form a single equivalent class. If d_A≤ d_B < 2d_A, then all ZUSs are pure and can be turned into each other by unitary transformations on ${{\mathcal{H}}}_{{\rm{B}}}$. These results hold as long as the transition graph $G({\mathscr{B}})$ is connected, even if ${\mathscr{B}}$ consists of only two nearly identical bases, so that the corresponding observables are only weakly incompatible, as quantified by the commutator or incompatibility robustness^36,37,38.

Theorem 1 establishes a simple and precise connection between zero uncertainty and maximum entanglement, which is independent of specific uncertainty and entanglement measures. This connection offers a fresh perspective for understanding the uncertainty principle in the presence of a quantum memory⁸. It may also shed light on uncertainty-reality complementarity given the close relation between the notation of uncertainty and that of reality^7,30,31,32.

ZUSs with respect to reducible basis sets

Next, we determine ZUSs with respect to a reducible basis set ${\mathscr{B}}$.

Theorem 2 Suppose ${\mathscr{B}}$ is a set of orthonormal bases in ${{\mathcal{H}}}_{{\rm{A}}}$ and has g irreducible components with component subspaces ${{\mathcal{H}}}_{{\rm{A}},a}$, component projectors P_a, and component ranks r_a for a = 1, 2, …, g. Let ρ be a bipartite state on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ and $\rho_a=(P_a\otimes 1_B) \rho(P_a\otimes 1_B)$. Then ρ is a ZUS with respect to ${\mathscr{B}}$ iff the following three conditions hold: r_a≤ d_B whenever $\mathrm{tr}\,({\rho }_{a})>0$; each ρ_a with $\mathrm{tr}\,({\rho }_{a})>0$ is a (subnormalized) MES on ${{\mathcal{H}}}_{{\rm{A}},a}\otimes {{\mathcal{H}}}_{{\rm{B}}}$; all ${\mathrm{tr}\,}_{{\rm{A}}}({\rho }_{a})$ have mutually orthogonal supports.

Theorem 2 follows from Theorem 1. Recall that the basis set ${\mathscr{B}}$ can be regarded as a direct sum of irreducible basis sets ${{\mathscr{B}}}^{a}$ defined on component subspaces ${{\mathcal{H}}}_{{\rm{A}},a}$. So ρ is a ZUS with respect to ${\mathscr{B}}$ iff its restriction ρ_a on ${{\mathcal{H}}}_{{\rm{A}},a}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ is a ZUS with respect to ${{\mathscr{B}}}^{a}$ and, in addition, all ${\mathrm{tr}\,}_{{\rm{A}}}({\rho }_{a})$ have mutually orthogonal supports. Note that coherence between different component subspaces are useless to constructing ZUSs. In addition, the dimension d_B of ${{\mathcal{H}}}_{{\rm{B}}}$ must satisfy ${d}_{{\rm{B}}}\ge {r}_{\min }$ in order to construct a ZUS, where ${r}_{\min }=\mathop{\min }\nolimits_{1\le a\le g}{r}_{a}$ is the minimum component rank. When the lower bound is saturated, every ZUS is a pure MES on ${{\mathcal{H}}}_{{\rm{A}},a}\otimes {{\mathcal{H}}}_{{\rm{B}}}$, where ${{\mathcal{H}}}_{{\rm{A}},a}$ is a component subspace of dimension ${r}_{\min }$. Furthermore, ${r}_{\min }$ determines the minimum entanglement required to construct a ZUS, as shown in the Methods section.

In the case of pure states, ZUSs admit a much simpler characterization, as shown in the following corollary.

Corollary 2 A bipartite pure state $\left|{{\Psi }}\right\rangle$ in ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ is a ZUS with respect to ${\mathscr{B}}$ iff the reduced state ρ_A is a weighted sum of component projectors in ${\mathscr{P}}({\mathscr{B}})$.

Corollary 2 is a special case of Theorem 2 and also follows from Lemma 2 and Supplementary Lemma 2. Here ρ_A is a weighted sum of component projectors iff ρ_A is diagonal with respect to each basis ${\mathcal{B}}$ in ${\mathscr{B}}$ (cf. Supplementary note C). As an implication of Corollary 2, the reduced state ρ_A of any (pure or mixed) ZUS ρ with respect to ${\mathscr{B}}$ is a weighted sum of component projectors in ${\mathscr{P}}({\mathscr{B}})$, given that any ZUS is a convex mixture of pure ZUSs. The equivalent classes of pure ZUSs are determined in the Methods section.

Applications to quantum certification and verification

Our results on ZUSs have immediate implications for the verification of MESs. Suppose Alice and Bob want to create the MES $\left|{{\Phi }}\right\rangle =\mathop{\sum }\nolimits_{j = 0}^{{d}_{{\rm{A}}}-1}\left|jj\right\rangle /\sqrt{{d}_{{\rm{A}}}}$ in this way: Bob first creates a MES in his lab and then sends one particle of the entangled pair to Alice via a quantum channel. To verify the resulting state ρ, they can perform tests based on correlated local projective measurements such that only the target state can pass all tests with certainty^{39,40,41,42,43}. Suppose Alice can perform projective measurements from the set ${\mathscr{B}}={\{{{\mathcal{B}}}_{x}\}}_{x = 1}^{m}$ in which ${{\mathcal{B}}}_{x}$ is chosen with probability μ_x > 0. For each choice ${{\mathcal{B}}}_{x}$, she asks Bob to perform the measurement on the conjugate basis ${{\mathcal{B}}}_{x}^{* }$ and return the outcome. The test is passed if Bob and Alice obtain the same outcome⁴¹.

If Bob is honest, then the average probability that ρ passes each test is $\mathrm{tr}\,(\rho {{\Omega }})$, where ${{\Omega }}=\mathop{\sum }\nolimits_{x = 1}^{m}{\mu }_{x}P({{\mathcal{B}}}_{x})$⁴¹ is known as the verification operator and

$$P({{\mathcal{B}}}_{x}):=\sum _{\left|\psi \right\rangle \in {{\mathcal{B}}}_{x}}\left|\psi \right\rangle \left\langle \psi \right|\otimes \left|{\psi }^{* }\right\rangle \left\langle {\psi }^{* }\right|$$

(8)

is a test projector. Note that $\left|{{\Phi }}\right\rangle$ is an eigenstate of $P({{\mathcal{B}}}_{x})$ and Ω with eigenvalue 1 and so can pass each test with certainty. In addition, $\left|{{\Phi }}\right\rangle$ can be reliably verified by this protocol iff the maximum eigenvalue of Ω is nondegenerate, that is, the pass eigenspace of Ω has dimension 1^40,41,42,43. This is the case iff the basis set ${\mathscr{B}}$ is irreducible by the following theorem proved in the Supplementary Information.

Theorem 3 Suppose ${\mathscr{B}}={\{{{\mathcal{B}}}_{x}\}}_{x = 1}^{m}$ is a set of orthonormal bases in ${{\mathcal{H}}}_{{\rm{A}}}$, and ${{\Omega }}=\mathop{\sum }\nolimits_{x = 1}^{m}{\mu }_{x}P({{\mathcal{B}}}_{x})$ with μ_x > 0 and $\mathop{\sum }\nolimits_{x = 1}^{m}{\mu }_{x}=1$. Then the degeneracy of the maximum eigenvalue 1 of Ω equals the number of connected components of the transition graph $G({\mathscr{B}})$. This eigenvalue is nondegenerate iff the basis set ${\mathscr{B}}$ is irreducible.

Next, suppose Bob is not honest. Then Alice cannot distinguish states that are equivalent under the local operations of Bob. Nevertheless, she can still verify the MES $\left|{{\Phi }}\right\rangle$ up to equivalence. Thanks to Theorem 1, the uncertainty game described before actually provides a verification protocol whenever the basis set ${\mathscr{B}}$ of Alice is irreducible. Note that Bob can pass each test (guess each measurement outcome) of Alice with certainty only if the state ρ prepared is a MES. Surprisingly, the requirement on the measurement bases of Alice remains the same when Bob becomes dishonest. In addition, the measurements of Bob required to attain the maximum guessing probability are essentially uniquely determined by the counterpart of Alice. These results are of interest to semi-device-independent quantum certification and verification^{18,23,24,25,26}

Implications for quantum steering

Our study also has implications for Einstein-Podolsky-Rosen steering or quantum steering^{7,17,18,19,20}, which is clear if we interchange the measurement order in the above verification protocol. In each test Alice asks Bob to perform the measurement on the basis ${{\mathcal{B}}}_{x}^{* }$ with probability μ_x > 0 for x = 1, 2, …, m and return the outcome. Then Alice performs the projective measurement on ${{\mathcal{B}}}_{x}\in {\mathscr{B}}$, and the test is passed if she obtains the same outcome as Bob. Alternatively, Alice can choose the two-outcome POVM $\{\left|{\psi }_{xk}\right\rangle \left\langle {\psi }_{xk}\right|,{1}_{{\rm{A}}}-\left|{\psi }_{xk}\right\rangle \left\langle {\psi }_{xk}\right|\}$ if Bob obtains outcome k. Suppose Alice and Bob share the state ρ and Bob performs the POVM ${\{{{{\Pi }}}_{xk}\}}_{k}$ instead of the projective measurement on ${{\mathcal{B}}}_{x}^{* }$. Then the probability that Bob passes the test reads

$$\sum _{k}\left\langle {\psi }_{xk}\right|{\sigma }_{xk}\left|{\psi }_{xk}\right\rangle ,\quad {\sigma }_{xk}={\mathrm{tr}}_{{\rm{B}}}[\rho ({1}_{{\rm{A}}}\otimes \Pi_{xk})],$$

(9)

which is a variant of Eq. (2). The subnormalized states σ_xk satisfy the normalization condition ∑_kσ_xk = ρ_A and form an ensemble of ρ_A for each x. The collection of ensembles ${\{{\{{\sigma }_{xk}\}}_{k}\}}_{x}$ is known as an assemblage^19,20,44. If Bob is honest, then the assemblage generated is ${\{{\{\left|{\psi }_{xk}\right\rangle \left\langle {\psi }_{xk}\right|/{d}_{{\rm{A}}}\}}_{k}\}}_{x}$. When ${\mathscr{B}}$ is irreducible, it turns out only this assemblage can pass each test with certainty, as shown in the following lemma and proved in the Supplementary Information.

Lemma 3 Suppose ${\mathscr{B}}={\{{{\mathcal{B}}}_{x}\}}_{x = 1}^{m}$ with ${{\mathcal{B}}}_{x}={\{\left|{\psi }_{xk}\right\rangle \}}_{k}$ is an irreducible set of orthonormal bases in ${{\mathcal{H}}}_{{\rm{A}}}$. Suppose ${\{{\{{\sigma }_{xk}\}}_{k}\}}_{x}$ is an assemblage for ρ_A that satisfies ${\sum }_{k}\left\langle {\psi }_{xk}\right|{\sigma }_{xk}\left|{\psi }_{xk}\right\rangle =1$ for each x. Then ρ_A is completely mixed, and ${\sigma }_{xk}=\left|{\psi }_{xk}\right\rangle \left\langle {\psi }_{xk}\right|/{d}_{{\rm{A}}}$ for each x and k.

Here the condition ${\sum }_{k}\left\langle {\psi }_{xk}\right|{\sigma }_{xk}\left|{\psi }_{xk}\right\rangle =1$ means the assemblage ${\{{\{{\sigma }_{xk}\}}_{k}\}}_{x}$ can pass each test of Alice with certainty. By virtue of Theorem 1, we can further show that the assemblage ${\{{\{\left|{\psi }_{xk}\right\rangle \left\langle {\psi }_{xk}\right|/{d}_{{\rm{A}}}\}}_{k}\}}_{x}$ can only be generated by a MES, as stated in the following theorem and proved in the Supplementary Information.

Theorem 4 Given the basis set ${\mathscr{B}}$ in Lemma 3, suppose ρ is a bipartite state on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ that can generate the assemblage ${\{{\{\left|{\psi }_{xk}\right\rangle \left\langle {\psi }_{xk}\right|/{d}_{{\rm{A}}}\}}_{k}\}}_{x}$ under the measurements of Bob. Then d_B≥ d_A, and ρ is a MES and a ZUS with respect to ${\mathscr{B}}$.

Thanks to Lemma 3 and Theorem 4, the tests of Alice can verify the assemblage ${\{{\{\left|{\psi }_{xk}\right\rangle \left\langle {\psi }_{xk}\right|/{d}_{{\rm{A}}}\}}_{k}\}}_{x}$, which in turn can verify the MES whenever ${\mathscr{B}}$ is irreducible. In addition, Theorem 4 offers a general recipe for constructing assemblages that are characteristic of MESs. These results establish intimate connections between uncertainty relations, quantum entanglement, and quantum steering, which are of intrinsic interest to foundational studies. Meanwhile, these results are instructive to studying remote state preparation^21,22 and semi-device-independent self testing^{18,23,24,25,26}.

Discussion

ZUSs in the presence of a quantum memory are particular quantum states that can eliminate uncertainties of incompatible von Neumann observables once assisted by suitable measurements on the memory. In this work, we determined all ZUSs with respect to any given set of nondegenerate observables in the presence of a quantum memory. To achieve this goal we introduced several useful tools that apply to an arbitrary set of observables, in sharp contrast with most previous approaches, which only apply to two observables or complementary observables. In addition, we determined the minimum entanglement required to construct a ZUS. Our study shows that all ZUSs are MESs for a generic set of two or more observables even if these observables are only weakly incompatible. In this way, we establish a simple and precise connection between ZUSs and MESs. This connection may shed light on the uncertainty principle in the presence of a quantum memory. It is of intrinsic interest to studying a number of fascinating topics, including the uncertainty principle, quantum entanglement, and quantum steering. Moreover, it has direct applications in semi-device-independent quantum certification and verification, which is currently an active research field.

Methods

ZUSs with least entanglement

Here we determine the minimum entanglement required to construct a ZUS, following the premises and notations in Theorem 2.

Given the basis set ${\mathscr{B}}$ in Theorem 2, define ${{{\Lambda }}}_{{\mathscr{B}}}$ as the CPTP map acting on quantum states on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ that removes coherence between different component subspaces, that is,

$${{{\Lambda }}}_{{\mathscr{B}}}(\rho )=\sum _{a}({P}_{a}\otimes {1}_{{\rm{B}}})\rho ({P}_{a}\otimes {1}_{{\rm{B}}})=\sum _{a}{\rho }_{a}=\bigoplus _{a}{\rho }_{a},$$

(10)

where ρ_a = (P_a ⊗ 1_B)ρ(P_a ⊗ 1_B) and P_a are component projectors defined in Eq. (7). Note that the map ${{{\Lambda }}}_{{\mathscr{B}}}$ can be realized by LOCC. In addition, ρ is a ZUS with respect to ${\mathscr{B}}$ iff ${\rho }_{{\mathscr{B}}}:={{{\Lambda }}}_{{\mathscr{B}}}(\rho )$ is. When ρ is a ZUS, ${\rho }_{{\mathscr{B}}}$ is a direct sum of subnormalized MESs ρ_a according to Theorem 2.

The component vector is defined as

$${\bf{q}}(\rho ,{\mathscr{B}}):={({q}_{a})}_{a},\quad {q}_{a}:=\mathrm{tr}\,[\rho ({P}_{a}\otimes {1}_{{\rm{B}}})]=\mathrm{tr}\,({\rho }_{a});$$

(11)

it is invariant under the local operations of Bob and is very useful to studying the entanglement properties and equivalent classes of ZUSs. Note that ${\rho }_{{\mathscr{B}}}$ and ρ share the same component vector. The following theorem is proved in the Supplementary Information.

Theorem 5 Suppose E is an entanglement measure, then any ZUS ρ with component vector ${\bf{q}}(\rho ,{\mathscr{B}})={({q}_{a})}_{a}$ satisfies

$$\ \ E(\rho )\ge E({\rho }_{{\mathscr{B}}})\ge \sum _{a}{q}_{a}E(\left|{{\Phi }}({r}_{a})\right\rangle )\ge E(\left|{{\Phi }}({r}_{\min })\right\rangle ),$$

(12)

where $\left|{{\Phi }}({r}_{a})\right\rangle$ is a MES of Schmidt rank r_a. The second inequality in Eq. (12) is saturated if E is a convex entanglement measure.

Here ${r}_{a}=\mathrm{tr}\,({P}_{a})$ is the component rank defined in Eq. (7), and ${r}_{\min }=\mathop{\min }\nolimits_{1\le a\le g}{r}_{a}$ is the minimum component rank. Theorem 5 applies to any entanglement measure E that is monotonic under selective and nonselective LOCC. In addition, the lower bounds for E(ρ) only depend on the values of the measure E at pure MESs.

When ${\rho }_{{\mathscr{B}}} \, \ne \, \rho$, the inequality $E(\rho )\ge E({\rho }_{{\mathscr{B}}})$ in Eq. (12) is strict for many entanglement measures, including the entanglement of formation, as shown in Corollary 5 below. To determine least entangled ZUSs, we can assume the condition $\rho ={\rho }_{{\mathscr{B}}}$, so ρ has no coherence between different component subspaces. Such a ZUS is called economical. In addition, the third inequality in Eq. (12) is usually strict unless q_a = 0 when ${r}_{a} \, > \, {r}_{\min }$ (cf. Corollary 6 below). An economical ZUS ρ with q_a = 0 for all ${r}_{a} \, > \, {r}_{\min }$ is called a ZUS with least entanglement (ZUSLE) since it can saturate the ultimate lower bound in Eq. (12) for every convex entanglement measure. Such a state can be expressed as follows,

$$\rho ={\rho }_{{\mathscr{B}}}=\sum _{a| {r}_{a}={r}_{\min }}{\rho }_{a}=\bigoplus _{a| {r}_{a}={r}_{\min }}{\rho }_{a}.$$

(13)

It has no coherence between different component subspaces, and its local support for Alice can only contain component subspaces with the minimum component rank ${r}_{\min }$. The operational significances of ZUSLEs can be summarized as follows.

Corollary 3 Every ZUS on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ with respect to ${\mathscr{B}}$ can be turned into a ZUSLE by LOCC. In addition, all ZUSLEs can be turned into each other by LOCC.

Corollary 4 A ZUS on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ with respect to ${\mathscr{B}}$ is a ZUSLE iff it can be created from $\left|{{\Phi }}({r}_{\min })\right\rangle$ by LOCC.

Corollary 3 follows from Theorem 2 and Corollary 1. Corollary 4 follows from Corollary 3 and Corollary 6 below. This operational characterization of ZUSLEs is independent of specific entanglement measures, which complements the operational definition of ZUSs in the main text.

Corollary 5 Any ZUS ρ with component vector ${\bf{q}}(\rho ,{\mathscr{B}})={({q}_{a})}_{a}$ satisfies ${E}_{{\rm{F}}}(\rho )\ge {\sum }_{a}{q}_{a}{\mathrm{log}\,}_{2}{r}_{a}$. The lower bound is saturated iff $\rho ={\rho }_{{\mathscr{B}}}$.

Corollary 6 Any ZUS ρ with respect to ${\mathscr{B}}$ satisfies ${E}_{{\rm{F}}}(\rho )\ge {\mathrm{log}\,}_{2}{r}_{\min }$, which is saturated iff ρ is a ZUSLE.

Corollary 5 is proved in the Supplementary Information. Corollary 6 follows from Corollary 5 (cf. Theorem 5). When ${\mathscr{B}}$ is irreducible, the bound ${E}_{{\rm{F}}}(\rho )\ge {\sum }_{a}{q}_{a}{\mathrm{log}\,}_{2}{r}_{a}$ reduces to ${E}_{{\rm{F}}}(\rho )\ge {\mathrm{log}\,}_{2}{d}_{{\rm{A}}}$, which is expected in view of Theorem 1 and Lemma 1. In general, the lower bound may be seen as a weighted average of bounds associated with individual irreducible components of ${\mathscr{B}}$. Incidentally, the bounds in Corollaries 5 and 6 still hold if E_F is replaced by any entanglement measure that coincides with E_F on pure states, such as the relative entropy of entanglement²⁷.

Equivalent classes of ZUSs

Here we clarify the equivalent classes of ZUSs under the local operations of Bob. Suppose ρ is a ZUS with respect to ${\mathscr{B}}$ and has a component vector ${\bf{q}}(\rho ,{\mathscr{B}})={({q}_{a})}_{a}$. According to Corollary 2, (cf. Theorem 2, Lemma 1, and Corollary 1), ρ_A is a weighted sum of component projectors,

$${\rho }_{{\rm{A}}}=\sum _{a}\frac{{q}_{a}{P}_{a}}{{r}_{a}}.$$

(14)

Two ZUSs have the same reduced state and thus same measurement statistics for Alice iff they have the same component vector. So the equivalent classes of pure ZUSs are completely characterized by component vectors.

Corollary 7 Two pure ZUSs with respect to ${\mathscr{B}}$ are equivalent iff they have the same component vector.

Given a ZUS ρ with respect to the basis set ${\mathscr{B}}$, denote by ${{\mathcal{H}}}_{{\rm{B}},a}$ the support of ${\mathrm{tr}}_{{\rm{A}}}({\rho }_{a})$ and Q_a the corresponding projector; then Q_a and Q_b are orthogonal whenever a ≠ b by Theorem 2. In addition, we have

$${\rho }_{a}=({1}_{{\rm{A}}}\otimes {Q}_{a})\rho ({1}_{{\rm{A}}}\otimes {Q}_{a}),$$

(15)

$${\rho }_{{\mathscr{B}}}=\sum _{a}({1}_{{\rm{A}}}\otimes {Q}_{a})\rho ({1}_{{\rm{A}}}\otimes {Q}_{a}).$$

(16)

So ρ can be turned into ${\rho }_{{\mathscr{B}}}$ by local operations of Bob. Thanks to Corollary 1, ${\rho }_{{\mathscr{B}}}$ can further be turned into a direct sum of pure MESs of the form ${\bigoplus }_{a}{q}_{a}\left|{{{\Phi }}}_{a}\right\rangle \left\langle {{{\Phi }}}_{a}\right|$, where $\left|{{{\Phi }}}_{a}\right\rangle$ is a normalized MES in ${{\mathcal{H}}}_{{\rm{A}},a}\otimes {{\mathcal{H}}}_{{\rm{B}},a}$ (a product state when r_a = 1). These observations lead to the following corollary, which complements Corollary 7.

Corollary 8 Every ZUS on ${{\mathcal{H}}}_{{\rm{A}}}\otimes {{\mathcal{H}}}_{{\rm{B}}}$ with respect to ${\mathscr{B}}$ can be turned into an economical ZUS with the same component vector by local operations of Bob. Two economical ZUSs are equivalent iff they have the same component vector.

Thanks to Corollary 8, equivalent classes of economical ZUSs with respect to ${\mathscr{B}}$ are in one-to-one correspondence with component vectors, which form a probability simplex of dimension g − 1, where g is the number of irreducible components of ${\mathscr{B}}$. In particular, two ZUSLEs are equivalent iff they have the same component vector. If there is only one component subspace of dimension ${r}_{\min }$, then all ZUSLEs are equivalent.