Entanglement formation in continuous-variable random quantum networks

Abstract

Entanglement is not only important for understanding the fundamental properties of many-body systems, but also the crucial resource enabling quantum advantages in practical information processing tasks. Although previous works on quantum networks focus on discrete-variable systems, light—as the only traveling carrier of quantum information in a network—is bosonic and thus requires a continuous-variable description. We extend the study to continuous-variable quantum networks. By mapping the ensemble-averaged entanglement dynamics on an arbitrary network to a random-walk process on a graph, we are able to exactly solve the entanglement dynamics. We identify squeezing as the source of entanglement generation, which triggers a diffusive spread of entanglement with a "parabolic light cone”. A surprising linear superposition law in the entanglement growth is predicted by the theory and numerically verified, despite the nonlinear nature of the entanglement dynamics. The equilibrium entanglement distribution (Page curves) is exactly solved and has various shapes depending on the average squeezing density and strength.

Introduction

Quantum information science has brought to us capabilities to enhance the performance of computing¹, sensing², and communication^3,4, through entangling local or distant processing nodes. Therefore, a quantum network⁵ that enables entanglement^6,7,8 establishment is important for achieving the promised quantum advantages. The study of entanglement formation and quantum information scrambling has been fruitful in complex systems such as random quantum networks^9,10,11, and circuits^{12,13,14,15,16}, many-body systems^{17,18,19,20,21,22,23,24,25,26}, quantum graphs^27,28,29, models of holography^30,31,32,33, and quantum gravity^{34,35,36,37,38,39,40,41,42,43,44,45,46}. Universal scaling laws and dynamical models of entanglement formation has been established, based on nonlinear surface growth models^12,13. Recently, experimental probing^21,47,48 of scrambling is also made possible; from the quantum network perspective, protocol design^49,50,51,52 for entanglement establishment has also been a recent focus.

The above works, across multiple disciplinaries, mainly focus on entanglement in discrete-variable (DV) systems, which is natural for computing. However, light as the only carrier of quantum information in network transmission, is bosonic and requires a continuous-variable (CV) description. Moreover, various applications in the photonic or microwave domain, including cluster-state-based quantum computing⁵³, quantum sensing applications^{54,55,56,57,58,59,60,61}, and entanglement-assisted communication^62,63, require CV entanglement in the form of Gaussian states⁶⁴. In this regard, noiseless linear amplifiers⁶⁵ and error correction codes^66,67 provide initial tools for CV networking, and an out-of-time-order correlator (OTOC) has revealed a squeezing-dependent butterfly-velocity of operator spreading⁶⁸.

In this paper, we study quantum information scrambling in CV quantum networks (see Fig. 1) focusing on the entanglement formation dynamics. Inspired by the classical statistical theory of complex networks^69,70,71, we consider random quantum networking protocols to enable analytical solutions, through a mapping to a random-walk process on graph. We study the dynamics and equilibrium, of bipartite and multipartite entanglement, on local and general network topologies, as we detail in the following paragraphs.

Fig. 1: Quantum networks and graph random walk.

a Schematic of a quantum network. Through entanglement distribution, the nodes get entangled to enhance communication, sensing and computation tasks. Cyan nodes have squeezers, whereas green nodes do not have. Solid and dashed lines represent quantum and classical links. b Random unitary gates correspond to random walk on a graph. The probability distribution among three output ports (dashed cyan circles) of a photon (cyan circle) initially at the center passing through two beamsplitters is equivalent to that of a random walk with proper transition probabilities. See Section "Mapping to random walk on graphs'' for more details. c A general graph $({\mathcal{G}},{\mathcal{E}})$, where ${\mathcal{G}}$ denotes all the vertices and ${\mathcal{E}}$ denotes all edges. Time evolution of the entanglement entropy between the subsystem ${\mathcal{L}}$ inside the dashed circle (vertices 1–5) and the rest ${\mathcal{R}}$ (vertices 6–9) depends on the random walk on the boundary $\partial {\mathcal{L}}$ (edges 3–6, 4–7, and 5–8). Vertices 3, 4, and 5 form the inner boundary $\partial {{\mathcal{L}}}^{-}$ (vertices of ${\mathcal{L}}$ connected to ${\mathcal{R}}$); vertices 6, 7, and 8 form the outer boundary $\partial {{\mathcal{L}}}^{+}$ (vertices in ${\mathcal{R}}$ but connected to ${\mathcal{L}}$).

We provide an analytical formula connecting the entanglement entropy to weights in the passive linear optical transforms, therefore establishing a mapping between (ensemble-averaged) entanglement dynamics to the probability evolution of a (Markovian) random-walk process on a general graph (see Fig. 1), with a transition matrix determined by the graph connectivity. Through the mapping, we also connect the scrambling time—the time it takes for the entire system to be maximally entangled—directly to the mixing time of the random walk.

At infinite time, the equilibrium entanglement distribution (Page curve^72,73,74) can be solved analytically from the stationary state of the random walk. Surprisingly, the Page curve is independent of the topology of the network, as long as the graph is connected. And, in general, it depends on two statistical properties of the quantum network—the squeezer’s density and the average squeezing strength.

To go beyond the bipartite characterization of entanglement through entanglement entropy, we also give an operational witness of multipartite entanglement, based on the precision in distributed sensing protocols⁶⁷. Maximum values of the entanglement witness are achieved towards the late time, therefore verifying the full scrambling of the entire network. This entanglement witness adds to the toolbox of CV entanglement characterization, including the separability criteria^{8,75,76,77,78,79}, entanglement of formation^{80,81,82,83,84}, tangle and cotangle^85,86,87, and Rényi entropy-based measures⁸⁸ (see Supplementary Note 1 for details).

Although our theory works for general graphs, we also apply to networks respecting “locality” of interactions—D-dimensional Cartesian graphs where links only exist between nearest neighbors (see Fig. 2). In this regard, we identify a diffusive "parabolic entanglement light cone” at the early time, which divides the regions with almost no entanglement and regions with substantial entanglement. After the parabolic light cone reaches each node, there is a period of entanglement sudden growth, where the entanglement entropy quickly gets close to its equilibrium value. In the end, there is a long period of saturation, determined by the mixing time ~M² quadratic in the length M on each dimension.

Fig. 2: Schematic of the Cartesian quantum networks and the corresponding heatmap of ensemble-averaged entanglement entropy.

a–d are for the 1-D case and e–g are for the 2-D case. In the schematic plots, cyan squares are single-mode squeezers, whereas the orange rectangles are the two-mode beamsplitters (combining phase shifters). In the entanglement plots, the green dashed line represents the parabolic entanglement light cone (t = T₁) and the black dashed line represents the characteristic time-scale T₁ + T₂ of entanglement growth. a The 1-D hopping quantum network. Each empty circle denotes a local mixing operation by beamsplitters and the dashed arrows indicate the transmission of optical modes in the network. The cyan lines indicate the linear light cone starting from the vertex with the single-mode squeezer. b The corresponding 1-D local circuit. The red dashed line represents the linear light cone from the center. c, d Entanglement evolution of the single-squeezer (r = 8 at the center shown as a cyan box) and multiple-squeezer case (r₁ = 5 at $\tilde{x}=0,t=0$, r₂ = 3 at $\tilde{x}=-0.35,t=200$, and r₃ = 7 at $\tilde{x}=0.2,t=500$, shown as cyan boxes). Number of modes M = 2N + 1 = 201. e, f The 2-D Cartesian graph and its corresponding repeating time steps. g Snapshots of entanglement entropy in 2-D Cartesian of 25 × 25 modes at t = 4, 12, 20, ∞. Single squeezer of r = 5 is placed at the center of system at t = 0. Subsystem ${\mathcal{L}}$ is chosen to be each mode at x = (x₁, x₂). Results with alternative choices of ${\mathcal{L}}$ can be found in Fig. 5e, f.

Our theory framework provides a complement to the DV counterparts^{12,13,14,15,16,23}. And our results provide insights into not only CV quantum networks being engineered, but also quantum information scrambling in various physical systems, as any form of bosonic radiation is intrinsically CV.

Results

Modeling and main results

Our overall goal is to characterize generic entanglement formation dynamics towards equilibrium in a CV quantum network (see Fig. 1 for a schematic). In general, a quantum network can have complicated topology, which makes the problem difficult. Moreover, each node can possess multiple optical modes, and perform local operations (LO) coordinated by classical communication (CC) to entangle them. Considering the optical modes, we can reduce a general entanglement generation protocol to a quantum circuit on a graph, as we illustrate in an one-dimensional (1-D) hopping quantum network in Fig. 2a. To establish entanglement, each node performs the following protocol repetitively: it receives a light mode from a neighbor, which gets entangled with a stored mode through a local unitary; then, it sends out a mode to another neighbor and stores one mode locally. For simplicity, the nodes send light to the left and right neighbors alternatively in even and odd steps. If we focus on the dynamics of the optical modes, the above protocol reduces to a 1-D local circuit in Fig. 2b, where local gates apply alternatively on the light modes⁶⁸.

The transmission links in a quantum network are in general lossy. To cope with loss, error correction⁶⁶ can be applied in each link transmission. On the physical layer, this means including additional components that seemingly complicate the analyses. However, on the logical layer, up to some small residual errors from imperfect error correction, the state being protected is identical to the state being generated in a lossless quantum network, as demonstrated in ref. ⁶⁷ for sensing purposes. Therefore, we start with the lossless case.

With the mapping between quantum networks and quantum circuits in mind, we specify the setup of the circuits on an arbitrary (undirected) graph (see Fig. 1c). In general, the topology can be described by an undirected graph $({\mathcal{G}},{\mathcal{E}})$, where ${\mathcal{G}}$ denotes the set of all vertices, each described by a coordinate system x. Since unconnected components can simply be regarded as two separate networks, we consider connected graph without loss of generality. The set of edges ${\mathcal{E}}$ can be described by a generalized connection matrix ${E}_{{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}$. When ${E}_{{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}=1$, the vertices ${\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}$ are connected by an edge $\overline{{\boldsymbol{x}}{{\boldsymbol{x}}}^{\prime}}$, zero when not connected. For simplicity, we write the set of vertices that are directly connected to x (neighbors) as ${\mathcal{N}}({\boldsymbol{x}})$. We are interested in the entanglement between a set of vertices ${\mathcal{L}}$ and the rest ${\mathcal{R}}={\mathcal{G}}\backslash {\mathcal{L}}$.

Unitaries are applied on the edges ${\mathcal{E}}$. We separate the edges into disjoint sets ${\{{{\mathcal{E}}}_{k}\}}_{k = 1}^{K}$, such that the edges in each set ${{\mathcal{E}}}_{k}$ do not have common vertices. The dynamics repeat in a period of K steps; in the k-th step of each period, one applies unitaries ${U}_{t,{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}$ on each edge $\overline{{\boldsymbol{x}}{{\boldsymbol{x}}}^{\prime}}\in {{\mathcal{E}}}_{k}$. The particular separation of the unitaries is not essential to the dynamics and equilibrium. As an example, in a 1-D local circuit, K = 2 and we alternative between gates {U_t,k,k+1} on k odd and even; in a 2-D local circuit, we have K = 4, as shown in Fig. 2f.

To produce the Gaussian states that enable various applications in communication, sensing, and computing, we consider Gaussian unitaries⁶⁴, which are unitaries generated by Hamiltonians that are second order in the quadrature operators (see details in Supplementary Note 2). Gaussian unitaries include squeezing, which creates asymmetry in quadrature noises; and passive linear optics, which includes beamsplitters and phase-shifters.

Squeezing is essential for entanglement generation. However, as an “active” component, squeezing is relatively difficult to implement. Thus, we consider the gates $\{{U}_{t,{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}\}$ to be passive linear-optics gates. And squeezing operations are added in between in a sparse way. As an example, in Fig. 2b, to establish entanglement, in this case a single vertex performs a squeezing operation (the cyan box), and then entanglement is generated by passing it around through passive components (the orange boxes), with vacuum on the other input modes.

We expect random protocols to reveal universal characteristics, therefore we choose the passive linear optics gates $\{{U}_{t,{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}\}$ to be Haar random (see details in Supplementary Note 2). This is also justified by the following reasons: (1) In classical complex network theory^69,70,71, various networks can be modeled as random networks with a proper degree distribution. (2) In condensed matter theory, random quantum circuits and Hamiltonian systems^{12,13,14,15,16,23} are able to capture the essential quantum information spreading features in generic many-body interacting systems. (3) In real quantum networks, the form of entanglement required can be complicated, depending on the purpose, e.g., the weights of the global parameter of interest in a distributed sensing protocol⁵⁸.

We aim to characterize the entanglement dynamics in the above random circuits. The entanglement entropy, measured by von Neumann entropy or Rényi entropy, can be numerically evaluated efficiently (see details in Supplementary Note 3). Two 1-D examples of time evolution of von Neumann entropy between the left part ${\mathcal{L}}=[-N,x]$ and the right part ${\mathcal{R}}=[x+1,N]$ of the system are given in Fig. 2c, d. In Fig. 2c, we have a single squeezer at the center in the first step, which is identical to the case depicted in Fig. 2b. The entanglement entropy grows diffusively from the source of squeezing. Different from the DV case, we can identify a parabolic entanglement light cone (green lines), which is the boundary between regions with substantial entanglement and regions with almost-zero entanglement. These phenomena can also be found in higher dimensional random local circuits, as shown in Fig. 2g for the 2-D case. When choosing a subsystem ${\mathcal{L}}$ as an individual mode at (x₁, x₂), we can see similar parabolic entanglement light cone (green dashed).

As shown in Fig. 1b and detailed in Section "Mapping to random walk on graphs”, the above entanglement dynamics can be solved by mapping to a random walk of the squeezed vacuums on a graph. Although involving non-classical states with squeezing and entanglement, the mapping can be understood through the evolution of probability distribution of a single photon after going through the two beamsplitters. We can therefore obtain the exact ensemble-averaged entanglement entropy $\left\langle S({\mathcal{L}},t)\right\rangle$ as a function of the total probability ${\eta }_{{\mathcal{L}},t}$ of having the walker in region ${\mathcal{L}}$ in the corresponding random walk,

$$S({\eta }_{{\mathcal{L}},t})=g\left[\left(\sqrt{1+4{\eta }_{{\mathcal{L}},t}(1-{\eta }_{{\mathcal{L}},t}){\sinh }^{2}(r)}-1\right)/2\right],$$

(1)

where g(x) is the (von Neumann or Rényi) entropy of a thermal state with mean photon number x (see details in Supplementary Note 3) and r is the original squeezing strength. Note that the mapping holds for arbitrary graphs beyond the local Cartesian graphs shown above. The scrambling time—the time that the entire system becomes maximally entangled—can be calculated by the mixing time of the random walk. The mapping also gives the Page curves—the late-time equilibrium entanglement entropy

$$\left\langle S({\mathcal{L}},\infty )\right\rangle =S(| {\mathcal{L}}| /| {\mathcal{G}}| )$$

(2)

as the CV analog to Page curve, while the fluctuation can be solved as $\propto | {\mathcal{L}}| | {\mathcal{R}}|$. Moreover, when there are multiple squeezers, we can regard the entanglement dynamics as the superposition of all single-squeezer dynamics, as depicted in Fig. 2d. Therefore, combining the results, we have a complete understanding of the entanglement dynamics in a CV quantum network.

Statistical theory of quantum networks

Now we present a statistical theory of the entanglement growth. We will focus on the single squeezer case in Fig. 2c, whereas the extension to multiple squeezers is presented in the later part. We first introduce the mapping between random unitary circuits and random walk on a graph, which allows us to solve the Page curves and scrambling time for general graphs. Explicit closed-form solutions can be obtained for local Cartesian graphs of an arbitrary dimension. Finally, we present the entanglement witness for multipartite entanglement.

Mapping to random walk on graphs

Consider the entire unitary evolution U(t) of the random circuit. In the single-squeezer case, the mode annihilation operator a_x,t at vertex ${\boldsymbol{x}}\in {\mathcal{G}}$ experiences a passive transform, which in general can be expressed as

$${a}_{{\boldsymbol{x},t}}={e}^{i{\theta }_{{\boldsymbol{x},t}}}\sqrt{{w}_{{\boldsymbol{x},t}}}{a}_{{\rm{SV}}}+{\rm{vac}},$$

(3)

where mode a_SV is in a squeezed-vacuum (SV) state with strength r and “vac” denotes all vacuum terms that complete the commutation relation. Here the phase θ_x,t is entirely random, and the positive weights ${{\boldsymbol{w}}}_{t}\equiv {\{{w}_{{\boldsymbol{x},t}}\}}_{{\boldsymbol{x}}\in {\mathcal{G}}}$ describe the overall energy splitting of the single SV among all modes.

For any subsystem ${\mathcal{L}}$, we can design a passive linear optics circuit to concentrate all the squeezing parts to a single mode

$${a}_{{\mathcal{L}},t}=\sqrt{{\eta }_{{\mathcal{L}},t}}{a}_{{\rm{SV}}}+{\rm{vac}},$$

(4)

with the total transmissivity

$${\eta }_{{\mathcal{L}},t}= \mathop {\sum}\limits_{{\boldsymbol{x}}\in {\mathcal{L}}}{w}_{{\boldsymbol{x},t}},$$

(5)

and all other modes are in vacuum required by energy conservation. Because unitary operations preserve entropy, the entanglement entropy of ${\mathcal{L}}$ can be calculated from the entropy of mode ${a}_{{\mathcal{L}},t}$ as

$$S\left({\mathcal{L}},t\right)=S\left({\eta }_{{\mathcal{L}},t}\right)$$

(6)

$$\simeq \frac{1}{2}{\mathrm{log}\,}_{2}\left[{\eta }_{{\mathcal{L}},t}\left(1-{\eta }_{{\mathcal{L}},t}\right)\right]+\frac{1}{\mathrm{ln}\,2}\left(r+1\right)-1,$$

(7)

where $S({\eta }_{{\mathcal{L}},t})$ is defined in Eq. (1). We will focus on von Neumann entropy, but all of our results can be adapted to Rényi entropy easily. At the large squeezing limit of $\sqrt{{\eta }_{{\mathcal{L}},t}(1-{\eta }_{{\mathcal{L}},t})}{e}^{r}\gg 1$, for von Neumann entropy we have Eq. (7) to the leading order. When ${\eta }_{{\mathcal{L}},t}=0,1$, subsystem ${\mathcal{L}}$ has zero or entire portion of the SV, indeed from Eq. (6) we have $S\left({\mathcal{L}},t\right)=0$. When ${\eta }_{{\mathcal{L}},t}=1/2$, we have the maximum entropy ${S}_{0}(r)=g({\sinh }^{2}(r/2))$.

So far we have the exact result $S\left({\eta }_{{\mathcal{L}},t}\right)$ of the entanglement entropy of an arbitrary subsystem ${\mathcal{L}}$, given the weights w_t (which determines ${\eta }_{{\mathcal{L}},t}$) obtained in each random circuit realization. Owing to the self-averaging in the random circuit, we expect

$$\left\langle S\left({\eta }_{{\mathcal{L}},t}\right)\right\rangle =S\left(\left\langle {\eta }_{{\mathcal{L}},t}\right\rangle \right)$$

(8)

up to corrections that decay with the system size. Thus, we have reduced the problem of solving the ensemble-averaged entanglement dynamics to solving the ensemble-averaged dynamics of the weights $\left\langle {{\boldsymbol{w}}}_{t}\right\rangle$.

We start by focusing on a single gate ${U}_{t,{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}$ on the modes at x and ${{\boldsymbol{x}}}^{\prime}$. By considering the Haar random ensemble averaging, we can derive the exact equation of motion of the weights as (see details in Supplementary Note 4)

$$\left\langle {w}_{{\boldsymbol{x}},t+1}\right\rangle =\left\langle {w}_{{{\boldsymbol{x}}}^{\prime},t+1}\right\rangle =\frac{1}{2}\left(\left\langle {w}_{{\boldsymbol{x}},t}\right\rangle +\left\langle {w}_{{{\boldsymbol{x}}}^{\prime},t}\right\rangle \right).$$

(9)

The overall dynamics alternates in K steps, in the k-th step the transition of Eq. (9) on all edges in ${{\mathcal{E}}}_{k}$ is applied.

An immediate observation from Eq. (9) is that the change of the entanglement entropy of ${\mathcal{L}}$, determined by the total weights $\left\langle {\eta }_{{\mathcal{L}},t}\right\rangle$, is related only to the boundary $\partial {\mathcal{L}}$ (schematic in Fig. 1c), in the sense that

$$\left\langle {\eta }_{{\mathcal{L}},t+1}\right\rangle -\left\langle {\eta }_{{\mathcal{L}},t}\right\rangle =\frac{1}{2}\left[ \mathop {\sum}\limits_{{\boldsymbol{x}}\in \partial {{\mathcal{L}}}^{+}}\left\langle {w}_{{\boldsymbol{x},t}}\right\rangle - \mathop {\sum}\limits_{{\boldsymbol{x}}\in \partial {{\mathcal{L}}}^{-}}\left\langle {w}_{{\boldsymbol{x}},t}\right\rangle \right],$$

(10)

which equals the net flow of the weights from the vertices on the outer boundary $\partial {{\mathcal{L}}}^{+}$ toward ${\mathcal{L}}$ and the weights from the inner boundary $\partial {{\mathcal{L}}}^{-}$ out from ${\mathcal{L}}$.

Another observation is that the weights update rule in Eq. (9) also describes the probability evolution of a lazy symmetric random-walk step, where the walker has half probability of staying and half probability of taking a step along $\overline{{\boldsymbol{x}}{{\boldsymbol{x}}}^{\prime}}$ (see Fig. 3). Combining the K steps, the underlying transition matrix for the weights

$${{\mathbb{E}}}_{{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}=\mathop{\prod }\limits_{k=1}^{K}\frac{1}{2}\left(I+{E}_{k,{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}\right),$$

(11)

where I is the identity matrix and ${E}_{k,{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}$ describes the adjacency matrix for the corresponding graph $({\mathcal{G}},{{\mathcal{E}}}_{k})$ (an isolated mode is regarded as a vertex with a loop). Eq. (11) describes a modified symmetric random walker on the graph (see Fig. 3), with K steps combined to implement a single random-walk step from the current position x to all neighbors ${\mathcal{N}}({\boldsymbol{x}})$ (including x) with equal probability.

Fig. 3: Random circuits and the corresponding modified random walk in 1-D and 2-D Cartesian graphs ${{\mathcal{G}}}_{D}$.

a, b Schematic of a K-step cycle of gates that implements a random-walk step, independent on each direction. c, d Examples of the modified random walk in 1-D and 2-D, following the rule in Eq. (11). In 1-D, the time trajectories up to t = 500 of different instances are plotted in different colors. In 2-D, the trajectories are shown up to t = 5000 for three different instances.

Utilizing the K-step transition matrix, the ensemble-averaged weights can be solved at any time t as

$$\left\langle {{\boldsymbol{w}}}_{t}\right\rangle =\left\langle {{\boldsymbol{w}}}_{0}\right\rangle {{\mathbb{E}}}_{{\boldsymbol{x}},{{\boldsymbol{x}}}^{\prime}}^{[t/K]},$$

(12)

with the initial condition $\left\langle {{\boldsymbol{w}}}_{0}\right\rangle ={\delta }_{{{\boldsymbol{x}}}_{0}}$ as the Kronecker delta at the squeezer position x₀. Thus, one can obtain $\left\langle {\eta }_{{\mathcal{L}},t}\right\rangle$ and the exact result of $S(\left\langle {\eta }_{{\mathcal{L}},t}\right\rangle )$ from Eq. (6) on any graph.

We give examples of the random walk in Fig. 3 in 1-D and 2-D Cartesian graphs, whose entanglement evolution can be found in Fig. 2. For the later use, we also introduce a general D dimensional Cartesian lattice ${{\mathcal{G}}}_{D}$, with the coordinates x = (x₁, ⋯, x_D) on a grid (x_d ∈ [ − N, N]). The total number of modes is $| {{\mathcal{G}}}_{D}| ={M}^{D}$, with M = 2N + 1 modes on each dimension.

In the following, we will consider the equilibrium and the dynamics. Some results hold for general graphs, while some analytical results are made possible by considering the special case of ${{\mathcal{G}}}_{D}$.

Page curves and scrambling time

In this section, we focus on the Page curves—the equilibrium entanglement distribution at infinite time. In order to share entanglement, squeezers are applied, which are then followed up by the random beamsplitters and phase shifters. As the layers of gates increases, the overall passive linear transform will approach the Haar measure (see details in Supplementary Note 2). Therefore, we can regard the equilibrium entanglement distribution as the CV analog to Page curves.

Considering the mapping from the circuit to the random walk, the equilibration of the entanglement also corresponds to the full mixing of the random walk on the graph. Assuming the full connectivity of the graph, owing to the special transform matrix in Eq. (11), the equilibrium (stationary) state of weights is uniform, i.e.,

$$\left\langle {{\boldsymbol{w}}}_{{\boldsymbol{x,\infty }}}\right\rangle =1/| {\mathcal{G}}| ,$$

(13)

where $| {\mathcal{G}}|$ is the total number of vertices, despite how one arranges the set of edges ${{\mathcal{E}}}_{k}$. Therefore, the total transmissivity (i.e., total weights)

$$\left\langle {\eta }_{{\mathcal{L}},\infty }\right\rangle =| {\mathcal{L}}| /| {\mathcal{G}}| .$$

(14)

In fact, assuming fully random weights from a Haar random unitary, one can obtain the probability density of total weights as (see details in Supplementary Note 5)

$$P({\eta }_{{\mathcal{L}},\infty }=\eta )\propto {\eta }^{| {\mathcal{L}}| -1}{(1-\eta )}^{| {\mathcal{R}}| -1}.$$

(15)

From Eq. (6), the Page curve is therefore given by

$$\left\langle S({\mathcal{L}},\infty )\right\rangle =S(\frac{| {\mathcal{L}}| }{| {\mathcal{G}}| })$$

(16)

$$\simeq \frac{1}{2}{\mathrm{log}\,}_{2}\left[\frac{| {\mathcal{L}}| }{| {\mathcal{G}}| }\left(1-\frac{| {\mathcal{L}}| }{| {\mathcal{G}}| }\right)\right]+\frac{1}{\mathrm{ln}\,2}\left(r+1\right)-1.$$

(17)

The maximum is achieved at $| {\mathcal{L}}| /| {\mathcal{G}}| =1/2$, which equals $\left\langle {S}_{0}(r)\right\rangle$ introduced following Eq. (6). The second equality is the leading order result similar to Eq. (7).

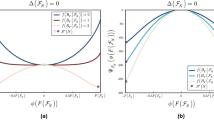
Note that in terms of Page curves, the graph topology is irrelevant as the entire dynamics is equivalent to a single passive global Haar unitary; therefore, it then suffices to verify our theory of Page curves in ${{\mathcal{G}}}_{1}$, which allows simple visualization. In the ${{\mathcal{G}}}_{1}$, consider a subsystem ${\mathcal{L}}$ with x + N modes, we have $\left\langle {\eta }_{{\mathcal{L}},\infty }\right\rangle =| {\mathcal{L}}| /| {\mathcal{G}}| =(x+N)/(2N+1)\simeq \tilde{x}+1/2,$ where we introduced $\tilde{x}=x/2N\in [-0.5,0.5]$. Therefore, it is convenient to choose the parameterization $\tilde{x}$. Fig. 4a plots $\left\langle S(\tilde{x},\infty )\right\rangle$ for various squeezing values of r and system sizes of M, where we see perfect overlapping among curves with identical r for different system sizes. And they all agree with Eq. (16) very well, as shown in Fig. 4b. As a by-product, the maximum entanglement—the maximum height of the Page curve $\max{}_{x}\left\langle S(x,\infty )\right\rangle$—agrees with the theory prediction $\left\langle {S}_{0}(r)\right\rangle$ following Eq. (6), as shown in Fig. 4b inset.

Fig. 4: Page curves.

a Page curves with a single squeezer, r = 2, 5, 8 shown by the red, blue and green lines separately. The overlapping scatter points, solid, dashed, dash-dot, and dotted lines corresponds to system of M = 21, 101, 201, 301, 401. Error bars representing the numerical precision for the case M = 21 lie in the empty circles. Invisible shadow area shows the numerical precision. b Re-scaled Page curves of those in a. Black dashed lines show the theory results of Eq. (16). The inset is the dependence of maximum height S₀ on the single squeezer r. Numerical results in system M = 201 (orange dots) and analytical results (black dashed line) Eq. (6) with ${\eta }_{{\mathcal{L}},t}=1/2$ agree well.

The same analyses can be extended to derive the fluctuations of the equilibrium entanglement entropy, where we find the variance $\propto | {\mathcal{L}}| | {\mathcal{R}}|$. The analytical formula are then numerically verified (see Supplementary Note 6 for details).

The entanglement scrambling time—the time for the system to be maximally entangled and reach the equilibrium is an important quantity for many physical problems, especially those related to the black hole^34,39. In the CV quantum network, this scrambling time can be directly obtained from the mixing time ${t}_{\epsilon }^{\star }$ of random walks on a graph, where the probability measure (weights) get ϵ-close to the stationary state in Eq. (13). Utilizing the mixing time, we can obtain the scaling of the scrambling time as ${t}_{\epsilon }^{\star }\propto D{M}^{2}$ (see details in the Supplementary Note 7).

Closed-form solutions to Cartesian graphs

With the understanding of the equilibrium Page curves, we now proceed to characterize the dynamical evolution towards the equilibrium. We will focus on the Cartesian graphs ${{\mathcal{G}}}_{D}$, which allows closed-form solutions. In particular, we identify a parabolic entanglement light cone, followed by an entanglement sudden growth phenomenon in CV networks, as has already been shown in Fig. 2.

In Cartesian graphs, the random walk analog to Eq. (9) can be understood as independent along each dimension. Thus, we modify the Pascal’s triangle from a usual random walk to obtain the solution

$$\left\langle {{\boldsymbol{w}}_t} \right\rangle ^{({\mathrm{Bi}})} = \left\{ {\frac{1}{{2^{t + D}}}\mathop {\prod }\limits_{d = 1}^D \left( {\begin{array}{*{20}{c}} {n_t} \\ {n_{x_d,t}} \end{array}} \right){\mathrm{ }}} \right\}_{x_d = - N},$$

(18)

with ${n}_{t}=[t/D],{n}_{{x}_{d},t}=[\frac{{x}_{d}}{2}]+[\frac{t}{2D}]$ and $\left(\begin{array}{c}a\\ b\end{array}\right)$as the binomial factor of a-choose-b.

With the weights in hand, we can calculate the entanglement entropy of an arbitrary subsystem ${\mathcal{L}}$. For example, we can consider ${\mathcal{L}}=\{{{\boldsymbol{x}}}^{\prime}| {x}_{d}^{\prime}\,<\,{x}_{d},1\le d\le D\}$, i.e., the system is cut into two parts by a high-dimensional plane. Then, we can obtain the ensemble-averaged total transmissivity

$${\left\langle {\eta }_{{\mathcal{L}},t}\right\rangle }^{({\rm{Bi}})}= \mathop {\sum}\limits_{{\boldsymbol{x}}\in {\mathcal{L}}}{\left\langle {w}_{{{\boldsymbol{x}}}^{\prime},t}\right\rangle }^{({\rm{Bi}})}=\mathop{\prod }\limits_{d=1}^{D}\left[1-\frac{1}{{2}^{t}}\left(\begin{array}{c}{n}_{t}\\ 1+{n}_{{x}_{d},t}\end{array}\right)\times F(1,1-{n}_{t}+{n}_{{x}_{d},t},2+{n}_{{x}_{d},t},-1)\right],$$

(19)

where F is the hypergeometric function. Numerical evaluation (see details in Supplementary Note 8) shows a good agreement up to rounding errors between the exact solution of weights $\left\langle {{\boldsymbol{w}}}_{t}\right\rangle$ from numerically solving Eq. (12) and the binomial solution of weights ${\left\langle {{\boldsymbol{w}}}_{t}\right\rangle }^{({\rm{Bi}})}$ in Eq. (18). Moreover, in Fig. 5a–d we verify the agreement between the entanglement dynamics via numerically solving Eq. (12)) and real random circuit evolution.

Fig. 5: Ensemble-averaged entanglement entropy evolution in Cartesian graphs.

Comparison between theory (blue) vs numerical results (red) at various times (indicated by the arrows) for 1-D shown in (a, b) and 2-D shown in (c, d). e, f are 2-D heatmap plots of entanglement entropy at various times till equilibrium. Details are given as follows; a, b A 1-D system of $| {\mathcal{G}}| =501$ with a single squeezer r = 5 placed (a) at the center and (b) at x = −200. c–f A 2-D graph of 25 × 25 modes with a single squeezer r = 5 placed at the center. Subsystem ${\mathcal{L}}=[-12,{x}_{1}]\times [-12,{x}_{2}]$ in (c) and (e); whereas ${\mathcal{L}}=[-| {x}_{1}| ,| {x}_{1}| ]\times [-| {x}_{2}| ,| {x}_{2}| ]$ in (d) and (f). To enable the comparison, in (c) and (d) we choose x₂ = x₁ to reduce to 1-D plots. e, f Area surrounded by red dashed lines shows the subsystem ${\mathcal{L}}$. Brown dots represent the spots with maximal entanglement in equilibrium state (up to numerical precision). Indeed, in the subfigure of (e) with t = ∞ the equi-entanglement line has the shape of (x₁ + N)(x₂ + N) = M²/2, whereas in the subfigure of (f) with t = ∞ it is 4x₁x₂ = M²/2. The error bar represents the numerical precision in the averaging.

In general, the entanglement dynamics highly depend on the choice of subsystem ${\mathcal{L}}$. We consider the 2-D case as an example. In Fig. 2g, ${\mathcal{L}}$ is chosen as each single mode at (x₁, x₂). There, we can see a clear light cone similar to the 1-D case. Here, we consider two alternative choices. First, as an analog to the 1-D choice, we can choose rectangles on the corner, as shown in Fig. 5e. We see a gradual saturation to the equilibrium, where entanglement entropy along $({x}_{1}+N)({x}_{2}+N)={\rm{constant}}$ are about equal, as the total weights ${\eta }_{{\mathcal{L}},t}$ are equal along this line. Second, we can choose rectangles centered at the center. In Fig. 5f, We can also see gradual saturation to equilibrium, where now the entanglement entropy along $| {x}_{1}| | {x}_{2}| ={\rm{constant}}$ are equal.

In the above, we see the entanglement entropy from the exact ensemble-averaged evolution of Eq. (12) (combined with Eq. (6)) and the actual results from numerically solving the entropy agree well, therefore verifying the underlying random-walk model. Taking the continuum limit, the binomial distribution can be approximated as Gaussian and the system is governed by a diffusive PDE (see details in Supplementary Note 8). Below, we further address the parabolic entanglement light cone.

Parabolic entanglement light cone and sudden growth

We now proceed to consider the entanglement evolution. One of such an evolution is depicted in Fig. 2c, where we see entanglement diffusively spreads from the source at the origin. We can introduce a parabolic entanglement light cone (green lines) and a wave front of the entanglement sudden growth (black lines), as will be explained in the following paragraphs.

To further understand the dynamics, we focus on particular modes and consider $\left\langle S(x,t)\right\rangle$ as a function of t (see Fig. 6a for examples). We observe a three-stage evolution: (1) In the first period 0 ≤ t < T₁, the entanglement $\left\langle S(x,t)\right\rangle$ is almost zero. This is the time period before the parabolic entanglement light cone reaches location x. As we see in Fig. 2c, the green curves show the threshold T₁ for spots at different distances ${{\Delta }}\tilde{x}$ to the initial squeezer—a parabolic entanglement light cone much slower than the usual linear light cone of operator spreading. (2) In the second period T₁ ≤ t < T₁ + T₂, the parabolic entanglement light cone reaches the spot and causes a rapid increase in $\left\langle S(x,t)\right\rangle$, after which $\left\langle S(x,t)\right\rangle$ gets close to $\left\langle S(x,\infty )\right\rangle$. As we see in Fig. 2c, the black curve depicts the threshold T₁ + T₂ for spots at different distances ${{\Delta }}\tilde{x}$. The parabolic shape again indicates a diffusion behavior. (3) In the last period, T₁ + T₂ ≤ t, $\left\langle S(x,t)\right\rangle$ gradually saturates towards $\left\langle S(x,\infty )\right\rangle$.

Fig. 6: Evolution of entanglement entropy of various spots in a 1-D system.

Squeezer r = 6 is placed at the center of the M = 801 modes. Thresholds for determining T₁ and T₂ is 1% and 70% of the static value. a Time evolution of entanglement entropy at different spots. T₁ and T₂ for the mode at x = −350 are labeled. Shadow areas show the standard deviation of the time evolution curves. b Dependence of T₁ + T₂ and T₁ on their relative distance to the squeezer ${{\Delta }}\tilde{x}$ represented by black and green lines. Solid lines represent the fitting results $\sim \!{({{\Delta }}\tilde{x})}^{2}$. The dots represent T₁, T₂ for the ensemble-averaged entropy $\left\langle S(x,t)\right\rangle$, whereas the error bar indicates the precision due to finite sample size. The background heatmap shows the entropy distribution $\left\langle S(x,t)\right\rangle$ among the system.

This parabolic light cone can be explained by our statistical theory. We want a constant fraction of the maximum entanglement $\epsilon {S}_{0}(r)=S({\eta }_{{\mathcal{L}},t})$ in Eq. (6), combining with Eq. (19) we can solve T₁, T₁ + T₂ precisely, despite the analytical formula being lengthy, one immediately recognizes the scaling

$${T}_{1},{T}_{2} \sim {({{\Delta }}\tilde{x})}^{2}f(r),$$

(20)

with some function f of the squeezing strength r. Indeed, as shown by Fig. 6b, the green curve (parabolic entanglement light cone) and the black curve (entanglement sudden growth) both agrees well with the quadratic fitting. This is indeed consistent with the OTOC diffusion identified in ref. ⁶⁸, revealing a universal behavior intrinsic to CV quantum networks and absent in DV circuits^12,13.

Growth of multipartite entanglement

So far, we have focused on bipartite entanglement between a subsystem ${\mathcal{L}}$ and its complement ${\mathcal{R}}$. In quantum networks, many applications often require multipartite entanglement, which is in general difficult to characterize⁸⁹. Here, we take an operational approach from a quantum sensing perspective. An important application of the entanglement generated in such a random quantum network is distributed sensing^58,59,60,61, where multipartite entanglement enables an improvement in the measurement sensitivity. In the case of measuring uniform real displacements of amplitude α on all modes, one can prove that considering a total mean photon number $| {\mathcal{G}}| {N}_{S}$, the optimum $| {\mathcal{G}}|$-mode separable state can only offer a variance

$${V}_{{\rm{C}}}=\frac{1}{4}\frac{1}{| {\mathcal{G}}| {(\sqrt{{N}_{S}+1}+\sqrt{{N}_{S}})}^{2}} \sim \frac{1}{16| {\mathcal{G}}| {N}_{S}}$$

(21)

in estimating the displacement α (the standard quantum limit). Therefore, beating the above precision limit is an evidence of entanglement. In fact, one can show that the optimum precision attainable by all entangled state is

$${V}_{{\rm{E}}}=\frac{1}{4}\frac{1}{| {\mathcal{G}}| {(\sqrt{| {\mathcal{G}}| {N}_{S}+1}+\sqrt{| {\mathcal{G}}| {N}_{S}})}^{2}} \sim \frac{1}{16| {\mathcal{G}}{| }^{2}{N}_{S}},$$

(22)

which possesses the Heisenberg scaling of ${V}_{{\rm{E}}} \sim 1/| {\mathcal{G}}{| }^{2}$ that is only possible with multipartite entanglement. Therefore, we can define an entanglement witness for any $| {\mathcal{G}}|$-mode state ρ with total energy $| {\mathcal{G}}| {N}_{S}$ as

$${\mathcal{E}}(\rho )=\mathop{\max }\limits_{{{\rm{LOCC}}}^{\prime}}{\mathrm{log}\,}_{2}\left({V}_{{\rm{C}}}/V(\rho )\right),$$

(23)

where V(ρ) is variance achievable by performing energy-conserved LOCC on the input ρ (hence ${{\rm{LOCC}}}^{\prime}$). We maximize over all such LOCC schemes. We have ${\mathcal{E}}(\rho )=0$ for all separable states, as one can simply prepare the optimum separable state in the LOCC and discard the original input, and ${\mathcal{E}}(\rho )\le {\mathrm{log}\,}_{2}({V}_{{\rm{C}}}/{V}_{{\rm{E}}}) \sim {\mathrm{log}\,}_{2}| {\mathcal{G}}|$ for all states. Moreover, similar to Eq. (22) the optimum performance given at most K modes being entangled and $| {\mathcal{G}}| {N}_{S}$ total mean photon number is ${\left[4K{(\sqrt{| {\mathcal{G}}| {N}_{S}+1}+\sqrt{| {\mathcal{G}}| {N}_{S}})}^{2}\right]}^{-1}$, one can obtain a lower bound on the number of modes K being entangled as

$$K\ge \frac{{2}^{{\mathcal{E}}(\rho )}| {\mathcal{G}}| {(\sqrt{{N}_{S}+1}+\sqrt{{N}_{S}})}^{2}}{{(\sqrt{| {\mathcal{G}}| {N}_{S}+1}+\sqrt{| {\mathcal{G}}| {N}_{S}})}^{2}} \sim {2}^{{\mathcal{E}}(\rho )}.$$

(24)

Fig. 7: Schematic of the sensing process for multipartite entanglement witness.

LO local operations. CC classical communication. After the energy-preserving LOCC, each mode of the input state goes through a displacement D(α); an estimator of the displacement amplitude $\tilde{\alpha }$ is generated from a joint measurement.

For the state ρ(t) generated in the single-squeezer random network at time step t, we can design an estimator to obtain a lower bound of ${\mathcal{E}}(\rho (t))$. Given the weight {w_x,t} on distributing the SV state to $| {\mathcal{G}}|$ modes, we can design the following measurement protocol. First, we perform a phase rotation on each mode such that the displacements act on the corresponding squeezed quadrature; then we perform homodyne measurements on the corresponding quadratures to obtain the results ${\{{\tilde{\alpha }}_{{\boldsymbol{x,t}}}\}}_{{\boldsymbol{x}}\in {\mathcal{G}}}$. The estimator $\tilde{\alpha }={\sum }_{{\boldsymbol{x}}\in {\mathcal{G}}}\sqrt{{w}_{{\boldsymbol{x}},t}}{\tilde{\alpha }}_{{\boldsymbol{x}},t}/{\sum }_{{\boldsymbol{x}}\in {\mathcal{G}}}\sqrt{{w}_{{\boldsymbol{x}},t}}$, which gives the variance

$$V(t)=\frac{1}{4}\frac{1}{\overline{| {\mathcal{G}}| }{(\sqrt{| {\mathcal{G}}| {N}_{S}+1}+\sqrt{| {\mathcal{G}}| {N}_{S}})}^{2}},$$

(25)

where the effective number of modes $\overline{| {\mathcal{G}}| }={({\sum }_{{\boldsymbol{x}}\in {\mathcal{G}}}\sqrt{{w}_{{\boldsymbol{x}},t}})}^{2}\in [1,| {\mathcal{G}}| ]$ that are entangled provides the advantage.

Combining the weights in Eq. (18), we can obtain the effective entangled mode number for the D dimensional Cartesian graph $\overline{| {\mathcal{G}}| }\simeq {(2{(2\pi t/D)}^{1/2})}^{D}$, which leads to the entanglement witness

$${\mathcal{E}}(\rho (t))\ge {\mathrm{log}}_{2}\left({V}_{{\rm{C}}}/V(t)\right)\simeq \frac{D}{2}{\mathrm{log}}_{2}(8\pi t/D),$$

(26)

before the boundary effect comes in, when the effective modes become comparable to $| {\mathcal{G}}|$ at $t \sim | {\mathcal{G}}{| }^{2}$.

Multiple squeezers: sparse limit

So far, we have focused on random networks with a single squeezer and presented a thorough theory for the entanglement dynamics and equilibrium, via an exact mapping to random walk on a graph. Quantum networks are likely to have multiple squeezers; therefore, we extend our analyses to random networks with multiple squeezers in this section. A surprising linear superposition law is numerically observed and theoretically explained.

We begin with an intuitive example of three squeezers in the 1-D Cartesian graph in Fig. 2d. The overall evolution of the entanglement entropy looks like a linear superposition of three independent squeezers, despite the nonlinearity of the entanglement dynamics. Following this observation, we consider a random circuit ${\mathbb{C}}$ with N_q squeezers at different space-time coordinates ${\{{{\boldsymbol{\xi }}}_{k}^{\star } = ({{\boldsymbol{x}}}_{k}^{\star },{t}_{k}^{\star })\}}_{k = 1}^{{N}_{q}}$, with squeezing strengths ${\{{r}_{k}\}}_{k = 1}^{{N}_{q}}$. Linear superposition (spp) means the entanglement entropy of subsystem ${\mathcal{L}}$, $\left\langle S({\mathcal{L}},t)\right\rangle \simeq \left\langle {S}_{{\rm{spp}}}({\mathcal{L}},t)\right\rangle$, where

$$\left\langle {S}_{{\rm{spp}}}({\mathcal{L}},t)\right\rangle =\mathop{\sum }\limits_{k = 1}^{{N}_{q}}\left\langle {S}_{k}({\mathcal{L}},t)\right\rangle$$

(27)

is a simple sum of the ensemble averages $\left\langle {S}_{k}({\mathcal{L}},t)\right\rangle$. Here ${S}_{k}({\mathcal{L}},t)$ is generated from a random circuit ${{\mathbb{C}}}_{k}$ with a single squeezer of strength r_k at ${{\boldsymbol{\xi }}}_{k}^{\star }$, therefore can be calculated by the random-walk mapping in Eqs. (12) and (6). Note that the random beamsplitters in all N_q single-squeezer circuits ${\{{{\mathbb{C}}}_{i}\}}_{k = 1}^{{N}_{q}}$ and the original circuit ${\mathbb{C}}$ are independent. To test the linear superposition law, we numerically calculate the deviation per mode

$${{\Delta }}{S}_{{\rm{spp}}}(t)=\frac{1}{| {\mathcal{G}}| }\parallel \left\langle S({\mathcal{L}},t)\right\rangle -\left\langle {S}_{{\rm{spp}}}({\mathcal{L}},t)\right\rangle {\parallel }_{1}.$$

(28)

To evaluate the relative deviation, we can also rescale the deviation relative to the steady state value, as ${\delta }_{{\rm{spp}}}(t)={{\Delta }}{S}_{{\rm{spp}}}(t)/(\parallel \left\langle S({\mathcal{L}},\infty )\right\rangle {\parallel }_{1}/| {\mathcal{G}}| )$. Both deviations are system-size independent in the continuum limit.

In Fig. 8a, we evaluate the deviation for the 1-D three-squeezer case considered in Fig. 2d. We see that the relative deviation δ_spp(t) is small (<2%) through the entire dynamical evolution. To be more explicit, in Fig. 8b, c, we directly plot $\left\langle S(\tilde{x},t)\right\rangle$ (blue) at various times, which agrees well with the superposition result $\left\langle {S}_{{\rm{spp}}}(\tilde{x},t)\right\rangle$ (red).

Fig. 8: Superposition in a three-squeezer case.

The example is identical to Fig. 2d. a Relative deviation from linear superposition. The orange line is the mean and the yellow area shows the precision owing to a finite sample size. Cyan dots show the time when the three squeezers are applied accordingly. Arrows represent the time when snapshots in (b) and (c) are taken. b, c Snapshots of entanglement entropy curves at t = 600, 1000. Blue and red lines are $\left\langle S(\tilde{x},t)\right\rangle$ and superposition $\left\langle {S}_{{\rm{spp}}}(\tilde{x},t)\right\rangle$; whereas green, purple, and brown ones show $\left\langle {S}_{i}(\tilde{x},t)\right\rangle$ generated by each of the three squeezers.

Following the above observation, we provide a theory at the sparse squeezers limit. The analyze is possible through concatenating the single-squeezer case sequentially to distill a set of squeezed vacuums (see Supplementary Note 9 for details). From the theory, we predict linear superposition for both the equilibrium Page curves and the dynamical evolution.

Page curves with multiple squeezers

In terms of Page curves, as we explained previously, the graph topology is irrelevant; therefore, we can simply consider the 1-D case. Furthermore, one can show that each Page curve is only characterized by a list of squeezing strength ${\{{r}_{k}\}}_{k = 1}^{{N}_{q}}$ (see details in Supplementary Note 10). In this case, as long as ${N}_{q}\ll M,| {\mathcal{L}}|$, we can regard the squeezers as sparse, and superposition $\left\langle S({\mathcal{L}},\infty )\right\rangle \simeq \left\langle {S}_{{\rm{spp}}}({\mathcal{L}},\infty )\right\rangle$ holds, with each single-squeezer result given in Eq. (16). In the large squeezing limit, we can further utilize Eq. (17) to obtain

$$S\left({\mathcal{L}},\infty \right)\simeq M\overline{{n}_{q}}\left\{\frac{1}{2}{\mathrm{log}\,}_{2}\left[\frac{| {\mathcal{L}}| }{| {\mathcal{G}}| }\left(1-\frac{| {\mathcal{L}}| }{| {\mathcal{G}}| }\right)\right]+\frac{1}{\mathrm{ln}\,2}\left(\overline{r}+1\right)-1\right\},$$

(29)

We see a dependence on statistical quantities $\overline{r}\equiv \mathop{\sum }\nolimits_{\ell = 1}^{{N}_{q}}{r}_{\ell }/{N}_{q}$ and $\overline{{n}_{q}}\equiv {N}_{q}/M$, whereas the shape of the curve is invariant in the bulk at the large squeezing limit (see details in Supplementary Note 10).

We numerically examine the validity of the linear superposition in Page curves in Fig. 9a–c. Indeed when the squeezer density is low, we see a good agreement, as shown in Fig. 9b; whereas when the squeezers are dense, substantial deviation can be found, as shown in Fig. 9c. The transition is captured by the relative deviation δ_spp(∞) in Fig. 9a, where δ_spp(∞) increases linearly with the squeezer density $\overline{{n}_{q}}$.

Fig. 9: Superposition for dynamic and equilibrium entanglement entropy in 1-D with multiple squeezers.

a, d show the deviation (measured in 1-norm) between the real and the superposition results, whereas the rest are examples of the entanglement entropy curves with solid lines for real results and dashed lines for superposition. Details are given as follows; A 1-D system of M = 200 modes is considered. a–c Relative 1-norm deviation δ_spp(∞) is shown in (a). Solid lines represent the results of circuits with identical ${r}_{i}=\overline{r}$ squeezers, whereas scatter dots show results of circuit where random squeezers r_i uniform in a range $[0.5\overline{r},1.5\overline{r}]$ with fixed total squeezing strength ${N}_{q}\overline{r}$. Page curves with $\overline{{n}_{q}}=0.03$ and $\overline{{n}_{q}}=0.5$ are shown in (b) and (c). Red and blue lines correspond to $\overline{r}=3$ and $\overline{r}=6$. d–f Absolute 1-norm deviation (per mode) of superposition measured by ΔS_spp(t) is shown in d, with different minimum distances between random squeezers d. Time t is fixed at early (t = 200, green), medium (t = 500, blue), and late time (t = 900, red). The shaded areas show the fluctuations in different squeezer space-time configurations. In comparison, the entanglement per mode $\parallel \left\langle S(\tilde{x},\infty )\right\rangle {\parallel }_{1}/M$, averaged over configurations with fixed d are plotted in orange. Squeezers with random strength r_i ∈ [1, 3] are randomly distributed before t = 500 following Poisson disk sampling. e and f are ensemble-averaged entanglement entropy evolution for the setup with d = 60 and d = 20 separately. Curves from bottom to top show the curve at time t = 200, 500, 900.

Although when $\overline{{n}_{q}}$ is not small, superposition does not hold, we numerically find that typical Page curves are mainly characterized by statistical quantities $\overline{r},\overline{{n}_{q}}$, which indicates a well-defined continuum limit of CV Page curves (see details in Supplementary Note 10).

Dynamics with linear superposition

To verify superposition in a more general setting beyond Fig. 8, we consider circuits with squeezers randomly distributed in space-time. To control sparsity, we adopt the Poisson sampling method⁹⁰ to obtain random circuits with various minimum distances d between the squeezers.

With the squeezers randomly chosen, we evaluate the entanglement dynamics for circuits with random squeezers of different minimum distances. Two examples are given in Fig. 9d–f: When the squeezers are sparse, the superposition results $\left\langle {S}_{{\rm{spp}}}(\tilde{x},t)\right\rangle$ (dashed lines) agree well with the true values $\left\langle S(\tilde{x},t)\right\rangle$ (solid lines) at various time steps in Fig. 9e; when the squeezers are dense, substantial deviations from the linear superposition can be observed, as demonstrated in Fig. 9f.

To systematically examine the transition from “dense” to “sparse” squeezers, we calculate the deviation Δ_spp(t) for distances 0 ≤ d ≤ 500 at various time steps in Fig. 9d, where the deviation decreases monotonically with d up to the numerical precision. Although for a smaller d, the deviation is larger, the relative deviation is still below 10% of the static value $\parallel \left\langle S(\tilde{x},\infty )\right\rangle {\parallel }_{1}/M$ (orange). Therefore, we conclude that in generic CV quantum networks with sparse squeezers, linear superposition of entanglement growth holds.

Discussion

In this paper, we reveal a mapping between entanglement formation dynamics in random CV networks to random walk on general graphs. This mapping allows analytical solutions of the entanglement entropy dynamics, Page curves and scrambling time for an arbitrary network topology. On networks respecting locality, the solution enables the understanding of three major features of entanglement formation dynamics—a parabolic entanglement light cone, an entanglement sudden-growth period and parameter-dependent Page curves.

Our results have implications in quantum network protocol design, e.g., the parabolic entanglement light cone will give an estimation on the latency in entanglement distribution in a protocol without well-controlled phases, and also on the fundamental understanding of many-body systems. Note that optimized protocols, with well-controlled optical phases across the system to generate a specific entangled state, can take less time. At last, let us point out some future directions: it will be interesting to extend the parabolic entanglement light cone to long-range interacting systems; extending the multipartite entanglement witness to more general input states will bring further insights of quantum entanglement; exploration of the connection between entanglement dynamics with statistical properties of random networks such as connectivity distribution will lead to a full statistical theory of CV quantum networks. Our random walk mapping is based on the weight of annihilation operators evolution, extension to quantum random-walk^91,92,93,94 can be possible by applying the gates in a superposition⁹⁵ (see Supplementary Note 11 for further discussions).

Methods

Entanglement entropy

The entanglement entropy $S({\mathcal{L}},t)$ can be efficiently calculated by keeping track of the covariance matrix of ${\mathcal{L}}$ (Equivalently, one can consider the covariance matrix of subsystem ${\mathcal{R}}$.)

$${{\boldsymbol{V}}}_{ij}=\left\langle \{{{\boldsymbol{X}}}_{i},{{\boldsymbol{X}}}_{j}\}\right\rangle ,i,j\in {\mathcal{L}},$$

(30)

where {, } is the anti-commutator and X_i, X_j are components of quadrature operators X that corresponds to subsystem ${\mathcal{L}}$. Under the dynamics of each local unitary U_S, the covariance matrix evolves as V → SVS^T. From the symplectic eigenvalues⁶⁴ $\{{\nu }_{i},1\le i\le | {\mathcal{L}}| \}$ of V, we can obtain the von Neumann entropy of ${\mathcal{L}}$ (which equals that of ${\mathcal{R}}$ due to purity of the global system)

$$S\left({\mathcal{L}},t\right)=S({\mathcal{R}},t)=\mathop{\sum }\limits_{i = 1}^{| {\mathcal{L}}| }g(\left({\nu }_{i}-1\right)/2),$$

(31)

where each term $g(x)=(x+1){\mathrm{log}\,}_{2}(x+1)-x{\mathrm{log}\,}_{2}\left(x\right)$ is the entropy of a thermal state with mean photon number x. Alternatively, we can also choose the Rényi entropy of the order α, which can be calculated as

$${S}_{\alpha }({\mathcal{L}},t)=\frac{1}{\alpha -1}\mathop{\sum }\limits_{i = 1}^{| {\mathcal{L}}| }{\mathrm{log}}_{2}{g}_{\alpha }(({\nu }_{i}-1)/2),$$

(32)

where the ${g}_{\alpha }\left(\cdot \right)$ is defined as ${g}_{\alpha }(x)={\left(x+1\right)}^{\alpha }-{\left(x\right)}^{\alpha }$.