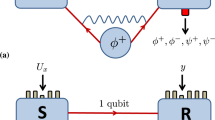
Abstract
We propose, analyze, and evaluate a technique for the joint measurement of time–frequency entanglement between two photons. In particular, we show that the frequency sum and time difference of two photons could be simultaneously measured through the sum-frequency generation process, without measuring the time or frequency of each individual photon. We demonstrate the usefulness of this technique by using it to design a time–frequency entanglement based continuous variable superdense coding and a quantum illumination protocol. Performance analysis of these two protocols suggests that the joint measurement of strong time–frequency entanglement of non-classical photon pairs can significantly enhance the performance of joint-measurement based quantum communication and metrology protocols.
Similar content being viewed by others
Introduction
Time and frequency correlation have been formidable resources in a rich range of applications from metrology and spectroscopy to communication and security1,2,3. In particular, time–frequency entanglement (TFE), that there are substantial and simultaneous correlations between two photons in both time and frequency, enables a plethora of advantages beyond what is achievable by classical correlations in the domains of metrology4 and communication5 applications. These advantages are brought about due to the continuous variable nature and loss resilient property6 of TFE. Recent years have witnessed rapid advances in the generation of TFE with attractive properties7,8,9. Thus far, TFE has already been used for entanglement based protocols such as quantum key distribution5,10 and continuous variable Bell test11. Such protocols only feature separate measurements of the time or frequency degree of freedom of each individual photon. In contrast, many other entanglement based applications require a joint measurement of the two entangled photons, that is, measuring a joint variable of the entangled system without resolving the property of each individual photon. One such example is continuous variable superdense coding12, in which the sum of the in-phase amplitude x1 + x2 and the difference of the out-of-phase amplitude p1 – p2 of two beams are simultaneously measured. In principle, such joint measurement based protocols could also be implemented with TFE photon pairs, since the time and frequency operator of a single photon obey the same commutation relation as x and p13.
Despite the progress on the front of TFE, to the best of our knowledge, TFE within non-classical photon pairs has not been used in quantum information and sensing applications that require joint measurement, where the sum of frequencies ω1 + ω2 and difference of times t1 − t2 of two photons are measured simultaneously. The frequency sum (time difference) of two photons has to be measured without measuring the frequency (time) of each individual photon, to avoid altering the subsequent measurement of the time difference (frequency sum). If such a measurement could indeed be implemented in a practical fashion, it could have a significant impact on many entanglement based applications that would have their performance depend on such joint measurements. Those include quantum teleportation14, quantum superdense coding15, and quantum metrology16,17.
Compared to the joint measurement, the generation of TFE is much more developed. To date, the most widely adopted approach to generating TFE photon pairs is continuous-wave spontaneous parametric down-conversion (SPDC). The TFE of SPDC photon pairs is closely related to the properties of SPDC sources. In particular, it has been shown that the temporal correlation and frequency anti-correlation of TFE photon pairs could be tailored with great flexibility with different designs of the waveguide structure of the photon-pair source8. Given the close connection between the SPDC process and TFE, a natural line of inquiry would be to utilize the time-reversal of the SPDC process, namely sum frequency generation (SFG), to help obtain an effective route for a TFE joint-measurement based protocol. In this paper, we show through theoretical analysis that the SFG process could be used as the joint measurement of TFE. In particular, we show that SFG could be used for the joint measurement of superdense coding and quantum illumination. These two examples show the potential of SFG as a measurement technique for practical quantum communication and sensing protocols.
Results
SFG of photon pairs
The SFG process in a χ(2) nonlinear medium could be modeled as the following evolution operator18:
where photons in the signal mode as(ωs) and idler mode ai(ωi) are annihilated to generate photons in the pump mode ap(ωp) and ϵ characterizes the interaction strength. The time reversed process of SFG, the SPDC process, can also be described by the same evolution operator V. Note that the function f0(ωp, ωs, ωi)δ(ωp − ωs − ωi) is the joint spectral amplitude of SPDC photon pairs if the pump mode is occupied by strong coherent light at frequency ωp. Given the fact that the SPDC process can create TFE photon pairs, it is natural to ponder whether the SFG process can be used to resolve the TFE between two photons. To investigate this while balancing the rigorousness and complexity of the analysis, we assume that the factor
is independent of the pump frequency ωp = ωs + ωi. This indicates that the SPDC process is assumed to be broadband phase matched for any pump frequency. Using this form of the SFG evolution operator V and work in the Heisenberg picture, the spectral density operator \({a}_{{\rm{p}}}^{\dagger }(\omega ){a}_{{\rm{p}}}(\omega )\) of the pump light at the SFG output could be expressed as (See Supplementary Section 1.3):
where \(O({a}_{{\rm{p}}}({\omega }_{{\rm{p}}}),{a}_{{\rm{p}}}^{\dagger }({\omega }_{{\rm{p}}}))\) is a sum of normal ordered operators that are at least linear in ap(ωp) or \({a}_{{\rm{p}}}^{\dagger }({\omega }_{{\rm{p}}})\). This term could be neglected due to the absence of pump photons at the input of the SFG process. It could be further shown that in the limit of infinite SPDC photon bandwidth (\(f(({\omega }_{{\rm{s}}}-{\omega }_{{\rm{i}}})/\sqrt{2})=1\)):
where P(ωp, 0) is the probability density operator for the input signal–idler photon pair of the SFG process to have their frequency sum ωs + ωi = ωp and zero time difference ts − ti = 0, simultaneously (see the Methods section). The general probability density operator P(ωp, t) for the frequency sum ωs + ωi = ωp and time difference ts − ti = t could be constructed from P(ωp, 0) by temporally displacing either the signal or the idler photon. Therefore (3) and (5) show that frequency resolved detection (i.e. using a single photon spectrometer, hence carrying out a classical measurement) of a pump photon generated in the SFG process reveals the simultaneous time and frequency correlation (hence TFE) ωp = ωs + ωi, ts − ti = 0 of the input signal–idler photon pair, in the limit of infinite SPDC photon bandwidth. Intuitively, such a joint measurement of TFE could be understood as a quantum interference effect: only photon pairs that have frequency sum ωp = ωs + ωi can possibly generate a pump photon at frequency ωp due to the energy conservation constraint. Meanwhile in the time domain, a non-zero time difference between the signal and idler photon will induce different phase shift for different frequency components of the photon-pair state, and the corresponding probability amplitude of SFG will interfere destructively, leading to a decreased probability of generating a pump photon.
Time–frequency entanglement based continuous variable superdense coding
Having shown that the SFG process could be utilized for the joint measurement of TFE, the question remains now is that whether it could benefit any quantum communication and sensing application that needs joint measurement. An important example is continuous variable superdense coding12, which utilizes entanglement between two particles to surpass the classical limit of channel information capacity. The previous proposal12 and implementation19 of continuous variable superdense coding are based on the joint-measurement of amplitude–quadrature entanglement, compared to which the joint measurement of TFE is more difficult to implement. However, the utilization of TFE can also provide additional advantages compared to the amplitude–quadrature entanglement. First, unlike the amplitude–quadrature entanglement, the strength of TFE (the Schmidt number of the photon pair) is not limited by the source power, which may translate to a larger information capacity enhancement compared to the two-fold enhancement achievable by amplitude–quadrature entanglement12. Second, the TFE has been demonstrated to be resilient to channel losses6, which is favorable for practical long haul superdense coding applications.
In what follows, we propose a proof-of-principle protocol of TFE based continuous variable superdense coding (TFE SDC). In particular, we will show that one can encode (decode) an arbitrarily large amount of information into (out of) both the time and frequency degree of freedom of the signal photon (that is entangled with the idler photon), simultaneously. The basic steps of the TFE SDC protocol are as follows. First Alice generates an entangled photon-pair state \(\left|{\rm{pair}}\right\rangle\) as the entanglement source:
Such a photon pair could be generated by pumping the χ(2) medium with a strong coherent beam of light in pump mode mode (ap(ωp)) that has (square normalized) complex spectral amplitude \(\frac{1}{{\root 4 \of 2}}h(\frac{{\omega }_{{\rm{p}}}}{\sqrt{2}})\). To simplify the calculation, we assume the factor h(ω) and \(f(({\omega }_{{\rm{s}}}-{\omega }_{{\rm{i}}})/\sqrt{2})\) to be Gaussian:
where the SPDC pump bandwidth and SPDC photon bandwidth are proportional to σ+ and σ−, respectively, and ω0 is the center frequency of the SPDC pump light. Note that if \(\sigma_{+}=\sqrt{2}\sigma_{-}\) the SPDC photon pair is not entangled. Alice then stores the idler photon locally and sends the signal photon to Bob. Bob will encode information by shifting both the frequency and time of the signal photon by Δω and Δt, which could be done with nonlinear frequency conversion20 and a tunable delay line. The encoded signal photon is sent back to Alice. Then the information coded photon-pair state for Alice to measure is given by
Alice will perform SFG with the encoded photon pair to obtain the final state \(\left|{\rm{SFG}}\right\rangle\):
The generated pump photon in state \(\left|{\rm{SFG}}\right\rangle\) is sent to a single photon spectrometer. The frequency spectrum S(ω) of the generated pump photon is given by the expectation value of the spectral density operator \({a}_{{\rm{p}}}^{\dagger }({\omega }_{{\rm{p}}}){a}_{{\rm{p}}}({\omega }_{{\rm{p}}})\)(See Supplementary Section 2):
The total probability of generating a pump photon is given by the integral of S(ωp):
The mean frequency and frequency variance of the generated pump photon are given by
As could be seen in (15) and Fig. 1, the probability NSFG of generating a pump photon decreases rapidly as the signal photon time shift Δt exceeds the inverse SPDC photon bandwidth 1/σ−. In contrast, the frequency shift Δω does not affect much NSFG as long as Δω ≪ σ−. Equations (16) and (17) show that the center frequency and bandwidth of the generated pump photon is identical to that of the SPDC pump light, aside from the frequency shift Δω that Bob encode into the photon pair.
Based on (15), (16), and (17), the joint measurement scheme of the TFE SDC protocol could be designed as follows. After receiving the signal photon from Bob, Alice first apply an additional time shift Δtextra to the signal photon and then let the encoded photon pair go through the SFG process. A pump photon will be generated through SFG with non-negligible probability only if the total time shift Δt + Δtextra is close to zero (≤1/σ−). The encoded photon pair will remain unchanged after SFG if no pump photon is generated. In such cases, the encoded photon pairs could be reused and go through the SFG process repeatedly until a pump photon is finally generated (see Fig. 2 for the schematic of the experimental setup). Over this SFG feekback loop, the extra time delay Δtextra is swept continuously and repeatedly. When the feedback loop terminates (a pump photon is generated) with the extra time delay set to Δtextra, the posterior probability distribution of the time shift Δt is centered around −Δtextra with variance \({\rm{var}}\{\Delta {\rm{t}}\}=1/{\sigma }_{-}^{2}\). The frequency shift Δω is obtained by measuring the frequency of the generated pump photon, with variance \({\rm{var}}\{\Delta \omega \}={\sigma }_{+}^{2}\). The measurement of Δt and Δω could be arbitrarily precise simultaneously:
which implies that arbitrarily large amount of information could be coded in Δt and Δω simultaneously. Such information capacity cannot be achieved without using entanglement. To see this, consider a classical coding protocol where the time shift Δω and frequency shift Δt information are coded on a single photon. Then the readout of Δt and Δω information can only be done through measuring the time and frequency of the encoded photon. But the time and frequency of a single photon cannot be simultaneously measured with arbitrarily high accuracy due to the uncertainty principle21.
a Setup of the SFG feedback loop for the TFE SDC protocol. SFG: a χ(2) medium where the SFG process takes place; DM: a dichroic mirror to separate the generated pump photon from the photon pair; TTD: tunable time delay Δtextra; OSA: single-photon optical spectral analyzer. SM: switch mirror. After the signal and idler pass by the switch mirror SM, SM will flip and form a ring cavity. b Setup of the TFE QI protocol. Target: the target object to be detected, modeled as a unballanced beamspliter with reflection η (η = 0 when the object is absent), SP: short pass filter, MRPD: mode resolved single photon detector that detects pump photon generated in mode A0.
As could be seen in (15) and (17), the performance of the TFE SDC protocol depends on the χ(2) medium that is used for the SPDC photon-pair generation and the SFG measurement: the SPDC photon bandwidth σ− dictates the maximal frequency shift Δω that can be encoded such that NSFG is constantly \({\epsilon }^{2}/\sqrt{2}\) as well as the readout variance of the time shift Δt. The nonlinear conversion efficiency ϵ2 determines the number of the SFG feedback loops that are needed for the joint measurement, hence the speed of the communication. This outcome demonstrates how TFE could be used for superdense coding, where it offers advantages over existing superdense proposals and demonstrations in that it pivots in its performance on the TFE of the photon pairs, which is not limited by the power of the source, and is resilient to losses.
Time–frequency entanglement based quantum illumination
While advantages offered by TFE to superdense coding can clearly benefit channel capacity in communication systems, they can also benefit a number of sensing applications. In this work we aim to explore the possibility of utilizing TFE to enhance the target detection sensitivity in a noisy and lossy environment, i.e. the quantum illumination protocol. The quantum illumination protocol is closely related to the superdense coding protocol in that they are both based on the same fashion of quantum entanglement enhancement16. The basic steps of the general quantum illumination protocol are as follows (see Fig. 1): The signal photon of the entangled photon pair is sent to probe the target while the idler photon is stored locally. The signal photon is reflected on the target object and collected with total transmission η (η = 0 if the target is absent). Regardless of the presence or absence of the target object, a constant level of environmental noise light is always collected into the detection system. The joint measurement of the collected (signal or noise) photon and the idler photon is performed to predict the presence and absence of the target object. For TFE based quantum illumination protocol, the joint measurement consists of the SFG process of the idler photon and the collected photon, and the detection of the generated pump photon at the sum frequency ωp = ωs + ωi. The entanglement enhancement provided by TFE results from the fact that only the signal photon that is strongly correlated in both time and frequency (hence TFE, which is not possible for uncorrelated photon pairs) with the idler photon can generate a pump photon at frequency ωp = ωs + ωi. Therefore, the detection of the generated pump photon is resilient to the background noise photons that are not correlated with the idler photon. Note that this protocol is entanglement based and is different from the target detection protocol using classical time and frequency correlation22. In what follows, we analyze the TFE QI protocol using a new mathematical formalism instead of that used for the superdense coding protocol. The formalism utilized here is chosen as it better highlights the connection between TFE and SFG (an analysis of the TFE QI protocol that parallels the analysis of the TFE SDC protocol could be found in Supplementary Section 5).
We shall start directly from the general form of the evolution operator V(1) without applying any approximation or assumption. In general, the χ(2) evolution operator V could be expressed as a discrete sum through a “two-step Schmidt decomposition process” (see the Methods section):
Equation (19) is obtained through the Schmidt decomposition between the pump and the “signal–idler” joint system with the singular values given by \(\{{\lambda }_{m}^{(1)}\}\). Equation (20) is obtained through the Schmidt decomposition of each “signal–idler” joint system with the singular values given by \(\{{\lambda }_{m,n}^{(2)}\}\). The operators {Am} and {Fm,n},{Gm,n} (with fixed m and different n) form complete orthogonal sets of annihilation operators for the pump, signal and idler mode, respectively. The definitions of the mode operators could be found in the Methods section. The photon-pair source of the TFE QI protocol is chosen to be \(\left|{\rm{pair}}\right\rangle ={B}_{0}^{\dagger }\left|0\right\rangle\), which could be approximated by SPDC twin beams generated by coherent pump light in the mode A0(neglecting the vacuum term and multiple pair terms). Note that if condition (2) is satisfied, then the mode A0 can be specified arbitrarily and \({\lambda }_{m}^{(1)}=1/\sqrt{2}\) (See Supplementary Section 3). The noise and loss of the signal photon in the target detection channel is modeled as mixing with the background noise mode on a virtual beam-splitter with transmission η for the signal photons. The evolution operator Uloss of the beam-splitter can be expressed as
where \({F}_{0,n}^{({\rm{b}})}\) is the discrete mode operator for the noise photon that has the same spectral amplitude as the signal mode F0,n. Equivalence between Uloss and the usual beam-splitter transform is shown in Supplementary Section 4.1. To avoid technical complexities, we assume that the background noise mode is occupied by a noise state ρb that satisfies the following conditions:
where μb is the average number of noise photons per mode. The above conditions mean that the noise photons are evenly distributed in every spectral mode \({F^{(b)}_{0,n}}\) with random phases and there is no coherence between each mode. It could be shown that such noise is broadband and continuous-wave white noise (See Supplementary Section 4.2). The density operator ρSFG of the SFG output can be expressed as
In the limit of perfect signal photon transmission (η = 1), the SFG process can only generate pump photons in mode A0 (See Supplementary Section 4.3). For this reason, in the following analysis only the photon detection event in mode A0 is taken into consideration. After some algebraic manipulation (See Supplementary Section 4.3), it can be shown that the photon detection probability Pd,QI on mode A0 is given by
where \({\rm{S}}N=1/{\sum }_{n}{({\lambda }_{0,n}^{(2)})}^{2}\) is the Schmidt number of the SPDC photon-pair state \(\left|{\rm{pair}}\right\rangle\). The Schmidt number being larger than unity is a indication of TFE. It can be shown that the conversion efficiency \({\lambda }_{0}^{(1)}{\epsilon }^{2}\) is also the SPDC conversion efficiency (See Supplementary Section 4.5). For comparison, we shall also consider a classical target detection (CI) protocol where a probe photon in an arbitrary temporal-spectral mode F is sent to probe the target16. It is easy to see that the photon detection probability is Pd,CI = η + μb. Comparison between Pd,CI and Pd,QI shows that the TFE QI protocol is equivalent to a CI protocol with detection efficiency \({\epsilon }^{2}{\lambda }_{0}^{(1)}\) and noise photon per mode reduced to μb/SN.
As could be seen in (24), the performance of the TFE QI protocol is limited by the nonlinear efficiency \({\epsilon }^{2}{\lambda }_{0}^{(1)}\) and the Schmidt number SN of the entangled photon-pair source. If SPDC twin beams are used as the TFE QI source, the Schmidt number SN could be approximated as the ratio of the SPDC photon bandwidth σ− and the SPDC pump bandwidth σ+23. Therefore ideally the χ(2) medium should have very large phase-matching bandwidth. For bulk χ(2) crystal there is a trade-off between the SPDC photon bandwidth and the length of the crystal(hence the nonlinear conversion efficiency). Therefore it may not be optimal for the TFE QI protocol. Integrated semiconductor χ(2) waveguide7 could be an ideal alternative because it offers high nonlinear conversion efficiency in a compact form factor (\({\epsilon }^{2}{\lambda }_{0}^{(1)}\simeq 2.1\times 1{0}^{-8}\) for a 1 mm long waveguide). Moreover, semiconductor waveguide can provide very large SPDC photon bandwidth with specific structure designs8.
It is important to highlight that the noise reduction being directly proportional to the Schmidt number SN is very similar to that in the first quantum illumination protocol reported in16. Therefore the TFE QI protocol proposed here could be considered as an implementation of16. However, it could be shown that the TFE QI protocol has large performance enhancement over the coherent light/homodyne detection scheme under high noise condition (See Supplementary Section 6.2). This extends the result in24 that shows that the first quantum illumination protocol16 cannot outperform coherent detection in the low noise limit μb ≪ 1. In addition, as could be seen in (24), the entanglement enhancement of the TFE QI protocol can effectively reduce the environmental noise power down to zero in the limit of large entanglement SN ≫ 1. Such a result does not contradict the previous finding25 that at most 6 dB of performance advantage could be achieved by Gaussian state quantum illumination. This is because for TFE QI the photon-pair source is assumed to be non-Gaussian \(\left|{\rm{pair}}\right\rangle ={B}_{0}^{\dagger }\left|0\right\rangle\). However, in practice, the SPDC twin beams are commonly used as an approximation of \(\left|{\rm{pair}}\right\rangle\) by neglecting the vacuum term and the multiple pair terms. Then, it must be remembered that SPDC twin beams are in Gaussian state and a TFE QI protocol with SPDC twin-beam source can achieve 6 dB enhancement of target detection performance at most. Lastly, the proposed TFE QI protocol is similar to the SFG quantum illumination protocol26 but with a simpler setup. However, the discussion of the TFE QI protocol here provides a different perspective of the performance advantage achievable by SFG detection from a TFE standpoint.
Discussion
In this paper, we propose a technique to jointly measure the time–frequency entanglement between two photons based on the SFG process. We also apply this technique to propose a time–frequency entanglement based continuous variable superdense coding protocol and a quantum illumination protocol and analyze their performances. In particular, a theoretical analysis of the quantum illumination protocol shows that the effect of background noise on target detection accuracy can be reduced to zero in the limit of infinite time–frequency entanglement between the signal and idler photon. The performance limiting factor of this joint measurement technique is that its efficiency is limited by the strength of χ(2) nonlinearity. To overcome this limit for the superdense coding protocol, we propose a feedback loop based setup to effectively enhance the interaction of the signal and idler photon inside the nonlinear medium. Other approaches to improving the efficiency may include resonance enhanced SFG of entangled photon pairs27 and enhancing the effective nonlinearity with high confinement waveguide design7.
Methods
The probability density operator P(ω, t) for time difference and frequency sum of two photons
Define first the frequency sum projection operator Pδω(ω) that selects two photon states with the frequency sum of the signal and idler photon satisfying ∣ωs + ωi − ω∣ ≤ δω/2:
where Gate(x) = 1 for ∣x∣ ≤ 1/2 and Gate(x) = 0 otherwise. The time difference projection operator that selects two photon states with the time difference of the signal and idler photon satisfying ∣ts + ti − t∣ ≤ δt/2 can be similarly defined as
where the instantaneous annihilation operator \({\tilde{a}}_{x}(t)\) is defined as
The probability density operator P(ω, t) for time difference and frequency sum of two photons can then be defined as the product of Pδt(t) and Pδω(ω) in the limit of δω → 0, δt → 0:
It can be shown that (See Supplementary Section 1.2)
where
As can be seen Bp equals B defined in (4) in the limit of \(f(({\omega }_{{\rm{s}}}-{\omega }_{{\rm{i}}})/\sqrt{2})\to 1\) and t = 0.
The two-step Schmidt decomposition
To simplify the analysis of the SFG process, the evolution operator could be discretized from the integral form (1) to a discrete sum form via a ‘two-step Schmidt decomposition’. First, the function δ(ωp − ωs − ωi)f0(ωp, ωs, ωi) could be decomposed through the first step Schmidt decomposition:
where {ψA,m(ωp)} is a complete set of orthonormal functions for the complex amplitude of the pump photons and {ψB,m(ωs, ωi)} is a (not complete) set of orthonormal functions for the joint spectral amplitude of the signal and idler photon pairs. Then the function ψB,m(ωs, ωi) could be further decomposed through the second step Schmidt decomposition:
where {ψF,m,n(ωs)}(for fixed m) and {ψG,m,n(ωi)}(for fixed m) are two complete sets of orthonormal functions for the signal and idler photon complex spectral amplitude, respectively. Therefore the evolution operator V could be written in a discrete sum form:
Data availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
References
Liu, H. et al. Enhancing lidar performance metrics using continuous-wave photon-pair sources. Optica 6, 1349–1355 (2019).
Yabushita, A. & Kobayashi, T. Spectroscopy by frequency-entangled photon pairs. Phys. Rev. A 69, 013806 (2004).
Lavoie, J., Kaltenbaek, R. & Resch, K. J. Quantum-optical coherence tomography with classical light. Opt. Express 17, 3818–3826 (2009).
Pe’Er, A., Dayan, B., Friesem, A. A. & Silberberg, Y. Temporal shaping of entangled photons. Phys. Rev. Lett. 94, 073601 (2005).
Mower, J., Zhang, Z., Desjardins, P., Lee, C., Shapiro, J. H. & Englund, D. High-dimensional quantum key distribution using dispersive optics. Phys. Rev. A 87, 062322 (2013).
Zhang, Q. et al. Distribution of time-energy entanglement over 100 km fiber using superconducting single-photon detectors. Opt. Express 16, 5776–5781 (2008).
Horn, R., Abolghasem, P., Bijlani, B. J., Kang, D., Helmy, A. S. & Weihs, G. Monolithic source of photon pairs. Phys. Rev. Lett. 108, 153605 (2012).
Abolghasem, P., Hendrych, M., Shi, X., Torres, J. P. & Helmy, A. S. Bandwidth control of paired photons generated in monolithic bragg reflection waveguides. Opt. Lett. 34, 2000–2002 (2009).
Svozilík, J., Hendrych, M., Helmy, A. S. & Torres, J. P. Generation of paired photons in a quantum separable state in bragg reflection waveguides. Opt. Express 19, 3115–3123 (2011).
Khan, I. A. & Howell, J. C. Experimental demonstration of high two-photon time-energy entanglement. Phys. Rev. A 73, 031801 (2006).
Tittel, W., Brendel, J., Zbinden, H. & Gisin, N. Violation of bell inequalities by photons more than 10 km apart. Phys. Rev. Lett. 81, 3563 (1998).
Braunstein, S. L. & Kimble, H. J. In Braunstein, S. L. & Pati, A. K. (eds), Quantum Information with Continuous Variables 95–103 (Springer, 2000).
Shalm, L. K., Hamel, D. R., Yan, Z., Simon, C., Resch, K. J. & Jennewein, T. Three-photon energy–time entanglement. Nat. Phys. 9, 19 (2013).
Furusawa, A., Sørensen, J. L., Braunstein, S. L., Fuchs, C. A., Kimble, H. J. & Polzik, E. S. Unconditional quantum teleportation. Science 282, 706–709 (1998).
Bennett, C. H. & Wiesner, S. J. Communication via one-and two-particle operators on einstein-podolsky-rosen states. Phys. Rev. Lett. 69, 2881 (1992).
Lloyd, S. Enhanced sensitivity of photodetection via quantum illumination. Science 321, 1463–1465 (2008).
Zhuang, Q., Zhang, Z. & Shapiro, J. H. Entanglement-enhanced lidars for simultaneous range and velocity measurements. Phys. Rev. A 96, 040304 (2017).
O’Donnell, K. A. & U’Ren, A. B. Time-resolved up-conversion of entangled photon pairs. Phys. Rev. Lett. 103, 123602 (2009).
Li, X., Pan, Q., Jing, J., Zhang, J., Xie, C. & Peng, K. Quantum dense coding exploiting a bright einstein-podolsky-rosen beam. Phys. Rev. Lett. 88, 047904 (2002).
Kobayashi, T. et al. Frequency-domain hong–ou–mandel interference. Nat. Photonics 10, 441 (2016).
Qi, B. Single-photon continuous-variable quantum key distribution based on the energy-time uncertainty relation. Opt. Lett. 31, 2795–2797 (2006).
Zhang, Y. et al. Multidimensional quantum-enhanced target detection via spectrotemporal-correlation measurements. Phys. Rev. A 101, 053808 (2020).
Bogdanov, A. Y., Bogdanov, Y. I. & Valiev, K. A. Schmidt information and entanglement of quantum systems. Mosc. Univ. Computational Math. Cybern. 31, 33–42 (2007).
Shapiro, J. H. & Lloyd, S. Quantum illumination versus coherent-state target detection. N. J. Phys. 11, 063045 (2009).
Tan, S.-H. et al. Quantum illumination with gaussian states. Phys. Rev. Lett. 101, 253601 (2008).
Zhuang, Q., Zhang, Z. & Shapiro, J. H. Optimum mixed-state discrimination for noisy entanglement-enhanced sensing. Phys. Rev. Lett. 118, 040801 (2017).
Sensarn, S., Ali-Khan, I., Yin, G. Y. & Harris, S. E. Resonant sum frequency generation with time-energy entangled photons. Phys. Rev. Lett. 102, 053602 (2009).
Author information
Authors and Affiliations
Contributions
L.H. carried out the derivation and calculation of the result with assistance of A.H. Both authors contributed to writing the paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, H., Helmy, A.S. Joint measurement of time–frequency entanglement via sum frequency generation. npj Quantum Inf 6, 66 (2020). https://doi.org/10.1038/s41534-020-00293-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00293-y
This article is cited by
-
Compact all-fiber quantum-inspired LiDAR with over 100 dB noise rejection and single photon sensitivity
Nature Communications (2023)