Abstract
One of the hallmarks of quantum mechanics is the impossibility of simultaneous measurement of non-commuting observables with projective measurements. This, however, can be circumvented by using continuous quantum measurements. Here we investigate the temporal correlations of the output signals of detectors continuously and simultaneously measuring the qubit observables σz and σz cosφ + σx sinφ, for various angles φ. Using the quantum Bayesian formalism, we obtain analytical expressions for the correlators, which we find to be in good agreement with those obtained from experimentally measured output signals. The agreement is particularly good for cross-correlators, even at times shorter than the cavity modes decay time. We further discuss how the correlators can be applied for parameter estimation, and use them to infer a small residual qubit Hamiltonian arising from calibration inaccuracy in the experimental data. Our work opens up new possibilities to perform quantum metrology based on temporal correlations of measured data.
Similar content being viewed by others
Introduction
Continuous quantum measurements (CQMs) have become a unique platform to explore fundamental aspects of quantum phenomena and have potential applications to quantum information science. They have been discussed theoretically in various contexts (e.g.,1,2,3,4,5,6,7,8,9,10), and in the past decade superconducting qubits have become the main experimental system for the realization of CQMs.11,12,13,14,15,16,17 CQMs are shedding new light on our understanding of the quantum measurement process, and there is also a growing interest in CQM applications, including quantum feedback,13,16,18,19,20 rapid state purification,21 preparation of entangled states,22,23,24 and continuous quantum error correction.25,26
While a simultaneous measurement of non-commuting observables is impossible with instantaneous projective measurements, nothing theoretically forbids such a measurement using CQMs. (This is so because a CQM can be regarded as a series of infinitesimally weak quantum measurements, and partial measurements of non-commuting observables become commuting with each other in the limit of infinitesimally weak strength.) Aside from new physics, such a protocol may open up new areas of applications, inaccessible to projective measurements. The theoretical discussion of a simultaneous measurement of incompatible observables has a long history.27,28,29,30 For the measurement of non-commuting observables of a qubit, statistics of time-integrated detector outputs and fidelity of state monitoring directly via time-integrated outputs has been analyzed in Ref. 31. The evolution of the qubit state due to simultaneous measurement of incompatible variables has been described theoretically in Ref. 32, and has been recently demonstrated experimentally in Ref. 33.
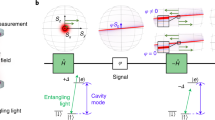
In this work, we focus on the temporal correlations of the output signals from two linear detectors measuring continuously and simultaneously the qubit observables σz and σφ ≡ σz cosφ + σx sinφ, where σx and σz are the Pauli matrices and φ is an angle between the two measurement directions on the Bloch sphere (Fig. 1). The experimental setup is described in detail in Ref. 33; it is based on a Rabi-rotated physical qubit, which is measured stroboscopically34 using symmetric sideband pumping of a coupled resonator, so that σz and σφ for an effective rotating-frame qubit are being measured. Description of such a measurement based on the theory of quantum trajectories8,9,35,36 has been developed in Ref. 33. In this work we will use a simpler approach based on quantum Bayesian theory.10,37,38,39 The quantum Bayesian description of the rotating-frame experiment33 is developed in Supplementary Note 1.
We will also show that the considered correlators can be used as a sensitive tool for parameter estimation. This scheme is different from conventional quantum metrology schemes (e.g., see Ref. 40 and references therein) because it is not necessary to initialize the qubit state; in fact, the considered correlators are insensitive to the initial state even before the steady state is formed. Furthermore, the continuous measurement capability may enable monitoring of correlators in real time to perform parameter estimation of slowly time-varying parameters. Access to two different measurement channels (corresponding to σz and σφ) also enhances the parameter estimation capability by circumventing the ubiquitous problem of spurious slow fluctuations of the measurement signals offset, affecting mainly self-correlators but not much cross-correlators, since noise in different amplifiers is usually not correlated. We will demonstrate such correlator-based parameter estimation scheme by finding a small frequency mismatch, \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\), between the frequency of stroboscopic measurement and the Rabi-oscillations frequency, using the cross-correlator for φ = π/2.
The goals of this paper are (i) calculation of the time-correlators for the output signals measuring σz and σφ, and their comparison with experimental data, and (ii) demonstration that these correlators may be a useful tool for sensitive parameter estimation in an experiment. The considered correlators are also important in the analysis of quantum error detection and correction based on simultaneous measurement of non-commuting operators.41 We note that the analyzed output signal correlators are different from qubit-state correlators.42
Results
Quantum Bayesian theory
A simultaneous continuous measurement (Fig. 1) of the qubit observables σz and σφ by two linear43 (non-switching) detectors produces noisy output signals Iz(t) and Iφ(t), respectively.32,37,38,39
where ρ(t) is the qubit density matrix and τz and τφ are the “measurement” (collapse) times needed for an informational signal-to-noise ratio of 1 for each channel. Note the chosen normalization for Iz and Iφ. In the Markovian approximation, the noises ξz and ξφ are uncorrelated, white, and Gaussian with two-time correlators
and \(\left\langle {\xi _z(t){\kern 1pt} \xi _\varphi (t^\prime )} \right\rangle\) = 0. The qubit state is characterized in the Bloch-sphere representation as \(\rho (t)\) ≡ \(\left[ {1 + x(t)\sigma _x + y(t)\sigma _y + z(t)\sigma _z} \right]{\mathrm{/}}2\). The experimental method of simultaneous measurement of σz and σφ for the effective qubit is rather involved (see Methods and Ref. 33); however, its theoretical description can be based on the standard quantum Bayesian approach for the circuit QED measurement. Note that the measured operator “direction” φ is determined by a phase shift between the applied sideband tones, so parameters of the σφ-measurement channel do not depend on φ. Each of the two channels uses a separate phase-sensitive amplifier, with the amplified quadrature determined by the phase of the local oscillator (parametric pumping). Here we assume that in each channel, the optimal (informational) quadrature is amplified, so that the qubit evolution due to measurement is not affected by the phase backaction related to fluctuations in the orthogonal (non-informational) quadrature.35,36,37,38,39 Then there is only the quantum informational backaction, which for measurement of σz and σφ is described32,37,38,39 by the evolution equations (in the Itô interpretation, see Supplementary Note 1)
Here Γz and Γφ are the ensemble dephasing rates due to measurement, so that the quantum efficiencies37,38,39 for the two channels are ηz = 1/(2τzΓz) and ηφ = 1/(2τφΓφ). In the experiment ηz ≈ 0.49 and ηφ ≈ 0.41 (note that ηφ is a characteristic of the measurement channel and therefore does not depend on φ).
Equations (4)–(6) describe evolution of the effective qubit due to measurement only. We also need to add terms due to unitary evolution and due to decoherence not related to measurement. We assume the Hamiltonian H = \(\hbar {\tilde{\mathrm \Omega }}_{\mathrm{R}}\sigma _y{\mathrm{/}}2\), describing Rabi oscillations about y-axis with frequency \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\). In the experiment, \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) = ΩR − Ωrf is a small (kHz-range) undesired mismatch between the Rabi frequency ΩR of the physical qubit and rotating frame frequency Ωrf defined by detuning of sideband pumps,33 see Supplementary Note 1. Decoherence of the effective qubit arises from the decoherence of the physical qubit, which is characterized (in the laboratory frame) by energy relaxation time T1 and dephasing time T2 [the pure dephasing rate is then \(T_{{\mathrm{pd}}}^{ - 1} = T_2^{ - 1} - \left( {2T_1} \right)^{ - 1}\); note that \(T_1^{ - 1}\) may have a significant contribution from qubit hybridization with leaking resonator, i.e., the Purcell effect]. To find decoherence of the effective (Rabi-rotating-frame) qubit, we need to average physical decoherence over fast rotations \({\mathrm{\Omega }}_{\mathrm{R}} \gg T_2^{ - 1}\). As derived in Supplementary Note 1, the corresponding decoherence of the effective qubit (with added unitary evolution) is
Evolution of the effective qubit is described by adding terms from Eqs. (4)–(6) and (7).
Correlators
Our goal is to calculate the two-time correlators, Kij(τ), for the output signals,
Self- and cross-correlators correspond to i = j and i ≠ j, respectively. The averaging in Eq. (9) is over an ensemble of measurements with the initial qubit state ρin prepared at time tin ≤ t1. We will see, however, that somewhat surprisingly, the result does not depend on ρin, tin, and t1 (even during initial non-steady-state regime), so Eq. (9) can also be understood as averaging over time t1. Note that this statement is correct only because of unital (symmetric) evolution in Eq. (7). We assume that the parameters describing strength of measurement, decoherence, and unitary evolution in Eqs. (4)–(7) do not change with time. By assuming τ > 0, we avoid considering the trivial zero-time contribution to the self-correlators, ΔKii(τ) = τiδ(τ).
As shown in Supplementary Note 2, calculation of the correlators from Eqs. (1)–(7) is equivalent to the following recipe:44 we replace an actual continuous measurement at the (earlier) time moment t1 with a projective measurement of σi, so that the measurement result Ii(t1) is ±1 with probability {1 ± Tr[σi ρ(t1)]}/2, and the qubit state collapses correspondingly to the eigenstate \(\left| {1_i} \right\rangle\) or \(\left| {0_i} \right\rangle\) of σi (\(\sigma _i\left| {1_i} \right\rangle = \left| {1_i} \right\rangle\), \(\sigma _i\left| {0_i} \right\rangle = - \left| {0_i} \right\rangle\)). We emphasize that this recipe does not assume a steady-state measurement process and does not assume a unital evolution. The recipe gives the correlator
where ρav(t1 + τ|1i) is the ensemble-averaged density matrix at time t1 + τ with the initial condition ρav(t1|1i) = \(\left| {1_i} \right\rangle \left\langle {1_i} \right|\); similarly, ρav(t1 + τ|0i) starts with ρav(t1|0i) = \(\left| {0_i} \right\rangle \left\langle {0_i} \right|\). The evolution of ρav is given by Eqs. (4)–(7) without noise, ξz = ξφ = 0 (because of the Itô form), so that
These equations have an analytical solution presented in Supplementary Note 2 (note that the evolution of the y-coordinate is not important in our analysis). Thus we obtain the following correlators (alternative methods for the derivation are also discussed in Supplementary Note 2):
Because of the rotational symmetry, the results for the correlators Kφφ(τ) and Kφz(τ) can be obtained from Eqs. (14) and (15) by exchanging Γz ↔ Γφ and φ → −φ. The rotational symmetry also makes the correlators insensitive to a y-rotation in both measurement directions, z → φadd, φ → φ + φadd, by any angle φadd.
We emphasize that the obtained correlators do not depend on the qubit state ρ(t1) and therefore on ρin and tin (this property would not hold in the presence of phase backaction or non-unital evolution). We also emphasize that the correlators depend on Γz and Γφ, but do not depend on τz and τφ and therefore on the quantum efficiencies ηz and ηφ. Physically, this is because non-ideal detectors can be thought of as ideal detectors with extra noise at the output.37,38,39 Since the extra noises are uncorrelated and have short (zero) correlation time, they only affect the zero-time self-correlators Kii(0).
Let us discuss some special cases for the results (14)–(16). (i) At small times, τ → + 0, we obtain correlators
(ii) For \(\left| \varphi \right| \ll 1\) and sufficiently small \(T_2^{ - 1}\) and \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\), we have Zeno pinning near the states \(\left| 0 \right\rangle\) and \(\left| 1 \right\rangle\) with rare jumps between them with equal rates Γjump. This produces cross-correlator45 Kzφ(τ) ≈ exp(−2Γjumpτ) with jump rates
(iii) In the case \({\tilde{\mathrm \Omega }}_{\mathrm{R}} = T_1^{ - 1} = T_2^{ - 1} = 0\), we have full correlation for φ = 0, Kzφ(τ) = Kzz(τ) = 1, full anticorrelation for φ = π, Kzφ(τ) = −Kzz(τ) = −1, and no correlation for φ = π/2, Kzφ(τ) = 0, while Kzz(τ) = \(e^{ - {\mathrm{\Gamma }}_\varphi \tau }\) and Kφφ(τ) = \(e^{ - {\mathrm{\Gamma }}_z\tau }\). (iv) In the case \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) = 0, the cross-correlator is symmetric, Kzφ(τ) = Kφz(τ), for any φ.
Comparison with experimental results
Experimental data have been taken in the same way as in Ref. 33(see also Methods). Experimental parameters correspond to well-separated frequency scales, as needed for the theoretical results, \(( {T_1^{ - 1},T_2^{ - 1},| {{\tilde{\mathrm \Omega }}_{\mathrm{R}}}|} ) \ll ( {{\mathrm{\Gamma }}_z,{\mathrm{\Gamma }}_\varphi } ) \ll ( {\kappa _z,\kappa _\varphi } ) \ll {\mathrm{\Omega }}_{\mathrm{R}}\), with T1 = 60 μs, T2,Ramsey = 30 μs (T2,echo = 40 μs), \({\mathrm{\Gamma }}_z^{ - 1} = {\mathrm{\Gamma }}_\varphi ^{ - 1}\) = 1.3 μs, damping rates of the two measurement resonator modes κz/2π = 4.3 MHz and κφ/2π = 7.2 MHz, and ΩR ≈ Ωrf = 2π × 40 MHz. For this work we use 11 values for the angle φ between the Bloch-sphere directions of simultaneously measured qubit observables: φn = nπ/10, with integer n between 0 and 10. While φn is determined by well-controlled phases of applied microwaves,33 the effective φ includes a small correction δφ = (κφ − κz)/2ΩR ≈ 0.036 (see Supplementary Note 1), so that φ = φn + δφ. We have used about 200,000 traces per angle for the output signals \(\tilde I_z(t)\) and \(\tilde I_\varphi (t)\), each with 5 μs duration and 4 ns sampling interval. The traces are selected by heralding the ground state of the physical qubit at the start of a run and checking that the transmon qubit is still within the two-level subspace after the run (this procedure eliminates about 15% of traces). The recorded signals \(\tilde I_i(t)\) are linearly related to the normalized signals Ii(t) in Eqs. (1) and (2) as \(\tilde I_i(t)\) = \(({\mathrm{\Delta }}\tilde I_i{\mathrm{/}}2){\kern 1pt} I_i(t) + \tilde I_i^{{\mathrm{off}}}\), where responses \({\mathrm{\Delta }}\tilde I_i\) have been calibrated using ensemble-averaged \(\langle {\tilde I_i(t)} \rangle\) (see details in Supplementary Note 3), giving in arbitrary units \({\mathrm{\Delta }}\tilde I_z\) = 4.0 and \({\mathrm{\Delta }}\tilde I_\varphi\) = 4.4. The offsets \(\tilde I_i^{{\mathrm{off}}}\) are approximately zeroed individually for each trace by measuring the non-rotating physical qubit after each run. Additional offset removal, \(|\tilde{I}_i^{\rm off}|\) ≈ 0.15–0.20, for all traces with the same φ is done using \(\langle {\tilde I_i(t)} \rangle\), see Supplementary Note 3. For calculating the correlators, we average over the ensemble of ~200,000 traces and additionally average over time t1 in Eq. (9) within the 0.5 μs range 1 μs ≤ t1 ≤ 1.5 μs (first 1 μs is not used to avoid transients in the experimental procedure, and longer averaging reduces the range for τ; we also used averaging over 1 μs duration with similar results). Note that in the experiment the applied microwave phases in the two measurement channels actually correspond to angles ±φn/2; however, because of rotational symmetry, we still label the first measured operator as σz and the second operator as σφ. Also note that we use subscripts z and φ in various notations (\(\tilde I_i\), κi, etc.) simply to distinguish the first (“z”) and second (“φ”) measurement channels.
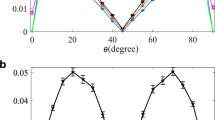
Figure 2a shows the agreement between the theory and the experimental data, where the solid lines show the symmetrized cross-correlator [Kzφ(τ) + Kφz(τ)]/2 calculated from the experimental traces for 11 values of the angle φ, while the dashed lines correspond to the theoretical result, Eq. (15). For the analytics we used \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) = 0; however, there is practically no dependence on \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) for the symmetrized cross-correlator, since the dependence comes only via Eq. (16). Note that because of the Markovian assumption, our theory is formally valid only for τ ≳ \(\kappa _i^{ - 1}\) ~ 30 ns; however, the experimental results agree with the theory even at \(\tau < \kappa _i^{ - 1}\) (experimental curves do not show any extra features in this range, and they are also not expected theoretically). Figure 2b shows the same symmetrized cross-correlator at τ = 0 as a function of φ. The agreement between the theory (cosφ, line) and the experiment (crosses) is also very good. Note a minor discrepancy between the theory and experimental results in Fig. 2a for φ ≈ π, while there is no discrepancy at φ ≈ 0; the physical difference between these two cases stems from different effective initial states (see Supplementary Note 3), so that we expect the largest contribution from transients for φ ≈ π.
Comparison between normalized experimental and theoretical correlators for the detector output signals. We used 11 angles between the measurement axes: φ = φn + δφ where φn = nπ/10, n = 0, 1, … 10 and δφ ≈ 0.036. Solid and dashed lines in all panels correspond to experimental and analytical results, respectively. a The symmetrized cross-correlator [Kzφ(τ) + Kφz(τ)]/2 for 11 values of φ, from n = 0 (top) to n = 11 (bottom). b The crosses show φ-dependence of experimental cross-correlators from a at τ = 0, while the dashed line, cosφ, corresponds to Eq. (17). c The self-correlator Kzz(τ) for 11 values of φ [n = 0 and 10 at the top, n = 5 at the bottom, the same colors as in a]. d Deviation of experimental self-correlators (for φn = π/2) from the theory at small τ due to finite bandwidth of amplifiers and filters; the thick black line at the left illustrates the theoretical δ-function
The self-correlator Kzz(τ) as a function of τ is shown in Fig. 2c for 11 values of φ (results for Kφφ are similar). The agreement between the theory (dashed lines) and experiment (solid lines) is in general good, except for small τ (discussed below). A significant discrepancy at relatively long τ for values of φ close to π/2 is probably caused by slow variations in time of the signal offsets \(\tilde I_i^{{\mathrm{off}}}\), so that they are different from trace to trace and cannot be fully removed. The corresponding slight increase of the correlators become especially visible when Kzz is small (because of the logarithmic scale), i.e., for φ close to π/2 and long τ. Note that the lines in Fig. 2c come in pairs, corresponding to angles φn and π − φn. The separation of the analytical lines in the pairs is due to δφ, while separation of experimental lines is smaller, probably indicating a smaller value of δφ (partial compensation could be due to imperfect phase matching of applied microwaves or their dispersion in the cable).
Looking at the experimental self-correlators Kzz(τ) and Kφφ(τ) at small τ for φn = π/2 (Fig. 2d), we see that in contrast to the theoretical results, there is a very significant increase of Kii(τ) at τ ≲ 0.1 μs. The discrepancy is due to the assumption of delta-correlated noise in our theory, while in the experiment the amplifying chain has a finite bandwidth (the Josephson parametric amplifiers have a half-bandwidth of 3.6 MHz and 10 MHz for σz and σφ channels, respectively), and the output signals \(\tilde I_i(t)\) are also passed through analog filters with a quite sharp cutoff at ~25 MHz (this cutoff produces clearly visible oscillations with ~40 ns period). Therefore, the theoretical delta-function contribution τi δ(τ) to Kii(τ) becomes widened in experiment. As shown in Supplementary Note 4, it is interesting to note that, somewhat counterintuitively, a finite bandwidth of measurement resonator modes does not produce a contribution to Kii(τ) at 0 < τ ≲ \(\kappa _i^{ - 1}\) when \({\mathrm{\Gamma }}_i \ll \kappa _i\) (\(\kappa _z^{ - 1}\) ≈ 37 ns, \(\kappa _\varphi ^{ - 1}\) ≈ 22 ns). This can be understood by considering a resonator without a qubit; then a finite bandwidth κi does not affect the amplified delta-correlated vacuum noise, so that only classical fluctuations of the resonator field (e.g., due to parameter fluctuations or elevated resonator temperature) will produce output fluctuations with 2/κi time scale. We have checked that the lines in Fig. 2d do not contain noticeable exponential contributions with decay time of 2/κi (small expected contributions with amplitude on the order of Γj/κi are below experimental accuracy, see Supplementary Note 4). Note that there is no contribution from the amplifier noise at small τ in Fig. 2a because the noises in the two amplifiers are uncorrelated.
Estimation of residual \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\)
We now show that the antisymmetrized cross-correlator is a useful tool and can be used to estimate small residual Rabi oscillations frequency \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) in the experiment. From Eq. (15) we find
Since in the case \(| {{\tilde{\mathrm \Omega }}_{\mathrm{R}}} | \ll {\mathrm{\Gamma }}_{z,\varphi }\) we can neglect \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) in Eq. (16) for Γ±, Eq. (19) gives a direct way to find \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) from the experimental antisymmetrized cross-correlator. The solid line in Fig. 3 shows Kzφ(τ) − Kφz(τ) from the experimental data for φ = π/2. Fitting this dependence on τ with Eq. (19) (dashed line), we find the value \({\tilde{\mathrm \Omega }}_{\mathrm{R}}{\mathrm{/}}2\pi\) ≈ 12 kHz, which is within the experimentally expected range of frequency mismatch between ΩR and Ωrf. Note that the overall shapes of the solid and dashed lines agree well with each other. Estimation of \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) via the antisymmetrized cross-correlation is a very sensitive method and can be used to further reduce \(| {{\tilde{\mathrm \Omega }}_{\mathrm{R}}} |\) in an experiment, in which a direct measurement of 40 MHz Rabi oscillations with a few kHz accuracy is a difficult task.
Estimation of the residual Rabi frequency \({\tilde{\mathrm \Omega }}_{\mathrm{R}}\) from the antisymmetrized cross-correlator Kzφ(τ) − Kφz(τ). Solid line shows experimental results for φn = π/2, while dashed line represents Eq. (19) with the fitted value \({\tilde{\mathrm \Omega }}_{\mathrm{R}}{\mathrm{/}}2\pi\) = 12 kHz. Averaging over ~200,000 experimental traces produces a clearly-visible difference signal, though with a significant noise
Discussion
Using the quantum Bayesian theory for a simultaneous measurement of non-commuting qubit observables, we obtained analytical results for the self- and cross-correlators of the output signals from the measurement. Their comparison with experimental results shows a very good agreement. The correlators can be used for sensitive parameter estimation, in particular, to estimate and eliminate the mismatch between the Rabi oscillations and the sideband frequency shift used for measurement.
Our theoretical method and results can be applied to a range of related problems. In particular, in subsystem error detection/correction codes operated with continuous measurements,41 the error syndrome is based on correlators from measurement of a set of non-commuting observables. Therefore, the analysis of correlators is necessary for logical error analysis as well as for diagnosis of spurious dynamics of gauge qubits and deviations of monitored observables from intended observables. Our method can also be extended to multi-time correlators46 and to experimental systems with phase backaction. Another possible application is to exploit continuous measurements to track slow variations of Rabi frequencies due to 1/f noise. It may also be possible to stabilize the Rabi frequencies by quantum feedback13 based on cross-correlators from several measurement channels.
Methods
Experimental setup
The experimental setup is the same as the one used in the experiment,33 where full details can be found. For clarity we briefly describe the experimental apparatus for simultaneously applying and controlling two measurement observables. We use a transmon qubit placed inside an aluminum cavity, such that it is dispersively coupled to the two lowest modes of the cavity. The cavity has two outputs, each primarily coupled to a different mode. The outputs of these modes are amplified using two lumped-element Josephson parametric amplifiers (LJPA) operated in phase sensitive mode. Each mode is then used to measure an observable of the qubit, as described below. The apparatus is cooled to 30 mK inside a dilution refrigerator.
We drive Rabi oscillations ΩR/2π = 40 MHz on the qubit by applying a resonant microwave tone modulated by an arbitrary waveform generator. In the frame rotating with ΩR, this produces an effective low frequency qubit. To couple the effective qubit to the cavity modes for measurement, we apply a pair of microwave sidebands to each mode. The sidebands are detuned above and below the two cavity modes by ΩR, which leads to a resonant interaction between the qubit Rabi oscillations and the mode. This coupling may be understood as a stroboscopic measurement of the qubit oscillations. The relative phase of the sidebands determines which quadrature of the qubit oscillations is measured. This coupling causes the cavity mode state to displace in a way that depends on the state of the qubit. We couple to the internal cavity field using a small antenna that protrudes into the cavity, allowing read out the cavity state as described above. Quantum trajectory reconstructions are validated using post-selection and tomographic measurements.
Data availability
All relevant data can be obtained from the authors upon request.
References
Kraus, K States, effects and operations: fundamental notoins of quantum theory. (Springer: Berlin, 1983).
Caves, C. M. Quantum mechanics of measurements distributed in time. A path-integral formulation. Phys. Rev. D. 33, 1643 (1986).
Menskii, M. B. Decoherence and the theory of continuous quantum measurements. Phys. Usp. 41, 923 (1998).
Belavkin, V. P. Quantum stochastic calculus and quantum nonlinear filtering. J. Multivar. Anal. 42, 171 (1992).
Braginsky, V. B. & Khalili, F. Ya Quantum measurement. (Cambridge University Press, Cambridge, UK, 1992).
Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351 (1988).
Dalibard, J., Castin, Y. & Mølmer, K. Wave-function approach to dissipative processes in quantum optics. Phys. Rev. Lett. 68, 580 (1992).
Carmichael, H. J An open systems approach to quantum optics. (Springer: Berlin, 1993).
Wiseman, H. M. & Milburn, G. J. Quantum theory of field-quadrature measurements. Phys. Rev. A. 47, 642 (1993).
Korotkov, A. N. Continuous quantum measurement of a double dot. Phys. Rev. B 60, 5737 (1999).
Katz, N. et al. Coherent state evolution in a superconducting qubit from partial-collapse measurement. Science 312, 1498 (2006).
Palacios-Laloy, A. et al. Experimental violation of a Bell’s inequality in time with weak measurement. Nat. Phys. 6, 442 (2010).
Vijay, R. et al. Stabilizing Rabi oscillations in a superconducting qubit using quantum feedback. Nature 490, 77 (2012).
Hatridge, M. et al. Quantum back-action of an individual variable-strength measurement. Science 339, 178 (2013).
Murch, K. W., Weber, S. J., Macklin, C. & Siddiqi, I. Observing single quantum trajectories of a superconducting quantum bit. Nature 502, 211 (2013).
de Lange, G. et al. Reversing quantum trajectories with analog feedback. Phys. Rev. Lett. 112, 080501 (2014).
Campagne-Ibarcq, P. et al. Observing interferences between past and future quantum states in resonance fluorescence. Phys. Rev. Lett. 112, 180402 (2014).
Wiseman, H. M. & Milburn, G. J. Quantum theory of optical feedback via homodyne detection. Phys. Rev. Lett. 70, 548 (1993).
Ruskov, R. & Korotkov, A. N. Quantum feedback control of a solid-state qubit. Phys. Rev. B 66, 041401 (2002).
Sayrin, C. et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature 477, 73 (2011).
Jacobs, K. How to project qubits faster using quantum feedback. Phys. Rev. A. 67, 030301(R) (2003).
Ruskov, R. & Korotkov, A. N. Entanglement of solid-state qubits by measurement. Phys. Rev. B 67, 241305(R) (2003).
Risté, D. et al. Deterministic entanglement of superconducting qubits by parity measurement and feedback. Nature 502, 350 (2013).
Roch, N. et al. Observation of measurement-induced entanglement and quantum trajectories of remote superconducting qubits. Phys. Rev. Lett. 112, 170501 (2014).
Ahn, C., Doherty, A. C. & Landahl, A. J. Continuous quantum error correction via quantum feedback control. Phys. Rev. A. 65, 042301 (2002).
Sarovar, M., Ahn, C., Jacobs, K. & Milburn, G. J. Practical scheme for error control using feedback. Phys. Rev. A. 69, 052324 (2004).
Arthurs, E. & Kelly, J. L. On the simultaneous measurement of a pair of conjugate observables. Bell Syst. Tech. J. 44, 725 (1965).
Busch, P. Indeterminacy relations and simultaneous measurements in quantum theory. Int. J. Theor. Phys. 24, 63 (1985).
Stenholm, S. Simultaneous measurement of conjugate variables. Ann. Phys. 218, 233 (1992).
Jordan, A. N. & Büttiker, M. Continuous quantum measurement with independent detector cross correlations. Phys. Rev. Lett. 95, 220401 (2005).
Wei, H. & Nazarov, Yu. V. Statistics of measurement of noncommuting quantum variables: Monitoring and purification of a qubit. Phys. Rev. B 78, 045308 (2008).
Ruskov, R., Korotkov, A. N. & Mølmer, K. Qubit state monitoring by measurement of three complementary observables. Phys. Rev. Lett. 105, 100506 (2010).
Hacohen-Gourgy, S. et al. Quantum dynamics of simultaneously measured non-commuting observables. Nat. (Lond.) 538, 491 (2016).
Averin, D. V. Quantum nondemolition measurements of a qubit. Phys. Rev. Lett. 88, 207901 (2002).
Wiseman, H. M. & Milburn, G. J. Quantum measurement and control (Cambridge Univ. Press, Cambridge, UK, 2010).
Gambetta, J. et al. Quantum trajectory approach to circuit QED: quantum jumps and the Zeno effect. Phys. Rev. A. 77, 012112 (2008).
Korotkov, A. N. Selective quantum evolution of a qubit state due to continuous measurement. Phys. Rev. B 63, 115403 (2001).
Korotkov, A.N. Quantum Bayesian approach to circuit QED measurement. Preprint at http://arxiv.org/abs/1111.4016 (2011).
Korotkov, A. N. Quantum Bayesian approach to circuit QED measurement with moderate bandwidth. Phys. Rev. A. 94, 042326 (2016).
Pang, S. & Jordan, A. N. Optimal adaptive control for quantum metrology with time-dependent Hamiltonians. Nat. Commun. 8, 14695 (2017).
Atalaya, J., Bahrami, M., Pryadko, L. P. & Korotkov, A. N. Bacon-Shor code with continuous measurement of noncommuting operators. Phys. Rev. A. 95, 032317 (2017).
Chantasri, A. & Jordan, A. N. Stochastic path-integral formalism for continuous quantum measurement. Phys. Rev. A. 92, 032125 (2015).
Clerk, A. A., Devoret, M. H., Girvin, S. M., Marquardt, F. & Schoelkopf, R. J. Introduction to quantum noise, measurement, and amplification. Rev. Mod. Phys. 82, 1155 (2010).
Korotkov, A. N. Output spectrum of a detector measuring quantum oscillations. Phys. Rev. B 63, 085312 (2001).
Korotkov, A. N. Persistent Rabi oscillations probed via low-frequency noise correlation. Phys. Rev. B 83, 041406 (2011).
Atalaya, J., Hacohen-Gourgy, S., Martin, L. S., Siddiqi, I. & Korotkov, A. N. Multitime correlators in continuous measurement of qubit observables. Phys. Rev. A. 97, 020104(R) (2018).
Acknowledgements
We thank Justin Dressel and Andrew Jordan for useful discussions. The work was supported by ARO Grant no. W911NF-15-1-0496. L.S.M acknowledges support from the National Science Foundation (NSF) Graduate Fellowship Grant no. 1106400. All statements of fact, opinion or conclusions contained herein are those of the authors and should not be construed as representing the official views or policies of ARO, NSF or the US Government.
Author information
Authors and Affiliations
Contributions
J.A. and A.N.K. performed the theoretical analysis. S.H.-G., L.S.M. and I.S. contributed with the experiment realization. J.A. analysed the experimental correlators and made the comparison with analytical results. J.A. and A.N.K. wrote the manuscript. All authors discussed and reviewed the final version of the manuscript. All work was carried out under supervision of A.N.K. and I.S.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Atalaya, J., Hacohen-Gourgy, S., Martin, L.S. et al. Correlators in simultaneous measurement of non-commuting qubit observables. npj Quantum Inf 4, 41 (2018). https://doi.org/10.1038/s41534-018-0091-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-018-0091-1
This article is cited by
-
Simultaneous weak measurement of non-commuting observables: a generalized Arthurs-Kelly protocol
Scientific Reports (2018)