An anisotropic lattice Boltzmann - phase field model for dendrite growth and movement in rapid solidification of binary alloys

Abstract

A model coupling the lattice Boltzmann and the phase field methods with anisotropic effects is proposed, which is used to numerically describe the growth and movement of dendrites in rapid solidification of alloys. The model is quantitatively validated by the simulation of the continuous growth and the drafting-kissing-tumbling phenomenon of two falling particles, and then applied to investigate the effects of dendrite movement and interfacial non-equilibrium on evolution of dendritic patterns for Si-9.0at%As and the CET for Al-3.0wt%Cu alloys. Both the growth and remelt processes of isolated dendrites are studied, and the result reveals the remelting influences on dendrite growth and solute micro-segregation in the condition of directional solidification. This work demonstrates that the proposed model has a wide range of applicability and great potential to simulate the microstructure evolution with various solidification conditions.

Introduction

Dendrite growth is a ubiquitous phenomenon in nature and industry. It includes a set of multiscale thermodynamic and dynamic processes, such as, heat and mass transfer, melt flows liquid-solid transition and solid phase remelting^1,2. During the dendrite growth in solidification of alloys, the free solid fragments originating from fragmentation, nucleation and external impurity, which could grow, remelt and move, play a crucial role in microstructure evolution. Experimental studies^3,4 and numerical simulations^5,6 have been conducted for the behavior of free solid fragments during solidification. However, experimental observations can usually only infer the solidification process backwards from the results, while the above numerical studies are mostly limited to the macro scale, which makes it difficult to further reveal the underlying mechanism of the microstructure evolution.

The phase field (PF) method based on free energy functional has been widely used in modeling of dendrite growth and microstructure evolution for its good thermodynamic consistency and the ability of avoiding explicit interface tracking^7,8,9,10,11. Various factors affecting dendrite growth and microstructure evolution include convection^12,13, heat and solute distribution^14,15, stress¹⁶, anisotropy¹⁷ and crystal interactions¹⁸ were studied with the PF modeling technique. However, many models based on the PF method are suffering from the lower computational efficiency compared with the models of sharp-interface methods. Numerical techniques are therefore developed and applied to reduce the computational resources. Medvedev¹⁹ proposed a composite phase field-Boltzmann scheme and apply it to dendritic growth form a supercooled melt. Nestler²⁰ combined the lattice Boltzmann method for incompressible fluid flow and phase field model, and investigated the permeability in porous media. In the above model, the LBM is only used for the flow field and temperature field, and the discretization of the phase field equation still depends on the traditional numerical method. Afterwards, Cartalade and Younsi^21,22 attempted to solve the PF and the convective-diffusion equations by the lattice Boltzmann (LB) method for its natural parallel merit and numerical stability. Later, Sun et al.^23,24,25 proposed the anisotropic LB-PF scheme and simulated dendrite growth with melt convection and heat transfer. Zhan²⁶ proposed a diffuse-interface model and a diffuse-interface multi-relaxation-time lattice Boltzmann method for the dendritic growth with thermosolutal convection. Wu²⁷ developed a unified lattice Boltzmann-phase field scheme for solutal dendrite growth with convection in which solute transport equation, NS equation and phase field equation are all solved by LBM. These studies imply the advantages of LB method in modeling of fluid flows and dendrite growth, but they are inefficient at the movement of growing dendrite, which is actually quite commonnly observed in solidification of alloys and has an important impact on the microstructure evolution²⁸. Ratkai et al.^29,30,31 studied the columnar to equiaxed transition of Ti-Al binary alloys in the presence of melt flows. After that, Ren et al.³² simulated motion and growth of multiple dendrites based on vector-valued PF method. Takaki and co-workers^33,34,35 studied multiple dendrite growth with motion, collision and coalescence and subsequent grain growth using a LB-PF coupled model. Meng et al. coupled the LB-PF model and the immersed boundary method³⁶ to simulate the moving dendrite growth with melt convection. Recently, Sun et al.³⁷ developed a hybrid scheme with the LB and finite volume method, and then simulated the growth and sedimentation of dendrite in the gravity environment.

The above studies were all carried out with the assumption of equilibrium solidification, and thus it is difficult to achieve actual industrial processes by using these models. For example in additive manufacturing, the dendrite growth is close to the rapid solidification range driven by large temperature gradients and large undercoolings compared to conventional solidification processes. The dendrite growth in rapid solidification condition would give rise to notable solute trapping and solute drag effects that render the original model inapplicable³⁸. Pinomaa^39,40 and Kavousi at al.⁴¹ proposed a quantitative PF model of solute trapping and continuous growth kinetics in quasi-rapid solidification successively and simulated the rapid resolidification of Al-Cu thin films⁴². This model can be seen as an extension of the classical model proposed by Karma⁸, where velocity related solute trapping/drag and kinetic supercooling are not considered. After that, Lindroos et al.⁴³ investigated the dislocation density in cellular rapid solidification. These models extend the classical PF model to the rapid solidification range, but only pertain to fixed dendrites. It is straight forward to combine the applicability of PF and efficiency of LB to develop a model for rapid solidification of alloys.

In this paper, an anisotropic LB-PF coupled model is developed and applied to the dendrite growth and movement in rapid solidification of binary alloys. The melt flow is described by using a two-relaxation-time (TRT) LB scheme, and the growth kinetics of dendrite is modeled and solved by the LB-PF scheme. Particularly, a separate equation of motion is utilized for solid migration, and it is solved by using a WENO-Z scheme. The proposed model is validated by simulations of the continuous growth of dendrites and the drafting, kissing and tumbling phenomenon of two falling particles. After that, the model is used to study the effect of inclusion melting and settling on microstructure evolution during rapid solidification processes. Finally, some conclusions are summarized.

Results and Discussion

Model validation

In order to investigate the melting-resolidification and growth-movement dynamics of dendrites in the non-equilibrium solidification, the present model is firstly validated to ensure its accuracy and reliability.

Validation of the anisotropic LB-PF model for rapid solidification

The anisotropic LB-PF model for dendrite growth in the equilibrium solidification condition was validated in our previous work²⁴. Only the validation of the anisotropic LB-PF model for rapid solidification is considered in the present work. According to Eqs. (7) and (24), both a₂ and a_t revert back to that of equilibrium solidification model with k^PF = k_e when A = 0. Thus, the solute partition coefficient is selected as a reference for model validation. In the non-equilibrium solidification process, the solute partition coefficient, k^PF(V), is correlated to the interface growth rate, described implicitly by a transcendental equation as³⁹

$${k}^{{{{\rm{PF}}}}}(V)={k}_{{{{\rm{e}}}}}\exp \left(\sqrt{2}\left(1-{k}^{{{{\rm{PF}}}}}(V)\right)V/{V}_{{{{\rm{D}}}}}^{{{{\rm{PF}}}}}\right).$$

(1)

The rapid solidification model used in this paper originated from the continuous growth model (CGM), which is a sharp interface model based on the assumption that standard diffusion is accompanied by attachment-limited kinetics at the interface^44,45. The velocity ${V}_{{{{\rm{D}}}}}^{{{{\rm{PF}}}}}$ was chosen by numerical comparing with

$${k}^{{{{\rm{CGM}}}}}(V)=\left({k}_{{{{\rm{e}}}}}+V/{V}_{{{{\rm{D}}}}}^{{{{\rm{CGM}}}}}\right)/\left(1+V/{V}_{{{{\rm{D}}}}}^{{{{\rm{CGM}}}}}\right),$$

(2)

where ${V}_{{{{\rm{D}}}}}^{{{{\rm{CGM}}}}}$ is the characterise solute trapping velocity in CGM³⁹.

Four cases corresponding to both equilibrium and non-equilibrium conditions were simulated: Case 1. non-equilibrium condition with solute drag and β > 0; Case 2. non-equilibrium condition with no solute drag and β > 0; Case 3. equilibrium condition with β > 0; Case 4. equilibrium condition with β = 0. The grid size was set as δx = 0.6W₀ and time interval, δt = 0.01τ₀, where W₀ and τ₀ are calculated by Eq. (6). Other parameters used in the simulation are listed in Table 1, and the capillary length can be obtained by ${d}_{0}=\Gamma /(1-{k}_{{{{\rm{e}}}}})| {m}_{1}^{0}| {c}_{1}^{0}$. Here, a constant dimensionless undercooling is assumed to driven solidification process, which is defined as $\Delta T\equiv ({T}_{1}-T)/(1-{k}_{{{{\rm{e}}}}})| {m}_{1}^{0}| {c}_{1}^{0}$, and fixed at −0.65. Periodic boundary conditions are applied to all boundaries.

Table 1 Material characteristics and simulation parameters for Si-9.0at%As alloy

Figure 1 displays the simulated free dendrite and the composition distribution across the solid-liquid interface. Considering the data across the solid-liquid interface varies smoothly in the whole region, which will cause a derivation error in the partition coefficient calculation, we get the concentration of the solid-liquid interface at ϕ = 0 by an interpolation method as shown in Fig. 1.

Fig. 1: The interpolated composition (blue bold dashed line) of the solid–liquid interface (red fine dashed line).

The composition and order parameter are extracted along the A–B line in the left figure, and the gray dashed line represents the position of the solid–liquid interface. The intersection point of the black dotted line and the gray dotted line is the projection interface concentration.

The simulated partition coefficient and total amount of solute as functions of tip growth rate are presented in Fig. 2a. It can be seen that the solute partition coefficient k(V) increases with the acceleration of interface velocity, and converges to the equilibrium solute partition coefficient k_e with zero velocity. The simulated data also shows good agreement with the theoretical values. The error, which increases with the accelerating interface velocity, is kept within a certain range. At a larger interface velocity (0.04 m s⁻¹), the error reaches to 3.7%. In Fig. 2b, the solute conservation of the present model is ensured and the results show good agreement with the theoretical data in a wide range of conditions.

Fig. 2: Validation of solute repartition and conservation.

a convergence of the partition coefficient of different phase field simulations (discrete point sets) to that of CGM sharp interface model (solid black line)³⁹ and equilibrium solidification theory (broken black line) for Si - 9.0at%As alloys with parameters in Table 1; b total amount of solute of the region in different examples.

Validation of the fluid-solid and the solid-solid interactions

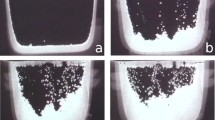
The short-range solid-solid interaction is introduced to the present model, which is used to describe collisions between solid particles and dendrites. The drafting, kissing and tumbling (DKT) process of two falling particles⁴⁶ is taken as a benchmark sample to validate the model. Figure 3 illustrates the initial and boundary conditions of the DKT process. The two-dimensional cartesian coordinates with x, y is utilized. We set the vertical direction, y, along gravity, and the horizontal direction, x, orthogonal to it. Initially, two particles are placed in the top zone of a rectangular channel. The left and right sides of the channel are solid walls. The computation domain is set as W × H = D × 4D. The diameter, D, of the particles is 0.002 m. The solid-liquid density ratio is set to be ρ_s/ρ₁ = 1.01, the fluid kinematic viscosity is ν = 1.0 × 10⁻⁶m² s⁻¹, and the acceleration of gravity is g = 9.8 m s⁻¹. In the simulation, the domain was divided uniformly into 250 × 1000 grids, the no-slip condition was applied to the left and right boundaries, and the full development boundary (∂V_f/∂y = 0) was applied to the top and bottom boundaries.

Fig. 3: Schematic diagram of initial geometric conditions of DKT example.

The width and length of the domain are W and H, respectively, the diameter of the two particles is D, and the spacing between them is 2D. The left and right boundaries are solid walls with no-slip condition, and the top and bottom boundaries are liquid with the full development boundary.

As shown in Fig. 3, the two particles are released along the centerline at a height of 0.072 m (red) and 0.068 m (blue), respectively. The two particles then fall and collide under the gravity and hydrodynamic forces. The horizontal and vertical trajectories of the two particles are tracked and compared with the data given by Jafari⁴⁷ in Fig. 4. The appropriate interaction constant, κ, in Eq. (34) was obtained through series of numerical experiments with various κ. Finally, as shown in Fig. 4, the simulation recovers the DKT process of the two falling particles, and the particles trajectories converge quantitatively to the benchmark.

Fig. 4: The positions of two particles in DKT benchmark.

a horizontal displacement; b vertical displacement. The results were compared with those of Jafari⁴⁷.

Investigation of dendrite behavior and its affects on microstructure evolution and segregation

Non-equilibrium solidification is a ubiquitous phenomenon in industry, and the extreme solidification conditions in advanced technology such as additive manufacturing provides conditions for rapid solidification. The non-equilibrium effects in the above process greatly changes the micro-segregation mode of the alloy, which has a significant influence on the microstructure evolution and ultimately affects the material properties. In addition, the behavior of isolated dendrites, such as growth, melting and movement, also changes the melt convection and heat transfer, thus affecting the micro-segregation and microstructure. In this section, the effects of non-equilibrium solidification conditions and dendrite behavior on microstructure evolution and segregation are studied.

In total, three solidification conditions were investigated. For brief description, the three conditions were defined as follows: Condition 1 (NTND), without solute trapping or solute drag; Condition 2 (WTND), with solute trapping but without solute drag; Condition 3 (WTWD), with solute trapping and solute drag.

Dendrite growth and movement in several solidification conditions

This section demonstrates the solute trapping effect on dendrite growth, as well as the influence of the solute drag, dendrite movement and melt convection. The same physical parameters of Si-9.0at%As alloy in the above section was also chosen in the present simulation. The growth of single dendrite was firstly investigated with initial supersaturation S = −0.65. The computational domain was set as 1000 × 1000 grids and the seeds were fixed at center of the domain. The simulated morphology and solute distribution at the time t = 2.0 × 10⁻⁴ s, 6.9 × 10⁻⁵s and 3.5 × 10⁻⁴ s were recorded for conditions 1, 2 and 3, respectively. The boundary condition of the solute field is no flux boundary condition, and the boundary of the flow field is the development boundary.

Figure 5 a shows that the dendrite arms become coarser with solute drag effect while slender with solute trapping effect, which results from the the non-equilibrium distribution of solute at the interface. Figure 5b depicts that the solid concentration of the solute trapping condition is larger than that of equilibrium condition while the distributions of liquid concentrations are reversed for these conditions, which is consistent with the principle of solute conservation. On contrary, the solute drag can transfer solutes from solid to liquid, which is in competition with the solute trapping effect, resulting in lower supersaturation and slower advancement of the dendrite tips. In the presence of solute drag, the concentration of solute in both solid and liquid phases is higher than that of equilibrium. The enrichment of solutes in the liquid phase caused by solute drag weakens the anisotropy of the crystal interface, resulting in a slow growth rate and larger radius. At later stages of solidification, the liquid phase region would shrink which will result in a higher concentration than that in the equilibrium condition.

Fig. 5: Dendrite profile and solute distribution with interfacial non-equilibrium effect.

a the dendrite profile under various conditions; b distribution of solutes along the dendrite horizontal midline.

Figure 6 illustrates the simulated dendrite tip growth speed and tip radius in three different solidification conditions. It can be found that the dendrite growth promoted by the solute trapping effect and weakened by the solute drag effect. Considering the Gibbs-Thomson relation,

$${c}_{1}/{c}_{1}^{0}=1-(1-k){d}_{0}{{{\mathcal{K}}}}-(1-k){\beta }_{0}{V}_{{{{\rm{n}}}}},$$

(3)

It can be concluded that the dendritic tip radius ($1/{{{\mathcal{K}}}}$) of the case with solute drag should be larger than that equilibrium, and the dendritic tip radius of the case with solute trapping but without solute drag should be smaller than equilibrium.

Fig. 6: Comparison of dendrite tip growth rate a and tip radius b with different solidification conditions.

equilibrium solidification (green lines), rapid solidification with solute trapping but without solute drag (red lines) and rapid solidification with solute trapping and solute drag (blue lines).

The presences of dendrite movement and melt flow play a crucial role in altering heat and mass transfer. They can significantly influence the dendrite growth behavior and the solute distribution. We attempted to reveal the coupling mechanism of multiple physical fields by simulations of the movement and growth of individual dendrites in three solidification conditions. The solid-liquid density ratios were set as ρ_s/ρ₁ = 1.05, 1.10 and 1.15, respectively. Figure 7a–c show the growth of fixed dendrites with forced convection from bottom to top. Figure 7d–l depict the sedimentation and growth of free dendrites with different solid-liquid density ratios under the gravity. Figure 7m displays the comparison of the dendrite profiles, the solute distributions and the velocity field as the lower tips of the dendrite reached the bottom of the calculated region, and recorded the lower tip radius and time.

Fig. 7: Comparison of flow field, solute distribution and phase profile of dendrites with different solid–liquid density ratio.

The direction and size of the arrow indicate the direction and speed of the flow respectively, and the solid–liquid density ratios are ρ_s/ρ_l = 1.05 (d–f), 1.10 (g–i) and 1.15 (j–l). The fixed dendrites with flow are shown in (a–c). Three kinds of solidification conditions are considered: NTND (a, d, g, j), WTND (b, e, h, k) and WTWD (c, f, i, l). The growth time and radius of each dendrite are shown in (m).

It can be seen that the melt flow greatly changes the morphology of dendrite in case of forced convection and dendrite movement. The growth of dendrite arms in the upstream direction is significantly accelerated, while that in the downstream direction is inhibited. The dendrites settle down under the gravity. Meanwhile, the melt flows upward relative to the dendrites. As a result, the solute is carried away from the upstream to the downstream region, leading to a higher level of supersaturation in the southern tip area. At the same time, the horizontal tips agitates the fluid to cause eddy currents. Therefore, the surrounding melt carries solute to the upper tip region, resulting in a lower supersaturation in this region. This is an important reason for the difference in growth of different tips.

Furthermore, the solid-liquid density ratio has a significant impact on the intensity of the melt flow. The larger solid-liquid density ratio leads to a more vigorous flow, resulting in a more significant tip growth difference and ultimately resulting in a larger tip radius in the direction of gravity compared to cases with smaller density ratios. The dendrite with a relatively small density falls for a long time, resulting in a weaker flow and a longer and smoother dendrite arm. Conversely, when the density is relatively high, the falling time is short, causing severe eddy current, and the dendrite that reaches the bottom is relatively, but the interface appears rough and exhibits significant instability.

By comparing the dendrite patterns in the conditions, we can find that the growth of the upstream dendrite arm are accelerated and the arms become elongated when only solute trapping is considered. In this condition, the concentration in the upstream tip is clearly higher than that of other tips due to the faster tip growth speed. In addition, it is worth mentioning that the dendrite growth is more ”regular” with the solute trap effect, and the lateral tip is almost distributed along the line between the south tip and the horizontal tip. The possible reason is that the solute is heavily enriched in the liquid phase of the solid-liquid interface due to the solute drag effect. Meanwhile, the enriched solute is distributed along the streamline with the action of the flow field, which inhibits the growth of the secondary dendrite arm in this region.

Non-equilibrium effect on columnar growth in directional solidification

We now simulated the microstructure evolution in the directional solidification to investigate the non-equilibrium interfacial effect. In the simulation, a flat solid-liquid interface is initially set at the bottom of the computation domain, and the temperature distribution is set by T = T_ref + G(z − V_pt). Here, G is the temperature gradient and V_p is the pulling rate. The cooling rate V_c can be obtained by V_c = G × V_p. A Gaussian noise was introduced at the interface to simulate thermodynamic disturbance⁴⁸. The computational domain was divided into 1500 × 1500 grids, the time interval was set as δt = 0.01τ₀. Periodic boundary conditions are used on the left and right sides, for top and bottom sides, no flux boundary was used for solute field and the development boundary was used for flow field. The solute trapping and solute drag effects on the microstructure and segregation at different cooling rates, V_c, were firstly discussed. The cooling rates were set as 9000, 900 and 90 K s⁻¹. Figure 8 gives the simulated columnar growth with V_c = 9000 K s⁻¹. As it is shown, the planar interface is unstable with thermodynamic perturbation and the resulting primary dendrite arms grow driven by both temperature and constitutional supercooling. In order to elucidate the synergistic and competitive mechanism of temperature and composition involved, we investigated the primary dendrite arm spacing (PDAS), solute segregation and solidification rates in different solidification processes. The segregation degree is defined by

$${I}_{{{{\rm{s}}}}}=\frac{1}{{V}_{{{{\rm{I}}}}}}{\int}_{{\!V}_{{{{\rm{I}}}}}}\frac{\left\vert c-{c}_{0}\right\vert }{{c}_{0}}{{{\rm{d}}}}{V}_{{{{\rm{I}}}}}$$

(4)

where V_I is the volume of computation domain and c₀ the initial concentration.

Fig. 8: Morphology of columnar growth and solute distribution with different solidification conditions, the cooling rate was set as V_c = 9 × 10³ K s⁻¹.

a–c condition 1 (NTND); d–f condition 2 (WTND); g–i condition 3 (WTWD).

Figure 9 shows the comparison of PDAS in the different conditions. It can be found that the PDAS decreased with increasing cooling rate, while the solute trapping effect reduced the PDAS and the solute drag effect increased it.

Fig. 9

Comparison of PDAS in equilibrium solidification and rapid solidification at different cooling rates. A total of three conditions are shown, namely, NTND, WTND and WTWD. The red line with diamond represents the cooling rate is 9000 K s⁻¹. The green line with triangle represents the cooling rate is 900 K s⁻¹, and blue line with inverted triangle 90 K s⁻¹.

Figure 10 displays the solidification rates and solute segregation effects in the three different solidification conditions. It can be seen in Fig. 10a that the solidification rate of the case of condition 2 is much higher than the other two conditions (without trapping and drag, with trapping and drag) at the initial stage of solidification, which indicated that the constitutional supercooling drives the grain growth much more than temperature supercooling. However, at the end of solidification, the solidification rate of condition 1 with V_c = 9 × 10³ K s⁻¹ exceeds that of condition 2 with V_c = 9 × 10² and V_c = 90 K s⁻¹. It indicates that the temperature undercooling is higher than constitutional supercooling at the solidification front and plays a leading role in driving the solidification process.

Fig. 10: Effects of different cooling rates and solidification conditions on solidification rates and solute segregation.

a variation of solidification rate with time; b solute segregation index; c segregation rates at different solid-phase fractions.

As shown in Fig. 10b and c, the segregation degree increases with the solidification process, and the segregation degree of condition 2 is always larger than that of condition 1 with the same cooling rate. In case of condition 3, the solidification rate was reduced significantly compared with the other two conditions, which also indicated the dominant role of constitutional supercooling at the initial solidification stage. This phenomenon is related to the solute distribution of single dendrite growth mentioned above.

Figure 11 displays the simulated morphology and solute distribution in different solidification conditions. It can be seen that the solidified structures are closer together at such high cooling rate. The microstructure of condition 1 remains columnar, and the primary dendrite arm spacing is smaller. However, in condition 2 and 3, the microstructure develop into seaweed crystals, and the crystals of condition 3 are coarser than that of condition 2, which can be attributed to the different solute partition rules in the solid-liquid front. As summarized above, constitutional undercooling plays a leading role in driving liquid-solid transformation at the initial solidification stage. In condition 2, there is a higher level of constitutional supercooling compared to condition 1. Conversely, condition 3 exhibits lower constitutional supercooling.

Fig. 11: Simulated morphology and solute distribution in different solidification conditions, the cooling rate was set as V_c = 3 × 10⁴ K s⁻¹.

a–c condition 1 (NTND); d–f condition 2 (WTND); g–i condition 3 (WTWD).

Figure 12 shows the solidification rate, solute segregation index and segregation rate in the simulation of various V_cs. As depicted in Fig. 12a, different undercooling can lead to contrasting solidification rates. Consequently, condition 2 forms seaweed crystals. However, at the end of solidification, temperature undercooling greatly exceeds constitutional supercooling, which becomes the leading driving force for crystal growth of condition 3, and meanwhile, the enriched solute at the solid-liquid front leads to the instability of the interface, and seaweed crystals arises with the larger total supercooling.

Fig. 12: Effects of solidification conditions on solidification rates and solute segregation with large cooling rate, V_c = 6 × 10⁴ K s⁻¹.

a variation of solidification rate with time; b solute segregation index; c segregation rates at different solid-phase fractions.

Effects of solid settlement and remelting on microstructure evolution

In this subsection, the growth and remelting behavior of free solid particles in a molten pool was investigated. Initially, three seeds were placed in the top region of the computational domain. The computational domain was divided into 1200 × 1200 grids, the cooling rate was set fixed at V_c = 6.0 × 10⁴ K s⁻¹. The results are shown in Figs. 13 and 14.

Fig. 13: Effect of free equiaxed crystals on directional solidification microstructure with V_c = 6 × 10⁴ K s⁻¹.

a–c without solute trapping and drag; d–f with solute trapping but without solute drag; g–i with solute trapping and drag.

Fig. 14: Effects of free equiaxed crystals on solidification rates and solute segregation with large cooling rate, V_c = 6 × 10⁴ K s⁻¹.

a variation of solidification rate with time; b solute segregation index; c segregation rates at different solid-phase fractions.

The free dendrites (grains) can greatly changes the final microstructure and solute segregation. Initially, the free seeds are surrounded by the supercooled melt and grow into dendrites, while the seeds at the bottom grow as columnar crystals along the temperature gradient. It can be seen from Fig. 14a and c that the nucleated grains can accelerate the solidification speed and the segregation rate. Subsequently, the free dendrites approach with each other which increases the solute concentration and decreases the undercooling, and thus the growth was inhibited at the approaching region. Meanwhile, the solidification speed and the solute segregation rate decrease to lower levels, as shown in Fig. 14. Figure 13 also illustrates that the solidification behaviors are significantly different in the above process. In condition 1 and condition 3, the solidification speeds are slower, the advance speed of columnar structure front is slow. Columnar crystals of condition 1 are obstructed by equiaxed dendrite arms, and equiaxed dendrites continue to grow and occupy the upper space. However, the free crystals of condition 3 grow so slowly and lose their anisotropy in the low constitutional supercooling environment. Thus, the bottom columnar crystals enclose free grains and develop together into seaweed crystals. In condition 2, solute trapping effect significantly increased the solidification speed. The free dendrites occupy the growth space of the bottom columnar pattern and avoid their growth into seaweed morphology. Meanwhile, the secondary dendrite arms are formed rapidly on the arms of free dendrites, and grow along the temperature gradient to become the dominant structure in the residual region.

Figures 15 and 16 show the remelting, sedimentation of high concentration solid particles in the molten pool and its effect on the directional solidified microstructure. The impurity particles were put at the top of melt pool as the primary dendrite arms reached a certain length. It can be seen from Fig. 16 that the solidification and segregation trends are similar in different conditions, while the microstructure are quite different as Fig. 15 shown. At the early stage, the impurity particles melt and settle, forming a solute channel with positive segregation along the wake, as shown in Fig. 15. The particles formed a solute rich region after fully remelted at the front of the bottom columnar crystals, where the constitutional supercooling is very small and the dendrites grown slowly and even melt, as shown in Fig. 15b, e, h. However, the dendrites on both sides were less affected and grow rapidly along the temperature gradient until the solute rich region surrounded. Finally, the residual liquid phases region solidified with the decreasing temperature, and the solid phase concentration was significantly higher than the surrounding area due to its slowly diffusion in solid.

Fig. 15: Effect of high concentration impurity particles on directional solidification microstructure with V_c = 6 × 10⁴ K s⁻¹.

a–c condition 1 (NTND); d–f condition 2 (WTND); g–i condition 3 (WTWD).

Fig. 16: Effects of high concentration impurity particles on solidification rates and solute segregation with large cooling rate, V_c = 6 × 10⁴ K s⁻¹.

a variation of solidification rate with time; b solute segregation index; c segregation rates at different solid-phase fractions.

In the above solidification processes, there were obvious differences between different conditions of microstructure evolution. Firstly, it can be seen from Fig. 16 that the high concentration inpurities significantly reduces the solidification rates and increases the degree of solute segregation. Different from condition 1, the solidified microstructure in condition 2 and 3 are seaweed crystals, which are relatively compact, while the dendrite arms in condition 1 are sparse as shown in Figs. 11 and 15. The small crystal arms between the two larger dendrite arms grow slowly and easily melt in condition 1. Therefore, the influence of the solute rich region on the microstructure in condition 1 is much larger than that in the other two conditions, as shown in Fig. 15c, f, i. It can be seen from Fig. 16a that the solidification rate of condition 1 slowed down and was less than that of the other two conditions, after putting the high concentration impurity. Compared with condition 2, dendrite in condition 3 grow slowly, resulting in a larger solute enrichment region. When reaching the solidification front, the solid particles agitated the melt to produce two vortices on both sides, which brought the solute to both sides, so that the dendrites in the middle could grow rapidly until the solute rich region was divided into two parts, as Fig. 15h, i show. This is an important factor that caused the difference in microstructure between condition 2 and 3.

Simulation of the columnar-to-equiaxed transition of Al-3.0wt%Cu alloy in non-equilibrium solidification

In this subsection, we simulated the CET process of Al-3wt%Cu alloy and investigated the transition rule and solutal interactions in equ- and non-equilibrium. A total of three cases (NTND, WTND, and WTWD) were simulated, and all cases shared the same material properties listed in Table 2. Initially, four seeds were set at the bottom of the computational domain, then, several equiaxed grains nucleated after a period of cooling, grown, and settled. It was assumed that the equiaxed grains nucleate at a fixed temperature,T_N, behind the liquidus isotherm, T_L(c₀), as shown in Fig. 17b. The directional solidification shown in Fig. 17a was characterized by a frozen temperature approximation with G = 3.0 × 10³ K m⁻¹ and V_p = 5.0 × 10⁻² m s⁻¹. Periodic boundary conditions are used on the left and right sides, for top and bottom sides, no flux boundary was used for solute field and the development boundary was used for flow field.

Table 2 Material characteristics and simulation parameters for Al-3.0wt%Cu alloy

Fig. 17: Predicted microstructure and concentration profile for three conditions: NTND, WTND and WTWD.

a microstructure morphology and solute distribution; b concentration profile along line I−I, II−II, III−III and schematic illustration of the frozen temperature approximation.

Figure 17 a shows the predicted microstructure and solute concentration for three conditions: NTND, WTND and WTWD. It can be seen that the solute trapping effect accelerates tip advance velocity and promotes dendrite side branches which solute drag effect inverses. Figure 17b gives the concentration profiles along line I−I, II−II and III−III of Fig. 17a and the fit lines represented by colored dashed lines, c¹(I−I, II−II, III−III). ${c}_{0}^{1}(T)$ represents the liquidus equilibrium concentration which is a function of temperature. It can be seen that solute trapping effect reduced the solute concentration at the columnar front, as a result, the undercooling, ${T}_{{{{\rm{L}}}}}-T={m}_{1}({c}_{1}-{c}_{0}^{1})$, which is proportional to the distance between c₁ and ${c}_{0}^{1}$, was deduced. This lead to a larger advancing velocity of columnar front in non-equilibrium, the opposite is true when the solute drag effect is considered.

Figure 18 shows the concentration distribution at the tips, a, and roots, b, of columnar crystals for three conditions. In Fig. 18a, the maximum concentration occurred at the columnar tips and the minimum concentration occurred inside the columnar crystals. With the columnar front advancing, the solute was rejected into liquid and diffused around, which resulted in such concentration profiles in Fig. 18a. Besides, the liquid concentration for three conditions was ${c}_{{{{\rm{WTWD}}}}}^{1} \,>\, {c}_{{{{\rm{NTND}}}}}^{1} \,>\, {c}_{{{{\rm{WTND}}}}}^{1}$ and in solid, the relationship was changed as ${c}_{{{{\rm{NTWD}}}}}^{{{{\rm{s}}}}}\,>\, {c}_{{{{\rm{NTND}}}}}^{{{{\rm{s}}}}}\,>\, {c}_{{{{\rm{WTWD}}}}}^{{{{\rm{s}}}}}$, which is consistent with Figs. 5 and 17b. Figure 18b gives the solute profile along an isotherm at the columnar roots in Fig. 17a (line A-A), the solute concentration is almost homogenous in the solid and liquid phases. In roots of columnar crystals, the concentration in liquid is close to liquidus equilibrium concentration, ${c}_{0}^{1}$, and the undercooling almost vanished. The growth of crystals almost stopped and solute fully diffused.

Fig. 18: Predicted concentration profile for three conditions: NTND, WTND and WTWD.

a solute concentration at columnar tips along line B-B, C-C and D-D; b solute concentration along line A-A.

Figure 19 shows the predicted microstructure and solute distribution during the CET process for three conditions. It assumed that the temperature at the dashed gray line in Fig. 19 reached the nucleation temperature at about 1.04 s. Then, the equiaxed grains nucleated, grown, and settled to the columnar front, a large amount of solute was rejected into the liquid, the growth of columnar crystals stopped and CET occurred. It can be seen from Figs. 19 and 17 that the columnar crystal heights are very different at nucleation time, which directly lead to the differences in the time and location of CET occurrence for three conditions. In the WTND case, the columnar front advanced faster than those in the NTND and WTWD cases, the equiaxed grains settled to the columnar front in a short period of time after nucleating, and the CET occurred faster and at a higher position. The size of the equiaxed dendrites is smaller than those in the two other cases. In addition, there is higher constitutional supercooling at the liquid side of the solid-liquid interface, the equiaxed grains became highly dendritic in the NTND and WTND cases. In the WTWD case, the columnar crystal length was shorter, and equiaxed crystals took longer to settle and grow, the CET occurred later and at a lower position. Meanwhile, the solute drag effect caused the lower constitutional supercooling in liquid, the nucleated crystals grew slower and remained somewhat globulitic.

Fig. 19: Predicted microstructure and solute concentration during CET process for three conditions.

a, b NTND; c, d. WTND; e, f WTWD. The dashed gray line indicates that the nucleation temperature has reached at this location and exquixed dendrites nucleated here.

Figure 20 gives the total solid fraction a, segregation degree, b, solidification rate, c, and segregation rate, d, in the domain change with time for three conditions. It can be seen from Fig. 20a that the relationship of solidification rates in three cases is: V_WTND > V_NTND > V_WTWD and the relationship of solute segregation degrees is: I_WTND > I_NTND > I_WTWD. In the initial stage of solidification, the solidification rate and segregation rate quickly reached a small peak due to the large constitutional supercooling at the solid-liquid front, as shown in Fig. 20c, d. Subsequently, the solidification rate and segregation rate decreased rapidly with the influence of the rejected solute, and slowly increased with time. The growth of columnar crystals reached a relatively stable stage. The moments that equiaxed crystals nucleated and the CET occurred were given by the colored dashed lines in Fig. 20a–d. It can be seen that there is a sudden increase in the solidification rate and solute segregation rate at the moment equiaxed crystals nucleated and a sudden decrease when the CET occurred, which can assit in determining whether nucleation and the CET are occurring.

Fig. 20: Effects of CET process on solidification rates and solute segregation of Al-3.0% Cu alloy.

The total solid fraction (a), segregation degree (b), solidification rate (c), and segregation rate (d) in the domain change with time for three conditions. The dashed gray lines indicate that the moment equixed nucleation occurred, the colored dashed lines represent the occurrence of CET for three conditions: green, WTND; red, NTND; blue, WTWD.

We should note that the present work were carried out in two-dimensional space, and the dendrite growth and solute transport are quite different in the three-dimensional case, which is worthy of future study. When considering the 3D case, the movement and collision of dendrites may lead to locally more violent flows, and the case of turbulence may need to be considered. Furthermore, in the present model, dendrite orientation and rotation are described with Euler angles which can be superimposed in 2D. However, in 3D case, Euler angles cannot be simply superimposed, so it may be necessary to consider quaternons to achieve rotation. Besides, in the 3D case, the influence of curvature is more obvious, the dendrite morphology is more complex, and the lateral branches are more obvious than the 2D case.

Methods

Anisotropic lattice Boltzmann equation for dendrite growth

The quantitative PF equation is used to mathematically describe the dendritic growth in quasi-rapid solidification. The governing equation of the order parameter, ϕ, which varies continuously from −1 in liquid to +1 in solid, is given as ref. ¹⁰

$$\tau ({{{\bf{n}}}})\frac{\partial \phi }{\partial t}=\nabla \cdot ({W}^{2}({{{\bf{n}}}})\nabla \phi )+{W}_{0}^{2}\nabla \cdot {{{\boldsymbol{{{{\mathcal{N}}}}}}}}+(\phi -{\phi }^{3})-\lambda {M}_{1}{c}_{1}^{0}S{(1-{\phi }^{2})}^{2},$$

(5)

where τ(n) characters the anisotropic attachment time of interfacial atoms, and it depends on the interface unit normal vector n with ${\bf{n}} = - {\nabla}\,{\phi}\big/|\,{\nabla}\,{\phi}\,|$. W(n) = W₀⋅a_s(n), where W₀ is the spatial scale. The coupling coefficient λ evaluates the driving force of supersaturation, S, on phase transition, M₁ is the scaled magnitude of the liquidus slope m₁. In the present work, we set ${M}_{{{{\rm{c}}}}}=\frac{| {m}_{1}| (1-{k}_{{{{\rm{e}}}}})}{{L}_{{{{\rm{h}}}}}/{c}_{{{{\rm{p}}}}}}{c}_{\infty }$. Here, k_e is the equilibrium solute partition coefficient, L_h is the latent heat, c_p is the thermal capacity, and c_∞ is the concentration far from the interface that equals the initial value ${c}_{1}^{0}$.

In the PF method, W(n) and τ(n) are related to the solutal capillary length d₀ and the kinetic coefficient β₀ via³⁹,

$$\begin{array}{l}{d}_{0}\cdot {a}_{{{{\rm{s}}}}}({{{\bf{n}}}})\,=\,{a}_{1}\frac{W({{{\bf{n}}}})}{\lambda },\\ {\beta }_{0}\cdot {a}_{{{{\rm{k}}}}}({{{\bf{n}}}})\,=\,{a}_{1}\frac{\tau ({{{\bf{n}}}})}{\lambda W({{{\bf{n}}}})}-{a}_{1}{a}_{2}\frac{W({{{\bf{n}}}})}{{D}_{1}},\end{array}$$

(6)

where ${a}_{{{{\rm{s}}}}}({{{\bf{n}}}})=1-3{\varepsilon }_{{{{\rm{c}}}}}+4{\varepsilon }_{{{{\rm{c}}}}}({n}_{{{{\rm{x}}}}}^{4}+{n}_{{{{\rm{y}}}}}^{4}+{n}_{{{{\rm{z}}}}}^{4})$ and ${a}_{{{{\rm{k}}}}}({{{\bf{n}}}})=1+3{\varepsilon }_{{{{\rm{k}}}}}-4{\varepsilon }_{{{{\rm{k}}}}}({n}_{{{{\rm{x}}}}}^{4}+{n}_{{{{\rm{y}}}}}^{4}+{n}_{{{{\rm{z}}}}}^{4})$. Here, a_s(n) and a_k(n) are the capillary function and the kinetic anisotropic function, respectively. D₁ is the diffusive coefficient of solute in the liquid phase. Let β = β₀⋅a_k(n) for simplification. With the known β and D₁, the τ(n) can be obtained from Eq. (6). When β = 0, Eq. (6) can be rewritten as $\tau ({{{\bf{n}}}})={\tau }_{0}\cdot {a}_{{{{\rm{s}}}}}^{2}({{{\bf{n}}}})={a}_{2}W({{{\bf{n}}}})/{D}_{1}$, where τ₀ is the time scale. a₁ and a₂ are the asymptotic analysis constants, and a₁ = 0.8839. a₂ can be computed by

$${a}_{2}={a}_{2}^{\pm }=\frac{4\sqrt{2}}{5}\left(0.0638+\frac{\sqrt{2}\ln 2}{2}-0.0505A+\frac{\sqrt{2}\,\mp\, 2\sqrt{2}}{4}A\right),$$

(7)

where +/− corresponds to zero/full solute drag. A is the trapping parameter determined by $A={D}_{1}/({V}_{{{{\rm{D}}}}}^{{{{\rm{PF}}}}}{W}_{0})$ and equals to zero in equilibrium solidification, ${V}_{{{{\rm{D}}}}}^{{{{\rm{PF}}}}}$ is the characteristic velocity. The anisotropic vector ${{{\boldsymbol{{{{\mathcal{N}}}}}}}}$ in Eq. (5) is defined as

$${{{\boldsymbol{{{{\mathcal{N}}}}}}}}({{{\bf{x}}}},t)=| \nabla \phi {| }^{2}{a}_{{{{\rm{s}}}}}({{{\bf{n}}}})\left(\frac{\partial {a}_{{{{\rm{s}}}}}({{{\bf{n}}}})}{\partial \left({\partial }_{{{{\rm{x}}}}}\phi \right)},\quad \frac{\partial {a}_{{{{\rm{s}}}}}({{{\bf{n}}}})}{\partial \left({\partial }_{{{{\rm{y}}}}}\phi \right)},\quad \frac{\partial {a}_{{{{\rm{s}}}}}({{{\bf{n}}}})}{\partial \left({\partial }_{{{{\rm{z}}}}}\phi \right)}\right).$$

(8)

To model the dendrite growth with arbitrary preferring orientations, we should define a new Cartesian coordinates in which the (x, y, z)-axes are set parallel to the [100], [010], [001] directions of the dendrite. The relation between the two Cartesian coordinates (x, y, z)∣_old and (x, y, z)∣_new is characterized by three Euler angles (θ_x, θ_y, θ_z). For the two-dimensional (2D) dendrite growth, we set θ to be the angle between the x-axes in the two coordinates. The calculation of n and ${{{\boldsymbol{{{{\mathcal{N}}}}}}}}$ are executed with respect to the new Cartesian coordinates rather than the original coordinates. After that, the calculated n and ${{{\boldsymbol{{{{\mathcal{N}}}}}}}}$ are transformed into the original coordinates with θ.

Indeed, Euqation(5) can be regarded as a convective diffusion equation with an additional anisotropic factor τ(n) in front of the time derivative²¹. In order to handle the anisotropic factor and $\nabla \cdot {{{\boldsymbol{{{{\mathcal{N}}}}}}}}$, an anisotropic LB scheme is applied to solve the PF equation, which can be written in the following formula

$$\begin{array}{r}{g}_{i}({{{\bf{x}}}}+{{{{\bf{c}}}}}_{i}\delta t,t+\delta t)=\frac{{\tau }_{0}}{\tau ({{{\bf{n}}}})}\left\{{g}_{i}({{{\bf{x}}}},t)-(1-\tau ({{{\bf{n}}}})){g}_{i}({{{\bf{x}}}}+{{{{\bf{c}}}}}_{i}\delta t,t)\right.\\ -\left.\frac{1}{{\eta }_{\phi }({{{\bf{x}}}},t)}\left[{g}_{i}({{{\bf{x}}}},t)-{g}_{i}^{{{{\rm{eq}}}}}({{{\bf{x}}}},t)\right]+{w}_{i}{Q}_{\phi }({{{\bf{x}}}},t)\delta t\right\},\end{array}$$

(9)

where g_i(x, t) (i = 0, 1,…,q−1, q represents the number of directions of the discrete velocity c_i) is the distribution function of ϕ at position x and time t, and ${g}_{i}^{{{{\rm{eq}}}}}({{{\bf{x}}}},t)$ is the corresponding equilibrium distribution function. η_ϕ is the relaxation time, δt is the time step, and Q_ϕ represents for the source term. In the present work, the ${g}_{i}^{{{{\rm{eq}}}}}$ is chosen as

$${g}_{i}^{{{{\rm{eq}}}}}({{{\bf{x}}}},t)={w}_{i}\left(\phi ({{{\bf{x}}}},t)-\frac{{{{{\bf{c}}}}}_{i}\cdot {{{\boldsymbol{{{{\mathcal{N}}}}}}}}({{{\bf{x}}}},t)}{{c}_{{{{\rm{s}}}}}^{2}}\frac{{W}_{0}^{2}}{{\tau }_{0}}\frac{\delta t}{\delta x}\right),$$

(10)

where w_i is the weight coefficient and where c_s is the lattice sound speed. η_ϕ is calculated by

$${\eta }_{\phi }({{{\bf{x}}}},t)=\frac{1}{{c}_{{{{\rm{s}}}}}^{2}}{a}_{{{{\rm{s}}}}}^{2}({{{\bf{n}}}})\frac{{W}_{0}^{2}}{{\tau }_{0}\delta t}+\frac{1}{2}.$$

(11)

The source term Q_ϕ coupled the supersaturation, described as

$${Q}_{\phi }({{{\bf{x}}}},t)=\left(\phi -{\phi }^{3}\right)-\lambda {\left(1-{\phi }^{2}\right)}^{2}S.$$

(12)

The macroscopic order-parameter ϕ is related with the distribution functions g_i and ${g}_{i}^{{{{\rm{eq}}}}}$ through

$$\mathop{\sum }\limits_{i=0}^{q-1}{g}_{i}^{{{{\rm{eq}}}}}=\mathop{\sum }\limits_{i=0}^{q-1}{g}_{i}=\phi$$

(13)

Two-relaxation-time lattice Boltzmann equation for melt flow

The melt flow can influence the heat and mass transport in dendrite growth, and can significantly influence the evolution of solidification microstructure. The melt flow is usually treated as governing by the Navier-Stokes (N-S) equations,

$$\begin{array}{ll}\frac{\partial {\rho }_{1}}{\partial t}+\nabla \cdot ({\rho }_{1}{{{{\bf{u}}}}}_{{{{\rm{f}}}}})\,=\,0,\\ \frac{\partial ({\rho }_{1}{{{{\bf{u}}}}}_{{{{\rm{f}}}}})}{\partial t}+\nabla \cdot ({\rho }_{1}{{{{\bf{u}}}}}_{{{{\rm{f}}}}}{{{{\bf{u}}}}}_{{{{\rm{f}}}}})\,=\,-\nabla p+\nabla \cdot ({\rho }_{1}\nu (\nabla {{{{\bf{u}}}}}_{{{{\rm{f}}}}}+{\nabla }^{{{{\rm{T}}}}}{{{{\bf{u}}}}}_{{{{\rm{f}}}}}))+{{{\boldsymbol{F}}}},\end{array}$$

(14)

where ρ₁ is the melt density, u_f the flow velocity, p the pressure in fluid ν the kinematic viscosity and F the external force. In the present work, the TRT-LB scheme is chosen to solve N-S equations for its numerical stability and computational efficiency. The evolution equation of the TRT-LB scheme for the melt flow can be expressed as

$$\begin{array}{r}{f}_{i}\left({{{\bf{x}}}}+{{{{\bf{c}}}}}_{i}\delta t,t+\delta t\right)-{f}_{i}({{{\bf{x}}}},t)=-\frac{1}{{\eta }_{{{{\rm{f}}}}}^{+}}\left[{f}_{i}^{+}({{{\bf{x}}}},t)-{f}_{i}^{{{{\rm{+,eq}}}}}({{{\bf{x}}}},t)\right]\\ -\frac{1}{{\eta }_{{{{\rm{f}}}}}^{-}}\left[{f}_{i}^{-}({{{\bf{x}}}},t)-{f}_{i}^{{{{\rm{-,eq}}}}}({{{\bf{x}}}},t)\right]+{F}_{i}^{{{{\rm{trt}}}}},\end{array}$$

(15)

where f_i(x, t) and ${f}_{i}^{{{{\rm{eq}}}}}({{{\bf{x}}}},t)$ are the density distribution function and equilibrium distribution function in i-th direction, and $\bar{i}$ for the opposite direction of the i-th direction. ${f}_{i}^{+}=({f}_{i}+{f}_{\bar{i}})/2$ and ${f}_{i}^{-}=({f}_{i}-{f}_{\bar{i}})/2$ are the symmetric and asymmetric forms of the density distribution functions, respectively. The symmetric and asymmetric relaxation time, ${\eta }_{{{{\rm{f}}}}}^{+}$ and ${\eta }_{{{{\rm{f}}}}}^{-}$ are correlated by

$$\Lambda =\left({\eta }_{{{{\rm{f}}}}}^{+}-\frac{1}{2}\right)\left({\eta }_{{{{\rm{f}}}}}^{-}-\frac{1}{2}\right),$$

(16)

where ${\eta }_{{{{\rm{f}}}}}^{+}$ is related to the kinematic viscosity ν by $\nu =\left({\eta }_{{{{\rm{f}}}}}^{+}-\frac{1}{2}\right){c}_{{{{\rm{s}}}}}^{2}\delta t$ and Λ is fixed as 0.25⁴⁹. ${F}_{i}^{{{{\rm{trt}}}}}$ is the force term which can be constructed with external force on the fluid.

The equilibrium distribution function, ${f}_{i}^{{{{\rm{eq}}}}}$, is given as

$${f}_{i}^{{{{\rm{eq}}}}}={\omega }_{i}{\rho }_{1}\left[1+\frac{{{{{\bf{c}}}}}_{i}\cdot {{{{\bf{u}}}}}_{{{{\rm{f}}}}}}{{c}_{{{{\rm{s}}}}}^{2}}+\frac{{\left({{{{\bf{c}}}}}_{i}\cdot {{{{\bf{u}}}}}_{{{{\rm{f}}}}}\right)}^{2}}{2{c}_{{{{\rm{s}}}}}^{4}}-\frac{{{{{\bf{u}}}}}_{{{{\rm{f}}}}}^{2}}{2{c}_{{{{\rm{s}}}}}^{2}}\right],$$

(17)

In this paper, a two dimensional D2Q9 model⁵⁰ with nine discrete velocities is used, and i = 0,1, 2,…,8. The fluid density, ρ₁ and the fluid velocity, u_f are computed by ${\rho }_{1}=\mathop{\sum }\nolimits_{i = 0}^{8}{f}_{i}^{+}=\mathop{\sum }\nolimits_{i = 0}^{8}{f}_{i}$ and ${\rho }_{1}{{{{\bf{u}}}}}_{{{{\rm{f}}}}}=\mathop{\sum }\nolimits_{i = 0}^{8}\left({{{{\bf{c}}}}}_{i}{f}_{i}^{-}+{F}_{i}^{-}/2\right)=\mathop{\sum }\nolimits_{i = 0}^{8}\left({{{{\bf{c}}}}}_{i}{f}_{i}+{F}_{i}/2\right)$. In the D2Q9 model, the discrete velocities are defined as

$${{{{\bf{c}}}}}_{i}=\left\{\begin{array}{ll}(0,0)c,\quad &i=0\\ (\cos [(i-1)\pi /2],\sin [(i-1)\pi /2])c,\quad &i=1-4\\ (\cos [(2i-9)\pi /4],\sin [(2i-9)\pi /4])\sqrt{2}c,\quad &i=5-8\end{array}\right.$$

(18)

where the lattice speed c. It can be calculated by δx/δt, and ${c}^{2}=3{c}_{{{{\rm{s}}}}}^{2}$.

The force term in TRT-LB equation is constructed as²⁵

$${F}_{i}^{{{{\rm{trt}}}}}=\left(1-\frac{1}{2{\eta }_{{{{\rm{f}}}}}^{+}}\right){F}_{i}^{+}+\left(1-\frac{1}{2{\eta }_{{{{\rm{f}}}}}^{-}}\right){F}_{i}^{-},$$

(19)

where ${F}_{i}^{+}=({F}_{i}+{F}_{\bar{i}})/2$ and ${F}_{i}^{-}=({F}_{i}-{F}_{\bar{i}})/2$. The format of F_i can be expressed as⁵¹ :

$${F}_{i}={\omega }_{i}\left[\frac{{{{{\bf{c}}}}}_{i}-{{{{\bf{u}}}}}_{{{{\rm{f}}}}}}{{c}_{{{{\rm{s}}}}}^{2}}+\frac{{{{{\bf{c}}}}}_{i}\cdot {{{{\bf{u}}}}}_{{{{\rm{f}}}}}}{{c}_{{{{\rm{s}}}}}^{4}}{{{{\bf{c}}}}}_{i}\right]{{{\bf{F}}}}\delta t.$$

(20)

Governing equation for solute transfer with dendrite growth

The solute transport during dendrite growth is governed by the following convective-diffusion equation

$$\begin{array}{ll}&\frac{1}{2}[1+{k}_{{{{\rm{e}}}}}-(1-{k}_{{{{\rm{e}}}}})\phi ]\left(\frac{\partial S}{\partial t}+{{{\bf{v}}}}\cdot \nabla S\right)\\ &=\nabla \cdot \left(\frac{1-\phi }{2}{D}_{1}\nabla S+{a}_{{{{\rm{t}}}}}[1+(1-{k}_{{{{\rm{e}}}}})S]\frac{\partial \phi }{\partial t}\frac{\nabla \phi }{| \nabla \phi | }\right)+{Q}_{{{{\rm{S}}}}}({{{\bf{x}}}},t),\end{array}$$

(21)

where v is the advection velocity of solute. S is the supersaturation of the binary solution, representing for the composition caused by solute distribution during phase transition. It is an essential driving force of dendrite growth in the isothermal condition. S is related with the solute concentration c through

$$S=\left[\frac{2c/{c}_{1}^{0}}{1+{k}_{{{{\rm{e}}}}}-(1-{k}_{{{{\rm{e}}}}})\phi }-1\right]/(1-{k}_{{{{\rm{e}}}}}).$$

(22)

The advection velocity v is computed by

$${{{\bf{v}}}}=\left\{\begin{array}{ll}{{{{\bf{u}}}}}_{{{{\rm{s}}}}},\quad &(\phi \,\geqslant\, 0),\\ {{{{\bf{u}}}}}_{{{{\rm{f}}}}},\quad &(\phi \,<\, 0).\end{array}\right.$$

(23)

Here, u_s is the local velocity in solid phase, u_f is the local velocity in fluid zone. The second term in parentheses on the right-hand side of Eq. (21) represents the modified anti-trapping current, which is constructed artificially to counteracting solute dissipation caused by the diffusion interface. a_t denotes the anti-trapping coefficient and is modified as³⁹

$${a}_{{{{\rm{t}}}}}=\frac{1}{2\sqrt{2}}\left(1-A\left(1-{\phi }^{2}\right)\right).$$

(24)

The source term, Q_S, in Eq. (21) denotes the solute redistribution caused by phase transition, which is computed by

$${Q}_{{{{\rm{S}}}}}({{{\bf{x}}}},t)=\frac{1}{2}[1+(1-{k}_{{{{\rm{e}}}}})S]\frac{\partial \phi }{\partial t}.$$

(25)

Equation (21) can be solved by using an explicit scheme of either the finite volume method or the finite difference method. It is straightforward to couple the explicit schemes with the LB schemes.

Governing equation for migration and collision of dendrites

In the condition of either gravity or other external force environment, the dendrite seeds and solid fragments will settle and drift with melt flow in the liquid. The dynamic of solid movement is described by using the following equations of rigid body motion^31,37

$$\begin{array}{ll}m\frac{{{{\rm{d}}}}{{{{\bf{V}}}}}_{{{{\rm{T}}}}}}{{{{\rm{d}}}}t}\,=\,{{{{\bf{F}}}}}_{{{{\rm{f}}}}}+{{{\bf{{F}}}_{{{{\rm{b}}}}}}}+{{{\bf{{F}}}_{{{{\rm{p}}}}}}},\\ {I}_{{{{\rm{m}}}}}\frac{{{{\rm{d}}}}{{{\boldsymbol{\Omega }}}}}{{{{\rm{d}}}}t}\,=\,{{{{\bf{T}}}}}_{{{{\rm{f}}}}}.\end{array}$$

(26)

Here, the mass m and rotational inertia I_m can be computed by summing the density of all solid phase grid points and their spatial moments, respectively. V_T and Ω are translational velocity and angular spin rate of solid particle. For the 2D dendrite growth, the angle θ can be calculated via Ω_z = dθ/dt. F and T are the force and torque on solid. Their subscripts represent different sources.

The hydrodynamic force and torque on a particle can be calculated by

$${{{{\bf{F}}}}}_{{{{\rm{f}}}}}=\mathop{\sum}\limits_{{{{{\bf{x}}}}}_{{{{\rm{w}}}}}\in \Xi }\mathop{\sum}\limits_{i}\delta {{{{\bf{F}}}}}_{i}\left({{{{\bf{x}}}}}_{{{{\rm{w}}}}}\right),$$

(27)

$${{{{\bf{T}}}}}_{{{{\rm{f}}}}}=\mathop{\sum}\limits_{{{{{\bf{x}}}}}_{{{{\rm{w}}}}}\in \Xi }\mathop{\sum}\limits_{i}\left({{{{\bf{x}}}}}_{{{{\rm{w}}}}}-{{{{\bf{x}}}}}_{{{{\rm{c}}}}}\right)\times \delta {{{{\bf{F}}}}}_{i}\left({{{{\bf{x}}}}}_{{{{\rm{w}}}}}\right),$$

(28)

where Ξ represents the solid-liquid interface region. x_w is the intersection positions on the lattice link of solid-liquid interface marked by ϕ = 0, as shown in Fig. 21. x_c is the centroid position of the moving solid particle. Δ_w is defined as the interpolation parameter, which represents the fractīion of the intersected link within the fluid region, and Δ_w = ∣x_f − x_w∣/∣x_f − x_b∣.

Fig. 21: Schematic diagram of solid–liquid interface meshing and curved boundary.

Δx is the node size. There are four types of nodes:fluid node represented by x_f and x_ff, solid node represented by x_s, boundary node represented by x_b and boundary wall represented by x_w. c_i is the discrete velocity in i-th direction in LBM and its opposite discrete velocity, c_ï.

In this work, a momentum exchange method with Galilean invariance is used to get δF_i(x_w)⁵²

$$\delta {{{{\bf{F}}}}}_{i}\left({{{{\bf{x}}}}}_{{{{\rm{w}}}}}\right)=\left({{{{\bf{c}}}}}_{i}-{{{{\bf{u}}}}}_{{{{\rm{w}}}}}\right){\tilde{f}}_{i}\left({{{{\bf{x}}}}}_{{{{\rm{f}}}}},t\right)-\left({{{{\bf{c}}}}}_{\bar{i}}-{{{{\bf{u}}}}}_{{{{\rm{w}}}}}\right){\tilde{f}}_{\bar{i}}\left({{{{\bf{x}}}}}_{{{{\rm{b}}}}},t\right),$$

(29)

where u_w is the velocity of solid-liquid interface, x_b is the boundary node within solid region, and ${{{{\bf{x}}}}}_{{{{\rm{f}}}}}={{{{\bf{x}}}}}_{{{{\rm{b}}}}}+{{{{\bf{c}}}}}_{\bar{i}}\delta t$, as shown in Fig. 21. The density distribution function within fluid region, $\tilde{{f}_{i}}({{{{\bf{x}}}}}_{{{{\rm{f}}}}},t)$, is computed by Eq. (15), while ${\tilde{f}}_{\bar{i}}({{{{\bf{x}}}}}_{{{{\rm{b}}}}},t)$ is to be determined in the solid region.

The geometry of flow region is constructed by the dendrites with growth, remelting and sedimentation. The geometry of fluid zone will become very complex. A suitable method should be chosen to reconstruct the ${\tilde{f}}_{\bar{i}}({{{{\bf{x}}}}}_{{{{\rm{b}}}}},t)$. A fictitious equilibrium distribution function, ${f}_{i}^{* }({{{{\bf{x}}}}}_{{{{\rm{b}}}}},t)$ is introduced to realize above procedure. The reconstruction of the unknown distribution functions is described by⁵³

$${\tilde{f}}_{\bar{i}}\left({{{{\bf{x}}}}}_{{{{\rm{b}}}}},t\right)=(1-\chi ){\tilde{f}}_{i}\left({{{{\bf{x}}}}}_{{{{\rm{f}}}}},t\right)+\chi{f}_{i}^{* }\left({{{{\bf{x}}}}}_{{{{\rm{b}}}}},t\right)+2{w}_{i}\rho \frac{1}{{c}_{{{{\rm{s}}}}}^{2}}{{{{\bf{c}}}}}_{\bar{i}}\cdot {{{{\bf{u}}}}}_{{{{\rm{w}}}}},$$

(30)

and

$$\begin{array}{ll}{f}_{i}^{* }\left({{{{\bf{x}}}}}_{{{{\rm{b}}}}},t\right)\,=\,{w}_{i}\rho \left({{{{\bf{x}}}}}_{{{{\rm{f}}}}},t\right)\left[1+\frac{1}{{c}_{{{{\rm{s}}}}}^{2}}\left({{{{\bf{c}}}}}_{i}\cdot {{{{\bf{u}}}}}_{{{{\rm{bf}}}}}\right)+\frac{1}{2{c}_{{{{\rm{s}}}}}^{4}}{\left({{{{\boldsymbol{c}}}}}_{i}\cdot {{{{\bf{u}}}}}_{{{{\rm{f}}}}}\right)}^{2}-\frac{1}{2{c}_{{{{\rm{s}}}}}^{2}}{{{{\bf{u}}}}}_{{{{\rm{f}}}}}^{2}\right]\\ \,\qquad\qquad=\,{f}_{i}^{{{{\rm{eq}}}}}\left({{{{\bf{x}}}}}_{{{{\rm{f}}}}},t\right)+{w}_{i}\rho \left({{{{\bf{x}}}}}_{{{{\rm{f}}}}},t\right)\frac{1}{{c}_{{{{\rm{s}}}}}^{2}}{{{{\bf{c}}}}}_{i}\cdot \left({{{{\bf{u}}}}}_{{{{\rm{bf}}}}}-{{{{\bf{u}}}}}_{{{{\rm{f}}}}}\right),\end{array}$$

(31)

where χ is the weight coefficient and u_f is the fluid velocity at x_f. u_bf is the interpolated fictitious velocity, which is defined as

$$\begin{array}{ll}{{{{\bf{u}}}}}_{{{{\rm{bf}}}}}=\,{{{{\bf{u}}}}}_{{{{\rm{ff}}}}},\,\chi =\frac{(2\Delta -1)}{{\tau }_{{{{\rm{f}}}}}^{+}-2},\,0 \,<\, \Delta \,<\, \frac{1}{2},\\ {{{{\bf{u}}}}}_{{{{\rm{bf}}}}}=\,\frac{\Delta -1}{\Delta }{{{{\bf{u}}}}}_{{{{\rm{f}}}}}+\frac{1}{\Delta }{{{{\bf{u}}}}}_{{{{\rm{w}}}}},\,\chi =\frac{(2\Delta -1)}{{\tau }_{{{{\rm{f}}}}}^{+}},\,\frac{1}{2}\,\leqslant\, \Delta \,\leqslant\, 1.\end{array}$$

(32)

Here, ${{{{\bf{u}}}}}_{{{{\rm{ff}}}}}={{{{\bf{u}}}}}_{{{{{\bf{x}}}}}_{{{{\rm{f}}}}}+{\bar{{{{\bf{c}}}}}}_{i}\Delta t}$ is the fluid velocity of the node on the lattice link outside interface region within fluid, and it could improve the accuracy and robustness.

In Eq. (26), F_b denotes the buoyancy force originating from the density difference between solid and liquid, and is expressed as

$${{{{\bf{F}}}}}_{{{{\rm{b}}}}}=m\left(1-\frac{{\rho }_{1}}{{\rho }_{{{{\rm{s}}}}}}\right){{{\bf{g}}}}.$$

(33)

The force of the exerted on the α-th dendrite F_p is formulated as the interaction with its neighbours, ${\alpha }^{{\prime} }$-th dendrite⁴⁶,

$${{{{\bf{F}}}}}_{{{{\rm{p}}}}}({{{\bf{x}}}})=\kappa \mathop{\sum }\limits_{{\alpha }^{{\prime} }}^{{\alpha }^{{\prime} }\ne \alpha }{\phi }_{\alpha }({{{\bf{x}}}}){\phi }_{{\alpha }^{{\prime} }}({{{\bf{x}}}})\times \left[\nabla {\phi }_{\alpha }({{{\bf{x}}}})-\nabla {\phi }_{{\alpha }^{{\prime} }}({{{\bf{x}}}})\right],$$

(34)

where the interaction strength constant κ is fixed by classical benchmark.

Then, the translational velocity and rotational angular velocity of solid particles can be calculated combining Eq. (26), and then, the velocity of each node in the particles, u_s can be obtained by

$${{{{\bf{u}}}}}_{{{{\rm{s}}}}}={{{{\bf{V}}}}}_{{{{\rm{T}}}}}+{{{\boldsymbol{\Omega }}}}\times \left[{{{\bf{x}}}}-{{{{\bf{x}}}}}_{{{{\rm{c}}}}}\right].$$

(35)

An advection equation with u_s is introduced to model the movement of dendrites, which is written as

$$\frac{\partial {\phi }_{{{{\rm{m}}}}}}{\partial t}+{{{{\bf{u}}}}}_{{{{\rm{s}}}}}\cdot \nabla {\phi }_{{{{\rm{m}}}}}=0.$$

(36)

The three-order total variation diminishing (TVD) Runge-Kutta scheme for the time derivative term and the fifth-order WENO-Z scheme^54,55,56,57 for the advection term are utilized to solve Eq. (36) for their high accuracy. More details on the TVD Runge-Kutta scheme and WENO-Z scheme can be found in Supplementary methods. After that, an additional source term should be added to Eq. (9), given as

$${Q}_{{{{\rm{m}}}}}({{{\bf{x}}}},t)={w}_{i}\frac{{\phi }_{{{{\rm{m}}}}}({{{\bf{x}}}},t+\delta t)-{\phi }_{{{{\rm{m}}}}}({{{\bf{x}}}},t)}{\delta t}.$$

(37)

Computational procedure of the anisotropic LB-PF model

The consecutive computational procedure is as follows:

• (1) Initialize the computational domain, including the flow field, solute field and order parameter;

• (2) Compute the phase field via solving Eq. (9) and calculate the order parameter, ϕ; calculate the mass, m, centroid position, r_a, and moment of inertia, I_m of the dendrites;

• (3) Compute the dimensionless supersaturation, S, via solving Eq. (21);

• (4) Implement the streaming and collision steps of f_i(x, t) using Eq. (15), calculate the melt density, ρ, and the flow velocity, u_f;

• (5) Reconstruct the f_i(x_b, t) on interfacial grids, calculate the hydrodynamic F_f, solid interaction F_p and torque T_f with Eqs. (27-30,34);

• (6) Calculate the solid velocity u_s and the growth preferring orientation angle θ;

• (7) Calculate the source term of Eq. (9) with Eq. (12) and Eq. (37);

• (8) Repeat steps (2-7).