X-ray scattering tensor tomography based finite element modelling of heterogeneous materials

Abstract

Among micro-scale imaging technologies of materials, X-ray micro-computed tomography has evolved as most popular choice, even though it is restricted to limited field-of-views and long acquisition times. With recent progress in small-angle X-ray scattering these downsides of conventional absorption-based computed tomography have been overcome, allowing complete analysis of the micro-architecture for samples in the dimension of centimetres in a matter of minutes. These advances have been triggered through improved X-ray optical elements and acquisition methods. However, it has not yet been shown how to effectively transfer this small-angle X-ray scattering data into a numerical model capable of accurately predicting the actual material properties. Here, a method is presented to numerically predict mechanical properties of a carbon fibre-reinforced polymer based on imaging data with a voxel-size of 100 μm corresponding to approximately fifteen times the fibre diameter. This extremely low resolution requires a completely new way of constructing the material’s constitutive law based on the fibre orientation, the X-ray scattering anisotropy, and the X-ray scattering intensity. The proposed method combining the advances in X-ray imaging and the presented material model opens for an accurate tensile modulus prediction for volumes of interest between three to six orders of magnitude larger than those conventional carbon fibre orientation image-based models can cover.

Introduction

Fibre-reinforced composite materials have become indispensable in numerous applications in various industries such as automotive, aerospace, and construction, due to their exceptional mechanical properties. The key for understanding and predicting the mechanical properties of these composites lies in realistic modelling of their micro-scale structures. It is at the fibre scale that critical macroscopic properties such as stiffness and strength are determined. Over the last decade, X-ray micro-computed tomography (micro-CT) has become state-of-the-art for imaging heterogeneous materials that consist of these intricate micro-structures¹.

For a meaningful numerical prediction of material properties, mere image analysis is not sufficient. Such a prediction necessitates image-based modelling, typically characterised by a finite element model of the micro-structure detected in an image dataset². X-ray micro-computed tomography information has proven effective for numerically predicting the mechanical properties of various fibre-reinforced composites, including carbon^3,4, glass^5,6,7, and flax fibre⁸ reinforced composites. The choice of modelling strategy significantly influences the predicted material behaviour predictions. For example, Wilhelmsson et al.⁹ numerically modelled compressive failure in carbon fibre-reinforced composites based on X-ray computed tomography data. Sencu et al.¹⁰ used multi-scale modelling to perform damage analysis of a carbon fibre-reinforced composite based on high-resolution images. In addition to traditional methods, deep learning methods have also emerged for predicting mechanical behaviour of materials^11,12. While those methods are capable of providing accurate predictions of the mechanical behaviour, they are contingent on the availability of extensive amount of experimental data. Despite the notable progress in the numerical prediction of mechanical properties for fibre-reinforced composites utilising micro-computed tomography data, several significant challenges remain to be addressed.

Firstly, traditional absorption-based X-ray imaging methods struggle with low contrast in carbon or natural fibre-reinforced composites, complicating fibre segmentation for further analysis. Secondly, the trade-off between the length scale of interest and the desired field-of-view (FOV) is a limiting factor, often necessitating the stitching of multiple scans to achieve a comprehensive view. For example, detecting the orientations of carbon fibres, with a diameter of 5 μm, in a 2 × 2 × 2 cm³ would require approximately 1000 micro-computed tomography scans of 2000 × 2000 × 2000 voxels, with a voxel-size of 1 μm for each scan. This approach would generate a massive 32 TB dataset from 8 trillion voxels expressed in 4-byte wide unsigned integers, posing daunting challenges in terms of both data processing and experiment duration.

In contrast, small-angle X-ray scattering (SAXS) imaging offers a promising alternative. Small-angle X-ray scattering does not require resolving individual fibres, thus easing spatial resolution requirements. By leveraging small-angle X-ray scattering signals, imaging setups with lower resolution¹³ and higher acquisition rates¹⁴ can serve as a tool for analysing the mechanical properties of fibre-reinforced composites in a comprehensive volumetric field-of-view. To be specific, micro-structural details such as fibre orientations and distributions, that are orders of magnitude smaller than the voxel-size can be non-destructively captured by measuring and decoding the local small-angle X-ray scattering signals. This technique effectively separates the length scale of interest and the desired field-of-view.

One of the experimental techniques to acquire local two-dimensional small-angle X-ray scattering signals is to use phase modulator X-ray optics composed of an array of circular gratings^15,16. Circular fringes that resemble the circular grating patterns are formed at a certain distance downstream at the detector. Omnidirectional scattering information can be extracted in each image pixel by measuring the change in the circular fringes before and after inserting the sample into the beam path. The measurement of local two-dimensional small-angle X-ray scattering signals is repeated at different sample angular poses with respect to the incoming beam. Due to the omnidirectional scattering sensitivity of the circular gratings, the measurement time to acquire local small-angle X-ray scattering signals is considerably shorter compared to other experimental methods^17,18. After reconstructing the local two-dimensional small-angle X-ray scattering signals, scattering tensors, representing the local three-dimensional scattering property of each voxel within the sample^13,19, are computed. This method is referred to as X-ray scattering tensor tomography.

In this study, we demonstrate the comprehensive capabilities of X-ray scattering tensor tomography in quantitative modelling of mechanical properties. We address the challenges inherent in low-resolution image-based modelling that have previously not been adequately tackled. In particular, our approach integrates, for each voxel, the distribution of fibre orientation and fibre volume fraction (instead of a single value) into the finite element model. This methodology is particularly relevant for voxels with sizes up to fifteen times larger than the fibre diameter. Consequently, we have developed a method that updates the material’s stiffness tensor at a local level, harnessing the detailed sub-voxel information available through tensor tomography.

In summary, this work takes advantage from the advanced capabilities of X-ray scattering tensor tomography and paves the way for more accurate and significantly more efficient modelling of fibre-reinforced composites. This approach marks a significant advancement in the field, leveraging the comprehensive information available in X-ray scattering tensor tomography, enhancing our ability to study these materials.

Results

Scattering tensor tomography analysis

Figure 1 shows the fibre orientations reconstructed using the proposed X-ray scattering tensor tomography method with 50 Simultaneous Iterative Reconstruction Technique (SIRT) iterations. The fibres have different orientations in different regions of the cylindrical sample. The fibres are in general aligned perpendicularly to the axial axis, i.e. x-axis, of the cylindrical sample (Fig. 1a), except for the centre and the extreme periphery where they are aligned parallel to the sample axis. The Mean Scattering signal (MS) is higher in the core region compared to the peripheral region (Fig. 1b). This implies that the fibre volume fraction is higher in the core region. In contrast, no conspicuous variation in Fractional Anisotropy (FA), except for a slight drop in the core region (Fig. 1c), can be found. Consequently, there are no regions with more aligned fibres than others. Moreover, the Fractional Anisotropy (FA) values are rather low (less than 0.2 in most regions, while the maximum is 1). This implies that the fibres in general do not have particular alignment orientation in any region.

Fig. 1: Rendered and clipped view of the reconstructed results of the scattering tensor tomography.

Only half of the cylindrical sample is shown to better visualise the inner structures surrounding the core. For a better visual interpretation, streamlines calculated based on the Runge-Kutta method are used (tool provided by the Paraview Guide⁵⁰). Note, that those streamlines do not represent single fibres but a dominant material orientation. The three-dimensional fibre orientations p_i in (a) are colour-coded according to the colour sphere, which maps the absolute values of the orientation vector coordinates ∣x, y, z∣ to the RGB colour components. The colours in (b) and (c) represent the Mean Scattering MS ∈ [0, 1] and the Fractional Anisotropy FA ∈ [0, 1] signals, respectively.

Stiffness matrix analysis

Only voxels which spatially contain an integration point are used to map and update information for the finite element model. One element covers a region corresponding to 64 voxels. Therefore, with eight integration points per element, only 1/8 of the image information is incorporated into the model. In Fig. 2, the stiffness matrix components C₁₁ are compared for the full image data and the actual mapped (reduced) data. The observed difference is almost invisible, even for a logarithmic scale. Consequently, it is verified that 7/8 of the image information can be neglected in the stiffness matrix computation. This is important from a computational cost perspective. In case local stresses and strains are of interest, e.g., when modelling compressive failure, the choice not to homogenise around an integration point can be important. Through homogenisation, extreme values, e.g. significant local fibre misalignments, are always reduced in their severity due to the averaging with the neighbouring values.

Fig. 2: Stiffness matrix component distribution histogram for C₁₁, which is oriented along the dominant fibre orientation, for each voxel of the full image data (orange) and voxels that were actually used in the mapping process (red).

C₁₁ can range between 40.7 and 8.79 GPa given the chosen constituent properties (see Supplementary Information) and for a fibre volume fraction of 19.9%. The values are normalised over the integration point or voxel count, respectively. Note the logarithmic scale.

Tensile modulus analysis

In total, three simulation variants are considered. In Simulation A, only the dominant fibre orientation is mapped, and the global fibre volume fraction of 19.9% is used. Simulation B incorporates a sub-voxel fibre orientation information from the scattering tensor and the global fibre volume fraction of 19.9%. Finally, Simulation C considers the sub-voxel fibre volume fraction in addition to the sub-voxel fibre orientation information from the scattering tensor. More details on the integration of sub-voxel information can be found the Method. Simulations A to C are performed to numerically predict the rod’s tensile modulus. Simulation C provides the best predictions, with the predicted modulus only deviating by −1.6% from the experimental value, see Table 1¹. The assignment of a sub-voxel fibre volume fraction as well as the considered sub-voxel fibre orientation spread leads to a substantial improvement. It can be stated that only exploiting the full scattering tensor data with sub-voxel fibre orientation information and sub-voxel fibre volume fraction allows to accurately predict the tensile modulus of the investigated sample.

Table 1 Comparison of the experimentally measured tensile modulus and the numerically predicted tensile modulii of the three simulation variants

Since the investigated rod is axisymmetric, the stiffness matrix components and stresses can be expressed in a global cylindrical coordinate system with the x-direction along the axial direction, r in radial and Θ in the circumferential direction. The influence of the implementation of the sub-voxel fibre orientation update and the sub-voxel fibre volume fraction on the stiffness matrix component C_xx is depicted in Fig. 3. In general, it can be seen that the greater part of the integration points are assigned with a stiffness C_xx < 10 GPa. In Simulation C also, the effect of a sub-voxel fibre volume fraction is included. The sub-voxel fibre volume fraction leads to a larger spread of the stiffness matrix component values, as locally lower and higher fibre volume fractions also widen the possible range of the stiffness matrix component values. The stiffness component histograms for the radial and circumferential directions can be found in the Supplementary Information.

Fig. 3: Comparison of the stiffness matrix component C_xx for all three simulation variants.

Simulation A uses the dominant fibre orientation and a global fibre volume fraction of 19.9 %. Simulation B incorporates sub-voxel fibre orientation information from the scattering tensor and a global fibre volume fraction of 19.9%. In Simulation C, additionally to the sub-voxel fibre orientation information, a sub-voxel fibre volume fraction is assigned.

Stress distribution analysis

The stress distributions for the sample loaded in tension from Simulations A, B and C, respectively, are plotted in Fig. 4a–c. In the plot for Simulation A, effects of the dominant fibre orientation are clearly visible. In the centre, an area of high σ_xx is evident. In the outermost layer also stresses of a similar magnitude are visible, indicating that the fibres are oriented along the axial direction. These results match with the visualisations of the scattering tensor (Fig. 1), and thus indirectly validate the fibre orientation mapping method. The observed differences in results from Simulation A and Simulation B are small in this plot. Only a more smeared stress distribution can be seen in Simulation B. The influence of the implemented sub-voxel fibre volume fraction is readily seen in the results from Simulation C. Due to the higher fibre volume fraction in the core region of the rod, a stress concentration of σ_xx is found in this region. The stress plots for σ_rr and σ_ΘΘ are depicted in the Supplementary Information.

Fig. 4: Comparison of stresses in axial direction for all three simulation variants.

Simulation A (a) uses the dominant fibre orientation and a global fibre volume fraction of 19.9%. Simulation B (b) incorporates sub-voxel fibre orientation information from the scattering tensor and a global fibre volume fraction of 19.9%. In Simulation C (c), additionally to the sub-voxel fibre orientation information, a sub-voxel fibre volume fraction is assigned. The stress histograms of all simulations are presented in (d).

In Fig. 4d, the histogram for σ_xx is presented. The main peak of Simulation B is slightly shifted to the higher stresses. Most prominent, however, is the much lower peak for Simulation C. Hence, the primary explanation stems from the broader width of this peak, originating from the allocation of local fibre volume fraction. Regions where the fibre volume fraction is lower/higher than the mean fibre volume fraction experience diminished/elevated stress levels in comparison to the areas within Simulation B. The stress histograms for σ_rr and σ_ΘΘ are depicted in the Supplementary Information.

Discussion

The proposed approach overcomes one of the main issues of image-based numerical modelling of fibrous composites; the necessity of high-resolution images in order to resolve fibres. This is in turn problematic as the possible volume of interest decreases with the resolution increase cubed. We show that accurate prediction of the tensile modulus of short fibre composites, with significant variation in local fibre orientation distribution, can be made from image information with voxel-sizes of approximately fifteen times the fibre diameter. Regular micro-computed tomography scans of carbon fibre-reinforced composites use voxel-sizes between 1 and 5 μm^9,20,21. Comparing the proposed method (voxel-size 100 μm) with a micro-computed tomography scan with a voxel-size of 1 μm, the volume of interest is increased by six orders of magnitude, i.e., a factor of 1,000,000. This marks a tremendous step towards the goal to accurately analyse volume of interests in the decimetre to metre range. However, more research on both the imaging and modelling part is needed.

For example, currently the X-ray optical element only allows for a voxel-size of 100 μm. However, updates of the X-ray optical elements are being developed by the authors to adjust voxel-sizes for different micro-structures and investigate the influence of the resolution. Moreover, higher energies and flux available after the upgrade of the Swiss Light Source will allow to address higher fibre volume fractions within larger volumetric field of views. Simultaneously, the imaging technology is transferred to a lab-based system and a commercial prototype, which is expected to deliver similar results²².

In the introduction of a new image-based model, precision in capturing both fibre orientation and fibre volume fraction becomes paramount. Through achieving a robust match with experimentally tested tensile modulus values, our ultra low-resolution image-based model successfully captures these critical aspects – fibre orientations and volume fractions – that significantly influence the tensile modulus. This effective validation emphasises the primary focus of our study, which focuses on the introduction of an innovative method in ultra low-resolution image-based modelling. The observed stress distribution naturally arises from the distribution of fibre orientations. However, it remains for future research to introduce targeted low-resolution failure models, which must be thoroughly validated through additional mechanical tests. This step will contribute to a more comprehensive understanding of the model’s predictive capabilities and further enhance its applicability in practical scenarios.

Although a tensile test has been chosen to validate the presented method, it does not provide an efficient, alternative way to predict the tensile modulus. Testing the tensile modulus directly remains a more cost-effective and faster alternative compared to scanning the sample and creating an image-based model. The primary future application of the method lies in the image-based prediction of stress states in fibre-reinforced composites, significantly surpassing the capabilities of state-of-the-art image-based models in terms of size. Even though we successfully introduce a sub-voxel update for fibre orientation and fibre volume fraction, limitations arise due to the given voxel-size. In scenarios involving compression load cases, even a small number of misaligned fibres can potentially lead to the ultimate failure of the material. Despite the innovative approach in constructing the stiffness matrix presented here, the impact of these few misaligned fibres may not be fully captured.

As we have opened the field of ultra low-resolution image-based modelling, there is a manifold of other approaches to be investigated. However, the presented way to recalculate the 30 stiffness matrix components, based on the shape of the scattering tensor, represents a fast and efficient method. The assumed linear correlations for the computation of the sub-voxel fibre angle spread and sub-voxel fibre volume fraction has been taken due to lack of information. A Gaussian distribution instead of a linear correlation between the sub-voxel fibre angle spread and the Directional Anisotropy (DA) has also been tested; however, the results differ only marginally. Further investigations on the relation between the sub-voxel fibre angle spread and sub-voxel fibre volume fraction as well as the Directional Anisotropy (DA) are necessary for more accurate modelling.

It has been demonstrated that sub-voxel fibre orientations and fibre volume fraction can alter the predicted mechanical stiffness behaviour of fibrous composites. Thus, the proposed modelling approach to define the material’s stiffness matrix including the fibre direction, the Directional Anisotropy (DA), and the Mean Scattering (MS) is indispensable for low-resolution image-based modelling. In addition, sub-voxel fibre orientations and fibre volume fractions can also influence strength. Therefore, in a similar fashion, as the stiffness matrix update, the strength, σ^max or ϵ^max, can be recalculated based on the sub-voxel fibre distribution and fibre volume fraction.

Only image-based numerical models consequently targeted on the available image data will lead to research progress. The presented work emphasises the need for targeted approaches for ultra low-resolution image-based modelling and it opens for further research in large field-of-view image-based modelling.

The successful demonstration of low-resolution small-angle X-ray scattering tensor tomography in image-based numerical modelling is evident in the accurate prediction of the tensile modulus for the examined short carbon fibre reinforced polyether ether ketone. Notably, this method requires voxel-sizes approximately fifteen times the diameter of carbon fibres in the composite, in contrast to conventional image-based models that depend on high-resolution image data with voxel-sizes closely matching the fibre diameter. The advancements presented in this study significantly expand the potential volume of interest for carbon fibre orientation image-based modelling, enlarging it by three to six orders of magnitude compared to current state-of-the-art approaches. While these results are promising, further research is imperative, particularly in refining the imaging setup to accommodate various voxel-sizes and diverse material systems. Additionally, extending the method to incorporate material failure prediction will unveil the full potential of X-ray scattering tensor tomography based finite element modelling.

Method

In this study, we perform ex-situ X-ray scattering tensor tomography based finite element modelling of a short carbon fibre-reinforced composite under tensile load, see Fig. 5. The fibre diameter is approximately 7 μm, while the three-dimensional image voxel-size is 100 × 100 × 100 μm³. It is important to highlight that, for the experimental tensile tests, three rods measuring 30 cm in length are employed, whereas the scanned sample has a length of only 14 mm. Due to the inherent characteristics of the pultrusion process, variations in fibre orientations occur primarily in the radial dimension and not along the axial dimension. Exploiting this aspect, an image-based model applied to a shorter sample proves effective in predicting the tensile modulus. This choice reduces both acquisition and computation time.

Fig. 5: Proposed method from image acquisition to the final finite element model in order to compute the mechanical properties of the carbon fibre reinforced polyether ether ketone (PEEK) rod.

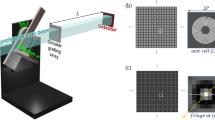
a Setup for small-angle X-ray scattering tensor tomography with circular gratings in a synchrotron beamline. This figure is reproduced from²⁸ (b) Element of the finite element model with eight integration points (black crosses), which are assigned with the voxel’s scattering information in form of the reconstructed scattering tensor and the local fibre volume fraction V_f computed based on the local Mean Scattering (MS). c Stress distribution in the 19 mm diameter carbon fibre-reinforced polyether ether ketone rod loaded in tension using the scattering tensor-based numerical model.

In Table 2 important characteristics of the newly developed X-ray scattering tensor tomography-based finite element modelling are compared with a state-of-the-art synchrotron micro-computed tomography-based finite element modelling. The X-ray scattering tensor tomography reconstruction time is calculated using an iterative reconstruction (Simultaneous Iterative Reconstruction Technique - SIRT) with a single thread implementation (2.10 GHz CPU) in a memory-sharing cluster environment with a NVIDIA Quadro P4000 GPU whereas the micro-computed tomography reconstruction time is estimated using an analytic reconstruction without use of a GPU. It is worth noting that the X-ray scattering tensor tomography reconstruction time will be two orders of magnitude shorter by using the direct reconstruction method²³. The statistics for fibre orientation analysis and homogenisation/mapping in the context of micro-computed tomography-based finite element modelling are projected for a single AMD EPYC 7351 processor, operating at 2.9 GHz with 16 cores (based on the experiences in^7,13). It becomes evident that the adoption of smaller voxel-sizes, essential for resolving carbon fibres through micro-computed tomography, causes an enormous increase in both scanning and analysis time.

Table 2 Essential characteristics of the presented approach with X-ray scattering tensor tomography-based finite element modelling (XSTT-FEM) and classical synchrotron micro-computed tomography-based finite element modelling (Micro-CT-FEM)

Material characterisation

A short carbon fibre-reinforced polyether ether ketone (PEEK) extruded rod with a diameter of 19 mm from Ensinger GmbH, Germany, is studied²⁴. It contains short fibres, which, in general, require more advanced material modelling, compared to long (continuous) fibres. The fibre orientations and fibre volume fraction regimes within the rod are expected to vary due to the manufacturing process. This adds to the importance of imaging techniques that are capable of detecting micro-scale fibre orientations within a centimetre-scale large field-of-view. The tensile modulus was experimentally measured for three full-diameter rods. Each sample was tested using four repeating load/unload sequences with loading up to a low strain level of 0.3% at a displacement rate of 0.016 mms⁻¹. The modulus was evaluated as the secant between the strains 0.05% and 0.25%. Strains were measured with two extensometers with an initial gauge length of 50 mm and a displacement of ± 2.5 mm. Additionally, the fibre volume fraction was determined by comparing the density of the composite to the density of a pure polyether ether ketone sample from the same manufacturer. The volumes of the samples were determined using a gas pycnometer from Quantachrome, type UltraPyc 1200e. The mass of the samples was measured using an analysis scale from Mettler Toledo, type XS204. The density of pure polyether ether ketone is found to be 1.30 kgm⁻³. With a fibre density of 1.81 kgm⁻³ and a measured density of the carbon fibre reinforced polyether ether ketone of 1.40 kgm⁻³, a fibre volume fraction of 19.9% is obtained.

Local small-angle X-ray scattering acquisition

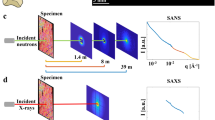
The acquisition experiment was performed at the synchrotron X-ray beamline TOMCAT, Swiss Light Source, Paul Scherrer Institute in Switzerland. A π-shift circular grating array, with a fine period g = 1.46 μm and a coarse period P = 49.5 μm (see Fig. 5a), was placed at a distance L = 49.5 cm from the detector (Fig. 5). The sample was measured by a parallel monochromatic X-ray beam with an energy of 17 keV and a bandwidth of 2–3%. The experimental system is most sensitive to the scattering signals from the micro-structure at a scale that corresponds to its autocorrelation length ξ = 730 nm. The autocorrelation length is approximately 10% of the fibre diameter. Nevertheless, half of the maximum scattering sensitivity, which would be obtained with an autocorrelation length equal to the fibre diameter, is still expected²⁵. A LuAG:Ce scintillator with a thickness of 300 μm was used to convert the X-rays to visible light. The converted visible light is collected by a high numerical aperture 1x microscope optics (Optique Peter, France) and arrives at the in-house GigaFRoST²⁶ CMOS detector with a pixel size of 11 μm. A 9 × 9 detector pixel grid (unit cell), which corresponds to an effective image pixel in the retrieved image, is used to resolve the circular fringe.

The probed scattering signals depend on the relative orientation between the incident beam and the underlying micro-structure²⁷. Therefore, multiple tilted rotation axes along the beam direction are necessary for tomographic reconstruction of the scattering tensor with high accuracy²⁸. In this study, the sample pose is manipulated by a 2-axis stage with which the rotation axis can be tilted ± 45°, following the procedure by Kim et al.¹³. The sample is measured at in total 1000 angular poses: 100 rotation angles [0°, 3.6°, …, 356.4°] at 10 tilt angles [0°, 5°, …, 45°]. The available field-of-view is limited by the optics and beam size to 15.2 mm × 5.4 mm. To be able to cover the entire sample which exceeds this field-of-view in both the horizontal and vertical direction, at each pose 21 image tiles (3 × 7) have been acquired and stitched together to generate a new composed image. The resulting total field-of-view is 40.8 mm × 29.2 mm for each stitched image. The exposure time for each projection tile is 10 ms. Therefore, the effective scan time, with the 1000 projections each containing 21 image tiles, is approximately 210 s and the total scan time is approximately 420 s, including the time required for sample stage movement between each tilt angle and the stitching position.

The visibility of the circular fringe along different scattering angles is extracted from the projection images in each unit cell. For this purpose, a radial line profile going through the circular fringe is modelled by a cosine function with two periods¹⁶. Therefore, the visibility V_s,m and V_f,m are calculated as the ratio of the second to the zeroth component of the discrete Fourier transform (DFT) of the measured intensity along such line profile:

$${V}_{{{{\rm{s}}}},m}=\frac{{\tilde{I}}_{{{{\rm{s}}}},m}(n=2)}{{\tilde{I}}_{{{{\rm{s}}}},m}(n=0)}\,,\,\,{V}_{{{{\rm{f}}}},m}=\frac{{\tilde{I}}_{{{{\rm{f}}}},m}(n=2)}{{\tilde{I}}_{{{{\rm{f}}}},m}(n=0)}\,$$

(1)

The subscript s stands for the sample measurement, f stands for the flat measurement (without sample), and $\tilde{I}(n)$ is the n^th angular component of the discrete Fourier transform in the polar coordinates. The subscript m keeps track of each single visibility measurement. The projected local small-angle scattering signal D_m is calculated by measuring the visibility reduction of the circular fringe as

$${D}_{m}=\frac{{V}_{{{{\rm{s}}}},m}}{{V}_{{{{\rm{f}}}},m}}\,.$$

(2)

From the projection data with directional scattering signals, the small-angle scattering tensor can be tomographically reconstructed.

Scattering tensor calculation

In tensor tomography, multiple tensor component values instead of a single scalar are reconstructed for each voxel. For example, each reconstructed voxel contains scattering signal values μ_k along the sampling directions (channels) k = 1, 2, …, K(K ≥ 6). In this study, K is chosen to be 7 based on an empirical optimisation. The scattering signal D_m is known to follow the Beer-Lambert law^29,30,31. However, due to the rotational dependence of the scattering signal, the probed scattering signal intensity depends on the relative orientation of the samples’ micro-structures, beam direction, as well as the direction along which the scattering signals are extracted from the projection images. Therefore, the measured scattering signal D_m’s negative logarithm p_m is modelled as follows:

$${p}_{m}=-\ln {D}_{m}=\mathop{\sum}\limits_{k}{\nu }_{m,k}{\int}_{{L}_{m}}{\mu }_{k}({{{\bf{x}}}})d{{{\bf{x}}}},$$

(3)

where the weighting constant ν_m,k takes the rotational dependence into account³² and L_m indicates the beam path. Then, Equation (3) is expanded for all measurement indices m, so that

$${{{\bf{p}}}}={{{\bf{A}}}}\mu .$$

(4)

The matrix A is the system matrix that defines the geometry of our tensor tomography problem²³. In this study, Equation (4) is solved with the Simultaneous Iterative Reconstruction Technique (SIRT), which minimises $\parallel {{{\bf{p}}}}-{{{\bf{A}}}}\mu {\parallel }_{2}^{2}$. After running the Simultaneous Iterative Reconstruction Technique, μ is tomographically reconstructed for each voxel.

Using principal component analysis (PCA), one can compute the ellipsoid that best fits the reconstructed μ³³ (see Fig. 6b). As final result, a second-order tensor is computed, where its eigenvector with the minimum eigenvalue is chosen to represent the dominant orientation of the carbon fibres embedded in the corresponding voxel, while the other two eigenvalues indicate how well the fibres are aligned in each voxel. With the three eigenvalues λ_i, metrics for the normalised Mean Scattering (MS ∈ [0, 1]) and the Fractional Anisotropy (FA ∈ [0, 1]) per voxel can be computed according to Equation (5) and (6). A higher Fractional Anisotropy (FA) indicates a better alignment of fibres in the regarded voxel. Several works have shown the use of such eccentricity of the scattering tensor as a sensible indicator^13,34,35. For example, equally large eigenvalues will lead to a spherical shape and indicate a random fibre distribution (see Fig. 6c), with the Fractional Anisotropy (FA) value being 0. In contrast, a small third eigenvalue compared to larger first and second eigenvalues indicates that fibres in the voxel have a preferred orientation, with the Fractional Anisotropy (FA) value being closer to 1. A large first eigenvalue, while the other two eigenvalues are small, would indicate that the fibres are rather randomly oriented in a plane. A region with a higher Mean Scattering (MS) than its neighbourhood implies that the region contains a higher volume fraction of the scattering structures (e.g., fibres).

$${{{\rm{MS}}}}=\frac{{\lambda }_{1}+{\lambda }_{2}+{\lambda }_{3}}{\mathop{\max }\limits_{volume}({\lambda }_{1}+{\lambda }_{2}+{\lambda }_{3})},$$

(5)

$${{{\rm{FA}}}}=\frac{\sqrt{{({\lambda }_{1}-{\lambda }_{2})}^{2}+{({\lambda }_{2}-{\lambda }_{3})}^{2}+{({\lambda }_{3}-{\lambda }_{1})}^{2}}}{\sqrt{2({\lambda }_{1}^{2}+{\lambda }_{2}^{2}+{\lambda }_{3}^{2})}}$$

(6)

In Equation (5) the sum of eigenvalues is normalised by the maximum sum ($\mathop{\max }\limits_{volume}$) in the entire reconstructed volume.

Fig. 6 : Voxel-wise scattering signal sampling and ellipsoid modelling of the scattering distribution.

a Schematic image acquisition for one voxel. b For this voxel, the scattering signals are sampled along multiple direction vector ${\hat{{{{\bf{s}}}}}}_{k}$ (here k = 1, …, 7). Then the three principal axes of an ellipsoid that fit the scattering distribution can be computed using principal component analysis (PCA). c Possible shapes of ellipsoids that voxel-wise model the scattering distribution depending on the micro-structures. For example, a voxel that mostly contains isotropic (spherical) structures has a sphere-shaped scattering distribution whereas a voxel with fibre-like structures has a flat-ellipsoid-shaped distribution as in the left-bottom part in (c). (a, b) are reprinted with permission from²³. (Copyright 2024 by the American Physical Society).

Material modelling

As the constituents inside the composite are not resolved due to the low resolution, full-field models, which assume heterogeneous stress and strain fields inside the constituents of the micro-structure, are not feasible. Mean-field homogenisation models³⁶, on the other hand, offer an advantageous solution to this problem. They assume average stress and strain states in the different constituents of a composite. Mean-field homogenisation approaches have been described in several studies^{37,38,39,40,41} and their differences have been recently discussed by Raju et al.⁴² and Hessman et al.⁴³. The Mori-Tanaki scheme^41,44 is particularly popular among the mean-field homogenisation methods as its formulation is easily understood and implemented which is essential in this study where the primary objective is to introduce a methodology for modelling ultra low-resolution image datasets. The Mori-Tanaka scheme, which is a commonly employed method in composite modelling⁴², serves in this context of this study as a secondary aspect rather than the core focus of the study. It assumes that all fibres are embedded in an infinitely large matrix and behave independently of each other. As boundary condition a far-field mean strain is applied. Additionally, the Mori-Tanaka scheme can account for short fibres and the anisotropic character of carbon fibres.

For the Mori-Tanaka scheme the strain localisation tensor A^MT, is formulated according to Benveniste et al.^44,45, following the theory by Eshelby³⁷, that the strain for a homogeneous and ellipsoidal inclusion in an infinite matrix is constant. It depends on the fourth order identity tensor I, the stiffness tensor for the matrix C^m, the stiffness tensor for the fibre C^f and Eshelby’s tensor P. The strain localisation tensor is then a fourth-order tensor and can be expressed as

$${{{{\bf{A}}}}}^{{{{\rm{MT}}}}}={\left[{{{\bf{I}}}}+{{{\bf{P}}}}\!:\left({\left({{{{\bf{C}}}}}^{{{{\rm{m}}}}}\right)}^{-1}:{{{{\bf{C}}}}}^{{{{\rm{f}}}}}-{{{\bf{I}}}}\right)\right]}^{-1}$$

(7)

Using Voigt form, fourth-order tensors can also be expressed as 6 × 6 matrices. This is discussed in greater detail in the Supplementary Information. Eshelby’s tensor solely incorporates the inclusion geometry and the matrix Poisson’s ratio. Here, the inclusion is represented by a single carbon fibre. Details about the calculation of Eshelby’s tensor can also be found in the Supplementary Information.

The final Mori-Tanaka stiffness tensor C^MT can also be expressed as a 6 × 6 matrix in Voigt form. It also includes I, C^m, C^f as well as the scalar value of the fibre volume fraction V_f. In tensor notation, the Mori-Tanaka stiffness tensor is given by

$$\begin{array}{l}{{{{\bf{C}}}}}^{{{{\rm{MT}}}}}={{{{\bf{C}}}}}^{{{{\rm{m}}}}}+{V}_{{{{\rm{f}}}}}\left({{{{\bf{C}}}}}^{{{{\rm{f}}}}}-{{{{\bf{C}}}}}^{{{{\rm{m}}}}}\right):{{{{\bf{A}}}}}^{{{{\rm{MT}}}}}{\left[(1-{V}_{{{{\rm{f}}}}}){{{\bf{I}}}}+{V}_{{{{\rm{f}}}}}{{{{\bf{A}}}}}^{{{{\rm{MT}}}}}\right]}^{-1}\\ \end{array}$$

(8)

The Mori-Tanaka stiffness tensor does not account for the fibre orientations. Therefore, it has to be rotated according to local fibre orientations. Advani and Tucker⁴⁶ introduced a second-order fibre orientation tensor O_ij with a fibre orientation probability distribution function Ψ(p). The fibre orientation tensor is given by

$${O}_{ij}=\oint {p}_{i}\,{p}_{j}\,{{\Psi }}({{{\bf{p}}}})\,d{{{\bf{p}}}},$$

(9)

where p denotes the orientation and is expressed as a unit vector with Cartesian coordinates⁴⁷, i.e.

$${p}_{i}=\left\{\begin{array}{c}{p}_{1}\\ {p}_{2}\\ {p}_{3}\end{array}\right\}=\left\{\begin{array}{c}cos(\varphi )sin(\theta )\\ sin(\varphi )sin(\theta )\\ cos(\theta )\end{array}\right\}.$$

(10)

The angle φ is the in-plane angle between the x-axis and the xy-projection of the unit vector and θ is the angle between the z-axis and the unit vector. The fibre angles are schematically illustrated in the Supplementary Information.

Here, such a fibre orientation probability distribution function Ψ(p) is not needed as the reconstructed scattering signal already incorporates the fibre orientation distribution. The reconstructed scattering signal represents the X-ray scattering signal of all fibres present in one voxel and yields a second-order tensor, which can be decomposed into three eigenvectors and eigenvalues. The eigenvector with the smallest eigenvalue is interpreted as the dominant fibre orientation.

Using the eigenvector with the smallest eigenvalue of the scattering tensor as material orientation for the stiffness tensor is however ambiguous, as there are many fibres present within one voxel. This problem can be further explained with the following example: A voxel with nine fibres embedded and oriented in xy-plane at 15°, 45°, and 75° (Fig. 7a) has a mean fibre orientation of 45°. This, however, does not represent the correct mechanical behaviour. The mean of the three different stiffness components (C₁₁ in this example) does not coincide with the mean of the fibre orientations (Fig. 7b), as the elastic modulus and fibre angle are not linearly dependent. This illustrates how a systematic error is introduced in an image-based model where the voxel-size is much larger than the fibre diameter.

Fig. 7: Influence of the non-linear relation between fibre orientation and mechanical stiffness properties.

a In case there are three different fibre orientation regimes with 15°, 45° and 75° within one voxel with a size of 100 μm the mean fibre orientation is 45°, indicated by the black dot. b The mean of stiffness matrix components C₁₁, indicated by the black triangle, however, does not coincide with the mean orientation due to the non-linear correlation between fibre orientation and stiffness property.

To overcome this issue we propose to formulate a specific material’s constitutive law for low-resolution image-based modelling (Equation (11)). This approach is founded on the full information extraction of the scattering tensor. Based on Equation (8), the material’s stiffness tensor therefore becomes a function of the fibre orientation p_i, and the scalar values Mean Scattering (MS) (Equation (5)) and Directional Anisotropy (DA) (Equations (12), (13)). The construction of the material’s stiffness tensor is described in more detail in the next section.

$${C}_{ij}={C}_{ij}\left({p}_{i},{{{\rm{DA}}}},{{{\rm{MS}}}}\right)$$

(11)

In contrast to the Fractional Anisotropy (FA), which only reflects a general anisotropy, the term Directional Anisotropy (DA) is introduced to account for the sub-voxel fibre orientation spread in both xy- and xz-plane. The ratio (Equation (12)) of the third eigenvalue λ₃ and first eigenvalue λ₁ of the scattering tensor represents the sub-voxel fibre orientation distribution in the xy-plane, while the ratio (Equation (13)) of the third eigenvalue λ₃ and second eigenvalue λ₂ represents the sub-voxel fibre orientation distribution in the xz-plane.

$${{{{\rm{DA}}}}}_{{{{\rm{xy}}}}}=\frac{{\lambda }_{3}}{{\lambda }_{1}}$$

(12)

$${{{{\rm{DA}}}}}_{{{{\rm{xz}}}}}=\frac{{\lambda }_{3}}{{\lambda }_{2}}$$

(13)

Here, a ratio of 1 represents a fully random orientation, and a value of 0 implies perfect alignment. The fibre orientation p_i is expressed in φ and θ (Equation (10)). Therefore, these ratios can be correlated to a sub-voxel fibre angle spread φ^S and θ^S of 0 to 90° (Equation (14) and (15)), where the superscript S stands for spread. As no other information is available a linear correlation is the given choice.

$${\varphi }^{{{{\rm{S}}}}}={{{{\rm{DA}}}}}_{{{{\rm{xy}}}}}\,\pi /2$$

(14)

$${\theta }^{{{{\rm{S}}}}}={{{{\rm{DA}}}}}_{{{{\rm{xz}}}}}\,\pi /2$$

(15)

Additionally, the local Mean Scattering signal MS^local is used to calculate a local sub-voxel fibre volume fraction (Equation (16)). It builds on the premises that in a voxel with only matrix the mean scattering signal is lower than in a voxel with fibres. The more fibres are present in one voxel the higher the scattering signal. For this relation a linear dependency is assumed. This is again an assumption forced by lack of information. The Mean Scattering of pure matrix material MS_m represents 0 % fibre volume fraction, while the Mean Scattering of all voxels MS_c corresponds to the mean fibre volume fraction ${V}_{{{{\rm{f}}}}}^{{{{\rm{mean}}}}}$ of 19.9 %.

$${V}_{{{{\rm{f}}}}}^{{{{\rm{local}}}}}=-\frac{{V}_{{{{\rm{f}}}}}^{{{{\rm{mean}}}}}}{{{{{\rm{MS}}}}}_{{{{\rm{c}}}}}-{{{{\rm{MS}}}}}_{{{{\rm{m}}}}}}{{{{\rm{MS}}}}}_{{{{\rm{m}}}}}+\frac{{V}_{{{{\rm{f}}}}}^{{{{\rm{mean}}}}}}{{{{{\rm{MS}}}}}_{{{{\rm{c}}}}}-{{{{\rm{MS}}}}}_{{{{\rm{m}}}}}}{{{{\rm{MS}}}}}^{{{{\rm{local}}}}}$$

(16)

By the presented approach to construct the material’s constitutive law it becomes possible to account for sub-voxel fibre orientations and fibre volume fractions, as shown in in Fig. 8. All voxels A, B, C have the same dominant fibre orientation p_i, but yield different ellipsoidal shapes representing the X-ray scattering tensor. Voxels A and B have the same amount of fibres, which results in the same local Mean Scattering (MS) value but show a different fibre orientation distribution, leading to different Directional Anisotropies (DA)s. Voxels A and C have the same fibre orientation distribution but Voxel C has a higher amount of fibres which yields to a higher local Mean Scattering (MS) value.

Fig. 8: Three voxels with different sub-voxel fibre orientation distribution and fibre volume fraction.

A The fibres in this voxel have a mean orientation of 45° with two fibres deviating from the mean orientation. B The fibres in this voxel also have a mean orientation of 45° but with a smaller deviation. C The fibres in this voxel have the same orientation distribution as in (A) but there are twice as many fibres present. Even though all voxels show the same dominant fibre orientation, they yield different ellipsoid shapes representing the X-ray scattering tensor. These different shapes are used to construct different stiffness matrices C_ij (Equation (11)). Consequently, the stiffness matrix depends on the dominant fibre orientation p_i (Equation (10)), the Directional Anisotropy (DA) (Equation (12), (13)) and the Mean Scattering (MS) (Equation (5)).

Finite element modelling

The image-based model is set-up in a Python script, which can be found open access in⁴⁸. The reconstructed tensor tomography data, containing voxel-wise information about the scattering tensors’ eigenvectors and eigenvalues, is loaded into the Python script.

Based on the image data, a voxel-based regular hexahedral mesh with 8-node three-dimensional brick elements, each with 8 integration points, is created. Four voxels in all three spatial directions are combined into one element. Each element spatially covers 64 voxels, resulting in an element length of 400 μm. By this the number of integration points is kept at a reasonable level of approximately 500,000. In the Supplementary Information a mesh size study can be found. Further, elements are only created in voxels that exceed 10% Mean Scattering value (MS) in order to exclude voxels containing air (i.e., outside the sample) from the meshing process. Minor manual adjustments are necessary to remove elements that represent the scanned sample holder.

In each integration point of the finite element mesh, an individual stiffness matrix is calculated based on the originally defined Mori-Tanaka stiffness tensor (Equation (8)), which is updated by scattering information of the voxel spatially containing the integration point. This means that for each element in the finite element model, the information of 64 − 8 = 56 voxels is neglected. The stiffness matrix is computed with respect to the sub-voxel fibre volume fraction and the sub-voxel fibre orientation spread. The sub-voxel fibre volume fraction is calculated according to Equation (16), while the implementation of the sub-voxel fibre orientation spread is much more extensive. For each integration point, the fibre orientation angles φ and θ (Equation (10)) are calculated given the dominant fibre orientation. Around these nominal fibre orientation angles, an angular range, representing the sub-voxel fibre angular spread, is spanned. This spread depends on the Directional Anisotropy (DA) ratios and is computed according to Equations (14) and (15). Each spread is parameterised with ten angles distributed equally around the nominal fibre orientation direction. Each of the 30 independent stiffness matrix components is computed as mean of 100 possible combinations for each φ and θ in their respective interval. This is computationally heavy. In total 1.7 billion stiffness matrix components, all consisting of sine and cosine functions, are computed. Nevertheless, with the implementation of the Python Numba package, the computation time on 16 CPUs is kept to around 40 min. For each integration point, the 30 stiffness matrix components are then output in a Fortran file format, similar to what is described in ref. 49.

The final finite element model of the rod is applied with boundary conditions, where the lower surface is fixed, and the upper surface is displaced in the axial direction, corresponding to an axial strain of 1 %. For each integration point, the 30 independent stiffness matrix components generated in the Python script are read into an Abaqus user-defined material model (UMAT), where the final stiffness matrix is constructed. The simulation runs for approximately 12 minutes on one CPU.