Introduction

The study of bulk photovoltaic effect (BPVE) has a long history1,2,3, and recently it has attracted great renewed interest because it potentially allows the energy conversion efficiency to surpass the Shockley-Queisser limit4,5. The shift-current effects are believed to be the primary intrinsic contribution to the BPVE3,6. They offer an alternative to the photocurrent generated by traditional semiconductor p-n junctions7,8. It has been demonstrated that the photovoltage generated by shift-current effects can far exceed the band gap9,10,11,12.

The high priority of current studies in the field is to discover materials that have high shift-current conductivities. Cook et al. proposed principles for designing shift current materials using an effective two-dimensional model and successfully applied them to the monochalcogenide GeS8. In addition to conventional ferroelectric materials13,14, special attention has been given to Weyl semimetals because of the special topological nature of their band structures15,16. Ahn et al.17 theoretically studied the low-frequency properties of BPVEs in topological semi-metals and revealed the relationship between the shift current, injection current, and the quantum geometry of the material near the Weyl point. Recent studies18,19,20 indicate a significant potential for substantial nonlinear optical responses in layered two-dimensional materials, including BPVE and second harmonic generation.

In this work, we investigate the nonlinear optical properties of the two-dimensional ferroelectric material SnTe monolayer21 using first-principles methods. We find that it has giant shift current conductivities near the valley points. More remarkably, the linear optical absorption coefficient at this energy is very small, which leads to an enormous Glass coefficient of four orders of magnitude larger than that of bulk BaTiO31,5,22. We develop a minimal three-band model to analyze the mechanism of the giant shift-current effect in the SnTe monolayer. We find that the giant shift-current effects are induced by the nontrivial band structure geometry, where the shift-vector diverges at the valley point. We further show that the giant shift-current is related to the derivatives of the imaginary part of the quantum geometric tensor near the point. The mechanism is different from the previous works on the Weyl semimetals17, and therefore opens a play ground for the fascinating physical properties that are determined by the band structure geometries.

Results

Crystal structure

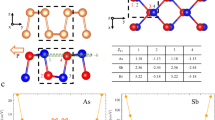
In 2016, Chang et al.21 reported that the SnTe monolayer exhibits robust in-plane ferroelectricity with a Curie temperature of up to 270 K, which is significantly higher than its bulk counterpart at 98 K. The SnTe monolayer has a hinge-like structure similar to that of phosphorene, as shown in Fig. 1, and belongs to the Pmn21 space group with mirror (Mxz) and glide mirror (G) symmetries. The in-plane ferroelectricity of the SnTe monolayer is oriented along the x-axis23,24,25,26. Due to its lack of inversion symmetry, the SnTe monolayer is expected to exhibit shift-current effects.

Fig. 1: Crystal structure and band gap of SnTe monolayer.
figure 1

a Top view, (b) side view along the x direction and (c) side view along the y direction of the crystal structure of the SnTe monolayer. The unit cell is indicated by the dashed rectangle in a. d The band gap between the lowest conduction band and the highest valence band in the Brillouin zone, where k0, \({\bar{{{{\bf{k}}}}}}_{0}\,{{{{\bf{k}}}}}_{1}\) and \({\bar{{{{\bf{k}}}}}}_{1}\) are the valley points.

Full size image

Band structure and shift current conductivities

We perform first-principles calculations to investigate the shift-current effects in the SnTe monolayer. Details of the calculations are presented in the METHODS section.

The band structures of SnTe monolayer with and without spin-orbit coupling (SOC) are shown in Supplementary Fig. 1. There are four valley points of the band structure in the first Brillouin zone. Two valley points, k0 = (0.416, 0.0), k1 = (0.0, 0.415), are situated on the Γ − X line and Γ − Y line, respectively, in direct coordinates. The other two valley points are obtained by the time inversion symmetry of the aforementioned two k-points, namely \({\bar{{{{\bf{k}}}}}}_{0}=-{{{{\bf{k}}}}}_{0}\) and \({\bar{{{{\bf{k}}}}}}_{1}=-{{{{\bf{k}}}}}_{1}\), as displayed in Fig. 1d. The band gaps at points k0 (\({\bar{{{{\bf{k}}}}}}_{0}\)) and k1 (\({\bar{{{{\bf{k}}}}}}_{1}\)) are 1.21 eV and 1.45 eV, respectively. The positions of the valley points are only slightly altered upon the introduction of SOC, as shown in Supplementary Fig. 1.

The lack of inversion symmetry in the SnTe monolayer results in a shift current, which is a nonlinear dc photocurrent induced by illumination1,2,3,

$${J}^{a}=2{\sigma }^{abc}(0;\omega ,-\omega ){E}_{b}(\omega ){E}_{c}(-\omega ),$$
(1)

where σabc(0; ω, − ω) is the shift-current conductivity tensor, and a (b, c) = x, y, z are the crystal axes. As the SnTe monolayer is a 2D material, we do not consider the current in the z-direction, nor do we consider the electric field applied in the z-direction. Because of the mirror symmetry Mxz of the SnTe monolayer, only σxxx, σxyy, and σyxy = σyyx are nonzero.

The first-principles calculated shift-current conductivities3,27,28,29 are consistent with the above symmetry analysis. The 3D-like conductivities are obtained assuming an active single-layer thickness of 3.12 Å28,30. Although the results with and without SOC show some quantitative differences, the inclusion of SOC does not affect the main conclusions of this study (see Supplementary Fig. 3). Therefore, we only discuss the results without SOC here, and the analysis can be equally applied to the results with SOC.

Figure 2a shows the largest component of the shift-current conductivity tensor, σyxy, and the results for σxxx and σxyy are displayed in Supplementary Figs. 4 and 5, respectively. σyxy exhibits the highest peak at ℏω0 = 1.21 eV, with \({\sigma}_{3D}^{yxy}\) = 284 μA V−2. This value is significantly larger than the shift-current conductivity of the known high BPVE material GeS, which is of the order of 150 μA V−2, and the values of 250 μA V−2 reported in state-of-the-art Si-based solar cells28,30,31.

Fig. 2: Shift current spectra, absorption, and Glass coefficient of SnTe monolayer.
figure 2

a Shift current conductivity \({\sigma }_{3D}^{yxy}\) of the SnTe monolayer. There are three peaks at 1.21, 1.59, and 2.73 eV, respectively. b The absorption coefficient α[110] and (c) the Glass coefficient of the SnTe monolayer, respectively.

Full size image

It has been suggested that a large joint density of states (JDOS) is necessary to have a large shift current7,8,28. However, surprisingly, we find that the JDOS at ℏω0 = 1.21 eV is extremely small, as shown in Supplementary Fig. 2. Consequently, the absorption coefficient α[110] is also very small around ℏω0 = 1.21 eV, as shown in Fig. 2b. It is noteworthy that the absorption coefficient αyy is zero at this energy, which is strongly counterintuitive given that σyxy is enormous.

The above results have significant physical implications. We compute the Glass coefficient1,7,9,27gabc = α−1σabc, and the calculated gyxy is shown in Fig. 2c. At ℏω0 = 1.21 eV, gyxy has a sharp peak due to the giant σyxy and small α[110]. The calculated Glass coefficient gyxy of the SnTe monolayer is 1.8 × 10−5 cm V−1 (ref. 30) at this energy, which is four orders of magnitude higher than g31 = 3 × 10−9 cm V−1 of the bulk (001)-oriented BaTiO3 crystal1,5,22. The Glass coefficient g plays essential roles in the shift current related physical properties. For example, the photovoltaic field generated by the shift current1,5 can be estimated as,

$${E}_{{{{\rm{pv}}}}}\approx \frac{g}{\phi {(\mu \tau )}_{{{{\rm{pv}}}}}}\frac{\hslash \omega }{e}\,,$$
(2)

where ϕ is the quantum yield, ℏω is the incident photon energy and μ and τ are the mobility and lifetime of the carriers responsible for photoconductivity. A large value of the Glass coefficient g can result in a significant increase in the photovoltaic field Epv because, in such cases, the shift current dominates over the “leaking current” caused by photoconductivity. The photovoltaic power conversion efficiency is also closely related to the Glass coefficient1, where the maximum efficiency is \({\eta }_{\max }=g{E}_{{{{\rm{pv}}}}}/4\).

To experimentally explore this giant shift current effect, we could apply light with an electric field polarized along the [110] direction, and measure the resulting shift current along the y direction, which gives,

$${J}^{y}=2{\sigma }^{yxy}{E}_{x}(\omega ){E}_{y}(-\omega ).$$
(3)

It has been shown that strong excitonic effects may further enhance the shift-current effects in 2D materials32,33. To enable the unambiguous detection of the shift-vector-induced effects while minimizing potential interference from other effects (e.g., the exciton effect), one may use laser energy that matches the band-to-band transition energy, which is typically much higher than the exciton absorption energy. Investigating how many-body effects change the shift-current in SnTe will be an interesting topic for future investigation.

Discussion

It is particularly interesting and important to explore the underlying mechanism of the giant shift-current conductivity and Glass coefficient in the SnTe monolayer. The shift-current tensor is given by3,

$${\sigma }^{abc}(0;\omega ,-\omega )=\frac{\pi {e}^{3}}{{\hslash }^{2}}\int\frac{d{{{\bf{k}}}}}{8{\pi }^{3}}{\sum }_{n,m}{f}_{nm}{{{\rm{Im}}}}\left[{I}_{mn}^{abc}+{I}_{mn}^{acb}\right]\delta \left({\omega }_{mn}-\omega \right)\,,$$
(4)

where fnm = fn − fm and ℏωnm = En − Em are differences between Fermi occupation factors and band energies, respectively. \({I}_{mn}^{abc}={r}_{mn}^{b}{r}_{nm;a}^{c}\), where \({r}_{nm}^{a}\) is the inter-band dipole matrix, and \({r}_{nm;a}^{b}\) is the generalized derivative of the dipole matrix, i.e.,

$${r}_{nm}^{a}=(1-{\delta }_{nm}){A}_{nm}^{a},$$
(5)
$${r}_{nm;b}^{a}={\partial }_{b}{r}_{nm}^{a}-i\left({A}_{nn}^{b}-{A}_{mm}^{b}\right){r}_{nm}^{a}.$$
(6)

Here, \({A}_{nm}^{a}\) is the non-Abelian Berry connection. Although \({r}_{nm}^{a}\) and \({r}_{nm;a}^{b}\) are gauge dependent, their norm \(| {r}_{nm}^{a}|\) and \(| {r}_{nm;a}^{b}|\), as well as \({I}_{mn}^{abc}\) are gauge invariant28. Note that \({r}_{nm}^{a}\) and \({r}_{nm;a}^{b}\) and \({I}_{mn}^{abc}\) are all k dependent, but we drop the k index here for simplicity.

We calculate \({\sum }_{n,m}{f}_{nm}{{{\rm{Im}}}}\left[{I}_{mn}^{yxy}+{I}_{mn}^{yyx}\right]\delta \left({\omega }_{mn}-{\omega }_{0}\right)\) in the first BZ at ℏω0 = 1.21 eV. We find that the contribution only arises from the transition between the highest valence (v) band and the lowest conduction (c) band near the valley points k0 and \({\bar{{{{\bf{k}}}}}}_{0}\) as shown in Supplementary Fig. 6a.

Because only the valley points contribute to the optical transitions at ℏω0, the corresponding JDOS and linear absorption coefficient is very small. Furthermore, as shown in Supplementary Fig. 6b, \({I}_{vc}={{{\rm{Im}}}}\left[{I}_{vc}^{yxy}+{I}_{vc}^{yyx}\right]\), has a bright spot at k0, which gives rise to the giant shift-current conductivity.

Figure 3a shows the norm of \({r}_{vc}^{x}\) and \({r}_{vc}^{y}\) along ky passing through k0, represented by the red and blue solid lines, respectively. We observe that \(| {r}_{vc}^{x}|\) reaches a maximum at ky = 0, whereas \(| {r}_{vc}^{y}|\) = 0 at k0 due to the mirror symmetry Mxz. However, as seen from Fig. 3a, \(| {r}_{vc}^{y}|\) changes rapidly along ky around k0. One may speculate that \({r}_{vc}^{y}\) may have a large partial derivative in Eq. (6) along ky at the valley point. Indeed, as shown in Fig. 3b, \(| {r}_{cv;y}^{y}|\) exhibits a peak at k0. We plot Ivc in Fig. 3c. Interestingly, we find that \({I}_{vc}\approx | {r}_{vc}^{x}| | {r}_{cv;y}^{y}|\) around k0. Both \({r}_{vc}^{x}\) and \({r}_{cv;y}^{y}\) reach their maximum values at k0, leading to the giant Ivc.

Fig. 3: DFT and model analysis of dipole matrix, its generalized derivatives, and shift current contribution along ky.
figure 3

a The norm of dipole matrix \({r}_{vc}^{x}\) and \({r}_{vc}^{y}\) along ky, where v and c are highest valence band and lowest conduction band, respectively. b The norm of the generalized derivative of dipole matrix, \({r}_{cv;y}^{y}\), along ky. c The \({I}_{vc}={{{\rm{Im}}}}\left[{I}_{vc}^{yxy}+{I}_{vc}^{yyx}\right]\) along ky. The results obtained from DFT and model calculations are shown in solid and dashed lines, respectively.

Full size image

To gain a deeper insight into the physics involved, we construct a minimal three-band model around the valley point k0,

$$H({{{\bf{k}}}})={H}_{0}+{\mathbb{A}}\delta {k}_{x}+{\mathbb{B}}\delta {k}_{y}+{\mathbb{C}}\delta {k}_{x}^{2}+{\mathbb{D}}\delta {k}_{x}\delta {k}_{y}+{\mathbb{E}}\delta {k}_{y}^{2},$$
(7)

up to the quadratic terms of δk, where δk = k − k0. More specifically, δkx = kx − 0.416, δky = ky. We therefore do not distinguish ky and δky below. In the model, the 1st band is the highest valence band, whereas the 2nd band and 3rd band correspond to the lowest two conduction bands in the DFT calculations. We fit the Hamiltonian matrix H(k) and velocity matrix vmn(k) from DFT calculations around k0. The fitted parameters of the model are given in Supplementary Information.

We first (numerically) calculate \(| {r}_{12}^{x}|\), \(| {r}_{12;y}^{y}|\), and I12 of the three-band model, and the results are compared with those from DFT calculations in Fig. 3a–c, respectively. The three-band model can reproduce the results of the DFT calculations semi-quantitatively, and the discrepancies can be attributed to the omission of other bands in the model.

Around k0, the three-band model can be analytically solved using second order perturbation theory, and consequently \({r}_{nm}^{a}\) and \({r}_{nm;b}^{a}\) can also be calculated analytically. Especially, at k0 we have \({v}_{nm}^{x}({{{{\bf{k}}}}}_{0})={{\mathbb{A}}}_{nm}\) and \({v}_{nm}^{y}({{{{\bf{k}}}}}_{0})={{\mathbb{B}}}_{nm}\), therefore by using Eq. (18) in METHOD section, we have

$${r}_{nm}^{x}({{{{\bf{k}}}}}_{{{{\bf{0}}}}})=\frac{{{\mathbb{A}}}_{nm}}{i{\omega }_{nm}},\quad {r}_{nm}^{y}({{{{\bf{k}}}}}_{{{{\bf{0}}}}})=\frac{{{\mathbb{B}}}_{nm}}{i{\omega }_{nm}}.$$
(8)

Because \({{\mathbb{A}}}_{12}\ne 0\), and \({{\mathbb{B}}}_{12}=0\), which is actually imposed by the mirror symmetry, we have \({r}_{12}^{x}({{{{\bf{k}}}}}_{0})\ne 0\), but \({r}_{12}^{y}({{{{\bf{k}}}}}_{0})=0\). This means that the linear (or direct) optical transition between the 1st and 2nd bands along ky is forbidden. Similarly we calculate the \({r}_{nm;a}^{b}\) of the valley point k0, and we have,

$${r}_{21;y}^{y}({{{{\bf{k}}}}}_{{{{\bf{0}}}}})=\frac{i}{{\omega }_{21}}\left[{{\mathbb{B}}}_{23}{{\mathbb{B}}}_{31}\left(\frac{1}{{\omega }_{31}}+\frac{1}{{\omega }_{32}}\right)-2{{\mathbb{E}}}_{21}\right].$$
(9)

In the model, the value of \({r}_{21,y}^{y}\) (and therefore \({I}_{12}^{yxy}\)) depends mainly on the virtual transitions \({{\mathbb{B}}}_{23}{{\mathbb{B}}}_{31}\), which corresponding to the last term of Eq. (19) in METHOD section. The first term of Eq. (19) vanishes, because \({{\mathbb{B}}}_{12}\) = 0. This is remarkable that the linear (direct) optical transition between the 1st band and the 2nd band in the y direction is forbidden, but the nonlinear transition may occur because both the 1st band and 2nd band have strong coupling with the 3rd-band, which leads to the giant shift-current effect. This effect is quite different from that of the two-band models for Weyl semimetals17.

The giant shift-current effects in SnTe have even more profound origins. An alternative expression for the shift-current conductivity is written as17,

$$\begin{array}{l}{\sigma }^{yxy}=-\frac{\pi {e}^{3}}{{\hslash }^{2}}{\int}_{{{{\bf{k}}}}}\mathop{\sum}\limits_{n,m}{f}_{nm}\left({R}_{mn;y}^{y}-{R}_{nm;y}^{x}\right){r}_{nm}^{x}{r}_{mn}^{y}\\\qquad\qquad \delta \left({\omega }_{mn}-\omega \right)\,,\end{array}$$
(10)

where,

$${R}_{mn;a}^{b}=i{\partial }_{a}\ln {r}_{mn}^{b}+{A}_{mm}^{a}-{A}_{nn}^{a},$$
(11)

is known as the shift vector, which characterizes the displacement of electrons in real space during the inter-band transition1,34,35. The shift vector is a gauge invariant quantity and can be viewed as a quantum geometric potential36. According to the perturbation theory, near k0, \({r}_{12}^{y}({{{\bf{k}}}})={f}_{4}\,{k}_{y}+{f}_{5}\,\delta {k}_{x}{k}_{y}\), where f4 and f5 are constants. In the model, \({A}_{11}^{a}({{{{\bf{k}}}}}_{0})=0\) and \({A}_{22}^{a}({{{{\bf{k}}}}}_{0})=0\) at k0, and both are small around k0. We can therefore neglect them in the following calculations. As k approaches k0 along ky, i.e., δkx = 0, we have,

$${R}_{12;y}^{y}=i{\partial }_{y}\ln \left({f}_{4}\,{k}_{y}\right)=\frac{i}{{k}_{y}}\,,$$
(12)

i.e., \({R}_{12;y}^{y}\) is purely imaginary and goes to infinity. Therefore, k0 is a singular point for the shift vector \({R}_{12;y}^{y}\), which is a monopole in k-space. When ky is approaching zero, \({r}_{12}^{y}\) is also approaching zero as discussed in previous sections, and \({R}_{21;y}^{x}{r}_{21}^{x}{r}_{12}^{y}\) vanishes, but \({R}_{12;y}^{y}{r}_{21}^{x}{r}_{12}^{y}\) is still finite (actually very large) and purely real (Fig. 3). The introduction of SOC will not break the mirror symmetry, and therefore the above analyses remain valid. The shift vector would diverge at the valley points, as evidenced by Supplementary Fig. 3. Even after the introduction of SOC, the Glass coefficient at the valley points remains significantly large.

The shift vectors also play important roles in second harmonic generation17,37,38. It is therefore expected that the SnTe monolayer would have non-trivial second harmonic responses. The divergence of the shift vector at the so-called “optical zero” was discussed in ref. 39. However, the relation between the giant shift current and the divergent shift vector has not been revealed.

Very recently, nonlinear optical transitions have been related to the Riemannian geometry of the energy bands17,40. We may define the quantum geometric tensor between two bands m and n,

$${Q}_{ba}^{mn}={r}_{nm}^{b}{r}_{mn}^{a}\equiv {g}_{ba}^{mn}-\frac{i}{2}{F}_{ba}^{mn}\,,\,\,a,b=x,y,z$$
(13)

where \({g}_{ba}^{mn}\) is the band-resolved quantum metric, \({F}_{ba}^{mn}\) is the band-resolved Berry curvature, and the two geometric quantities are related to U(1) quantum metric and Berry curvature as \({g}_{ba}^{n}={\sum }_{m\ne n}{g}_{ba}^{mn}\) and \({\Omega }_{c}^{n}={\sum }_{m\ne n}{\epsilon }_{cba}{F}_{ba}^{mn}/2\)41,42.

In our case, we consider the transition between the 1st band and the 2nd band, and the quantum geometric tensor of the two bands is given by \({Q}_{xy}^{12}={r}_{12}^{x}{r}_{21}^{y}\). We have \({Q}_{xy}^{12}({{{{\bf{k}}}}}_{{{{\bf{0}}}}})=0\) because \({r}_{21}^{y}({{{{\bf{k}}}}}_{{{{\bf{0}}}}})=0\). However, we show that the partial derivative of the imaginary part of \({Q}_{xy}^{12}\) is related to \({I}_{12}^{yxy}\), i.e.,

$${{{\rm{Im}}}}\left[{I}_{12}^{yxy}({{{{\bf{k}}}}}_{{{{\bf{0}}}}})\right]={\partial }_{y}{{{\rm{Im}}}}{\left.\left[{Q}_{xy}^{12}\right]\right\vert }_{{{{\bf{k}}}} = {{{{\bf{k}}}}}_{0}}=-\frac{1}{2}{\left.{\partial }_{y}{F}_{xy}^{12}\right\vert }_{{{{\bf{k}}}} = {{{{\bf{k}}}}}_{0}}.$$
(14)

Fig. 4a illustrates the distribution of \({{{\rm{Im}}}}[{Q}_{xy}^{12}]\) near k0 and its derivative with respect to ky is shown in Fig. 4b. \({{{\rm{Im}}}}[{Q}_{xy}^{12}]\) has a maximum (minimum) at δky = 0.05 (δky = −0.05) and δkx = 0, which is very similar to the Berry curvature distribution in Fig. 2a of ref. 26. Furthermore, \({{{\rm{Im}}}}[{Q}_{xy}^{12}]\) changes rapidly around δky = 0, and as a consequence, \({{{\rm{Im}}}}\left[{I}_{12}^{yxy}({{{{\bf{k}}}}}_{0})\right]\) has a maximum at k0, which is consistent with that from direct calculations.

Fig. 4: Quantum geometric tensor near valley point k0.
figure 4

The distributions of (a) \({{{\rm{Im}}}}\left[{Q}_{xy}^{12}\right]\) and (b) \({\partial }_{y}{{{\rm{Im}}}}\left[{Q}_{xy}^{12}\right]\) around the valley point k0.

Full size image

We have demonstrated that the giant shift-current and Glass coefficient are directly induced by the divergent shift-vector near the valley points. Our three-band model has revealed several crucial requirements for achieving these effects. Firstly, the band structure should possess valley points located on a k-line with mirror symmetry, ensuring the divergence of the shift vector. Additionally, the structure should break the inversion symmetry within the mirror plane to have non-zero \({r}_{nm}^{x}\). Notably, there are numerous materials that meet these conditions, such as the MX family, including GeS, GeSe, GeTe, SnS, SnSe30,43, which exhibit similar properties.

In summary, our study unveils a significant shift current effect and an extremely large Glass coefficient in the ferroelectric SnTe monolayer. These effects stem from the divergence of the shift-vector near valley points, highlighting the influence of band geometry on nonlinear optical transitions. These findings present remarkable evidence of measurable physical effects arising from shift-vector divergence in semiconductors. They also offer valuable guidance in the search for materials with significant shift current effects, holding promise for their application in photoelectric devices.

Methods

Self-consistent calculations

The first-principles calculations are carried out with the Atomic orbital Based Ab-initio Computation at UStc (ABACUS) code44,45. The Heyd-Scuseria-Ernzerhof (HSE) exchange-correlation functional46 is used. The ABACUS code is developed to perform large-scale density functional theory calculations based on numerical atomic orbitals (NAO)44,47 and supports for large-scale HSE calculations48,49,50. The optimized norm-conserving Vanderbilt (ONCV)51 fully relativistic pseudopotentials52 from the PseudoDojo library53 are used. The valence electrons for Sn, Te are 4d105s25p2, and 4d105s25p4, and the NAO bases for Sn and Te are 2s2p2d1f and 2s2p2d1f, respectively47.

In the self-consistent and band structure calculations, the energy cut-off for the wave functions is set to 150 Ry. The Brillouin zone is sampled using a Γ-centered 16 × 16 × 1k-point mesh. The structure is fully optimized until all forces are less than 1 meV Å−1.

Shift-current conductivity

After the self-consistent calculations, the tight-binding Hamiltonian,

$${H}_{\mu \nu }({{{\bf{R}}}})=\langle {{{\bf{0}}}}\mu | H| {{{\bf{R}}}}\nu \rangle ,$$
(15)

the overlap matrices,

$${S}_{\mu \nu }({{{\bf{R}}}})=\langle {{{\bf{0}}}}\mu | {{{\bf{R}}}}\nu \rangle ,$$
(16)

and the dipole matrices (between the NAOs),

$${{{{\bf{r}}}}}_{\mu \nu }({{{\bf{R}}}})=\langle {{{\bf{0}}}}\mu | {{{\bf{r}}}}| {{{\bf{R}}}}\nu \rangle ,$$
(17)

in the NAO bases are generated, where \(\left\vert {{{\bf{R}}}}\nu \right\rangle ={\phi }_{\nu }\left({{{\bf{r}}}}-{\tau }_{\nu }-{{{\bf{R}}}}\right)\) is the ν-th NAO in the R-th cell, and τν is the center of the ν-th NAO in the unit cell.

The dipole matrix \({r}_{nm}^{a}\) and its generalized derivative \({r}_{nm;b}^{a}\) in the shift current Eqs. (5)–(6) are calculated as follows3,8,28 (here we drop the k index for simplicity),

$${r}_{nm}^{a}=\frac{{v}_{nm}^{a}}{i{\omega }_{nm}}\quad (m\,\ne\, n),$$
(18)

and

$$\begin{array}{l}{r}_{nm;b}^{a}=\frac{i}{{\omega }_{nm}}\left[\right.\frac{{v}_{nm}^{a}{\Delta }_{nm}^{b}+{v}_{nm}^{b}{\Delta }_{nm}^{a}}{{\omega }_{nm}}-{w}_{nm}^{ab}\\\qquad\quad+\mathop{\sum}\limits_{p\ne n,m}\left(\frac{{v}_{np}^{a}{v}_{pm}^{b}}{{\omega }_{pm}}-\frac{{v}_{np}^{b}{v}_{pm}^{a}}{{\omega }_{np}}\right)\left.\right]\quad (m\ne n),\end{array}$$
(19)

where,

$$\begin{array}{rcl}{v}_{nm}^{a}&=&\frac{1}{\hslash }\left\langle {u}_{n{{{\bf{k}}}}}\left\vert {\partial }_{a}H({{{\bf{k}}}})\right\vert {u}_{m{{{\bf{k}}}}}\right\rangle ,\\ {\omega }_{nm}&=&{E}_{n}-{E}_{m},\\ {\Delta }_{nm}^{a}&=&{\partial }_{a}{\omega }_{nm}={v}_{nn}^{a}-{v}_{mm}^{a},\\ {w}_{nm}^{ab}&=&\frac{1}{\hslash }\left\langle {u}_{n{{{\bf{k}}}}}\left\vert {\partial }_{ab}^{2}H({{{\bf{k}}}})\right\vert {u}_{m{{{\bf{k}}}}}\right\rangle .\end{array}$$
(20)

The velocity matrix elements \({v}_{nm}^{a}\) are calculated by the ab initio tight-binding Hamiltonian Eqs. (15)–(17)54,55. The calculated shift-current conductivities and Glass coefficients are converted to effective 3D values, following refs. 28,30. More details can be found in Supplementary Information.

The band structures and the optical properties, such as the shift current are calculated using the tight-binding Hamiltonian implemented in the PY-ATB code56.