Unravelling ultralow thermal conductivity in perovskite Cs₂AgBiBr₆: dominant wave-like phonon tunnelling and strong anharmonicity

Abstract

Understanding the lattice dynamics and heat transport physics in the lead-free halide double perovskites remains an outstanding challenge due to their lattice dynamical instability and strong anharmonicity. In this work, we investigate the microscopic mechanisms of anharmonic lattice dynamics and thermal transport in lead-free halide double perovskite Cs₂AgBiBr₆ from first principles. We combine self-consistent phonon calculations with bubble diagram correction and a unified theory of lattice thermal transport that considers both the particle-like phonon propagation and wave-like tunnelling of phonons. An ultra-low thermal conductivity at room temperature (~0.21 Wm⁻¹K⁻¹) is predicted with weak temperature dependence( ~ T^−0.34), in sharp contrast to the conventional ~T⁻¹ dependence. Particularly, the vibrational properties of Cs₂AgBiBr₆ are featured by strong anharmonicity and wave-like tunnelling of phonons. Anharmonic phonon renormalization from both the cubic and quartic anharmonicities are found essential in precisely predicting the phase transition temperature in Cs₂AgBiBr₆ while the negative phonon energy shifts induced by cubic anharmonicity has a significant influence on particle-like phonon propagation. Further, the contribution of the wave-like tunnelling to the total thermal conductivity surpasses that of the particle-like propagation above around 310 K, indicating the breakdown of the phonon gas picture conventionally used in the Peierls-Boltzmann Transport Equation. Importantly, further including four-phonon scatterings is required in achieving the dominance of wave-like tunnelling, as compared to the dominant particle-like propagation channel when considering only three-phonon scatterings. Our work highlights the importance of lattice anharmonicity and wave-like tunnelling of phonons in the thermal transport in lead-free halide double perovskites.

Introduction

Halide perovskite materials, with a general chemical formula ABX₃, where A is a monovalent cation (Cs⁺, methylammonium (CH₃NH₃⁺) or formamidinium (CH(NH₂)₂⁺)), B is a bivalent cation (Pb²⁺ or Sn²⁺), and X is a halide anion (Cl⁻, Br⁻ or I⁻), have emerged as a new class of materials with outstanding optoelectronic properties. Generally, lead-based halide perovskites possess unique merits as optoelectronic materials, exhibiting long carrier lifetime and diffusion length, tuneable direct bandgap, high absorption coefficient and low trap density^1,2,3. These properties make halide perovskites an ideal option for photovoltaic and optoelectronic devices in recent years. However, lead-based perovskite materials still encounter two crucial challenges, i.e., poor long-term stability and the toxicity of lead elements³. A promising strategy to tackle these issues is to replace the divalent Pb²⁺/ Sn²⁺ cation with one monovalent and one trivalent metal cation in the lead halide perovskites to form the so-called lead-free double perovskites A₂B⁺B³⁺X₆ (A = K, Rb, Cs; B⁺ = Li, Na, K, Rb, Cs, Ag; B³⁺ = Al, Ga, In, Sb, Bi, Sc, Y, and X = F, Cl, Br, I)^3,4. The structural and functional diversity and the long-term stability of lead-free double perovskites render them attractive candidates for optoelectronic devices.

Apart from the optoelectronic properties, halide perovskites also attract research interest in lattice dynamics and thermal transport characteristics, which affect their thermodynamical stability⁵, opto-electronic and photovoltaic performances⁶. Particularly, the effects of lattice vibrations on electronic and optoelectronic properties have been widely investigated to slow down the cooling of charge carriers in halide perovskites^7,8,9. Besides, the experimentally reported ultra-low thermal conductivity κ_L^{10,11,12,13,14,15}, high carrier mobilities^12,16,17 in conjunction with large Seebeck coefficient^16,17 make halide perovskites attractive for thermoelectric applications. A high ZT of 1~2 in hybrid halide perovskite was predicted by ab initio calculations¹⁸. Importantly, the ultra-low κ_L of halide perovskites was attributed to the low phonon group velocities and short phonon lifetimes¹⁹ stemming from the complicated crystal structures and extremely strong lattice anharmonicity. Despite the progress in experimentally and theoretically observed thermal properties of halide perovskites^{12,13,14,15,20}, oxide and fluoride perovskites²¹, an accurate quantitative prediction of their lattice dynamical properties and a comprehensive microscopic understanding of their thermal transport properties are still in infancy.

The outstanding challenges in theoretical understanding of phonon-related properties in halide perovskites can be traced back to the strong lattice anharmonicity, which makes the conventional approaches within the harmonic approximation framework fail^22,23,24,25. To overcome the shortcoming of harmonic approximation, the anharmonic phonon renormalization techniques^22,23,24,26 have been applied to predict the phase transition temperature and thermal properties of halide perovskites at finite temperatures^27,28,29. However, most of works consider only cubic-anharmonicity and the explicit treatment of effects of both cubic- and quartic-anharmonicities on phonon energies and transport channels remains challenging. Also, the particle-like phonon picture in describing thermal transport physics generally breaks down in highly anharmonic materials when the phonon linewidths are larger than the interbranch spacings^30,31,32,33. For example, using the conventional first-principles-based Peierls-Boltzmann transport equation (PBTE) method³⁴, Lee et al.¹² failed to reproduce the experimentally measured ultra-low κ_L in all-inorganic halide perovskites. Going beyond the conventional particle-like description of phonons in PBTE, Simoncelli et al.³⁰ explained the experimentally observed lattice thermal conductivity in the complex perovskite CsPbBr₃ by further considering wave-like tunneling of phonons. The unified theory of thermal transport adopted in the above literature³⁰ can accurately reproduce the κ_L; however, it considers only the three-phonon scattering processes within the harmonic approximation treatment (The error cancellation due to phonon renormalization and four phonon scattering rates may occurs in the κ_L of CsPbBr₃, similar to that observed in PbTe³⁵). Therefore, a comprehensive understanding of the lattice dynamics and thermal properties in lead-free halide double perovskites have been rarely reported.

In this paper, we systematically investigate the anharmonic lattice dynamics and thermal transport properties in a benchmark lead-free halide double perovskite Cs₂AgBiBr₆ at the atomic level. We have applied a state-of-the-art unified theory of thermal transport to predict the lattice thermal conductivity κ_L in perovskite Cs₂AgBiBr₆ by considering the isotope-, three- (3 ph) and four-phonon (4 ph) scatterings, anharmonic phonon renormalization from both cubic and quartic anharmonicities, particle-like propagation and wavelike tunneling transport channels. Using the anharmonic phonon renormalization technique, we find that the soft modes are associated with the tilting of the AgBr₆ and BiBr₆ octahedra units and become hardened with increasing temperature. The cubic-to-tetragonal phase transition temperature of Cs₂AgBiBr₆ is predicted as ~119–138 K, agreeing well with the experimental value. Using the unified theory of thermal transport, we show that both the 4 ph scattering processes and wavelike tunneling of phonons play a crucial role in predicting the κ_L of Cs₂AgBiBr₆. Particularly, considering only the 3 ph scattering, the populations’ conductivity accounts for more than 50% of the total κ_L over the entire temperature range. By further considering 4 ph scatterings, the coherences’ conductivity ascribing from the wave-like tunneling channel dominates the total κ_L above ~310 K. This study highlights the importance of wave-like tunneling and quartic anharmonicity in describing heat conduction in Cs₂AgBiBr₆.

Results and discussion

Lattice dynamics and anharmonicity

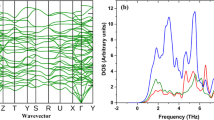
We start by investigating the vibrational properties of double perovskite Cs₂AgBiBr₆ in its cubic phase (as shown in Fig. 1a, b) using the static harmonic approximation (HA) approach. The calculated harmonic phonon dispersions (represented by dark blue dash lines) and density of states (DOS) of Cs₂AgBiBr₆ are shown in Fig. 1c. One of the most notable characteristics of the harmonic phonon dispersions in cubic Cs₂AgBiBr₆ is the occurrence of soft modes with negative phonon energies, which are observed at the Γ and X points in the Brillouin zone. This feature suggests the presence of dynamical instability at low temperatures [see in Fig. 1c]. Upon analyzing the vibrational properties of Cs₂AgBiBr₆, we have observed that the soft modes at the Γ and X points are associated with the tilting of the AgBr₆ and BiBr₆ octahedra units, respectively, which was also reported by Klarbring et al.²⁹. By applying a comprehensive anharmonic phonon renormalization technique, these soft modes are found to become significantly hardened with increasing temperature [see anharmonically renormalized phonon dispersions and DOS in Fig. 1c]. The soft modes in Cs₂AgBiBr₆ are primarily contributed by Br atoms, which is evident from the atom-decomposed partial DOS [see the right panel in Fig. 1c] and atomic participation ratio of Br atoms projected onto the phonon bands [see Supplementary Fig. 1 (See Supplementary Information for additional figures illustrating harmonic and anharmonic phonon properties, along with thermal transport properties, and further discussions)]. Apart from the Br-dominated soft modes, the low-frequency phonon modes (≤2.2 THz), contributed by Cs atoms, also undergo a gradual stiffening [see Fig. 1c and Supplementary Fig. 1]. The temperature-dependent stiffening behavior of low-frequency modes is attributed to the large atomic displacements that arise from the relatively weak bonding interactions [see Supplementary Fig. 2]. In contrast, the high-frequency phonon modes (>2.2 THz) in Cs₂AgBiBr₆ are predominantly contributed by Ag and Br atoms [see Supplementary Fig. 1] and exhibits a temperature-dependent softening, consistent with experimental observations³⁶.

Fig. 1: Crystal structure and phonon properties.

a Crystal structure of the cubic double perovskite Cs₂AgBiBr₆, which features two different sub-lattices formed by AgBr₆ and BiBr₆ octahedra units, respectively, together with Cs atoms. The solid green lines inside the sub-lattice depict a conventional unit cell, and the green, white, blue, and brown spheres represent Cs, Ag, Bi and Br atoms, respectively. b View of the yz plane of the crystal structure. c Calculated anharmonically renormalized phonon dispersions at finite temperatures (from T = 100 to 700 K) compared with the phonon dispersions computed by the harmonic approximation treatment at T = 0 K. The calculated atom-decomposed partial and total phonon densities of states at T = 0, 300, and 700 K are shown on the right panel, respectively. d Calculated temperature-dependent squared phonon frequency of soft modes at the Γ and X points using the SCP and SCPB approximations, respectively. The empty red circle indicates the experimentally measured phase transition temperature (~122 K)^36,39,40, and the empty blue pentagon indicates the experimental phonon energies of the soft mode at the Γ point at 135 and 300 K, respectively⁴⁰. e Calculated temperature-dependent renormalized phonon dispersions along the high-symmetry paths compared with experimental results at 300 K⁴⁰.

It is worth noting that in some crystals, the phonon energy shifts resulting from 3 ph interaction processes, specifically the bubble diagram (including those in the SCPB approximation), can be ignored due to their minor contributions³⁷ and computational complexity³⁸. In the case of crystalline Cs₂AgBiBr₆, considering only 4 ph processes, i.e., the loop diagram (SCP approximation), in anharmonic phonon renormalization shows only phonon stiffening [see Supplementary Fig. 3]. Additionally, the anharmonically renormalized phonon energies in Cs₂AgBiBr₆ are stabilized above 50 K when considering only 4 ph processes [see Fig. 1d]. This value is close to the prediction of Klarbring et al.²⁹ but significantly lower than the experimental value of approximately 122 K^36,39,40. The observed discrepancy in the phase transition temperature of Cs₂AgBiBr₆, between the value computed solely from 4 ph processes and the experimental result, underscores the crucial role of the negative phonon energy shifts from 3 ph processes in accurately determining phonon energies. By incorporating the 3 ph processes in phonon renormalization calculations, it predicts that the cubic-to-tetragonal phase transition of Cs₂AgBiBr₆ occurs at ~119 K (phonons collapse at X point) and ~138 K (phonons collapse at Γ point) [see in Fig. 1d], in good agreement with experimental measurements^36,39,40. Furthermore, in comparison to the SCP approximation, the SCPB approximation provides more accurate predictions for the phonon energies of the soft mode at Γ point, as observed in experiments conducted at 135 and 300 K [see in Fig. 1d]⁴⁰. To validate out calculations, we compared the phonon dispersions along high-symmetry paths calculated using the SCPB approximation with the experimental results obtained from inelastic neutron scattering measurements⁴⁰. The comparison shows good agreement between the calculated and experimental values [see Fig. 1e and Supplementary Figs. 4 and 5]. The importance of both 3 ph and 4 ph processes in reproducing the experimental lattice vibrational properties of Cs₂AgBiBr₆ crystal is highlighted by these results, as has been demonstrated for several other compounds, e.g., BaZrO₃, CsPbBr₃ and SnSe^38,41,42.

To gain insight into lattice instability, anharmonicity, and phonon energy shift in Cs₂AgBiBr₆ crystal, we mapped out the 2D potential energy surface (PES)⁴³ of soft modes at the Γ and X points. The PES was plotted along two corresponding normal-mode coordinates (Q₁, and Q₂) [see Fig. 2a]. The soft modes at the Γ and X points are associated with the out-of-phase and in-phase tilting of the AgBr₆ and BiBr₆ octahedra units, respectively, as shown in Fig. 2b, c. As anticipated, the minimum energy is located outside the zero-tilt amplitude (${Q}_{1}={Q}_{2}=0$) of both soft modes at the Γ and X points, indicating lattice instability or dynamical instability [see Fig. 2a]⁴³. The 2D PES mapping in Fig. 2a reveals that the minimum energy of the soft mode at Γ point is lower than that of soft mode at the X point. This observation suggests the dominant role of the out-of-phase tilting mode, associated with the AgBr₆ octahedra, in the cubic-to-tetragonal phase transition of Cs₂AgBiBr₆. Although the minimum energies exist outside the zero-tilt amplitude for both soft modes, the corresponding minima are relatively shallow, with values of about −0.79 and −0.45 meV∙atom⁻¹, respectively. This observation suggests that the high-temperature cubic phase of Cs₂AgBiBr₆ crystal is effectively an average structure at relatively low temperatures, similar to the specific phase of some previously reported compounds such as CsSnI₃, CsSnBr₃ and CsSnCl₃^44,45,46.

Fig. 2: Calculated 2D potential energy surfaces, displacement pattern and 1D potential energy surfaces.

a Calculated two-dimensional (2D) potential energy surface of Cs₂AgBiBr₆ as a function of normal mode coordinates Q₁ and Q₂. Here the soft modes at the Γ and X points associated with the out-of-phase and in-phase tilts are selected to generate the corresponding configurations. b Crystal structure of Cs₂AgBiBr₆ with displacement pattern of the soft mode at the Γ point, wherein the red and light blue circles with arrows are depicted for the displacements of AgBr₆ and BiBr₆ octahedron units (out-of-phase tilting), respectively. c The same as b, but with displacement pattern of the soft mode at the X point and (in-phase tilting). d DFT-calculated double well potential energy surface (solid green disks) of the soft mode at the Γ point as a function of the vibrational amplitude (Q₁) in the normal mode coordinate. The blue, yellow and green dash lines show the potential energy surface decomposed to the second, fourth and sixth orders, respectively. The blue, brown and pink solid lines represent the renormalized harmonic potentials at T = 300, 500, and 700 K, respectively. e The same as d, but for soft mode at the X point and the normal mode coordinate (Q₂).

To gain a more intuitive understanding of the lattice anharmonicity of Cs₂AgBiBr₆, we projected the 2D PES onto 1D PES for both the soft modes at Γ and X points [see Fig. 2d, e]. As expected, each soft mode forms a double-well potential, suggesting strong lattice anharmonicity⁴⁷. Indeed, the anharmonic double-well potentials of soft modes can be decomposed up to the sixth order, although the contribution of the sextic terms is minor [see Fig. 2d, e]. Additionally, the harmonic potential (blue dash line) of soft modes has a negative coefficient, which is responsible for the imaginary frequency [see Fig. 1b], and therefore leads to the failure of the conventional harmonic approximation (HA) treatment^22,34,47. It is worth mentioning that although the PESs of the soft modes exhibit anharmonic behavior up to the sixth-order terms, the contribution of these higher-order terms is minor. Therefore, in our anharmonic phonon renormalization calculations, we only consider the anharmonic contributions up to fourth-order terms. The lattice anharmonicity was utilized in the anharmonic phonon renormalization to gradually transform the negative harmonic potentials of the soft modes into positive ones at finite temperatures, such as 300 K, 500 K and 700 K [see Fig. 2d, e]. These positive potentials represent the effective harmonic potential with temperature effects taken into account.

Lattice thermal conductivity

Next, we investigate the effects of phonon energy renormalization and multi-phonon interaction from both cubic and quartic anharmonicities on lattice thermal conductivity κ_L. To achieve this, we employ a hierarchy of theoretical approaches with increasing accuracy, as depicted in Fig. 3a. Due to the failure of conventional harmonic approximation (HA) treatment in capturing the lattice dynamics of Cs₂AgBiBr₆, we begin our analysis by examining the κ_L obtained using the SCP+3 ph model. The populations’ thermal conductivity ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ was computed using the SCP+3 ph model, which takes into account renormalized phonon energies from only quartic anharmonicity and employs only 3 ph scattering processes. The resulting value at 300 K is ~0.38 ${\rm{W}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}$, as shown in Fig. 3b. This predicted ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ is consistent with the result reported by Klarbring et al.²⁹, although their method utilized the temperature-dependent effective potential approach based on AIMD simulations. As discussed earlier, the anharmonic phonon renormalization using only quartic anharmonicity can lead to an overestimation of the phonon energies and phase transition temperature of Cs₂AgBiBr₆. To account for extra phonon energy shifts from cubic anharmonicity, we move up the theory level progressively to the SCPB+3 ph model. As a result, we observe a remarkable decrease in ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ from ~0.38 to ~0.17 Wm⁻¹ K⁻¹ (~55.95% reduction) at 300 K, as demonstrated in Fig. 3b. This observation highlights the significant influence of cubic anharmonicity not only on lattice dynamics but also on phonon transport in crystalline Cs₂AgBiBr₆. A similar phenomenon has been reported for simple cubic perovskites, e.g., CsSnBr₃, BaZrO₃ and CsPbBr₃, in previous studies^28,38,41. To properly account for the anharmonicity of highly anharmonic compounds, it is necessary to include multi-phonon scatterings resulting from quartic anharmonicity^25,47. By further incorporating 4 ph scattering processes into the SCPB+3 ph model, the improved SCPB+3,4 ph model predicts a further reduction in ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$. Specifically, the predicted ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ decreases to ~0.11 and ~0.06 Wm⁻¹ K⁻¹ (~34.6 and 51.8% reduction) at 300 and 700 K, respectively [see Fig. 3b]. This highlights the crucial role of 4 ph scattering processes in determining the ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ of highly anharmonic Cs₂AgBiBr₆. Recent studies have emphasized the importance of coherences’ contributions from non-diagonal terms of heat flux operators, i.e., wave-like tunneling channel, in compounds with ultra-low κ_L or/and strong anharmonicity^30,31,47,48. By incorporating the wave-like tunneling transport channel^30,48 through non-diagonal terms of heat flux operators, beyond the phonon-gas model, the SCPB+3,4 ph+OD model results in a substantial increase in κ_L to 0.21 and 0.16 Wm⁻¹ K⁻¹ (~93.9 and 184.2% enhancement) at 300 and 700 K, respectively. Interestingly, using the SCPB+3,4 ph+OD model reveals that the total κ_L contributed from the wavelike tunneling channel comprises more than 50% of the total κ_L above 310 K [see Fig. 3b, c]. In contrast, when considering only 3 ph scatterings, the phonon propagation channel dominates the total κ_L, accounting for more than 50% of the total heat conduction over the entire temperature range [see Fig. 3c]. The presence of strong 4 ph scatterings triggers the inter-conversion of the dominant role of heat conduction between the particle-like phonon propagation and the wave-like tunneling channels in Cs₂AgBiBr₆. This observation emphasizes the limitations of the conventional phonon-gas model and highlights the importance of considering higher-order anharmonicity and coherences’ effects in advanced thermal transport models to accurately describe the thermal transport of Cs₂AgBiBr₆.

Fig. 3: Thermal transport models, theoretically predicted and experimentally measured thermal conductivity.

a A schematic diagram depicting the prediction accuracy of lattice thermal conductivity using various hierarchical thermal transport models, namely, the HA+3 ph, SCP+3 ph, SCPB+3 ph, SCPB+3,4 ph, and SCPB+3,4 ph+OD models, respectively. The ellipsis indicates the theory of thermal transport beyond the SCPB+3,4 ph+OD model and it may further include anharmonic heat flux operators⁶¹. b Calculated temperature-dependent lattice thermal conductivity ${\kappa }_{{\rm{L}}}$ using different levels of thermal transport theory including the SCP/SCPB+3 ph, SCPB+3,4 ph+OD models. The yellow and pink shaded areas show the contributions from phonon and coherence thermal transport channels calculated using the SCPB+3,4 ph+OD model, respectively. c Temperature-dependent populations’, coherences’ and total thermal conductivity calculated using SCPB+3 ph+OD model and the coherences’ contributions, percentage wise, to total thermal conductivity calculated using SCPB+3/3,4 ph models. d Comparison of our predicted lattice thermal conductivity of crystalline Cs₂AgBiBr₆ with other experimentally measured ultra-low thermal conductivity of all-inorganic halide perovskites at room temperature^{12,13,14,15,51,52}.

The dominant role of coherences’ contributions ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ to the total κ_L over a wide range of temperatures implies that the heat transfer physics in Cs₂AgBiBr₆ exhibits similar features to those observed in glasses. We proceed to analyze the temperature dependence of the lattice thermal conductivity of Cs₂AgBiBr₆ calculated using different levels of theory. The predicted ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ predicted by the SCP+3 ph model follows an extremely weak temperature dependence of $\sim {T}^{-0.28}$ in the temperature range of 300–700 K [see Fig. 3b]. This observation challenges the conventional understanding that the ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ computed by the lowest-order perturbation theory⁴⁹ follows a temperature dependence of $\sim {T}^{-1}$. Using the SCPB+3 ph model, the temperature dependence of the ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ becomes stronger and follows $\sim {T}^{-0.40}$, which is a result of the softening of phonon frequency. Further including 4 ph scattering processes leads to a significant change in the temperature dependence of the ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$, which is remarkably enhanced to $\sim {T}^{-0.75}$. This observation is consistent with the findings of Feng et al.⁵⁰ and Zheng et al.⁴¹ By utilizing the SCPB+3,4 ph+OD model, the κ_L exhibits a weak temperature dependence of $\sim {T}^{-0.34}$, resembling the experimentally observed out-of-plane temperature-dependent behavior of κ_L in Cs₂PbI₂Cl₂¹⁴ [see Fig. 3b].

To validate our computational results, we compared the calculated κ_L of Cs₂AgBiBr₆ with the available experimental data for all-inorganic halide perovskites at 300 K^{12,13,14,15,51,52}, as illustrated in Fig. 3d. Our predicted total κ_L for Cs₂AgBiBr₆ is within the same order of magnitude (≤0.64 Wm⁻¹ K⁻¹) as the κ_L values reported for other halide perovskites [see Fig. 3d]. After a thorough examination, we discovered that the experimental κ_L of halide perovskites tends to decrease as the structural complexity increase. Structural complexity is typically characterized by the size of the unit-cell and the types of elements present in the halide perovskite crystal. An experiment recently reported an ultralow room-temperature κ_L of 0.31 Wm⁻¹ K⁻¹ in crystalline Cs₂SnI₆⁵¹. Given the similarity in structure and phonon dispersions between Cs₂SnI₆ and Cs₂AgBiBr₆⁵³, we can expect a similar result for Cs₂AgBiBr₆. Furthermore, the frequency of soft mode at Γ point in Cs₂SnI₆ is around 0.6 THz, which is higher than that in Cs₂AgBiBr₆ (~0.4 THz) at 300 K. Therefore, we can expect a lower experimental κ_L in Cs₂AgBiBr₆ as compared to Cs₂SnI₆. An even lower κ_L value of 0.19 Wm⁻¹ K⁻¹ was observed for the halide perovskite Cs₃Bi₂I₆Cl₃, which has a higher structural complexity than Cs₂AgBiBr₆, in a recent experiment at room temperature¹⁵. Therefore, the κ_L of Cs₂AgBiBr₆ is expected to be higher than 0.19 Wm⁻¹ K⁻¹. Overall, the predicted total κ_L of Cs₂AgBiBr₆ in this study is considered to be reasonably reliable and can be verified by future experimental investigations.

Microscopic mechanisms of populations’ conductivity

To better illustrate the effect of anharmonic phonon renormalization and higher-order phonon scattering processes on the ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ of Cs₂AgBiBr₆, we present the spectral and cumulative κ_L in Fig. 4a, b calculated using SCP+3 ph and SCPB+3/3,4 ph models at 300 and 700 K, respectively. For all the three levels of theory, our results consistently show that most of populations’ thermal conductivity ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ in Cs₂AgBiBr₆ is carried by phonons with a frequency less than 3 THz across the temperature range of 300–700 K [see Fig. 4a, b]. Additionally, we observed that optical phonons with a frequency higher than 1.2 THz play a dominant role in the ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ from the particle-like propagation channel. This behavior is commonly observed in cubic SrTiO₃ with strong anharmonicity and low-${\kappa }_{{\rm{L}}}^{{\rm{P}}}$²², and is attributed to the suppression of acoustic phonons by highly anharmonic optical modes.

Fig. 4: Calculated populations’ thermal conductivity and phonon scattering rates.

a Calculated spectral and cumulative phonon thermal conductivities at T = 300 K using the SCP+3 ph and SCPB+3/3,4 ph models, respectively. b The same as a, but T = 700 K. c Calculated 3 ph and 4 ph scattering rates at T = 300 K using the SCP+3 ph and SCPB+3/3,4 ph models, respectively. d The same as c, but T = 700 K.

The spectral and cumulative ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ obtained from the SCP+3 ph model show a reduction compared to the results from the SCPB+3 ph model. This decrease in ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ is mainly contributed by the phonons with frequency less than 3 THz [see Fig. 4a, b]. This is because the cubic anharmonicity contributes negative phonon energy shifts, which results in the softening of phonons and enhancement of phonon scattering processes [see Fig. 4c, d]. With the additional 4 ph scattering processes, the reduced ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ obtained by SCPB+3,4 ph relative to SCPB+3 ph is primarily contributed by phonons with a frequency less than 3 THz at both 300 and 700 K. This can be attributed to the inherently strong 4 ph scattering rates of specific modes, such as rattling-like flat modes, which will be demonstrated later.

By examining the group velocity, specific heat, and scattering rates, in computing ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$³⁴, the reduction in ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ in two improved models (SCPB+3/3,4 ph) relative to the SCP+3 ph model is mainly attributed to the scattering rates [see Fig. 4c, d]. This is due to the fact that the difference in group velocity and specific heat between the SCP and SCPB approximation is negligible in Cs₂AgBiBr₆, as demonstrated by see Supplementary Figs. 6 and 7. Indeed, previous studies have shown that the group velocity and specific heat of certain crystals are relatively insensitive to phonon energy shifts resulting from lattice anharmonicity^25,41,47,54. As shown in Figs. 3b and 4a, b, the inclusion of additional 4 ph scatterings in the calculation of ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ (using the SCPB+3,4 ph model) leads to a significant reduction compared to considering only 3 ph processes (using the SCPB+3 ph model). Specifically, the reduction in ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ is 34.6 and 51.8% at 300 and 700 K, respectively. This can be ascribed to the large 4 ph scattering rates, which are roughly as high as those of 3 ph processes at 300 K, and even become dominant at 700 K, particularly for phonons with frequency less than 2 THz, as shown in Fig. 4c, d.

It is worth noting that both the 3 ph and 4 ph scattering rates decrease with increasing frequency for phonons below 1 THz (shown in the upper left part of Fig. 4c, d). Upon analysis of the distribution of scattering rates and atomic participation ratios [see Fig. 4a, b and Supplementary Fig. 1], we have found that the observed phenomenon can be attributed to the presence of Br-dominated soft modes, and a similar phenomenon was also reported for other compounds, e.g., SrTiO3, PbSe and PbTe^22,55. Generally, the ultra-low κ_L observed in halide perovskites is attributed to the combination of strong scattering rates and small group velocity^19,56. The small group velocity with a maximum value of ~2.35 Km∙s^-1 observed in Cs₂AgBiBr₆ may lead to the ultra-low κ_L[see Supplementary Fig. 6]. However, neglecting the contribution from Br-dominated soft modes in 3 ph scattering processes calculation leads to a significant enhancement of ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$, with a value of ~87 Wm⁻¹ K⁻¹ at 300 K [see Supplementary Figs. 8 and 9]. Similarly, neglecting Cs-dominated modes leads to an increase in ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ to 18 from ~0.17 Wm⁻¹ K⁻¹ calculated using SCPB+3 ph [see Supplementary Figs. 8 and 9]. This illustrates the important role of the Br-dominated soft modes with strong anharmonicity [see Supplementary Figs. 8, 10 and 11] in contributing to the ultra-low ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ of Cs₂AgBiBr₆. Overall, the strong anharmonicity and resulting high scattering rates are the dominant factors in the ultra-low κ_L of Cs₂AgBiBr₆.

To reveal the correlation between the negative phonon energy shift due to cubic anharmonicity and the resulting change in phonon scattering rates, we compare scattering phase space^57,58 calculated using the SCP and SCPB approximation at 300 and 700 K, as shown in Fig. 5a, b. The scattering phase space of emission processes computed with SCPB+3 ph is substantially larger relative to the SCP+3 ph results for phonons with a frequency less than 3 THz at 300 and 700 K. This observation suggests that the negative phonon shifts resulting from cubic anharmonicity leads to enhance the scattering phase space and thus stronger phonon scattering rates. Similar observations have been also reported in other crystals such as BaZrO₃ and CsPbBr₃^38,54. Similarly, the enhanced scattering rates for phonons with frequencies greater than 3 THz between the SCP+3 ph and SCPB+3 ph models can be attributed to the enhanced scattering phase space of absorption processes. Note that another key quantity in calculating scattering rates, namely, the scattering matrix element, is insensitive to the phonon energy shift due to lattice anharmonicity⁴¹.

Fig. 5: Calculated multi-phonon scattering phase space.

a Comparison of mode-resolved 3 ph scattering phase space calculated using SCP and SCPB approximations at T = 300 K, respectively. The 3 ph scattering phase spaces are decomposed to the absorption ($q+{q\text{'}}\to {q\text{'}\text{'}}$) and emission ($q\to {q}^{{\prime} }+{q\text{'}\text{'}}$) processes, respectively. b The same as a, but at T = 700 K. c Mode-resolved 4 ph scattering phase space calculated using SCPB approximation at T = 300 K, wherein the 4 ph scattering phase spaces are decomposed to the recombination ($q+{q}^{{\prime} }+{q\text{'}\text{'}}\to {q\text{'}\text{'}\text{'}}$), redistribution ($q+{q}^{{\prime} }\to {q\text{'}\text{'}}+{q\text{'}\text{'}\text{'}}$) and splitting ($q\to {q}^{{\prime} }+{q}^{{\text{'}\text{'}}}+{q\text{'}\text{'}\text{'}}$) processes, respectively. d The same as c, but at T = 700 K.

To gain a deeper insight into the microscopic origin of strong 4 ph scattering rates in Cs₂AgBiBr₆, we calculated the scattering phase space for 4 ph processes at 300 and 700 K, respectively, as shown in Fig. 5c, d. We found that the scattering phase space for 4 ph processes, specifically for the redistribution processes ($q+{q}^{{\prime} }\to {q}^{{\text{'}\text{'}}}+{q\text{'}\text{'}\text{'}}$), is remarkably strong in Cs₂AgBiBr₆, with magnitudes comparable to those of 3 ph processes at 300 K and even surpassing them at 700 K [see Fig. 5a–d]. This observation is in line with the magnitude distribution between the 3 ph and 4 ph scattering rates [see Fig. 4c, d] and provides further evidence that the large 4 ph scattering phase space contributes to strong 4 ph scattering rates in Cs₂AgBiBr₆ [see Fig. 5c, d]. The peak region of the 4 ph redistribution processes in Cs₂AgBiBr₆ was found to coincide with the partial DOS of Cs atoms [see Figs. 1c and 5c–d], which suggests that Cs atoms play a significant role in the strong 4 ph scattering rates. Additionally, the atom participation ratio calculated in Supplementary Fig. 12 reveals that Cs atoms contribute to flat phonon bands and exhibit rattling-like behaviors (This observation can be attributed to the loose bonding of Cs atoms [see Supplementary Fig. 13]), which are known to result in strong scattering phase space and scattering rates^47,59. Flat rattling-like modes contributing to strong 4 ph scatterings have also been observed in other materials such as crystalline AgCrSe₂⁶⁰ and Cu₁₂Sb₄S₁₃ Tetrahedrites⁴⁷.

Microscopic mechanisms of coherences’ conductivity

As shown in Fig. 3b, c, the dominant contribution to the total κ_L above ~310 K is from the coherences’ contributions. Specifically, using the SCPB+3,4 ph+OD model, the coherences’ conductivity ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ accounts for 48.4 and 60.3% of the total κ_L at 300 and 700 K, respectively. To uncover the microscopic origin of wavelike conduction in crystalline Cs₂AgBiBr₆, we calculated the phonon lifetime as a function of frequency from 3 ph and 4 ph processes at 300 and 700 K, respectively, as shown in Fig. 6a, b. Recently, a new concept called the Wigner limit in time proposed by Simoncelli et al.⁴⁸ was used to separate phonons into different thermal transport regimes, mainly including particle-like propagation and wave-like tunneling regimes. The Wigner limit in time is defined as $\tau ={3N}_{{at}}/{\omega }_{\max }$, where N_at is the number of atoms in the primitive cell and ω_max is the maximum phonon frequency. Using the criterion of Wigner limit in time, phonons with a lifetime above this limit behave in a particle-like propagation and mainly contribute to the populations’ thermal conductivity; on the contrary, phonons behave in a wave-like tunneling and mainly contribute to the coherences’ thermal conductivity.

Fig. 6: Calculated multi-phonon lifetimes.

a Calculated phonon lifetimes as a function of frequency at T = 300 K within SCPB+3/3,4 ph models, respectively. The green solid line depicts the Wigner limit in time⁴⁸ and can be written as $\tau ={\left[\Delta {\omega }_{{avg}}\right]}^{-1}$, where $\Delta {\omega }_{{avg}}$ is the average phonon inter-band spacing and can be defined as ${\omega }_{\max }/3{N}_{{at}}$, where ${\omega }_{\max }$ denotes the highest frequency and ${N}_{{at}}$ denotes the number of atoms in primitive cell. Phonons with lifetime larger than this limit mainly contribute to populations’ thermal conductivity; on the contrary, phonons mainly contribute to coherences’ thermal conductivity. The Cyan dots indicates the Ioffe-Regel limit in time⁷⁷, i.e., $\tau =2\pi /\omega$, $\omega$ is the phonon frequency with unit of cm⁻¹. Phonons with lifetime larger than the Ioffe-Regel limit in time are recognized as well-defined and can be handled by the unified theory of thermal transport³⁰. b The same as a, but T = 700 K.

For the transport regimes in crystalline Cs₂AgBiBr₆, after considering both 3 ph and 4 ph scattering processes, most phonons have a lifetime below the Wigner limit in time at both 300 and 700 K, highlighting the necessity of evoking wavelike tunneling transport channel [see Fig. 6a, b]. These findings suggest that the coherences’ conductivity from wavelike tunneling channel may dominate over the total thermal conductivity in Cs₂AgBiBr₆, consistent with the results shown in Fig. 3b, c. When only 3 ph scattering processes are considered, it is shown in Fig. 6a, b that there are many phonons with a lifetime above the Wigner limit in time. This suggests that the wave-like tunneling channel may be as important as the particle-like propagation channel in Cs₂AgBiBr₆ [see Fig. 3c and Supplementary Fig. 14]. Interestingly, compared with the ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ calculated by the SCPB+3 ph+OD model, further including 4 ph scattering processes, namely, SCPB+3,4 ph+OD, significantly suppresses the particle-like propagation channel. As a result, the wave-like tunneling channel plays a dominant role in thermal transport in Cs₂AgBiBr₆ [see Fig. 3c]. This indicates the conversion of dominant thermal transport channels between the particle-like phonon propagation and wave-like tunneling channels. These findings emphasize the inadequacy of the conventional phonon-gas model in describing thermal transport in Cs₂AgBiBr₆. They also highlight the crucial role of comprehensive modeling, such as the SCPB+3,4 ph+OD model, in gaining a deeper understanding of the actual heat transfer mechanism in Cs₂AgBiBr₆.

To gain a better understanding of microscopic mechanisms behind the coherences’ thermal conductivity ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ in Cs₂AgBiBr₆, we calculated the 1D-spectral and cumulative mode-specific contributions to coherences’ conductivity at 300 and 700 K, respectively, as shown in Fig. 7a, b. Similar to the spectral populations’ conductivity ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ of Cs₂AgBiBr₆ in Fig. 4a, b, the majority of the coherences’ conductivity from the wavelike tunneling channel is carried by the phonons with a frequency less than 3 THz at both 300 and 700 K [see Fig. 7a, b]. This can be attributed to the small inter-band spacing (due to dense phonon dispersions [see Fig. 1b]) in conjunction with large linewidths (large scattering rates [see Fig. 4a, b] or strong anharmonicity³⁰) within frequency region below 3 THz⁴⁸. This phenomenon is consistent with the observation presented in Fig. 6a, b.

Fig. 7: Calculated coherences’ thermal conductivity.

a Calculated spectral and cumulative coherences’ thermal conductivity using SCPB+3,4 ph+OD model at T = 300 K. The contribution of phonon mode j in coherence couplings between two phonon modes (q, j) and (q, jʹ) is evaluated by ${c}_{{\boldsymbol{q}}j}/\left({c}_{{\boldsymbol{q}}j}+{c}_{{\boldsymbol{q}}{j}^{{\prime} }}\right)$, where ${c}_{{\boldsymbol{q}}j}$ is the phonon mode-specific heat. b The same as a but at 700 K. c Two-dimensional (2D) modal ${\kappa }_{{\rm{L}}}^{{\rm{C}}}\left({\omega }_{{\boldsymbol{q}}j},{\omega }_{{\boldsymbol{q}}{j}^{{\prime} }}\right)$ of the contributions to the coherences’ thermal conductivity calculated using the SCPB+3,4 ph+OD model at T = 300 K. The diagonal data points $({\omega }_{{\boldsymbol{q}}j}={\omega }_{{\boldsymbol{q}}{j}^{{\prime} }})$ indicate phonon degenerate eigenstates. d The same as c but T = 700 K. e The same as c but using SCPB+3 ph+OD model. f The same as e but at T = 700 K.

Figure 7c, d show that the contributions to coherences’ thermal conductivity in Cs₂AgBiBr₆, calculated using SCPB+3,4 ph+OD at 300 and 700 K, can be resolved in terms of the phonon energies, namely, ${\omega }_{q{\boldsymbol{j}}}$ and ${\omega }_{q{\boldsymbol{j\text{'}}}}$, of two coupled phonons. In contrast to the ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ in CsPbBr₃ at 50 K³⁰ and La₂Zr₂O₇ at 200 K⁴⁸, where quasi-degenerate phonon states dominate, the phonons contributing to the ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ of Cs₂AgBiBr₆ at both 300 and 700 K have relatively different frequencies [see Fig. 7c, d]. This suggests that the contributions to the ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ are driven by the strong anharmonicity and the corresponding heat transfer physics of wave-like coherences in Cs₂AgBiBr₆ is intrinsically different from that of harmonic glasses. By comparing the contributions to the ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ in Fig. 7c, d, it is observed that couplings between phonons with large frequency differences begin to contribute to the ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ with increasing temperature [for instance, when considering coupling pairs with a frequency difference larger than 2 THz, their coherences’ contribution ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ increases by ~6.9% with the temperature rising from 300 to 700 K]. This is because the scattering rates of phonons, i.e., their linewidths, also increase as the temperature increases. Additionally, a comparison between the contributions to the ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$ calculated using SCPB+3 ph+OD and SCPB+3,4 ph+OD models [see Fig. 7c–f] reveals that the additional 4 ph scattering rates result in more scattered contributions to ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$. This is because the large 4 ph scattering rates allow phonons with relatively large frequency differences to couple, particularly those involving the Cs rattling-like modes. This phenomenon is similar to what was observed in Cu₁₂Sb₄S₁₃ Tetrahedrites⁴⁷.

To this end, the application of the SCPB+3,4 ph+OD model has provided a reliable prediction of the κ_L in crystalline Cs₂AgBiBr₆, and has elucidated its microscopic mechanism of heat transport within the temperature range of 300–700 K. However, further improvement may be possible by accounting for (i) the anharmonic contributions of heat flux operators⁶¹, (ii) simultaneously evaluating phonon energy shifts and broadening.

In conclusion, we have performed the DFT calculations to investigate the anharmonic lattice dynamics and unravel the microscopic mechanisms of thermal transport in crystalline Cs₂AgBiBr₆. Our results show that the unstable soft modes correspond to the in-phase and out-of-phase tilting of the AgBr₆ and BiBr₆ octahedra units in real space. The anharmonic stabilization of the soft modes is observed to occur at ~119–138 K in excellent agreement with experiments. We found that the negative phonon energy shifts arising from cubic anharmonicity plays a crucial role in accurately reproducing experimental phonon dispersions. The accurate reproduction of experimental phonon energies by the SCPB approximation underscores the significance of considering both cubic and quartic anharmonicities in anharmonic phonon renormalization.

With advanced unified theory of thermal transport, the κ_L of Cs₂AgBiBr₆ is predicted to be ultra-low, with a value of 0.21 Wm⁻¹ K⁻¹ at 300 K, which can be mainly attributed to the inherently strong scatterings rather than small group velocities. The negative phonon energy shifts from cubic anharmonicity leads to enhanced phonon scattering rates, thus reducing κ_L in Cs₂AgBiBr₆. Additionally, our results indicate that the 4 ph scatterings significantly suppress the κ_L in Cs₂AgBiBr₆. Through analysis of the phonon scattering phase space for 3 ph and 4 ph processes, we attribute the strong 4 ph scattering rates to the flat phonon modes dominated by Cs atoms.

It is also revealed that the coherences’ conductivity dominates the total κ_L above 310 K, highlighting the breakdown of the conventional phonon gas model in accurately predicting the κ_L of Cs₂AgBiBr₆. The comparison of the results obtained from SCPB+3 ph+OD and SCPB+3,4 ph+OD models shows that the inclusion of 4 ph scattering processes alters the dominance of wave-like tunneling and particle-like phonon propagation channels in thermal transport of Cs₂AgBiBr₆. Thus, both cubic and quartic anharmonicities are critical in determining not only the anharmonic lattice dynamics but also lattice thermal conductivity. Our study provides insights into the microscopic mechanisms of thermal transport in halide double perovskites with ultra-low κ_L and strong anharmonicity.

Methods

First-principles calculations

In this work, the ab-initio calculations within the framework of density functional theory (DFT)⁶² using the Vienna Ab-initio Simulation Package (VASP)⁶³ were performed for structural optimization of Cs₂AgBiBr₆ crystal, wherein the projector-augmented wave (PAW)⁶⁴ method was used to treat the Cs(5s²5p⁶6s¹), Ag(4d¹⁰5s¹), Bi(5d¹⁰6s²6p³) and Br(4s²4p⁵) shells as valence states. The revised Perdew-Burke-Ernzerhof (PBE) version for solids, i.e., PBEsol⁶⁵, of the generalized gradient approximation (GGA)⁶⁶ was used for the exchange-correlation functional. The ionic positions and unit cell geometry were fully optimized using a plane-wave cutoff energy of 800 eV and a 10 × 10 × 10 Monkhorst-Pack electronic k-point mesh, with a tight force convergence criterion of 10⁻⁵ eV·Å⁻¹ and a tight energy convergence criterion of 10⁻⁸ eV. The resulting relaxed lattice constant is a = b = c = 5.602 Å, in good agreement with the experiment (a = 5.639 Å)^39,67 for Cs₂AgBiBr₆ crystal with a ${\boldsymbol{Fm}}\bar{{\boldsymbol{3}}}{\boldsymbol{m}}$ space group. Considering that the long-term dipole-dipole interaction in the polar Cs₂AgBiBr₆ crystal will lead to the longitudinal (LO) and transverse optical (TO) phonon modes splitting near the Brillouin zone center, the non-analytic corrections are further included in the dynamical matrix and the dielectric tensor ε and the Born effective charges Z of Cs₂AgBiBr₆ are calculated using the density functional perturbation theory (DFPT)⁶⁸. The corresponding parameters are computed to be ε^∞ = 5.392, ${Z}^{* }\left({\rm{Cs}}\right)=1.356,{Z}^{* }\left({\rm{Ag}}\right)=1.795,{Z}^{* }\left({\rm{Bi}}\right)=4.805,{{Z}^{* }\left({\rm{Br}}\right)}_{\perp }=-0.769,$ and ${{Z}^{* }\left({\rm{Br}}\right)}_{{\rm{II}}}=-3.114$, which are consistent with previous theorectical calculations²⁹. Given the experimental thermal expansion of Cs₂AgBiBr₆ in the temperature range of 100–300 K is relatively small (~0.53% – from 11.21 to 11.27 Å)³⁹, we have opted not to consider the thermal expansion in the current calculations [For more details, please refer to Supplementary Fig. 15].

The 0-K harmonic interatomic force constants (IFCs) calculation was performed using the finite-displacement approach⁶⁹, with a 2 × 2 × 2 supercell and 4 × 4 × 4 Monkhorst-Pack electronic k-point mesh, and a plane-wave cutoff energy of 800 eV in VASP. Additionally, the same supercell dimensions and DFT calculation settings were used to map out the potential energy surfaces (PESs). To extract anharmonic IFCs efficiently, the machine-learning-based method called the compressive sensing lattice dynamics method (CSLD) was used^70,71, where the compressive technique⁷² was implemented to collect the physically important terms of the anharmonic IFCs using the limited displacement-force datasets²². Within the framework of the CSLD method, the ab initio molecular dynamics (AIMD) simulation was performed with a 2 × 2 × 2 supercell to generate the random atomic displacements, with a 2 × 2 × 2 Monkhorst-Pack electronic k-point mesh and an energy convergence criterion of 10⁻⁵ eV. The AIMD simulation of the NVT ensemble with the Nosé Hoover thermostat at 500 K was ran for 3000-time steps using a 2-fs time step. By disregarding the first 500 steps from the obtained AIMD trajectories, 100 atomic structures were sampled at equal intervals. After that, a random-direction displacement of 0.1 Å for all atoms was imposed to reduce the cross-correlations between the atomic structures. Furthermore, accurate DFT calculations were performed to obtain the training and cross-validation data, on the basis of the sampled atomic structures, with 4 × 4 × 4 Monkhorst–Pack electronic k-point mesh and energy convergence better than 10⁻⁸ eV. Finally, using the displacement-force datasets and 0-K harmonic IFCs obtained, the least absolute shrinkage and selection operator (LASSO) technique⁷³ was used to extract the anharmonic IFCs up to the sixth order. The real-space cutoff radii of 8.47 Å, 6.35 Å, 4.23 Å and 3.18 Å were applied for the cubic, quartic, quintic, and sextic IFCs extraction, respectively. We observe a relative fitting error of 6.2% for higher-order IFCs in the context of atomic force. It is noteworthy that this error is exceptionally small, mirroring values consistently reported in the existing literatures^22,25,71. In this work, the IFCs estimation was performed by using the ALAMODE package^22,37,74.

Anharmonic phonon renormalization

The anharmonic phonon energy renormalization was performed using the self-consistent phonon approximation (SCP) formulated in the reciprocal space^26,37, as implemented in the ALAMODE package^22,37. Considering only the first-order correction from quartic anharmonicity, i.e., the loop diagram, the resulting SCP equation in the diagonal form neglecting polarization mixing (PM) can be written as

$${\varOmega }_{q}^{2}={\omega }_{q}^{2}+2{\varOmega }_{q}{I}_{q},$$

(1)

where ω_q is the bare harmonic phonon frequency associated with the phonon mode q, and Ω_q is the anharmonically renormalized phonon frequency at finite temperatures. The quantity I_q can be defined as

$${I}_{q}=\frac{1}{8N}\sum _{{q}^{{\prime} }}\frac{{\rm{\hslash }}{V}^{\left(4\right)}\left(q{\rm{;}}-q{\rm{;}}{q}^{{\prime} }{\rm{;}}-{q}^{{\prime} }\right)}{4{\varOmega }_{q}{\varOmega }_{{q}^{{\prime} }}}\left[1+2n\left({\varOmega }_{{q}^{{\prime} }}\right)\right],$$

(2)

where N, ℏ, n and ${V}^{(4)}\left({q;}-{q;q\text{'};}-{q\text{'}}\right)$ are the total number of sampled phonon wavevectors in the first Brillouin zone, the reduced Planck constant, the Bose-Einstein distribution and the reciprocal representation of 4^th-order IFCs, respectively. Note that the off-diagonal terms of the phonon loop self-energy for PM²² were found to be crucial for some crystal systems^41,54, thus, we also further included it in the anharmonic phonon energy renormalization calculations. In this work, the q-mesh of the SCP calculations was set to 2 × 2 × 2, which is equivalent to a 2 × 2 × 2 supercell adopted by the real-space-based phonon energy renormalization technique. Meanwhile, the SCP q-mesh of 2 × 2 × 2 was used to correspond to the supercell dimensions of the second-order IFCs extracted in the real space.

Using the above first-order SCP technique that only obtains the renormalized phonon energies resulting from the quartic anharmonicity, i.e., the loop diagram, the anharmonic phonon energies of highly anharmonic compounds may be overestimated^38,47. On top of the renormalized phonon energies calculated by the first-order SCP, the renormalized phonon energies arising from the cubic anharmonicity, i.e., the dominant bubble diagram, can be estimated using the following self-consistent equation within quasi-particle approximation³⁸

$${\left({\varOmega }_{q}^{{\rm{B}}}\right)}^{2}={\varOmega }_{q}^{2}-2{\varOmega }_{q}\mathrm{Re}{\sum }_{q}^{{\rm{B}}}\left[G,{\varPhi }_{3}\right]\left(\varOmega ={\varOmega }_{q}^{{\rm{B}}}\right),$$

(3)

where ${\sum }_{q}^{{\rm{B}}}[G,{\varPhi }_{3}]\left({\Omega }_{q}\right)$ is the phonon frequency-dependent bubble self-energy, B denotes the bubble diagram, ${\varPhi }_{3}$ is the third-order force constant explicitly included in the anharmonic self-energy calculation. Note that several treatments within quasiparticle (QP) approximation including QP[0], QP[S] and QP-NL can be employed to solve Eq. (3) and obtain the fully renormalized phonon energies due to cubic and quartic anharmonicities³⁸. The QP-NL treatment was used in this work due to its reliable predictions. Additionally, the extra phonon energy shifts arising from the tadpole diagram due to the cubic anharmonicity were found to be small and negligible, which was also reported for many crystals^41,47,54. Note that the SCP and SCPB were denoted as the shorthand notation of the first-order SCP calculation and SCP calculation with bubble diagram correction in this work.

Phonon scattering rates and unified thermal transport theory

With the renormalized harmonic (2^nd-order) and original anharmonic IFCs (3^rd and 4^th-order), the phonon scattering rates resulting from phonon-phonon and phonon-isotope interaction processes, as the key ingredients entering the thermal transport equation³⁴, can be calculated using Fermi’s golden rule of perturbation theory⁵⁰. In this study, the intrinsic multi-phonon interaction mainly includes three-phonon (3 ph) and four-phonon (4 ph) scattering processes and the corresponding expressions within single-mode relaxation time approximation (SMRTA) can be written as^25,47,50

$${\Gamma }_{q}^{3{\rm{ph}}}={\sum }_{{q}^{{\prime} }{q}^{{\rm{\text{'}\text{'}}}}}\left\{\frac{1}{2}\left(1+{n}_{{q}^{{\prime} }}^{0}+{n}_{{q}^{{\rm{\text{'}\text{'}}}}}^{0}\right){\zeta }_{-}+\left({n}_{{q}^{{\prime} }}^{0}-{n}_{{q}^{{\rm{\text{'}\text{'}}}}}^{0}\right){\zeta }_{+}\right\},$$

(4)

$${\Gamma }_{q}^{4{\rm{ph}}}={\sum }_{{q}^{{\prime} }{q}^{{\rm{\text{'}\text{'}}}}{q}^{{\rm{\text{'}\text{'}\text{'}}}}}\left\{\frac{1}{6}\frac{{n}_{{q}^{{\prime} }}^{0}{n}_{{q}^{{\rm{\text{'}\text{'}}}}}^{0}{n}_{{q}^{{\rm{\text{'}\text{'}\text{'}}}}}^{0}}{{n}_{q}^{0}}{\zeta }_{--}+\frac{1}{2}\frac{\left(1+{n}_{{q}^{{\prime} }}^{0}\right){n}_{{q}^{{\rm{\text{'}\text{'}}}}}^{0}{n}_{{q}^{{\rm{\text{'}\text{'}\text{'}}}}}^{0}}{{n}_{q}^{0}}{\zeta }_{+-}+\frac{1}{2}\frac{{\left(1+{n}_{{q}^{{\prime} }}^{0}\right)\left(1+{n}_{{q}^{{\rm{\text{'}\text{'}}}}}^{0}\right)n}_{{q}^{{\rm{\text{'}\text{'}\text{'}}}}}^{0}}{{n}_{q}^{0}}{\zeta }_{++}\right\},$$

(5)

where ${\zeta }_{\pm }$ and ${\zeta }_{\pm \pm }$ are defined as

$${\zeta }_{\pm }=\frac{{\rm{\pi }}{\rm{\hslash }}}{4N}{\left|{V}^{\left(3\right)}\left(q,\pm {q}^{{\prime} },-{q}^{{\rm{\text{'}\text{'}}}}\right)\right|}^{2}{\triangle }_{\pm }\frac{\delta \left({\varOmega }_{q}\pm {\varOmega }_{{q}^{{\prime} }}-{\varOmega }_{{q}^{{\rm{\text{'}\text{'}}}}}\right)}{{\varOmega }_{q}{\varOmega }_{{q}^{{\prime} }}{\varOmega }_{{q}^{{\rm{\text{'}\text{'}}}}}},$$

(6)

$${\zeta }_{\pm \pm }=\frac{{\rm{\pi }}{{\rm{\hslash }}}^{2}}{8{N}^{2}}{\left|{V}^{\left(4\right)}\left(q,\pm {q}^{{\prime} },\pm {q}^{{\rm{\text{'}\text{'}}}},-{q}^{{\rm{\text{'}\text{'}\text{'}}}}\right)\right|}^{2}{\triangle }_{\pm \pm }\frac{\delta \left({\varOmega }_{q}\pm {\varOmega }_{{q}^{{\prime} }}\pm {\varOmega }_{{q}^{{\rm{\text{'}\text{'}}}}}-{\varOmega }_{{q}^{{\rm{\text{'}\text{'}\text{'}}}}}\right)}{{\varOmega }_{q}{\varOmega }_{{q}^{{\prime} }}{{\varOmega }_{{q}^{{\rm{\text{'}\text{'}}}}}\varOmega }_{{q}^{{\rm{\text{'}\text{'}\text{'}}}}}},$$

(7)

where ${\Gamma }_{q}^{3{ph}}$ and ${\Gamma }_{q}^{4{ph}}$ denote the 3 ph and 4 ph scattering rates, respectively, the phonon mode q is a shorthand notation for a composite index of the wavevector q and phonon branch j, ${V}^{\left(3\right)}\left(q,\pm {q}^{{\prime} },-{q}^{{\text{'}\text{'}}}\right)$ and ${V}^{\left(4\right)}\left(q,\pm {q}^{{\prime} },\pm {q}^{{\text{'}\text{'}}},-{q}^{{\text{'}\text{'}\text{'}}}\right)$ are the reciprocal representation of 3^rd- and 4^th-order IFCs, respectively⁵⁷, the delta function $\delta \left(\varOmega \right)$ describes the selection rules for energy in both 3 ph and 4 ph scattering processes, the Kronecker deltas ${\triangle }_{\pm }$ and ${\triangle }_{\pm \pm }$ are shorthand notation for ${\triangle }_{{\boldsymbol{q}}{\boldsymbol{\pm }}{\boldsymbol{q\text{'}}}{\boldsymbol{-}}{\boldsymbol{q\text{'}\text{'}}}{\boldsymbol{,}}{\boldsymbol{Q}}}$ and ${\triangle }_{{\boldsymbol{q}}{\boldsymbol{\pm }}{{\boldsymbol{q}}}^{{\boldsymbol{{\prime} }}}{\boldsymbol{\pm }}{{\boldsymbol{q}}}^{{\boldsymbol{\text{'}\text{'}}}}{\boldsymbol{-}}{\boldsymbol{q\text{'}\text{'}\text{'}}}{\boldsymbol{,}}{\boldsymbol{Q}}}$, respectively, and account for the selection rules for momentum, where the reciprocal lattice vector Q = 0 indicates the normal (N) process and Q ≠ 0 the Umklapp (U) process.

The phonon scattering term resulting from isotope can be written as⁷⁵

$${\Gamma }_{q}^{{\rm{isotope}}}=\frac{\pi {\varOmega }_{q}^{2}}{2N}{\sum }_{i\in u.c.}g\left(i\right){\left|{e}_{q}^{* }\left(i\right)\cdot {e}_{{q}^{{\prime} }}\left(i\right)\right|}^{2}\delta \left(\varOmega -{\varOmega }^{{\prime} }\right),$$

(8)

where the mass variance, $g\left(i\right)$, is defined as$g\left(i\right)=\sum _{s}{f}_{s}\left(i\right){\left[1-{M}_{s}\left(i\right)/\bar{M}\left(i\right)\right]}^{2}=\sum _{s}{f}_{s}\left(i\right){\left[\Delta {M}_{s}\left(i\right)/\bar{M}\left(i\right)\right]}^{2}$, where ${f}_{s}\left(i\right)$ and ${M}_{s}\left(i\right)$ are the concentration and mass of the ${sth}$ isotope of atom $i$, respectively. $\bar{M}\left(i\right)$ denotes the average mass of the ith atom in the primitive cell. ${e}_{q}\left(i\right)$ denotes the eigenfunction of phonon mode q at the atom i.

Using Matthiessen’s rule, the total phonon scattering rate Γ_q can be expressed as

$${\Gamma }_{q}={\Gamma }_{q}^{3{\rm{ph}}}+{\Gamma }_{q}^{4{\rm{ph}}}+{\Gamma }_{q}^{{\rm{isotope}}},$$

(9)

The lattice thermal conductivity κ_L can be calculated by a unified theory of thermal transport incorporating populations’ and coherences’ conductivities/contributions³⁰, and the detailed formula for κ_L under the SMRTA is given as follows^30,47,48:

$${\kappa }_{{\rm{L}}}^{{\rm{P}}/{\rm{C}}}=\frac{{{{\hslash }}}^{2}}{{k}_{{\rm{B}}}{T}^{2}{VN}}\sum _{{\boldsymbol{q}}}\sum _{j,{j}^{{\prime} }}\frac{{\varOmega }_{{\boldsymbol{q}}j}+{\varOmega }_{{\boldsymbol{q}}{j}^{{\prime} }}}{2}{\upsilon }_{{\boldsymbol{q}}j{j}^{{\prime} }}\otimes {\upsilon }_{{\boldsymbol{q}}{j}^{{\prime} }j}\cdot \frac{{\varOmega }_{{\boldsymbol{q}}j}{n}_{{\boldsymbol{q}}j}\left({n}_{{\boldsymbol{q}}j}+1\right)+{\varOmega }_{{\boldsymbol{q}}{j}^{{\prime} }}{n}_{{\boldsymbol{q}}{j}^{{\prime} }}\left({n}_{{\boldsymbol{q}}{j}^{{\prime} }}+1\right)}{4{\left({\varOmega }_{{\boldsymbol{q}}j}-{\varOmega }_{{\boldsymbol{q}}{j}^{{\prime} }}\right)}^{2}+{\left({\Gamma }_{{\boldsymbol{q}}j}+{\Gamma }_{{\boldsymbol{q}}{j}^{{\prime} }}\right)}^{2}}\left({\Gamma }_{{\boldsymbol{q}}j}+{\Gamma }_{{\boldsymbol{q}}{j}^{{\prime} }}\right),$$

(10)

where the superscripts P and C denote the populations’ and coherences’ contributions, respectively, k_B is the Boltzmann constant, T is the temperature, V is the unit-cell volume and υ is the group velocity matix including both the intra- and inter-branch terms⁷⁶. In Eq. (10), when $j={j\text{'}}$, it calculates the populations’ contribution (PBTE calculation result) $\left({\kappa }_{{\rm{L}}}^{{\rm{P}}}\right)$, i.e., particle-like phonon propagation described by the diagonal terms of heat flux operators, otherwise, it gives the coherences’ contribution $\left({\kappa }_{{\rm{L}}}^{{\rm{C}}}\right)$, i.e., wave-like tunelling of phonons described by the off-diagonal terms of heat flux operators (The terminology, i.e., diffuson, is also used to describe this operator In galsses). The total lattice thermal conductivity κ_L can be obtained by summing over ${\kappa }_{{\rm{L}}}^{{\rm{P}}}$ and ${\kappa }_{{\rm{L}}}^{{\rm{C}}}$, namely ${\kappa }_{{\rm{L}}}={\kappa }_{{\rm{L}}}^{{\rm{P}}}+{\kappa }_{{\rm{L}}}^{{\rm{C}}}$. In this work, the q mesh for 3 ph scattering processes was set to 12 × 12 × 12, which gives well-converged results for the crystalline Cs₂AgBiBr₆. Considering the huge computational cost, a q mesh of 8 × 8 × 8 with a scalebroad parameter of 0.06 were used for 4 ph scattering processes. Note that the iterative scheme to PBTE is only applied for 3 ph scattering processes in this work, while the 4 ph scattering processes are treated at the SMRTA level considering the exceptionally large memory demands^47,57. Thermal transport calculations including particle-like propagation and wave-like tunneling transport channels were performed by using the ShengBTE⁵⁸ and FourPhonon⁵⁷ packages, as well as our in-house code⁴¹.