Accelerating the transition to cobalt-free batteries: a hybrid model for LiFePO₄/graphite chemistry

Abstract

The increased adoption of lithium-iron-phosphate batteries, in response to the need to reduce the battery manufacturing process’s dependence on scarce minerals and create a resilient and ethical supply chain, comes with many challenges. The design of an effective and high-performing battery management system (BMS) for such technology is one of those challenges. In this work, a physics-based model describing the two-phase transition operation of an iron-phosphate positive electrode—in a graphite anode battery—is integrated with a machine-learning model to capture the hysteresis and path-dependent behavior during transient operation. The machine-learning component of the proposed “hybrid” model is built upon the knowledge of the electrochemical internal states of the battery during charge and discharge operation over several driving profiles. The hybrid model is experimentally validated over 15 h of driving, and it is shown that the machine-learning component is responsible for a small percentage of the total battery behavior (i.e., it compensates for voltage hysteresis). The proposed modeling strategy can be used for battery performance analysis, synthetic data generation, and the development of reduced-order models for BMS design.

Introduction

The positive electrode of a lithium-ion battery (LIB) is the most expensive component¹ of the cell, accounting for more than 50% of the total cell production cost². Out of the various cathode technologies available on the market today, iron phosphate (LiFePO₄, also referred to as LFP) cathodes³ offer superior thermal and chemical stability, resulting in a safer cathode material that does not decompose at high temperatures, as compared to nickel- and cobalt-based cathodes⁴. The absence of cobalt and nickel suggests a pathway for a resilient battery supply chain, and contributes to the creation of an ethical energy market, owing to the concerns about cobalt mining working conditions and child labor in countries such as the Democratic Republic of Congo (the top supplier)^5,6.

LFP batteries are notoriously cheaper and offer better cycle life compared to the NCA or NMC cathode LIBs (approximately 4–5x longer) and withstand high rates of charge and discharge (up to 20C⁷). Major LIB manufacturers are investing in this technology. In 2020, the Chinese automaker and battery company BYD unveiled a new generation of LFP batteries, called “Blade”^8,9, followed by Tesla who in 2020 first announced the use of iron phosphate in LIBs manufactured for the Chinese electric vehicle market⁹, and later in 2021 extended to LIBs manufactured globally^10,11.

The known weakness of LFP batteries is their low energy density and low electrical and ionic conductivity. It has been shown that metal doping and the addition of conductive coatings are effective solutions to enhance electronic conductivity¹². The low energy density—120 Wh kg⁻¹ (ref. ¹²)—is of particular concern for the transportation sector, because of the reduced battery range it can provide¹³. However, recent advancements in LFP technology set the Chinese company SVolt to reach a specific energy of 230 Wh kg⁻¹ in 2023¹⁴. In 2023, Gotion High Tech unveiled a new lithium manganese iron phosphate (LMFP) battery to enter mass production in 2024 that, thanks to the addition of manganese in the positive electrode, is poised to reach 240 Wh kg⁻¹ (ref. ¹⁵).

Lithium-ion batteries are electrochemical energy storage devices in which lithium is exchanged between the positive and the negative electrode. During discharging (positive current), lithium leaves the negative electrode (deintercalation) and enters the positive one (intercalation). During charging (negative current), the positive electrode experiences deintercalation, and lithium intercalates into the negative electrode.

The open circuit voltage (OCV) is the thermodynamic equilibrium potential of the battery, a function of its chemistry, and is defined as the difference between the open circuit potentials (OCPs) of the positive and negative electrodes. LFP batteries use LiFePO₄ and graphite as positive and negative electrode active materials, respectively. In this paper, the two-phase transition behavior of the positive electrode, which results in a flat positive electrode OCP characteristic and a voltage plateau around 3.45 V vs. Li/Li⁺ (see Supplementary Fig. 1)^16,17, is modeled. In particular, in the positive electrode, there are three distinct stages: lithium-rich (LiFePO₄), two-phase transition, and lithium-poor (FePO₄)^18,19,20. According to ref. ¹⁸, in the two-phase transition region coexist a lithium-rich phase Li_βFePO₄ referred to as β (with β ≃ 1), and a lithium-poor phase Li_αFePO₄ referred to as α (with α ≃ 0).

The presence of a two-phase transition in the positive electrode results in a flat OCV curve, which makes the task of estimating the state of charge (SOC) challenging as it causes a lack of observability of the system’s states from the voltage output measurements²¹. Moreover, a pronounced hysteresis²², and path dependence behavior, i.e., for the same SOC the battery relaxes to different OCV values depending on whether it was charging or discharging, pose additional challenges in the design of battery management system (BMS) strategies.

Hysteresis results from thermodynamic effects, mechanical stress, and microscopic distortions within the active material particles caused by dopants²³. Thermodynamic effects are related to the electrodes being composed of multiple particles and to the heterogeneity of the lithium insertion rate. Mechanical hysteresis is associated with the different lattice constants of lithiated and delithiated phases that cause mechanical stress at the phase barrier.

In LiFePO₄/graphite batteries, the positive electrode is the main contributor to OCV hysteresis and it is modeled in this paper. In ref. ²⁴, this is modeled in terms of the coexistence of lithium-rich and lithium-poor phases in a core-shell paradigm. During charge, the core and shell are characterized by a lithium-rich and a lithium-poor phase, respectively, and vice versa for discharge. In ref. ²⁵, the thermodynamic origin of hysteresis is attributed to different lithium insertion rates in the particles of the positive active material. Such a non-uniform insertion rate leads to heterogeneous lithium concentrations within the individual particles and non-uniform potentials. The overall electrode potential is a blend of the potentials of the active material particles and, depending on the intercalation/deintercalation path taken to reach a given SOC, hysteresis is shown.

According to ref. ¹⁷, there is no complete agreement among researchers on how the lithium-poor and lithium-rich phases are created during the positive electrode phase transition. From scanning transmission X-ray microscopy (STXM), in ref. ²⁰ it is shown that spatial variations in the lithium-ion insertion rate lead to the formation of nonuniformities inside the positive electrode particles that do not experience a clear separation between poor and rich phases. Conversely, STXM results recently published in ref. ²⁶ show the formation of two separated phases in a core-shell type of structure.

This dispute has led to the development of different models describing the lithium insertion dynamics in LiFePO₄ cathodes. In ref. ²⁵, the authors propose a many-particle model where lithium is exchanged between individual particles, and sequential lithiation and delithiation are demonstrated. Kinetic and transport equations are ignored, making the model inappropriate at a high C-rate or when an accurate description of electrochemical phenomena is required. In ref. ¹⁹, a domino-cascade model is used to describe lithium insertion in the positive electrode. In this model, the phase transition is described via a front moving inside the lattice. The authors of ref. ²⁷ investigate a mosaic model where small nucleation sites, each undergoing a phase change during charge and discharge, are created inside a bigger active material particle.

In ref. ²⁸, a core-shell model is used to describe phase transitions in the positive electrode. While assuming isotropic diffusion, lithium intercalation, and deintercalation are modeled with a moving boundary controlling the core-shell phase transition. Similar approaches are used in refs. ⁴ and ²⁹, for the pseudo-two-dimensional (P2D) and single particle model (SPM), respectively. In ref. ⁴, the formation of multiple phase transition layers in an “onion” structure is modeled. Through the addition of a mass balance equation that describes the moving boundary between the core and shell phases, the model, experimentally validated over LFP/graphite coin cell data, allows to track the lithium-rich and lithium-poor phases.

In ref. ³⁰, the formulation of a core-shell enhanced single particle model (ESPM), blending the predictive capabilities of ESPM with the core-shell modeling paradigm in the positive electrode, is proposed and experimentally validated. In ref. ³¹, this model is further enhanced through an average core-shell ESPM formulation, where the bulk-normalized concentration is used to prevent discontinuity of the positive particle lithium surface concentration arising from the transition between one-phase to two-phase regions³².

When used in applications such as electric vehicles (EVs) or battery energy storage systems (BESSs), a BMS must be designed to guarantee the functionality, safety, and reliability of the system during operation. A critical task of the BMS is the estimation of SOC, which is particularly challenging for the battery chemistry under study due to the flatness and hysteresis of the OCV. In this paper, we model hysteresis and path-dependent dynamics of LFP batteries for BMS design. Empirical models, initially proposed by ref. ³³, have been widely used to model battery hysteresis^13,21,34,35. The accuracy of such models though depends on a careful calibration upon ad hoc crafted experimental data consisting of major and minor loops. Major loops aim at capturing the major OCV boundaries and require the battery to be fully charged and discharged, whereas minor loops are meant to capture partial charge and discharge events at different loading conditions to assess the local hysteretic behavior and the path-dependent dynamics, and they are a function of both SOC and C-rate. For example, in ref. ³⁴, the minor loop hysteresis test is composed of a sequence of five charge pulses followed by five discharge pulses; at each pulse, the battery is relaxed for 3 h to its OCV. As minor loops must be repeated at different SOCs and C-rates to capture the hysteretic behavior and path dependence over the whole battery operating region, this could lead to experimental campaigns of the order of weeks or months.

The flat OCV-SOC relationship and the prominent hysteresis challenge the status quo in lithium-ion battery modeling. Similar to what was done in ref. ³⁶ to improve battery safety, in this paper, we combine the strengths of physics-based and machine-learning approaches by leveraging the aptness of the average core-shell ESPM model³¹ (to track the cathode lithium concentration) integrated with a machine-learning hysteresis model (Fig. 1).

Fig. 1: Workflow.

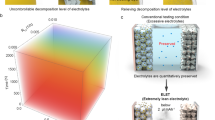
a Starting from field data (electric vehicles, grid, or home stationary storage), the proposed hybrid model merges the strengths of physics-based and machine-learning approaches for improved prediction performance. In this paper, we use EV driving data to train the machine-learning hysteresis model. b The hybrid model can be employed in battery performance analysis, synthetic data generation, and as the basis for reduced-order models.

The output voltage of the battery cell using the proposed hybrid model is given as:

$$\begin{array}{l} V \,=\, V_{\mathrm{cs}} + V_{\mathrm{h}}\\\quad\,=\, \underbrace{\left(U_{\mathrm{p}}^{\mathrm{ch}} + U_{\mathrm{p}}^{\mathrm{dis}}\right)/2 - U_{\mathrm{n}} + \eta_{\mathrm{p}} - \eta_{\mathrm{n}} +{\Delta}{\Phi}_{\mathrm{e}} - I\cdot R_{\mathrm{l}}({\mathrm{SOC}},I)}_{{V_{\mathrm{cs}}}} + V_{\mathrm{h}}\\\quad\,=\, \underbrace{U_{\mathrm{p}}^{\mathrm{avg}} - U_{\mathrm{n}} + \eta_{\mathrm{p}} - \eta_n +{\Delta}{\Phi}_{\mathrm{e}} - I\cdot R_{\mathrm{l}}({\mathrm{SOC}},I)}_{{V_{\mathrm{cs}}}} + V_{\mathrm{h}}\\\quad\,=\, \underbrace{V_{\mathrm{OCV}}^{\mathrm{avg}} + \eta_{\mathrm{p}} - \eta_{\mathrm{n}} +{\Delta}{\Phi}_{\mathrm{e}} - I\cdot R_{\mathrm{l}}({\mathrm{SOC}},I)}_{{V_{\mathrm{cs}}}} + V_{\mathrm{h}}\end{array}$$

(1)

where the term V_cs collects the information from a core-shell physics-based model, and the term V_h models the hysteresis via a machine-learning method described later. The term V_cs depends on the OCP of the negative electrode U_n, the OCP of the positive electrode in charge (${U}_{{{{\rm{p}}}}}^{{{{\rm{ch}}}}}$), and the OCP of the positive electrode in discharge (${U}_{{{{\rm{p}}}}}^{{{{\rm{dis}}}}}$). These latter terms are then combined to produce the average positive electrode OCP defined as $({U}_{{{{\rm{p}}}}}^{{{{\rm{ch}}}}}+{U}_{{{{\rm{p}}}}}^{{{{\rm{dis}}}}})/2$ and shown in Fig. 2c. Moreover, V_cs depends on the positive and negative electrode overpotentials, η_p and η_n, and the electrolyte overpotential, ΔΦ_e, which are derived according to ref. ³⁷ as described in Supplementary Note 1. Lastly, the Ohmic loss term (I ⋅ R_l(SOC, I)) accounts for the battery’s high-frequency resistance (lumping both electro-migration in the electrolyte and contact resistance), which is a function of input current and SOC. This resistance is computed from galvanostatic intermittent titration technique (GITT) experiments performed at C/6, C/3, C/2, and 1C, as described in Supplementary Note 2. These experimental data are made available at the link provided at the end of the paper.

Fig. 2: Battery modeling and phase transitions.

Lithium-ion battery schematic (a). Electrodes are composed of multiple particles which differ in shape and size. The physics-based model is formulated by approximating the battery’s positive and negative electrodes as two spherical particles (b). x and r indicate the Cartesian and radial coordinates, respectively. The thicknesses of negative particle, separator, and positive particle domains are L_n, L_s, and L_p, respectively. Phase transitions experienced by the positive particle during a discharge from 100% to 0% SOC are shown in c. The positive particle is first initialized at a concentration ${\theta }_{{{{\rm{p}}}}}^{{{{\rm{bulk}}}}} \,<\, {\theta }_{{{{\rm{p}}}}}^{\alpha }$ (one-phase), then, it transitions to a two-phase region where the lithium solid phase concentration is described by the core-shell paradigm, and finally, the particle returns to one-phase for ${\theta }_{{{{\rm{p}}}}}^{{{{\rm{bulk}}}}} \,>\, {\theta }_{{{{\rm{p}}}}}^{\beta }$ and stays in this phase until 0% SOC is reached.

The term V_h captures the deviation of the simulated battery cell voltage from the average OCV, defined as ${V}_{{{{\rm{OCV}}}}}^{{{{\rm{avg}}}}}=({U}_{{{{\rm{p}}}}}^{{{{\rm{avg}}}}}-{U}_{{{{\rm{n}}}}})$ and shown in Supplementary Fig. 2, due to hysteresis and model uncertainties. The hysteresis assumes negative values over the 100% to 0% SOC discharge range (because the battery voltage trajectory is below the ${V}_{{{{\rm{OCV}}}}}^{{{{\rm{avg}}}}}$) and positive over the 0% to 100% SOC charge range (because the battery voltage trajectory is above the ${V}_{{{{\rm{OCV}}}}}^{{{{\rm{avg}}}}}$). In this paper, we refer to the term V_h as pseudo-hysteresis to account for both hysteresis and model uncertainties, the latter due primarily to the limitations of the physics-based model to capture all the underlying electrochemical dynamics³⁸.

This model copes with both static and dynamic hysteresis. The static hysteresis is associated with the battery equilibrium potentials being different whether coming from charge or discharge. Instead, dynamic hysteresis arises from the switching between charge and discharge conditions and is a function of the battery history, and local and instantaneous operating conditions (SOC and C-rate).

The hybrid model proposed in this paper can increase the predictive capabilities of traditional battery models³⁹. The physical understanding of lithium intercalation and deintercalation is preserved in all the stages of the model development, which reaffirms the key role of physics. Moreover, the pseudo-hysteresis machine-learning model pursued in this work is not constrained within a fixed model structure, like semi-empirical approaches.

The machine-learning component learns the hysteretic behavior from both simulated features (from the core-shell ESPM) and experiments and it is trained and validated over 19 and 15 h of EV real-driving profiles, respectively. Data are obtained from a 49Ah LiFePO₄/graphite pouch cell—currently in the design phase—under real-world EV operation. The approach proposed allows us to step away from the need to have major and minor loops-based testing, providing a simplified approach to learning the dynamic hysteresis behavior—along with any unmodeled dynamics—when switching between charge and discharge conditions. Along with GITT experiments, EV real-driving profiles are also made available at the link provided at the end of the paper.

Results

Physics-based model: average core-shell ESPM

As shown in Fig. 2a, b, the average core-shell ESPM approximates the battery positive and negative electrodes as two, spherical, single particles where transport of lithium ions in the solid (the single particle) and electrolyte phase is expressed by mass conservation equations, charge conservation is used in the electrolyte phase, and phase transitions in the positive particle are modeled with a mass balance equation and a moving boundary³¹.

Figure 2c shows phase transitions experienced by the positive particle and the corresponding regions on the charge and discharge OCPs. In line with the arguments of ref. ²², at a given stoichiometry, the battery OCP in discharge ${U}_{{{{\rm{p}}}}}^{{{{\rm{dis}}}}}$ (lithiation) is lower than the one in charge ${U}_{{{{\rm{p}}}}}^{{{{\rm{ch}}}}}$ (delithiation). The red dashed line between charge and discharge OCPs is the average positive electrode potential (${U}_{{{{\rm{p}}}}}^{{{{\rm{avg}}}}}$), as defined in Equation (1).

The bulk-normalized lithium concentration ${\theta }_{i}^{{{{\rm{bulk}}}}}$ is used to describe the solid phase concentration in both electrodes³¹. For the positive electrode, when ${\theta }_{{{{\rm{p}}}}}^{{{{\rm{bulk}}}}} \,<\, {\theta }_{{{{\rm{p}}}}}^{\alpha }$ and ${\theta }_{{{{\rm{p}}}}}^{{{{\rm{bulk}}}}} \,>\, {\theta }_{{{{\rm{p}}}}}^{\beta }$ the particle is in the one-phase region. The stoichiometric values ${\theta }_{{{{\rm{p}}}}}^{\alpha }$ and ${\theta }_{{{{\rm{p}}}}}^{\beta }$ define the transition points from one-phase to two-phase (and, vice versa) and are identified using optimization algorithms such as particle swarm optimization³⁰. In the two-phase region, α-phase and β-phase coexist inside the particle, which experiences a phase transition from α to β (during discharge). This phase transition is described by the moving boundary r_p (in the Supplementary Equation (34)), modeling the shrinking phenomenon replacing the core phase with the shell phase.

The use of the bulk-normalized concentration in the average core-shell ESPM was introduced to remove the positive particle surface concentration discontinuity arising in the traditional core-shell modeling paradigm during the transition from one-phase to two-phase region³¹. Model equations for the core-shell ESPM are summarized in Supplementary Tables 1, 2, and 3.

In this paper, we also extend the applicability of the physics-based model to real-world current profiles, characterized by a combination of charge and discharge events which translates into continuous switching between scenarios ${{{\mathcal{A}}}}$ and ${{{\mathcal{B}}}}$ in Fig. 2c. This switching is implemented by means of the transition conditions described in Supplementary Note 3 (Supplementary Equations (5) and (7)), which ensure the conservation of mass. The characteristic of the proposed approach is that it always enforces a positive particle structure with “one shell” and “one core”. For example, when transitioning from charge to discharge, the positive particle β-core and α-shell are remapped into α-core and β-shell while ensuring mass conservation and the opposite happens during discharge-to-charge transitions. This allows to track the evolution of the two phases while avoiding the creation of an “onion” structure with multiple α and β layers⁴, and reduces the complexity of the model and the computational burden required for its numerical solution.

Machine-learning model: pseudo-hysteresis

The machine-learning model capturing static and dynamic voltage hysteresis and model uncertainties is formulated as follows:

$${V}_{{{{\rm{h}}}}}=f([I\,\Psi ])$$

(2)

where V_h is the pseudo-hysteresis, expressed as a function f of the input current profile I and the vector Ψ which collects simulated electrochemical features extracted from the solution of the average core-shell ESPM. In this work, different machine-learning models are trained and Ψ formulation depends on whether manual or automatic feature selection is used, as described in the next paragraphs.

A distinct challenge of machine learning is the selection of the model class to describe the input/output behavior. Batteries are nonlinear systems, hence, nonlinear machine-learning approaches might provide the most benefits. In this work, we explore three techniques for the solution of nonlinear regression problems: feedforward neural networks (FNNs), regression trees (RTs), and random forests (RFs)^40,41. Contrary to FNNs and RTs, which are based on the training of a single model, RFs are based on an ensemble of regression trees that provide an effective framework for feature selection while reducing data overfitting.

The accuracy of machine-learning models is highly sensitive to the input feature selection and hyperparameters configuration. Two feature selection approaches are used in this work: manual and automatic. In the manual approach, a total of three features are chosen to get information on electrochemical states, namely, bulk-normalized positive particle solid phase concentration, ${\theta }_{{{{\rm{p}}}}}^{{{{\rm{bulk}}}}}$, average electrolyte concentration, c^avg, and input current (experimental data). The manually selected feature vector is used to train FNNs and RTs. In the automatic method, used for the RT design, features are selected by combining the strength of correlation analysis with RF. Given a current profile and the simulated quantities from the average core-shell ESPM (i.e., positive and negative electrode solid phase concentration, electrolyte concentrations, moving boundary, SOC, bulk-normalized concentrations—see Supplementary Note 4 for details), correlation analysis is used to select a subset of informative features and reduce the feature space. This subset is then used to train an RF model, which creates and merges predictions of several regression trees trained with different combinations of features.

For the training of FNN, RT, and RF, both input features and output are needed. In this work, the output is a vector containing the information on static/dynamic hysteresis and model uncertainties, and it is computed as the difference between the simulated output voltage from the purely physics-based model (which accounts for overpotentials and Ohmic losses) and experimental data. While training FNN, RT, and RF, the model hyperparameters are optimized. In FNNs, the number of hidden layers and neurons within each hidden layer plays a key role in modeling the nonlinearities in the system. As mentioned in⁴¹, the selection of features and hyperparameters is generally done through background knowledge of the problem or, as done in this work, with grid search. The performance of RTs, in terms of the description of nonlinearities, is a function of the maximum depth. Being an ensemble of regression trees, RFs performances are a function of the maximum depth and number of trees used for prediction.

Table 1 summarizes the feature selection and hyperparameters optimization process for FNN, RT, and RF. For further information on feature selection, hyperparameters optimization, and training of the data-driven models, readers are referred to Supplementary Note 6.

Table 1 Feature selection and hyperparameters optimization.

Hybrid modeling strategy

Figure 3 shows the hybrid model schematic combining the first-principle understanding with the learning capability of the machine-learning component to create an accurate battery model able to capture and dynamically reproduce the system pseudo-hysteresis. On top, the physics-based model equations are summarized, where current is the input to the model. At the bottom, the machine-learning model is shown. Input to the machine-learning model is the experimental current profile I and the simulated feature vector Ψ. As shown in Equation (1), the output of the hybrid model is the battery voltage as given by the summation of physics-based (V_cs) and machine-learning (V_h) voltages.

Fig. 3: Hybrid model architecture.

The physics-based model (average core-shell ESPM), describing the battery behavior from mass and charge conservation, feeds the machine-learning model through the feature vector Ψ. Both the physics-based and machine-learning models use current as input. The overall battery output voltage V is given by the summation of V_cs and V_h, outputs of the physics-based and machine-learning models, respectively. In this figure, the machine-learning model is shown in the form of a FNN.

Table 2 summarizes the current profiles used for the training of the machine-learning model, #1, #2, and #3, and the ones used for testing the hybrid model, i.e., #4, #5, #6, and #7. These profiles were specifically designed to emulate EV applications, with discharge and charge events corresponding to the vehicle’s acceleration/cruising and regenerative braking, respectively. For each current profile shown in Fig. 6 (in the “Experimental procedures” section), Table 2 collects the SOC range, minimum and maximum currents, mean values, and standard deviations. The last two columns show the root mean square errors (RMSEs) in terms of voltage response and SOC, before the introduction of the machine-learning pseudo-hysteresis model. According to Equation (5), RMSEs are computed between the purely physics-based average core-shell ESPM output and experimental data (the experimental SOC is obtained from Coulomb counting (CC)).

Table 2 Current profiles for training and testing of the hybrid model.

With respect to SOC, the physics-based model ensures satisfactory performances, with RMSEs always below 1%. The machine-learning compensation is limited to the voltage output profile and does not affect the SOC output of the physics-based model. In Table 3, instead, the voltage RMSEs of the hybrid model (either using FNN, RT, or RF), quantifying the performance before and after the introduction of the machine-learning model are tabulated and compared. It can be seen that compared to the benchmark solution from the purely physics-based model, the hybrid models (irrespective of the FNN, RT, or RF compensation) lead to a substantial improvement of the voltage RMSEs: of ~95% for training datasets, consistently across the three machine-learning methods, and between 83% and 47% in testing. Compared to FNN, the RT shows a tendency to overfit the training data, with RMSEs improving for current profiles #1, #2, and #3 and worsening for #4, #5, and #7. At the cost of increasing the complexity of the model, the RF provides the best trade-off. This is expected since the output of the RF is based on the average of predictions performed by its ensemble of regression trees. Compared to FNN, performances are improved in training and, except for profiles #5 and #7, also during testing (the difference between ${{{{\rm{RMSE}}}}}_{V}^{{{{\rm{FNN}}}}}$ and ${{{{\rm{RMSE}}}}}_{V}^{{{{\rm{RF}}}}}$ for profiles #5 and #7 is lower than or equal to 0.15mV). As shown in the Supplementary Note 5, we argue that differences between training and testing datasets are responsible for the higher RMSEs during testing.

Table 3 Performance of feedforward neural network, regression tree, and random forest over training and testing datasets.

The performances of the hybrid model—using the RF machine leaning compensation—for profiles #4 and #7 are shown in Fig. 4 (in Supplementary Fig. 14, simulation results for the training current profile #3 are shown). In Fig. 4a, b, simulation results with (signal V) and without (signal V_cs) of the machine-learning pseudo-hysteresis model are compared to experimental data. In Supplementary Fig. 3, for profile #4, the machine-learning compensation V_h is compared to the maximum polarization computed from charge and discharge OCPs ($-({U}_{{{{\rm{p}}}}}^{{{{\rm{ch}}}}}-{U}_{{{{\rm{p}}}}}^{{{{\rm{dis}}}}})/2$)¹³, describing the theoretical deviation from the average OCP caused by hysteresis only. As shown in the figure, the compensation (on average of −32 mV) is of the same order of magnitude as the maximum polarization, indicating that voltage hysteresis is the major contributor to the deviation between the physics-based model and experimental data. Other fluctuations are related to V_h compensating for physics-based model uncertainties.

Fig. 4: Hybrid model performance.

Comparison between experimental data and simulation results for current profiles #4 (a) and #7 (b), where the hybrid model adopts the RF machine-learning compensation. As shown in both the zoomed portions, the hybrid model reduces the discrepancy between simulated and experimental voltage profiles. In a, the contribution of the machine-learning model (V_h) to the overall voltage profile (V) is on average −32 mV. In (b), a −32 mV average contribution is seen only inside the SOC range [10, 90]% and, for SOC higher than 90%, the pseudo-hysteresis increases to 43 mV. For both a, b, the bottom left plots show the good agreement of the physics-based model SOC (Sim.) with the SOC from Coulomb counting.

In Fig. 4b, one can notice that the discrepancy between model and experimental data increases for SOC values lower than 12%, leading to an ${{{{\rm{RMSE}}}}}_{V}^{{{{\rm{RF}}}}}$ of 27.03 mV (see Table 3 also for detailed RMSE modeling errors across all the profiles). As described in Supplementary Note 5, current-voltage operating conditions for driving cycle #7 differ from the training dataset by 4.2%. We argue that the difference between training and testing datasets (together with the evidence that ~75% of the training points fall inside the current and voltage ranges [−7,17.8]A and [3.2,3.3]V, respectively) is responsible for the overpredicting behavior in Fig. 4b. This behavior could be improved by increasing the population of the training dataset and performing ad hoc experiments in the low SOC region.

As shown in Fig. 4, driving cycles #4 and #7 deplete the battery from 50% to 10% and 100% to 0% SOC, respectively. Since the battery is overall discharging, the positive electrode is characterized by a lower OCP compared to the average OCP, and consequently, negative values of V_h are expected. For driving cycle #7, inside the SOC range [10, 90]%, and driving cycle #4, the pseudo-hysteresis holds an average value of −32 mV. For driving cycle #7 and SOC higher than 90%, the pseudo-hysteresis increases to 43 mV, indicating that the cell is starting from a full charge condition and then polarized towards the positive electrode charge OCP.

To further assess the performance of the hybrid model, modeling errors before (e₁) and after (e₂) the introduction of the machine-learning pseudo-hysteresis component are computed:

$$\begin{array}{l}{e}_{1}\,=\,{V}_{\exp }-{V}_{{{{\rm{cs}}}}}\\ {e}_{2}\,=\,{V}_{\exp }-({V}_{{{{\rm{cs}}}}}+{V}_{{{{\rm{h}}}}})={V}_{\exp }-V\end{array}$$

(3)

Figure 5 (top plots) shows the statistical distributions of e₁ and e₂ for the three machine-learning models proposed, namely FNN, RT, and RF (using current profile #7). The advantage of the hybrid model is two-fold: first, it shifts the error distribution to zero-mean (the purely physics-based model is overpredicting) and, second, it reduces the error variance by shrinking the distribution. Finally, the bottom plots in Fig. 5 show the energy contribution of physics-based (${E}_{{V}_{{{{\rm{cs}}}}}}$) and machine-learning (${E}_{{V}_{{{{\rm{h}}}}}}$) models computed integrating over time the electrical power:

$$E={E}_{{V}_{{{{\rm{cs}}}}}}+{E}_{{V}_{{{{\rm{h}}}}}}=\int\nolimits_{0}^{{t}_{{{{\rm{f}}}}}}| {V}_{{{{\rm{cs}}}}}I| \,dt+\int\nolimits_{0}^{{t}_{{{{\rm{f}}}}}}| {V}_{{{{\rm{h}}}}}I| \,dt$$

(4)

with t_f the time duration of the current profile. The energy analysis shows that the contribution of the machine-learning component is small, around 1.1%, and acts as a low energy compensation of voltage hysteresis and model uncertainties. The modeling error distribution and energy characterization for all current profiles is shown in Supplementary Figs. 15 and 16.

Fig. 5: Hybrid model energetic analysis.

Modeling error distributions and energetic analysis for profile #7, considering FNN, RT, and RF. On top, of error distributions before (e₁) and after (e₂) the introduction of the machine-learning model. The hybrid model leads to a shift of the distributions to the right (zero-mean) and to a reduction of the error variance. The energy analysis shows that the machine-learning model contributes a small percentage to the overall output prediction.

Discussion

The hybrid model developed in this paper merges the strengths of physics-based modeling with the machine-learning model’s ability to describe unknown physics. While preserving the physical understanding of lithium-ion transport and intercalation provided by the average core-shell ESPM, machine learning is leveraged to learn hysteresis from 19 h of driving cycle data and compensate for model uncertainties. To show the potential of the proposed architecture, the hybrid model is tested over 15 h of driving cycle data. The hybrid model copes with voltage hysteresis reducing the voltage RMSE by ~95% in training datasets, and between 83% and 47% in testing (last row of Table 3). The worst case, with an average percentage improvement of 47%, is obtained for driving cycle #7, where, at low SOC, the hybrid model starts overpredicting due to the limitations of the training dataset described in Supplementary Note 5. Nevertheless, the hybrid model outperforms the purely physics-based one. The proposed approach could be extended to simulate the whole electric vehicle operation characterized by both driving and constant current charge. During charge, instead of the machine-learning pseudo-hysteresis model, the charge OCP would be used as the true positive particle OCP (as done in ref. ³⁰).

In this work, we followed a data-centric approach to develop the machine-learning-based pseudo-hysteresis model—as opposed to a big-data approach—where data are systematically engineered⁴². This approach reduces the experimental time, creating highly informative and low-dimensional datasets. Specifically, the training and testing of the pseudo-hysteresis machine-learning model was achieved with 34 h of EV real-driving data, whereas an empirical hysteresis model would have required weeks or months for the collection of the major and minor loops data¹³. In the field of modeling and life span prediction of batteries, where experimental testing still remains the biggest bottleneck to push timely innovations, a data-centric solution could be used to enable optimized and more flexible procedures. For an effective pseudo-hysteresis machine-learning model:

• the training data should carry information on the switching between charge and discharge positive particle OCPs, i.e., the current profile should be composed of both charge and discharge events. This is a key requirement to learn voltage hysteresis;

• the training data should cover the whole SOC window, ideally from 100% to 0% SOC, to assess the hysteretic behavior over the whole battery operating region;

• the C-rate of the training data should be reflective of the target application (e.g., transportation or stationary storage).

The hybrid model developed in this paper has also the potential to improve the analysis of battery performance, generate meaningful synthetic data, and enable model order reduction for BMS applications (Fig. 1).

Battery performance. The hybrid model captures both the positive electrode phase transition and voltage hysteresis. This allows us to perform realistic sensitivity analysis, and potentially assess the effect of modifications of transport parameters and geometrical properties on the output voltage, performance, and solid and electrolyte phase concentration dynamics.

Synthetic data generation. The description of pseudo-hysteresis and phase transitions could make this model suitable for the generation of synthetic data covering the whole current input range (function of the target application) and, in particular, corner cases (e.g., high/low SOC and high C-rate scenarios). This would contribute to reducing experimental campaign time and optimize costs.

Model order reduction. The hybrid model can be used as a basis for the derivation of reduced-order models to be used for BMS design for SOC estimation using, for example, an electrode-based observer framework⁴³. A poorly predictive model can lead to large SOC estimation errors, which could lead the battery to be improperly managed and be subject to premature aging. The proposed hybrid model is deemed to be a valuable tool for the control community for the development of phase transition/hysteresis-dependent observers for LFP batteries.

Methods

Experimental data

Data used in this paper are acquired from a 49Ah LiFePO₄/graphite opposed tab pouch cell tested at a temperature of 25 °C. Properties of the cell are summarized in Table 4.

Table 4 Technical specifications of the LiFePO₄/graphite pouch cell used in this study.

The negative electrode OCP is obtained by performing GITT experiments, on the other hand, the positive electrode charge and discharge OCPs are collected by constant charging and discharging the cell at a low C-rate (C/50). Experiments for both positive and negative electrode OCPs are performed on the half-cell, with a lithium metal electrode as a reference. Supplementary Fig. 1 shows experimental OCPs for both positive and negative electrodes.

Average core-shell ESPM parameters identification, described in Supplementary Note 7, is performed for constant current charge and discharge profiles at C/12 and C/6. Profiles at C/12 are used to identify geometrical parameters and stoichiometric coefficients, and C/6 data are used to identify solid phase diffusion coefficients and reaction rate constants. The battery high-frequency resistance as a function of both SOC and C-rate is computed from the C/6, C/3, C/2, and 1C current pulses in different GITT experiments, as shown in Supplementary Fig. 5. Between two pulses, a resting time of at least 2 h is implemented to ensure the battery is at equilibrium when computing the high-frequency resistance (details on the procedure are shown in Supplementary Note 2).

The hybrid model is trained and tested over seven different current profiles. These profiles were specifically designed to reproduce the operation of EV batteries in a laboratory setting and are used to learn the voltage hysteresis and model uncertainties. The profiles, characterized by properties listed in Table 2, are based on a sequence of discharging and charging events corresponding to the vehicle’s acceleration/cruising and regenerative braking, respectively, and are all shown in Fig. 6. An in-depth analysis of the operating conditions spanned by training and testing datasets is in the Supplementary Note 5.

Fig. 6: Training and testing datasets.

a Training current and Coulomb counting SOC profiles for driving cycles #1, #2, and #3 (from top to bottom). b Testing current and Coulomb counting SOC profiles for driving cycles #4, #5, #6, and #7 (from top to bottom).

Assessing physics-based and hybrid model performance

As proposed in⁴⁴, for the identification of unknown model parameters of the average core-shell ESPM (described in Supplementary Note 7) the voltage response and two SOCs, one for the positive and one for the negative electrode, are used to increase the parameters’ sensitivity and improve identification accuracy. Instead, to assess the performance of the physics-based model, only voltage response and positive electrode SOC are used. In lithium-ion batteries, the positive electrode generally limits the performance of the battery, because with a lower aerial capacity compared to the negative one. Hence, we decide to use the positive electrode state of charge (SOC_p) for performance evaluation.

The RMSEs for the physics-based model voltage response and positive electrode SOC are defined as follows:

$$\begin{array}{l}{{{{\rm{RMSE}}}}}_{V}\,[{{{\rm{mV}}}}]\,=\,1000\times \sqrt{\frac{1}{N}\mathop{\sum }\limits_{j=1}^{N}{\left({V}_{\exp }(j)-{V}_{{{{\rm{cs}}}}}(j)\right)}^{2}}\\ {{{{\rm{RMSE}}}}}_{{{{\rm{SOC}}}}}\,[ \% ]\,=\,100\times \sqrt{\frac{1}{N}\mathop{\sum }\limits_{j=1}^{N}{\left({{{{\rm{SOC}}}}}_{{{{\rm{cc}}}}}(j)-{{{{\rm{SOC}}}}}_{{{{\rm{p}}}}}(j)\right)}^{2}}\end{array}$$

(5)

where j is the time index, N is the number of samples, SOC_p is the simulated positive electrode state of charge (Supplementary Equation (48)), V_cs is the simulated voltage profile (output of the physics-based model), ${V}_{\exp }$ and SOC_cc are the experimental cell voltage and state of charge from Coulomb counting, respectively.

In the hybrid model, the machine-learning compensation is limited to the voltage output profile and does not affect the SOC. Hence, the performance of the hybrid model is assessed using the following reformulation of Equation (5) (on top):

$${{{{\rm{RMSE}}}}}_{V}^{\star }\,[{{{\rm{mV}}}}]=1000\times \sqrt{\frac{1}{N}\mathop{\sum }\limits_{j=1}^{N}{\left({V}_{\exp }(j)-V(j)\right)}^{2}}$$

(6)

where V is the output of the hybrid model (as in Fig. 3) and the ⋆ distinguishes between the use of FNN, RT, and RF as a machine-learning model.