Physics-informed neural networks for solving time-dependent mode-resolved phonon Boltzmann transport equation

Abstract

The phonon Boltzmann transport equation (BTE) is a powerful tool for modeling and understanding micro-/nanoscale thermal transport in solids, where Fourier’s law can fail due to non-diffusive effect when the characteristic length/time is comparable to the phonon mean free path/relaxation time. However, numerically solving phonon BTE can be computationally costly due to its high dimensionality, especially when considering mode-resolved phonon properties and time dependency. In this work, we demonstrate the effectiveness of physics-informed neural networks (PINNs) in solving time-dependent mode-resolved phonon BTE. The PINNs are trained by minimizing the residual of the governing equations, and boundary/initial conditions to predict phonon energy distributions, without the need for any labeled training data. The results obtained using the PINN framework demonstrate excellent agreement with analytical and numerical solutions. Moreover, after offline training, the PINNs can be utilized for online evaluation of transient heat conduction, providing instantaneous results, such as temperature distribution. It is worth noting that the training can be carried out in a parametric setting, allowing the trained model to predict phonon transport in arbitrary values in the parameter space, such as the characteristic length. This efficient and accurate method makes it a promising tool for practical applications such as the thermal management design of microelectronics.

Introduction

Thermal management of microelectronics is unprecedentedly crucial due to the rapid miniaturization in semiconductor technology, as it is essential to achieving high compactness along with high performance and reliability^1,2,3,4. With the application of electronic devices with higher power consumption in smaller packages, micro-/nanoscale thermal analysis is necessary to understand and predict the Joule-heating effect for the design and improvement of thermal packaging. In addition, the rapid advancement in the field of micro-/nanotechnology has led to the development of devices that exhibit characteristic dimensions comparable to or even smaller than the mean free path of phonons^5,6,7, which are the primary heat carriers in semiconductors. In such cases, phonon transport is not purely diffusive, but rather can be ballistic depending on the mean free path of specific phonon modes. Fourier’s law has been widely employed to analyze thermal conduction in the diffusive limit on the macroscale. However, this law is not suitable for accurately describing heat transfer in situations where the length scale is smaller than the phonon mean free path or when the time scale is shorter than the average phonon relaxation time. Instead, the phonon Boltzmann transport equation (BTE) is a more accurate method to describe phonon transport from the nanoscale to the macroscale and has been shown to model heat conduction in the mesoscale precisely^8,9,10,11,12. Although other techniques, such as molecular dynamics (MD) simulations^13,14 and first-principles¹⁵ calculations, can model phonon transport, they are impractical for mesoscale thermal analysis due to the high computation cost.

Despite the effectiveness in modeling micro-/nanoscale thermal transport, numerically solving the phonon BTE, a highly nonlinear integro-differential equation, can be very computationally demanding, particularly when considering mode-resolved phonon information and time evolution. Nevertheless, researchers can take advantage of some mature numerical schemes that are effective in solving various partial differential equations (PDEs), such as the finite difference method (FDM), finite volume method, finite element analysis (FEA), and their variants. By utilizing these numerical schemes, researchers can obtain precise and efficient solutions to the phonon BTE. The discrete ordinate method (DOM) has been used to solve BTE directly using FEA or FDM, but it often requires a large amount of computational memory and can be difficult to converge fast, especially in the diffusive limit^16,17. An implicit kinetic scheme has been developed to solve steady-state 1D and 2D phonon BTEs accurately within a few minutes¹⁸. However, with the use of large-scale parallel numerical solvers with even 400 processors, it still takes over an hour to run 3D steady-state phonon BTE calculations¹⁹. It is noted that the aforementioned numerical solvers only handle steady-state phonon BTE without considering the transient nature of thermal transport processes, which can be proven important in localized hotspots due to instantaneous spikes of power in electronic devices. Fortunately, researchers have developed methods to tackle the transient phonon BTE. For example, a combined FEA and DOM scheme has been utilized to investigate transient ballistic-diffusive phonon heat transport in a two-dimensional domain, as reported by Hamian et al.²⁰. But for Knudsen numbers exceeding 5, it has been noted that the standard DOM may not be appropriate, and modified methods should be applied to reduce the ray effect. Recently, a discrete unified gas kinetic scheme (DUGKS) has been developed to numerically predict transient heat transfer by solving 1D and 2D phonon BTEs with varying acoustic thicknesses. The DUGKS possesses asymptotic preserving properties for both the diffusive and ballistic regimes and can provide accurate solutions throughout the transition regime²¹. Additionally, the DUGKS has been extended to solve nongray (frequency-dependent) phonon BTE and is demonstrated to accurately capture the ballistic-diffusive transport phenomenon across a wide range of Knudsen number²². Later on, a semi-Lagrangian method is proposed to solve the nongray phonon BTE efficiently²³. However, it should be noted that while this method preserves asymptotic behavior in the ballistic limit, it may not preserve it in the diffusive limit. In general, the numerical solvers for phonon BTE discussed above can be resource-intensive to some extent, especially in the context of design and optimization. Additionally, the curse of dimensionality, which states that computational cost and complexity of nonlinear regression models increase exponentially with increasing dimensionality²⁴, may impede their practical applications in complicated phonon transport problems. Therefore, there is a pressing need to develop a new scheme that is computationally friendly for efficient analyses of the dynamic thermal behavior of multiscale devices.

Deep neural networks (DNNs) have been shown capable of approximating smooth functions²⁵, and they can overcome the curse of dimensionality in approximating the solutions to nonlinear PDEs²⁶. Deep learning can learn the solution to a PDE by minimizing the PDE residual while leveraging the automatic differentiation feature of the DNNs²⁷. Compared to mesh-based numerical solvers, the deep learning method eliminates the need for mesh generation and numerical differentiation between neighboring mesh points. For the deep learning method, the neural networks are trained to satisfy the governing laws of physics described by the PDEs, along with boundary/initial conditions, and/or labeled data. This is known as physics-informed machine learning, wherein the PDE constraints are integrated into the loss function during training. The idea of using physics-informed training to obtain solutions to differential equations was brought up by Meade and Fernandez²⁸, Dissanayake and Phan-Thien²⁹, and Lagaris et al.³⁰. The concept of physics-informed neural networks (PINNs) was introduced in 2019 when it was leveraged to solve forward and inverse fluid dynamics problems²⁷. PINNs are a type of deep neural network that can be trained to satisfy physical laws described by PDEs without significant reliance on labeled data, depending on the extent of prior knowledge of the underlying physics. In fact, if complete knowledge of the physics laws is available, labeled training data will not be required, and the training process becomes purely focused on satisfying the laws of physics by minimizing the residual of the governing equations. The success of PINNs in fields such as fluid dynamics and heat transfer^31,32,33,34 suggests their potential for application in broader research areas, including the anticipated utilization in solving phonon BTE. However, employing PINNs to study phonon transport can be quite challenging. Unlike the heat equation or Navier–Stokes equations, which typically involve two dimensions (spatial coordinates x and time t) in one-dimensional problems and three dimensions (x, y, and t) in two-dimensional problems^33,34,35,36, solving phonon BTE requires a five-dimensional input in one-dimensional problems and a seven-dimensional input in two-dimensional problems (to be discussed later). Furthermore, solving the phonon BTE entails highly nonlinear integro-differential processes characterized by intricate relationships between the independent and dependent variables, particularly when accounting for phonon dispersion and polarization. These inherent complexities pose additional challenges for DNNs to effectively approximate and capture such intricate relationships. We have recently extended PINNs to solve mode-resolved steady-state phonon BTE and demonstrated their great efficiency and extensibility in modeling problems with high-dimension geometries and large temperature gradients^37,38,39.

In this work, we show the capability of PINNs to solve time-dependent phonon BTE by demonstrating their efficiency and accuracy in modeling several thermal transport cases with different dimensions and boundary conditions. To be specific, PINNs are successfully applied to solving 1D and 2D micro-/nanoscale heat conduction problems, with periodic boundary conditions applied in the 1D problems and fixed temperature boundary conditions applied in the 2D problems. In contrast to the steady-state phonon BTE, the time-dependent phonon BTE exhibits a different equation form, incorporating a time derivative term on the left side. Furthermore, the dynamic behavior associated with the unsteady phonon BTE makes it difficult to effectively approximate the time-evolving solution using PINNs. Additionally, in order to establish a well-defined problem, both boundary and initial conditions should be applied, resulting in a more complex loss function compared to steady-state problems that only require boundary conditions. Moreover, the complexity of the loss function further increases due to the inclusion of the time derivative term in the governing equation. These complexities result in difficulties in accurately and efficiently predicting temperature distribution using the PINN model. While specific techniques, such as enforcing energy self-conservation and fine-tuning hyperparameters, have been applied in some testing cases, they are not the primary focus of the current work, and some details are beyond the scope of the paper. However, readers are encouraged to refer to the provided code for further insights.

Both gray and nongray models are investigated in this work, and the results are validated by either analytical or numerical solutions. By minimizing the residual of the phonon BTE, the law of energy conservation, and boundary/initial conditions, the PINNs are trained to accurately predict the spatio-temporal temperature distribution in a few seconds. The PINN method can be a promising tool for understanding mesoscale phonon transport physics and practical applications such as the thermal management design of microelectronics.

Results

Phonon Boltzmann transport equation

In this paper, we use single crystalline silicon, the most representative semiconductor in electronics, as the model material. In crystalline silicon (as well as in other crystalline solids), the atomic vibrations from equilibrium positions can set off waves traveling through the crystal at different frequencies and in different directions. These waves can be quantized as quasi-particles known as phonons, and the model system can be treated as a domain filled with a chaotic mix of phonons. The relationship between the angular frequency $\omega$ of a phonon and the wavevector k is described by the phonon dispersion relation. The phonon transport behavior can be captured by phonon BTE in the regime where wave effects and phase coherence effects can be neglected^10,40,41. To solve the phonon BTE, isotropic wave vector space and the single-mode relaxation time (SMRT) approximation are usually adopted to simplify the computation^10,42. Under the SMRT approximation, the energy-based phonon BTE can be written as,

$$\frac{\partial e}{\partial t}+{\boldsymbol{v}}\,\cdot\, \nabla e=\frac{{e}^{{eq}}-e}{\tau }$$

(1)

where $e\left({\boldsymbol{x}},{\boldsymbol{s}},k,p,t\right)={\hslash}\omega D\left(\omega ,p\right)[f-{f}^{{eq}}({T}_{{ref}})]$ is the phonon energy deviational distribution function, ${e}^{{eq}}\left(k,p,T\right)={\hslash }\omega D\left(\omega ,p\right)[{f}^{{eq}}\left(T\right)-{f}^{{eq}}({T}_{{ref}})]$ is the associated equilibrium phonon energy deviational distribution function, v is the phonon group velocity, and τ is the effective relaxation time. By using the SMRT approximation, a specific relaxation time is assigned to each phonon mode, reflecting the overall effect of various phonon scattering processes. The equilibrium phonon distribution function ${f}^{{eq}}\left(\omega ,T\right)$ conforms to the Bose-Einstein distribution,

$${f}^{{eq}}\left(\omega ,T\right)=\frac{1}{{e}^{\frac{{{\hslash }}\omega }{{k}_{B}T}}-1}$$

(2)

where ℏ is the reduced Planck’s constant, k_B is the Boltzmann constant, ω is the angular frequency, and T is the temperature. The phonon distribution function $f=f\left({\boldsymbol{x}},{\boldsymbol{s}},k,p,t\right)$ (or $f\left({\boldsymbol{x}},{\boldsymbol{s}},\omega ,p,t\right)$) is determined by the spatial vector x, directional unit vector ${\boldsymbol{s}}=({cos \theta,}\,{sin \theta cos \varphi,}\,{sin \theta sin \varphi})$ (θ is the polar angle and φ is the azimuthal angle), time t, wave number k (or angular frequency $\omega =\omega (k,p)$) and polarization p. If the temperature difference across the entire domain is much smaller than the reference temperature (i.e., $\left|\Delta T\right|\ll {T}_{{ref}}$), the equilibrium energy term can be linearized and we can use the following approximation⁴³,

$${e}^{{eq}}\left(k,p,T\right)={{\hslash }}\omega D\left(\omega ,p\right)\left[{f}^{{eq}}\left(\omega ,T\right)-{f}^{{eq}}\left(\omega ,{T}_{{ref}}\right)\right]\approx C\left(\omega ,p\right)\left(T-{T}_{{ref}}\right)$$

(3)

where $C(\omega ,p)=\hslash \omega D\left(\omega ,p\right)\frac{\partial {f}^{{eq}}}{\partial T}$ represents the modal heat capacity, and $D\left(\omega ,p\right)=\frac{{k}^{2}}{2{\pi }^{2}\left|{\boldsymbol{v}}\right|}$ is the phonon density of states. By assuming the small temperature difference, the problem can be significantly simplified. Additionally, the group velocity ${\boldsymbol{v}}={\nabla }_{k}\omega$ can be obtained by utilizing the phonon dispersion relation, and relaxation time $\tau (\omega ,p,T)$ can be derived from the Holland model^44,45. In order to ensure energy conservation of the scattering term, Eq. (4) must be satisfied.

$$\sum _{p}{\int_{0}^{{\omega }_{\max, p}}}{\int_{4\pi }}\,\frac{{e}^{{eq}}-e}{\tau }d\Omega d\omega =0$$

(4)

where ω_max,p is the maximum frequency. The local temperature can be obtained by substituting Eq. (3) into Eq. (4),

$$T={T}_{{ref}}+\frac{1}{4\pi }\left(\sum _{p}{\int_{0}^{{\omega }_{\max ,p}}}{\int_{4\pi }}\,\frac{e}{\tau }d\Omega d\omega \right)\times {\left(\sum _{p}{\int_{0}^{{\omega }_{\max,p}}}\frac{C}{\tau }d\omega \right)}^{-1}$$

(5)

This demonstrates that temperature can be determined once the phonon energy distribution is known, which can be obtained by solving the phonon BTE. Therefore, the spatio-temporal temperature distribution of micro-/nanoscale thermal transport problems can be obtained by solving the time-dependent phonon BTE (Eq. (1)). It is important to note that the aforementioned procedure is for the nongray model of phonon BTE, which is often used for greater accuracy in predicting the behavior of phonons. However, in practice, it is common to make assumptions such as the gray model, in which all phonon modes are assumed to have the same properties. In the gray model, average phonon group velocity and relaxation time are adopted in the phonon BTE, and they are treated as constants for all phonon modes to simplify the calculation.

Physics-informed neural networks

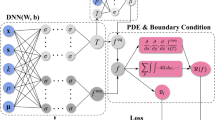
To solve the phonon BTE, a PINN scheme is constructed in accordance with the laws of physics, as shown in Fig. 1. The input variables to the neural networks are position vector x (including x, y, and z), solid angle ${\boldsymbol{s}}=({cos \theta,}\,{sin \theta cos \varphi,}\,{sin \theta sin \varphi})$ (including polar angle θ and azimuthal angle φ), wave number k, polarization p, and time t. Two neural networks are employed to approximate the equilibrium phonon energy distribution function ${e}^{{eq}}$ and non-equilibrium phonon energy distribution function ${e}^{{neq}}$ separately to enhance the training efficiency, due to the large difference between the magnitudes of ${e}^{{eq}}$ and ${e}^{{neq}}$. The total phonon energy ${e={e}^{{eq}}+e}^{{neq}}$ is then formulated to satisfy various physical constraints, including the PDE (i.e., phonon BTE), energy conservation, and boundary/initial conditions. For energy conservation, the integration of the scattering term vanishes, which is already demonstrated in Eq. (4). The loss function, which is composed of the mean squared error from each physical constraint, can be expressed as shown in Eq. (6),

$${\mathcal{L}}={{\Big\Vert}\frac{\partial e}{\partial t}+{\boldsymbol{v}}\,\cdot\, \nabla e-\frac{{e}^{{eq}}-e}{\tau }\Big\Vert}^{2}+{\Big\Vert\sum _{p}{\int_{0}^{{\omega }_{\max ,p}}}{\int_{4\pi }}\frac{{e}^{{eq}}-e}{\tau }d\Omega d\omega {\Big\Vert}}^{2}+\sum _{i}{\Big\Vert{{\mathcal{B}}}_{i}\Big\Vert}^{2}$$

(6)

where ${{\mathcal{B}}}_{i}$ is the inconsistency between the given boundary/initial values and the corresponding values predicted by the PINNs. The training process aims to minimize Eq. (6) by adjusting the weights and biases of the neural networks.

Fig. 1: Schematic of the PINN framework for solving transient phonon BTE.

Net 1 and Net 2 are used to approximate the equilibrium part (${e}^{{eq}}$) and non-equilibrium part (${e}^{{neq}}$) of the phonon energy distribution, respectively. The inputs are position vector x (x, y, and z), solid angle s (including polar angle θ and azimuthal angle φ), wave number k, polarization p, and time t. The Swish activation function, denoted as σ, is employed in this work.

It is noted that the partial derivatives of x, y, z, and t, can be calculated by taking advantage of the auto differentiation of neural networks, which uses the chain rule to compute derivatives analytically and efficiently during the back-propagation process. Thus, PINNs can compute the derivatives at any point in the domain without needing information from neighboring grid points, as is necessary in numerical methods. This is a significant advantage of PINNs compared to traditional numerical methods.

Gray model

To begin with, we use the gray model of phonon BTE to evaluate our PINN scheme and gain preliminary insight into our model performance. In contrast to the nongray model where mode-resolved properties are considered, all phonon modes are treated as having the same properties in the gray model. To some extent, the gray model can provide useful insights into phonon transport, such as ballistic transport and boundary scattering effects⁴⁶. In this section, we conduct numerical experiments to analyze the performance of our PINN scheme by solving the phonon BTE gray model for both 1D and 2D transient heat conduction problems.

First, we model a 1D transient thermal grating (TTG) process to test the PINN scheme. The laser-induced TTG technique allows non-contact measurements of thermal conductivity on nanostructured samples, without the use of metal heaters or other extraneous structures^47,48,49. We simulate the thermal relaxation process of a 1D TTG system, where a spatially sinusoidal temperature variation across a silicon thin film is induced by a laser interference⁴⁷, and the initial condition and boundary condition for the heat transport problem are described in Eq. (7),

$$\left\{\begin{array}{ll}T\left(x,0\right)={T}_{b}+{A}_{0}\cos \left(\frac{2{\rm{\pi }}x}{L}\right)\\ T\left(0,t\right)=T\left(L,t\right)\end{array}\right.$$

(7)

where ${T}_{b}$ is the background temperature, ${A}_{0}$ is the amplitude at the initial state, and L is the thickness of the silicon thin film (characteristic length). The periodic boundary condition is applied to the left and right boundaries. Therefore, the temperature deviation from the background temperature, $\Delta T=T-{T}_{b}$, can be approximated as $\Delta T=A\left(t\right)\cos \left(\frac{2{{\pi }}x}{L}\right)$, where A(t) is the amplitude of the temperature variation, and it can be obtained analytically⁴⁷,

$${\hat{A}}\left({t}^{* }\right)={sinc}\left(\xi {t}^{* }\right){e}^{-{t}^{* }}+{\int_{0}^{{t}^{* }}}{\hat{A}}\left({t}^{\prime}\right){sinc}\left[\xi \left({t}^{\prime}-{t}^{* }\right)\right]{e}^{\left({t}^{\prime}-{t}^{* }\right)}d{t}^{{\prime} }$$

(8)

where ${\hat{A}}=A/{A}_{0},$ ${t}^{* }=t/\tau$, and the rarefaction parameter $\xi =2{{\pi }}{\rm{Kn}}$. Knudsen number Kn is a dimensionless number defined as the ratio of phonon mean free path $\varLambda$ and characteristic length L of the modeled structure.

The previously derived PINN framework is applied to predict the thermal relaxation process of this 1D TTG case. A uniform grid of N_x points in the spatial domain and N_t points in the time domain is utilized to produce the training points for the DNNs. Moreover, the solid angle space s is discretized by using the Gauss–Legendre quadrature rule, with the number of sample points denoted as N_s. The values of N_x, N_t, and N_s are summarized in Table 1 for reference. After training, the temperature can be evaluated at new positions and times other than the trained points, given the interpolation ability of DNNs. The extrapolation study is also conducted, and the details are provided in the Supplementary Information. The rarefaction parameter $\xi$ is chosen to be 0.6, 4, and 36, indicating the characteristic length of the modeled structure can span from the regime where diffusive phonon transport dominates to the regime where ballistic phonon transport dominates. It is worth noting that parametric learning is achieved by incorporating the rarefaction parameter as a new input parameter to the DNNs. Parametric learning enables temperature prediction for new thermal relaxation processes that feature different thicknesses, even if such thicknesses were not encountered during the training phase of the DNNs. To be specific, we train the DNNs under $\xi$ = 0.45, 0.55, 0.65, and 0.75 to study thermal transport at the length scale exceeding the phonon mean free path and evaluate the model at $\xi$ = 0.6. Similarly, for length scales comparable to the phonon mean free path, the DNNs are trained under $\xi$ = 3, 5, 7, and 9, followed by testing the model at $\xi$ = 4. Likewise, to examine thermal transport at length scales smaller than the phonon mean free path, the DNNs are trained at $\xi$ values of 34, 38, 42, and 46, and tested at $\xi$ = 36.

Table 1 Training and testing information for the 1D TTG case with the gray model.

Figure 2a shows the schematic of the 1D silicon thin film, where a sinusoidal initial temperature and periodic boundary condition are applied. The obtained results are compared with the analytical solutions, as depicted in Fig. 2b–d, with PINN results in dashed lines, parametric-learning PINN results in triangular symbols and analytical solutions in solid lines. Both the PINN results and the parametric-learning PINN results show great agreement with the analytical solutions, which validates the capability of the PINN to accurately capture micro-/nanoscale phonon transport using a gray model. The results demonstrate that as the value of $\xi$ increases, thermal relaxation becomes faster. It is important to note that, for the case where $\xi$ = 36, we use a denser set of training points in both the spatial and time domains to ensure the accuracy of the model at this length scale. Moreover, in this particular case, the characteristic length of the silicon film L is smaller than the phonon mean free path $\varLambda$, which results in more ballistic and less diffusive phonon transport. To precisely capture the highly non-equilibrium phonon energy distribution near the ballistic limit, a finer spatial and temporal discretization is required. The training and testing information is summarized in Table 1. The training can be finished within several minutes, depending on the number of collocation points used. However, it should be noted that in the case of $\xi$ = 36, the training time significantly increases due to the adoption of additional layers and a higher number of neurons per layer, which are necessary in order to capture such drastic phonon energy gradients within this thin film. Once fully trained, the PINNs can produce accurate predictions within 1 ms. It is noted that all computational times presented in this study are based on an NVIDIA GeForce TITAN Xp GPU. However, with newer GPUs, these times may be significantly reduced.

Fig. 2: Results of the 1D TTG case with the gray model.

a Schematic of the 1D silicon thin film, where the sinusoidal initial temperature and periodic boundary condition are applied. b–d Amplitude of the temperature variation ${\hat{A}}$ predicted by the PINN framework is validated by the analytical solutions at $\xi =0.6$, $\xi =4$, and $\xi =36$, respectively. The comparison between the PINN results (dashed lines), parametric-learning PINN results (triangular symbols), and analytical solutions (solid lines) is presented at three time points in each case. X is the normalized coordinate.

In the second test case, phonon transport in a 2D square domain is considered, as depicted in Fig. 3a. The temperature at the top boundary is maintained at T_h, while the other boundaries are held at T_c (T_c < T_h). The fixed temperature boundary conditions are imposed on all the boundaries. At the initial state, the whole domain temperature is held at T₀ = T_c. Thermal transport is studied at different Kn numbers (i.e., Kn = 0.1 and Kn = 1) in order to evaluate the performance of our model at different length scales. When Kn is 0.1, diffusive phonon transport dominates, whereas when Kn is 1, ballistic phonon transport dominates. For the Kn values under consideration, the system takes 10τ/Kn to reach the steady states, where τ/Kn represent the time scale for thermal information to propagate from one boundary to another²⁰. As a result, we select a time range of [0, 100τ] for training the Kn = 0.1 case, and [0, 10τ] for the Kn = 1 case. Given the boundary conditions and the initial condition, the temperature distribution at any time within the aforementioned range can be predicted by the PINN framework. To improve the accuracy on the top boundary, non-uniform spatial training points are sampled, with denser points placed at the top corners. This is done in response to the abrupt temperature change at the corners, which is caused by the boundary conditions. The solid angles (polar angle θ and azimuthal angle φ) are discretized using the Gauss–Legendre quadrature rule with the number of sample points N_θ = 12 and N_φ = 12.

Fig. 3: Results of the 2D square case with the gray model.

a Schematic of the 2D square phonon transport domain. The higher temperature T_h is applied on the top boundary, and the lower temperature T_c is applied on the other boundaries. b Dimensionless temperature profiles T* at the vertical centerline (see dashed line in (a)) is validated by the numerical results when Kn is 0.1. Results are compared at t = 1τ, t = 10τ, and t = 100τ, respectively. c Dimensionless temperature profiles T* at the vertical centerline is validated by the numerical results when Kn is 1. Results are compared at t = 0.1τ, t = 0.7τ, and t = 10τ, respectively. Y is the normalized coordinate.

Although there is no analytical result available for direct validation of the PINN results, the temperature profiles along the vertical centerline at x = 0.5 L can be extracted and compared with the numerical results obtained by an FEA-DOM scheme²⁰, as shown in Fig. 3b, c. For both the Kn = 0.1 and Kn = 1 cases, the BTE solutions exhibit obvious ballistic phonon transport behavior. Specifically, it is observed that the dimensionless temperature (${T}^{* }=(T-{T}_{c})/({T}_{h}-{T}_{c})$) at the center of the top boundary (x = 0.5 L) slips down to 0.61 in Fig. 3b and 0.51 in Fig. 3c right after thermal transport occurs, and it gradually recovers to 0.89 and 0.62, respectively, as approaching the steady state. The presence of the temperature slip indicates a difference in the energy levels between the phonons emitted from the top boundary and those traveling towards it. As thermal information propagates through the domain, the energy level discrepancy between phonons and the top boundary decreases, resulting in smaller temperature slips, as depicted in Fig. 3b, c. Additionally, a comparison of Fig. 3b and Fig. 3c reveals a positive correlation between the Knudsen number and the magnitude of the temperature slip phenomenon. This observation can be attributed to the predominance of ballistic transport in the system with a smaller length scale. Overall, the PINN-predicted results agree well with the numerical results. It is noted that the ray effect, a common numerical artifact encountered in traditional numerical schemes, especially in DOM^50,51, is not observed in the PINN solution. In contrast, in the reference numerical solution, the presence of the ray effect in the Kn = 1 case, where the phonon energy distribution tends to be highly non-equilibrium, is obvious. This can be attributed to the lack of sufficient resolution in the numerical method to accurately capture the solution, resulting in errors that manifest as jagged features in the simulation output. Nonetheless, such anomalies are not found in the PINN solution. The associated training and testing details are succinctly presented in Table 2. While the training procedure typically takes approximately 20 h, the testing phase can be executed expeditiously within a few seconds. This implies that once the PINN framework is trained, it possesses the capability to predict temperature distribution at any time point within the training domain accurately.

Table 2 Training and testing information for the 2D square case with the gray model.

Nongray model

The gray model is widely used owing to its simplicity. Nevertheless, this approach assumes that all phonons share identical properties with constant group velocity and relaxation time, which can lead to considerable inaccuracies in some scenarios⁵². To address this issue, the nongray model is explored in this section. Specifically, we utilize a PINN framework to predict temperature evolution for the same geometry subjected to TTG (as shown in Fig. 2a), with ${T}_{b}$ = 300 K. We investigate thermal transport at different characteristic lengths, namely L = 1 μm and L = 10 μm. In particular, for the L = 1 μm case, we train the model using a time range of [0, 2000 ps], while for the L = 10 μm case, we use a larger time interval of [0, 80 ns]. The predicted temperature distributions for the two cases are presented in Fig. 4a, b, respectively. To verify the accuracy of our predictions, we compare our results with numerical solutions obtained from the DUGKS, as described in reference²². A summary of the pertinent training and testing information is provided in Table 3. Notably, the L = 1 μm case requires a longer training duration due to the larger number of training epochs required to achieve convergence. This outcome can be attributed to the non-equilibrium nature of the phonon energy distribution, which tends to become increasingly significant as the system length scale is reduced. Typically, the training period spans around 20 to 40 h, while testing can be completed within a few seconds.

Fig. 4: Results of the 1D TTG case with the nongray model.

a The amplitude of the temperature variation $\hat{A}$ is validated by numerical solution when L = 1 μm. Results are compared at t = 100 ps, t = 500 ps, and t = 1500 ps, respectively. b The amplitude of the temperature variation $\hat{A}$ is validated by numerical solution when L = 10 μm. Results are compared at t = 0, t = 20 ps, and t = 60 ps, respectively.

Table 3 Training and testing information for the nongray model cases.

In order to investigate transient mode-resolved phonon transport in 2D geometries, we extend the PINN scheme to solve the time-dependent 2D nongray phonon BTE in a square domain with fixed temperature boundary conditions. Specifically, a Gaussian temperature profile, mimicking a laser hot spot, is applied to the top surface of the square domain with a standard deviation of L/6, as illustrated in Fig. 5a. The temperature at the center of the hot spot is T_h = 300.5 K and gradually decreases to T_c = 299.5 K as approaches the corners, while the other three boundaries are maintained at T_c = 299.5 K. The initial temperature of the interior domain is T₀ = T_c = 299.5 K. By integrating these boundary and initial conditions into the PINN loss function during the training process, the trained model can accurately predict the temperature evolution within the simulation domain. The temperature contours predicted at different times are depicted in Fig. 5b–e. However, it is worth noting that there is a lack of a reference solution for direct comparison with the PINN results. In order to validate the accuracy of the PINN predictions, temperature profiles at the vertical center line (as indicated by the dashed line in Fig. 5a) are extracted at 10, 50, and 100 ns. These profiles are then compared with the corresponding COMSOL simulation results, which are based on Fourier’s law. In the current 2D nongray case, it is noted that the domain characteristic length is 10 μm. It already far exceeds the average phonon mean free path in silicon, which is approximately 300 nm. Consequently, phonon transport in this scenario occurs at the diffusive limit, where Fourier’s law is applicable. Figure 5f demonstrates that the temperature profiles extracted from the PINN predictions converge to the solutions obtained via Fourier’s law, which validates the accuracy of our PINN-predicted results. The training and testing information is summarized in Table 3. It is important to note that the training process can be executed in a parametric setting to improve computation efficiency, which we have previously demonstrated in the 1D TTG case. And we believe with newer GPUs, a significant reduction in computation time could be achieved.

Fig. 5: Results of the 2D square case with the nongray model.

a Schematic of the 2D square domain with a Gaussian hot spot on the top boundary. b–e Contours of dimensionless temperature at t = 0, t = 10 ns, t = 50 ns, and t = 100 ns, respectively. f Temperature profiles at the vertical centerline converge to the results of Fourier’s law for our case of L = 10 μm.

Discussion

In this work, transient phonon BTE is successfully solved based on our PINN framework and validated by comparing to either analytical or numerical results. The model accuracy including the training and validation loss is shown in the Supplementary Information. The proposed data-free PINN framework is appealing compared to learning solely from labeled data, where those data are sometimes expensive or impossible to obtain. PINN can predict temperature distribution and temperature evolution in a few seconds after training. While showing great promise, the current PINN framework can still be further improved to adapt to a wider range of applications. The current framework has been successfully implemented on 1D and 2D models, but the 3D model remains to be tested, which is currently hindered by the capability of our GPU hardware. However, we do not believe there is any algorithm difficulties in extending our model to 3D. Our PINN has already demonstrated its superiority by solving 2D transient nongray phonon BTE, which conventional numerical solvers often struggle with. We also note that while training takes much more time than prediction, it can be carried out in parametric settings, enabling the trained model to predict phonon transport in arbitrary values in the parameter space. For example, by training the model with system length as a parameter, the trained model can be utilized to study phonon transport in geometries with different lengths. While still at the early stage, the current work represents the first effort of using PINN to efficiently solve transient nongray phonon BTE, which could impact micro-/nanoscopic thermal transport research and facilitate the practical application of phonon BTE for device design and optimization.

Methods

Phonon properties

In this study, silicon is the material we use for modeling. The phonon dispersion relation in the [100] direction is employed for our analysis. The detailed phonon properties are described in the Supplementary Information. We use Matthiessen’s rule to calculate the effective relaxation time induced by the overall effect of impurity scattering, Umklapp, and normal phonon–phonon scattering.

Training

Training points are sampled from the input space using quasi-random low-discrepancy Sobol sequences. We construct two distinct full-connected neural networks to estimate the equilibrium and nonequilibrium phonon energy separately. Both neural networks consist of the same number of layers and neurons per layer, but they take different sets of input variables. The size of the neural networks depends on the complexity of the problems. Specifically, we employed 5 layers with 30 neurons per layer for gray models and 8 layers with 30 neurons per layer for the non-gray model. Both neural networks are trained simultaneously with a unified loss function. Adam optimizer is used, and the initial learning rate is set as 10⁻³. Additionally, we scale the spatial and temporal variables to the range of [0,1] prior to feeding them into the neural networks.