Introduction

Anomalous Nernst effect (ANE), for which the generated voltage drop is perpendicular to the temperature gradient without any assistance of an external magnetic field, attracts growing attention for energy harvesting1,2,3,4,5. The nature of transverse transport helps for device miniaturization during the energy conversion. Compared with the ordinary Nernst effect, where the carriers are driven by Lorentz force from the external magnetic field6, the driving force of ANE can be classified as extrinsic and intrinsic contributions. While the extrinsic contributions refer to the drags of magnon or the skew scattering and side jump due to strong spin-orbit coupling7,8, the intrinsic one is attributed to the effects of Berry curvature of the energy bands9,10. Berry curvature behaves as the magnetic field deflecting the electrons in momentum space, diverging at the band crossing points such as Weyl points or nodal lines. Therefore, the corresponding topological semimetals are favorable to exhibit large anomalous Hall conductivity (AHC)11,12,13,14,15,16,17. Similarly, recent studies pursuing materials candidates with large ANE also focus on topological semimetals. For example, sizable anomalous Nernst conductivity (ANC) [~ 0.1–10 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\)] is observed in topological materials Co2MnGa18, Co3Sn2S219, Mn3X (X = Sn, Ge)20, and Heusler family21,22, all of which possess multiple Weyl points or nodal lines. However, the ANC \(\alpha\) and the corresponding thermopower \(S\) are still too small for practical applications compared with magneto-thermoelectricity23.

The Mott relation4,24 reflects the connection between the AHC σ and ANC α, both of which are related to the integration of the Berry curvature through the Brillouin zone. At low temperature limit, the Mott relation expresses as:

$${\alpha }_{{ij}}=\frac{{{\rm{\pi }}}^{2}}{3}\frac{{k}_{B}^{2}T}{{\rm{e}}}{\sigma }_{{ij}}^{{\prime} }\left({{\rm{\varepsilon }}}_{{\rm{F}}}\right),$$
(1)

where \({k}_{B}\), \(T\), \({\rm{e}}\) and \({{\rm{\varepsilon }}}_{{\rm{F}}}\) are Boltzmann constant, temperature, elementary charge, and Fermi energy, respectively. The Mott relation indicates that the maximum value of ANC α occurs at the energy with the steepest slope of AHC σ. Thus, a band structure with opposite AHC peaks on the opposite side of the Fermi level \({{\rm{\varepsilon }}}_{{\rm{F}}}\) is expected to host large ANC. In addition, the ANC can be further enhanced if carriers are compensated at the current Fermi level. Although carriers of opposite charge play against each other in the Seebeck effect25, they synergically contribute to the ordinary Nernst effect, giving rise to a giant and non-saturating Nernst voltage26,27,28. To utilize a similar mechanism in ANE, it is necessary to design a system in which both types of carriers experience a fictitious magnetic field, i.e., Berry curvature, of the same sign. However, Among the various materials with ANE observed in experiments, they are almost discovered by chance or in some special material systems, e.g., Heusler compounds21,22. Moreover, for most theoretically proposed ANE materials, the maximum value of ANC, corresponding to a specific chemical potential, usually deviates from the pristine Fermi level. It means that to achieve the best performance, the Fermi level needs to be tuned to the optimal ANC through electron or hole doping. Therefore, it is desirable to conduct a material design from the fundamental electronic structure that hosts large ANE pinning close to the intrinsic Fermi level.

In this work, rather than resorting to a single material system, we theoretically illustrate that the target functionality of enhanced ANC pinning at the Fermi level can be treated as an electronic-structure design problem. Starting from a model Hamiltonian of a Dirac semimetal under Zeeman field, we reveal two pairs of Weyl points forming a “G-type” configuration of chirality in momentum space, leading to a double-peak feature of the AHC, odd distributed with respect to the chemical potential. Such a system also features compensated carriers, both types of which experience Berry curvatures of the same sign. As a result, a 300% enhanced ANC pinning at the Fermi level is obtained compared with a simple two-band Weyl semimetal model. Exemplified by two realistic Dirac materials Na3Bi29,30 and NaTeAu31,32, we then perform ANC calculations based on atomistic Hamiltonians obtained from density-functional theory and obtained sizable ANC in the vicinity of the Fermi level (~0.38 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\) and ~1.3 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\), respectively). Additionally, by substituting 50% Na with Fe in NaTeAu, we design an intrinsic ferromagnetic topological material NaFeTe2Au2. Its AHC curve shows a “double-peak” feature with respect to the chemical potential with a maximum value of ANC (\(3.7\,{\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\)) at the Fermi level. Our work paves an avenue for the material realization of large ANE materials.

Results

Double-peak AHC of a Dirac semimetal under Zeeman field

A Weyl point is the position of band crossing in momentum space, where the Berry curvature diverges, identified as the source or sink of Berry curvature10. It always connects with the large AHC and ANC. First, we study the electronic structure and properties of a tilted two-band Weyl model system. The minimal Hamiltonian for such a model can be written as33:

$$H=A\left({k}_{x}{\sigma }_{x}+{k}_{y}{\sigma }_{y}\right)+M\left({k}_{w}^{2}-{{\bf{k}}}^{2}\right){\sigma }_{z}+t{k}_{z},$$
(2)

where \(\sigma\) are Pauli matrices; \(A\) and \(M\) are related to the Fermi velocity and the inverse of effective mass near the band edge, respectively; \({k}_{w}\) characterizes the distance of the two Weyl points in momentum space and \(t\) describes the tilting of the band structure along \({k}_{z}\). Such a three-dimensional minimal model describes a pair of Weyl nodes locating at \((\mathrm{0,0},\pm {k}_{w})\), with an energy difference of \(2t{k}_{w}\). The monopole charges, i.e., chirality of Weyl nodes at \((\mathrm{0,0},\pm {k}_{w})\), are \(\mp 1\). Figure 1a displays the band structure of the tilted two-band Weyl model. The anomalous Hall conductivity is an even function with respect to the chemical potential (see Fig. 1b), with one peak \(\sim 220\,{{\Omega }^{-1}\,{\rm{cm}}}^{-1}\) locating at \({{\rm{E}}}_{{\rm{f}}}=0\,{\rm{eV}}\). The corresponding ANC curve is an odd function with respect to the chemical potential, consisting of the Mott relation. The two opposite peaks of ANC connect with the maximum slope of the AHC curve symmetrically locating above and below the Fermi level with the absolute value of about 1.1 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\) (see Fig. 1c). Such results are similar to the two-band Weyl model without band tilting34. In a word, a pair of Weyl points with opposite chirality generates only one AHC peak at the Fermi level. Such a single-peak Weyl model gives rise to a moderate ANE away from the Fermi level, while the ANE at the Fermi level is exactly zero.

Fig. 1: Electronic structures and transport properties of the Weyl model and Dirac model under the Zeeman field.
figure 1

a Band structure of the tilted Weyl semimetal and its b AHC and c ANC with respect to the chemical potential. d Band structure of the four-band Dirac model with Zeeman term and its e AHC and f ANC with respect to the chemical potential. The ANC curve in f behaves as an even function, with a maximum value of about 3.2 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\), which is almost 300% enhancement compared with that of the two-band Weyl model c. The signs “\(\pm\)” in the band structures a and d denote the chirality of Weyl points. The model parameters are \(A=0.18\,{\rm{eV}}\cdot {\rm{\mathring{A} }}\), \(M=2\,{\rm{eV}}\cdot {{\rm{\mathring{A} }}}^{2}\), \({k}_{w}={sqrt}\left(0.1\right){{\rm{\mathring{A} }}}^{-1}\), \(t=0.3\,{\rm{eV}}\cdot {\rm{\mathring{A}}}\) and \(S=0.05\,{\rm{eV}}\).

Full size image

To gain an enhanced ANC pinning at the Fermi level, we require the AHC curve is an odd function with two opposite peaks locating above and below the Fermi level within a narrow energy interval. This requires at least four Weyl nodes, with one pair locating below the Fermi level and the other above the Fermi level forming a “G-type” arrangement of chirality. Inspired by the results of the two-band Weyl model, we adopt a Dirac model, i.e., a two-band Weyl model connecting with its time-reversal partner, combined with a Zeeman term breaking the time-reversal symmetry35:

$$H=\left[\begin{array}{cc}\begin{array}{cc}({k}_{w}^{2}-{{\bf{k}}}^{2})M & A{k}_{x}-{iA}{k}_{y}\\ A{k}_{x}+{iA}{k}_{y} & -({k}_{w}^{2}-{{\bf{k}}}^{2})M\end{array} & \begin{array}{cc}0 & 0\\ 0 & 0\end{array}\\ \begin{array}{cc}0 & 0\\ 0 & 0\end{array} & \begin{array}{cc}({k}_{w}^{2}-{{\bf{k}}}^{2})M & -A{k}_{x}-{iA}{k}_{y}\\ -A{k}_{x}+{iA}{k}_{y} & -({k}_{w}^{2}-{{\bf{k}}}^{2})M\end{array}\end{array}\right]+\left[\begin{array}{cc}\begin{array}{cc}S & 0\\ 0 & S\end{array} & \begin{array}{cc}0 & 0\\ 0 & 0\end{array}\\ \begin{array}{cc}0 & 0\\ 0 & 0\end{array} & \begin{array}{cc}-S & 0\\ 0 & -S\end{array}\end{array}\right],$$
(3)

where \(A\), \(M\) and \({k}_{w}\) are parameters as that in Eq. (2), and S denotes the strength of the Zeeman term. Composed of two copies for different spin degrees of freedom, the Hamiltonian can be written in a concise form:

$$\,H=A\left({k}_{x}{\sigma }_{z}\otimes {\sigma }_{x}+{k}_{y}{\sigma }_{0}\otimes {\sigma }_{y}\right)+M\left({k}_{w}^{2}-{{\bf{k}}}^{2}\right){\sigma }_{0}\otimes {\sigma }_{z}+S{\sigma }_{z}\otimes {\sigma }_{0}.$$
(4)

Without the Zeeman term, the energy bands are doubly degenerate, with two Dirac nodes locating at \((0,0,\pm {k}_{w})\). Each Dirac node consists of two degenerate Weyl nodes with opposite chirality. Due to the time-reversal symmetry, both the AHC and ANC are vanishing. However, the compensation of the Weyl points for opposite spin channel ensures that when the time-reversal symmetry is slightly breaking, there could be significant response for AHC and ANC. As shown in Fig. 1d, by adopting the same parameters as that of the tilted Weyl model in Eq. (2) and a Zeeman term \(S=0.05\,{\rm{eV}}\), the four Weyl points emerge, with the chiralities forming a G-type configuration around the Fermi level (see Fig. 1d). The AHC is then odd distributed with respect to the chemical potential (see Fig. 1e), with two opposite peaks (\(\sim 219\,{{\Omega }^{-1}{\rm{cm}}}^{-1}\)) locating symmetrically above and below the Fermi level.

The corresponding ANC curve exhibits an even function with respect to the chemical potential, consistent with the Mott relation. Instead of being zero at the Fermi level in the single-peak Weyl model, the ANC curve in the two-peak Dirac model shows the maximum value right at the Fermi level, with the magnitude (3.2 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\)) almost 300% of the maximum value for the Weyl model (see Fig. 1c, f). Moreover, the two smaller symmetric peaks (~1.3\(\,{\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\)) locating on both sides of the Fermi level are also comparable to the maxima of the Weyl model. Thus, the minimal four-band Dirac model with a Zeeman term displays two peaks of AHC with an enhanced ANC at the Fermi level, providing a prototypical band feature for designing ANC materials.

We next consider the modulation of ANC for the four-band Dirac model with Zeeman term as a function of different physical parameters in Eq. (3). Here \(A\), \(M\), \({k}_{w}\) and \(S\) are related to the Fermi velocity, the inverse of the effective mass of the band edge, distance of the two Dirac nodes in momentum space and strength of the Zeeman field, respectively. In real materials, these physical parameters can be regulated by strain, element substitution, magnetic proximity effect and external magnetic field, etc. Figure 2 shows the variation of the maximum ANC peak at \({{\rm{E}}}_{{\rm{f}}}=0\) (see Fig. 1f) with respect to four physical parameters in Eq. (3) at different temperatures (see Supplementary Note 1). First, we study the ANC variations at room temperature (black lines). The peak value of ANC increases and then decreases with the Fermi velocity \(A\), which describes the slope of the energy band around Dirac points, with an optimal value ~0.16 \({\rm{eV}}\cdot {\rm{\mathring{A} }}\) (see Fig. 2a). The maximum value of ANC saturates with an increasing trend of the inverse of the effective mass \(M\), i.e., decrease with the effective mass near the band edge (see Fig. 2b). We suggest that a smaller effective mass near the band edge gives rise to a steeper band around the Dirac points and simultaneously a larger peak value of AHC, thus leading to a larger ANC.

Fig. 2: Modulation of ANC for the four-band Dirac model with Zeeman term.
figure 2

Variation of the maximum peak at \({{\rm{E}}}_{{\rm{f}}}=0\,{\rm{eV}}\) of ANC (see Fig. 1f) with respect to the four physical parameters in Eq. (3). ANC varies with the physical parameters a Fermi velocity (A), b inverse of the effective mass around band edge (M), c distance of the two Dirac nodes (\({k}_{w}\)) and d strength of the Zeeman field (S) in Eq. (3).

Full size image

With the increase of the distance of the two Dirac nodes \({k}_{w}\), the peak of ANC gradually increases, as shown in Fig. 2c. The strength of the Zeeman field relates to the energy splitting of the two spin channels (Fig. 1d) and the energy interval of the opposite peaks of AHC (Fig. 1e). A larger Zeeman field strength \(S\) represents a stronger breaking of time-reversal symmetry and hence a larger ANC, while a larger energy interval of the two peaks of AHC will lead to a smaller slope of AHC and suppresses the ANC. This competing mechanism makes the maximum value of ANC initially increase and then decrease, with an optimal value at about 60 meV (Fig. 2d). At 200 K, the ANCs vary similarly to that of the room temperature. Due to the temperature broadening effect, ANCs for a relative low temperature (i.e., 100 K) are obviously smaller than that of the high temperature. It is worth noting that the Mott relation is applicable for a large temperature range (i.e., up to 300 K) that the maximum of ANC \(\alpha\) corresponds to the steepest of AHC \(\sigma\). The dependence of the physical parameters for the peak value of ANC here offers a reference for real material regulation.

Candidate Dirac materials with enhanced ANC

Exemplified by two Dirac semimetals, we next perform ANC calculations based on atomistic Hamiltonians obtained from density-functional theory to further illustrate the role of the double-peak AHC feature. Alkali pnictides Na3Bi crystallizing in hexagonal \(P{6}_{3}/{mmc}\) is a widely studied three-dimensional Dirac semimetal29,30 (see Supplementary Note 2). With spin-orbit coupling (SOC), the low-energy states form massless Dirac fermions along the \(\Gamma -{\rm{{\rm A}}}\) line around the Fermi level, as shown in Fig. 3a. The Dirac points are accidental degeneracy protected by the C3 rotational symmetry. By adopting the Na-3s and Bi-6p states around Fermi energy, we construct a tight-binding model Hamiltonian \({H}_{{TB}}\) with Wannier orbitals36,37 and add a Zeeman term shown as follows:

$$H={H}_{{TB}}+{{\rm{g}}}_{{\rm{e}}}{\boldsymbol{\mu }}\cdot {\bf{B}},$$
(5)

where \({{\rm{g}}}_{{\rm{e}}}\), \({\boldsymbol{\mu }}\) and \({\bf{B}}\) are effective g-factor, magnetic moment and magnetic field, respectively. Figure 3b shows the band structure under a Zeeman field of 23 meV along the \(z\) axis. The broken time-reversal symmetry split the two-fold degenerate bands along the \(\Gamma -A\) line, while the branch with a lower Fermi velocity underwent a larger split than the steeper branches.

Fig. 3: Electronic structures and transport properties of Na3Bi under Zeeman field.
figure 3

a Crystal structure and band structure of Na3Bi with the Dirac points appearing along the \(\Gamma -A\) line. The c axis is set to the z axis. b Band structure of Na3Bi under a Zeeman field of 23 meV. c AHC and d ANC of Na3Bi under a Zeeman field with respect to the chemical potential.

Full size image

Due to the absence of time-reversal symmetry, the AHC (\({\sigma }_{{xy}}\)) of Na3Bi under a magnetic field shows a single maximum peak (~37 \({{\Omega }^{-1}{\rm{cm}}}^{-1}\)) near the Fermi level (see Fig. 3c), which is similar to the tilted Weyl model in Fig. 1b. This is because the band splitting between the two branches is very asymmetric (see inset of Fig. 3b). As a result, the corresponding ANC of \({\alpha }_{{xy}}\) exhibits two opposite peaks (~0.38 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\)) in the vicinity of the Fermi energy (see Fig. 3d). The curve of \({\alpha }_{{xy}}\) with respect to the chemical potential is approximately equal to the derivative of \({\sigma }_{{xy}}\), in consistent with the Mott relation of Eq. (4). On the other hand, since the Zeeman field here is only along the \(z\) axis, the \({yz}\) and \({zx}\) components of AHC and ANC are almost negligible compared with that of the \({xy}\) components.

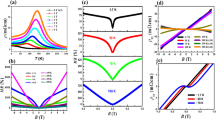
Since the steeper branches forming the Dirac nodes of Na3Bi hardly split under a Zeeman field, the feature of the double-peak AHC does not emerge. We next consider a ternary Dirac semimetal NaTeAu, which crystalizes in the honeycomb lattice with \(P{6}_{3}/{mmc}\) space group31,32 (see Supplementary Note 3). Te and Au atoms construct a honeycomb lattice positioned on the A and B sites, respectively; Na atoms form a triangular lattice, stacking alternately with the honeycomb lattice along the c direction. Figure 4a shows the Dirac nodes of NaTeAu locating along the \(\Gamma -A\) line, protected by \({C}_{3}\) rotational symmetry. By adopting the Na-3s Te-5s, 5p and Au-5d, 6s states around Fermi energy, we construct an effective Hamiltonian for NaTeAu with a Zeeman term as shown in Eq. (5). Figure 4b shows the band structure under a Zeeman field of 29 meV along the \(z\) axis, exhibiting a symmetric band splitting for the two branches and the “G-type” arrangement of two pairs of Weyl points (one pair is shown in the inset of Fig. 4b).

Fig. 4: Electronic structures and transport properties of NaTeAu under Zeeman field.
figure 4

a Crystal structure and band structure of NaTeAu with the Dirac points appearing along the \(\Gamma -A\) line. The c axis is set to the z axis. b Band structure of NaTeAu under a Zeeman field of 29 meV. c AHC and d ANC of NaTeAu under a Zeeman field with respect to the chemical potential. e AHC and f ANC of intrinsic ferromagnetic topological material NaFeTe2Au2 with respect to the chemical potential.

Full size image

Owing to the spin-split Dirac band structure, the AHC (\({\sigma }_{{xy}}\)) of NaTeAu shows two peaks with opposite sign at E = 0.01 eV and E = 0.13 eV, leading to a sharp slope near the Fermi level (see Fig. 4c). The maximum value of \({\sigma }_{{xy}}\) is about 81 \({{\Omega }^{-1}{\rm{cm}}}^{-1}\). Accordingly, the ANC curve of \({\alpha }_{{xy}}\) exhibits one peak ~1.3 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\) at E = 0.07 eV (see Fig. 4d), consistent with the feature of our four-band Dirac model. On the other hand, the \({yz}\) and \({zx}\) components of AHC and ANC are almost zero compared with that of the \({xy}\) components, given that the Zeeman field is along the \(z\) axis. Assuming an effective g-factor of 20, for Na3Bi (NaTeAu) with a Zeeman splitting 23 meV (29 meV), the magnetic field is estimated as 20 T (25 T), respectively. We note that in Na3Bi and NaTeAu, the transverse Nernst conductivity, dubbed ANE here, is driven by the Berry curvature effect, where the presence of an external magnetic field is to induce Zeeman splitting. This is distinct from the ordinary Nernst effect38,39, where the lateral movement of charge carriers is driven by the Lorentz force from the external magnetic field. At a small magnetic field (i.e., 1 T), the ANCs become non-zero (Supplementary Fig. 6). On the other hand, the optimal temperature of ordinary Nernst effect is usually very low (e.g., 13.5 K for Mg3Bi223), while for ANE it maintains a finite value over a wide temperature range (see Supplementary Fig. 8 for NaTeAu). Therefore, the ANE could be comparable to the ordinary Nernst effect at high temperature.

Besides the external magnetic field, the intrinsic exchange interaction, such as magnetic doping or magnetic proximity effect, can also give rise to Zeeman splitting yet without ordinary Nernst conductivity. By substituting 50% Na by Fe in NaTeAu, we design an intrinsic magnetic topological material NaFeTe2Au2 (Supplementary Fig. 9). The Fe ions form a ferromagnetic structure, providing intrinsic Zeeman splitting. As expected, its AHC curve shows a “double-peak” feature with respect to the chemical potential with a maximum value of ANC (\(3.7\,{\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\)) at the Fermi level, as shown in Fig. 4e, f. Additionally, we artificially designed a full Heusler ferromagnetic material Co2PdGe (Supplementary Fig. 10), which also exhibits a large ANC around the Fermi level (\(\sim 6.2 \,{\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\) at \({E}_{\rm{f}}=0.16\,{\rm{eV}}\)) (Supplementary Fig. 7).

Discussion

In summary, we illustrate that enhanced ANC pinning at the Fermi level can be treated as an electronic-structure design problem. Starting from a model Hamiltonian, we elucidate that Dirac semimetals under a Zeeman field exhibit a double-peak AHC feature and compensated carriers experiencing the Berry curvature of the same sign, leading to about 300% enhanced ANC pinning at Fermi level compared to an ideal Weyl semimetal. For realistic material candidates, we find that the classic Dirac semimetal Na3Bi with a Zeeman field manifests two symmetric peaks around the Fermi level, with a maximum ANC value of about 0.38 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\). We then predicted that Dirac semimetal NaTeAu exhibits the required double-peak AHC feature, leading to a maximum ANC peak of about 1.3 \({\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\) near the Fermi level. To demonstrate our approach, we also artificially design two intrinsic ferromagnetic topological materials NaFeTe2Au2 and Co2PdGe, exhibiting maximum ANC values of \(3.7\,{\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\) and \(6.2\,{\rm{A}}{{\rm{m}}}^{-1}{{\rm{K}}}^{-1}\), respectively, in the vicinity of the Fermi level. Our work provides a design guideline and a protype band structure with enhanced ANC pinning at the Fermi level. This will promote the search of large ANC system and the inverse design of other specific functional materials based on electronic structure.

Methods

Calculation of AHC and ANC for anomalous transport properties

The anomalous Hall conductivity (AHC) \(\sigma\), evaluated via the Kubo formula, is formulated as:

$${\sigma }_{{ij}}=\frac{{{\rm{e}}}^{2}}{{{\hslash }}}\sum _{n}\int \frac{{d}^{3}k}{{(2{{\pi }})}^{3}}{\Omega }_{{ij}}^{n}{f}_{n},$$
(6)

where \({ij}\), \(n\), \(\Omega\), and \(f\) are direction indicator, band index, Berry curvature and Fermi-Dirac distribution function, respectively. The anomalous Nernst conductivity (ANC) proposed by Xiao et al.9,10 can be obtained by substituting the Fermi-Dirac distribution function \(f\) by a Gaussian-like function \(w\), that is:

$${\alpha }_{{ij}}=\frac{{{\rm{e}}}^{2}}{{{\hslash }}}\sum _{n}\int \frac{{d}^{3}k}{{(2{{\pi }})}^{3}}{\Omega }_{{ij}}^{n}{w}_{n}.$$
(7)

Here \(w\) is a function of the temperature \(T\):

$${w}_{n}=-\frac{1}{{\rm{e}}T}\left[\left({\varepsilon }_{n}-\mu \right){f}_{n}+{k}_{B}T\mathrm{ln}\left(1+\exp \frac{{\varepsilon }_{n}-\mu }{-{k}_{B}T}\right)\right],$$
(8)

where \({\varepsilon }_{n}\) and \(\mu\) are the energy of \(n\)-th band and the chemical potential, respectively. Comparing the Fermi-Dirac distribution function \(f\) and Gaussian-like function \(w\) with respect to the chemical potential \(\mu\), the Gaussian-like function \(w\) is approximate the derivative of the Fermi-Dirac distribution (see Supplementary Fig. 1). At low temperature, this intrinsic relation explicitly reduces to

$${\alpha }_{{ij}}=\frac{{{\rm{\pi }}}^{2}}{3}\frac{{k}_{B}^{2}T}{{\rm{e}}}{\sigma }_{{ij}}^{{\prime} }\left({{\rm{\varepsilon }}}_{{\rm{F}}}\right),$$
(9)

which is known as the Mott relation4,24. That is to say that the extreme value of ANC \(\alpha\) occurs at the maximum slope of AHC \(\sigma\). And a band structure with opposite AHCs on either side of the Fermi level \({{\rm{\varepsilon }}}_{{\rm{F}}}\) is expected. At a relative high temperature, such a guide rule to obtain large ANC \(\alpha\) is also applicable, although the position of the maximum ANC \(\alpha\) will slightly shift.

The Berry curvature \(\Omega\) adopted in Eq. (1) and Eq. (2) is evaluated via the Kubo formula10,40:

$${\Omega }_{{ij}}^{n}=i\sum _{m\ne n}\frac{\left\langle n\Big|\frac{\partial H}{\partial {k}_{i}}\Big|m\right\rangle \left\langle m\Big|\frac{\partial H}{\partial {k}_{j}}\Big|n\right\rangle -(i\leftrightarrow j)}{{({E}_{n}-{E}_{m})}^{2}},$$
(10)

where \({|n} >\) and \({E}_{n}\) are the eigenvector and eigenvalue of the H. The Berry curvature acts as the magnetic field in the momentum space, deflecting the carrier transverse to the temperature gradient. The Berry curvature will diverge at the band crossing point, i.e.,\({E}_{n}={E}_{m}\), what is the Weyl point or nodal line in topological semimetals. In the next section, we will introduce how to construct an efficient Weyl configuration to enhance the ANE.

First-principles DFT calculations

Electronic structure calculations for real materials were based on the density-functional theory (DFT)41 implemented in the Vienna ab initio simulation package (VASP)42,43, where the exchange-correlation potential was treated by generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) functional44 and the ionic potential was based on the projector augmented wave (PAW) method45,46. Owing to the strong relativistic effect in Bi, Te and Au, spin-orbit coupling (SOC) was also considered for the energy band dispersion calculations. The tight-binding model Hamiltonian adapted for the Wannier interpolation of AHC calculations implemented in the WannierTools package36,37 (i.e., electrical conductivity calculation) was constructed by the Wannier90 software47 using the maximally localized Wannier function approach48,49,50. For ANC calculations, a subroutine was added to WannierTools package by substituting the Fermi-Dirac function\(\,f\) in Eq. (1) by the \(w\) function of Eq. (3). The s orbits of Na, s, p orbits of Bi and Te, and s, d orbits of Au were selected as the initial projectors for Wannier90 software.