Introduction

Electric and strain field effects are highly important ingredients in the tight control of solid-state spin defects for quantum technology applications. The accurate knowledge of the couplings to these perturbations can be harnessed either actively, e.g., for tuning the magneto-optical properties of the defect, or passively, e.g., for sensing its close environment. Particular attention is currently given to spin defects embedded in two-dimensional (2D) van der Waals materials1,2,3,4. The main advantage of a 2D host is the proximity of the quantum defect to the surface, which improves both its optical efficiency5 and sensing capabilities4. One of these 2D materials is hexagonal boron nitride (hBN), which can be exfoliated down to the mono-layer limit without compromising its chemical stability6,7. Owing to its large optical band gap (~6.0 eV8), hBN hosts optically-active point defects in a wide range of wavelengths. Once isolated at the individual scale, defects in hBN were first studied as single-photon emitters, providing narrow and tunable emission lines, high brightness, and perfect photostability9,10,11,12,13,14,15,16,17. In addition, it was recently shown that the electron spin resonance frequencies of some defects can be inferred through optically detected magnetic resonance (ODMR) methods, providing a central resource for quantum sensing applications18,19,20,21,22,23,24.

To date, the negatively-charged boron-vacancy centre (\({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\)) is the only point defect in hBN possessing an ODMR response whose microscopic structure has been unambiguously identified24,25,26,27. This defect, which can be readily created by irradiation, ion-implantation and laser writing techniques28,29,30,31,32, has been recently employed for sensing magnetic fields33,34,35,36,37, strain38,39, and temperature33,37,40. In this context, the purpose of the present work is to provide an accurate description of the coupling of \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centres in hBN to strain and electric fields.

Under optical illumination, the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre exhibits a very broad emission in the near-infrared24. Although an experimental work has reported a zero-phonon-line (ZPL) at 773 nm41, a recent theoretical study has claimed that the full emission is phonon-assisted since optical transitions between electronic states are forbidden42. As a consequence, the optical emission is intrinsically dim and only dense ensembles of \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centres could be detected in experiments so far. Theory further identified that the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre has a spin triplet ground state (S = 1) with D3h symmetry26. In the absence of external perturbations, the ground state spin Hamiltonian only involves spin-spin interaction and reads as

$${\hat{H}}_{{{\mbox{SS}}}}=D\left({\hat{S}}_{z}^{2}-\frac{S\left(S+1\right)}{3}\right).$$
(1)

The axial zero-field-splitting (ZFS) parameter D separates the mS = 0 and mS = ± 1 spin sublevels, the notation mS referring to the spin projection along the c axis (z) of the hBN crystal. Interestingly, ODMR spectra recorded on ensembles of \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centres usually indicate two magnetic resonances at frequencies D ± E, with D ~ 3.47 GHz and E ~ 50 MHz24. These measurements thus reveal an additional orthorhombic splitting (E) of the mS = ± 1 levels, which is in contradiction with the D3h symmetry of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre. While this splitting was originally attributed to strain effects in the hBN crystal leading to a reduced symmetry of the defect24,31, a recent study suggested that it results instead from the interaction with a local electric field43. However, no microscopic picture has been applied to interpret these results. More generally, there is an urgent need to understand the coupling of strain and electric fields to \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) defect spins, which is an exemplary quantum sensor in a van der Waals material.

In this paper, we employ first-principles simulations to determine the effect of external electric and strain fields on the ground state electronic spin structure of \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centres in hBN. We show that in most of the experimental conditions the defect experiences fluctuating electric fields that leads to an orthorhombic splitting in ODMR spectra recorded at zero external magnetic field. We identify the microscopic origin of this effect and determine the spin-strain and spin-electric field coupling parameters. We then compare these results to experimental ODMR spectra recorded from neutron-irradiated hBN crystals containing different densities of \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centres. Our study proves that the orthorhombic ZFS is caused by fluctuating electric fields and suggest that the coupling strengths of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centres to strain and electric fields are comparable to those of the nitrogen-vacancy (NV−) centre in diamond44,45.

Results

Defect structure and spin-spin interaction

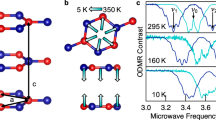
The \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre in hBN is a single vacancy at the boron site in the negatively-charged state possessing D3h point symmetry (Fig. 1a). In the following, the spin properties of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre are calculated using a large hydrogen-terminated mono-layer flake model (see Methods). The coordinate frame is defined as {x, y} span the plane of the hBN layer, with x and y along the zigzag and armchair directions of the hexagonal lattice, respectively. The Kohn–Sham levels in the spin-polarised calculations are plotted in Fig. 1b, showing nearby double-degenerate \({e}^{{\prime} }\) and e″ levels and non-degenerate \({a}_{1}^{{\prime} }\) and \({a}_{2}^{{\prime\prime} }\) levels leaving two holes in the \({e}^{{\prime} }\) orbital of the spin minority spin channel. This constitutes the \({}^{3}{A}_{2}^{{\prime} }\) spin triplet ground state of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre, in agreement with previous calculations25,26,46. Importantly, the spin density is dominantly localised in-plane on the three dangling bonds of the neighbouring nitrogen atoms (Fig. 1a), as recently confirmed experimentally by pulsed electron-nuclear double resonance techniques47.

Fig. 1: Geometry and electronic structure of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre in hBN.
figure 1

a Visualisation of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre and its ground state electronic spin density (yellow) in the mono-layer flake model used in the calculations. Green, blue, and white balls represent boron, nitrogen and hydrogen atoms, respectively. b Kohn–Sham level structure of the defect calculated with PBE0 functional. The orbitals are labelled according to the irreducible representations in D3h point group symmetry. The subspace of occupied orbitals is indicated in the figure. As these lie close to each other, their labels are ordered in ascending energy from bottom to top. The spin density of the triplet ground state originates from the unoccupied double-degenerate \({e}^{{\prime} }\) orbital.

Full size image

Starting with an unperturbed D3h symmetry, the mono-layer flake model leads to an axial ZFS parameter D = 3263 MHz [see Eq. (1)], a value in fair agreement with the experimental results D ≈ 3470 MHz. In Supplementary Note 1, we show that the mono-layer flake model well represents the bulk environment around the defect because the spin density is fully localised into the hBN plane. Although there is ~6% discrepancy in the absolute value of the D parameters obtained from our theoretical approach and the experimental data, the accuracy in the variation of the zero-field-splitting parameters upon external perturbations can be reliably obtained thanks to the cancellation of numerical errors in partial derivatives.

In the next sections, we compute the coupling coefficients of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre to strain and electric fields. We assume that the strengths of these fields are much smaller than the Coulomb interaction between the electrons, so that strain and electric fields can be considered as perturbations. We analyse how these interactions can lead to an orthorhombic ZFS parameter, that splits the mS = ± 1 levels upon axial symmetry breaking.

Strain field interaction

We start the analysis of external perturbations with the strain field case. We construct the interaction Hamiltonian analogously to previous calculations performed on the NV− centre in diamond featuring C3v symmetry48. In the linear approximation, the bi-linear forms of the second rank tensor of the external strain are connected to the bi-linear forms of the \(\hat{S}\circ \hat{S}\) second rank tensor by scalar coupling coefficients g. We write the interaction in a symmetry-adapted form to retain only the linearly independent couplings, i.e., we construct the irreducible representation basis in D3h symmetry from the components of the strain and spin tensors. These transform as quadratic spatial coordinates, e.g., zz and xx + yy both belong to the totally symmetric \({A}_{1}^{{\prime} }\) irreducible representation. The interaction Hamiltonian is totally symmetric, thus only the products of the same irreducible representations of the strain and spin are valid combinations.

According to the theory of invariants, the Hamiltonian describing the interaction of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre with strain can be formulated as

$$\begin{array}{lll}{\hat{H}}_{{{\mbox{strain}}}}\,=\,\left({\varepsilon }_{xx}+{\varepsilon }_{yy}\right){g}_{1}{\hat{S}}_{z}^{2}\\ \qquad\qquad\quad+\left({\varepsilon }_{xx}-{\varepsilon }_{yy}\right)\left[{g}_{2}\left({\hat{S}}_{x}^{2}-{\hat{S}}_{y}^{2}\right)+{g}_{2}^{{\prime} }\left({\hat{S}}_{x}{\hat{S}}_{y}+{\hat{S}}_{y}{\hat{S}}_{x}\right)\right]\\ \qquad\qquad\quad+\left({\varepsilon }_{xy}+{\varepsilon }_{yx}\right)\left[{g}_{3}\left({\hat{S}}_{x}^{2}-{\hat{S}}_{y}^{2}\right)+{g}_{3}^{{\prime} }\left({\hat{S}}_{x}{\hat{S}}_{y}+{\hat{S}}_{y}{\hat{S}}_{x}\right)\right]\end{array}$$

where gi are the coupling coefficients between ε bi-linear forms of the strain matrix elements and \(\hat{S}\) bi-linear forms of the spin projection operators reflecting a symmetry-adapted form of \({A}_{1}^{{\prime} }\times {A}_{1}^{{\prime} }+{E}^{{\prime} }\times {E}^{{\prime} }\). Note that the out-of-plane strain components {εzx, εy, εzz} are not included in the Hamiltonian because we consider a single-layer flake model. However, these couplings are expected to be minor for a bulk model as well since out-of-plane (z) distortions have a small impact on the in-plane hBN structure that contains the spin density of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre (see Supplementary Note 2).

To calculate the coupling coefficients gi, we specify uniform strain of a single element in the strain tensor in each calculation and apply it to our model (see Methods). We do so for each symmetrically non-equivalent components in Eq. strain, i.e., for εxx and εxy. We then calculate the resulting axial and orthorhombic ZFS parameters (see red data in Fig. 2a, b and Supplementary Fig. 3) and obtain the coupling coefficients gi as the partial derivatives

$$\begin{array}{lll}{g}_{1}\,=\,\frac{\partial D}{\partial {\varepsilon }_{xx}}=(-19.2\pm 0.2)\,\frac{{{{\rm{GHz}}}}}{{{{\rm{strain}}}}},\\ {g}_{2}\,=\,\frac{\partial ({D}_{xx}-{D}_{yy})/2}{\partial {\varepsilon }_{xx}}=(2.6\pm 0.8)\,\frac{{{{\rm{GHz}}}}}{{{{\rm{strain}}}}},\\ {g}_{2}^{{\prime} }\,=\,\frac{\partial ({D}_{xy}+{D}_{yx})/2}{\partial {\varepsilon }_{xx}}=0,\\ {g}_{3}\,=\,\frac{\partial ({D}_{xx}-{D}_{yy})/2}{\partial {\varepsilon }_{xy}}\approx 0,\\ {g}_{3}^{{\prime} }\,=\,\frac{\partial ({D}_{xy}+{D}_{yx})/2}{\partial {\varepsilon }_{xy}}=(5.8\pm 0.1)\,\frac{{{{\rm{GHz}}}}}{{{{\rm{strain}}}}},\end{array}$$

where Dij are components of the ZFS D-matrix defined by alternate form of the interaction \(\hat{H}=\hat{{{{\bf{S}}}}}{{{\bf{D}}}}\hat{{{{\bf{S}}}}}\). The negative sign of g1 implies a larger (smaller) axial ZFS parameter D = 3Dzz/2 for compressive (tensile) external strain, in line with the decrease (increase) of the distance between the localised spin density lobes. We note that coupling coefficient pairs of \({E}^{{\prime} }\) symmetry correspond to the two basis functions spanning the two-dimensional irreducible representation. As such, these can be arbitrarily transformed by a rotation in the subspace. The zero values of \({g}_{2}^{{\prime} }\) and g3 are a consequence of our choice of reference aligned with one of the dangling bonds.

Fig. 2: Response to an external strain component εxx.
figure 2

a Axial ZFS parameter D as a function of the external strain. b Orthorhombic ZFS parameter E as a function of the external strain. The cases of fixed and relaxed atomic positions are compared (blue and red points), as explained in the main text. c Local strain response for the externally applied strain. Blue dots show the one-to-one correspondence when the atomic positions are not allowed to relax. Red and green points show the enhanced local εxx strain and the activated local εyy strain around the defect, respectively, when its close vicinity is allowed to relax under the strain applied to the crystal.

Full size image

We now analyse how the microscopic structure of the defect affects the response to the strain. To this end, we carried out calculations for which we strained the lattice of the defective model without allowing any local ionic relaxation around the defect and then calculated the change in the ZFS parameters (blue points in Fig. 2a, b). After allowing local relaxation under the externally applied strain (red points in Fig. 2a, b), we can define the local geometry changes in the close vicinity of the defect. The local strain is defined from the deformation of the triangle spanned by the three neighbouring nitrogen atom positions. We plot this local strain as a function of the external εxx strain in Fig. 2c. We identify a large increase in the same component (εxx) of the local strain after relaxation. Moreover, an additional εyy component is also activated. We attribute this effect to the smaller local stiffness at the vacancy site originating from the broken bonds. During the relaxation of the defect under external strain, it is energetically favourable for the vacancy site to accommodate an increased strain compared to the externally applied one, thus lowering the strain enthalpy of the host material in its vicinity. Generally, the same strain enhancement is expected in defects with dangling or weaker bonds than the ones in its host material, making this type of qubits more sensitive strain sensors. The increased local strain after relaxation reflects in the increase of the ZFS strain coupling strength as well. Note that relaxation under external sheer strain (εxy) shows a similar trend in the ZFS coupling strength.

Finally, we convert the strain-spin coupling strengths to stress couplings, as stress is usually more accessible and controllable in experiments than strain. Based on the experimentally available elastic parameters of C11 = 811 GPa and C12 = 168 GPa in bulk hBN49, we calculate the hi stress coupling coefficients as:

$$\begin{array}{rcl}{h}_{1}&=&\frac{{g}_{1}}{{C}_{11}+{C}_{12}}=(-19.6\pm 0.2)\,\frac{{{{\rm{MHz}}}}}{{{{\rm{GPa}}}}}\\ {h}_{2}&=&\frac{{g}_{2}}{{C}_{11}-{C}_{12}}=(4.04\pm 1.2)\,\frac{{{{\rm{MHz}}}}}{{{{\rm{GPa}}}}},\end{array}$$

where Cij elements are the second-order elastic constants (stiffness tensor) in the Voigt notation. The relation between the strain (ε) and stress (σ) can be then formulated in linear elasticity as

$$\left(\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\end{array}\right)=\left(\begin{array}{cc}{C}_{11}&{C}_{12}\\ {C}_{12}&{C}_{11}\end{array}\right)\left(\begin{array}{c}{\varepsilon }_{xx}\\ {\varepsilon }_{yy}\end{array}\right).$$
(2)

With the above conversion, the Hamiltonian takes a similar form to Eq. strain using the stress coupling coefficients

$$\begin{array}{lll}{\hat{H}}_{{{\mbox{stress}}}}\,=\,{h}_{1}\left({\sigma }_{xx}+{\sigma }_{yy}\right){\hat{S}}_{z}^{2}\\ \qquad\qquad\quad+\,{h}_{2}\left({\sigma }_{xx}-{\sigma }_{yy}\right)\left({\hat{S}}_{x}^{2}-{\hat{S}}_{y}^{2}\right).\end{array}$$

Importantly, our calculations already indicate that ∣h1∣ > ∣h2∣, such that spin-stress coupling mostly leads to variations of the axial ZFS parameter D without inducing a significant orthorhombic splitting.

Electric field interaction

The Hamiltonian of the electric field coupling is constructed analogously to the strain coupling as

$${\hat{H}}_{{{\mbox{elec}}}}={d}_{\perp }\left[{{{{\mathcal{E}}}}}_{y}\left({\hat{S}}_{x}^{2}-{\hat{S}}_{y}^{2}\right)+{{{{\mathcal{E}}}}}_{x}\left({\hat{S}}_{x}{\hat{S}}_{y}+{\hat{S}}_{y}{\hat{S}}_{x}\right)\right]$$
(3)

where d⊥ is the coupling coefficient between \({{{\mathcal{E}}}}\) linear forms of the electric field vector and \(\hat{S}\) bi-linear forms of the spin projection operators reflecting a symmetry-adapted form of \({E}^{{\prime} }\times {E}^{{\prime} }\). We note that the parallel component of the electric field (\({{{{\mathcal{E}}}}}_{z}\)) with respect to the hBN plane normal vector belongs to the \({A}_{2}^{{\prime\prime} }\) irreducible representation, and it cannot couple to either \({A}_{1}^{{\prime} }\) or \({E}^{{\prime} }\) representations of the spin operators. As a result, the interaction with an electric field only introduces an orthorhombic splitting without inducing variations of the axial ZFS parameter D.

We apply homogeneous electric field to the defective hBN model. The coupling coefficient can be calculated as the partial derivative of the ZFS parameter (see Figure 3a)

$${d}_{\perp }=\frac{\partial E}{\partial {{{{\mathcal{E}}}}}_{y}}=(20.72\pm 0.02)\,\frac{{{{\rm{Hz}}}}\,{{{\rm{cm}}}}}{{{{\rm{V}}}}}.$$
(4)

We note that recent experimental work has estimated the coupling strength of the E parameter to the electric field as d⊥ = 35 Hz cm/V43, which is in the same order of magnitude as our first-principle results.

Fig. 3: Response to an external electric field component \({{{{\mathcal{E}}}}}_{y}\).
figure 3

a Orthorhombic ZFS parameter E as a function of the external electric field. The cases of fixed and relaxed atomic positions are compared (blue and red points). b Estimated local strain from the piezo effect induced by the external electric field.

Full size image

We now analyse the geometry relaxation under the applied external electric field similarly as for the case of the strain perturbation discussed above. We can identify an accompanying piezo effect resulting in (εxx − εyy) and (εxy + εyx) additional strains for the applied \({{{{\mathcal{E}}}}}_{y}\) and \({{{{\mathcal{E}}}}}_{x}\) electric fields, respectively. The former calculation is shown in Fig. 3b. This effect enhances the coupling strength to the electric field by a factor of 1.5 (compare blue and red points in Fig. 3a).

The microscopic origin of the piezo enhancement effect can be explained by changes in electrostatic interactions in the vicinity of the defect under the applied external electric field. We obtain a significant change in the partial charge distribution of the strongly polarised bonds around the vacancy defect depending on the relative direction of the external electric field. This implies a redistribution of the electron density by the electric fields, which generates quantum mechanical forces on the ions. The origin of this effect can be detailed in the example of the vacancy-neighbour nitrogen atom in the y direction and its boron neighbours. Without the external electric field applied, the B-N bonds are polarised with an effective dipole moment pointing from N to B. The applied field in the positive (resp. negative) direction increases (resp. decreases) the original charge separation and the effective dipole moment. This results in an additional effective attractive (resp. repulsive) force along the B-N bond and an outward (resp. inward) relaxation of the nitrogen atom relative to the vacancy site. We identify this additional relaxation as the εyy piezo response. Thus, the relaxation of the nitrogen atom is in the same direction as the electric field. This finally enhances the symmetry-breaking effect of the electric field and consequently its coupling to the E parameter.

ODMR simulation

In the experimental ODMR signal of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre, a small orthorhombic E splitting was reported despite its contradiction with the defect symmetry. Recently, the effect was attributed to the local electric field originating from nearby charged defects without providing arguments from microscopic picture of the defect43. Firstly, we simulate the ZFS parameters of a single \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) defects affected by the presence of uniformly distributed random local strain or electric fields of given magnitudes. We sample 1000 random configurations for each given magnitude and visualise the corresponding mS = ± 1 eigenvalues of the ZFS Hamiltonian as a scatter plot as a function of the perturbation magnitude. From the simulations shown in Fig. 4, we conclude that the E splitting can be exclusively attributed to the local electric field, while the effect of strain leads to a broadening of the signal. The sharp splitting originates from the large difference in the magnitudes of the couplings of the D and E parameters to the external fields. We can describe this with the ratio gD/gE of the coupling strengths. In the case of the electric field, the D parameter coupling is symmetry forbidden, gD/gE ≈ 0, leading to a sharp splitting of the magnetic resonances. In the case of the strain field, we calculate gD/gE = 7.38, which leads to a dominating shift in the ODMR signal with broadening of the integrated spectrum. We note that a similar effect was already observed and simulated for the NV− centre in diamond50.

Fig. 4: Simulated ZFS of the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre in random perturbation environments.
figure 4

a ZFS distribution as a function of normal strain magnitude. b ZFS distribution as a function of electric field magnitude.

Full size image

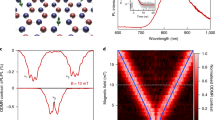
We now use our theoretical predictions to analyse experimental ODMR spectra recorded at zero external magnetic fields. To this end, we rely on three hBN crystals (S1, S2 and S3) with different densities of V\({}_{{{{\rm{B}}}}}^{-}\) centres created by neutron irradiation. Their optical properties are analysed with a confocal microscope operating at room temperature under green laser illumination (see Methods). All crystals exhibit the characteristic emission spectrum of V\({}_{{{{\rm{B}}}}}^{-}\) centres with a broad spectral line in the near-infrared. The relative density of V\({}_{{{{\rm{B}}}}}^{-}\) centres is estimated by recording the evolution of the PL signal with the optical excitation power (Fig. 5a). In the considered power range, the PL signal increases linearly with a slope proportional to the density ρ of V\({}_{{{{\rm{B}}}}}^{-}\) centres. By analysing these data, we obtain ρS2 ~ 4.8 × ρS1 and ρS3 ~ 8.5 × ρS1.

Fig. 5: PL properties and ODMR spectra of hBN crystals with different concentration of \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centres.
figure 5

a PL signal as a function of the optical excitation power for the three hBN crystals (S1, S2, and S3). The dashed lines are linear fit. b ODMR spectra recorded for S1, S2 and S3 crystals from top to bottom. The solid lines are the results of the fitting procedure based on the microscopic charge model described in the main text, from which we extract the charge density ρc. c Charge density ρc as a function of the relative density of V\({}_{{{{\rm{B}}}}}^{-}\) centres in the hBN crystal. The dashed line is a linear fit.

Full size image

The ODMR spectra recorded at zero external magnetic field are shown in Fig. 5b. For the three crystals, we detect the two characteristic magnetic resonances of the V\({}_{{{{\rm{B}}}}}^{-}\) centre with frequencies at D ± E. Importantly, the D parameter is identical for all spectra while the E splitting increases with the density of V\({}_{{{{\rm{B}}}}}^{-}\) centre. To understand these results, we rely on a microscopic charge model originally introduced for NV− defects in diamond50. We consider that negatively-charged V\({}_{{{{\rm{B}}}}}^{-}\) centres are associated with positively-charged defects in order to ensure charge neutrality of the hBN crystal. These charges produce a local electric field that depends on the charge density ρc. The Hamiltonian describing the interaction of a central V\({}_{{{{\rm{B}}}}}^{-}\) centre with this electric field is constructed from Eqs. (1) and (3) using the calculated coupling coefficient d⊥. Moreover, we include the hyperfine splittings from the first neighbour 14N nuclear spins with a coupling strength of 47 MHz26,51. We keep this value fixed in the simulation according to the obtained negligible effect of the external electric field on the hyperfine parameters. We note that the hyperfine constants are, however, sensitive to the strain (see Supplementary Note 4). For the microscopic model of the charge environment, a specific number of elementary point charges are placed at the atomic sites of hBN in a simulation radius of 10 nm, corresponding to an average charge density ρc in the simulation sphere. Their position vectors relative to the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) defect at the origin of the sphere are sampled randomly from the standard normal distribution. The resulting total electric field at the origin is supplied to the Hamiltonian as an effective external electric field. The obtained spectrum is collected for 104 different random charge configurations. We then optimise the charge density and the ODMR contrast to fit to the experimental spectra.

As shown in Fig. 5b, all ODMR spectra are well fitted by this microscopic charge model, leading to charge densities ρc,S1 = 0.018(3) nm−3, ρc,S2 = 0.046(4) nm−3 and ρc,S3 = 0.141(8) nm−3. These results indicate that the density of charges increases linearly with the density of V\({}_{{{{\rm{B}}}}}^{-}\) centres in the hBN crystal (Fig. 5c), as expected from the microscopic charge model.

Discussion

We calculated the coupling strengths of the ZFS parameters to the symmetry-adapted components of strain and electric fields for the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) defect in 2D hBN from first principles. In order to place these values in a broader context, we briefly compare them to those of the popular NV− defect in diamond. The calculated and experimental values of the stress coupling on the axial ZFS parameter of the NV− centre is −5.17 MHz/GPa48 and −4.4 MHz/GPa44, respectively. These values are weaker than that obtained for the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre h1 = −19.6 MHz/GPa. On the other hand, the experimental perpendicular electric field coupling d⊥ was reported to be 17 Hz cm/V for NV− centres45, which is close to the result of our calculation of ~21 Hz cm/V for the \({\,{{\mbox{V}}}}_{{{\mbox{B}}}\,}^{-}\) centre in hBN.

For the strain perturbation, the coupling to the axial ZFS parameter D dominates, while it is forbidden by symmetry for electric field perturbations. Consequently, we identify the electric field perturbation as the source of the symmetry-breaking orthorhombic E splitting in the ODMR experiments. Our numerical simulations based on the calculated couplings can accurately model the experimental ODMR signal in the presence of electric field perturbations originating from point charges in the lattice sites of the bulk hBN host. Furthermore, we identify a correlation in the defect density created by neutron irradiation with the simulated density of point charges and ultimately with the effective E splitting in the ODMR signal.

Moreover, our DFT calculations reveal a local enhancement effect in the coupling strengths for both strain and electric fields. The former is specific to the vacancy nature of the defect. The latter is attributed to the local piezo effect, i.e., an accompanying strain response under the external electric field effect. In other words, the local piezo effect strengthens the response of the ZFS to the external electric field which is a significant effect of about 50%. We note that this effect goes to the opposite of one 3D qubit system, the divacancy qubit in 4H silicon carbide52. In that case, the local piezo effect rather generates such quantum mechanical forces on the ions that compensate for the effect of the external electric field and reduce the spin-electric field coupling by ~10%.

In summary, the spin-strain and spin-electric field couplings of V\({}_{{{{\rm{B}}}}}^{-}\) centre in hBN were determined. We proved that fluctuating electric fields around the V\({}_{{{{\rm{B}}}}}^{-}\) spins are at the origin of the orthorhombic splitting commonly observed in ODMR spectra of ensembles V\({}_{{{{\rm{B}}}}}^{-}\) centres at zero external magnetic field. We showed that the piezo effect is strong in the spin-electric field coupling parameters, which may be generalised for other vacancy-type defects in hBN. This work might guide future applications of V\({}_{{{{\rm{B}}}}}^{-}\) centres in hBN, such as quantum sensing under high pressure and electrometry.

Methods

Density functional theory calculations

The nano-flake model used in the calculation is a hydrogen-terminated hBN mono-layer of up-to-the fourth hexagon neighbours around the boron-vacancy defect, consisting of 147 atoms in total. Its electronic structure was calculated by density functional theory (DFT) using the PBE0 functional53 and split valence polarisation Karlsruhe basis set (def2-SVP)54, as implemented in the ORCA code55. The spin-spin ZFS tensor is calculated using the restricted spin density obtained from the singly occupied unrestricted natural orbitals56. During the relaxation of the defect structure under external strain applied, the outshell hBN hexagons were fixed in the atomic positions that are associated the strain environment acting on the inner part of the model.

Numerical simulations

ZFS simulation of the defect under external strain and electric field perturbations is calculated in a home-built Python code. We iterate over the magnitude of the perturbation in 1000 steps for the simulation range. In each iteration, we adaptively sample (scaled by the magnitude) the random configurations of effective perturbation vectors ε = (εxx, εyy) and \({{{\mathcal{E}}}}=({{{{\mathcal{E}}}}}_{x},{{{{\mathcal{E}}}}}_{y})\) for the normal strain and electric fields, respectively. The component are sampled from uniform random distribution and the vector is normalised. In the ODMR simulation, we sample a uniform random distribution of positions inside a sphere, representing parasitic charged defects around the target boron-vacancy defect. To this end, we sample the elements of the position vector from standard normal distribution and multiply with \(d=r\root 3 \of {x}\) random distance, where x is sampled from a uniform random normalised distribution and r is the simulation sphere radius. Then we define an underlying lattice of bulk hBN and project the positions to the nearest lattice sites. We optimise two parameters, the charge density and the ODMR contrast, to fit to the experimental spectrum. The optimisation is done by the least squares method using parallelised brute force method on a two-dimensional parameter grid refined in three consecutive optimisation cycles.

hBN crystals

The three hBN crystals used in this work were synthesised through the metal flux growth method described in ref. 57, and irradiated at the Ohio State University Research Reactor, which produces a thermal neutron flux of 1012 cm−2 s−1. The crystal S1 is isotopically purified with 11B (99.4%) and was irradiated with a neutron dose of 2.6 × 1017 cm−2. The two other crystals, S2 and S3, are purified with 10B (99.2%) and irradiated with a dose of 2.6 × 1016 cm−2 and 2.6 × 1017 cm−2, respectively. Neutron irradiation creates V\({}_{{{{\rm{B}}}}}^{-}\) centres (i) through damages induced by neutron scattering across the crystal and (ii) via neutron absorption leading to nuclear transmutation doping. The latter process strongly depends on the isotopic content of the hBN crystal since the neutron capture cross-section of 10B is orders of magnitude larger than that of 11B. As a result, neutron irradiation creates more efficiently V\({}_{{{{\rm{B}}}}}^{-}\) centres in hBN crystals isotopically enriched with 10B.

Experimental details

The optical properties of hBN crystals are studied with a confocal microscope operating at ambient conditions. A laser excitation at 532 nm is focused onto the sample with a high numerical aperture microscope objective (NA = 0.95). The PL signal is collected by the same objective and directed to a silicon avalanche photodiode operating in the single-photon counting regime. ODMR spectra are recorded by monitoring the PL signal while sweeping the frequency of a microwave field applied through a copper microwire deposited on the hBN crystal surface.