Introduction

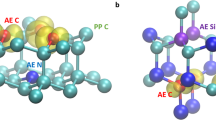
Defects in solid-state semiconductors often introduce additional electronic states with energy lower than the band-gap, leading to color centers. Tens of different color centers are known for only diamond1 and Silicon Carbide2 and their presence often enriches the original material’s optical and magnetic properties, enabling interesting applications in the fields of sensing, photonics, and more. In particular, the negative nitrogen-vacancy (NV−) center in diamond, represented in Fig. 1, consists of a spin-1 system, with spin density localized at the defect site. NV− centers hold a special role in the quantum technology ecosystem thanks to some ideal properties, including long relaxation and coherence times (T1 and T2, respectively) at ambient temperature3,4, chemical and mechanical robustness5, and the possibility to optically address and initialize the spin states6,7. NV− centers have thus found immediate application in quantum technologies, going from sensing5,8,9 to quantum communications10. On the verge of NV− success, other materials with similar properties have been individuated leading to a fast-growing family of solid-state spin qubits11. This includes negative boron vacancies in hexagonal boron-nitride (\(\mathop{\rm{V}}\nolimits_{\rm{B}}^{-}\)), reported in Fig. 1, which has emerged as a promising 2D-material-based qubit with an optimal spin-optical interface and mechanical properties12,13,14.

Fig. 1: Defects’ Structure.
figure 1

Left panel: The structure of the defects NV− in the unit cell of the diamond. Right panel: the structure of \({\rm{V}}_{{{{\rm{B}}}}}^{-}1\) embedded on a 6x6 supercell of h-BN. Carbon atoms are ported in grey, nitrogen atoms in blue, and boron atoms in pink. The vacancy is highlighted by the presence of a fictitious yellow atom.

Full size image

Spin coherence is key for any quantum application and ultimately sets the limit of sensing accuracy or computation fidelity. Despite its central role in the physics of paramagnetic defects, the contribution of spin-phonon interaction to relaxation and decoherence has not yet been fully understood and experiments are invariably interpreted by means of phenomenological models based on a simplistic Debye picture of phonons11,15. Such a state of affairs effectively prevents the establishment of a rigorous understanding of spin dynamics in solid-state qubits and several outstanding questions are left unanswered. For instance, it is yet not clear which mechanism of spin relaxation is the driving one at non-cryogenic temperatures, with one- (Direct and Orbach) and two-phonon (Raman) mechanisms often interchangeably cited as possible relaxation routes13,16. Moreover, spin-phonon relaxation has been shown to limit spin coherence at ambient temperature, but with significant deviations from the commonly expected limit T2 = 2T14, suggesting that additional vibronic contributions to decoherence might play an important role. Besides the importance of such questions from a fundamental science point of view, the current limits to our understanding of the microscopic processes determining spin coherence in paramagnetic solid-state materials pose serious challenges for their use as quantum sensors, namely one of the main applications for such compounds. In a typical experiment, the information on the spin’s environment is obtained through the study of spin-environment fingerprints present in the spin dynamics17. Such protocol is inherently connected to our ability to build reliable and quantitative models for spin-environment interactions and dynamics, of which spin-phonon coupling and relaxation are topical examples. Last but not least, from a materials science point of view, the lack of robust structure-property relations for these compounds makes the identification of paramagnetic defects with desired properties an outstanding challenge, so far mostly left to serendipity.

Ab initio methods have been applied to the problem of spin relaxation in the context of molecular systems in the last few years18,19,20,21,22,23, leading to insights into the physics of spin systems. On the other hand, only very recent attempts to apply ab initio strategies to solid-state defects are available24,25,26, and a full picture of what is the leading relaxation mechanism at ambient temperature in both 3D and 2D semiconductors, the role of phonons on coherence, and what type of vibrations are responsible for such processes have not yet been fully elucidated. Here we extend the state-of-the-art in this nascent field22,27 to solid-state compounds and obtain a quantitative microscopic picture of spin relaxation and decoherence in NV− and \({{{{\rm{V}}}}}_{\rm{B}}^{-}\). Our results can be exported to the rest of the increasingly large family of S = 1 spin qubits11,28 and have the potential to provide guidance toward the design of materials with optimal features for quantum technologies.

Results

Our computational strategy for the simulation of spin-phonon relaxation and decoherence has two fundamental steps. Fistly, ab initio simulations are used to determine i) the static spin properties of the two defects, ii) spin-phonon coupling coefficients, and iii) phonons’ frequencies and normal modes. All these details are then used to inform open quantum system models, which solution provides the time evolution of the spin states as a function of temperature. Results are presented following the same steps of the computational framework.

Static Spin Interactions

The ground state of both NV− and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\) is well described by a S = 1 Hamiltonian

$${\hat{H}}_{S}=\overrightarrow{{{{\bf{S}}}}}\cdot {{{\bf{D}}}}\cdot \overrightarrow{{{{\bf{S}}}}}+{\mu }_{{{{\rm{B}}}}}\overrightarrow{{{{\bf{S}}}}}\cdot {{{\bf{g}}}}\cdot \overrightarrow{{{{\bf{B}}}}},$$
(1)

where the Bohr’s magneton, μB, and the Lande’s tensor, g, mediate the interaction with the external field \(\overrightarrow{{{{\bf{B}}}}}\), and \(\overrightarrow{{{{\bf{D}}}}}\) is the zero-field splitting matrix. By expressing this Hamiltonian in a reference frame with the z-axis parallel to the defect’s pseudo C3 symmetry axis, the first term of Eq. (1) reduces to \({\hat{H}}_{S}=D{S}_{z}^{2}\), with D = 0.117 cm−1 and D = 0.096 cm−1 as determined experimentally for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\)13 and NV−16, respectively, whereas g closely matches the free electron value for both compounds. The zero-field splitting stabilizes the \({\hat{S}}_{z}\) eigenstate \(\left\vert 0\right\rangle\) with respect to the pair \(\left\vert \pm 1\right\rangle\) by an energy amount of D. Finally, the degeneracy of \(\left\vert \pm 1\right\rangle\) is broken by the Zeeman interaction (see Supplementary Figure 7). Density functional theory (DFT) applied to a small cluster of atoms around the defect (see Methods and Supplementary Figure 1) predicts D = 0.118 cm−1 and D = 0.092 cm−1 for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\), and NV−, respectively, nicely reproducing these experimental values. As illustrated in Supplementary Tables 1 and 2, these quantities are well converged with respect to the size of the cluster used to approximate the crystalline environment of the defects. This approach is used to describe the defects’ spin properties throughout this work.

Spin-phonon coupling

The interaction between the defect’s spin and the phonons is modeled by the spin-phonon Hamiltonian22

$${\hat{H}}_{{{{\rm{S-Ph}}}}}=\mathop{\sum}\limits_{\alpha }\left(\frac{\partial {\hat{H}}_{S}}{\partial {q}_{\alpha }}\right){q}_{\alpha }+\frac{1}{2}\mathop{\sum}\limits_{\alpha ,\beta }\left(\frac{{\partial }^{2}{\hat{H}}_{S}}{\partial {q}_{\alpha }\partial {q}_{\beta }}\right){q}_{\alpha }{q}_{\beta },$$
(2)

where we assume the phonons qα to be quantum harmonic oscillators of frequency ωα/2π. Here we consider the modulation of the zero-field splitting D as the source of spin-phonon coupling and numerically compute its first and second-order derivatives. In order to reduce the computational overheads associated with a second-order numerical differentiation, we trained a neural network on a set of D values computed with DFT over 1600 random distortions of the considered cluster20,29. The neural network is tested over 400 residual distortions not used during the training and shows a remarkable ability to predict the values of D for unseen geometries with a root-mean-squared error of only 1.8 × 10−4 cm−1 for NV− and 2.6 × 10−4 cm−1 for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\), see Supplementary Figures 9–11. The net is then used to perform a 6- and 36-point numerical differentiation of D for first- and second-order, respectively. Differentiation is carried out with respect to atomic Cartesian coordinates and then mapped to the representation of normal modes by means of Eqs. (13) and (14), as detailed in the Methods section. Convergence of results with respect to the size of the cluster is confirmed also in the case of spin-phonon coupling. As shown in Supplementary Figure 2, only the atoms closest to the defect are in fact contributing to spin-phonon coupling.

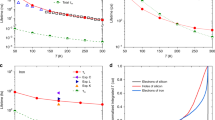
Phonons, computed with periodic DFT as described in the Methods section, are studied to extract the vibrational density of states, shown in Fig. 2. In order to individuate the coupling strength of each phonon we studied the function

$$V(\omega )=\mathop{\sum}\limits_{\alpha }\mathop{\sum }\limits_{ij}^{3}{\left(\frac{\partial {D}_{ij}}{\partial {q}_{\alpha }}\right)}^{2}\delta (\omega -{\omega }_{\alpha }).$$
(3)

V(ω) is plotted in Fig. 2, together the phonon density of states, and shows that strongly coupled vibrations are present over the entire spectrum. A visual inspection of the strongly coupled modes for NV− (mode M1 and M2 at ~350 cm−1 and ~500 cm−1 in Fig. 2a) shows that spin-phonon coupling is promoted by either compressive waves of diamonds (Fig. 2c) and distortions localized at the defect site (Fig. 2d). Similarly, the analysis of modes for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\) (modes M3 and M4 at ~20 cm−1 and ~75 cm−1 in Fig. 2b) shows that spin-phonon coupling is effectively originated by both long-wavelengths out-of-plane modes of the 2D material, which locally distort the defect’s structure (Fig. 2e), and distortions localized at the defect site, such as the mode M4 depicted in Fig. 2f.

Fig. 2: Phonon density of state, spin-phonon coupling and atomic displacements.
figure 2

Results for spin-phonon coupling and density of states for NV− and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\) are reported in panels (a) and (b), respectively. Red curves report the phonon density of states, while the blue curves report the spin-phonon coupling density V(ω). M symbols point to the phonon modes displayed in the panels (c–f). Panels (c) and (d) report the atomic displacements associated with modes M1-2 of NV−, respectively. Panels (e) and (f) report the atomic displacements associated with modes M3-4 of \({\rm{V}}_{{{{\rm{B}}}}}^{-}\), respectively. Atomic displacements are reported as both positive and negative distortions ( ± qα) of the equilibrium structure (central geometry).

Full size image

Spin-Phonon Relaxation

Spin-phonon relaxation is described by means of density-matrix perturbation theory, where phonons, namely the perturbation, act as a thermal reservoir with infinite specific heat and instantaneous relaxation time. In this framework, the Markovian time-evolution of the reduced spin density matrix in the interaction picture, \({\hat{\rho }}_{s}(t)\), is described by22

$$\frac{d\hat{{\rho }_{s}}}{dt}=\left({\hat{\hat{\bf{R2}}}}\!{\,}^{1-{{{\rm{ph}}}}}\,+\,{\hat{\hat{\bf{R2}}}}\!{\,}^{2-{{{\rm{ph}}}}}\,+\,{\hat{\hat{\bf{R4}}}}\!{\,}^{2-{{{\rm{ph}}}}}\right){\hat{\rho }}_{s}(t),$$
(4)

where \({\hat{\hat{\bf{R2}}}}\!{\,}^{1-{{{\rm{ph}}}}}\) describes resonant single-phonon processes arising from the first term of the Hamiltonian in Eq. (2) and second-order density matrix perturbation theory. As shown in Fig. 2, phonons’ energies largely exceed the zero-field splitting of the spin qubits, resulting in the absence of one-phonon processes, namely direct and Orbach relaxation mechanisms, which would require degeneracy among spin and phonon states. In principle, low-energy phonons would appear by increasing the size of the cell used for phonons simulations, thus recovering the long-wavelength acoustic modes of the lattice. However, as shown for molecular qubits18,30, these modes have vanishingly small spin-phonon coupling and become relevant to spin dynamics only in the low-temperature relaxation regime24,31. Low-temperature spin relaxation is also strongly affected by cross-relaxation, as shown by experiments conducted on samples with different defect concentrations16, and does not represent an ideal regime to compare simulations and experiments. Therefore, we neglect the contribution \({\hat{\hat{\bf{R2}}}}{\,}^{1-ph}\) to spin dynamics and focus on the more application-relevant high-temperature limit dominated by two-phonon processes.

The term \({\hat{\hat{\bf{R2}}}}{\,}^{2-{{{\rm{ph}}}}}\) accounts for two-phonon processes leading to Raman relaxation and originates from the quadratic spin-phonon coupling terms of Eq. (2) at the second-order of perturbation theory. In this approximation, the dynamics of the diagonal elements of \({\hat{\rho }}_{s}\) reads

$$R{2}_{bb,aa}^{2-{{{\rm{ph}}}}}=\frac{\pi }{4{\hslash }^{2}}\mathop{\sum}\limits_{\alpha \beta }{V}_{ba}^{\alpha \beta }{V}_{ab}^{\alpha \beta }{G}^{2-{{{\rm{ph}}}}}({\omega }_{ba},{\omega }_{\alpha },{\omega }_{\beta })$$
(5)

where \({V}_{ab}^{\alpha \beta }\) stands for \(\left\langle a\right\vert ({\partial }^{2}{\hat{H}}_{{{{\rm{s}}}}}/\partial {q}_{\alpha }\partial {q}_{\beta })\left\vert b\right\rangle\). The function G2−ph accounts for three possible processes involving two phonons: absorption of two phonons, emission of two phonons, and simultaneous emission of one phonon and absorption of a second one. Among all the possible two-phonon processes, two-phonon absorption/emission is negligible as they require phonons with energy lower than the zero-field splitting, absent in our framework. Therefore, the simultaneous emission/absorption of two phonons is the only process that enables energy-conserving two-phonon spin transitions, for which G2−ph reads

$${G}^{2-{{{\rm{ph}}}}}({\omega }_{ba},{\omega }_{\alpha },{\omega }_{\beta })=\delta ({\omega }_{ba}-{\omega }_{\alpha }+{\omega }_{\beta }){\bar{n}}_{\alpha }({\bar{n}}_{\beta }+1).$$
(6)

Finally, the term \({\hat{\hat{\bf{R4}}}}{\,}^{2-{{{\rm{ph}}}}}\) accounts for those two-phonon processes due to linear spin-phonon coupling at the fourth-order perturbation theory and reads

$$R{4}_{bb,aa}^{2-ph}=\frac{\pi }{2{\hslash }^{2}}\mathop{\sum}\limits_{\alpha \beta }{\left\vert {T}_{ba}^{\alpha \beta ,+}+{T}_{ba}^{\beta \alpha ,-}\right\vert }^{2}{G}^{2-ph}({\omega }_{ba},{\omega }_{\alpha },{\omega }_{\beta }),$$
(7)

where the terms

$${T}_{ba}^{\alpha \beta ,\pm }=\mathop{\sum}\limits_{c}\frac{\left\langle b\right\vert (\partial {\hat{H}}_{s}/\partial {q}_{\alpha })\left\vert c\right\rangle \left\langle c\right\vert (\partial {\hat{H}}_{s}/\partial {q}_{\beta })\left\vert a\right\rangle }{{E}_{c}-{E}_{a}\pm \hslash {\omega }_{\beta }},$$
(8)

include the contributions of virtual excited states \(\left\vert c\right\rangle\).

We compute \({\hat{\hat{\bf{R2}}}}{\,}^{2-{{{\rm{ph}}}}}\) and \({\hat{\hat{\bf{R4}}}}{\,}^{2-{{{\rm{ph}}}}}\) with the spin-phonon coupling coefficients and phonon frequencies determined by electronic structure calculations and simulate the relaxation dynamics of both defects with the software MolForge22,32. In accordance with the experimental setup, we initialize the system in \(\left\vert 1\right\rangle\) and then monitor the population recovery of \(\left\vert 0\right\rangle\) in time in the presence of a field of 1 mT13,16. As shown in Supplementary Figure 6 we observe a mono-exponential profile that leads to a single relaxation rate constant \({({T}_{1})}^{-1}\). Figure 3 reports the simulated \({({T}_{1})}^{-1}\) as function of temperature obtained by applying \({\hat{\hat{\bf{R2}}}}{\,}^{2-{{{\rm{ph}}}}}\) to both defects. The comparison with experimental data reveals a striking agreement for both materials, and simulations nicely reproduce both the T-dependence and the trend in relaxation rates. On the other hand, simulations carried out with \({\hat{\hat{\bf{R4}}}}{\,}^{2-{{{\rm{ph}}}}}\) lead to much slower relaxation rates (see Supplementary Figure 5), thus leading to the conclusion that two-phonon relaxation due to quadratic spin-phonon coupling is the most relevant pathway in solid-state defects. The robustness of our conclusions is demonstrated by performing simulations with different phonons cell sizes, as shown in Supplementary Figure 3.

Fig. 3: Spin-phonon relaxation.
figure 3

The left panel reports the simulated rate \({({T}_{1})}^{-1}\) (black solid line) as a function of T for NV− defect in diamond together with the experimental rates (red squares)16. The dashed yellow line represents the fitting with Eq. (9). Dashed blue and green lines are the two separate contributions of Eq. (9). The right panel reports the simulated rate as a function of T for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\) (solid black line) together with experimental rates (red squares)13. The dashed yellow line represents the fitting with the function AT2.

Full size image

The accuracy of simulations validates the computational approach and allows us to revisit the interpretation of spin relaxation in these systems. Firstly, our simulations reveal that no one-phonon Orbach process is involved in the spin relaxation of either NV− and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\) defects at high-temperature, as previously hypothesized in the fitting of experimental data16. Our finding is in agreement with spin energy-conservation arguments and the low-energy cut-off frequency of the phonons’ density of states. Moreover, the fitting of experimental data accounted for the Raman contribution to spin relaxation by means of a power-law expression \({({T}_{1})}^{-1}=A{T}^{5}\)16. Such expression was derived over 60 years ago by assuming the term \({\hat{\hat{\bf{R4}}}}{\,}^{2-{{{\rm{ph}}}}}\) as the dominating driving mechanism for Raman relaxation, a Debye-like structure of the phonons’ density of states, and the absence of low-energy spin excited states15. Our simulations show that contrary to this model’s assumptions, Raman relaxation does instead proceed through the term \({\hat{\hat{\bf{R2}}}}{\,}^{2-{{{\rm{ph}}}}}\) and that the phonons relevant to spin relaxation are not at all well described by a Debye model. The analysis of our simulations indeed shows that a strict \({({T}_{1})}^{-1}\propto {T}^{5}\) relation does not hold and that the T-dependence of spin relaxation has a more complex profile. As suggested by the T-dependence of the function G2−ph, we successfully modelled the simulations of NV− by means of the expression

$${({T}_{1})}^{-1}=A\frac{{e}^{-B/{k}_{B}T}}{{({e}^{-B/{k}_{B}T}-1)}^{2}}+C\frac{{e}^{-D/{k}_{B}T}}{{({e}^{-D/{k}_{B}T}-1)}^{2}},$$
(9)

with optimal coefficients A=252.1 s−1, B=326.3 cm−1, C=496.0 s−1, and D=576.1 cm−1. The parameters B and D nicely correspond to the first few peaks in the spin-phonon coupling density V(ω) reported in Fig. 2, in qualitative agreement with a recent work26. The same type of expression would apply to \({\rm{V}}_{\rm{B}}^{-}\), but differently from NV−, the spin relaxation of the \({\rm{V}}_{\rm{B}}^{-}\) is determined in the high-T regime (kBT > ℏω) with respect to the first available modes, thus leading to a simple \({({T}_{1})}^{-1}=A{T}^{2}\) contribution, also in nice agreement with the experimentally determined T2.5 power-law13. To corroborate the interpretation that the first available phonons are indeed the prominent ones for spin relaxation, we simulate T1 by imposing a variable cut-off on the energy of phonons included in the computation of \({\hat{\hat{\bf{R2}}}}{\,}^{2-{{{\rm{ph}}}}}\) and show that even the inclusion of the first few available phonons is enough to obtain the correct order of magnitude of relaxation rate, with the inclusion of phonons up to 800 cm−1 and 80 cm−1 to entirely recover the converged value of T1 for NV− and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\), respectively (see Supplementary Figure 8). This is in agreement with previous findings for magnetic molecules22 and provides a simple rationale for explaining the striking difference among the relaxation rate of NV− and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\). Indeed, despite being both materials with stiff chemical bonds, the 2D nature of h-BN enables low-energy out-of-plane flexural vibrations that are sensibly populated even at low-T.

Spin-phonon decoherence

Finally, we turn to the study of the limits imposed to spin coherence by spin-phonon relaxation by studying the dynamics of the out-of-diagonal elements of \({\hat{\rho }}_{s}\). Considering the contribution of the super-operator \({\hat{\hat{\bf{R2}}}}{\,}^{2-{{{\rm{ph}}}}}\) (reported in full in Eq. 4 of Supplementary Notes) to the decoherence of a superposition among states a and b, namely \({({T}_{2})}^{-1}=R{2}_{ab,ab}^{2-{{{\rm{ph}}}}}\), we obtain the analytical result

$${({T}_{2})}^{-1}={(2{T}_{1})}^{-1}+{({T}_{2}^{* })}^{-1},$$
(10)

where the first term on the r.h.s. is the commonly reported upper bound of coherence due to a finite spin lifetime and reads

$$\begin{array}{lll}\frac{1}{2{T}_{1}}\propto \mathop{\sum}\limits_{j\ne a}{V}_{aj}^{\alpha \beta }{V}_{ja}^{\alpha \beta }{G}^{2-{{{\rm{ph}}}}}({\omega }_{ja},{\omega }_{\alpha },{\omega }_{\beta })\\\qquad\;\;\;+\mathop{\sum}\limits_{j\ne b}{V}_{bj}^{\alpha \beta }{V}_{jb}^{\alpha \beta }{G}^{2-{{{\rm{ph}}}}}({\omega }_{jb},{\omega }_{\alpha },{\omega }_{\beta }).\end{array}$$
(11)

The term \({T}_{2}^{* }\) represents the pure-dephasing term and reads

$$\begin{array}{lll}\frac{1}{{T}_{2}^{*}}\propto \mathop{\sum}\limits_{\alpha ,\beta }\left(-2{V}_{aa}^{\alpha \beta }{V}_{bb}^{\alpha \beta }+{V}_{aa}^{\alpha \beta }{V}_{aa}^{\alpha ,\beta }+{V}_{bb}^{\alpha \beta }{V}_{bb}^{\alpha \beta }\right)\cdot \\\qquad\;\;\cdot{G}^{2-{{{\rm{ph}}}}}(0,{\omega }_{\alpha },{\omega }_{\beta }).\end{array}$$
(12)

Such a mechanism thus involves an energy-conserving simultaneous emission and absorption of two degenerate phonons. If the two phonons have different spin-phonon coupling, this process leads to decoherence, equivalently to the flip-flop nuclear spin transitions limiting the coherence of a central electronic spin33,34,35. These two processes are schematically shown in the top panel of Fig. 4 Notably, the corresponding expression of pure dephasing for one-phonon processes leads to a null contribution, as energy conservation would require zero-frequency phonons. Recently, it has been shown that pure spin dephasing is an active decoherence mechanism in molecular S = 1/2 spin qubits29. Here we test the possibility for this process to also be influencing the values of T2 for NV− observed in dynamical decoupling experiments4. In such experimental conditions, the contribution of spin-spin dipolar interactions to dephasing is systematically removed by applying several refocusing π pulses, revealing the contribution of phonons to decoherence and allowing us to compare simulations and experimental results. In line with the analysis above, we determine the decoherence time for the state \(\left\vert {{\Psi }}\right\rangle =(\left\vert 0\right\rangle +\left\vert 1\right\rangle )/\sqrt{2}\), typically generated in experiments through a π/2 pulse resonant with the transition \(\left\vert 0\right\rangle \to \left\vert 1\right\rangle\)4, by computing the corresponding term \({({T}_{2})}^{-1}=R{2}_{ab,ab}^{2-{{{\rm{ph}}}}}\) (see full expression from Eq. 4 in Supplementary Notes). The middle panel of Fig. 4 reports the ratio between the values of T2 and T1 at different values of temperature for NV−. The comparison between simulations and experimental results shows a remarkable agreement between the two, with simulations correctly capturing the experimentally observed trend T2 ~ 0.5T1, demonstrating the origin of such relation in the presence of pure dephasing. Interestingly, the simulations for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\) reported in the bottom panel of Fig. 4 show an even more drastic reduction of T2, namely T2 ~ 0.1T1.

Fig. 4: Pure dephasing mechanism and correlations between spin-phonon relaxation time (T1) and coherence time (T2).
figure 4

Top panel: schematic representation of two-phonon pure dephasing mechanism. Two degenerate phonons exchange population and lead to dephasing through the spin-phonon coupling interaction \({\hat{V}}_{sph}\), similarly to the pure dephasing due to nuclear spin flip-flop processes among spins with identical gyromagnetic factors γα = γβ. Middle panel: Black and red symbols represent the simulated and experimental4 results for NV−. The dashed line reports T2 = 0.56T1. Bottom panel: Black symbols represent the simulated results for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\). The dashed line reports T2 = 0.1T1.

Full size image

Discussion

The theory of spin relaxation in solid-state paramagnetic defects or impurities has a long-standing tradition with roots in the early days of magnetic resonance. Seminal contributions to the theory of spin relaxation36 were rapidly followed by a proliferation of phenomenological models based on varied assumptions about the details of spin-phonon coupling and materials’ vibrational density of states27,37. Until very recently, such models have remained the only tool available for the interpretation of experimental relaxation data. However, experimental data has proved to be far from easy to interpret and multiple models can often be equally good explanations of experimental evidence. The field of paramagnetic defects is no exception and no clear understanding of spin relaxation in this class of materials has yet been established. Providing a clear interpretation of the mechanism of spin relaxation is one of the main results of this work. Ab initio simulations, free from any adjustable parameter, enabled the identification of two-phonon Raman relaxation due to the quadratic coupling of low-energy optical phonons and zero-field splitting as the main relaxation pathway for NV− and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\). Although alternative relaxation pathways might be operative in spin qubits with different spin multiplicities or low-lying excited electronic states22, these results are likely exportable to all spin qubits exhibiting zero-field splitting, as suggested by their validity for defects in both 3D and 2D materials. In particular, we note that our approach is based on the spin Hamiltonian approximation, where only the first 2S + 1 electronic states are considered, and all the remaining excited states are neglected. This is expected to be a good approximation in fairly isotropic systems such NV− and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\), but generalizing beyond this formalism might be important in other cases. Work in this direction is currently pursued within the remit of single-reference electronic structure theory such as DFT38,39. As a consequence of the correct reinterpretation of the spin relaxation mechanism, we were also able to unravel the role of phonons on spin decoherence. The latter is invariably found to be bound from above by T14,40 instead of the way around, as suggested by one-phonon relaxation theories. As shown, two-phonon processes introduce a pure dephasing mechanism and naturally explain such apparent deviations, leading to a coherent picture of spin dynamics.

The present results have far-reaching consequences and suggest several possible pathways for future development. For instance, the relevance of low-energy phonons for the coherence dynamics of S = 1 spin qubits has several important consequences for the design of spin qubits. Although bulk diamond probably already offers the best environment possible in terms of the (high) energy of optical vibrations, spin qubits can be searched among materials with high-energy optical vibrations and a natural low density of nuclear spins41 in order to simultaneously minimize the effect of both spin-phonon coupling and spin-spin dipolar interactions.

Moreover, our results suggest that low-energy vibrational states of shallow defects and nano-diamonds might play a role in reducing the coherence time of electron spins in these substrates42. Indeed, it has recently been shown that the drastically reduced T1 observed for NV− nano-diamonds has a temperature profile consistent with phonon-induced relaxation43. DeGuillebon et al. invoked the presence of magnetic impurities at the surface of the nano-diamonds to interpret their results43, but our simulations suggest that surface vibrational states, qualitatively similar to those of \({\rm{V}}_{{{{\rm{B}}}}}^{-}\), might be enough to explain the drastic reduction in T1. 2D materials hetero-structures and tailored surface coating might also offer a rich playground to tune the vibrational properties of spin qubits’ host environment.

Overall, our simulations open a window on the fine details of spin-phonon coupling in solid-state paramagnetic defects that can eventually inform several applications. Indeed, the coupling of vibrations and electronic states are responsible for the temperature-dependent shift in spin energy transitions often used as a sensing strategy of the spin environment44, as well as for the optical polarization of defects’ spin states45. Moreover, whilst minimizing the effect of spin-phonon coupling is a key future challenge to increase coherence time at high-temperature, a tailored strong coupling with surface or bulk acoustic waves holds great promise towards the control and coupling of multiple spin systems in solid-state architectures46,47,48. The proposed computational framework has a strong potential to aid the development of all these areas.

In conclusion, we have here used ab initio spin dynamics simulations to determine the spin-phonon coupling coefficients in two prototypical solid-state qubits and demonstrated how this interaction leads to spin relaxation and decoherence. By using a fully parameter-free computational approach we have provided insights into the nature of two-phonon Raman relaxation and revealed low-energy phonons as the main source of decoherence in solid-state qubits at high temperatures. We anticipate that our results will facilitate the interpretation of experimental relaxation data in spin qubits and speed up the identification of quantum sensors.

Methods

Crystal structures

The defects’ structure has been generated starting from a supercell of the pristine materials, diamond and h-BN, respectively. Cell optimizations and simulation of phonons for both the defects have been performed for two sizes of the supercell, i.e 3x3x3 and 4x4x4 diamond supercells for NV− and of 9x9 and 12x12 h-BN supercells for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\). Supercells of 3x3x3 and 4x4x4 for NV− contain 215 atoms and 511 atoms, respectively, whereas, 9x9 and 12x12 supercells for V\({}_{{{{\rm{B}}}}}^{-}\) contain 161 atoms and 287 atoms. The supercells are shown in Supplementary Figure 1. All results presented in the main text have been obtained with the largest supercell available.

Electronic structure and phonons simulations

Cell optimizations and phonon calculations for all the supercells of NV− defect in diamond and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\) defect in h-BN were performed within the framework of periodic density functional theory using CP2K49. All the optimization and phonon calculations were done at Γ-point. A very tight force convergence criteria of 10−7 a.u. and SCF convergence criteria of 10−10 a.u. for the energy were employed for the cell optimizations. A plane wave cutoff of 1000 Ry with DZVP-MOLOPT Gaussian basis sets and Goedecker-Tetter Hutter pseudopotentials50 were used for both systems. The Perdew-Burke-Ernzerhof (PBE) functional and DFT-D3 methods for dispersion corrections had been used51,52. The second-order force constants, i.e. the Hessian matrix, has been computed for the periodic structures after optimization by employing a two-step numerical differentiation of atomic forces. The latter have been computed with the software CP2K by applying a displacement step of 0.01 Å to each lattice Cartesian degree of freedom independently. Cartesian force constants, phonons’ frequencies, and normal modes have then be computed with the software MolForge22,32.

Density Functional Theory, as implemented in the software ORCA53, had been used to compute the anisotropy tensor D. Clusters (passivated with H) created from atoms around the defect had been used for this purpose. A convergence test for different sizes of clusters had been performed to select the smallest cluster size, which can reproduce the experimental D value, see Supplementary Table 1. A similar strategy had been taken for the choice of the basis set and the DFT functional. Convergence tests had been performed to select the best ones in comparison to the experiments. A detailed comparison of different basis sets and different functionals has been presented in Supplementary Table 2. Based upon this comparison, we have used 5 Å cluster and BHANDHLY54 functional for NV− and 7.5 Å cluster and PBE055 functional for \({\rm{V}}_{{{{\rm{B}}}}}^{-}\), respectively. The basis set of DKH-def2-SVP had been used for all the atoms present in both the defects NV− and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\). The hydrogenated clusters of NV− defect (5 Å) and \({\rm{V}}_{{{{\rm{B}}}}}^{-}\) (7.5 Å) defect have been shown in Supplementary Figure 1.

Training of neural network and test set generation

The training sets for the neural network have been generated by calculating the D-tensor for over 2000 distorted structures. The distorted structures were obtained by displacing all the Cartesian coordinates of all the atoms from the optimized geometry. The displacement was given by a random value in the range from − 0.05 Å to 0.05 Å. Among the total of 2000 distorted geometries, 1600 were used for training the ML models, while 400 were used for validation. The neural network we used has 3 hidden layers consisting of 128, 64, and 16 nodes, respectively. The input layer has 3N nodes, where N is the number of atoms present in the cluster, and the output layer has 9 nodes. Each hidden layer has a sigmoid as the activation function and L2-regularization.

Calculation of spin-phonon coupling coefficients

All the relaxation rates presented in the main manuscript have been obtained using the spin-phonon coupling coefficients calculated from the machine learning model trained with D-tensor values obtained from DFT calculations. Numerical differentiation has been used to calculate the spin-phonon coupling coefficients. One-dimensional grids of 6 points and two-dimensional grids of 36 points have been used to determine the first-order and second-order coefficients of spin-phonon coupling. Machine learning models have been used to calculate the D-tensor values for all the points. Each one of these 2-dimensional grids of points was interpolated using a third-order polynomial, P(x, y) = a30x3 + a03y3 + a21x2y + a12xy2 + a20x2 + a02y2 + a11xy + a10x + a01y + a00. The coefficients a01 and a10 correspond to first-order spin-phonon coupling coefficients, \((\partial {\hat{H}}_{s}/\partial {X}_{i})\), and coefficient corresponding to a11, a20 and a02 represents the mixed and pure second-order Cartesian derivatives \(({\partial }^{2}{\hat{H}}_{s}/\partial {X}_{i}\partial {X}_{j})\), where the indexes i, j runs over all the 3N degrees of freedom of the cluster. Once these parameters have been computed, the spin-phonon coupling coefficients are obtained by means of the relations

$$\left(\frac{\partial {\hat{H}}_{s}}{\partial {q}_{\alpha }}\right)=\mathop{\sum }\limits_{i}^{3N}\sqrt{\frac{\hslash }{{\omega }_{\alpha }{m}_{i}}}{L}_{i\alpha }\left(\frac{\partial {\hat{H}}_{s}}{\partial {X}_{i}}\right),$$
(13)

and

$$\left(\frac{{\partial }^{2}{\hat{H}}_{s}}{\partial {q}_{\alpha }\partial {q}_{\beta }}\right)=\mathop{\sum }\limits_{ij}^{3N}\sqrt{\frac{\hslash }{{\omega }_{\alpha }{m}_{i}}}\sqrt{\frac{\hslash }{{\omega }_{\beta }{m}_{j}}}{L}_{i\alpha }{L}_{j\beta }\left(\frac{{\partial }^{2}{\hat{H}}_{s}}{\partial {X}_{i}\partial {X}_{j}}\right),$$
(14)

where Liα are the eigenvectors of the Hessian matrix. It should be noted that there is a mismatch between the number of atoms in the cell used to simulate phonons and the atoms in the cluster used to compute the Cartesian derivatives. This ambiguity is resolved by only considering the effect of phonon displacements for the atoms appearing in both the cell and the cluster, e.g. the Hydrogen used to terminate the cluster are not displaced and they do not contribute to spin-phonon coupling.