Introduction

Hierarchical materials with specific architecture at different length scales are observed everywhere in nature1, like in bone2 and wood3. Adding architecture to structures can enhance mechanical properties and provides an extra design lever on top of atomic-level microstructure and macroscopic-level part dimensions1,4,5,6. Investigations into hierarchically architected materials have thus been of great interest, with efforts to control fatigue tolerance7, energy absorption8, and stiffness and strength9, among many others. Design approaches for architected materials have included inspiration from existent crystalline material microsctructure10, finite element topology optimization11, and experimentation with rapidly fabricated additively manufactured samples12,13,14,15. Honeycomb structures are of particular interest due to their ultra-low weight and outstanding mechanical properties, with a variety of applications across automotive, railway, and aerospace industries16. Therein, the mechanics of honeycomb compression features varied stages of deformation, including elastic deformation, mechanisms of cell wall buckling and densification with ultimate compaction.

Recent advances in artificial intelligence have afforded emerging capabilities for architectural design. For example, there have been successes in achieving bioinspired hierarchical composites17, in using semi-supervised approaches with graph neural networks18, and in implementing natural language inputs for generative design19,20,21,22,23,24 of architected materials. Concurrently, machine learning models have been used in other material platforms for the prediction of a multitude of mechanical properties including fracture25,26,27, compliance28, and buckling29,30.

Here we demonstrate a full workflow to tackle compression design of architected honeycomb materials, utilizing simulation to determine initial insights into the space of hierarchical honeycomb lattices, machine learning and genetic algorithms to generate candidates for desired behavior, and additive manufacturing to rapidly test top structural candidates. This approach is generalizable to multiple material property targets, with 4 levels each of stiffness and stress illustrated here.

Results

Coarse-grained modeling of honeycomb deformation

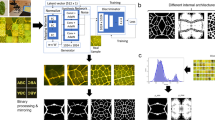
We simulate the compressive behavior of honeycomb structures as in Fig. 1a via a coarse-grained molecular dynamics approach31, in which we represent the honeycomb lattice as a series of interconnected beads subject to harmonic bond interactions, harmonic bond angle interactions, and a repulsive Lennard-Jones potential to avoid penetration. This model was designed to capture the salient principles of honeycomb compression mechanics (and the associated stress-strain behavior), including elastic deformation (captured via the harmonic bonds to describe the elasticity the constituting material), cell wall buckling (captured through the interplay of compressive response via harmonic bonds and bending response via harmonic bond angle potentials), and densification with ultimate compaction (captured via the repulsive Lennard-Jones potential). An advantage of this generic approach is that it captures a broad range of structure-property relationships, important here for our generative deep learning strategy that requires us to develop a training set of such data. The training set captures the behavioral space of physical behavior obtained by creating complex patterns (as shown in Fig. 1) of hierarchical honeycomb structures.

Fig. 1: Data representation of MD simulations.
figure 1

a MD simulation of honeycomb structures allows us to predict compressive behavior. b Depending on the hierarchical architecture of the super-honeycomb, different stress behaviors result. c We subsequently encode different super-honeycomb lattices into vectors representing structure, and slice stress curves into progressive windows of stress evolution. In doing so, we train an ML model to predict stress curves given an initial structure and stress condition. d Once trained, the model can be deployed on a hierarchical honeycomb structure, parametrized by the cell wall thicknesses of each hierarchical hexagonal ring, at an initial unstressed state to predict the full stress-strain behavior.

Full size image

A shortcoming of this approach are challenges in fitting the material behavior to a specific material. To address this, 2D finite element beams could be used to model these honeycomb structures. The framework developed here, however, could be directly applied by retraining or transfer-learning the model against new datasets. We use this strategy since we wish to develop a fundamental understanding of how hierarchical honeycomb design relates with resulting stress-strain behavior to form a training set for deep learning that captures a broader design space. Moreover, molecular dynamics was used because it can efficiently handle a variety of more complex, non-beam-based structures and could thus be easily adapted to deal with various nanoscale materials in the future (e.g., graphene honeycombs, nano-architected polymers, etc.). Hence, this strategy provides a flexible foundation to the approach that increases its applicability to more general cases.

We then define an initial set of distinct hierarchical honeycomb structures. These structures are comprised of a regular honeycomb lattice, onto which an additional longer-range hexagonal lattice is superimposed. Specifically, this superlattice is formed by adjusting the thicknesses of cell walls in a higher order hexagonal pattern. Here we vary both the repeat length of the superlattice and the cell wall thicknesses of each hexagonal ring within the superlattice to obtain a variety of structures with diverse compressive behaviors, as shown in Fig. 1b. These super-honeycomb structures are encoded as vectors, in which each entry of the vector dictates the relative thickness of the corresponding hexagonal arrangement of cell walls within the superlattice. Stress curves are natively representable as vectors, and are sliced into progressive time series in order to provide sections of compressive behavior at different timesteps.

Formatting structure and stress data in these ways allows us a natural way to map a cause and effect relationship between structure and property. Specifically, we append snapshot stress states to each structure vector, and pair off each such appended vector with its subsequent window of stress evolution. We then train a machine learning model to learn the relationship between a structure at a particular stress state as input and its subsequent stress behavior for the upcoming time window as output, as shown in Fig. 1c. In Fig. 1d, the final trained model can be deployed to make full predictions of the stress strain curve, starting from an initial unstressed structure. A zoomed in image of a hierarchical honeycomb structure is shown, to illustrate how encoded structural parameters correspond to the geometry. Details of MD simulation and data representation are provided in the Methodology section.

Deep learning and inverse design

Over 1000 MD simulations with randomized superlattice sizes and cell wall thicknesses, sliced into over 26,000 input-output training pairs, provide a training dataset with diverse stress behaviors, as shown in Fig. 2a. Training a convolutional LSTM model, suitable for learning time dependent data such as stress progression32, yields accurate predictions of compression behavior. Fig. 2b compares real versus predicted stress values and illustrates a linear fit with an r2 = 0.95. Figure 2c shows good agreement between training and validation losses, indicating the model is not simply overfitting on the training data, with a validation loss of 0.00058. Using the trained model to predict stress curves of the four samples presented in Fig. 1b shows a good ability to accurately predict a wide variety of compressive stress behaviors. Further details of ML model and training are provided in the Methodology section.

Fig. 2: LSTM model training.
figure 2

a An ensemble of 1445 MD simulations were used to train the convolutional LSTM network. b Predicted ML stresses align well with real MD stresses, with an r2 = 0.95 and (c) validation loss = 0.00058. d Predicted curves across a range of stress behaviors align well with MD, with the samples from Fig. 1b provided as example.

Full size image

We subsequently leverage this model to tackle the inverse design problem, in which we start out with a desired material property and predict a structure that exhibits it. Specifically, we employ an iterative genetic algorithm approach as in our previous work25, which alternates between stages of structure generation and evaluation, with specific steps outlined in Fig. 3 and using structure encodings as the genes subject to evolution.

Fig. 3: Inverse design procedure.
figure 3

The stress prediction ML model directly solves the forward design problem, where we input an arbitrary structure vector and rapidly receive its stress strain curve. Here, we solve the inverse design problem via genetic algorithm, which comprises an iterative two stage process of generation and evaluation, to obtain structures given a desired stress behavior as input.

Full size image

Briefly, an initial population of structures is randomly generated. Then, two structures are randomly chosen to serve as parents for derived children structures, which have some combinations of features similar to the parent structures. Additional sources of structure diversity are introduced through the mutation, specialization, and migration of next-generation structures, in which added structures are either randomly perturbed from existing structures, accentuated in features from existing structures, or newly instantiated completely randomly, respectively.

At the end of this multistep generative process, we have an enlarged population of structures to evaluate. To do this, we first use the ML model to rapidly characterize each structure’s compressive stress response. Next, we rank each structure’s behavior by a chosen fitness function. For example, we could calculate the initial slopes of each stress strain curve to extract values for material stiffness, and compare these calculated values to a desired target value. Then, proximity to the target value is used as the fitness function. Finally, we screen the ranked structures to reduce the population back to its initial size before moving on to the generation stage in the next iteration of the cycle.

Once structure fitness reaches a threshold value, we break out of the loop and select the best structures from the evaluated population. These structures are identified as likely candidates for possessing the mechanical properties we desire. To increase confidence in their properties, we subject these candidate structures to MD simulation. Figure 4 shows a selection of 8 candidate structures designed for a range of stiffness and ultimate stress values, with good agreement between ML predictions and MD simulations.

Fig. 4: Inverse design of stiffness and ultimate stress.
figure 4

a We input a series of desired stiffness values, and the approach generates a diversity of super-honeycomb structures predicted to meet these criteria. b These AI-generated structures are subsequently confirmed to have the desired behavior by MD simulation. c We do the same for a different property, such as ultimate stress, and again (d) confirm desired progression of structures with increasing stress by MD simulation.

Full size image

Experimental validation

After this corroboration with MD, we experimentally verify that candidate structures indeed possess desired properties. To do this, we use additive manufacturing to rapidly fabricate the candidate super-honeycombs out of thermoplastic polyurethane (TPU) and subsequently subject them to compression tests. The set of experiments tests whether the design principles learned by the model, and utilized during the generative design phase, can successfully be applied to achieve a desired mechanical outcome.

Figure 5a illustrates four candidate structures designed to have a specific progression of stiffness values, and their additively manufactured physical instantiations subjected to compression testing. The resultant force displacement curves in Fig. 5b initially overlap, likely representing the shared response of the base printing material. However, the curves diverge after 10 mm with the onset of different buckling behavior across the different architectures. Starting from this point, comparison with MD shows experimental compressive behavior qualitatively aligns with simulated behavior for the following 10 mm of displacement. Calculated stiffnesses from this divergence point, as the collection of slopes from 8 mm to 13 mm in 3 mm increments, provide a relative progression of values that align well with the desired targets, with error bars corresponding to the standard deviation of these slopes. A comparison plot showing good agreement between target stiffness, ML predictions, MD corroboration, and experimental verification is provided in Fig. 5c.

Fig. 5: Experimental verification of stiffness design.
figure 5

a We 3D print the AI-generated candidate structures and subject them to experimental compression tests. b All samples have similar initial force displacement curves, but differences in superlattice architecture lead to different buckling responses after 10 mm. In this 10–20 mm region, compressive behavior qualitatively corresponds to simulated stress curves. c Quantitatively, the relative experimental stiffnesses measured from this divergence point align well with the target behavior, ML predictions, and MD simulation.

Full size image

We perform similar experimental verification for structures designed to have specific maximum stress values. Like before, we fabricate structures via additive manufacturing and subject them to compression testing in Fig. 6a. Furthermore, the 10–20 mm region of force displacement curves again qualitatively correspond to simulated behavior with error bars corresponding to the standard deviation of values within a 5 mm range centered about 20 mm, as shown in Fig. 6b. And quantitatively, experimental maximum force values within this region correspond well with ultimate stress values of desired targets, ML predictions, and MD corroboration in Fig. 6c.

Fig. 6: Experimental verification of stress design.
figure 6

a We 3D print the AI-generated candidates stress design and subject them to experimental compression tests, which (b) again correspond to simulation in the 10–20 mm range and (c) quantitatively align to the desired targets, ML, and MD.

Full size image

Discussion

The trained ML model provides an effective tool for the forward design problem, in which a given super-honeycomb structure can have its compressive behavior directly and rapidly predicted without having to set up, run, and analyze a physics-based simulation. A genetic algorithm search validated by simulation and experimentation enables effective interrogation of the inverse design problem.

It should be noted that stress curve predictions that form the training data were ultimately based on a simplified coarse-grained model that captures the material behavior using a set of interactive potentials that operate at the mesoscale (bond, angle, and pair style interactions) without any specific information on what base materials would be used to fabricate structures. The coarse grain model is not tuned to replicate the specific performance of only one material, such as the TPU used in this study, as our approach may be of interest to many different material platforms. This means that the model generally captures results within a particular material choice and honeycomb design space are consistent (defined via the interplay of elastic deformation, cell wall buckling, and densification/compaction) but phenomenological. This is because the absolute values of these depend on a particular material choice. This shortcoming could be addressed by developing an additional training data set specific to a particular material platform (either from additional molecular modeling, finite element simulation results, or experimental data); in such a case, the predictions would be quantitative rather than generally mechanistic. Herein, transfer learning can be an effective strategy to adapt our model, where one could start from the model trained against our existing dataset and fine-tune the parameters to predict behavior quantitatively. Since the general physics of deformation is expected to be similar (some interplay of the key physical mechanisms like elastic deformation, cell wall buckling, and densification/compaction), we anticipate that such a task could be relatively easily be accomplished, even with small datasets.

Moreover, even though deformation in experiment is conducted at slow rates, resultant discrepancies, such as experimental force displacement curves corresponding to predictions after 10 mm, are not unexpected. No doubt, if one were particularly interested in honing in on some selected base material, a trained model specifically incorporating data on the unique properties of that particular material would likely outperform the results here. This limitation is evidenced in why the comparisons between computation and experiment are presented in relative rather than absolute terms—one could easily instantiate structures that are stiffer in an absolute sense if one simply used a stiffer polylactic acid (PLA) filament instead of a flexible TPU filament, of course.

However, and most importantly, even in the absence of such specific material property information, the predictions made here align to the crucial deformation steps around when buckling initiates in terms of both qualitative behavior and overall trends. The rankings for highest to lowest stiffness or ultimate stress remain consistent, as do the quantitative relative distances between values, per Figs. 5c and 6c. Indeed, the aim here was not to create a specific model tailored to precisely predict the properties of TPU structures, but rather to tackle the challenge of architectural design in a more general material agnostic manner, offering a broad framework that can be widely applied. If one is interested in designing for more granular scale-dependent localizations, future work may be interested in training the deep convolutional LSTM model on explicit representations of them. Other than mechanical properties, thermodynamics and kinetic theories can also be considered as coarse-grained models31. Hence, other material properties such as thermal conductivity may be treated by an ML inverse design approach, given a proper training dataset. This provides one of out many avenues for future directions that could build on this work.

Aside from training the predictive model on parameters of real material properties for better consistency with specific experimental cases, further space for advancement lies in the direction of structure generation. For example, future work may be done in modeling more direct, bidirectional translation between structure and property. In a literal sense, the growing field of machine translation33 of languages may find great utility here, if we treat structural encodings as “words in one language” that should translate to equivalent stress vector “words in a second language”. A model fluent in these two languages would be a valuable tool to both forward and inverse design tasks. And a model that gains some understanding of semantic rules and forbidden statements in either “language” may be helpful in putting bounds on the possible structures or properties that can be attained20,21.

Another recent development in state-of-the-art image generation concerns diffusion models like DALL·E, which have found successes in generating images based on complex prompts or conditioning parameters21,34,35,36. It may be fruitful to train diffusion models that learn how to architect structures based on prompts detailing mechanical property requirements that can then be added to yield a structural training set.

Regardless of such advancements, which may increase the performance of our approach if they were to pan out, we demonstrated our approach is a successful end-to-end process for compression design from ideated property requirements to actualized material structures. Furthermore, it is not difficult to imagine how such a process can be implemented at scale, with other material architecture platforms, and for other properties of interest. This can provide alternative avenues at the intersection of simulation, artificial intelligence, and experiment that can synergistically empower materials design in the future.

Methods

Stress simulation by molecular dynamics

Structures are encoded as 10-D vectors, where each entry corresponds to the cell wall thicknesses of successive hexagonal rings in the superlattice, as shown in Fig. 1d. As we simply join adjacent hexagonal cells along their cell walls, strut thicknesses are determined as the sum of the two adjacent cell thicknesses. For superlattices less than 10 hexagonal units in circumradius, the remaining entries in the 10-D vector are set to zero.

To generate an initial set of data, we randomly instantiate a set of 1500 structures. For each structure, we select a random number from 2 to 10 from a uniform distribution to serve as the superlattice length. Then, each entry in the superlattice is assigned a random relative cell thickness from 2 to 15, also from a uniform distribution. These structural parameters are used to generate coarse-grained representations of super-honeycomb structures, wherein each structure is comprised of 14,309 coarse-grain beads arranged in a hexagonal lattice, strut thicknesses are normalized to ensure consistent mass across all samples and isolate the effect of material redistribution, and the bead masses and interaction coefficients are adjusted to emulate the behavior of thicker or thinner walls.

First, the average strut thickness A of the honeycomb is obtained by the following Eq. (1):

$$A=\mathop{\sum }\limits_{i=1}^{N}{T}_{i}\cdot {L}_{i}/\mathop{\sum }\limits_{i=1}^{N}{L}_{i}$$
(1)

for N struts with thicknesses Ti and lengths Li. Then, the strut thicknesses Ti are divided by the average A to yield a set of normalized thicknesses t that yield a structure with an average thickness of 1. We then use the normalized thicknesses t to determine bead masses m as in the following Eq. (2):

$$m=\rho {r}_{0}t$$
(2)

with density ρ, and equilibrium bead distance r0 set to 5 Å. Then the harmonic bond interactions Ub are determined by the following Eq. (3):

$${U}_{b}=\frac{{Et}}{2{r}_{0}}{(r-{r}_{0})}^{2}$$
(3)

for elastic modulus E set to 100 MPa. This representative value of 100 MPa is applicable to a wide variety of materials, falling within the typical ranges for foams and natural materials with complex hierarchical architecture, and between traditional polymers and elastomers37.

Similarly, the harmonic angle interactions Ua are determined by the following Eq. (4):

$${U}_{a}=\frac{E{t}^{3}}{2{4r}_{0}}{(\theta -{\theta }_{0})}^{2}$$
(4)

with equilibrium bead angle θ0 set to 180° within the struts and to 120° at the vertices. We add a Lennard-Jones pair style potential with a cutoff of 2.5 nm to prevent particle penetration with the following Eqs. (5), (6), and (7):

$${U}_{p}=4{\rm{\varepsilon }}({\left(\frac{{\rm{\sigma }}}{r}\right)}^{12}-{\left(\frac{{\rm{\sigma }}}{r}\right)}^{6})$$
(5)
$${\rm{\sigma }}=\frac{t}{{2}^{1/6}}$$
(6)
$$\varepsilon =\frac{0.02E{{\rm{\sigma }}}^{2}}{{r}_{0}t}$$
(7)

with well size σ calculated so that the contacting force approaches 0 when two beads are in the distance of the wall thickness and well depth ε calculated as to fit the stiffness of beads contacting at the distance of cell wall thickness, which are both dependent on normalized strut thicknesses t. The MD variables in the bond, angle, and pair interactions parametrize the physics of the system and can be readapted for different specific materials.

These MD parameters can capture the reality of deformation by defining the coarse grain bead interaction potentials. Then, the application of Newtonian physics to the energy potentials allows for the calculation of emergent behaviors and properties as an output of simulation parameters. Specifically, yield strength and buckling limit can be tuned by elastic modulus E, while strain hardening and relative density over compression can be tuned by potential well size σ and well depth ε. And while changes in beam connectivity are not modeled here, reactive potentials such as AIREBO have been used in the literature to model breakage38.

These structures are then subject to compression testing with MD simulations using LAMMPS39, with initial equilibration using the microcanonical ensemble (NVE) and additional temperature rescaling to maintain 10 K during a brief finite temperature equilibration phase before energy minimization. The structures all share the same width, height, mass, and thus density. The difference between structures is in the distribution of this mass within the designated sample area. The equilibration and compression conditions are kept consistent between samples to isolate the effect of varying structure by material redistribution. Compression is implemented by iteratively deforming the simulation box and performing energy minimization via the Polak-Ribiere version of the conjugate gradient algorithm at each increment. For each structure, we obtain a stress strain curve, which we then slice into progressive sequences that highlight evolution over time.

The stress strain relation is naturally embedded in the outcome of the coarse grain MD simulations, obtained via LAMMPS compute pressure, as the sum of contributions from bond, angle, and pair interactions. As our focus lay in designing stress strain behavior of each structure as a whole, we did not systematically observe local scale-dependencies. Of the 1500 generated structures, 1445 full stress strain curves are obtained, as some structures fail during compression and yield incomplete stress curves.

The final format for simulation data, amenable for subsequent training of a machine learning model, is paired up in relationships of input-output. Input data are comprised of 13-D vectors, 10 of which correspond to the previously described structure encoding and 3 of which correspond to the current strain step, current stress state, and next stress state of the structure, respectively. Output data are comprised of 4-D vectors representing the subsequent 4 stress steps for a given input. In total, we obtain 34,680 input-output pairs after slicing each original stress curve into stress progressions from 24 different timesteps.

The coarse grain beads have an equilibrium spacing of 5 Å, compared to a simulation sample width of 173 nm. When translated to the printed samples, which are scaled up to a sample width of 100 mm, this corresponds to a coarse grain size of 289 µm.

Stress prediction by machine learning

We use a deep convolutional LSTM model40 suitable for learning temporal relationships between data. Training is done using an Adam optimizer41 with a learning rate of 0.0001, decay of 0.001, and batch size of 32. 75% of the MD data is used for training, while 25% is reserved for validation. The specific layer architecture used is described in Table 1.

Table 1 Summary of the ML model architecture.
Full size table

We use an iterative process similar to our previous work with LSTM models26,29 for obtaining total stress predictions. Here, we use previous predictions to update the “current” stress and strain values used for subsequent predictions. As 4 steps of prediction are output for each input, and we advance forward inputs 1 timestep at a time, we save a running list of up to 4 potential predicted stress values for each timestep. Once we reach a given timestep and need to use it as input for the next prediction, we average all previous output predictions for that timestep and finalize this as the most likely current value. We continue this process until all desired timesteps are filled.

Rapid fabrication by additive manufacturing

2D images of candidate honeycomb structures were extruded into 100 mm × 67.17 mm × 22.4 mm blocks and sliced to .3mf files with PrusaSlicer 2.5.0. Samples were printed on an Original Prusa i3 MK3 using a 1.75 mm green NinjaFlex TPU filament.

Experimental verification by compression testing

Compression testing was performed using a 5 kN Instron Universal Testing Instrument. Compression tests were conducted at a rate of 10 mm/min to a final displacement of 30 mm. Videos of samples under compression were taken with a Samsung Galaxy Note20 Ultra 5 G 108 MP wide-angle camera. We do not expect a direct quantitative correspondence between simulated and experimental stress values due to the omission of material specific parameters in the coarse grain MD simulations. To avoid potential confusion of conflating material-agnostic values from coarse grain MD simulation with the specific values from TPU experimentation, we do not represent the two sets of curves as direct comparisons of stress and strain. Rather, the experimental compression tests are provided in their native load-displacement format, and comparisons are made by relative trends.