Abstract
An approach to supervised classification and regression of superconductive materials is proposed which builds on the DeepSet technology. This enables us to provide the chemical constituents of the examined compounds as an input to the algorithm, while avoiding artefacts that could originate from the chosen ordering in the list. The performance of the method are successfully challenged for both classification (tag a given material as superconducting) and regression (quantifying the associated critical temperature). We then searched through the International Mineralogical Association list with the trained neural network. Among the obtained superconducting candidates, three materials were selected to undergo a thorough experimental characterization. Superconductivity has been indeed confirmed for the synthetic analogue of michenerite, PdBiTe, and observed for the first time in monchetundraite, Pd2NiTe2, at critical temperatures in good agreement with the theory predictions. This latter is the first certified superconducting material to be identified by artificial intelligence methodologies.
Similar content being viewed by others
Introduction
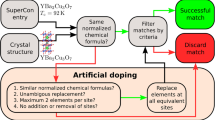
Finding new superconductors represents a complex task, which heavily relies on individual experience and intuition. Indeed, it was shown that sampling from a large gallery of candidate materials, only a limited fraction, accredited in the range of 3%1 of the total, displays superconducting behavior. This is a rather dissatisfying score which severely impacts on the reported success rate, when chasing for novel superconductors via conventional methodologies. It is therefore crucial to devise novel strategies for identifying materials which can putatively display superconducting behaviors beyond state-of-the-art approaches. At the forefront of current developments, machine learning (ML) technologies are steadily gaining popularity as credible tools for complex data-sets handling. As such, they have been successfully applied to a wide range of problems, transcending disciplinary boundaries2,3,4,5,6,7,8 and with specific reference to those realms of applications where classification and/or regression are needed. Multi-layered feedforward neural networks are prototypical architectures extensively used for their inherent versatility. They are constituted by a collection of adjacent layers made by individual computing units, the neurons, where information is punctually processed. More concretely, the information gets manipulated by a nested sequence of linear (across layers) and non-linear (localized on the nodes) operations, from the input to the output stack. In essence ML seeks at solving a global optimization problem by minimizing a suitably defined loss function, which compares the output produced at the exit layer to the expected target for a class of exemplary items supplied as an input during training stages. The ultimate aim is to self-consistently assign the weights of the links that connect pair of nodes belonging to contiguous layers, so that the trained network can cope with the specific task for which it was assembled. At the same time, the network should perform equally well when confronted with data non included in the reservoir that defines the training set, although belonging to the same category of pertinence. A first attempt to apply ML technology to a large superconducting database was reported in ref. 9, where variants of random forest methods10 have been used to predict the critical temperature Tc (restricted to the range Tc > 10 K). Importantly, several chemical characteristics—as e.g., atomic mass, band gap, atomic configuration, melting temperature— are provided in ref. 9 with a discretional choice that could in principle reverberate in unfortunate bias. To overcome this limitation, a convolutional neural network was employed in ref. 11, which enables the operator to bypass the feature extraction phase, namely the process of a priori selecting a suitably engineered chart of the relevant chemical information. Specifically, stoichiometries of the materials under scrutiny are entered into the two-dimensional periodic table. The latter is then divided into four sub-tables which bear information on the orbital characteristics of the valence electrons. Convolutional layers allow hence to resolve the relative positions of the elements, and the regression problem is brought back to a standard image processing task. Also in this case, however, the outcome of the analysis senses patterns and trends as stemming from the rows and columns of the periodic table. Although universally shared, this is just one out of several other viable strategies to display the data in two dimensions. Starting from these premises, we here propose an approach to supervised classification and regression of superconductive materials which builds on the Deep Sets technology12, a family of deep learning algorithms that is specifically designed to operate on sets defined by the finite enumeration of distinct members (or elements). The modeling of sets is a subfield of paramount importance at the frontier of machine learning research. The computational architecture of Deep Set can be rationalized from an encoder-decoder perspective. The encoder embeds datasets into an appropriate vector space of variable size. Each input element of the set if transformed by a mapping function that is parameterized by a neural network. The resulting elements are summed up (pooling operation) and the output is in turn transformed by means of a non-linear filter. The advantages of this procedure are manifolds, when applied to the problem of classifying superconducting material and anticipating their associated critical temperature. On the one side, the examined compound is associated to a set—of variable dimension—which reflects its chemical composition. In other words, we are feeding the neural network with the atomistic description of the material, a foundational approach solidly grounded on first principles that wipes out the load of arbitrariness intrinsic to any heuristic recipe. Feature engineering is carried out self-consistently, from the input set toward the ensuing aggregated representation, with no a priori imposed bias. Then, the extracted features are combined linearly at the pooling stage. This makes it possible to gauge the contribution of each individual atom to the onset of the superconductive transition: the whole is here the sum of its parts, a remarkable outcome of the automated feature selection strategy that is settled upon training. Interestingly, the encoding space can be successfully squeezed, even compactified to yield just one scalar output, so providing a handy and immediate proxy of the chemical propensity to superconductivity.
The performance of the fully trained Deep Set is challenged against the so called Hosono dataset1,11: a significant portion of the materials certified as superconductors are correctly spotted by the network, and the associated transition temperatures predicted with a high degree of confidence. Further, given that the study of the materials formed by Nature, i.e., the minerals, has been always the basis for the greatest breakthroughs in chemistry and solid state physics13, we searched within the complete mineralogical catalogue to look for plausible candidates, as tagged by the trained classification algorithm. This choice has several advantages. First, it is not biased toward superconductivity properties, as this is a property seldom investigated or looked for in minerals. Second, the chemical stability of the material is warranted by the existence of the mineral, even if the conditions in which the mineral has formed might be very far from those used in synthesis protocols. A list of minerals identified as putative superconductors was extracted by the trained network: 44% of the selected candidates were already reported to display superconducting behavior. We then focused our attention on a sublist of three minerals, extracted from the above pool of candidates, which were never reported as superconductors in literature or were poorly described about 60 years ago14. The promising minerals are: temagamite Pd3HgTe3, michenerite PdBiTe and monchetundraite Pd2NiTe2. Next, given the rarity of the selected minerals and their occurrence only as micron-sized grains, we carried out a systematic experimental characterisation of the structural and magnetic properties of their synthetic analogues. Remarkably enough, the synthetic equivalent of michenerite and monchetundraite were found to exhibit superconducting transitions with critical temperatures in good agreement with those predicted by the Deep Set algorithm.
Results
Training and application of the machine learning technology
In the following, we will begin by illustrating the results of the analysis for what concerns regression and classification. The specific aspects that pertain the implementation of the Deep Set algorithm are discussed in the Method section. In Fig. 1, we report the predicted Tc against the corresponding values, as measured in direct experiments. Blue circles refer to materials of the SuperCon dataset11 that were not presented to the Deep Set during training stages. The error bar is computed by gathering data from 50 independent realisations of the trained device. Hence, for any given material, the number of averaged entries is at most 50 (if the material has never been selected for a training session). Only materials that have been selected at least 10 times are considered. Data align along the bisectrix of the quadrant (depicted with a dashed line), an observation that points to the predictive adequacy of the procedure implemented. To cast this finding on quantitative grounds we computed root mean squared error that is equal to 9.5 K, while r2 = 0.92. It should be remarked that the r2 value, typically employed for assessing the goodness of a regression task, proves often inadequate, as it may convey a biased, thus distorted, meaning. As a matter of fact, r2 values can be directly confronted only when referring to an identical test set. To elaborate further on the limited interest of the r2 metric focus on the work by Li et al.15, which is pertinent to the class of problems here inspected. In ref. 15, the authors report a r2 equal to 0.9 for a regression task aimed at assessing the temperature of superconducting materials. However, the associated root mean square error is relatively large, quantified in about 80 K in ref. 15 (an for a subset of materials smaller than the one here considered). In our analysis, the root mean square error drops significantly to reach 9.5 K, while the r2 stays comparable to that claimed in ref. 15. The proposed scheme can be further improved by employing ensemble techniques that enable us to reduce the root mean square error to 9 K, with r2 = 0.93 (see SI). To the best of our knowledge, the root mean square error reported in our paper is indeed the smallest claimed in the literature with a correct handling of the (large) analyzed dataset (i.e., by removing duplicate samples).
Predicted vs. measured critical temperature, Tc (K). The blue circles refer to materials from the SuperCon database. A fraction of 20% of the total is randomly selected as part of the testset, while the remaining 80% is used for training. The operation is repeated 50 times and the collected temperatures from each independent run stored for further processing. The displayed data refer to the 328 materials selected to be part of the testset at least 10 times, out of 50 trials. The orange diamonds refer to the 39 superconducting materials (all tested 50 times by independent DeepSet realizations) that are present in the Hosono database. This latter contains a total of 207 (superconducting and non-superconducting) compounds. Symbols stand for the average temperature, while the error bars are the computed standard deviation.
The diamonds depicted in orange in Fig. 1 stand for the entries of the Hosono database1,11. By visual inspection, one can immediately appreciate the correspondence between the predicted and measured Tc. In this case, the root mean squared error is found to be 7 K (r2 = 0.84). Summing up, the results displayed in Fig. 1 testify on the inherent ability of the Deep Set network to satisfactorily reproduce the critical temperature of a superconducting material, starting from its description in terms of constitutive elements. The results here presented refer to a latent space of dimension (size of the vector where information are stored) d = 300. In the annexed Supplementary Information (SI), we show that the recorded predictions are remarkably accurate also when the dimension of the latent space gets dramatically reduced. Assuming d = 1, which amounts to impose a scalar embedding in the latent space, yields a modest drop in the regression performance as quantified by the associated root mean squared error. By operating in this setting, it paves the way for a straightforward interpretation of the obtained results (see "Discussion").
As concerns the classification task, the aim is to identify putative superconductors materials. To this end we train the Deep Set on a sub-portion of the SuperCon database, potentiated with additional data from the Crystallography Open Database (COD), as convened by the garbage in procedure discussed in the “Methods” section. The trained Deep Set is then used against the test-sets of interest—the remaining data within the SuperCon augmented with COD and the Hosono database. At the end of the assessment of each individual item, the Deep Set returns a scalar quantity \(\tilde{\rho }\), ranging from zero (the material is deemed non superconducting) to unit (it is classified as superconductor). The scalar quantity can be interpreted as an effective measure of the level of confidence in the achieved prediction. The material is then classified as superconducting if \(\tilde{\rho }\, > \,{\epsilon }_{{{{\rm{th}}}}}\), for an apt threshold ϵth (see Methods). The analysis is repeated over 60 independent realizations and the results of each run stored for further analysis.
In particular, to test the performance of the method, we refer to two complementary measures. These are the precision (p), namely the fraction of relevant (i.e., correctly classified) items among the retrieved instances, and the recall (r) computed as the fraction of relevant instances that were effectively retrieved. The precision-recall curve is routinely employed as a measure of the success in carrying out the prediction, when the examined classes are imbalanced (i.e., when the number of representative elements per class is not homogeneous). In Fig. 2a the precision is plotted (green symbols) versus the recall for the SuperCon database (with the inclusion of the COD data). Different points stand for different thresholds ϵth (by increasing ϵth the precision increases smoothly and the curve is traveled from right to left). More specifically, at the exit node and for any supplied entry item, the DeeptSet returns a scalar quantity (termed ρ). If ρ > ϵth, the material is deemed superconductor, viceversa otherwise. Symbols refer to the average precision/recall over the performed, statistically independent, runs. The computed standard deviation is smaller than the size of the employed symbols. The classifier threshold ϵth can be chosen so as to return accurate results (high precision), with a rather modest quota of false negative (high recall). The results for the Hosono database, as depicted with blue symbols in Fig. 2a, are instead less captivating. To improve on this, we propose a more stringent approach to the classification which consists in designation of the material as superconductor only if this is a shared conclusion by the majority of the performed independent runs, for a given choice of the threshold. Different points (as displayed in Fig. 2b) refer to distinct choices of the threshold amount ϵth which is now operated on an ensemble made of independently trained DeepSet models.
a The performance of the classifier are challenged in the plane precision vs. recall. Green symbols refer to the SuperCon database, potentiated with data from COD. Blue symbols refer to the Hosono database. Each symbol is computed as the average over 60 independent realizations and the shadowed region reflects the associated standard deviation. b the precision vs. recall curve is plotted for the Hosono database by using the majority rule, as described in the main text: a material is classified superconducting if the majority of runs (over 60 realizations), each associated to ϵth = 0.85, leads to this conclusion. The horizontal dashed line is a benchmark reference computed by assuming random guessing for the Hosono dataset.
By applying this strategy to the analysis of the Hosono dataset yields a much more satisfactory scenario as outlined in Fig. 2b. By assuming in particular ϵth = 0.85, we identified 29 out of 39 superconductors of the Hosono database, with 19 false positive. This is a particularly satisfactory outcome given the fact that the Hosono database contains samples that are pre-filtered by experts in the field. Hence all materials are in principle reasonably good superconducting candidates.
The performance of the method, as quantified above, are superior to those displayed by other competing approaches and so far reported in the literature9,11, as we shall elaborate in the following. The algorithms developed in ref. 9 seek to separate materials (all superconducting a priori) into two distinct groups depending on whether Tc is above or below a given threshold. Modulating the imposed threshold makes it in principle possible to implement a pipeline that integrates classification and regression, and so eventually decide on the nature of the examined material. It should be stressed however that only superconducting materials are used in the training of the algorithm discussed in ref. 9. The trained network has never been taught to handle non superconducting materials. Consequently, the response obtained when presenting as an input a non-superconducting material (as one should do for classification purposes) cannot be deemed a priori meaningful. In our study, the network is instead directly trained to distinguish between superconducting and non-superconducting materials, by leveraging on the garbage in idea introduced in refs. 12.
In Figure 2 of ref. 9, the precision and recall are quantified and fall consistently below 90%, in classifier modality (to be questioned for the reasons illustrated above). As a benchmark reference, one can consider the above Fig. 2 where the curve recall versus precision is plotted for same dataset (SuperCon, green symbols) as employed in ref. 9: by properly tuning the threshold ϵth, we can push both the precision and the recall well beyond 90%, for the considered classification. Again, and thanks to the garbage in procedure, in our case we deal with a genuine classification task between superconducting and non-superconducting materials (non-superconducting materials are in fact definitely seen by the DeepSet during training stages). Notice also that the scores obtained in ref. 9 for the limited subset of materials contained in both SuperCon and the Inorganic Crystal Structure Dataset (ICSD)—just 1500 compounds—are significantly smaller (0.74 and 0.66 are reported to be found for, respectively, precision and recall) than the homologous quantities here obtained for the closest benchmark possible, the SuperCon dataset complemented with COD (Fig. 2). Remarkably the score reported in ref. 9 for the intersection between SuperCon and ICSD is worse than that obtained by applying the DeepSet method to the Hosono database. As recalled above, this is a particularly challenging testbed as it contains pre-filtered samples and thus materials are in principle reasonably good superconducting candidates. By setting the recall in between 0.6 and 0.7 for the Hosono database, we can in fact still have precisions above 0.8.
More straightforward is the comparison with the work by Konno et al.11, where deep learning tools are operated to achieve a classification of the supplied materials. When it comes to classification, the scores for both precision and recall as displayed by our method are superior to those reported in ref. 11. This can be appreciated by inspection of Table 1 in ref. 11 for the case of the aforementioned Hosono database, as well as by looking at the results reported in Section XIV C in the supplementary material of ref. 11 (the top score precision 0.52 reported in ref. 11 to be compared with 1, as obtained with our method, for suitable choices of the recall, against the same dataset). Also the F1 metric (the harmonic mean of precision and recall) for the same dataset (characterized by a baseline precision of 20%) is found to be 0.71 to be compared with the 0.63 reported in ref. 11.
Following the above validation, we applied the trained Deep Set, in this latter version that implements the majority rule, to the analysis of the updated list (September 2021) of minerals accepted by the International Mineralogical Association. As for the above setting, we assumed ϵth = 0.85 and averaged out 60 independent runs. In the SI we report the list of minerals classified as superconductors, when setting ϵth = 0.85. Interestingly enough, about 44% of the minerals selected by the trained network were indeed already verified to be superconductors (this information is displayed in the the annexed SI, together with the indication of corresponding study). Notice that none of the samples contained in the mineral catalogue was supplied during training. In the current version of the implementation we do not keep track of additional annotations as, e.g., high pressure or thin layers. This is a worthwhile direction of further investigation which however necessitates investing on the quality of the existing database. For the sake of completeness, we can recalculate the percentage of success of the DeepSet prediction by excluding from the pool superconducting materials at high pressure and thin films. The computed percentage is in this case 29%, still quite remarkable.
Magnetic characterization of the selected materials
Motivated by this success, we decided to focus on a subset of candidate materials, that have not yet been characterized—or poorly characterized14—in the literature, with reference to their potential superconducting behavior. In particular, we focus on the synthetic analogues of a sublist of minerals (see also Methods and Table 1) that were tagged at superconducting by the DeepSet technology. These are Pd3HgTe3 (the analogue of the mineral temagamite), PdBiTe (the analogue of the mineral michenerite), and Pd2NiTe2 (the analogue of the mineral monchetundraite). As concerns the critical temperatures, we predicted Tc of 1.8(1.8) K, 1.6(0.8) K and 1.18(0.7) K, respectively.
We employed magnetic ac susceptometry to investigate the synthesized analogues of the three minerals expected to exhibit superconductivity. Ac susceptibility \({\chi }_{{{{\rm{ac}}}}}^{{\prime} }\), measured in zero static magnetic field is a simple and sensitive technique to evidence the presence of superconducting phases through the detection of a diamagnetic signal that is proportional to the volume fraction exhibiting flux line expulsion16,17,18. The onset of the diamagnetic signal is to be considered the intrinsic Tc of the superconductors, while at lower temperatures the coupling between SC grains can result in a further increase of the diamagnetic signal.
Figure 3 collects the temperature dependence of the real part of the ac susceptibility, χac, of the four investigated samples. Given the limited availability of the 3He set-up only the Zero Field Cooled (ZFC) magnetic susceptibility was measured. The two samples of temagamite (blue and magenta) do not reveal any sizeable diamagnetic susceptibility, while the clear onset of diamagnetic shielding is visible at T = 2.10 K for PdBiTe (michenerite, red) and, even more pronounced, at T = 1.06 K for Pd2NiTe2 (monchetundraite, black).
Temperature dependence of the real part of the susceptibility (\({\chi }_{{{{\rm{ac}}}}}^{{\prime} }\)) measured in zero static field for the four investigated samples: Pd3HgTe3 (blue and magenta for sample prepared at 350 and 500 ∘C, respectively), PdBiTe (red), and Pd2NiTe2 (black). A zoom around the transition of Pd2NiTe2 is provided in the inset with \({\chi }_{{{{\rm{ac}}}}}^{{\prime} }\) as squares and \({\chi }_{{{{\rm{ac}}}}}^{{\prime\prime} }\) as triangles.
Given the more pronounced SC behavior of Pd2NiTe2, we extended the investigation. First, we checked that the employed oscillating magnetic field, Hac, is not too large to significantly affect the transition. Supplementary Fig. 14 in SI shows the susceptibility data taken at Hac = 1 and 3 Oe. The susceptibility curves are superimposable, confirming that the width of the transition is intrinsic.
To get an insight into the critical field of this superconducting phase, we also measured both ac susceptibility and dc magnetization under the effect of a variable dc magnetic field at T = 0.50 (±0.02) K. Figure 4 reveals that at this temperature a first critical field is observed at ~20 Oe, as evidenced by the minimum in M vs. H plot and the drop in \({\chi }^{{\prime} }\) vs. H plot, as well as by the onset of irreversibility in χ″ curves. Such a behavior can be either ascribed to the onset of an intermediate state in type I superconductors or to the 1st critical field in type II superconductors. The irreversibility in the \({\chi }^{{\prime} }\) vs. H curves is almost negligible and significantly weaker than in the M vs. H curves, in agreement with the fact that only minor hysteresis loops are detected. Importantly, diamagnetism is fully suppressed in a field of around 160 Oe, from ac measurements, and only at around 70 Oe from dc measurements. This behavior is indicative of a complex dynamics and points to a type II superconductor.
Field dependence of the ac susceptibility measured for Pd2NiTe2 with \({\chi }_{{{{\rm{ac}}}}}^{{\prime} }\) as squares and \({\chi }_{{{{\rm{ac}}}}}^{{\prime\prime} }\) as triangles at T = 0.50 K. In the inset the dc magnetization measured at the same temperature. Red and black symbols refer to the direction of the scanning field as indicated by the arrows.
It is interesting to correlate our experimental findings to the predicted critical temperatures. A very good agreement is observed for PdBiTe and Pd2NiTe2, for which a relatively small standard deviation was computed, while Pd3HgTe3 does not show any superconductivity down to 0.45 K, despite being predicted with the highest Tc.
We must however keep in mind that some contaminants present in the synthesized materials (Table 1, see Methods) also exhibit SC properties. Unfortunately, quantification of the SC phases remains an issue in the absence of additional investigations. First of all, the diamagnetic susceptibility depends on the shape of the sample due to the demagnetization factor. When loose crystalline powders are employed, as in our case, the signal can be considered as the sum of the individual grains, and the demagnetization factor is assumed to be that of the sphere N = 4π/3 in cgs units.
The largest measured diamagnetic signal corresponds to ca 2% and 5% of volume fraction for PdBiTe and Pd2NiTe2, respectively, though it is evident that complete diamagnetic shielding is not achieved even at the lowest temperature, as the diamagnetic susceptibility is still increasing. Last but not least, many materials, including some elemental metal and type II superconductors, do not exhibit a complete Meissner effect even in low magnetic fields16. Values as small as 2% of diamagnetic shield were observed for loose small grains of high Tc SC and attributed to the field penetration depth being comparable to the grain size19. Interestingly, the diamagnetic signal of the high Tc SC gradually increases on lowering the temperature, as observed in our case.
In the case of PdBiTe, the only detectable impurity is αPdBi2, whose Tc = 1.7 K20 is however significantly lower than the observed one. In addition the measured diamagnetism exceeds that expected considering that only the impurity is a superconductor with complete Meissner shielding. These findings suggest that the observed susceptibility is intrinsic of michenerite. Unfortunately, we cannot compare our results with those of the previous study14, as the authors just listed PdBiTe as superconductor without reporting any experimental data.
In the case of Pd2NiTe2, the detected impurity has the PdTe structure but no anomaly is observed at the expected Tc of 4.5 K21. Interestingly this is also true for the two samples of Pd3HgTe3, which also contain this impurity (see Supplementary Fig. 15). However, a recent study has shown that the replacement of Pd with Ni in PdTe induces a significant lowering of Tc. Even if we cannot exclude the presence of a superconductivity impurity with complex composition, this latter is unlikely to be the cause of the peak in the imaginary component of the susceptibility (see inset of Fig. 3) because: (i) for the experimental composition of the impurity (Pd0.7Ni0.3Te), Goyal et al. did not detect any SC transition above 2 K22; (ii) for lower Ni content the transition becomes very broad22 while it is rather abrupt in our sample of Pd2NiTe2. We can thus reasonably conclude that also for this sample the results suggest an intrinsic superconductivity, as predicted by our ML approach. Optimized synthetic processes calibrated so as to significantly reduce the presence of impurities could yield improved samples for further investigations.
To improve on the quality of the existing database it is crucial to keep track of materials which have been shown not to display a superconducting phase. To contribute along this line, while at the same time testing the predictions of the proposed method from a different perspective, we have also measured the ac susceptibility of three compounds tagged as non-superconducting by DeepSet. These are the synthetic analogues of polarite (PdHg), telluropalladinite (Pd9Te4), and paolovite (Pd2Sn). The experiments show that none of them present superconducting features down to 0.5 K in agreement with what anticipated by DeepSet (see SI).
Discussion
In this study we have proposed and thoroughly tested a machine learning scheme that could contribute with a decisive boost in the search for novel superconducting materials. The peculiar architecture of the neural network employed enables us to deal with sets, rather than individual entries. This proves fundamental in correctly handling the supplied input, the actual chemical composition of the examined crystal, without bias that could in principle originate from the chosen ordering in the designated list. Moreover, the final output follows a pooling operation that enables one to trace back the impact of each element in the chemical formula. This proves particularly intriguing when the latent space is compactified in a manifold of reduced dimensionality, a choice that allows to markedly enhance the interpretability of the result at a modest detriment of the recorded performance. Particularly illuminating is the limiting setting when d = 1. Each element of the periodic table is connected to a characteristic scalar attribute, termed x1 (see SI). To illustrate the main idea, focus on the regression task (determining the associated critical temperature). The parameter x1 can be hence interpreted as the individual endowment of every single atom to the estimated critical temperature, by recalling that distinct contributions are combined linearly in the latent space as in the spirit of the Deep Set technology. The larger x1, the more significant the shift to the ensuing critical temperature as stemming from the considered element. The predicted value of x1 can be used to re-plot the periodic table with an apt color code as shown in Fig. 5. Working in this limiting setting, the obtained predictions are indeed less accurate ad compared to the reference choice d = 300, though still remarkable. Indeed, one can associate to each chemical composition a reference value that is computed as the sum of the estimated x1, each referred to the atoms that compose the examined compound. This information can be used—for example—to discriminate superconducting materials that display a critical temperature below/above 10 K, as in the spirit of the analysis carried out in ref. 9. Proceeding along these lines, we eventually obtain an accuracy of 84% (that corresponds to say that more than 4/5 of the analyzed materials are correctly assigned to their reference group), for a threshold in x1 set to −2.5.
The periodic table is plotted by associating to each case its corresponding x1 entry (the latent space has d = 1), displayed with an appropriate color code. Atoms that contribute to increasing the critical temperature are those characterised by larger (positive) x1 amount (see SI for further details).
Direct inspection of Fig. 5 suggests that Ca is identified by the trained neural network (in its minimal implementation) as one of the key elements for high Tc superconductors. This conclusion should be handled with care, as it could—to some extent—reflect the choice of operating with the smallest possible latent space. On the other hand, it should be also remarked that the superconductor with the highest transition temperature at ambient pressure is the cuprate of mercury, barium, and calcium, in line with the model prediction. More into depth, the median of the critical temperature of superconducting material containing Ca is 73 K, to be compared with that associated to materials containing Cu (58.8 K) and Fe (20.88 K). In general, 50% of the superconductors containing Ca displays a critical temperature in the range 41–88 K.
Additional information are provided in the SI where the problem of classification (deciding whether a material is indeed superconducting) for the case d = 1 is also discussed.
The Deep Set algorithm set to operate with d = 300 is challenged with reference to both classification and regression. Particularly relevant results are obtained when challenging the trained network against the database of Hosono and collaborators1: in this case the list of materials is in fact pre-filtered by experts in the field to yield a selection of candidates that are worth of investigation as potential superconducting candidates, for their structural characteristics. The Deep Set trained on a set of independent data, not including the entries of the Hosono database, is capable of identifying a large fraction of the materials certified as superconductors in refs. 1,11, following dedicated experiments. Furthermore, the critical temperature of the superconductors is nicely predicted. Motivated by this finding we applied the Deep Set methodology to the list of minerals provided by the International Mineralogical Association and obtained a sublist of materials that, according to our analysis, are plausible superconducting candidates. Among these, we selected three different materials and carried out direct experiments to test the adequacy of our predictions. Superconductivity has been observed for two of the investigated mineral analogues of michenerite and monchetundraite at critical temperatures in very good agreement with the predictions. Though these results need to be confirmed by more detailed investigations on samples of improved purity, they should be regarded as an additional proof of the success of the proposed method. Monchetundraite is in particular the first certified superconducting material to be identified by articial intelligence methodologies.
To take one step in the direction of improving the quality of the current database, we also report on the results of experiments carried out on three compounds—the synthetic analogues of polarite (PdHg), telluropalladinite (Pd9Te4), and paolovite (Pd2Sn)—tagged as non-superconducting by DeepSet. The experiments bring evidence that the examined materials are indeed non-superconducting, a finding that confirms in turn the validity of the analysis from a different, though less stringent, standpoint.
Methods
Deep Set architecture
Deep Set enables us to extend the input space of machine learning algorithms, to generic sets, rather than vectors, as customarily done. By set one signifies an unordered collection of objects. A valid function defined on a set should be invariant under permutations of the elements belonging to the very same set, supplied as an input. Assume a set to be made by an unordered collection of elements. Then, each permutation that promotes an internal reshuffling of a pre-existing order, should yield the same functional output. Stated differently, the produced output should be insensitive to the imposed permutation, a requirement that translates into an invariant constraint. It can be shown that any function \(f:{2}^{{{{\mathscr{H}}}}}\to {\mathbb{R}}\), with \(| {{{\mathscr{H}}}}|\, < \,{\aleph }_{0}\) (the cardinality of the countably infinite), acting on a set X is a valid function, i.e., invariant under permutation of the instances of X, if and only if it can be cast in the form ρ(∑x∈Xϕ(x)), for two appropriate transformations ρ and ϕ. The problem of obtaining a valid function f, defined on sets, is therefore equivalent to identify a suitable function ρ, which takes instances from the set, as an input, upon filtering by ϕ. Standard neural networks can be employed to approximate the aforementioned functions ϕ and ρ, at desired precision level. Deep Set architectures can be applied to either classification or regression problems, as other neural networks of standard conception. For the specific case at hand, the elemental composition of the examined crystal is supplied as an input and define the set of interest. More specifically, and as outlined below, each element is characterised by a list of 22 instances, stored in a vector. The stoichiometric integer of the selected atom is also provided, as an additional entry of the vector. In Fig. 6 a schematic outline of the applied Deep Set architecture is provided.
A schematic layout of the Deep Set architecture here employed. The input of the Deep Set is the set of elements that compose the analyzed compound. Each element is associated to 22 chemical/physical instances as described in the main body of the paper. The stoichiometric contribution of a given element defines an additional entry of the supplied vector. The input is processed by the non linear function ϕ, represented as a feed forward neural network. The result of the processing are gathered together and further transformed by the application of a non linear filter ρ. This is also defined in terms of a neural network. The produced output is confronted to the expected target, during training stages, and the parameters of the networks ϕ, ρ tuned so as to minimise the assigned loss function.
From the set of elements that compose the material to the input set
The Deep Set receives as an input the set of elements that compose the examined material. Each element is associated to a vector of 22 instances drawn from the Mendeleev software23. This is a freely available Application Programming Interface (API), written in Python, for accessing various properties of elements from the periodic table. The 22 instances considered are respectively the atomic number, the atomic volume, the block in periodic table, the density at 295 K, the dipole polarizability, the electron affinity, the evaporation heat, the fusion heat, the group in periodic table, the lattice constant, the lattice structure symbol, the melting temperature, the period in the periodic table, the specific heat at 293.15 K (20 oC), the thermal conductivity at 293.15 K (20 oC), the Van der Waals radius, the covalent radius, the Pauling’s scale of electronegativity, the atomic weight, the atomic radius, the ionization energies (in eV), the valence. Missing data were recovered from atom datasets made available on Mathematica, and specifically those referred to density, electron affinity, fusion heat, lattice constant, specific heat and thermal conductivity. In the analysis we focused on atoms with atomic number smaller than 96. By gathering information from different datasets we could reduce the amount of missing data to about 4% of the total. The stoichiometric integer, i.e., the number of times the selected atoms appears in the chemical formula, is also supplied as one additional entry of the input vector. The non linear function ϕ maps every input vector into a latent space, as evident in the scheme depicted in Fig. 6. The dimensionality (d) of the target latent space (the space where the processed information is embedded by the trained network) can be tuned at will. The embedding of the input is self-consistently driven by data, thus allowing to overcome intrinsic bias that might arise when shaping the latent space with direct human intervention. Results reported in this study refer to two different settings. On the one side we shall assume a sufficiently large value for d to provide the Deep Set with a wide range of computational degrees of freedom. Then, in the SI, we report the conclusions for the setting d = 1 (see also Fig. 5 in the “Discussion” section): with this choice, one achieve a noticeable gain in terms of interpretability of the associated latent space, at the price of a modest drop in the overall performance of the method. In the SI, we also quantify the recorded performance as a function of the imposed latent space dimension, d (Supplementary Fig. 1). Upon application of ϕ, one hence obtains an output vector in d-dimensions. Vectors associated to different elements are summed together, before being further elaborated via a subsequent non linear transformation, denoted with ρ. The representation in the latent space can be also engineered to be linear, with respect to the stoichiometric index. Any compound is hence portrayed as a point in d-dimension: its location follows the linear superposition of distinct contributions, each coming from every single constitutive element, weighed with its stoichiometric coefficient.
Datasets employed for learning and testing
Data are extracted from the SuperCon database, which consists into two separate subsets: Oxide and Metallic compounds (inorganic materials containing metals, alloys, cuprate high-temperature superconductors, etc.) and Organic compounds (organic superconductors). Removing compounds with incompletely specified chemical compositions and accounting for multiple records yields a final collection of 16395 independent entries.
Roughly 5700 compounds are cuprates and 1500 are iron-based materials. The remaining set includes conventional phonon-driven superconductors, known unconventional superconductors like the layered nitrides and heavy fermions, and many materials for which the mechanism of superconductivity is still to be elucidated (such as bismuthates and borocarbides).
For the regression problem (i.e., determining the critical temperature Tc), we split the SuperCon database into training (80% of the total) and test (the residual 20%) sets. This partition follows a random implementation, thus leaving a mark of inherent stochasticity the reflects back in the obtained predictions. The analysis is repeated by 50 times, each realization being refereed to independent sampling of the available datasets into training and test sets.
For classification purposes (i.e., determining if a given, supposedly unknown compound is superconducting or not) and to access a larger set of materials that are presumably non superconductors, we adopted a technique pioneered in ref. 11 and termed garbage in. This latter is here applied to the Crystallography Open Database (COD). Since superconductors are just a few percent of the total, we label all materials belonging to COD as non superconductors. Then, the full database was randomly sampled to extract a collection of entries, that we used to thicken the population of superconductors. Since superconductors are rare, the errors (the inclusion of superconductors in the reservoir of non superconducting materials) are, in all probability, small: the benefits of enlarging the examined pool of materials, overcome the disadvantages, which stem from having contaminated the dataset with a few erroneous entries (garbage that is put in). The performance of the classification are shown to steadily increase as a function of the amount of material, selected from the COD as putative non superconductors, up to about 50,000 (see SI). This is the setting that we have assumed in the course of the analysis reported in this study.
Another employed database is that produced by Hosono et al.1. This latter paper examined a relatively short list of pre-selected materials, each of which chosen by experts with a background in solid state chemistry. Several superconductors were identified (3% of the total, as anticipated above) and thoroughly characterised. Importantly, the list of unsuccessful materials tested for superconductivity was also provided. In this study, we make use of a distilled version of the original database. This is discussed in ref. 11, and it will hereafter referred to as Hosono database. It contains 207 materials, 39 superconductors and 168 non superconductors. The Hosono database allows for an independent and more stringent test (since materials were pre-selected as possible superconductors) of the performance of Deep Set classificator.
Finally, we used the trained Deep Set against the updated list (September 2021) of minerals accepted by the International Mineralogical Association (https://www.ima-mineralogy.org/minlist.htm).
Training the Deep Set
To build and train the Deep Set model we used TensorFlow and leveraged on automatic build-in optimisers. For the regression problem, the non linear function ϕ is implemented as a neural network made of 7 layers, with a variable number of nodes, ranging from 96 to 992. The activation function chosen is the ReLu8 for all the layers except for the final layer (the one that populates the latent space), where it is set to be linear. The non linear function ρ is implemented with a neural network made of 13 layers, including the output one. The number of nodes range from 128 to 960. The ReLu activation function is used to filter the signal on the nodes, across different layers. The loss function employed for training the model is the mean square error. The produced (\(\rho ({\sum }_{x\in X}\phi (x))\to \tilde{\rho }\)) output is the predicted temperature.
For classification purposes, the non linear function ϕ is set to be a neural network made of 4 layers and 300 nodes per layer. The activation functions are chosen as for the regression problem. The non linear function ρ is a neural network made of 3 layers (in addition to the output layer) with number of nodes respectively fixed to 300, 300, and 100. A ReLu activation function is used in all layers, except for the last one where we chose a sigmoidal function. The loss function is the binary crossentropy. The produced output \(\rho ({\sum }_{x\in X}\phi (x))\to \tilde{\rho }\)) is a real number, ranging in the interval [0, 1]. Values close to zero imply that the inspected material is non superconducting. Conversely, the material is classified as superconducting, when \(\tilde{\rho }\) approaches one. To obtain a binary output, we introduce a threshold ϵth ∈ [0, 1] with the conditon that the material is indeed superconducting if \(\tilde{\rho }\, > \,{\epsilon }_{{{{\rm{th}}}}}\). The larger the value of ϵth the more certain the Deep Set ought to be before classifying the material as superconducting.
For training the Deep Set network, we made use of Adam optimiser8, by setting a learning rate of 0.001. The training proceeded for a maximum number of epochs equal to 400. We adopted an early stopping regularisation with patience settled to 40. During successive epochs the network was fed with batches of size 64. These hyperparameters follow the Hyperband algorithm, and are set so as to improve the performance of the model. The code employed, as well as a notebook to reproduce our results, can be found in the public repository of this project.
Synthesis and characterization of mineral analogues
The synthetic analogues of a few selected minerals from the list (i.e., Pd3HgTe3—an analogue of temagamite, PdBiTe—an analogue of michenerite, Pd2NiTe2—an analogue of monchetundraite, PdHg—an analogue of potarite; Pd2Sn - an analogue of paolovite; Pd9Te4—an analogue of telluropalladinite) were synthesized by using silica-glass tube methods as described in refs. 24,25. Temperature conditions and more details are given in SI.
Chemical analyses were performed with a CAMECA SX-100 EPMA in wavelength dispersive mode using an electron beam focused to 1–2 μm and an accelerating voltage of 15 keV, and a beam current of 10 nA on the Faraday cup. Pure elements were used as calibrants.
The powder X-ray diffraction data of the experimental products were collected on a Bruker D8 Advance diffractometer in Bragg-Brentano geometry using LynxEye XE detector and CuKα radiation. The initial phase identification was carried out by HighScore program26. Subsequent quantitative phase analysis was performed by Rietveld method using Topas 5 program27. The crystal structure models were taken from the Inorganic Crystal Structure Database 202128. The fundamental parameter approach for the peak shape description for all phases present in the samples was used. Only scale factors, unit-cell parameters and parameters describing profile (CrySize L and Strain G) were refined. No atomic coordinates were refined. Correction for preferred orientation (March-Dollase) of Pd3HgTe3 along [001] was applied. The X-ray powder patterns with the assigned phases of the studied samples are given in the SI, as Supplementary Figs. 6, 7, 8, 9, 10, 11 and 12.
The two synthesized Pd3HgTe3 samples resulted to be mainly constituted by the P3m1 phase (temagamite). Impurity of PdTe (P63/mmc, kotulskite) known to be a superconductor below 4.5 K21, was quantified to be 1.8% and 0.8% in weight for the sample prepared at 500 ∘C and 350 ∘C, respectively. PdBiTe sample was almost totally constituted by the P213 phase (michenerite) with 0.9% impurity of αPdBi2 (C2/m), which is a superconductor with Tc = 1.7 K20. Pd2NiTe2 sample comprises mainly the Ibam phase (monchetundraite) with 4.5% impurity of PdTe (P63/mmc, kotulskite). A more detailed analysis of the X-ray data combined with electron microprobe analysis indicated that the impurity has average composition Pd0.7Ni0.3Te.
PdHg and Pd9Te4 samples resulted to be mainly constituted by the P4/mmm and P21/c phases, which correspond to potarite and telluropalladinite, respectively. Pd2Sn sample comprises mainly the Pnma phase (paolovite) with 9% impurity of Pd3Sn2 (P63/mmc, stannopalladinite). In Table 1 the percentages of the various phases (main and impurities) are provided, together with the associated space group, for the examined samples.
Magnetic characterization
Static (dc) and dynamic (ac) magnetic measurements were performed on a Quantum Design MPMS magnetometer by using ball-shaped samples of loose microcrystalline powders wrapped in PTFE. Measurements were corrected for diamagnetic contributions of both PTFE (blank measurement) and compound (calculated with Pascal constants). Low temperature measurements (≤1.6 K) were performed using a Quantum Design 3He insert (iHelium3) adapted to the MPMS magnetometer. For both configurations, careful degaussing of the magnet was performed and the small remaining field (2 Oe) was compensated to ensure a measurement in zero-field conditions (Hdc = 0 Oe). Optimal data for dynamic magnetic measurements were obtained for Hac = 3 Oe and oscillating field frequency equal to 10 Hz.
Data availability
SuperCon dataset is available at the following link: https://mdr.nims.go.jp/collections/5712mb227. The so called Hosono database is made available here: https://github.com/tomo835g/Deep-Learning-to-find-Superconductors.
Code availability
Employed codes are made available at the following link: https://github.com/ClaudioPereti/From_individual_elements_to_macroscopic_materials.
References
Hosono, H. et al. Exploration of new superconductors and functional materials, and fabrication of superconducting tapes and wires of iron pnictides. Sci. Technol. Adv. Mater. 16, 033503 (2015).
He, H. et al. Amc: Automl for model compression and acceleration on mobile devices. In Proc. European Conference on Computer Vision (ECCV), 784–800 (2018).
Sutton, R. S. & Barto, A. G. Reinforcement Learning: An Introduction (MIT press, 2018).
Grigorescu, S., Trasnea, B., Cocias, T. & Macesanu, G. A survey of deep learning techniques for autonomous driving. J. Field Robotics 37, 362–386 (2020).
Biancalani, T. et al. Deep learning and alignment of spatially resolved single-cell transcriptomes with Tangram. Nat. Methods 18, 1352–1362 (2021).
Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning (MIT Press, 2016). http://www.deeplearningbook.org.
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Deng, L. & Yu, D. Deep learning: methods and applications. Found. Trends Signal Process. 7, 197–387 (2014).
Stanev, V. et al. Machine learning modeling of superconducting critical temperature. Npj Comput. Mater. 4, 29 (2018).
Ho, T. K. Random Decision Forests. In Proc. Third International Conference on Document Analysis and Recognition (Volume 1) - Volume 1, ICDAR ’95, 278–282 (IEEE Computer Society, M, 1995).
Konno, T. et al. Deep learning model for finding new superconductors. Phys. Rev. B 103, 014509 (2021).
Komiske, P. T., Metodiev, E. M. & Thaler, J. Energy flow networks: deep sets for particle jets. J. High Energy Phys. 121, 1–45 (2019).
Bindi, L., Nespolo, M., Krivovichev, S. V., Chapuis, G. & Biagioni, C. Producing highly complicated materials. Nature does it better. Rep. Prog. Phys. 83, 106501 (2020).
Hulliger, F. & Müller, J. Superconductivity and semiconductivity in cobaltite- and pyrite-type compounds. Phys. Lett. 5, 226 (1963).
Li, S. et al. Critical temperature prediction of superconductors based on atomic vectors and deep learning. Symmetry https://www.mdpi.com/2073-8994/12/2/262 (2020).
Shoenberg, D. Superconductivity. (Cambridge University Press, U.K., 1962)..
Francavilla, T., Hein, R. & Liebenberg, D. Magnetic Susceptibility of Superconductors and Other Spin Systems. (Springer, US, 1991).
Goldfarb, R. B., Lelental, M. & Thompson, C. A. Alternating-Field Susceptometry and Magnetic Susceptibility of Superconductors. (NIST Interagency/Internal Report (NISTIR), Gaithersburg, 1991)..
Thompson, J. R. et al. Studies of “Non-ideal” Superconductors using Dc Magnetic Methods, 157–176 (Springer US, Boston, MA, 1991). https://doi.org/10.1007/978-1-4899-2379-0_7.
Mitra, S. et al. Probing the superconducting gap symmetry of α − PdBi2: a penetration depth study. Phys. Rev. B 95, 134519 (2017).
Karki, A. B., Browne, D. A., Stadler, S., Li, J. & Jin, R. PdTe: a strongly coupled superconductor. J. Phys. Condensed Matter 24, 055701 (2012).
Reena, G., Rajveer, J., Brajesh, T., Ambesh, D. & Awana, V. P. S. Impact of Ni doping on critical parameters of PdTe superconductor. Supercond. Sci. Technol. 29, 075008 (2016).
Mentel, L. mendeleev – A Python resource for properties of chemical elements, ions and isotopes. https://github.com/lmmentel/mendeleev.
Vymazalová, A., Laufek, F., Grokhovskaya, T. & Stanley, C. Monchetundraite, Pd2NiTe2, a new mineral from the Monchetundra layered intrusion, Kola Peninsula, Russia. Mineral. Petrol. 114, 263–271 (2020).
Vymazalová, A., Laufek, F., Kristavchuk, A. V., Chareev, D. A. & Dr/’abek, M. The system Ag-Pd-Te: phase relations and mineral assemblages. Mineral. Mag. 79, 1813–1832 (2015).
PANalytical, B.V. HighScore 3.0. (Almelo, The Netherlands, 2011).
Bruker AXS. Topas 5, computing program. (Bruker AXS GmbH, Karlsruhe, Germany, 2014).
FIZ. FIZ Karlsruhe - Leibnitz Institute for Information Infrastructure, Inorganic Crystal Structure Database 2021, (Karlsruhe, Germany, 2021).
Acknowledgements
This research was supported by the Grant Agency of the Czech Republic (project No. 22-26485S), by the MIUR-PRIN2017 via project “TEOREM deciphering geological processes using Terrestrial and Extraterrestrial ORE Minerals”, prot. 2017AK8C32 and the Italian Ministero dell’Istruzione, dell’Università e della Ricerca through the “Progetto Dipartimenti di Eccellenza 2018-2022”.
Author information
Authors and Affiliations
Contributions
C.P., L.B., R.S., and D.F. conceived and designed the study; C.P. set up and trained the deep set architecture; T.G., K.B., and R.S. performed the experiments to characterize the magnetic properties of the samples; F.L. and A.V. provided the examined samples; C.P., L.B., R.S., and D.F. contributed to interpreting the results and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pereti, C., Bernot, K., Guizouarn, T. et al. From individual elements to macroscopic materials: in search of new superconductors via machine learning. npj Comput Mater 9, 71 (2023). https://doi.org/10.1038/s41524-023-01023-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-023-01023-6