Concurrent multi-peak Bragg coherent x-ray diffraction imaging of 3D nanocrystal lattice displacement via global optimization

Abstract

In this paper we demonstrated a method to reconstruct vector-valued lattice distortion fields within nanoscale crystals by optimization of a forward model of multi-reflection Bragg coherent diffraction imaging (MR-BCDI) data. The method flexibly accounts for geometric factors that arise when making BCDI measurements, is amenable to efficient inversion with modern optimization toolkits, and allows for globally constraining a single image reconstruction to multiple Bragg peak measurements. This is enabled by a forward model that emulates the multiple Bragg peaks of a MR-BCDI experiment from a single estimate of the 3D crystal sample. We present this forward model, we implement it within the stochastic gradient descent optimization framework, and we demonstrate it with simulated and experimental data of nanocrystals with inhomogeneous internal lattice displacement. We find that utilizing a global optimization approach to MR-BCDI affords a reliable path to convergence of data which is otherwise challenging to reconstruct.

Introduction

Bragg coherent diffraction imaging (BCDI) is a synchrotron-based characterization technique that utilizes coherent x-ray illumination and three-dimensional (3D) phase retrieval algorithms to interrogate the internal structure of sub-micron-sized crystalline materials at spatial scales of tens of nanometers^1,2. This is possible because Bragg coherent diffraction is sensitive to the shape of the crystal and its internal atomic lattice displacement field projected along the direction of the scattering vector. This information is encoded in the amplitude and phase of the complex-valued wave that creates a fringe pattern about the diffracted Bragg peak. However, as with other x-ray scattering techniques which face the crystallographic “phase problem,” BCDI measurements record only the intensity of the diffracted wave, providing no direct information as to the phase. Thus phase retrieval approaches are needed to gain access to the reconstructed 3D image of the crystal and its internal lattice distortion field. The typical approach to solving this phase problem in BCDI is via iterative methods^3,4,5 that update an estimate of the 3D image based on the error between its diffraction (emulated via a ‘forward model’) and the experimentally observed diffraction of a Bragg peak from the sample. BCDI of this sort uses a family of relatively straightforward iterative phase retrieval algorithms to reconstruct the spatial distribution of a single scalar component of the lattice distortion field of a nanocrystal, with many examples in the literature from diverse materials systems^6,7,8. BCDI methods have also been developed to directly retrieve the full 3D lattice distortion field in a nanocrystal by solving the phase retrieval problems for multiple BCDI datasets from different independent Bragg reflections of the same crystal.

The multi-reflection approach (MR-BCDI) involves a more complex measurement as compared to standard BCDI, requiring multiple Bragg peaks from a single nanoparticle to be measured⁹. This further complicates the image reconstruction process by imposing additional constraints, which then become difficult to reconcile simultaneously with the target image of interest. Various strategies of MR-BCDI image reconstruction have been developed that either utilize phase retrieval methods adapted from standard single-Bragg-peak approaches to reconstruct experimental data sets^10,11,12, or that explore more sophisticated multi-Bragg peak reconstruction concepts within the realm of simplified simulated data^13,14 that are more difficult to translate to as-measured MR-BCDI data sets.

In this work, we introduce an MR-BCDI reconstruction approach that can reconstruct experimental data directly and that is compatible with modern optimization methods. As compared to other MR-BCDI methods, our approach enables global fitting to the full set of intensity patterns from multiple Bragg peaks in order to determine the scattering volume of a crystal and its internal lattice distortion field, affording a much more reliable path to convergence. In this paper, we present this forward model, we implement it within the stochastic gradient descent optimization framework common in machine learning model training, and we demonstrate the method with simulated and experimental data. We focus in particular on enabling accurate reconstructions of crystals that contain discontinuities in their lattice distortion fields.

Results

The multi-reflection BCDI forward model

A comprehensive forward model for MR-BCDI must tackle several prominent challenges inherent to the geometry of the measurement. First, each Bragg peak measurement is sensitive to a specific projection of the displacement field u within the crystal sample along the reciprocal lattice vector G of the measured reflection. Second, the crystal and detector must be physically rotated to different orientations to satisfy each different Bragg reflection, resulting in different orientations (or views) of the sample with respect to the detector. Third, the reciprocal space sampling basis of each Bragg peak is generally different and non-orthogonal. This comes about because parallel 2D slices of the 3D diffraction intensity patterns about each Bragg peak are obtained via a fine angular scan (rocking curve) of the crystal by one of the sample rotation stages of the diffractometer after the sample and detector are oriented for diffraction. Thus, flexible multi-axis rotation and adaptable and accurate re-sampling of the sample object space to the different bases dictated by the measured data are needed.

A final requirement, as discussed in the next section, is that in order for this forward model to be suitable for inversion using modern numerical optimization toolkits available as part of machine learning packages, it should be composable of differentiable elementary functions. This allows global optimization of a loss function based on rapid evaluation of gradients through the numerical process of automatic differentiation, which has recently gained traction in x-ray coherent diffraction imaging¹⁵. As we describe here, our MR-BCDI forward model is designed to accommodate these requirements.

The forward model for MR-BCDI is built upon a reference frame in which relevant conventions and operations can be defined. To describe the nanocrystal containing a distortion field we wish to reconstruct, we adopt a right-handed ortho-normal laboratory frame $[{\hat{{{{\boldsymbol{s}}}}}}_{1}\,{\hat{{{{\boldsymbol{s}}}}}}_{2}\,{\hat{{{{\boldsymbol{s}}}}}}_{3}]$ (Fig. 1). This frame is defined such that the incident x-ray beam path k_i is coincident with ${\hat{{{{\boldsymbol{s}}}}}}_{3}$, and ${\hat{{{{\boldsymbol{s}}}}}}_{2}$ is vertically upward. In this frame, we define the following quantities needed for the forward model:

• The three-dimensional scalar field ${{{\mathcal{A}}}}({{{\bf{x}}}})$ and the 3D vector field u(x), respectively denoting the spatial distribution of scattering amplitude and the spatial distribution of the relative lattice displacement vector within the crystal at locations ${{{\bf{x}}}}\in {{\mathbb{R}}}^{3}$. We assume ${{{\mathcal{A}}}}({{{\bf{x}}}})\in [0,1]$ and define ${{{\mathcal{A}}}}:{{\mathbb{R}}}^{3}\to {\mathbb{R}}$ and ${{{\bf{u}}}}:{{\mathbb{R}}}^{3}\to {{\mathbb{R}}}^{3}$.

• The bounding box ${{{\mathcal{V}}}}$ that should be larger than the expected size of the crystal. Outside of this volume, the condition ${{{\mathcal{A}}}}({{{\bf{x}}}})=0$ and u(x) = 0 is enforced. ${{{\mathcal{A}}}}$ and u are discretized on a given grid within ${{{\mathcal{V}}}}$ with a voxel size s₀ along each of the Cartesian axes $[{\hat{{{{\boldsymbol{s}}}}}}_{1}\,{\hat{{{{\boldsymbol{s}}}}}}_{2}\,{\hat{{{{\boldsymbol{s}}}}}}_{3}]$. Typical voxel sizes s₀ for BCDI experiments are ~ 10-nm due to the resolution limits of the method, a length scale that spans many lattice unit cells in the physical crystal.

• The reciprocal lattice vectors corresponding to the multiple Bragg reflections (M in number) measured within a MR-BCDI data set are denoted by the set ${\{{{{{\bf{G}}}}}_{i}\}}_{i = 1}^{M}$. The physical units of the G_i are chosen to be the inverse of those chosen for u(x), i.e., ∥G_i∥ = 1/d_i, where d_i is the corresponding spacing of atomic planes diffracting to a given peak.

• The 3 × 3 rotation matrices ${\{{{{{\mathcal{R}}}}}_{i}\}}_{i = 1}^{M}$ that act upon the nanocrystal in the lab frame to bring its crystal lattice into each of the G_i Bragg conditions. This matrix represents a composite rotation of the object to orient the set of sample rotation stages and the detector positioning stages used in the MR-BCDI measurement, providing the orientation of the sample as viewed from the detector. We note that ${{{{\mathcal{R}}}}}_{i}$ represents an active rotation of the object that can be implemented by applying a complementary passive rotation ${{{{\mathcal{R}}}}}_{i}^{-1}$ to the coordinates of that object, as is done in this work.

• The 3 × 3 matrices ${\{{{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}\}}_{i = 1}^{M}$ whose columns form a basis of 3D sampling vectors in real space in the frame ${\hat{{{{\boldsymbol{k}}}}}}_{1}$, ${\hat{{{{\boldsymbol{k}}}}}}_{2}$, ${\hat{{{{\boldsymbol{k}}}}}}_{3}$ of the detector (see Fig. 1). The elements of ${\{{{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}\}}_{i = 1}^{M}$ are determined by the corresponding reciprocal basis matrix ${\{{{{{\bf{B}}}}}_{{{{\rm{recip}}}}}^{(i)}\}}_{i = 1}^{M}$ which depends on the detector pixel size, detector orientation, the angular increments of the rocking curve, sample rotation axis, and the signal-space array size chosen to encompass the Bragg peak. It is important to note that ${\{{{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}\}}_{i = 1}^{M}$ for every Bragg peak scan is unique.

• Dataset-dependent scaling factors ${\{{\chi }_{i}\left\vert {\chi }_{i}\in {\mathbb{R}}\right.\}}_{i = 1}^{M}$ for the scattering amplitude ${{{\mathcal{A}}}}$ that rescales the sample exit wave amplitude of the model to correspond to the relative intensities of the set of 3D Bragg peak measurements.

Fig. 1: BCDI measurement schematic.

BCDI setup at Beamline 34-ID-C of the Advanced Photon Source showing the laboratory and detector frames $[{\hat{{{{\boldsymbol{s}}}}}}_{1}\,{\hat{{{{\boldsymbol{s}}}}}}_{2}\,{\hat{{{{\boldsymbol{s}}}}}}_{3}]$ and $[{\hat{{{{\boldsymbol{k}}}}}}_{1}\,{\hat{{{{\boldsymbol{k}}}}}}_{2}\,{\hat{{{{\boldsymbol{k}}}}}}_{3}]$ for a single Bragg condition. The diffractometer rotations in this figure can be redefined as needed to generate forward models of MR-BCDI measurements at other synchrotron beam lines with differing geometries. k_i and k_f are drawn to satisfy the current diffraction condition with the area detector shown.

These elements can be used to make a MR-BCDI forward model that addresses the above-mentioned challenges and makes the inversion of the forward model tractable. The projection of u(x) along G_i allows the 3D complex-valued amplitude and phase of the crystal exit wave field for a given Bragg reflection to be determined as has been established in the BCDI literature: ${\psi }^{(i)}({{{\bf{x}}}})={{{\mathcal{A}}}}({{{\bf{x}}}})\exp [\iota 2\pi {{{{\bf{G}}}}}_{i}^{T}{{{\bf{u}}}}({{{\bf{x}}}})]$. The complex-valued object consistent with the i’th sample orientation in the reference frame of the detector is given by ${\psi }^{(i)}({{{{\mathcal{R}}}}}_{i}^{-1}{{{\bf{x}}}})\equiv {{{\mathcal{A}}}}({{{{\mathcal{R}}}}}_{i}^{-1}{{{\bf{x}}}})\exp [\iota 2\pi {{{{\bf{G}}}}}_{i}^{T}{{{\bf{u}}}}({{{{\mathcal{R}}}}}_{i}^{-1}{{{\bf{x}}}})]$ and represents the 3D object exit wave to be propagated to the far field for a particular Bragg reflection.

With the object in the detector coordinate frame, the issue of non-orthogonal reciprocal space sampling in BCDI and how to account for its impact in the reconstruction image space also needs to be accounted for. Here, we use the construction of B_real as derived in Reference^16,17 as a means to account for this effect. ${{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}$ is defined with respect to the i’th detector frame and originates from the reciprocal space sampling basis ${{{{\bf{B}}}}}_{{{{\rm{recip}}}}}^{(i)}$. Using the real space basis ${{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}$, the i’th object exit wave can be appropriately discretized by applying it to the 3D pixel array index space of the Bragg peak measurement. This can be implemented by defining m, a 3 × N_vox matrix of integer array coordinates with N_vox being the total number of voxels in the data of the BCDI scan under consideration. Thus, we can substitute x with the discretized ${{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}{{{\bf{m}}}}$:

$${\psi }_{{{{\bf{m}}}}}^{(i)}={\psi }^{(i)}\left({{{{\mathcal{R}}}}}_{i}^{-1}{{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}{{{\bf{m}}}}\right)=A\left({{{{\mathcal{R}}}}}_{i}^{-1}{{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}{{{\bf{m}}}}\right)\exp \left[\iota 2\pi {{{{\bf{G}}}}}_{i}^{T}{{{\bf{u}}}}\left({{{{\mathcal{R}}}}}_{i}^{-1}{{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}{{{\bf{m}}}}\right)\right]$$

(1)

The quantity B_realm produces a grid of sampling points in real space along a non-orthogonal basis. The discrete Fourier transform (DFT) of ${\psi }_{{{{\bf{m}}}}}^{(i)}$ from Equation (1) yields the far field diffraction pattern Ψ⁽ⁱ⁾ sampled on the conjugate grid ${{{{\bf{B}}}}}_{{{{\rm{recip}}}}}^{(i)}{{{\bf{n}}}}$ of the measurement data space, where the integer vector set n is equivalent to m. Both m and n define the equivalent 3D array index space of the diffraction pattern (n) and of the sample (m). We distinguish these indices in a manner consistent with the convention of DFT notation. This construction links the discrete sampling of both sample space and signal space via the DFT and affords significant flexibility to apply different rotation and coordinate transformations of the sample corresponding to different Bragg peak measurements:

$${\psi }_{{{{\bf{m}}}}}^{(i)}={\psi }^{(i)}\left({{{{\mathcal{R}}}}}_{i}^{-1}{{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}{{{\bf{m}}}}\right)\mathop{\rightleftharpoons }\limits_{{\mathcal{F}}^{-1}}^{\mathcal{F}}{{{\Psi }}}^{(i)}\left({{{{\mathcal{R}}}}}_{i}^{-1}{{{{\bf{B}}}}}_{{{{\rm{recip}}}}}^{(i)}{{{\bf{n}}}}\right)={{{\Psi }}}_{{{{\bf{n}}}}}^{(i)}$$

(2)

A necessary condition for implementing our forward model is that, prior to rotations into the detector frame, ${{{\mathcal{A}}}}({{{\bf{x}}}})$ and u(x) need to be discretized in the lab frame along an orthonormal grid with spacing s₀ that is similar to the magnitude of the values of B_real for the series of Bragg reflection data sets. As a consequence, the elements of all ${{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}$ should be narrowly distributed about a mean value, which can be used to designate s₀. Additionally, the degree of orthogonality of each ${{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}$ basis should be as high as possible. Both of these factors inform the design of angular rocking curve scans with suitable angular motors and angular increments at each Bragg peak. (More detail on this topic is found in the Supplementary Information.)

Another important aspect is the size of the object bounding box ${{{\mathcal{V}}}}$ relative to the total size of the buffered array in which it is nested. For each combined re-sampling and rotation transformation ${T}_{i}\equiv {{{{\mathcal{R}}}}}_{i}^{-1}{{{{\bf{B}}}}}_{{{{\rm{real}}}}}^{(i)}$, the object will be sheared, rotated, and rescaled, as will the bounding box. Since our implementation of the MR-BCDI forward problem uses the fast Fourier transform, it must be ensured that the bounding box ${{{\mathcal{V}}}}$, after transformation into each of the M detector frames, spans less than half of the number of voxels along each array axis. The implications of this requirement in terms of the measurement is that the intensity fringe pattern of each Bragg peak should be oversampled. This mirrors the well-known sampling condition for single-peak BCDI measurements.

A remaining requirement of the forward model, provided that our aim is to use modern optimization for its inversion, is that Equations (1) and (2) be implemented with readily differentiable operators. In order to achieve this efficiently, we used Fourier interpolation based operations akin to those in the image processing community^18,19,20 to implement the re-sampling and rotation T_i. More details regarding the operations we used are given in the Supplementary Information.

The MR-BCDI inverse problem

Having established a forward model for multi-reflection BCDI, establishing an inverse problem becomes a matter of expressing a loss function and implementing an automatic-differentiation-based optimization algorithm. The loss function we utilize for MR-BCDI, ${{{{\mathcal{L}}}}}_{{{{\rm{multi}}}}}$, represents the mean error in signal amplitude per BCDI data set, aggregated over the number of data sets:

$${{{{\mathcal{L}}}}}_{{{{\rm{multi}}}}}[A,{{{\bf{u}}}}]=\mathop{\sum }\limits_{i=1}^{M}\frac{1}{{N}_{{{{\rm{vox}}}}}}\mathop{\sum}\limits_{{{{\bf{n}}}}}{\left[\Big\Vert {{{\mathcal{F}}}}\left\{{\chi }_{i}{{{\mathcal{A}}}}({T}_{i}{{{\bf{m}}}}){e}^{\iota 2\pi {{{{\bf{G}}}}}_{i}^{T}{{{\bf{u}}}}({T}_{i}{{{\bf{m}}}})}\right\}{\Big\Vert }_{{{{\bf{n}}}}}-\sqrt{{I}_{{{{\bf{n}}}}}^{(i)}}\right]}^{2}$$

(3)

The quantities ${{{\mathcal{A}}}}$, u, and the global scaling factors χ_i are treated as parameters to be optimized. In this expression, χ represents the set of M scaling factors, and ${I}_{{{{\bf{n}}}}}^{(i)}$ is the measured diffraction data corresponding to the i’th Bragg reflection. The scaling factors χ are needed to reconcile the different diffraction signal strengths encountered at different Bragg peaks with the constraint that ${{{\mathcal{A}}}}\in [0,1]$. N_vox,the number of voxels in a single BCDI data set, is 128³ in all of the examples in this paper. We note that by using $\sqrt{I}$, the MR-BCDI loss function mirrors what is typically used in coherent diffraction phase retrieval approaches^21,22.

It is important to consider the degree to which the above optimization problem is overdetermined. This can be established by taking ${{{\mathcal{V}}}}$ to have an edge size of n voxels within a buffered array of size N (with n < N/2). Combining χ, ${{{\mathcal{A}}}}$, and the three scalar components of u yields M + 4n³ unknowns. The number of measurements (total pixels in the data constraint space) is given by MN³, for M BCDI scans. The MR-BCDI problem is therefore over-determined by a factor of MN³/(M + 4n³). In the case of our first numerical test presented below, M = 5, N = 128 and n = 46. This gives an overdetermination factor of ~ 27 which is significantly higher than the minimum required 1. We note further that we require M ≥ 3 Bragg peak measurements with non-coplanar G_i reciprocal lattice vectors to ensure that the optimization is overdetermined in u(x), as has been established in prior MR-BCDI literature^11,13,14,23.

It is convenient for optimization to implement the constraint ${{{\mathcal{A}}}}\in [0,1]$ analytically by defining an activation field α in order to reconcile the fact that the relative scaling of the expected values of ${{{\mathcal{A}}}}$ and the values of u may take on very different values and variances, which can complicate optimization. Thus, the scalar field α(x) is defined such that:

$${{{\mathcal{A}}}}({{{\bf{x}}}})=\frac{1}{2}\left[1+\tanh \left(\frac{\alpha ({{{\bf{x}}}})}{{\alpha }_{0}}\right)\right]$$

(4)

where the constant α₀ scales the rate of gradient descent of ${{{\mathcal{A}}}}$. This allows α to take on any value but will result in ${{{\mathcal{A}}}}$ being bracketed within the interval [0, 1]. With this definition, we see that ${{{\mathcal{A}}}}\simeq 0$ for α(x) ≪ 0 and ${{{\mathcal{A}}}}\simeq 1$ for α(x) ≫ 1. The transition between 0 and 1 in the neighborhood of α(x) = 0 is controlled by the positive hyperparameter α₀. Qualitatively, a larger value of α₀ results in a smaller gradient descent step for ${{{\mathcal{A}}}}$ at x (as is seen by differentiating Equation (4) with respect to α), and a more gradual and controlled approach of ${{{\mathcal{A}}}}$ to its intended value. Smaller α₀ results in ${{{\mathcal{A}}}}$ converging through sporadic switching between values close to 0 and 1, which is much less controlled. We found that α₀ = 1 best served our global convergence rate, and have used this for all reconstructions in this paper. Given this analytical framing of the constraint, the optimization problem to be solved in practice is:

$$\begin{array}{lll}{\alpha }^{\star },{{{{\bf{u}}}}}^{\star },{{{{\boldsymbol{\chi }}}}}^{\star }\,=\,\arg \mathop{\min }\limits_{\alpha ,{{{\bf{u}}}},{{{\boldsymbol{\chi }}}}}{{{{\mathcal{L}}}}}_{{{{\rm{multi}}}}}\left[{{{\mathcal{A}}}}[\alpha ],{{{\bf{u}}}},{{{{\chi }}}}\right]\\ \qquad\quad{{{{\mathcal{A}}}}}^{\star }\,=\,{{{\mathcal{A}}}}[{\alpha }^{\star }]\end{array}$$

(5)

where the ^⋆ indicates optimal values that produce minimum error.

The loss minimization problem framed above can be solved by implementing an optimization algorithm such as stochastic gradient descent (SCG)^24,25. Modern machine learning software toolkits offer the opportunity to do so efficiently and with relative ease. In each iteration of a gradient descent approach, the gradient of the loss function is evaluated with respect to the quantities of interest, and the quantities are updated via an increment proportional to the negative of the gradient. Thus, the total error is expected to be lower for the next iteration, and new gradients and updates are calculated and applied iteratively until improvements in error plateau. Stochastic gradient descent, which is applied in this work, applies gradient descent to different changing subsets of the constraint set. This strategy is valuable in cases where the starting guesses of the quantities of interest are likely far from the eventual solutions, and coarse updates based on gradients with respect to subsets of the full constraint space prove effective in reducing error in early iterations. In our work, α^⋆, u^⋆, χ^⋆ are updated first by constraining to two of the available Bragg peaks data sets. Then a gradually stricter global constraint to the data is imposed as the reconstruction progresses by constraining to an increasing number of Bragg peaks until the complete data set is used as the basis of the update.

Owing to the complexity of our MR-BCDI model, we implement SCG using automatic differentiation (AD) using the PyTorch toolkit, which simplifies evaluation of the loss function and its gradient. AD-based optimization evaluates the gradient automatically and exactly via the chain rule applied repeatedly to the constituent elementary functions. This feature allows increasingly complicated forward models of coherent diffraction to be developed corresponding to more sophisticated measurements, enabling image inversion without the need to derive loss function gradients analytically. Given the complexity of the forward model presented here, MR-BCDI leverages this ability. The use of AD optimization does require that the mathematical operations composing the forward model be differentiable, as we have taken care to enforce here. In this work, we implement the “Adam” optimization algorithm, which is an extension of SCG that is commonly used in machine learning, in a Python-based MR-BCDI reconstruction software²⁶ for CPU and GPU hardware using PyTorch²⁷.

Lastly, we note that the optimal solution in Equation (5) does not preclude the universal twin solution, akin to the twin image degeneracy in single-reflection BCDI²⁸. In other words, the crystal defined by the transformations ${{{\mathcal{A}}}}({{{\bf{x}}}})\to {{{\mathcal{A}}}}(-{{{\bf{x}}}})$ and u(x) → − u( − x) in the same lab frame is also a solution to the MR-BCDI problem, in that it results in indistinguishable diffraction patterns for the same diffraction geometry. Thus, no matter its implementation, MR-BCDI is still susceptible to a reconstruction degeneracy, but our global optimization will converge to one twin solution or the other without requiring intervention to align individual phase retrieval instances¹². Typical ambiguities associated with real-space coordinate origin and phase offset present in single-Bragg-peak BCDI are mitigated in our approach because a single object is the subject of iterative update from all Bragg peaks. This forces consistency of the spatial position of the object. Also, because our reconstruction problem aims to image lattice distortion rather than the phase of the exit wavefield, phase offsets are not an issue.

Method demonstration

In this section we present three reconstruction results with the MR-BCDI technique described above. Two of these use numerically synthesized coherent Bragg diffraction intensity data sets from digital nanocrystals. In the numerical studies, one crystal has a slowly varying continuous inhomogeneous distortion field and the other has a discontinuous, winding displacement field, which emulates two orthogonal screw dislocations within the crystal. The third reconstruction is from experimental diffraction data consisting of six Bragg reflections of a silicon carbide (SiC) nanocrystal measured using BCDI at Beamline 34-ID-C of the Advanced Photon Source. In each case, we present the MR-BCDI reconstruction of the scattering amplitude ${{{\mathcal{A}}}}({{{\bf{x}}}})$ and the lattice deformation u(x). All reconstructions were performed using a single Nvidia Tesla P100 GPU with 16 GB of RAM, and typical reconstruction times were 2-4 hours.

We have adopted the matrix coordinate convention for all the cross-section plots in this paper. As an example, a cross-section image labeled as X − Y implies that the X-axis is directed from top to bottom along the image, and the Y-axis from left to right. The third axis (in this example, the Z-axis) emerges out of the plane of the figure in order to maintain right-handedness. The X, Y, and Z axes correspond to the laboratory frame of reference (i.e., the ${\hat{{{{\boldsymbol{s}}}}}}_{1}$, ${\hat{{{{\boldsymbol{s}}}}}}_{2}$ and ${\hat{{{{\boldsymbol{s}}}}}}_{3}$ directions in Fig. 1, respectively). With this convention, we ensure that the reference frame of the reconstructed crystal is consistent with the programmed order of the array axes in the multi-dimensional FFT routines in Python and PyTorch.

Simulated crystal without dislocations

A synthetic crystal with arbitrary facets was generated on a Cartesian grid of size 128 × 128 × 128 voxels, with a voxel size of s₀ = 12 nm along each axis in the laboratory frame ($[{\hat{{{{\boldsymbol{s}}}}}}_{1}\,{\hat{{{{\boldsymbol{s}}}}}}_{2}\,{\hat{{{{\boldsymbol{s}}}}}}_{3}]$ in Fig. 1). To emulate realistic BCDI scans at a diverse set of sample and detector orientations, a face-centered cubic (FCC) gold lattice with a lattice constant of a₀ = 4.078 Å was assumed for the simulated particle. The orientation of the FCC unit cell with respect to the lab frame was assigned arbitrarily. A slowly-varying internal field u(x) was created by first generating uniform random samples for the three components of u(x) (−0.1a₀ ≤ u_i(x) ≤ 0.1a₀) and then retaining the long-period variations by convolving each u_i(x) with a low-pass filter. The crystal spanned (39, 39, 40) voxels along the laboratory frame axes, and a cubic bounding box ${{{\mathcal{V}}}}$ of size 46 × 46 × 46 voxels was chosen for the reconstruction.

Numerical MR-BCDI diffraction data were generated in a manner consistent with the measurement of a real FCC-structured crystal at the BCDI diffractometer at the APS Sector 34-ID-C beamline. The angular rotations available at that diffractometer (Fig. 1) were emulated as coordinate rotations about cardinal lab frame axes as follows: the sample rotation stage θ and the detector rotation stage δ were coordinate transformations about ${\hat{{{{\boldsymbol{s}}}}}}_{2}$, and the sample rotation stage ϕ and the detector rotation stage γ are coordinate transformations about ${\hat{{{{\boldsymbol{s}}}}}}_{1}$. With this convention, the orientations of θ, δ, and γ needed to satisfy the $[1\bar{1}\bar{1}]$, $[\bar{1}\bar{1}\bar{1}]$, $[\bar{2}\bar{2}0]$, $[20\bar{2}]$ and $[0\bar{2}\bar{2}]$ Bragg reflections with an x-ray energy of 9 keV were determined (with ϕ held at 0) and used to make up the composite rotation ${{{{\mathcal{R}}}}}_{i}$ as discussed in detail in²⁶. Since either the θ or ϕ sample rotation axes could be used to emulate the angular rocking curve for each Bragg peak, the rotation axis that provided a higher degree of orthogonality of the basis set [q_iq_jq_k] was chosen (details in the Supplementary Information). Following the forward model described above, ${\psi }_{{{{\bf{m}}}}}^{(i)}$ and ${{{\Psi }}}_{{{{\bf{n}}}}}^{(i)}$ were calculated for each Bragg peak. To create a simulated MR-BCDI data set, the ${{{\Psi }}}_{{{{\bf{n}}}}}^{(i)}$ were squared to generate the far-field intensity distributions, the peak intensities for each data set were scaled to 10⁵ photon counts in the highest-intensity pixel (consistent with high-quality experimental BCDI data), and Poissonian fluctuations consistent with the scaled intensity fields were added to emulate counting statistics.

For the MR-BCDI reconstruction, the crystal was initialized to a constant-amplitude cube (${{{\mathcal{A}}}}=1$) occupying the entire 46 × 46 × 46 bounding box with no interior lattice distortion (u = 0). This was achieved by setting α(x) from Equation (4) to 2 and α₀ = 1 for all pixels within ${{{\mathcal{V}}}}$. Each of the global scaling factors χ_i was initialized to match the total energy ∑_n∥Ψ_n∥² of the corresponding simulated Bragg intensity pattern. An Adam optimizer²⁹ with an initial learning rate of 0.005 was employed. A total variation (TV) regularizer was applied to α(x) with a coupling constant of 10⁻⁵. During optimization, u(x) was constrained so as not to extend beyond the magnitude of the lattice plane separations ± a₀/2 in each of the [100], [010] and [001] crystallographic directions of the model. This constraint may be employed without loss of generality and is discussed further in the Supplementary Information. The optimization was carried out sequentially over increasingly larger ‘minibatches’ of the BCDI data, as summarized in Table 1 of Methods. After each optimization epoch, a median filter with a kernel size of 3 × 3 × 3 voxels was applied to the reconstructed lattice distortion field u(x) in order to remove spurious isolated discontinuities induced by phase wraps. In the final epoch the full set of 5 Bragg peaks was used, and for the last 1000 iterations of this epoch, the voxels in the crystal for which ${{{\mathcal{A}}}}\, > \,0.2$ were optimized with the other voxels held constant to refine the solution within the crystal interior.

Table 1 Sequential optimization plan for dislocation-free crystal.

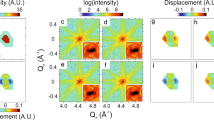
Figure 2 shows a comparison of the ground truth and the reconstructed quantities ${{{\mathcal{A}}}}({{{\bf{x}}}})$ and u(x) on the lab frame grid after the optimization schedule was completed. Orthogonal cross-sections of the three components of u(x) are shown from the reconstruction alongside those from the known model (ground truth). The degree of similarity between the ground truth and reconstructed u(x) quantities is evidenced by comparing the histograms of the voxel-by-voxel components of u(x) (Fig. 3b). Point-to-point residuals were also calculated for all voxels with ${{{\mathcal{A}}}} > 0.5$, and the histogram of these residuals is sharply peaked at u = 0, indicating good agreement between reconstruction and ground truth. The second peak in residuals originates from imperfect spatial alignment of the estimated object and ground truth, which results in higher residuals near the object edges. The spatial resolution of the reconstruction was estimated by fitting an error function to the density profile ${{{\mathcal{A}}}}({{{\bf{x}}}})$ along the dashed line shown in Fig. 3c. This error function has a characteristic width of σ = 0.788 pixels, which gives a spatial resolution estimate of $\sqrt{8\ln 2}\sigma \simeq 1.86$ pixels. Figure 4 shows the comparison of two-dimensional cuts of the reconstructed diffraction patterns at the end of the last epoch alongside the ground truth simulated diffraction used as constraints, showing good agreement.

Fig. 2: MR-BCDI results from simulated crystal.

a Ground truth (top) and reconstructed (bottom) cross-sections of the electron density ${{{\mathcal{A}}}}({{{\bf{x}}}})$ of the synthetic strained crystal with no internal dislocations. The array size represents the original bounding box chosen for reconstruction, i.e., 46 pixels along each lab frame axis. The spatial resolution was estimated by fitting an error function to the reconstructed electron density along the dashed line (see Fig. 3c). b Orthogonal cross sections of ground truth lattice distortion components u₁(x), u₂(x) and u₃(x) The length scale is the same as in a. c Corresponding sections of the reconstructed lattice distortion. The scales shown for u in this and subsequent Figures are in units of fractional lattice constant [ − 0.05α₀, 0.05α₀]. For comparison, this scale translates to a scale of [−0.1, 0.1] radians when considering the G^Tu scalar field projection corresponding to the [002] Bragg peak.

Fig. 3: Figures of merit for simulated crystal reconstruction.

a Trend in multi-reflection loss function given by Equation (3) for the dislocation-free synthetic crystal. The units of this loss function are chosen not to mirror a physical quantity, but as result of a noise model robust to Poissonian noise that is routinely used in BCDI phase retrieval approaches. The red lines denote the beginning of a new optimization epoch. b Histogram of the simulated and reconstructed components of the vector u(x), along with point-to-point residuals of each vector component. c Error function fit to the reconstructed profile along the dashed line in Fig. 2a (X-Y slice). The spatial resolution was estimated from this fit to be ≃ 1.86 pixels, or ≃ 23 nm.

Fig. 4: Comparison of simulated and reconstructed diffraction patterns.

Cross-sections of the noisy simulated (top) and reconstructed (bottom) coherent diffraction patterns from the five Bragg peaks chosen for the dislocation-free synthetic crystal. The reconstructed diffraction patterns are shown here without the scaling effect of the χ_i, but rather scaled to match the corresponding simulated intensity peaks. To fully match the color scales, each reconstructed diffraction was clipped below to the smallest nonzero photon count in the corresponding signal (i.e., 1 photon).

The progression of the loss function ${{{{\mathcal{L}}}}}_{{{{\rm{multi}}}}}[{{{\mathcal{A}}}},{{{\bf{u}}}}]$ over the entire optimization process is shown in Fig. 3a and has several noteworthy features. The dashed lines in Fig. 3a indicate the beginning of each new optimization epoch. Within each epoch, the rapid oscillations are attributed to the abrupt change in the loss function landscape due to each new randomized minibatch. For example, in the first epoch, the loss function is successively optimized over 400 sets of 2 randomly selected BCDI scans for 6 iterations each. Whenever a new randomized set of scans is used, the loss function landscape abruptly changes from its previous state, and the gradient descent evaluates a different error.

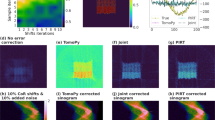
We also performed single-Bragg-peak phase retrieval of the 5 BCDI simulated data sets using standard methods^3,4 in order to demonstrate the advantage of our MR-BCDI method, and the results are shown in Supplementary Fig. 2. It is apparent that the MR-BCDI reconstructed electron density from Fig. 2a is more uniform than what was obtained from phase retrieval of individual peaks, indicating that applying the global set of constraints to a single ${{{\mathcal{A}}}}({{{\bf{x}}}})$ mitigates spurious fluctuations that are difficult to avoid in single-peak BCDI reconstructions. A deterioration of spatial resolution was also observed with the single-peak reconstructions (3.06 pixels resolution estimated by error function fitting), again stemming from the fact that single peak reconstructions do not benefit from a coupling across related data.

Simulated crystal with screw dislocations

A second synthetic crystal with arbitrary facets was generated on the same lab-frame grid as above (s₀ = 12 nm), and as before, the crystallographic lattice structure of gold was adopted with a new initial lab frame crystal orientation. Using this crystal lattice orientation frame, a u(x) field was calculated to simulate two spatially separated screw dislocations within the crystal volume, with dislocation lines along the orthogonal [111] and $[2\bar{2}0]$ crystallographic directions. For this simulation, the respective Burgers vector magnitudes ∥b∥ for the screw dislocations were set to: $\parallel {{{\bf{b}}}}{\parallel }_{111}={a}_{0}/\sqrt{3}$ and $\parallel {{{\bf{b}}}}{\parallel }_{2\bar{2}0}={a}_{0}/\sqrt{8}$. The u(x) fields for each dislocation were calculated with the continuum model of lattice distortion for screw dislocations, as in other BCDI work^30,31, and the net displacement field was modeled as the vector sum of the displacement fields of the pair of screw dislocations. The simulation procedure of calculating the BCDI data sets, including the selection criterion for Bragg reflections, selection of rocking directions, and introduction of Poisson noise, followed the same procedure as for the dislocation-free crystal. Four Bragg peaks with high reciprocal-space mutual orthogonality were chosen for modeling BCDI intensity patterns: [200], [002], [202] and $[2\bar{2}0]$. The simulation box ${{{\mathcal{V}}}}$ was chosen to be 40 × 40 × 40 voxels in size. The Adam optimizer was initialized with a learning rate of 0.02, the object initialization was done as in the previous example, and a similar optimization schedule was used (see Table 2 in Methods). The final optimization stretch for the interior voxels of the object was carried out for 5000 iterations constrained by all four Bragg peak data sets. A median filter of size 7 × 7 × 7 voxels was applied to the components of u(x) after each optimization epoch.

Table 2 Optimization plan for crystal with orthogonal screw dislocations along [111] and $[2\bar{2}0]$.

Figure 5 compares the simulated and reconstructed electron densities ${{{\mathcal{A}}}}({{{\bf{x}}}})$ and u(x), and Fig. 6 compares Bragg peak intensity distributions. (Reconstruction metrics are shown in Supplementary Fig. 4). As in the dislocation-free case, there is good agreement between the simulation and reconstructed images as well as in the diffraction intensity patterns. One noteworthy feature of this reconstruction is the presence of regions of low electron density where the discontinuous lattice distortion in the u(x) field intersects the plane of the figure (regions indicated with blue arrows) and the surface of the crystal (regions circled in red). This effect is attributed to the fact that the highest spatial resolution components of the signal (the “high-q” regions of the detector) are suppressed with the introduction of Poisson counting statistics into the simulated BCDI data sets, effectively imposing a low-pass spatial filter on the reconstructed image.

Fig. 5: MR-BCDI results from simulated crystal with dislocations.

a Ground truth (top) and reconstructed (bottom) electron density cross-sections of the synthetic strained crystal with two orthogonal screw dislocations. The array size represents the original bounding box chosen for reconstruction, i.e., 40 pixels along each lab frame axis. The arrows indicate the points of intersection of the dislocation cores with the figure plane. b Orthogonal cross sections of ground truth lattice distortion components u₁(x), u₂(x) and u₃(x). c Corresponding cross section for the reconstructed lattice distortion. The length scale is the same as a. The regions of discontinuity in the lattice distortion match with the drop in electron density in a. The arrows show the location of the modeled dislocation cores. The circled regions show imperfect reconstruction at locations where the lattice discontinuity meets the crystal surface.

Fig. 6: Comparison of simulated and reconstructed diffraction patterns.

Cross-sections of the noisy simulated (top) and reconstructed (bottom) coherent diffraction patterns from the five Bragg peaks chosen for the gold crystal with two orthogonal screw dislocations.

As before, a comparison was also made to BCDI images reconstructed from the individual Bragg peak data sets from the dislocated crystal lattice using convention phase retrieval approaches. The recipe used was the same for the dislocation-free crystal. A representative amplitude cross-section of a single-peak BCDI image from the [202] Bragg peak is show in Fig. 7. From this image, it is clear by comparing to Fig. 5 that the conventional phase retrieval approach from a single peak struggles to converge to the uniform amplitude distribution expected in the ground truth.

Fig. 7: Reconstructed amplitude from a single Bragg peak of the simulated data set.

a An individual amplitude reconstruction ∥ψ⁽ⁱ⁾∥ from phase retrieval applied to the BCDI virtual data set of the [202] Bragg peak of the crystal with screw dislocations, using the recipe in Section B of the Supplementary Information. The cross section shown displays prominent fluctuations in electron density that are not present in the MR-BCDI reconstructions by virtue of the coupling effect of multiple data sets in a single optimization of the object. Note that the aspect ratio of the central slice of the object is not as it appears in Fig. 5a because the output of standard single-peak BCDI phase retrieval is not shear corrected.

Silicon carbide nanocrystal

Here, we describe a MR-BCDI reconstruction from experimental data acquired from a silicon carbide (SiC) nanoparticle fabricated from a bulk substrate in a manner similar to fabrication methods of SiC quantum sensors^{32,33,34,35,36,37}. The sample was fabricated using lithography and wet etching methods from a bulk single crystal of single-polymorph SiC with a hexagonal 4H structure (lattice parameters a = 3.073 Å and c = 10.053 Å). (The fabrication process is described in the Methods Section.) The shape of the sample was intentionally chosen to be an asymmetric “D”-shaped column with tapering edges fabricated such that the macroscopic facets approximately aligned to low-index lattice planes in the underlying crystal, as shown schematically in Fig. 8a. The sample that was studied is shown in the scanning electron micrograph in Fig. 8b, oriented with the edge of the “D” shape laying flat on the silicon substrate that was used to support the crystal during BCDI measurement. As an intentional result of the fabrication process, only the region of the sample inside the red circle retained a highly crystalline structure and contributed to the measured BCDI peaks.

Fig. 8: Silicon carbide nanoparticle used for experimental demonstration of MR-BCDI.

a Schematic of the design of the lithographically fabricated SiC nanoparticle with facets aligned closely with crystallographic directions of the parent 4H single crystal substrate. b A scanning electron micrograph of the nanoparticle used in the study. The portion of the particle that retained a high degree of crystallinity from which BCDI scans were done is circled in red. c A central slice through the six Bragg peaks measured from this crystal (top row), alongside this same slice after MR-BCDI optimization and image reconstruction (bottom row).

The beamline at 34-ID-C of the Advanced Photon Source was used to measure BCDI data from six Bragg reflections from this crystal: $[10\bar{1}1]$, $[10\bar{1}0]$, $[01\bar{1}2]$, $[01\bar{1}0]$, $[01\bar{1}1]$ and $[10\bar{1}3]$. At each Bragg condition, rocking curves were performed via fine angular steps of the θ motor in order to record 3D coherent diffraction intensity data sets with a pixelated area detector, resulting in raw BCDI data sets of 256 × 256 images with 80 steps along the rocking curve. In terms of signal strength, the maximum pixel intensities in each of the 6 measured Bragg peaks were respectively: 40,980, 16,072, 32,661, 14,577, 34,123 and 7805 peak photons.

Several steps were taken to process this data for MR-BCDI reconstruction. The data sets were clipped to a size of 128 × 128 pixels in the detector plane, and the angular rocking curve dimensions of the data sets were zero-padded to a size of 128, resulting in a cubic data array space of 128 × 128 × 128 voxels for each Bragg peak. This uniform array size ensured that the T_i transformation operations acts as intended. The lab frame crystal orientation of the SiC particle was determined by a least squares optimization of the crystal orientation (expressed as a 3-parameter rotation vector) over the δ, γ and θ motor orientations of all 6 BCDI scans with the Nelder-Mead optimizer³⁸. From this crystal orientation, the set of appropriately oriented reciprocal space lattice vectors G_i that are needed for MR-BCDI reconstruction were generated.

The MR-BCDI reconstruction was performed on the data from the SiC particle in much the same was as for the simulated data. Figure 8c shows the measured and inferred diffraction patterns, showing close agreement, as in the previous cases. Figure 9a depicts the progression of the loss function for the optimization scheme described in Table 3 of the Supplementary Information. Figure 9b shows the electron density after optimization of the interior voxels with ${{{\mathcal{A}}}}\, > \,0.1$. Also shown is the contour at ${{{\mathcal{A}}}}=0.65$, depicting the approximate surface of the crystal. Figure 9c shows the reconstructed components of u(x) within this contour. Figure 10 shows the corresponding 3D isosurface plots of the components of u, with the color scale denoting the spatially varying lattice distortion in nanometers. We see from the absence of discontinuities in the u field that the particle contains a smoothly varying lattice displacement field and no dislocations. Further, morphological features of the reconstructed image correspond as expected with the features of the SiC crystal, including the “D”-shaped cross-section of the nanoparticle, the particle aspect ratio, and the tapering edges.

Fig. 9: Loss function and interior lattice displacement of SiC particle reconstruction.

a Loss function trend for the SiC crystal reconstruction, for the optimization plan shown in Table 3 of the Supplementary Information. b Final estimated SiC nanocrystal electron density ${{{\mathcal{A}}}}$, from a highly permissive mask threshold of 0.1. The red line is the contour at a threshold of ${{{\mathcal{A}}}}=0.65$, representing the approximate crystal surface. c Reconstructed components of the lattice distortion within the SiC crystal (centered at zero volume-averaged distortion in each dimension), within the estimated crystal surface at ${{{\mathcal{A}}}}=0.65$.

Fig. 10: Surface lattice displacement of SiC.

a–c Isosurface plots of the reconstructed u₁(x), u₂(x) and u₃(x) respectively in the SiC crystal (color scale in nanometers), with an isovalue of 0.65 in electron density.

Discussion

In this paper we demonstrated a method by which to reconstruct vector-valued lattice distortion fields within nanocrystals by optimization of a comprehensive forward model of multi-Bragg-peak BCDI data. This forward model flexibly accounts for important geometric factors that arise when making BCDI measurements, is amenable to efficient inversion with modern optimization toolkits, and allows for globally constraining a single image reconstruction to multiple Bragg peak measurements. A key feature of our method is the fact that the forward model we developed to reconcile multiple Bragg peak measurements from a single originating crystal does so by emulating the native measurement space associated with BCDI rocking curve data sets. We also note that our reconstruction approach obviates the need for trial-and-error fixed point projection recipes and reduces the need for intermittent support updates via the shrinkwrap algorithm⁴. Our formulation of MR-BCDI offers another potential advantage in that it permits the analytical interrogation of the high-dimensional solution space in the neighborhood of the true solution, opening the door to rigorous uncertainty analysis where fixed-point-iteration-based methods fall short.

In implementing our MR-BCDI method, we have demonstrated successful reconstructions of the 3D electron density and displacement field for both numerical and experimental data. Crucially, we have shown that crystals with both smoothly varying displacement fields as well as ones with discontinuities in lattice displacement due to, for example, the presence of dislocations, are reconstructable with our approach. In addition, this work brings coherent diffraction methods further into the scope of global optimization techniques^{15,39,40,41,42}, thereby enabling the use of highly optimized software packages capable of handling large data volumes and running on seemingly ever-improving high-performance computing hardware. The use of AD within a machine learning framework also makes the development and testing of more sophisticated cost functions that make use of regularizers based on a-priori information for potentially improved MR-BCDI reconstructions in certain situations.

The demonstration of lattice displacement reconstruction within an individual SiC nanoparticle motivates the use of MR-BCDI in science domains where structural inhomogeneities at nanometric length scales impact materials performance and properties. For example, the case of SiC demonstrated in this work is pertinent to the field of quantum sensing. In a SiC nanoparticle quantum sensor, the sensitivity of near-surface optically active point defects to changes in temperature, magnetic field, and mechanical stress is exploited in order to measure these quantities in media where the nanoparticles can be dispersed^{32,33,34,35,36,37}. Latent inhomogeneous lattice distortion fields within these crystal sensors detract from the precision of such measurements. Thus, quantum sensor fabrication methods aim to minimize such lattice distortion fields. As we demonstrated here, MR-BCDI provides a means by which to assess this key metric.

Methods

Sequential optimization plans

In Tables 1–3 we specify the optimization plans used in the three reconstructions corresponding to the simulated crystal without dislocations (Table 1), the simulated crystal with dislocations (Table 2), and the experimental data set from a nanoparticle of SiC (Table 3).

Table 3 Optimization plan for the silicon carbide nanocrystal.

Silicon carbide nanoparticle fabrication

Here, we specify the method of fabrication of the SiC crystal used in the experimental demonstration of our MR-BCDI approach. The SiC nanoparticles were fabricated from a single 4H-SiC wafer with an i-p-n doping structure. The wafer had a 400nm-thick intrinsic SiC layer with an intrinsice < 10¹⁵atoms/cm³ defect content, a 2μm-thick p-type layer with < 10¹⁹atoms/cm³ of aluminum dopant atoms, and a 0.5mm-thick n-type layer with < 10¹⁸atoms/cm³ of nitrogen dopant atoms. The wafer was diced (5 × 5 mm), electon-beam lithographically patterned (bi-layer PMMA 495K-A3/950K-A6; 1000μC/cm² dose, 3-minute development in 1:3 MIBK:IPA at room temperature), and metallized (10 nm of Ti and 60 nm of Cr via e-beam evaporation) to transfer the D-shaped array pattern onto the SiC. The D shape flat of the lithographic pattern was aligned to the crystallographic $[11\bar{2}0]$ direction (see Fig. 8 in the main text). To fabricate particles that adopt the profile of the surface pattern, the SiC was etched (SF6-Ar ICP/RIE dry-etching) with the Ti/Cr acting as a hard mask. The 1.2 μm etch depth exposed the p-type layer for subsequent photo-electrochemical (PEC) etching of the nano-particles. The etch-defined nanopillars were then PEC etched (0.2M KOH, -0.3V biased etch under 365nm UV illumination at < 500 mW) to partially and selectively remove the p-type SiC to allow for nanoparticle formation and subsequent detachment. For this particular experimental run, the p-type SiC was underetched, resulting in a weakly scattering, porous p-type tether remaining which did not contribute to the BCDI signal (as shown in Fig. 8b in the main text). These nanoparticle arrays were stamp-transferred to a PMMA-coated silicon substrate. The wafers were baked at the PMMA glass transition temperature, which locked the nanoparticles on the Si substrate. The nanoparticles were arranged on the Si wafer in 100 μm pitched arrays bordered by macroscopic fiducials consisting of tightly packed nanoparticles. Finally, the PMMA was O₂ etched away, leaving pristine SiC nanoparticle arrays on the Si substrate that were then conformally covered with alumina (22 nm thick) via ALD to help adhere them to the substrate.