Introduction

Stimuli-responsive materials with actuation and phase-changing capabilities have gained increasing interest due to their potential to enable advanced functionalities in various disciplines1,2,3,4,5. Among them, magneto-responsive materials, allowing untethered, rapid, and wireless actuation under magnetic fields, have been widely studied recently in the areas of robotics6,7,8,9,10, biomedicine11,12,13, metamaterial14,15, vibration mitigation16,17, sensing18,19, and more. Hard-magnetic soft material, achieved by embedding high-coercivity magnetic particles (e.g., neodymium iron boron alloy) into a soft matrix (e.g., rubber), has gained popularity4,20,21,22. The hard-magnetic soft material possesses enhanced programmability because both its geometry and the magnetization distribution of the embedded hard-magnetic particles can be programmed23. Under external magnetic fields, the pre-magnetized hard-magnetic particles produce torques to deform their surrounding soft matrix to align with the applied magnetic field, leading to complex yet programmable shape transformations4,21,22,23. In addition to complex shape transformation, the programmability of hard-magnetic soft materials is further explored to enable programmable properties by capitalizing the nonlinear interaction between the magnetic field and another stimulus, such as mechanical loading. In particular, researchers demonstrate that it is possible to enable switchable and tunable properties in those materials, which is typically challenging to achieve under single stimuli. Those properties include varying auxetic behavior (e.g., Poisson’s ratio)15, tunable buckling24, and reprogrammable force-displacement response14.

To design for programmable and tunable properties, the hard-magnetic soft material offers an enlarged design space containing both the geometry and magnetization pattern of the embedded hard-magnetic particles. To explore the design space, recent studies have established optimization-guided9,25,26 and machine learning-driven27,28,29,30,31 design approaches to enable computational design for mechanical or other stimulus-responsive materials (e.g., hard-magnetic soft materials). Topology optimization32,33 is a promising generative approach for the rational design of magnetic soft materials because of its ultimate capability to generate free-form designs by exploring the entire design space of geometry and magnetization patterns to optimize user-defined objectives under functional constraints. While topology optimization has been explored by few studies23,34 for the computational design of hard-magnetic soft materials for shape morphing and actuation performance under external magnetic fields, it has not been developed for designing multi-functional materials and structures with adaptable and reprogrammable properties under both magnetic and mechanical stimuli.

To enable the capability of altering behaviors without changing geometries or material constitutions for materials and structures, here we develop a multi-objective topology optimization framework to encode reprogrammable properties into magneto-mechanical metamaterials and metastructures. These metamaterials and metastructures possess optimized geometry and embedded magnetization to enable properties that are seamlessly reprogrammed by switching on and off the external stimuli fields. The framework is built upon the design space parameterization scheme in ref. 23. By simultaneously optimizing both geometries and remnant magnetization patterns, the generated designs are capable of realizing different programmed behaviors under purely mechanical load and simultaneous magneto-mechanical load with the magnetic field serving as a “switch” to alter those behaviors. To validate the performance of the optimized magneto-mechanical designs with switchable properties, we fabricate a representative design and conduct an experimental study. The complete procedure of the design process, fabrication, and experimental validation are described in Supplementary Videos 1, 2.

Notably, the proposed optimization-driven computational approach facilitates a systematic and automated discovery of programmable magneto-mechanical metamaterials and structures, whose properties can be reprogrammed and adapted by external magnetic fields. The obtained designs exhibit optimized geometry and magnetization patterns, and some of them are challenging to acquire by intuition. With programmable and adaptable properties, we can enable multiple functionalities within a single design for various relevant applications, such as adaptable actuators, programmable metamaterials, and adjustable energy absorbers. Although the focus in this work is on the magneto-mechanical materials, we remark that our multi-objective and multi-physics topology optimization framework is sufficiently general and could be extended to design reprogrammable and adaptable stimuli-responsive systems considering other or more physics stimuli (e.g., thermo-mechanical35,36,37,38 and thermo-magneto-mechanical39).

Results and discussion

Overview of the optimization-driven design approach

The proposed optimization-driven computational design approach and experimental validation are illustrated in Fig. 1. Given a design domain and prescribed multiple performance targets (i.e., desired functionalities) under purely mechanical and simultaneous magneto-mechanical loads, the proposed generative approach simultaneously optimizes both geometry and material magnetization distributions to produce magneto-mechanical material and structural designs to achieve the prescribed targets. Under prescribed applied magnetic fields, the magnetic torques are induced to align the materials with magnetization directions with the applied magnetic field direction, leading to programmed actuation at the desired locations. The readers are referred to the Methods section below and Supplementary Methods for detailed descriptions of the mathematical optimization formulation.

Fig. 1: Overview of the optimization-guided computational design approach and experimental validation for magneto-mechanical multi-functional metamaterials and structures.
figure 1

Given design domain and targets (top left), the proposed approach can optimize the three sets of design variables (middle left) to generate magneto-mechanical multi-functional metamaterials and structures (right), whose properties can be seamlessly reprogrammed by switching on and off the external stimuli. Fabrication and experimental validation (bottom) are developed to physically demonstrate the target reprogrammable behaviors are accurately achieved.

Full size image

We employ the proposed design approach to discover three multi-functional magneto-mechanical metamaterials and structures and experimentally validate one of the obtained designs (as shown in Fig. 1). Each of them can achieve multiple distinct yet switchable responses (summarized in Supplementary Note 1) under purely mechanical and simultaneous magneto-mechanical loads, respectively.

Multi-functional magnetic actuators

We first deploy the optimization-driven design approach to discover multi-functional magnetic actuators with both optimized actuation and maximized structural stiffness. The purpose is to design a multi-functional device, with sufficient structural stiffness to carry loads under mechanical load alone, and can be transformed into an actuator when switching on the external magnetic stimuli. As shown in Fig. 2a, we consider a rectangular (40 mm × 10 mm) design domain which is fixed on both sides and discretized by 300 × 75 quadrilateral finite elements. In the load case of purely downward mechanical force (F = 0.0125 N shown in Fig. 2), we use the downward displacement at the top middle point of the actuator to characterize its structural stiffness. The variable \({u}_{\alpha }^{({{{\rm{F}}}})}\) indicates the evaluated displacement at the αth degree of freedom (DOF), which ranges from 1 to ND (we set ND = 1 for this design problem). The variable \({u}_{\alpha }^{({{{\rm{F}}}})}\) with a smaller magnitude indicates a higher structural stiffness. In the load case of switching on the external upward magnetic field (while keeping the downward mechanical load), we use the upward displacement (\({u}_{\alpha }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\)) to represent the actuation performance. The variable \({u}_{\alpha }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\) with larger magnitude indicates better actuation performance. Given the above setting, we formulate a weighted-sum objective function J(⋅) (see Eq. 6 in Methods section for the detailed optimization formulation) to maximize both structural stiffness and actuation performance:

$$J({{{{\bf{u}}}}}^{({{{\rm{F}}}})},{{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})})\,=\,-\mathop{\sum }\limits_{\alpha \,=\,1}^{{N}_{{{{\rm{D}}}}}}\left({w}_{1}{u}_{\alpha }^{({{{\rm{F}}}})}\,+\,{w}_{2}{u}_{\alpha }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\right),$$
(1)

where u(F) and \({{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\) are the displacement vectors of the design under the purely mechanical load case and simultaneous magneto-mechanical load case, respectively. Both u(F) and \({{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\) take positive values in the upward direction. The parameters w1 and w2 are the weighting factors that can be tuned to generate whether a device with high structural stiffness (possessing small downward displacement), a magnetic actuator design (possessing large upward displacement), or a design combining both functionalities. The soft matrix is modeled by the compressible Ogden model (see Section Methods for more details) with initial elastic modulus E = 1 MPa and Poisson’s ratio ν = 0.499. We consider a total of Nm = 8 candidate magnetization vectors with uniform orientation space of 45∘ and the same magnitude of 100 mT. The applied magnetic field Ba is prescribed to be 50 mT pointing upward.

Fig. 2: Multi-functional magnetic actuators.
figure 2

a Design setup and target functionalities, i.e., high structural stiffness under mechanical load and large actuation performance under magneto-mechanical load; b Three optimized designs obtained by varying the weighting factors in Eq. 1. Notably, the design of Scenario 3 performs well in both target functionalities, i.e., structural stiffness and magnetic actuation.

Full size image

As shown in Fig. 2b, we vary the weighting factors, w1 and w2, under the same prescribed allowable total structural volume (i.e, 30% of the volume of the design domain) and generate three representative designs (i.e., Scenarios 1–3) with different targets. For Scenario 1, we set w1 = 1 and w2 = 0 to only maximize structural stiffness under the purely mechanical load case. The total volume usage ratio is 0.3. The obtained design resembles a conventional compliance-minimized design40 whose structural geometry (topology) enables efficient load paths to achieve a high structural stiffness. Because this scenario considers purely mechanical response, no optimized magnetization pattern is obtained for the design. Hence, this design does not exhibit actuation performance when the magnetic field is applied (i.e, \({u}_{1}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\) = \({u}_{1}^{({{{\rm{F}}}})}\) = − 0.18 mm). For Scenario 2, we set w1 = 0 and w2 = 1 to only focus on maximizing the actuation performance under simultaneous magneto-mechanical load case. Compared to Scenario 1, with the total volume usage ratio of this design is 27% (which is slightly smaller than the one in Scenario 1), thinner structural members appear to form a more compliant structural system, which leads to a larger actuated upward displacement (\({u}_{1}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\,=\,7.56\) mm). However, the increased compliance of the design significantly reduces the structural stiffness under the purely mechanical load case—the induced displacement at the top middle point \({u}_{1}^{({{{\rm{F}}}})}\) is −1.99 mm, which is 10 times larger than the design from Scenario 1.

For Scenario 3, the weighting factors are set to be w1 = 0.7 and w2 = 0.3 to generate a multi-functional device having both high structural stiffness and optimized magnetic actuation performance. The total volume usage ratio is 0.3. The obtained design has an overall geometry similar to that of the design from Scenario 1, enabling a relatively stiff structural performance under the purely mechanical load case (i.e., \({u}_{1}^{({{{\rm{F}}}})}\) = − 0.29 mm). Additionally, the thinner structural members on both sides (a feature similar to the design from Scenario 2), along with the optimized magnetization distribution, induce considerable bending deformations under the magnetic field to promote a large actuated upward displacement (\({u}_{1}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\,=\,2.81\) mm) at the top middle point under simultaneous magneto-mechanical load case. Compared to other designs, this optimized actuator design showcases a balanced performance between both functionalities of high structural stiffness and large magnetic actuation, having the potential to be applied in wireless actuation devices that also require certain stiffness. The magnetic field, serving as a ‘switch’, can enable the alternation between those two functionalities.

Magneto-active metastructures with adaptable snap buckling

Using the proposed optimization-driven design approach, we now focus on generating magneto-active metastructures with variable yet controllable snap-buckling behavior. As demonstrated in Fig. 3a, we consider a square (200 mm × 200 mm) design domain which is fixed on three sides and discretized by a 150 × 150 FE mesh. Displacement loadings are applied vertically at different locations in three design scenarios (see Fig. 3a). We denote the magnitude of applied displacement as D and the total force associated with the applied displacement as F. The sign of the force is taken to be positive in the same direction of the applied displacement and negative otherwise.

Fig. 3: Magneto-controllable buckling-induced metastructures with reprogrammable behaviors.
figure 3

a Design setup. Metastructures with switchable buckling behaviors enabled by magnetic stimuli under b compressive load; and c tensile load. d Metastructure with switchable multi-stage buckling behaviors under compressive load. Note: the deformed configurations at the circled locations on the FD curves demonstrate the ensured snap buckling through ‘switching on’ the magnetic field.

Full size image

To enable snap-buckling control through the external magnetic field, we first introduce a force constraint in the optimization formulation (see Eq. 6 in Methods section for more details). This constraint enforces that the total forces F under both pure mechanical and simultaneous magneto-mechanical load cases are larger than the prescribed positive lower bounds (denoted by \({F}_{\min }^{({{{\rm{F}}}})}\) and \({F}_{\min }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\) respectively) at a smaller applied displacement level D141,42. With this force constraint, we ensure the structure does not experience snap buckling at applied displacement level D1 under both load cases. We then formulate the objective function J(⋅) (incorporated in the formulation Eq. 6 in Methods section) as follows:

$$J({{{{\bf{u}}}}}^{({{{\rm{F}}}})},{{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})})\,=\,\max \left\{-F({{{{\bf{u}}}}}^{({{{\rm{F}}}})}{| }_{D \,=\, {D}_{2}}),F({{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}{| }_{D \,=\, {D}_{2}})\right\}.$$
(2)

Intuitively, this objective function aims to promote designs that experience snap buckling at applied displacement level D2 under simultaneous magneto-mechanical load case (by minimizing \(F({{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}{| }_{D \,=\, {D}_{2}})\)) and, at the same time, to prevent it from snap buckling under pure mechanical load case (by maximizing \(F({{{{\bf{u}}}}}^{({{{\rm{F}}}})}{| }_{D \,=\, {D}_{2}})\)). By changing the values of D1 and D2, the optimization formulation can generate various designs with distinct yet tunable snap-buckling displacements.

The matrix material is modeled by the compressible Ogden model with initial elastic modulus E = 0.25 MPa and Poisson’s ratio ν = 0.45. We consider a total of Nm = 8 candidate internal magnetization vectors with uniform orientation space of 45∘ and the same magnitude of 250 mT. The external applied magnetic field Ba is prescribed to be 60 mT (Scenario 1) or 40 mT (Scenarios 2–3) pointing upward. We note that to accurately capture the snap-through and snap-back buckling behaviors of the obtained designs, we employ the arc-length method43 to simulate the force-displacement (FD) curves. The maximized applied displacement for all the Scenarios is set as 50 mm.

Figure 3b–d show optimized structures obtained for the three Scenarios. The optimized design for Scenario 1 (with the volume being 15% of the design domain volume), which is obtained by applying compressive displacement and setting \({F}_{\min }^{({{{\rm{F}}}})}\,=\,{F}_{\min }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\,=\,30\) N, D1 = 20 mm, and D2 = 50 mm, is shown in Fig. 3b. Under the purely mechanical load case, this optimized structure maintains positive stiffness and does not experience snap buckling before the applied displacement level D2 = 50 mm. In contrast, when switching on the magnetic field while keeping the mechanical load, this structure buckles around applied displacement level D = 30 mm. Notably, we remark that such adaptable buckling behavior of the optimized structure is achieved by leveraging the nonlinear coupling between the mechanical behavior of a two-leg topology and magnetically-induced deformations. Under applied magnetic field, the optimized magnetization pattern produces magnetic torques in the two side members of the structure, which in turn induces finite rotations23 and promotes their snap buckling. Figure 3c shows the optimized design for Scenario 2 (with the volume being 15% of the design domain volume), which is obtained by applying tensile displacement and setting \({F}_{\min }^{({{{\rm{F}}}})}={F}_{\min }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}=7\) N, D1 = 18 mm, and D2 = 42 mm. Similar to the optimized design in Scenario 1, the optimized metastructure does not experience snap buckling under the purely mechanical load case whereas achieves snap buckling under the simultaneous magneto-mechanical load cases with the magnetic field ‘switched on’.

Both optimized metastructures in Scenarios 1 and 2 possess single-stage snap behavior. In Scenario 3, we aim to obtain a magneto-active metastructure with an adaptable multi-stage snap-buckling behavior. We use an initial design whose geometry combines the features of the optimized structures from Scenarios 1 and 2 (i.e., we flip the geometry of Scenario 2 and place it on top of the design from Scenario 1). The optimized design for Scenario 3 (with the volume being 30% of the design domain volume) is shown in Fig. 3d. The minimal forces for both mechanical and magneto-mechanical load cases at D1 = 16 mm are set to be the same, i.e., \({F}_{\min }^{({{{\rm{F}}}})}\,=\,{F}_{\min }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\,=\,40\) N. The resultant forces at D2 = 40 mm under the two load cases, \(F({{{{\bf{u}}}}}^{({{{\rm{F}}}})}{| }_{D \,=\, {D}_{2}})\) and \(F({{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}{| }_{D = {D}_{2}})\) are simultaneously maximized and minimized, respectively, by the optimization formulation. From simulated FD responses of the optimized structure, we observe that under the purely mechanical load case, only the two lower members of the structure experience snap buckling after applied displacement reaches D = 40 mm. In contrast, under the simultaneous magneto-mechanical load case, both lower and upper members of the structure experience snap buckling before applied displacement reaches D = 32 mm. In addition, the lower members experience snap buckling first around D = 16 mm, followed by the upper members buckling around D = 32 mm. We note that the three designs reported in this section do not contain members connecting to the bottom side of the design domain, which also has fixed-end support. When evaluated by an arc-length solver, the three designs show both snap-through buckling and snap-back buckling behaviors. Through the above-mentioned multiple design scenarios, we demonstrate the feasibility of using the magnetic field as a “switch” to reprogram the snap-buckling behavior of magneto-active metastructures and showcase the potential of the proposed optimization-driven approach to discover those metastructures, which could be promising in the applications of adaptable energy absorption and dissipation devices that leverage elastic buckling.

Magnetic metamaterials with reprogrammable deformation modes

Next, we aim to design magneto-active metamaterials that can switch between distinctive deformation modes under purely mechanical and magneto-mechanical loads. We optimize designs at the unit-cell level and then assemble the optimized unit design into periodic metamaterials to achieve similar switchable deformation modes. As shown in Fig. 4a, we consider a unit-cell (20 mm × 20 mm) design domain with its four corners fixed. Bilinear quadrilateral finite elements (150 × 150) are employed to discretize the domain. In addition, four springs are attached to the loading and control DOFs of the unit cell to account for the stiffness interactions between unit cells in the assembled metamaterial. We consider two load cases and aim to optimize unit designs that achieve reprogrammable deformation modes under these two load cases. In the first load case, purely mechanical loads (prescribed displacements denoted by Δ with a negative value indicating tension) are applied horizontally to induce the first deformation mode, which mimics the material behavior of positive Poisson’s ratio. In the second load case, in addition to the mechanical load, we simultaneously ‘switch on’ the magnetic field, aiming to reprogram the deformation mode to a distinctive one that mimics the material behavior of negative Poisson’s ratio. To achieve this optimization goal, we simultaneously maximize or minimize a total of ND control displacement DOFs (with \({u}_{\alpha }^{({{{\rm{F}}}})}\) and \({u}_{\alpha }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\), respectively, denoting the αth control DOF under purely mechanical and simultaneous magneto-mechanical loads) via a min-max objective function32, J(⋅), incorporated in the proposed formulation Eq. 6 in Methods section:

$$J({{{{\bf{u}}}}}^{({{{\rm{F}}}})},{{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})})\,=\,\mathop{\max }\limits_{\alpha \in \{1,\ldots ,{N}_{{{{\rm{D}}}}}\}}\left(-{u}_{\alpha }^{({{{\rm{F}}}})},{u}_{\alpha }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\right).$$
(3)
Fig. 4: Magneto-active metamaterial unit and assembly with reprogrammable deformation modes.
figure 4

a Design setup; b, c Two optimized units and their 3 × 3 assemblies under tensile and compressive mechanical loads, respectively.

Full size image

We note that, in the above objective function, the sign convention of both \({u}_{\alpha }^{({{{\rm{F}}}})}\) and \({u}_{\alpha }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\) needs to be defined appropriately to accommodate the desired target deformation modes. In this example, we define both \({u}_{\alpha }^{({{{\rm{F}}}})}\) and \({u}_{\alpha }^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\) to be positive in the deformation modes of mimicking “positive Poisson’s ratio” for both tensile and compressive loading scenarios. These control displacement DOFs are associated with the vertical displacements on the top middle and bottom middle of the design domain (i.e., ND = 2). To quantify the actuation performance of the optimized design, we also denote the displacement at the bottom control DOF as D (with a positive value corresponding to upward displacement). Given that we apply symmetric constraint44 and min-max formulation, the displacement at the top control DOF has the same magnitude and points to the opposite direction of the bottom DOF. The matrix material is modeled by the compressible Ogden model with initial Young’s modulus E = 0.25 MPa and Poisson’s ratio ν = 0.499. We consider a total of Nm = 8 candidate magnetization vectors with uniform orientation space of 45∘ and the same magnitude of 250 mT. The applied magnetic field Ba is set as 50 mT pointing upward.

The optimized designs under the two loading scenarios and their realized switchable deformation modes are presented in Fig. 4b, c, respectively. The volumes of the optimized designs for these two scenarios are set as 20% and 30% of the unit-cell volume, respectively. For Scenario 1, we apply a tensile displacement (Δ = −2 mm) horizontally and optimize the unit design to achieve two distinct deformation modes under purely mechanical and simultaneous magneto-mechanical load cases, respectively. From the optimized unit design (Fig. 4b), we observe that the optimized unit design produces a vertically contracting deformation (D = 1.84 mm) under purely mechanical load. By ‘switching on’ the magnetic field, its deformation mode is reprogrammed into a vertically expanding (D = −1.28 mm) one, primarily through the magnetically-actuated bending deformations of the four members in the center. Furthermore, when assembling the optimized unit design into a 3 × 3 metamaterial, the behavior of switchable deformation modes remains, as shown on the right side of Fig. 4b. Under the applied tensile displacement of Δ = −3 mm, the assembled metamaterial exhibits contracting and expanding deformation modes with D = 3.68 mm and D = −5.94 mm under mechanical and magneto-mechanical load cases, respectively.

For Scenario 2, we change the horizontal applied displacement to compression (i.e., Δ = 2 mm). Figure 4c shows the optimized unit design and the two distinct deformation modes realized under purely mechanical and magneto-mechanical loads, respectively. Under horizontal applied compressive displacement (Δ = 2 mm), the optimized unit design exhibit a vertically expanding deformation mode (D = −2.26 mm). With the magnetic field simultaneously ‘switched on’, the magnetic torques, which are generated by the interaction between the optimized magnetization pattern and the external magnetic field, bend the four middle structural members (members with blue and red colors in Fig. 4c) to achieve a vertically contracting deformation mode (D = 4.8 mm) which is similar to the auxetic behavior of negative Poisson’s ratio. After assembling the optimized unit design into a 3 × 3 metamaterial, the behavior of reprogrammed distinct deformation modes is still realized. Under compression (Δ = 3 mm), the assembled metamaterial achieves expanding (D = −5.6 mm) and contracting (D = 13 mm) deformation modes under purely mechanical and magneto-mechanical load cases, respectively. It is worth remarking that, for the scenario of compressive loading (Scenario 2), the displacement magnitudes of the contracting deformation mode are considerably larger than those of other deformation modes, which is due to buckling of the top and bottom members under the simultaneous magneto-mechanical load case.

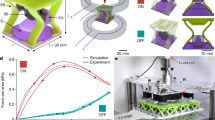
To support the numerical findings, we fabricate the optimized unit design in Scenario 2 using a hybrid 3D printing and casting approach45,46 (shown in Fig. 5a) and experimentally validate its switchable deformation modes under compression. The fabrication approach, material property characterization, and experiment setup are detailed in Supplementary Methods. Both the numerical and experimental designs use the dimensions of 60 mm × 60 mm × 8 mm, the applied magnetic field ∣Ba∣ = 25 mT, and boundary conditions as shown in Fig. 5. The simulation results are provided on the top row of Fig. 5b. Under purely mechanical compression (Δ = 12 mm), the unit design (undeformed configuration shown in Stage I-1) produces a vertically expanding deformation mode (Stage I-2) with a displacement of D = −11.4 mm. We define this deformation mode as the first stable state. On the other hand, under the purely magnetic field (without mechanical loading), the optimized design experiences a displacement of D = 6.2 mm. By fixing the magnetic field and then applying a horizontal compression simultaneously (Δ = 12 mm), we observe that the unit design is reprogrammed into another deformation mode, namely, the top and bottom sides each contract D = 14.2 mm (Stage II-2). Interestingly, when removing the magnetic field while maintaining the compression force, the contracting deformation recovers slightly from D = 14.2 mm to D = 13.6 mm. However, due to the locking of the four buckled members under compressive load, the unit design remains in a stable contracting deformation state, which we define as the second stable state (Stage II-3). The above-mentioned bistable behavior of the unit-cell enabled by the magneto-active design agrees with the findings of experimental investigations of magneto-actuated bistable designs47. It is noted that although bistability is not ensured with the objective function (3), one could tune the design domain, boundary conditions, and passive zones to promote such type of bistable designs. The experimental results are shown in the bottom row of Fig. 5b. By repeating the same loading sequence as in the simulation, we observe that the fabricated unit design realizes the first stable state under purely mechanical loading, and achieves the different second stable state by first applying and then removing the magnetic field while maintaining the mechanical loading. The recorded displacements (through image tracking) at different loading stages show good agreement with the ones obtained from the numerical simulation with less than 7% of relative errors. Supplementary Video 1 shows the deformation of the tested specimen and simulation. Hence, the experiment results agree with our numerical findings both qualitatively and quantitatively, validating that the optimized metamaterial unit design possesses bistability that can be ‘switched’ on and off by the external magnetic field.

Fig. 5: Numerical analysis and experimental validation of the bistability and reprogrammable deformation modes in the optimized magneto-active metamaterial unit design.
figure 5

a Illustrations of fabrication approach and experimental setup; b Comparison of numerical and experimental results.

Full size image

To probe the origin of the bistable behavior of the unit design and understand how this behavior is influenced by ‘switching on’ the applied magnetic field as well as varying its magnetic magnitude, we simulate the FD response and the energy landscape of this unit design. With the prescribed displacement on both sides held constant, we load the displacement at the top and bottom control DOFs simultaneously to deform the unit design to achieve the same contracting and expanding deformation modes as we observe in Fig. 5, under both mechanical and magneto-mechanical loads, respectively. The prescribed displacements of the bottom control DOF together with the associated forces (negative value corresponds to upward force) and the total Helmholtz free energy are evaluated and plotted in Fig. 6. We note that the total energy is computed by summing up the element-wise Helmholtz free energy (see Eq. 5) on the voxel-based mesh for the optimized design with the values of design variables being either 0 or 1.

Fig. 6: Force-displacement responses and energy landscapes to understand the underlying behavior of bistability.
figure 6

a Boundary condition illustration and force-displacement responses; b Energy landscapes; c, d 3D contour plots of force-displacement relations and energy landscapes, respectively (as functions of the bottom displacement and the magnitude of applied magnetic field).

Full size image

From the FD curve under pure mechanical load (i.e., the solid line in Fig. 6a, c), we observe that the design undergoes snap buckling. Stages I-2 and II-3 correspond to two stable states with the forces being zero and their energy landscapes forming two valleys (shown on the solid line in Fig. 6b, d). At D = 0 mm, the bottom force is positive (downward at the bottom control DOFs), and the energy landscape has a positive slope, indicating that the metamaterial unit prefers to expand vertically under purely mechanical load. By ‘switching on’ magnetic fields with different magnitudes, both the FD relations and energy landscapes are changed accordingly, as shown in Fig. 6. For the applied magnetic field with ∣Ba∣ = 25 mT, the bottom force becomes negative (i.e., upward force at the bottom control DOFs) at D = 0 mm, and the energy has a negative slope around D = 0 mm, implying that the unit design prefers the contracting mode (i.e., Stage II-2) to attain an energy valley. Going from this contracting mode at Stage II-2, we can ‘switch off’ the applied magnetic field, and the FD and energy landscape curves return back to the solid lines in Fig. 6, implying that the metamaterial unit goes to the nearest energy valley, which the second stable state at Stage II-3. Remarkably, we still observe the first energy valley (the one close to Stage I-2) with a magnetic field of ∣Ba∣ = 25 mT (the dashed lines in 6b, d), indicating that if we apply this magnetic field at Stage I-2, the metamaterial unit will get trapped at the expanding deformation mode and not go to the contracting one. However, this energy valley disappears by applying larger magnetic fields, e.g., ∣Ba∣ = 55 mT (the dash-dotted line in Fig. 6b, d). Additionally, the force no more passes through the zero-force line, indicating that no stable state exists for the expanding deformation mode. Therefore, if we apply the magnetic field of ∣Ba∣ = 55 mT at Stage I-2, the metamaterial unit will deform into the contracting deformation mode.

To conclude, we introduce a multi-objective, magneto-mechanical topology optimization approach for the systematic and rational design of metamaterials and metastructures with reprogrammable properties. Through the proposed approach, we present several magneto-active metamaterials and metastructures that realize a wide range of multi-functionalities and reprogrammable behaviors, including simultaneously-maximized actuation and structural stiffness, adaptable snap buckling, switchable deformation modes, and tunable bistability. The optimized magnetic soft material designs possess both organic geometries and magnetization distributions, some of which are challenging to design via intuition-based processes. Through numerical studies, we demonstrate that the external magnetic field can serve as a wireless ‘switch’ to reprogram the behaviors and functionalities of those magneto-active metamaterials and structures without the need of changing their geometries or magnetization patterns.

To validate the proposed computational approach, we fabricate the optimized design and perform an experimental study to physically demonstrate the target switchable behaviors are accurately achieved. Furthermore, we study the energy landscapes of the optimized magneto-active metamaterials with switchable deformation modes and reveal how their multi-stability can be reprogrammed by varying the external magnetic field. We envision that the proposed optimization-driven computational design approach could facilitate and accelerate the systematic discovery of multi-functional metamaterials and metastructures, which hold great potential for various applications, such as wireless actuators, soft robotics, and adaptable energy dissipation devices.

Methods

We present the proposed multi-objective topology optimization framework (including parameterization, interpolation of the energy function, and optimization formulation) in this section with details discussed in Supplementary Methods. The nonlinear modeling of hard-magnetic soft material and the experimental setup for the fabricated specimens are described in Supplementary Methods, respectively. The features of the discovered magneto-mechanical metamaterials and structures are summarized in Supplementary Note 1. Supplementary Videos 1, 2 document the design process, fabrication, and experimental validation of a representative optimized design.

Parameterization of matrix and magnetization distributions

The distribution of matrix characterizes the spatial occupancy of material through a density-based approach32. The matrix distribution is associated with the density variable ρ with ρe for the eth element. We apply the density filter48,49 and the Heaviside projection operator50 on the density variable to obtain the physical density variables \(\overline{{{{\boldsymbol{\rho }}}}}\).

The residual magnetic flux density at each location of the design is selected from a set of Nm pre-defined candidate residual magnetic flux densities, \({{{{\bf{B}}}}}_{{{{\rm{r}}}}}^{(1)},\ldots ,{{{{\bf{B}}}}}_{{{{\rm{r}}}}}^{({N}_{{{{\rm{m}}}}})}\), each pointing at one direction. The magnetization distribution is associated with the design variable ξ with \({\xi }_{e}^{(j)}\) for the eth element and jth residual magnetic flux density. Next, we introduce a physical design variable field, \(\overline{{{{\bf{m}}}}}\), to parameterize the magnetization distributions. We filter48,49 and project50 the design variable ξ to the physical variable \(\overline{{{{\bf{m}}}}}\). Formally, we define the residual magnetic flux density in element e as

$${{{{\bf{B}}}}}_{{{{\rm{r}}}},e}=\mathop{\sum }\limits_{j\,=\,1}^{{N}_{{{{\rm{m}}}}}}{\left({\overline{m}}_{e}^{(j)}\right)}^{{p}_{{{{\rm{m}}}}}}{{{{\bf{B}}}}}_{{{{\rm{r}}}}}^{(j)}.$$
(4)

where \({\overline{m}}_{e}^{(j)}\,=\,1\) means the jth candidate residual magnetic flux density \({{{{\bf{B}}}}}_{{{{\rm{r}}}}}^{(j)}\) is selected, and \({\overline{m}}_{e}^{(j)}\,=\,0\) means the jth candidate residual magnetic flux density \({{{{\bf{B}}}}}_{{{{\rm{r}}}}}^{(j)}\) is not selected. A penalization power, pm, is introduced to penalize the mixture of candidate magnetizations and to promote the convergence of the physical magnetization variables \({\overline{m}}_{e}^{(j)}\) to either 1 or 0. To promote discrete magnetization distribution and allow non-magnetized regions to appear in the design, the physical magnetization variables need to satisfy the following two constraints: (1) \(\mathop{\sum }\nolimits_{j \,=\, 1}^{{N}_{{{{\rm{m}}}}}}{\overline{m}}_{e}^{(j)}\,\le\, 1\) and (2) \({\overline{m}}_{e}^{(j)}\,\ge\, 0,\forall j\). We adopt the Hypercube-to-Simplex Projection (HSP) approach51,52 to define \({\overline{m}}_{e}^{(j)}\), which can satisfy the above-mentioned constraints (1) and (2) by construction. Through updating the variable field \(\overline{{{{\bf{m}}}}}\), the magnetization at each location is selected by the optimization formulation from the set of candidate magnetization vectors to minimize/maximize the objective function.

Interpolation of the Helmholtz free-energy function

Based on the modeling of hard-magnetic soft material20, we introduce the following interpolation of the Helmholtz free-energy function from the physical variables \(\overline{{{{\boldsymbol{\rho }}}}}\) and \({\overline{{{{\bf{m}}}}}}^{(j)},\,j\,=\,1,\ldots ,{N}_{{{{\rm{m}}}}}\) to describe the magneto-mechanical behaviors of the parameterized designs. The interpolated free-energy We of element e is given by

$$\begin{array}{ll}{W}_{e}\left({\overline{\rho }}_{e},{\overline{m}}_{e}^{(1)},\ldots ,{\overline{m}}_{e}^{({N}_{{{{\rm{m}}}}})},{{{{\bf{u}}}}}_{e}^{{{{\rm{L}}}}}\right)\\ =\,\left[\epsilon \,+\,(1\,-\,\epsilon ){({\overline{\rho }}_{e})}^{{p}_{\rho }}\right]{W}_{{{{\rm{E}}}}}\left({{{{\bf{u}}}}}_{e}^{{{{\rm{L}}}}},{\overline{\rho }}_{e}\right)\\ \quad\, +\,{({\overline{\rho }}_{e})}^{{p}_{\rho }}{W}_{{{{\rm{M}}}}}\left({{{{\bf{u}}}}}_{e}^{{{{\rm{L}}}}},{{{{\bf{B}}}}}_{r,e}({\overline{m}}_{e}^{(1)},\ldots ,{\overline{m}}_{e}^{({N}_{{{{\rm{m}}}}})})\right),\end{array}$$
(5)

where \({{{{\bf{u}}}}}_{e}^{{{{\rm{L}}}}}\) is the displacement vector in element e under mechanical load (L = (F)) or magneto-mechanical load (L = (F, Ba)); ϵ = 10−5 is a small value to avoid singular stiffness; pρ is the penalization parameter to promote a nearly discrete design. Additionally, the energy interpolation scheme53 depending on \({\overline{\rho }}_{e}\) is applied to the stored-energy WE to address the numerical instabilities of low stiffness regions.

Optimization formulation

With the introduced design space parameterization and free-energy interpolation schemes, we now present the topology optimization formulation to generate multi-functional metamaterial and structural designs under mechanical and magneto-mechanical loads, respectively. Formally, we formulate the topology optimization problem as:

$$\begin{array}{l}\,\mathop{\min }\limits_{{{{\boldsymbol{\rho }}}},{{{{\boldsymbol{\xi }}}}}^{(1)},\ldots ,{{{{\boldsymbol{\xi }}}}}^{({N}_{{{{\rm{m}}}}})}}\,J\left({{{{\bf{u}}}}}^{({{{\rm{F}}}})},{{{{\bf{u}}}}}^{({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})}\right),\\ \,{{{\rm{s.t.}}}}:\,\frac{{{{{\bf{v}}}}}^{T}\overline{{{{\boldsymbol{\rho }}}}}}{| {\Omega }_{{{{\rm{h}}}}}| }\le {v}_{\max },\\ \,F({{{{\bf{u}}}}}^{{{{\rm{L}}}}})\ge {F}_{\min }^{{{{\rm{L}}}}},\quad {{{\rm{L}}}}\in [({{{\rm{F}}}}),({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})],\\ \,{\left\{\mathop{\sum }\limits_{e \,=\, 1}^{{N}_{{{{\rm{e}}}}}}{\left[\frac{{w}_{\sigma }({\overline{\rho }}_{e})}{{v}_{e}}{\int}_{{\Omega }_{{{{\rm{h}}}},e}}{\sigma }_{{{{\rm{VM}}}}}({{{{\boldsymbol{\sigma }}}}}_{{{{\rm{E}}}}}({{{{\bf{u}}}}}^{{{{\rm{L}}}}})){{{\rm{d}}}}{{{\bf{X}}}}\right]}^{{p}_{{{{\rm{n}}}}}}\right\}}^{1/{p}_{{{{\rm{n}}}}}}\,\le\, {\sigma }_{\max }^{{{{\rm{L}}}}},\quad {{{\rm{L}}}}\in [({{{\rm{F}}}}),({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})],\\ \,{{{\bf{r}}}}(\overline{{{{\boldsymbol{\rho }}}}},{\overline{{{{\bf{m}}}}}}^{(1)},\ldots ,{\overline{{{{\bf{m}}}}}}^{({N}_{{{{\rm{m}}}}})},{{{{\bf{u}}}}}^{{{{\rm{L}}}}})\,=\,{{{\bf{0}}}},\quad {{{\rm{L}}}}\in [({{{\rm{F}}}}),({{{\rm{F}}}},{{{{\rm{B}}}}}_{{{{\rm{a}}}}})],\\ \,{{{\bf{0}}}}\,\le\, {{{\boldsymbol{\rho }}}}\,\le\, {{{\bf{1}}}},\\ \,{{{\bf{0}}}}\,\le\, {{{{\boldsymbol{\xi }}}}}^{(j)}\,\le\, {{{\bf{1}}}},\quad j\,=\,1,\ldots ,{N}_{{{{\rm{m}}}}},\\ \end{array}$$
(6)

where the mesh Ωh is composed of Ne elements, uL is the converged displacement vector under mechanical load (L = (F)) or magneto-mechanical load (L = (F, Ba)); v is the element volume vector with ve being the volume of element e; Ne is the number of elements; \({v}_{\max }\) is the assigned maximum volume for matrix materials. We note that the force constraint41,42 is used for designing magneto-active structures with adaptable snap buckling, with F being the summation of force at target degree of freedoms (DOFs) and \({F}_{\min }^{{{{\rm{L}}}}}\) being the prescribed minimum force. In addition, the above optimization formulation incorporates von-Mise stress constraints applied individually on the deformation state uL with the upper bound \({\sigma }_{\max }^{{{{\rm{L}}}}}\). To prevent the singularity issue in the stress-constrained topology optimization54,55,56, we adopt the relaxation approach and define \({w}_{\sigma }({\overline{\rho }}_{e})\,=\,\epsilon \,+\,(1\,-\,\epsilon ){\overline{\rho }}_{e}^{{q}_{\rho }}\) with qρ < 1. The stress constraint is handled by the p-norm approach55 with the power of pn. We emphasize that the stress constraints, as a numerical technique, are effective to prevent thin members and hinge-like connections from appearing in the optimized design as well as to restrict the level of local deformations23,57.

The proposed formulation (6) is solved by a gradient-based update algorithm. In this work, we adopt the method of moving asymptotes (MMA)58. The sensitivities information of objective and constraint functions with respect to the design variables are derived by the adjoint method32.