Introduction

In semiconductors and insulators, phonons dominate the lattice thermal conductivity (LTC) as the quanta of atomic vibrations1. Because of its ubiquity, knowledge of the phonon properties such as phonon dispersions and LTC in ordered structures is enormously important in the development of innovative energy-related technologies, such as energy conversion, thermal management, quantum computing, etc. Fast and accurate prediction phonon properties are necessary for the discovery of novel materials for those applications. Currently, the first-principles-based anharmonic lattice dynamics (ALD) method coupled with the phonon Boltzmann transport equation (BTE) is one of the most featured and accurate methods to obtain the phonon properties including LTC, which involves tedious calculations of harmonic and anharmonic interatomic force constants (IFCs) of crystalline structures relating the potential energy and atomic displacements2. Despite the parameter-free and predictive calculations of density functional theory (DFT), obtaining IFCs via the real-space supercell-based finite displacement method is very time and resource-consuming. This situation is even worse for high-throughput computation of a large number of materials3. Many efforts are put forth to circumvent this time-consuming nature of computing LTC with DFT, dubbed “DFT-LTC” here, to achieve the high-throughput discovery of materials for target LTCs. A primary route that recently has been taken by storm is machine learning (ML). Due to their demonstrated ability to fit complex non-linear, multi-dimensional functions at orders of magnitude faster than the traditional enumeration schemes, many ML methods have been incorporated to accelerate LTC computation. For instance, researchers have recently pursued data-driven approaches through the extraction of vital information from already existing DFT-LTC data to explore previously unseen structures4,5,6,7,8. Recently, Zhu et al. predicted the LTC of 92,919 materials with a 154-dimensional descriptor as the input to random forest prediction, with the three most important features for LTC prediction being the average volume per atom in the ground state, average bond length, and volume per atom7. Additionally, Miyazaki et al. incorporated combinations of atomic radii, atomic masses, and elements from 143 half-Heusler structures into a sequence of regression models to predict the lattice parameter and thermal conductivity of unseen half-Heuslers within 1% and 4% of the DFT results, respectively6.

While training ML models with material descriptors offer physical insights towards feature importance for LTC prediction, limitations are present when facing high throughput. Mainly, these models are still required to generate reference LTC data to serve as the target during training. ML models such as artificial neural networks (ANNs) depend on data diversity due to their interpolative nature, i.e., they cannot perform well when provided data are outside of the training set9,10. As such, the data generation for a sufficiently robust model is expensive and may limit the predictions to a small subset of materials. Additionally, because these models are usually trained on one temperature designed to output a single value of LTC, they are unable to provide the plethora of information that comes with DFT-LTC calculations4,5,6,7. Outputs such as phonon dispersion, scattering rates, temperature-dependent LTC, and off-diagonal thermal conductivity values in the LTC tensor are inaccessible, all of which are standard outputs from phonon calculators11,12,13,14.

To circumvent these issues, the LTC may be approached from a lower level, more specifically through the atomic forces, which are the fundamental input and starting point of the DFT-LTC procedure. Approaching BTE solvers with already computed atomic forces from ML maintains the rich output of information that comes standardly from phonon calculators. More importantly, training for the atomic forces has the potential to reduce the costly demand for training set generation. For traditional ML models, many DFT calculations are required for one LTC value, serving as a single data point for training. In contrast, training on atomic descriptors is advantageous in terms of data abundance per DFT run because each simulation provides (3N + 1) data corresponding to N atoms worth of force vectors and one total energy. Namely, machine learning potentials (MLPs) implicitly capture the electronic-level features from DFT by the representation of the potential energy surfaces as functions of the atomic nuclei' positions9. Due to the purely mathematical nature of ML models, the accuracy of MLPs strongly depends on the description of the atomic environment surrounding central atoms to capture the appropriate physics15. Many studies have shown an excellent representation of DFT-level energetics and realistic property prediction with MLPs such as the High Dimensional Neural Network Potential (HDNNP)16, Deep Potential Molecular Dynamics (DeePMD)17, and Gaussian Approximation Potential (GAP) with SOAP descriptors18. In the context of phonon property prediction, several studies have used MLPs as the force calculator19,20. Typically, these MLPs own a root mean square error (RMSE) of the force predictions within 10–100 meV/Å with approximately 103 faster evaluation time compared to DFT.

Undoubtedly, the robustness of the MLP has the potential to mitigate the current speed-related bottlenecks in the LTC workflow. However, to date, the majority of studies using MLPs share a common denominator in that the models are limited to a material-to-material basis. This is primarily due to the exponential scaling of model parameters with the number of atomic species or elements (Nelem). For example, the HDNNP requires Nelem element-specific networks each containing approximately Nelem radial and Nelem (Nelem + 1) angular symmetry functions21. When faced with data containing elements spanning the periodic table, the training efficiency and evaluation time is reduced significantly due to the \(\sim N_{\text{elem}}^2\) scaling of the input descriptors. Additionally, training of each element-specific network requires central atoms dedicated only to said element, meaning that little to no knowledge of atomic environments from other central atom species is shared. In general, recent MLPs represent atomic positions numerically, while the atomic elements depend on specific sub-models and/or order of the input descriptors, in turn diminishing prediction quality with ten or more elements. Overall, independent elemental scaling and centralized ML training are two major factors necessary for the evaluation of theoretical materials databases containing a plethora of structures and atomic species that would otherwise be too difficult to handle with modern MLPs. Computing forces across many atomic environments is especially challenging for high-throughput LTC considering the notoriously strict force accuracy requirements for the IFCs and the resulting LTC22,23.

In this work, we developed accurate force calculators called Elemental Spatial Density Neural Network Force Field (Elemental-SDNNFF) including the high scope of transferability between atomic structures and elements. The Elemental-SDNNFF shows an unprecedented <10 meV/Å force error for the atomic forces covering 11,866 structures including 55 elements spanning the periodic table as observed in Fig. 1. To easily access millions of data from costly DFT calculations, training on atomic forces allows an N-fold increase granting the current model abundant high-resolution force information, whereby N is the number of atoms per supercell. This is distinct from existing MLPs especially those with total energy as the output: although the addition of other properties like atomic forces and virial terms is standard, they involve a summation over all other properties providing a single training point per DFT run16,24. Here, we further the existing data size with data augmentation techniques, allowing for an average three-fold increase in the data size as explained in the Section “Data augmentation”. We also incorporate active learning techniques to generate data with little to no human intervention with the “query by committee” method, which is based on the uncertainty of atomic forces between several models as detailed in the Section “Active learning”. Demonstrating these methods, we train and apply the elemental-SDNNFF to a database containing quaternary (ABCD), half (ABC), and full (ABC2) Heusler structures, all of which are trending in research due to their capacity for high thermoelectric performance6,25,26. Because the atomic forces are predicted directly, our results show promise for the prediction of accurate high-throughput full phonon properties, such as phonon dispersions for thermodynamic stability and LTC calculations, at the fraction of the computational cost of traditional DFT-LTC. The such workflow may be easily extended to broader types of crystals such as noncubic structures with an arbitrary number of elements spanning the periodic table. Moreover, the concept of topological quantum states has recently been introduced to phonon systems27. Among them, Weyl semimetals in three dimensions are found in realistic materials28,29. Weyl points (WPs) are crossing points of two phonon bands, which can be described by the chiral Weyl equation. The band degeneracy is robust against small perturbations, meaning the position of a WP can move under small perturbations, but it will not disappear unless annihilated with an opposite WP. Topologically protected Fermi arc surface states connecting the projections of a pair of WPs can be found on the surface Brillouin zone30. Before this work, the predictions of WPs were based on DFT-derived phonon dispersions. Our Elemental-SDNNFF spanning the periodic table offers vast opportunities for exploring a large number of candidate Weyl semimetals in a more efficient way.

Fig. 1: Summary of the dataset in this work.
figure 1

a Pipeline performed here for full, half, and quaternary Heusler structures. Numbers on the right of the pipeline represent the number of ABC2 (red), ABC (green), and ABCD (blue) structures after passing through the adjacent filter. The final filter has a slightly reduced structure count from the removal of <0.1 and >200 W m−1 K−1 structures, which are assumed to be outliers. b Structures studied here with the corresponding number of structures from OQMD. c Total number of elements corresponding to central atoms included in training the Elemental-SDNNFF. Elements without color are not included in this study.

Full size image

Results and discussion

Testing the effect of Elemental-SDNNFF implementation

From the overall dataset including those from active learning and DFT-LTC, an 80–20% training-testing split of the structures after shuffling is performed, where the remaining 20% serves as the testing set to probe the ability of the network to predict previously unseen structures. We perform the split based on structures and not atomic configurations, whereby structures and corresponding atoms in the testing set may never have been previously observed by the model. Then, as shown in Fig. 2, four 7 Å, K = 12 networks are trained on the 80% training set and a comparison between DFT and predicted forces in the testing set is done. The first network is the original SDNNFF model labeled as the “Original SDNNFF”22. The jump in performance from the first to the second network is major, dropping by 62.9 meV/Å in testing RMSE. This is primarily attributed to the inability of the original SDNNFF to consider atomic species, i.e., no knowledge is trained to distinguish the 55 elements in the training set. From the second to the third network, the rotational covariance adds a very slight 0.35 meV/Å improvement to the RMSE. Finally, the added data augmentation paired with the rotational covariance bumps the RMSE to the sub-10 meV/Å mark. Overall, the 8.8 meV/Å testing RMSE with 6.7 meV/Å training RMSE shows the robustness of the network when facing new structures containing various atomic positions and species. The small difference between the training and testing RMSE also implies little overfitting in the current model.

Fig. 2: The force comparison curves with corresponding force RMSE and R2 on the testing set, where the y-axes are the predicted forces by the Elemental-SDNNFF model, and the x-axes are the DFT forces in eV/Å.
figure 2

Improvement in force prediction is seen with added features to the SDNNFF.

Full size image

Phonon frequency and LTC prediction

To compare the frequencies in the phonon dispersions from Elemental-SDNNFF with those from DFT, the RMSE across all bands is computed. Since the range of the phonon dispersions varies between structures, we divide the RMSE by the maximum phonon frequency to scale all structures equally, and is expressed as a percentage. To display the agreement of phonon dispersions, two ABC2 structures are taken from the testing pool for benchmark comparison. As seen in Supplementary Fig. 10 (Supplementary Information), the overlap with DFT for RuAuMg2 and CrFeTa2 is virtually perfect in the acoustic branches with near-perfect quality in the optical branches. The RMSE/range percentages for RuAuMg2 and CrFeTa2 are 0.5459% and 0.4931%, respectively, owing the performance to the quality of the 2nd-order IFCs and corresponding atomic forces. The quality of the phonon frequencies as a function of Elemental-SDNNFF cutoff is further investigated. The overall histogram containing the RMSE over the maximum phonon frequency ratio for all structures is shown in Fig. 3a. The increase of the force cutoff improves the accuracy for the predicted frequency from the observed push of the distribution towards the left of the figure. This is expected as the harmonic force constants are sensitive to long-ranged interactions which are truncated by the finite cutoff1, especially the existence of long-ranged dipole–dipole interactions in polar solids31. Additionally, the error in Supplementary Table 2 (Supplementary Information) seems to increase with decreasing average number density in the order ABCD, ABC2, and ABC corresponding with the possible truncation of atomic neighbors beyond the cutoff.

Fig. 3: Summary of predicted phonon properties on 1298 untrained structures.
figure 3

a Histogram containing the percentage of structures against the RMSE for the phonon frequencies normalized by their frequency ranges and b the lattice thermal conductivity comparison plot between Elemental-SDNNFF predicted and DFT values. The solid black line is to guide the eyes for perfect agreement, whereas the red lines indicate a factor of two.

Full size image

The LTC involves both the second and third-order IFCs, the latter being significantly more sensitive to the force error23. As seen in Fig. 3b, the agreement with DFT is very good following linear trends with observable outliers. The mean absolute error (MAE) of the LTC in the 8 Å-12 K model for ABCD, ABC2, and ABC are 0.0934, 0.123, and 0.2526 W m−1 K−1, respectively, with an overall MAE of 0.162 and R2 of 0.9353. The former two structure types are in agreement, especially when compared with the 0.12 MAE and 0.87 R2 predicted by Zhu et al.7. The ABC structures have relatively lower accuracy, which could be improved with further active learning iterations. Further insight into the effects of the cutoff on the LTC accuracy is provided by histograms in Supplementary Figs. 11–13 (Supplementary Information). Due to the wide range of computed LTC (~10−1 to 102 W m−1 K−1), the absolute percent difference of the LTC instead of the RMSE is used herein to quantify the performance. As seen by the histograms and Supplementary Table 3 (Supplementary Information), there is a weak correlation of absolute percent difference with respect to the cutoff. However, there is evidence of a slight leftward shift of ABC with increasing cutoff which is most likely due to the low density of ABC in which the 8 Å force cutoff is more likely to capture the interactions up to the third nearest neighbor as mentioned in Supplementary Methods (Supplementary Information). Overall, despite the accuracy of the second-order IFCs as shown by the phonon dispersions, the third-order IFCs are more challenging to capture across the many structures studied here. Nonetheless, a significant proportion of structures stay within a factor of 2 of the predicted LTC as seen by both the 2× margin in Fig. 3b and the high population of structures within an absolute percent error of 100% in the histograms of Supplementary Figs. 11–13 (Supplementary Information). It is worth pointing out that, for ultralow LTC prediction, this could be treated as a rule-of-thumb to filter structures by, for example, <1 W m−1 K−1. Given that the prediction is within 2× DFT-LTC values, structures with predicted LTC < 0.5 W m−1 K−1 are highly expected to lie within the target 1 W m−1 K−1 range. Therefore, our Elemental-SDNNFF is promising for the filtration of ultralow LTC structures.

A comparison of the LTC from the literature containing the first principles and experiments is provided in Supplementary Table 4 (Supplementary Information) along with our corresponding DFT and predicted values. As seen from the table, comparison of the DFT-LTC with those from other works holds an average percent difference of 4.955% which is expected considering differences in DFT parameters such as energy convergence criterion and pseudopotential or by the method of computing the force constants and associated parameters such as displacement distance and q-point mesh. Correspondingly, the agreement of our predictions with the DFT-LTC values from the literature inherits a similar 6.294% average percent difference and may be attributed to the difference in DFT parameters and corresponding forces from the training data. More importantly, the experimental values are emphasized here as the high-throughput predictive capabilities demonstrated above are designed for near-future synthesis and deployment of crucial thermal materials. Due to the little abundance of experimental data and large coverage of the structures studied here, only one structure with experimental LTC found in the literature was not once trained into our model. The structure is ZrNiSn whereby the average experimental LTC is 11.5 W m−1 K−132 with a literature DFT value of 10 W m−1 K−133 whereas this work’s DFT and prediction values are 15.1 and 14.5 W m−1 K−1, respectively. The existing difference in the experimental LTC with respect to DFT and prediction values is attributed to effects not considered in solving phonon BTE, such as defects, boundary scattering, phase separation, and electron–phonon interactions34,35,36. Because these effects are collective in defining the phonon scattering rates and therefore detract from the overall LTC, almost all the predictions via DFT or Elemental-SDNNFF are expectedly slightly higher than an experiment. Nonetheless, the filtration of high-performance thermal materials given this knowledge remains highly feasible provided the error is akin to that between DFT and the predictions for the entire pool of Heusler structures studied here. Indeed, the model presented here captures the forces and corresponding LTC for the previously unseen material ZrNiSn displaying successful prediction for unseen structures with unique composition and lattice size.

t-SNE analysis

Currently, the atomic weight of the central atom, the neighboring atomic positions, and neighboring species serve as the input to the Elemental-SDNNFF yielding the atomic forces on the central atom. These atomic forces are not directly related to the phonon properties but are necessary to construct the IFCs and subsequently solve phonon BTE. As such, the relationship between atomic-level information and global properties such as the LTC is not straightforward. Here, we instead pursue a higher-level understanding of phonon properties via the t-distributed stochastic neighbor embedding (t-sne) method37. The t-sne is a dimensionality reduction method allowing visualization of highly complex vectors into 2D/3D points, whereby the proximity of these points defines their correlation. To understand the Elemental-SDNNFF input vector, reduction to 20 dimensions by principal component analysis (PCA)38 followed by a further reduction to 2D by t-sne is performed on the entire pool of structures with predicted positive dispersions (7373). Additionally, because each structure contains several atoms, the SDNNFF mesh is instead centered about the entire primitive cell as opposed to each atom. This guarantees only one vector input per structure is plotted for t-sne analysis. Then, the points are colored based on global properties, including structure type, cell volume, number density, average atomic mass, mass density, and the predicted LTC to observe any structure–property relationships in Fig. 4.

Fig. 4: t-sne plots of Elemental-SDNNFF input, with each point representing a single structure.
figure 4

Colors are added for every six plots based on a structure type (red is ABC2, green is ABC, and blue is ABCD), b volume (Å3), c number density (atoms per Å3), d average atomic weight (amu), e mass density (g/cm3), and f predicted LTC (log(W m−1 K−1)).

Full size image

As seen in Fig. 4a colored based on structure type, the green ABC points are distinguishable from the mixed red ABC2 and blue ABCD points. Indeed, ABC structures, when compared with ABC2 and ABCD, own a missing lattice site, causing the isolation of ABC structures as they are clearly identified by the Elemental-SDNNFF input. On the other hand, the ABC2 and ABCD structures here share similar lattice sites with only difference lying in different elements on the lattice sites (ABCD structures have additional elements than corresponding ABC2 structures and thus have lower symmetry), and thus some overlap is expected. Interestingly, Fig. 4b, c clearly shows a plateau for the primitive cell volume and a valley for the number density at the center of the t-sne bordering the ABC and ABC2/ABCD clusters. Despite differences in the structure, all structure types are involved with the same gradients, i.e., a decrease in volume and an increase in number density approaching the outer edges of the plot. Indeed, the relative positions of atoms are expected to expand or contract depending on their occupied elements and corresponding bonding behavior. Thus, because the Elemental-SDNNFF captures the atomic positions with a constant cutoff, the volume and number density are characterized per structure. Fig. 4d, e are colored based on the average atomic weight and mass densities sharing similar distributions at a quick glance. Because these values involve summing over all atoms in the primitive cell, it is not expected that the t-sne plots own obvious trends like the volume or number density since the Elemental-SDNNFF considers the contribution of each atom individually. Nonetheless, these two plots offer some insight into the distribution of the dataset studied here. For instance, many of the ABC2/ABCD structures own either extremely low or high average atomic masses and mass densities, whereas ABC is somewhere in-between. Also, many of the structures with low volumes at the center also correspond with low mass density which is sensible.

The most interesting result is seen in Fig. 4f whereby the color is based on the LTC predicted by our Elemental-SDNNFF model. As seen from the plot, the ultralow LTC structures (<1 W m−1 K−1, corresponding to zero in logarithm scale) are toward the center of the plot and the high LTC structures exist toward the outer edge. This marks an interesting direct relationship with the number density and inverse relationship with the total volume, which is consistent with Zhu et al. in which volume-related features like average atomic ground state volume, average bond length, and volume per atom own high feature importance in the LTC7. In general, ultralow LTC structures are significantly more distinguishable when compared to the high LTC structures which are more scattered. Nonetheless, general conclusions could be made to categorize the thermal transport performance of these structures based simply on the number density. For instance, when comparing the number density and LTC plot, structures with 1 W m−1 K−1 or less are expected to own a number density up to ~0.0525 atoms/Å3, whereas structures with more than 30 W m−1 K−1 are expected to own a number density of at least 0.067 atoms/Å3. Note, these estimates should only apply to the ABCD, ABC2, and ABC Heusler structures studied herein. Additionally, a Pearson correlation plot is shown in Fig. 5 showcasing the strong positive correlation (+0.71) and negative (−0.64) correlation of the LTC with respect to the number density and volume of the primitive cell, respectively, whereas the other two properties show weak correlation as summarized by the t-sne plots. As validation, Supplementary Fig. 14 (Supplementary Information) provides a colored comparison between the predicted LTC and DFT-LTC for the 1298 structures serving as the test set. This is the same t-sne plot as before but with all other structures than those in the test set excluded. It is quickly realized that the predicted and DFT-LTC trends agree with previous observations. Overall, simple descriptors such as number density are extremely valuable for the quick filtration of structures in databases as they require little to no cost to compute. Discovering these trends are made possible by the rapid prediction capabilities of the Elemental-SDNNFF presented here, which we expect to expand to other structure types in the near future.

Fig. 5: The Pearson correlation plot containing a volume of the primitive cell (Å3), number density (number of atoms per Å3), average atomic weight (amu), mass density (g/cm3), and predicted LTC (log(W m−1 K−1)).
figure 5

Red indicates a positive correlation while blue indicates a negative correlation. Pearson correlation close to zero indicates no correlation.

Full size image

Insights into phonon anharmonicity from p-d orbital hybridization

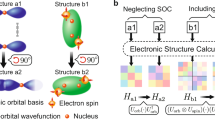
With the LTC of 7373 out of 11,866 thermodynamically stable Heusler structures with additional 1298 structures from the testing set accurately predicted, we are now in a position to provide deep insight into the phonon anharmonicity of crystalline materials. The mean atomic mass has long been regarded as a good predictor for LTC of several materials as Slack and Keyes’s formula state39,40. The higher the mean atomic mass with the same number of atoms between two materials, the lower LTC is and vice versa39,40. However, there are some exceptions that materials having the same atomic mass might have quite different LTC due to various anharmonicity mechanisms other than mean atomic mass. For example, CuBr, ZnSe, and GaAs have the same number of atoms (2 atoms per primitive cell, denoted as M–X with M for cations and X for anions) and a mean atomic mass of ~72 amu. However, CuBr, ZnSe, and GaAs possess different LTC of 1.25, 19, and 45 W m−1 K−1 at 300 K, respectively41. Such phonon anharmonicity mechanism was discovered by Jaffe et al.42 and Wei et al.43, which states that the hybridization in M-d orbitals and X-p orbitals can cause repulsion. The strength of the hybridization is reflected by the overlap and energy difference between the orbitals in M-d and X-p41,42,43. Moreover, the overlap and hybridization between M-d and X-p cause antibonding states below the Fermi level which causes more anharmonicity in the material41. We examine the phonon anharmonicity caused by p-d hybridization for the trained full-Heusler structures. Two materials, namely Li2PdAs and Li2CdGa, were selected from the Elemental-SDNNFF model as candidates for in-depth analysis with explicit DFT. One particular reason why these two materials are selected is that they have the same number of atoms in the primitive cell and almost the same mean atomic mass of ~49 amu. However, they have different values of LTC (1.92 W m−1 K−1 for Li2PdAs and 3 W m−1 K−1 for Li2CdGa) which ensures that the difference in LTC is caused by an anharmonicity mechanism other than the mean atomic mass. In fact, the p-d hybridization phenomenon is observed in Li2PdAs with reasonable p–d hybridization, while Li2CdGa has weak or non-existent p-d hybridization in Fig. 6. Since Li in both materials has neither p-orbitals nor d-orbitals, the analysis on orbitals is then only done on d-orbitals in Pd/Cd and p-orbitals in As/Ga in the orbital-projected band structures. The Crystal Orbital Hamilton Population (COHP) was also calculated in both materials to further explain the bonding and antibonding states especially the state below the Fermi level between Pd/Cd and As/Ga.

Fig. 6: Electronic band structure and COHP analysis of Li2PdAs and Li2CdGa.
figure 6

a Projected band structure for d orbitals in Pd and p orbitals in As in Li2PdAs, b the Crystal Orbital Hamilton Population (COHP) for Pd–As bond in Li2PdAs (negative COHP represents antibonding and positive COHP represents bonding), c projected band structure for d orbitals in Cd and p orbitals in Ga, d COHP for Cd-Ga bond in Li2CdGa. The Fermi energy is scaled to 0 eV in all the subplots.

Full size image

The difference between LTC can be explained by the Pd/Cd-d orbitals and As/Ga-p orbitals hybridization42,43. The orbital-projected band structure of Li2PdAs shown in Fig. 6a confirms the presence of hybridization between d-orbitals in Pd and p-orbitals in As. The colors red (d-orbitals in Pd) and blue (p-orbitals in As) below the Fermi level overlap with each other in Fig. 6a which indicates the hybridization between red (d-orbitals in Pd) and blue (p-orbitals in As). Moreover, the electronic density of states in Fig. 6a shows the overlap between the red d-orbitals in Pd with the blue p-orbitals in As. In Fig. 6b, the presence of antibonding negative COHP between Pd-As bond in Li2PdAs below Fermi level also confirms the presence of p-d hybridization in Li2PdAs between Pd-d orbitals and As-p orbitals. In Fig. 6c the orbital-projected band structure of Li2CdGa, the red (Cd-d orbitals), and blue (Ga-p orbitals) colors do not overlap in the orbital-projected band structure. Also, the density of states shows no overlap between red Cd-d orbitals and blue Ga-p orbitals partial density of states which confirms the weak or non-existent hybridization between Cd-d orbitals and Ga-p orbitals. In Fig. 6d, the non-existent antibonding (negative COHP) states below the Fermi level in Cd-As bond confirm the lower anharmonicity in Li2CdGa than in Li2PdAs. The difference in LTC may not be significant, which is due to the fact the p–d hybridization is weaker in Li2PdAs compared to the p–d orbitals hybridization in CuBr that occur between Cu-d orbitals and Br-p orbitals41. Despite the small hybridization between Pd-d orbitals and As-p orbitals in Li2PdAs, it is still worth taking it into consideration since it unravels a new understanding of phonons anharmonicity in materials caused by orbitals, which is expected to help design materials with ultralow LTC for vast applications such as thermoelectrics and thermal insulation.

To further analyze the chemistry effect on the LTC, Fig. 7 displays the bonding vs. antibonding for all 11,866 Heusler structures studied herein. Specifically, Fig. 7a contains the testing set structures colored by their corresponding DFT-LTC, whereby Fig. 7b includes all other structures colored by their LTC predicted by our Elemental-SDNNFF model. The bonding and antibonding value for each crystal structure are obtained via the integration of the COHP curve. When both figures are compared, the general trends are matching between DFT and predicted LTC and supports their agreement. One notable trend is seen in the group of structures at low bonding (<200) and high antibonding (>1). Here, only low LTC structures <100.5 W m−1 K−1 are observed and agree with the earlier discussion of highly anharmonic materials containing antibonding behavior. As seen by the insets, the logarithm of the bonding value is inversely related to the volume, and as the bonding decreases or volume increases, both DFT and predicted LTCs also generally decrease. This corresponds with the earlier finding in Fig. 4 whereby the volume is inversely proportional to the LTC. In essence, the high antibonding and low bonding behavior may be proposed as a method for quick filtration of insulating crystals necessitating only the unit cell in the DFT calculation. On the other hand, another trend is seen at the high bonding region (>200). Observably, the entirety of the LTC range is found here despite the antibonding, indicating the competing bonding-antibonding behavior for the LTC. However, only beyond this bonding region will high LTC > 100.5 W m−1 K−1 ever be observed, which may prove useful for the filtration of high-performance thermally conductive crystals.

Fig. 7: Bonding vs. antibonding colored by lattice thermal conductivity (LTC).
figure 7

Coloring is done for a 1298 structures from DFT calculations in the training set and b 7373 predicted stable structures in the current study. Insets: the unit cell volume vs. bonding colored to their corresponding LTC.

Full size image

Weyl points prediction

Until now, we have focused on phonon properties related to their eigenvalues, while topological effects of phonons originate from the correlation of their eigenvectors. Nevertheless, the topological classifications of phonons are obtained from harmonic force constants. Here, harmonic force constants from the Elemental-SDNNFF are used to perform the search due to their relatively high accuracy to DFT. An extensive search for WPs is performed on space group number 216 Heusler structures, revealing that 68.7% of ABC structures and 87.6% of ABCD structures have WPs as seen in Fig. 8a. Such a high success rate is much higher than the recent high-throughput study of electronic materials which found only 30% are topological44. Since all frequency ranges of phonons can be stimulated, this further demonstrates the advantage of phonons as a platform for studying topological states. All WPs are categorized according to their symmetry, including those on high symmetry lines, on high symmetry surfaces, and in bulk, as seen in Fig. 8b. Although the concept of metal and insulator breaks down when describing phonons, a clean semimetal in which the density of states vanish at gap closing point still benefits experimental verification. We found 85 and 92 clean WPs in ABC and ABCD Heusler structures, respectively, while the previous study has demonstrated clean WPs in half-Heusler materials45. Clean WPs are found between acoustic and optical branches, and between clusters of optical branches. We have found clean WPs between band 3/4 and band 6/7 in ABC structures and between band 3/4, band 6/7, and band 9/10 in ABCD structures. Interestingly, another class of two-band charge-2 WPs referred to as ‘double WPs’ is encountered, which has not been discovered in phonon systems previously. The double WPs are accompanied by a pair of chiral Fermi arcs, expecting novel transport properties. They also serve as parents of other topological phases, giving birth to two charge-1 WPs upon symmetry breaking. The double WPs predicted in this work may offer guidance on topological phase transition experiments. Note that there are also three-band charge-2 WPs and four-band charge-2 WPs28, but they are not included in this work because of the symmetry constraints of the Heusler structures. Unlike linear WPs with Chern number ±1, the double WPs have Chern number ±2 and exhibit quadratic dispersion near the band-crossing point46. The double WPs are listed in Supplementary Tables 5–6 (Supplementary Information) and a full list of all WPs is provided in the Excel file. The positions of all WPs are shown in Fig. 8d–g. Since our dataset includes 55 elements spanning the periodic table, our result can be viewed as a full evaluation of all possible WPs in Heusler structures. Most of WPs appear on high symmetry line XW and mirror plane ΓXWK, and the distribution is extensive. The frequencies of WPs in quaternary ABCD Heusler structures are found to be higher than those in ternary ABC Heusler structures, due to more atoms and denser packing in the unit cells of quaternary structures.

Fig. 8: Results of searching Weyl points (WPs) in 3212 Heusler structures with phonon dispersions predicted by our Elemental-SDNNFF.
figure 8

a Ratios of topological Weyl semimetals in ABC and ABCD structures. b Number of structures containing different types of WPs, including WPs with high symmetry (on XW, on ΓXWK, and on XWU), WPs without high symmetry (in bulk), clean WPs, and double WPs. The insets illustrate clean WPs and double WPs. c Plot of first Brillouin zone and irreducible Brillouin zone of space group 216. d–g Positions of WPs in bulk (d), on XWU (e), on ΓXWK (f), and on XW (g).

Full size image

Final remarks

In summary, we developed and trained a single deep neural network model dubbed Elemental-SDNNFF for predicting complete phonon properties of crystals with demonstrated high force accuracy and speed facing both observed and new compositions of the half, quaternary, and full Heusler structures. Benefited from the modified algorithm that enables million-scale atomic environments as training data, the accuracy of the predicted full phonon properties (phonon dispersions and lattice thermal conductivity as case studies) reflects the force accuracy with respect to DFT mimicking realistic electronic-level surfaces generated by atomic vibrations. The primary interest of the Elemental-SDNNFF is the capability of predicting full phonon properties of crystals in a single deep neural network model and the sustained DFT-level forces facing large-scale structures with substantial combinations of elemental compositions, effectively capturing bonding behaviors spanning the periodic table. Specifically, this is attributed to training directly on forces procuring an N × D dataset, where D is the number of DFT simulations and N is the number of atomic force vectors. Data augmentation further elevates the available data by three times for the Heuslers studied herein, providing the neural network with extremely abundant data for generalizing ab initio force fields. Additionally, we incorporated active learning allowing the models to prioritize those previously unseen structures with the highest error for subsequent training which is shown to drive improvement in understanding atomic environments undergoing lattice vibration. Made possible by the rapid evaluation of complete phonon properties of 11,866 materials, we realized the behaviors of lattice thermal conductivity trends based on physical and chemical properties. Mainly, we find a direct correlation of the number density with the lattice thermal conductivity, whereas a more complex relationship between bonding and antibonding is pinpointed. For instance, high antibonding and low bonding houses ultralow lattice thermal conductivity structures with p–d orbital hybridization, whereby antibonding is observed below the fermi level generating high anharmonicity and low lattice thermal conductivity. Moreover, given the expansive set of force constants evaluated by the model, novel physics are also discussed in light of Weyl points yielding new structures containing double Weyl points which provide unique topological phonon properties. Ultimately, our work is a medium for high-throughput evaluation and quantification of full phonon properties of large-scale materials to discover phononic crystals with exceptional or tailored phonon properties unraveling insightful physics for broad materials research.

Methods

Structural database and data preparation

To develop a pool of stable structures for this study, several filtration steps were done on a large pool of ABCD, ABC, and ABC2 Heusler structures with space group numbers 216, 216, and 225, respectively. The initial configuration of these structures was borrowed from the Open Quantum Materials Database (OQMD) lacking LTC data47 and was then reoptimized by the Vienna Ab initio Simulation Package (VASP)48,49,50 https://www.vasp.at/ using our own parameters. As seen in Fig. 1, the first step is to filter out structures containing lanthanide and actinide elements to limit the number of structures in this study for computational reasons, although future studies including these elements are certainly of consideration. Then, the structures are filtered by the formation energy after structure optimization with DFT, where lower formation energies have a higher tendency to be stable. The formation energy is quick to compute using DFT requiring only the primitive cells comprising 3–4 atoms. Finally, the energy above the hull (Ehull) provides the ground state stability of partial compounds with respect to all possible linear combinations of phases present in the compound phase diagram, which is also not time-consuming. The low Ehull value has a higher probability to yield thermodynamically stable structures, i.e., all positive frequencies in the phonon dispersion. The final pool in this study holds 2377 quaternary Heusler (ABCD), 2660 half-Heusler (ABC), and 6829 full-Heusler (ABC2) structures (totaling 11,866) from which the Elemental-SDNNFF model training and prediction of atomic forces, phonon dispersions, and LTC values are performed. After 21 iterations of retraining, 15 involving active learning iterations, the final dataset grew to 3.12 × 106 unique atomic configurations and is increased by a factor of 3 to 9.36 × 106 after data augmentation (see details below). When compared with the available 32,137 supercells for Elemental-SDNNFF training, this is a major leap in the dataset size and is inherently due to the N × D scaling from training on atomic forces. From Supplementary Fig. 7 (Supplementary Information), only 18.8% of the data is from active learning, whereas the remaining 32.9% and 48.3% are from the initial dataset and DFT-LTC data, respectively. Overall, 55 elements in Supplementary Fig. 3 (Supplementary Information) are included in this dataset and trained into the model, which is relatively large for modern MLPs.

Model development

The SDNNFF was originally inspired by the HDNNP wherein each atomic descriptor is a summation of atomic contributions in radially-dependent functions51. However, unlike in MLPs, the SDNNFF is designed to only model the atomic forces without the total energy, a so-called neural network force field (NNFF). In situations where the total energy is not required, an NNFF provides two major advantages: (a) the resolution of training on individual atomic force vectors in NNFFs, rather than a function of the total energy plus the summation of force components in MLPs, significantly augments (generally by two orders of magnitude) the available training data from D to N × D, where D is the number of supercells evaluated by DFT and N is the number of atoms in the supercell. Each DFT run, therefore, yields N data for training, and (b) prediction of the force vector directly eliminates the need to calculate the derivative of the total energy with respect to network inputs, or \(F_i = - \nabla _iE\) providing computational cost and time savings in training and evaluation. The former N data per supercell is the greatest motivator for SDNNFF development due to the improved yield in training data per costly DFT run. Although traditional MLPs also can take advantage of the force information, they are involved as a summation between DFT and prediction forces in the loss function for compatibility with the single energy value, effectively reducing the resolution of atomic forces and the overall number of training data16,24. This can be evidently seen from the RMSE for forces: <10 meV/Å for our Elemental-SDNNFF as compared to the several tens and even hundreds meV/Å for previous MLPs. Furthermore, since the IFCs for LTC calculation requires only the displaced positions and forces of atoms, the absence of the total energy in this application is not an issue.

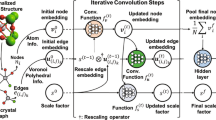
In our previous development of SDNNFF, the atomic environment is represented by a functional mapping of the 3D space rather than the polar space22. Following the previous model, the current solution for descriptor development including both atomic positions and elements requires only a single network scaling independently with respect to the available species in the training set. Let Rc as the cutoff radius, \(\mathop{R}\nolimits^{\rightharpoonup} _n\) as the distance between the central atom and atom n, and \(R_n^{\mathop{\alpha }\limits^{\rightharpoonup} }\) as the distance between grid point \(\mathop{\alpha }\limits^{\rightharpoonup}\) and atom n as detailed in the Supplementary Methods (Supplementary Information). Then, the modified SDNNFF model, dubbed the Elemental-SDNNFF, uses the following descriptors as input

$$\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^0 = \mathop {\sum}\limits_{n = 1}^N {\left\{ {\begin{array}{*{20}{c}} {\frac{1}{2} \ast f_c\left( {\left| {\mathop{R}\nolimits^{\rightharpoonup} _n} \right|} \right) \ast \left( {\cos \left( {\frac{\pi }{{\sqrt 3 L}} \ast R_n^{\mathop{\alpha }\nolimits^{\rightharpoonup} }} \right) + 1} \right)if\;R_n^{\mathop{\alpha }\limits^{\rightharpoonup} }\, < \,D \ast L} \\ {0\;{{{\mathrm{otherwise}}}}} \end{array}} \right.}$$
(1)
$$\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^1 = \mathop {\sum}\limits_{n = 1}^N {\left\{ {\begin{array}{*{20}{c}} {\frac{1}{2} \ast W_n \ast f_c\left( {\left| {\mathop{R}\nolimits^{\rightharpoonup} _n} \right|} \right) \ast \left( {\cos \left( {\frac{\pi }{{D \ast L}} \ast R_n^{\mathop{\alpha }\nolimits^{\rightharpoonup} }} \right) + 1} \right)if\;R_n^{\mathop{\alpha }\limits^{\rightharpoonup} }\, < \,D \ast L} \\ {0\;{{{\mathrm{otherwise}}}}} \end{array}} \right.}$$
(2)
$$\mathop{\varphi }\limits^{\rightharpoonup} = {{{\mathrm{concat}}}}\left( {W_{{{{\mathrm{central}}}}},\;{{{\mathrm{concat}}}}\left( {\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^0\;for\;all\;\mathop{\alpha }\limits^{\rightharpoonup} } \right),\;{{{\mathrm{concat}}}}\left( {\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^1\;for\;all\;\mathop{\alpha }\limits^{\rightharpoonup} } \right)} \right)$$
(3)

where \(\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^0\) is similar to the previous SDNNFF descriptor representing purely the spatial distribution of atoms, \(\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^1\) is the spatial-elemental descriptor, D is the width of the cosine functions centered at each grid point and is set to \(\sqrt 3\) as in the previous publication22, Wn is the atomic number of neighboring atom n, and Wcentral is the atomic number of the central atom. Additionally, the cutoff function \(f_c( {| {\mathop{R}\nolimits^{\rightharpoonup} _n} |} )\) as explained in the Supplementary Methods (Supplementary Information) was added to represent the decaying influence of atom n from the central atom, observably improving the force accuracy. Also, the only difference between \(\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^0\) and \(\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^1\) is the factor Wn where the density function is multiplied by the corresponding atomic number of neighboring atom n. As a result, the additional cost from \(\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^1\) is minimal since the already computed values from \(\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^0\) are simply multiplied with the corresponding atomic weights. Furthermore, \(\mathop{\varphi }\limits^{\rightharpoonup}\) is the finalized descriptor vector in which the central atom atomic number, the spatial descriptor vector, and the spatial-elemental descriptor vector are all concatenated in 1D. The basic idea of the added descriptor is to simultaneously capture the previously accurate spatial mapping of neighbors in addition to the influence of atomic elements on the signals measured at the same grid points. Two advantages arise from the elemental-SDNNFF descriptor: (1) The summation of weighted density functions in \(\varphi _{\mathop{\alpha }\limits^{\rightharpoonup} }^1\) eliminates the need for designated slots in the descriptor vector for each element and removes the scaling of input size with respect to number of elements, and (2) By providing Wcentral in \(\stackrel\rightharpoonup{\boldsymbol\varphi}\), the network can distinguish central atoms whereby individual element-specific SDNNFFs are not required. The result is a singular NNFF capable of modeling atomic systems spanning the periodic table without sacrificing network efficiency, demanding only one network for training with a fixed two times plus one inputs as the previous SDNNFF model.

Rotational covariance

As mentioned previously, the SDNNFF is constructed by a 3D mapping of space corresponding to the 3D forces as the output of the network. In the original version of the SDNNFF, the reference coordinate system was constructed by the input coordinates to the DFT system from the structure file containing atomic positions and Bravais lattice vectors. The grid point positions and consequentially the descriptor was dependent on the coordinate system of the reference DFT data the grid is always built along the reference x/y/z-directions. As a result, a rotation of the atoms in the system can yield dramatic changes to the input descriptor, and given the purely mathematical nature of neural networks, the resulting forces are likely to mismatch with those prior to the same rotation. Thus, it is beneficial to design an NNFF with rotational covariance. The advantage of rotational covariance is the capacity to model infinitely many possible rotations with fewer equivalent representations, reducing the redundancy in training similar but rotated atomic systems. Rotational covariance also helps reduce the number of DFT configurations needed for force accuracy convergence since redundant atomic neighborhoods of existing but rotated systems are already considered. Details about the implementation of rotational covariance are presented in the Supplementary Methods (Supplementary Information). Additionally, provided rotation of the local atomic environment by matrix \({{{\bf{{{{\mathcal{M}}}}}}}}\), the input descriptor is changed in comparison to that of the unrotated case. As a result, the problem arises that the rotated descriptor no longer lies in the original coordinate system of the DFT forces, and the training on these forces requires additional treatment. Thus, the approach here is to modify the architecture of the neural network model to train on rotationally covariant inputs and yield forces in the same crystalline coordinate system. Supplementary Fig. 2 (Supplementary Information) provides a schematic example of the neural network model for the current SDNNFF training. First, the rotationally covariant elemental SDNNFF input is generated from existing DFT data. Simultaneously, the inverse of the rotation matrix \({{{\bf{{{{\mathcal{M}}}}}}}}^{ - 1}\) is saved and serves as an input to the network model. The generation of \({{{\bf{{{{\mathcal{M}}}}}}}}\) is necessary for the descriptor vector and taking its inverse is relatively insignificant in terms of cost. Secondly, the input descriptor passes through several hidden layers. Thirdly, after the hidden layers, the number of nodes is deliberately set to three to represent a ‘pseudo-force’ vector described by the rotationally covariant nature of the input. During application, this force vector alone cannot represent the DFT force, so an additional dot layer is added. The dot layer multiplies the vector and the matrix \({{{\bf{{{{\mathcal{M}}}}}}}}^{ - 1}\), effectively converting the vector back into the cartesian space of the atomic system. Finally, this result yields the DFT-level forces from which the training program computes the loss function with respect to the reference DFT forces and performs back-propagation. Because the trainable parameters of the network lie between the rotationally covariant input descriptor and the dot layer, the model is trained on rotationally covariant information and is applicable to systems regardless of the rotation \({{{\bf{{{{\mathcal{M}}}}}}}}\).

Data augmentation

One of the objectives of this work is to minimize the number of DFT calculations for dataset generation. Following the existing N × D scaling of the dataset, gathering as much information as possible from each DFT run is imperative to improve the speed/cost ratio of NNFF training and evaluation. If the number of DFT calculations for network generation is close to or exceeds that required for LTC calculations for all materials in the data pool, then the NNFF quickly loses its novelty; the time for dataset generation and training could have been spent directly on LTC instead. As such, furthering the N × D scaling is therefore a critical aspect for the Elemental-SDNNFF. Here, the selection rule for rotational covariance is discussed in which two neighboring atoms relative to the central atom are selected: the first atom is the closest atom, and the second atom is (a) coordinated with the central atom and (b) forms the smallest angle with the first atom and the central atom. In this case, when provided a crystal with displaced atoms, the choice in the first and second atoms may vary greatly despite the similarity of atomic environments. This may artificially create gaps in knowledge due to the seemingly sporadic nature of the displaced atoms and the resulting rotation matrix. A simple way to fill these gaps in the data is to take several candidates for the second atom, i.e., those that are coordinated with the central atom but own similar angles as that with the smallest formed angle. These candidates are then used for rotation matrix generation for the same atomic environment and are included in the training set. Figure 9 shows an example of data augmentation performed on a single atom in ABCD structure provided a finite cutoff up to the first neighbor for clarity. The bottom right of Fig. 9 shows the closest atom as overlayed with a blue circle and similarly the second atom with green. In addition to the original scheme, similar atomic environments provided by the central and selected blue atoms may yield two more possibilities for the second atom. As a result, a 3× increase in data for training is expected in atomic environments for ABCD structure, as also observed in ABC and ABC2 structures in general and the dataset is augmented equally throughout. Markedly, the data augmentation performed here shows a significant increase in performance as mentioned in the Section “Structural database and data preparation” and detailed in the Supplementary Methods (Supplementary Information).

Fig. 9: Data augmentation of a single central atom performed on a displaced Quaternary Heusler (ABCD) structure.
figure 9

The periodic structure is broken down by atomic environments at fixed cutoff, where the nearest neighbors are extracted. Then, based on selection rules, several atomic pairs are selected for generating rotations used for data augmentation.

Full size image

Active learning

An important aspect of any ML process is to consider the quality of the dataset used for training. Ideally, the training data should contain sufficiently diverse data to cover all possible features within the domain of the application. However, judging the so-called quality and diversity of atomic force fields based on the simultaneous positions of atomic natures is not so trivial. Inspired by the work of Zhang et al., active learning is incorporated for Elemental-SDNNFF dataset generation and self-improvement52. Specifically, the ‘query by committee’ method is a form of active learning wherein several identical models are trained in parallel on the same dataset but own different initialized weights. After training, these models collectively evaluate a pool of structures, and a comparison of the predicted forces is performed. If the variance in the resulting forces is low for a particular structure, then the associated atomic configurations contain features that are well-considered in the training set. On the other hand, due to the interpolative nature of neural networks, a high variance implies that the atomic configuration owns features outside of the dataset, and the structure is pooled as a candidate for retraining. With this pool, DFT is performed, the new data is retrained for all the models in the committee, and the loop is repeated. Here, several Elemental-SDNNFF networks are trained on the initial dataset and serve as the committee. After training, we evaluate the atomic forces on a pre-generated set of displaced supercells. Like the work by Zhang et al., an indicator is computed for each atomic configuration serving as the uncertainty observed by the committee52. Further detail about the implementation of active learning in this work is provided in the Supplementary Methods (Supplementary Information).

Phonon property prediction and model verification

For verification, 553 ABCD, 649 ABC, and 583 ABC2 totaling 1785 structures are set aside for DFT-LTC calculation for comparison with those results from the SDNNFF. Details concerning the development of the initial model prior to and during active learning iterations, phonon property calculation details involving phonon dispersions and LTC from both predicted and DFT forces, and the active learning details and results, including methodology, efficiency, and cost, are provided in the Supplementary Methods (Supplementary Information).

Weyl points searching

The existence of WPs requires broken of either time-reversal symmetry or inversion symmetry27. Due to the lack of a time-reversal-breaking mechanism, only non-centrosymmetric materials can have WPs. Here the candidates are 1662 ABC and 1550 ABCD Heusler structures with non-centrosymmetric space group number 216 and phonon dispersions predicted by our Elemental-SDNNFF model. For each material, we first search for twofold degenerate points, then determine the Chern numbers of each degenerate node. For the search for gap-closing points, we use a 10 × 10 × 10 Γ center mesh as starting points. Then, a Limited-memory Broyden Fletcher Goldfarb Shanno Bound (L-BFGS-B) optimization procedure is applied to find the local minimum of the gap between two adjacent bands. To make sure the nodal point is isolated, i.e., it is not a point on a nodal line or surface, the gap on a surrounding surface is checked. After collecting the nodal points, they are transformed into the irreducible Brillouin zone (IBZ) by applying symmetry operations. Notice that the Chern numbers of two equivalent k-points are associated by the determinant of their rotation matrix. We only consider nodal points in the IBZ. Finally, we compute the Chern numbers of each nodal point using the Wannier charge center evolution approach53,54. Those with nonzero Chern numbers are identified as WPs.