Analytical and numerical modeling of optical second harmonic generation in anisotropic crystals using ♯SHAARP package

Abstract

Electric-dipole optical second harmonic generation (SHG) is a second-order nonlinear process that is widely used as a sensitive probe to detect broken inversion symmetry and local polar order. Analytical modeling of the SHG polarimetry of a nonlinear optical material is essential to extract its point group symmetry and the absolute nonlinear susceptibilities. Current literature on SHG analysis involves numerous approximations and a wide range of (in)accuracies. We have developed an open-source package called the Second Harmonic Analysis of Anisotropic Rotational Polarimetry (♯SHAARP.si) which derives analytical and numerical solutions of reflection SHG polarimetry from a single interface (.si) for bulk homogeneous crystals with arbitrary symmetry group, arbitrary crystal orientation, complex and anisotropic linear dielectric tensor with frequency dispersion, a general SHG tensor and arbitrary light polarization. ♯SHAARP.si enables accurate modeling of polarimetry measurements in reflection geometry from highly absorbing crystals or wedge-shaped transparent crystals. The package is extendable to multiple interfaces.

Introduction

The ability to combine and split photons using nonlinear optical interactions has had a dramatic impact on generating a broad and continuously tunable electromagnetic spectrum towards furthering both fundamental sciences as well as technological applications. Extreme 100th harmonics are used to generate x-rays and deep ultraviolet for spectroscopy, diffraction, and medical imaging; the near-infrared (IR) laser light at 1.55 μm powers the internet; the mid-and far-IR extending to the THz cover the fingerprint region for chemical sensing, environmental monitoring, free-space communication, gravitational wave detection, homeland security, aviation, medical imaging, and laser surgery^1,2,3,4,5. We are presently at the threshold of a new era of quantum communications. Nonlinear optics remains the primary means to generate entangled photons today, with the promise to revolutionize secure communications, sensing, and metrology⁶.

Optical second harmonic generation (SHG) is a nonlinear optical process in a material that combines two incident photons at frequency ω into one photon at frequency 2ω, i.e., $\omega + \omega = 2\omega$ indicating energy conservation. It is a specific instance of three wave-mixing processes in which the frequency of each of the three photons could be different, i.e., $\omega _1 \pm \omega _2 = \omega _3$where the positive sign corresponds to the sum-frequency generation (SFG) and the negative sign to the difference frequency generation (DFG). More generally, higher-order nonlinear optical processes involving four or more waves are also possible.

Electric-dipole optical SHG, the focus of this work, is described by the interaction ${{{\mathbf{P}}}}^{2\omega } = \varepsilon _0{{{\mathbf{\chi }}}}^{\left( 2 \right)}{{{\mathbf{E}}}}^\omega {{{\mathbf{E}}}}^\omega$, where χ⁽²⁾ is the SHG nonlinear susceptibility tensor relating the fundamental electric field vectors ${{{\mathbf{E}}}}^\omega$ with frequency ω inside the crystal to the creation of a nonlinear polarization, ${{{\mathbf{P}}}}^{2\omega }$ at frequency 2ω. The electric-dipole SHG tensor, χ⁽²⁾, is a third-rank polar tensor that keeps track of the polarizations of all three photons involved in the three-wave mixing process. As a consequence of Neumann’s principle⁷, it contains non-zero components only in materials that lack spatial inversion symmetry, or so-called non-centrosymmetric materials. Therefore, electric-dipole SHG is used as a sensitive probe of inversion symmetry breaking and polar order^8,9.

The classical, semi-classical, and quantum theories of nonlinear optical processes are well established^10,11,12. Based on the fundamental theories, analytical and numerical approaches have been utilized to model the nonlinear optical responses. The analytical approach is essential to derive a closed-form expression of the SHG intensity that connects experimental observations to fundamental material properties. If material properties are already established, numerical simulations can be used to predict the SHG responses of samples with inhomogeneous microstructures and/or with complex measurement geometries in which an analytical solution is intractable. The numerical approach solves Maxwell’s equations with well-defined boundary conditions using techniques, such as the finite-element method and finite difference time domain method¹³.

Bloembergen, Maker, and later Herman and Hayden and Shoji et al. laid out the analytical theory of SHG interactions at a single interface as well as in a slab geometry in both reflection and transmission geometries^{10,11,12,14,15,16,17}. Two common models used to quantitively obtain absolute SHG coefficients are the Maker fringes¹¹ technique and the Bloembergen and Pershan formulae¹⁰. The Maker fringes can be obtained by measuring the transmitted SHG intensity as a function of the incident angle of a slab sample with both surfaces parallel to each other. The SHG coefficients of the slab can then be accurately obtained by analyzing the envelope of the curve^12,18. Nevertheless, the Maker fringes technique is generally limited to the characterization of SHG properties of materials with negligible absorption, because of the transmission geometry. In contrast, other methods based on the reflection geometry provide greater flexibility, loosening the strict requirement for a transparent crystal, and allowing for the characterization of highly absorbing and reflecting bulk crystals such as metallic materials as well as ultrathin samples on an absorbing substrate such as few-layer flakes of 2D materials^19,20.

However, most of these theoretical studies adopt simplifications to keep the analytical solutions tractable. The probed crystals are generally limited to optically isotropic¹⁰, uniaxial^12,18, or sometimes orthorhombic (biaxial) crystals^14,21 but cut along a high-symmetry surface to reduce complexity. The material is also often assumed to be transparent and non-absorptive at the pump and second harmonic frequencies^10,12,21. A general analytical solution has not yet been established for modeling SHG polarimetry in nonlinear optical materials in all three optical classes (anaxial, uniaxial, biaxial)²², including absorption and dispersion, and for any surface orientation geometry. ♯SHAARP addresses this critical need.

In contrast to analytical methods, there have been many well-established numerical approaches in computational electromagnetics that can model nonlinear optical response^19,23,24. Based on these numerical approaches, commercial and open-source software packages are available, including COMSOL Multiphysics¹⁹, CST Studio Suite²³, and MEEP²⁴. Complementary to these tools, ♯SHAARP has advantages in the following respects. First, ♯SHAARP can provide fully analytical or semi-analytical solutions to the Maxwell’s equations for the reflected or transmitted SHG waves at a single interface (.si). (A code for multiple interfaces is under development). With these analytical expressions, users can fit their experimental measurements of the SHG polarimetry in a relatively straightforward manner. Particularly in this process, the users can determine whether to impose specific assumptions to simplify the final expression and evaluate quantitatively how each assumption can influence the results. It also standardizes the process and minimizes errors in publications, where each user does not have to derive specific (often messy) equations for their sample and their geometry. Second, since ♯SHAARP solves the Maxwell’s equations analytically, it can calculate the numerical results very efficiently. This feature allows one to predict the propagation directions and intensities of the SHG waves for a given system with known material properties in an on-demand modality without requiring running a numerical simulation for each desired change in variables. Third, ♯SHAARP is designed with a user-friendly GUI, which can guide the users to specify the inputs and conveniently export the output, including figure plots, numerical data, and analytical expressions. There is no need to build a finite-size system or specify the boundary conditions, and coding experience is not a prerequisite. Besides, ♯SHAARP is freely available to users via Mathematica® and Wolfram Player® and is expandable; while the former needs a license, the latter is free to use. The users may access the original code from GitHub and contribute to the code by optimizing it and adding new functionalities. We also plan to integrate new functionalities into ♯SHAARP in future versions, such as the SHG waves across slabs and multilayers. Based on these attributes, we believe ♯SHAARP can be a critical missing piece in the fields of nonlinear optics and optical materials research.

In this work, an open-source package, ♯SHAARP (Second Harmonic Analysis of Anisotropic Rotational Polarimetry), is developed to calculate analytical and numerical solutions for the polarization-dependent SHG generated from a single interface in the frequency domain. The software is designed to study the SHG of an absorbing bulk crystal or a wedged slab sample from a single interface in reflection geometry. Five key attributes are integrated into ♯SHAARP: arbitrary symmetry, arbitrary crystal orientation, arbitrary incident and measured polarizations of light, and the inclusion of dispersion and absorption. To benchmark the theoretical calculations, the reflective SHG intensity of three commercial crystals, namely, GaAs, LiNbO₃, and KTiOPO₄ (KTP), corresponding to the isotropic (anaxial), uniaxial, and biaxial classes, respectively, are experimentally measured and fitted using analytical solutions provided by ♯SHAARP to extract their nonlinear tensors and validate against published literature. Good agreement between this work and the literature demonstrates a robust means of understanding and characterizing anisotropic second harmonic response and nonlinear coefficients. An example is also given where ♯SHAARP aided the analysis of a new material, TaAs, as compared with the published literature^25,26.

Results and discussion

SHG polarimetry

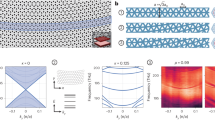
SHG measurement is often performed using SHG polarimetry in various geometries, as shown in Fig. 1. Polarimetry refers to the mapping of the SHG intensities for various combinations of the polarization of the incident fundamental photons at ω and the output SHG photon at 2ω. This can occur in transmission or reflection geometries, and the polarization of the incident and SHG light can each be, in general, elliptical with the special cases of linear and circular polarizations; these polarization states can further be either rotated or fixed. Figure 1a and d depict the schematics of two common experimental geometries where the red and blue rays are the fundamental and second harmonic light, respectively. Here, we will refer to Fig. 1a as the rotating polarizer, fixed analyzer (FA) geometry, and Fig. 1d as the rotating polarizer, rotating analyzer (RA) geometry, for the following discussion. The FA geometry in panel (a) is commonly achieved using a rotating half-wave plate to rotate the linear polarization of the incident fundamental wave while using a fixed analyzer in the s or p polarization geometries for the second harmonic wave. The RA geometry in panel (d) is achieved by either fixing both the half-wave plate and the analyzer while rotating the crystal or by rotating the half-wave plate and the analyzer simultaneously while fixing the sample orientation. The plane of incidence (PoI) is defined as the $L_1 - L_3$ plane, where $\left( {L_1,L_2,L_3} \right)$ are the lab coordinates as displayed in Fig. 1a and d. In both geometries, the incident linear polarization (${{{\mathbf{E}}}}^{{{{\mathrm{i}}}},\omega }$) is rotated, while second harmonic intensities are collected as a function of the azimuthal angle φ in two different ways. Here, superscripts i and ω, respectively, represent incident light and fundamental frequency. $\varphi = 0$ represents the p-polarized ω wave in the FA geometry, and the p-polarized $\omega ,2\omega$ waves in the RA geometry. In the FA geometry of Fig. 1a, the p and s polarized second harmonic intensities ($I_{{{\mathrm{p}}}}^{2\omega }(\varphi )$ and $I_{{{\mathrm{s}}}}^{2\omega }(\varphi )$) are measured as depicted in panels (b) and (c). In the RA geometry of Fig. 1d, the second harmonic intensities polarized either parallel or perpendicular to the incident fundamental polarization, namely, $I_\parallel ^{2\omega }(\varphi )$ and $I_ \bot ^{2\omega }(\varphi )$ are measured as depicted in panels (e) and (f). Figure 1c and f depict the calculated SHG polar plots of GaAs (111) obtained in the normal incidence geometry, which contains information about crystal symmetry, linear dielectric, or refractive index tensors at both ω and 2ω frequencies, and second-order nonlinear susceptibility tensor.

Fig. 1: Two common experimental geometries for SHG polarimetry and the resulting reflection SHG polarimetry for GaAs(111) surface in normal incidence.

a–c Rotating polarizer fixed analyzer (FA) geometry: SHG intensities of p- and s-polarized waves are recorded as a function of the azimuthal angle φ. d–f Rotating polarizer, rotating analyzer (RA) geometry: SHG intensities polarized parallel or perpendicular to the incident polarization are recorded as a function of the azimuthal angle φ. a, d Schematics of the experimental geometries are shown. $\left( {L_1,L_2,L_3} \right)$ is the lab coordinate system. The sample surface is located in the $L_1 - L_2$ plane, while the plane of incidence is parallel to the $L_1 - L_3$ plane. Red and blue waves indicate a pump beam at ω and a signal beam at 2ω frequency, respectively. b, e Schematics showing the relation between the incident polarization and SHG polarization projected in the $E_p - E_s$ plane for the two experimental geometries. c, f Polar plots of the calculated reflective SHG intensities for GaAs(111) surface subject to normal incidence using the two geometries.

Theoretical background

Consider an incident plane wave with the fundamental frequency ω onto a flat surface of a noncentrosymmetric crystal. The incident wave results in the generation of transmitted and reflective waves with ω and 2ω frequencies, as schematically illustrated in Fig. 2a. Each wave can be denoted by its wavevector k, the superscript of which indicates the frequency (ω or 2ω) as well as the birefringence. Here, e and o are for the two Eigen waves at each frequency, while ee, oo, and eo are for the nonlinear 2ω waves generated from three distinct combinations of the fundamental (ω) e and o waves. Note that the s and p polarization states are, in general, distinct from the e and o polarization states. The s and p polarization states are defined as the electric field (E) being perpendicular (s) or parallel (p) to the PoI (the plane defined by the incidence wavevector and the sample surface normal). The e and o polarization states are defined as the dielectric displacement (D) with a component along (e) or perpendicular to (o) the optical axes (0 optical axes for anaxial, 1 for uniaxial, and 2 for biaxial crystals). The extraordinary wave (e) is normal to D^o (ordinary polarized dielectric displacement)²⁷. The other superscripts, i, R, or T, corresponding to the incident, reflected, or transmitted beams, respectively. The angle θ represents the propagating angle of the associated wave with the wave vector k.

Fig. 2: Nonlinear waves and four coordinate systems for SHG process.

a Schematic example of different waves at both ω and 2ω frequencies for the specific measurement geometry where the optic axes are chosen to lie in the incidence plane for clarity sake. One optical axis is shown and the other one will be in the plane as well if it is biaxial material. ♯SHAARP does not in general have such a restriction, and can handle an arbitrary orientation of the optic axes with respect to the incidence plane. The green and blue rays are homogeneous waves at ω and 2ω frequency. The red rays are the inhomogeneous waves at 2ω. b Schematic of four different coordinate systems used for a monoclinic crystal structure. $\left( {L_1,L_2,L_3} \right)$, (a, b, c), $\left( {Z_1,Z_2,Z_3} \right)$, and $\left( {Z_1^{\mathrm{Principal}},Z_2^{\mathrm{Principal}},Z_3^{\mathrm{Principal}}} \right)$ are the lab, crystallographic, crystal physics, and principal coordinate systems, respectively. Only the crystallographic coordinate system is non-orthogonal.

Four different coordinate systems shown in Fig. 2b are necessary to describe the SHG measurement, and it is essential to clarify their mutual relationships. $\left( {L_1,L_2,L_3} \right)$ describe the lab coordinate system (LCS), where $L_3$ is defined as the normal to the sample surface, $L_2$ is selected as being perpendicular to the PoI, and L₁ is taken to the direction that ensures this coordinate system is orthogonal. For a crystal under study, the translation vectors of the unit cell of the crystal determine the crystallographic coordinate system (CCS) given by (a, b, c); these axes may not be orthogonal. The $\left( {Z_1,Z_2,Z_3} \right)$ represent the crystal physics coordinate system (ZCS) in which the material property tensors are represented; they are always orthogonal and their directions relative to (a, b, c) follow the IEEE standards as summarized in Supplementary Table 1^7,28. The $\left( {Z_1^{{{{\mathrm{Principal}}}}},Z_2^{{{{\mathrm{Principal}}}}},Z_3^{{{{\mathrm{Principal}}}}}} \right)$ is the principal coordinate system (PCS), in which the dielectric tensor, and hence the refractive index ellipsoid are diagonalized; this coordinate system is also always orthogonal. For an isotropic or uniaxial crystal structure, $\left( {Z_1,Z_2,Z_3} \right) = \left( {Z_1^{{{{\mathrm{Principal}}}}},Z_2^{{{{\mathrm{Principal}}}}},Z_3^{{{{\mathrm{Principal}}}}}} \right)$. For a biaxial crystal, the PCS is defined with the real part of the refractive indices along each axis following an ascending order²⁷ as follows:$n\left( {Z_1^{{{{\mathrm{Principal}}}}}} \right) < n\left( {Z_2^{{{{\mathrm{Principal}}}}}} \right) < n\left( {Z_3^{{{{\mathrm{Principal}}}}}} \right)$, while this is not true in general for refractive indices defined in the crystal physics coordinate system. Henceforth, we will adopt the notation $\tilde n\left( {Z_i^{{{{\mathrm{Principal}}}}}} \right) \equiv \tilde n_i^\omega$ for the eigenvalues of the refractive index tensor. In the PCS, the diagonal components of the relative dielectric tensor at an optical frequency can be conveniently written as ${{{\tilde{\boldsymbol{\varepsilon}}}}}^{{{{\mathrm{Principal}}}}} = \varepsilon _0\left( {{{{\tilde{\mathbf{n}}}}}} \right)^2$, where $\varepsilon _0$ is the vacuum permittivity. For a material with complex dielectric tensors and refractive indices, the complex quantities can be expressed as ${{{\tilde{\boldsymbol{\varepsilon}}}}} = {{{\boldsymbol{\varepsilon}}}}_{{{\mathrm{R}}}} + {{{\mathrm{j}}}}{{\boldsymbol{\varepsilon}}}_{{{\mathrm{I}}}}$ and ${{{\tilde{\mathbf n}}}} = {{{\mathbf{n}}}}_{{{\mathrm{R}}}} + {{{\mathrm{j}}}}{{{\mathbf{n}}}}_{{{\mathrm{I}}}}$. Subscripts R and I represent real and imaginary components of the tensors, and ${{{\mathrm{j}}}} = \sqrt { - 1}$. Therefore, the dielectric permittivity ${{{\tilde{\boldsymbol{\varepsilon}}}}}^\omega$ in the LCS can be expressed as

$$\begin{array}{*{20}{c}} {{{{\tilde{\boldsymbol{\epsilon}}}}}^\omega = {{{\mathbf{a}}}}_{{{{\mathrm{LZ}}}}}{{{\mathbf{a}}}}_{{{{\mathrm{ZP}}}}}\left( {\begin{array}{*{20}{c}} {\tilde n_1^\omega } & 0 & 0 \\ 0 & {\tilde n_2^\omega } & 0 \\ 0 & 0 & {\tilde n_3^\omega } \end{array}} \right)^2\left( {{{{\mathbf{a}}}}_{{{{\mathrm{LZ}}}}}{{{\mathbf{a}}}}_{{{{\mathrm{ZP}}}}}} \right)^{ - 1}} \end{array}$$

(1)

where ${{{\mathbf{a}}}}_{{{{\mathrm{LZ}}}}}$ is the rotation matrix from ZCS to the LCS, and ${{{\mathbf{a}}}}_{{{{\mathrm{ZP}}}}}$ is the rotation matrix from the PCS to the ZCS.

When a monochromatic plane wave at frequency ω is incident upon the interface, two refracted rays at frequency ω can propagate inside the medium with one of two possible orthogonal dielectric displacement vectors ${{{\mathbf{D}}}}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},\omega }$ and ${{{\mathbf{D}}}}^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},\omega }$. The two waves can be both ordinary, or one ordinary and one extraordinary, depending on the optical class of the material and the propagation direction of light. Without loss of generality, we denote the two transmitted (and subsequently refracted) waves at the single interface by superscript T, as shown in green in Fig. 2a. The two fundamental waves correspond to the Eigen solutions of the wave equation at the linear frequency, ω, given in the LCS as

$$\begin{array}{*{20}{c}} {{{{\mathbf{\nabla }}}} \times {{{\mathbf{\nabla }}}} \times {{{\mathbf{E}}}}^{{{{\mathrm{T}}}},\omega } + \left( {\begin{array}{*{20}{c}} {\varepsilon _{L_1L_1}^\omega } & {\varepsilon _{L_1L_2}^\omega } & {\varepsilon _{L_1L_3}^\omega } \\ {\varepsilon _{L_2L_1}^\omega } & {\varepsilon _{L_2L_2}^\omega } & {\varepsilon _{L_2L_3}^\omega } \\ {\varepsilon _{L_3L_1}^\omega } & {\varepsilon _{L_3L_2}^\omega } & {\varepsilon _{L_3L_3}^\omega } \end{array}} \right)\mu ^\omega \frac{{\partial ^2}}{{\partial t^2}}{{{\mathbf{E}}}}^{{{{\mathrm{T}}}},\omega } = 0} \end{array}$$

(2)

where $\varepsilon _{L_i,L_j}^\omega$ is the dielectric permittivity tensor at frequency ω in the LCS, and the μ^ω represents the magnetic permeability at ω²⁷. Typically, for a non-magnetic medium, $\mu ^\omega \sim \mu _0$, the vacuum permeability is assumed. In general, the anisotropic dielectric permittivity and magnetic permeability tensors of the medium are not diagonalized in LCS. Therefore, the non-collinearity between E and D, as well as B and H results in two separate orthogonal bases, namely, (k, D, B) and (S, E, H). Here, k, D, B, S, E, and H are, respectively, the wavevector, dielectric displacement, magnetic induction, Poynting vector, electric field, and magnetic field intensity²⁹. Note that E and H are not necessarily orthogonal to the wavevector k inside the medium.

The nonlinear polarization induced by second-order nonlinear susceptibility radiates nonlinear source waves at 2ω frequency, which can be written as

$$\begin{array}{*{20}{c}} {{{{\mathbf{P}}}}^{2\omega } = \varepsilon _0{{{\mathbf{\chi }}}}^{\left( 2 \right)}{{{\mathbf{E}}}}^{{{{\mathrm{T}}}},\omega }{{{\mathbf{E}}}}^{{{{\mathrm{T}}}},\omega }\exp {{{\mathrm{i}}}}\left( {{{{\mathbf{k}}}}^{{{\mathrm{S}}}} \cdot {{{\mathbf{r}}}} - \omega t} \right)} \end{array}$$

(3)

where ${{{\mathbf{P}}}}^{2\omega }$, ${{{\mathbf{E}}}}^{{{{\mathrm{T}}}},\omega }$, ${{{\mathbf{\chi }}}}^{\left( 2 \right)}$ are the nonlinear polarization, the electric field of the refracted ω waves, and the second-order nonlinear susceptibility. The term ${{{\mathbf{k}}}}^{{{\mathrm{S}}}}$ is the wavevector of the source wave (superscript S) that combines two linear wavevectors¹⁰, i.e., ${{{\mathbf{k}}}}^{{{\mathrm{S}}}} = 2{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},\omega }$, $2{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},\omega }$, or ${{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},\omega } + {{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},\omega }$. The electric fields radiated by the nonlinear polarization can then be calculated in the LCS using the wave equation

$$\begin{array}{*{20}{c}} {{{{\mathbf{\nabla }}}} \times {{{\mathbf{\nabla }}}} \times {{{\mathbf{E}}}}^{{{{\mathrm{T}}}},2\omega } + \left( {\begin{array}{*{20}{c}} {\varepsilon _{L_1L_1}^{2\omega }} & {\varepsilon _{L_1L_2}^{2\omega }} & {\varepsilon _{L_1L_3}^{2\omega }} \\ {\varepsilon _{L_2L_1}^{2\omega }} & {\varepsilon _{L_2L_2}^{2\omega }} & {\varepsilon _{L_2L_3}^{2\omega }} \\ {\varepsilon _{L_3L_1}^{2\omega }} & {\varepsilon _{L_3L_2}^{2\omega }} & {\varepsilon _{L_3L_3}^{2\omega }} \end{array}} \right)\mu ^{2\omega }\frac{{\partial ^2}}{{\partial t^2}}{{{\mathbf{E}}}}^{{{{\mathrm{T}}}},2\omega } = - \mu ^{2\omega }\frac{{\partial ^2}}{{\partial t^2}}{{{\mathbf{P}}}}^{2\omega }} \end{array}$$

(4)

where $\varepsilon _{L_i,L_j}^{2\omega }$ represents the dielectric permittivity tensor at frequency 2ω in the LCS, and the $\mu ^{2\omega }$ represents the magnetic permeability at 2ω^10,27,30. The homogeneous wave and inhomogeneous waves radiated by the nonlinear polarization correspond to the general and particular solutions of Eq. (4), respectively. The former component is also known as the ‘free wave’, and the latter is the radiated wave by the nonlinear polarization known as the ‘bound wave’^12,18. The total nonlinear wave can be expressed as a superposition of the general and particular solutions. To solve for the homogeneous wave at both linear (Eq. (2)) and nonlinear (Eq. (4)) frequencies, the congruence transformation, and generalized eigenequation are employed³¹. The two eigenvalues correspond to the effective refractive indices and the two eigenvectors correspond to the electric field directions for the two homogeneous e and o waves. Three inhomogeneous waves $\left( {{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega },{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega },{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega }} \right) = \left( {2{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},\omega },2{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},\omega },{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},\omega } + {{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},\omega }} \right)$, will be generated according to Eq. (3), as shown in Fig. 2a, due to the three-wave mixing process. Therefore, in principle, five waves at 2ω will be generated, as shown in Fig. 2a, where blue and red correspond to homogeneous and inhomogeneous waves, respectively. The inhomogeneous SHG fields can be written in the following form:

$$\begin{array}{l}{{{\mathbf{E}}}}^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega } = {{{\mathbf{C}}}}^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega }\exp {{{\mathrm{i}}}}\left( {{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega }.{{{\mathbf{r}}}} - \omega t} \right)\\ {{{\mathbf{E}}}}^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega } = {{{\mathbf{C}}}}^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega }\exp {{{\mathrm{i}}}}\left( {{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega }.{{{\mathbf{r}}}} - \omega t} \right)\\ \begin{array}{*{20}{c}} {{{{\mathbf{E}}}}^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2{\upomega}} = {{{\mathbf{C}}}}^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega }\exp {{{\mathrm{i}}}}\left( {{{{\mathbf{k}}}}^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega }.{{{\mathbf{r}}}} - \omega t} \right)} \end{array}\end{array}$$

(5)

where C is the field strength to be determined from Eq. (4) for a given ${{{\mathbf{P}}}}^{2\omega }$. By substituting Eqs. (3) and (5) into Eq. (4), the field strengths of the three inhomogeneous waves can be explicitly calculated with the associated second-order optical susceptibilities. Accordingly, the ${{{\mathbf{H}}}}^{2\omega }$ for the three inhomogeneous waves can be obtained by

$$\begin{array}{*{20}{c}} {{{{\mathbf{H}}}}^{2\omega } = \frac{1}{{\omega \mu _0}}{{{\mathbf{\mu }}}}^{ - 1}{{{\mathbf{k}}}}^{2\omega } \times {{{\mathbf{E}}}}^{2\omega }} \end{array}$$

(6)

Boundary conditions at the interface (here, the surface of the crystal) are important to accurately determine the propagation directions and the field strengths of waves³⁰. To satisfy the momentum conservation at both ω and 2ω frequencies, it is required that

$$\begin{array}{*{20}{c}} {k_{L_1}^{{{{\mathrm{i}}}},\omega } = k_{L_1}^{{{{\mathrm{R}}}},\omega } = k_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},\omega } = k_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},\omega }} \end{array}$$

(7)

$$\begin{array}{*{20}{c}} {k_{L_1}^{{{{\mathrm{R}}}},2\omega } = k_{L_1}^{{{{\mathrm{S}}}},2\omega } = k_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega } = k_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},2\omega }} \end{array}$$

(8)

from which the wavevectors and propagation angles of all refractive and reflective waves can be determined. The continuity across the interface of the components, $E_\parallel$ and $H_\parallel$, of the electric and magnetic fields parallel to the interface, respectively, also yields the boundary conditions for the ω and 2ω waves, given by

$$\begin{array}{*{20}{c}} {E_\parallel ^{{{{\mathrm{i}}}},\omega } + E_\parallel ^{{{{\mathrm{R}}}},\omega } = E_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},\omega } + E_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},\omega } = E_\parallel ^{{{{\mathrm{T}}}},\omega }} \end{array}$$

(9)

$$\begin{array}{*{20}{c}} {H_\parallel ^{{{{\mathrm{i}}}},\omega } + H_\parallel ^{{{{\mathrm{R}}}},\omega } = H_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},\omega } + H_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},\omega } = H_\parallel ^{{{{\mathrm{T}}}},\omega }} \end{array}$$

(10)

$$\begin{array}{*{20}{c}} {E_\parallel ^{{{{\mathrm{R}}}},2\omega } = E_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega } + E_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},2\omega } + E_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega } + E_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega } + E_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega } = E_\parallel ^{{{{\mathrm{T}}}},2\omega }} \end{array}$$

(11)

$$\begin{array}{*{20}{c}} {H_\parallel ^{{{{\mathrm{R}}}},2\omega } = H_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega } + H_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{o}}}},2\omega } + H_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega } + H_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega } + H_\parallel ^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega } = H_\parallel ^{{{{\mathrm{T}}}},2\omega }} \end{array}$$

(12)

where superscripts e and o represent homogeneous waves and ee, oo and eo are inhomogeneous waves at 2ω due to wave mixing. Using Eqs. (7)–(12), ${{{\mathbf{E}}}}^{{{{\mathrm{R}}}},2\omega }$ and ${{{\mathbf{E}}}}^{{{{\mathrm{T}}}},2\omega }$ can be calculated.

Outline of the ♯SHAARP code

We use a flowchart to illustrate the procedure for solving the equations using the boundary condition method for the ω and 2ω waves in Fig. 3. All the relevant input and output variables in ♯SHAARP are summarized in Supplementary Table 2. The two refracted linear waves are described by solving Eq. (2). Their actual field strengths can be obtained from the boundary conditions at the fundamental frequency ω, using Eqs. (7), (9), and (10). Given Eqs. (3) and (4), two homogeneous waves and three inhomogeneous waves at 2ω can be uniquely determined. Following the boundary condition analysis at 2ω using Eqs. (8), (11), and (12), analytical expressions for the second harmonic response can be derived and used for simulations of polarimetry as well as for fitting experimental polar plots and extracting intrinsic SHG tensor coefficients.

Fig. 3: Flowchart of calculation procedures in ♯SHAARP.

Flowchart illustrating the key steps in deriving the polarized second-harmonic fields generated by a nonlinear medium.

Notably, we have made no assumptions above on the crystal symmetry, surface orientation, or absorptive nature of the material in deriving Eqs. (1)–(12). Therefore, the procedure is generally applicable to material systems with arbitrary crystal orientation, dielectric permittivity tensor, and SHG tensor. This general routine enables us to predict the SHG responses for given linear and nonlinear optical properties and to determine nonlinear optical coefficients by fitting experimental SHG polarimetry measurements of new materials with arbitrary crystal symmetry, surface orientation, and absorptive properties.

To benchmark the theoretical results predicted by ♯SHAARP, we carried out SHG experiments on three typical nonlinear optical materials based on the FA geometry (cf. Fig. 1a). To verify the capability of ♯SHAARP for materials of arbitrary symmetry, we chose three materials, GaAs, LiNbO₃, and KTP, which corresponds to three different optical classes: isotropic (also called anaxial, or lacking any optic axes), uniaxial (with one optic axis), and biaxial (with two optic axes). We also studied (112)-cut TaAs where the surface is parallel to a non-trivial crystallographic plane. Notably, among the materials we have chosen, the semiconducting GaAs are known for exhibiting a finite absorption of the fundamental and SHG waves, which allows us to test the capability of ♯SHAARP in modeling materials systems with absorption.

Isotropic GaAs (111)

GaAs crystallize in a cubic structure with point group $\bar 43m$³². The CCS, ZPS, and PCS coincide and point in the same direction. It is one of the most widely used semiconductors, with a direct bandgap of around 1.42 eV^33,34,35, and can be patterned for quasi-phase-matching for nonlinear optical applications³⁶. Using the fundamental probing energy of 1.55 eV (as we have in this study), GaAs show a finite absorption at both fundamental and second harmonic frequencies and exhibit strong resonances at 2ω frequency³³. GaAs (111) single crystal is used for the study, and it is oriented such that the $[1\bar 10]$ is parallel to the $L_2$ direction as shown in Fig. 4a. The dark yellow line corresponds to the projection of the PoI ($L_1 - L_3$ plane) onto the viewing plane $L_1 - L_2$.

Fig. 4: Linear and nonlinear optical responses of GaAs (111).

a Crystal structure and experimental orientation. The $\left( {L_1,L_2,L_3} \right)$ and $\left( {a,b,c} \right)$ are the lab coordinate system and crystallographic coordinate system respectively. The dashed dark yellow line represents the projection of the plane of incidence to the $L_1 - L_2$ plane. b The effective complex refractive indices at ω frequency as a function of incident angle ($\theta ^i$), subscript R and I represent real and imaginary respectively. c and d p- and s-polarized second harmonic responses as a function of azimuthal angle (φ) at various incident angles ($\theta ^i$). The open circles are experimental results, and the solid lines are theoretical fits. e Comparison of the SHG coefficients with no approximations (labeled as ♯SHAARP, pale green background) as against those extracted with various approximations (pale orange background). ${{{\tilde{\boldsymbol{\varepsilon }}}}}_R$, and $\left| {{{{\tilde{\boldsymbol{\varepsilon }}}}}} \right|$ represent the real component of ${{{\tilde{\boldsymbol{\varepsilon }}}}}$, and the magnitude of the complex ${{{\tilde{\boldsymbol{\varepsilon}}}}}$, respectively.

At both the fundamental and second harmonic frequencies, the diagonalized complex dielectric tensors have three identical components due to the isotropic symmetry, i.e., $\tilde \varepsilon _{11} = \tilde \varepsilon _{22} = \tilde \varepsilon _{33}$. Consequently, the effective refractive index is independent of the incidence angle ($\theta ^{{{\mathrm{i}}}}$) as shown in Fig. 4b. The symmetry requires GaAs to possess only one independent nonzero second harmonic tensor component, i.e., $d_{14} = d_{25} = d_{36}$, while the other components vanish⁷.

The intensities of the p- and s-polarized SHG waves, $I_{{{\mathrm{s}}}}^{2\omega }\left( \varphi \right)$ and $I_{{{\mathrm{p}}}}^{2\omega }\left( \varphi \right)$, are recorded at four different incident angles ($\theta ^{{{\mathrm{i}}}} =$ 0°, 15°, 30°, and 45°). For non-normal incidence, each polar plot contains at least three independent equations, namely $\cos (4\varphi )$, $\sin (4\varphi )$, and $\sin \left( \varphi \right)\cos (\varphi )$. Two independent equations at normal incidence are $\sin ^2(2\varphi )$ and ${{{\mathrm{Cos}}}}^2(2\varphi )$. Thus, we used 20 equations to obtain the unique solution of five unknown parameters (one SHG susceptibility and four geometric factors). The data are fitted to extract the nonlinear susceptibilities of GaAs. As shown in Fig. 4c, d, the open circles, and solid curves represent experimental results and the theoretical fittings, respectively, which demonstrate quantitatively good agreements. The analytical expressions for the fittings were generated by ♯SHAARP for the $\bar 43m$ point group with the probing geometry described above. The analytical solutions of reflected 2ω waves for this most simplified case are given below

$$E_{{{\mathrm{p}}}}^{2\omega } = \frac{{\left( {C_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega } + C_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega } + C_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega }} \right)\left( {E_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega }\tilde n^{2\omega }\cos \theta ^{{{{\mathrm{T}}}},2\omega } - E_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega }\tilde n^\omega \cos \theta ^{{{{\mathrm{T}}}},\omega } + E_{L_3}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega }\tilde n^{2\omega }\sin \theta ^{{{{\mathrm{T}}}},2\omega }} \right) - \left( {C_{L_3}^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega } + C_{L_3}^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega } + C_{L_3}^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega }} \right)E_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega }\tilde n^\omega \sin \theta ^{{{{\mathrm{T}}}},\omega }}}{{E_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega } + \tilde n^{2\omega }\cos \theta ^{{{\mathrm{i}}}}\left( {E_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega }\cos \theta ^{{{{\mathrm{T}}}},2\omega } + E_{L_3}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega }\sin \theta ^{{{{\mathrm{T}}}},2\omega }} \right)}}$$

(13)

$$E_{{{\mathrm{s}}}}^{2\omega } = \frac{{\left( {C_{L_2}^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega } + C_{L_2}^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega } + C_{L_2}^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega }} \right)\left( {\tilde n^{2\omega }\cos \theta ^{{{{\mathrm{T}}}},2\omega } - \tilde n^\omega \cos \theta ^{{{{\mathrm{T}}}},\omega }} \right)}}{{\tilde n^{2\omega }\left( {\cos \theta ^{{{{\mathrm{T}}}},2\omega } + \cos \theta ^{{{\mathrm{i}}}}} \right)}}$$

(14)

where $\left( {E_{L_1}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega },E_{L_2}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega },E_{L_3}^{{{{\mathrm{T}}}},{{{\mathrm{e}}}},2\omega }} \right)$ = $\left( {\cos \theta ^{{{{\mathrm{T}}}},2\omega },0,\sin \theta ^{{{{\mathrm{T}}}},2\omega }} \right)$, is a unit vector describing the p-polarized electric field direction of one of the homogeneous waves at the 2ω frequency. The variables, ${{{\mathbf{C}}}}^{{{{\mathrm{T}}}},{{{\mathrm{ee}}}},2\omega }$, ${{{\mathbf{C}}}}^{{{{\mathrm{T}}}},{{{\mathrm{oo}}}},2\omega }$, ${{{\mathbf{C}}}}^{{{{\mathrm{T}}}},{{{\mathrm{eo}}}},2\omega }$ represent the amplitudes of the inhomogeneous waves radiated by the nonlinear polarization, and their explicit expressions are given in the Supplementary Note 5. Here, $\tilde n$ represents the complex refractive index. Subscripts $L_1$, $L_2$, and $L_3$ represent vector components along the lab coordinates, and $\theta ^{{{\mathrm{T}}}}$ and $\theta ^{{{\mathrm{i}}}}$ are the angles of refraction and incidence, respectively.

By fitting the data with expressions generated by ♯SHAARP, we have achieved very good fitting between the analytical theory and the polarimetry experiments for all incident angles $\theta ^{{{\mathrm{i}}}}$, which confirms the $\bar 43m$ point group of GaAs. The absolute SHG coefficients are further obtained by calibrating the SH intensities against a reference nonlinear optical crystal (LiNbO₃ in this study) under the same probing conditions. The extracted absolute SHG coefficient, $d_{36}$, at 800 nm is found to be $267 \pm 20$ pm V⁻¹, which agrees with the reported value, $310 \pm 50$ pm V⁻¹³⁷.

In many previous studies, various assumptions were made to simplify the analytical expressions in order to fit the experiments and extract the absolute values of the SHG coefficients. To evaluate the influence of these assumptions on the calculated SHG tensor coefficients, we obtained the corresponding analytical expressions under several assumptions using ♯SHAARP and evaluated the SHG intensities accordingly, as shown in Fig. 4e. The case labeled ‘♯SHAARP’ represents our results based on Eqs. (13) and (14) as described above. The results labeled ${{{\tilde{\boldsymbol{\varepsilon}}}}}_{{{\mathrm{R}}}}$ assume a negligible extinction coefficient, ${{{\tilde{\mathbf n}}}}_{{{\mathrm{I}}}}$, and only the real part of the dielectric permittivity tensor (i.e. real refractive indices, ${{{\tilde{\mathbf n}}}}_{{{\mathrm{R}}}}$) is used for deriving the analytical expression. Such assumptions are commonly employed in analyzing 2D materials with photon energy greater than their bandgaps, resulting in a largely uneven landscape of reported nonlinear susceptibilities^38,39. The results labeled by $\left| {{{{\tilde{\mathbf \varepsilon }}}}} \right|$ takes the magnitude of relative dielectric constants instead of the complex quantities into the analysis, which folds in the effect of the absorption indirectly. One can see that, for the specific case of GaAs (111) considered, the second-order nonlinear susceptibility tends to be underestimated by nearly 20% if the extinction coefficient is neglected. In contrast, no significant change in the SH intensity is observed in this case if only the magnitude of the complex dielectric constants ($\left| {{{{\tilde{\mathbf \varepsilon }}}}} \right|$) instead of the actual complex dielectric tensor is taken into account.

Uniaxial LiNbO₃ $(11\bar 20)$

LiNbO₃ is a uniaxial crystal (point group 3m) exhibiting ferroelectricity^40,41,42, piezoelectricity^43,44,45, and excellent nonlinear optical and electro-optic properties^46,47,48. The nonlinear optical properties of LiNbO₃ have been well characterized using the Maker fringes technique based on the transmission geometry^11,14. The bandgap of LiNbO₃ is reported to be ~3.78 eV^48,49, leading to no absorption at the fundamental pump energy of 1.55 eV and at the resulting SHG energy used in this study. Here we evaluate the absolute value of the SHG coefficient of LiNbO₃ by performing polarimetry experiments in the reflection geometry and using ♯SHAARP to fit the measured data. To exclude the contribution from the bottom surface of the LiNbO₃, a wedged crystal is used to select the contribution from only the top surface of the crystal.

The CCS can be expressed in hexagonal notation or trigonal notation, based on the choice of four or three basis vectors, respectively⁵⁰. X-cut LiNbO₃ is used in this study, which has the surface plane $(11\bar 20)$ and surface normal along $\left[ {11\bar 20} \right]$. The crystal is oriented in our measurement such that $[0001]\parallel L_1$ and $\left[ {11\bar 20} \right]\parallel L_3$ as illustrated in Fig. 5a. Since the optical axis is within the PoI, the extraordinary wave (transverse magnetic wave or the p-wave) experiences an effective refractive index as a function of the incidence angle ($\theta ^{{{\mathrm{i}}}}$) while the ordinary wave (transverse electric wave or the s-wave) experiences a constant refractive index, as shown in Fig. 5b. At 2ω frequency, two homogeneous and three inhomogeneous waves propagate inside the crystal with distinct phase velocities. Figure 5c, d show the p- and s-polarized second harmonic intensities, respectively, where open circles are experimental results and the solid curves are theoretically fitting from ♯SHAARP, respectively.

Fig. 5: Linear and nonlinear optical responses of LiNbO₃ ($11\bar 20$).

a Crystal structure and experimental orientation. b The real part of the effective refractive indices at ω frequency as a function of incident angle ($\theta ^i$). c and d p- and s-polarized second harmonic responses as a function of azimuthal angle (φ) at various incident angles ($\theta ^i$). e Comparison of ratios of SHG coefficients between ♯SHAARP (pale green background) and other forced approximations (pale orange background). Iso and KS, respectively, represent isotropic symmetry and Kleinman’s symmetry approximations, respectively. $Iso(\varepsilon _{ii})$ indicates that the component $\varepsilon _{ii}$ was assumed in all directions under the isotropic approximation, where $i$ is the direction index.

With the full consideration of anisotropic linear and nonlinear susceptibility and five nonlinear waves mixing, the fitting yields $\frac{{d_{33}}}{{d_{31}}} = 5.21 \pm 0.13$, which agrees well with the reported ratio ($\sim\!5.3$) measured using the Maker fringes¹⁴. Further referencing against a α-quartz (d₁₁ = 0.3 pm V⁻¹)^14,51,52 yields $d_{33}({{{\mathrm{LiNbO}}}}_3) = 28.5 \pm 0.2$ pm V⁻¹, which shows good agreement compared with the reported value of $26.2 \pm 2.8$ pm V⁻¹¹⁴. To examine the impact of various fitting assumptions commonly made in the literature, we refit the same experimental data using the analytical expressions generated by ♯SHAARP and forcing certain assumptions. The assumptions of isotropic symmetry and Kleinman’s symmetry were used to compare against the actual case as presented in Fig. 5e. Isotropic symmetry assumes isotropic dielectric permittivity and the absence of birefringence in the analysis. Here, we denote Iso($\varepsilon _{{{{\mathrm{ii}}}}}$) as the isotropic assumption of dielectric tensors, where $\varepsilon _{{{{\mathrm{ii}}}}}$ represents the dielectric components in the PCS. Kleinman symmetry^53,54,55 (abbreviated as KS) assumes that all three subscript indices of the SHG tensor (representing polarizations of the three waves) are fully permutable. This assumption has been widely used in determining nonlinear coefficients to reduce the number of independent variables⁵⁶, which leads to $d_{15} = d_{31}$ in LiNbO₃. With the assumption of isotropic dielectric permittivity, the ratios of coefficients exhibit an error within 10%. However, Kleinman symmetry can introduce a 20% error even for the nonresonant fundamental and SHG frequencies used in this study. Similar effects have been observed in other structures^57,58.

Biaxial KTP (100)

KTP is one of the most studied and widely applied NLO materials due to its large SHG coefficients and phase-matching properties^14,59,60,61. KTP crystallizes in an orthorhombic structure with the point group mm2 where the 2-fold axis is along the crystallographic c-axis⁶². The orthorhombic symmetry of KTP indicates that it belongs to the biaxial optical class characterized by three different refractive indices. The presence of two optical axes in such crystals often results in increased complexity in the analysis as compared with the uniaxial or isotropic classes²⁷. KTP (100) is used for this study which is oriented so that $[001]\parallel L_2$ and $[100]\parallel L_3$ as shown in Fig. 6a. In this case, both the optical axes deviate from the PoI. The propagation and effective refractive indices of the extraordinary and ordinary waves can be obtained by solving the generalized eigenvalue problem as shown in Fig. 6b. Since the optical axes lie in the $L_2 - L_3$ plane, the two refractive waves are, respectively, polarized, one extraordinary and one ordinary, which can be decomposed as transverse electric (s-polarized) and transverse magnetic (p-polarized) waves⁶³. The anisotropic SH signals reflected from the sample surface are collected at three incident angles ($\theta ^{{{\mathrm{i}}}} = 20^\circ ,30^\circ ,$ and 40°). In total, we have sufficient sets of experimental data to uniquely determine all independent variables, by fitting the analytical expression obtained from ♯SHAARP. The fitting results are shown in Fig. 6c and d.

Fig. 6: Linear and nonlinear optical responses of KTP (100).

a Crystal structure and experimental orientation. b The effective complex refractive indices at ω frequency as a function of incident angle ($\theta ^i$). c and d p- and s-polarized second harmonic responses as a function of azimuthal angle (φ) at various incident angles ($\theta ^i$). e Comparison of the correct ratios of nonlinear coefficients (pale green background) as against other forced approximations (pale orange background). Iso, and KS, respectively, represent isotropic symmetry and Kleinman symmetry approximations, respectively. $Iso(\varepsilon _{ii})$ indicates that the component $\varepsilon _{ii}$ was assumed in all directions under the isotropic approximation, where i is the direction index.

By using LiNbO₃ as the reference, the absolute d₃₃ is found to be $17.0 \pm 0.2$ pm V⁻¹ which agrees well with values reported in the literature ($16.4 \pm 0.7$ pm V⁻¹)¹⁴. The extracted full tensor components (see Table S1) are in agreement with the previous study utilizing the Maker-fringe technique¹⁴. In Fig. 6e we compared the fitted ratios of nonlinear coefficients based on the full analysis with no approximations against the analysis performed by forcing various assumptions such as the isotropic dielectric permittivity and the Kleinman symmetry assumptions, which have been described above in the case of LiNbO₃. It is found that the errors in the acquired SHG coefficients introduced by these assumptions can reach up to 40% if dielectric tensors with higher symmetry are used.

The agreement between our results on KTP and those reported in the literature not only demonstrates the capability of analyzing biaxial crystals using the ♯SHAARP, but also that single surface reflection can be an effective approach to characterizing the SHG coefficients, complementing the widely used methods based on Maker fringes and the Bloembergen–Pershan relations^11,12,18. All the extracted absolute SHG coefficients and ratios are summarized in Table 1.

Table 1 Comparison of ratios of SHG coefficients from ♯SHAARP and literature.

Weyl semimetal, TaAs (112)

TaAs is one of the first experimentally identified Weyl semimetals which host intriguing transport properties^64,65,66,67. Giant second harmonic response in TaAs was reported due to its intrinsic broken inversion symmetry and strong resonances^25,68. Using ♯SHAARP, we measure and analyze the SHG coefficients of TaAs crystals and compare our results with those reported in the literature. In this example, we also highlight two features of ♯SHAARP, namely, the ability to incorporate absorption and arbitrary crystal surface orientation. As indicated in Fig. 7a, the surface plane is (112), and $[1\bar 10]$ is set parallel to the L₂. The (112)-oriented plane results in a non-diagonalized dielectric tensor ${{{\tilde{\mathbf \varepsilon }}}}_{{{\mathrm{r}}}}$ in the lab coordinate system and, consequently, the noncollinearity between E and D. Figure 7b demonstrates the complex refractive index as a function of the incidence angle for both the ordinary and the extraordinary waves. The large extinction coefficient suggests large absorption at the pump wavelength. The anisotropic SHG intensities polarized along the L₁ and L₂ directions as a function of the polarization angle, $\varphi$ are measured, and then fitted with the analytical formula obtained using ♯SHAARP.

Fig. 7: Linear and nonlinear optical responses of TaAs (112).

a Crystal structure and experimental orientation. b The effective complex refractive indices at ω frequency as a function of incident angle ($\theta ^i$). c p- and s-polarized second harmonic responses as a function of azimuthal angle (φ) at various incident angles ($\theta ^i$). d Comparison of the correct ratios of nonlinear coefficients (pale green background) as against other forced approximations (pale orange background). Uni, Iso, and KS, respectively, represent uniaxial, isotropic symmetry, and Kleinman’s symmetry approximations. $Iso(\varepsilon _{ii})$ indicates that the component $\varepsilon _{ii}$ was assumed in all directions under the isotropic approximation, where i is the direction index. Uni($\left| {{{{\tilde{\boldsymbol{\varepsilon }}}}}} \right|$) and Uni(${{{\tilde{\boldsymbol{\varepsilon }}}}}_R$), respectively, mean using the magnitudes of complex relative dielectric permittivity and only the real part of the dielectric permittivity as tensor values while retaining the uniaxial dielectric permittivity tensor symmetry. Misoriented case represents analysis using the plane normal as [112] which is discussed in detail in Supplementary Note 2.

As seen in Fig. 7c, the intensity difference between $I_{L_1}^{2\omega }$and $I_{L_2}^{2\omega }$ indicates a strong anisotropy of the second-order nonlinear optical properties of TaAs probed with fundamental energy at 1.55 eV. Due to its metallic nature, TaAs exhibits multiple resonances near ω and 2ω frequencies leading to a resonance-enhanced SHG response⁶⁸. By calibrating with the SHG intensity of a well-studied nonlinear optical crystal (LiNbO₃ in our case), the absolute coefficients of TaAs can be uniquely determined. The saturation threshold of pump power was found to be around 50 μW (equivalent to a peak fluence of ~14 mJ cm⁻²). The second harmonic response was then collected in the non-saturation regime where quadratic dependence between pump power and SH intensity remains (see Supplementary Fig. 1). Using the equations generated by ♯SHAARP, the full absolute second harmonic tensor components can be evaluated, as shown in Fig. 7d (labeled as ♯SHAARP).

With the full consideration of anisotropy, absorption, and boundary conditions at the interface, our analysis yields values for |d₃₃|, |d₃₁| and |d₁₅| to be $827 \pm 39$, $12 \pm 15$, and $113 \pm 20$ pm V⁻¹, respectively. The strong anisotropy between d₃₃ and d₃₁ produces a large error bar for d₃₁. Figure 7d also demonstrates the variations of these coefficients created by forcing assumptions as shown in the pale orange-colored region. Here, Uni and Iso demonstrate the influence of birefringence on SHG response by constraining the dielectric tensors at both frequencies to be uniaxial and isotropic, respectively. To further explore the impact of optical resonances at the two frequencies on the SHG behavior, we adopted ${{{\tilde{\mathbf \varepsilon }}}}_{{{\mathrm{R}}}}$ as the constraint using only real components of dielectric permittivities and $\left| {{{{\tilde{\mathbf \varepsilon }}}}} \right|$ as the magnitude of dielectric permittivities. The non-absorbing assumption when analyzing materials with strong resonance may significantly underestimate the intrinsic SHG coefficients as presented in Uni(${{{\tilde{\boldsymbol{\varepsilon}}}}}_{{{\mathrm{R}}}}$) case. On the other hand, resonances due to interband transitions in TaAs⁶⁸ result in enhanced nonlinear optical susceptibilities, which make TaAs unsuitable for nonlinear optical frequency conversion applications due to their substantial absorption. Since utilizing photon energies below the bandgap is required for nonlinear optical frequency conversion applications, any direct comparison of TaAs or similar absorbing materials to transparent LiNbO₃ is not meaningful⁶⁹. The amplitude of the overall dielectric permittivity (presented as Uni($\left| {{{{\tilde{\boldsymbol{\varepsilon}}}}}} \right|$)) provides a closer estimation of the intrinsic properties as compared with the non-absorbing case. The study of Iso($\tilde \varepsilon _{{{{\mathrm{ii}}}}}$) cases provides a comprehensive picture of the influence of birefringence in TaAs, where $\tilde \varepsilon _{{{{\mathrm{ii}}}}}$ stands for the dielectric components used in the study. Iso($\tilde \varepsilon _{{{{\mathrm{ii}}}}}$) refers to the cases that directly apply Bloembergen and Pershan formulae¹⁰ to the studied material that has a symmetry lower than cubic²⁵. Due to the strong birefringence in TaAs, the isotropic dielectric permittivity assumption using $\tilde \varepsilon _{11}$ as the isotropic permittivity value (Iso($\tilde \varepsilon _{11}$)) leads to more than 20% underestimation of SHG coefficients, indicating the importance of a comprehensive and accurate model. Similarly, imposing Kleinman’s symmetry (presented as KS) results in large variations in d₃₁ and d₁₅, and cannot be used as a simplification in TaAs. The surface normal of TaAs (112) is $\left[ {\frac{1}{a}\frac{1}{a}\frac{2}{c}} \right]$ in the real space, where a and c are the lattice parameters⁷⁰. The ‘Misoriented’ case^25,26 in Fig. 7d represents analysis using out-of-plane direction as $\left[ {\frac{1}{a}\frac{1}{a}\frac{2}{a}} \right] = [112]$, assuming $a = c$. Due to the large c/a ratio, the misorientation leads to a dramatic change in the analysis (see Supplementary Fig. 2), and thus a large variation of the calculated d₃₃ in the analysis. Notably, the d₃₃ obtained without making these assumptions are found to be five times smaller as compared to the previously reported results^25,26. It is found that this discrepancy most likely originates from a misorientation of the crystal used in a previously published model (detailed discussion in Supplementary Note 2 and Supplementary Fig. 2 where we reproduce the derivations^25,26 and identify the deviation from ♯SHAARP analysis). Some differences due to the physical crystals are also possible, but the crystal used in this study shows that other properties of the crystals are comparable⁶⁸. Our results reveal that nothing more than a misorientation in modeling can lead to a huge overestimation of d₃₃ further emphasizing the importance of software tools such as ♯SHAARP that can eliminate such inadvertent human errors.

Table 1 summarizes absolute SHG coefficients and SHG ratios from this study and literature^14,25,37,48. We have benchmarked our analysis using three well-known nonlinear optical materials (GaAs, LiNbO₃, and KTP), covering all three optical classes, both transparent and absorbing systems, and both optical axes within and away from PoI. Good agreement has been achieved between this work and the literature for those three classical materials. We have examined how different assumptions made to simplify the analytical formulae of SHG intensities can influence the fitting results and thus the accuracy of the absolute values of SHG coefficients for the four different nonlinear optical crystals shown above. Overall in these examples, we found that including absorption and accurate crystal orientation, among other considerations, play significant roles in determining the nonlinear optical coefficients. Simply using the magnitude of the complex dielectric permittivity may result in an error of <10%, but neglecting extinction coefficients entirely may generate significant errors in the analysis (up to 90% for d₃₁ in TaAs). Simplifying the analysis by assuming higher symmetry of dielectric permittivity could introduce errors up to 20% or more, depending on the optical birefringence. However, assuming Kleinman’s symmetry results in much larger errors as compared with assuming higher symmetry for the cases presented in this study.

♯SHAARP demonstrates accurate and reliable analysis comparable with the Maker fringes, which have been used for six decades for the analysis of second harmonic response from transparent crystals^11,12,14,18. Maker fringes method is powerful for characterizing nonlinear susceptibilities, especially in analyzing transparent, thin crystals with high symmetry orientations along the LCS. However, the walk-off angle, the requirement of transmission geometry, simplified orientation, and high symmetry has limited the broader applications of this method. Moreover, the Maker fringes method mainly focuses on p- and s-polarized incident and SHG waves limiting the tunability of the detection schemes. On the other hand, we have demonstrated that the single-surface reflection method is as robust as the Maker fringes technique. This method provides more flexibility in materials selection regardless of their orientation, thickness, absorption, and symmetry. Polarimetry obtained through this method maps out the complete dependence of both input and output polarization, providing sufficient information on the nonlinear susceptibility tensor. Furthermore, various combinations of polarization settings provided in ♯SHAARP, including linear, elliptical, and circular polarized light, could promote more experimental designs, such as chiral structures. ♯SHAARP can be readily implemented in various frequency regimes from low-frequency radio waves to high-frequency extreme ultraviolet (XUV)^71,72 and X-rays^73,74 when the proper symmetry and probing intensity are taken into account. In particular, Curie groups implemented in ♯SHAARP ($\infty ,\infty m,\infty 2$) are useful for SHG from noncentrosymmetric plasma induced by hard x-rays^71,72,73,75.

In summary, we developed an open-source package, ♯SHAARP, for simulating SHG responses and extracting intrinsic SHG coefficients of nonlinear optical crystals based on a single-interface reflection geometry. The package is generally applicable to analyzing the reflective SHG of materials with arbitrary crystal symmetry, surface orientation, and absorption. To benchmark the results obtained by ♯SHAARP, we performed polarimetry experiments on representative nonlinear optical crystals, including GaAs, LiNbO₃, and KTP, to measure the reflective SHG intensities and fit the measurements with the analytical formula from ♯SHAARP. We extracted the absolute SHG coefficients of the three materials which show quantitative agreement with the previous works based on the transmission geometry using the Maker-fringe technique. We further applied ♯SHAARP to evaluate the SHG coefficients of topological Weyl semimetal TaAs. We found that the resonant SHG coefficient d₃₃ is nearly five times smaller than that reported in previous literature^25,26. Possible reasons for this deviation were discussed.

Looking forward, we believe that the open-source software, ♯SHAARP, will benefit studies of nonlinear optical materials in numerical modeling the polarimetry of known materials and extracting the absolute SHG coefficients of new materials. Moreover, the experimental scheme based on the single-interface reflection geometry will provide an alternative, more flexible way to the Maker fringe method in evaluating the SHG coefficients of nonlinear optical crystals, especially when the transmission experiment is challenging, e.g., for absorbing crystals. Meanwhile, we are building new functionalities into ♯SHAARP to enable the numerical and analytical modeling of the SHG based on transmission geometry through slabs and the Maker fringes. A version of ♯SHAARP for multiple-interface or multilayer system is under development.

Methods

Sample preparation

GaAs and LiNbO₃ single crystals were obtained from MTI Corporation. Note that X-cut based on MTI definition is different compared to convention^28,76 and we have specified the LiNbO₃ ($11\bar 20$) for clarity. The KTP crystal was obtained from CASTECH Inc. TaAs (112) was grown by chemical vapor transport at ~1000 °C for 4 weeks. Details can be found in the previous work⁶⁸. Wedged X-cut LiNbO₃ was prepared using 10 × 10 × 1 mm crystal with a wedged angle of around 5 degrees. The crystal was optically polished with 0.05 μm alumina suspension.

Second-harmonic generation

Second-harmonic polarimetry was performed using a Ti:Sapphire femtosecond laser system with the central wavelength at 800 nm (1 kHz, 100 fs). The incident linear polarized light was rotated through a zero-order half-wave plate and focused on the sample surface. A collecting lens was placed at the reflection geometry, and the SH signals were filtered by an analyzer and a bandpass filter before entering the photomultiplier tube (PMT). The SHG signals were then processed by the lock-in amplifier to filter out noise. The SHG fittings were then conducted using the expression generated by ♯SHAARP. All the SHG coefficients from the literature are recalibrated using Miller’s rule before the comparison⁷⁷.