Abstract
Image perception plays a fundamental role in the tomography-based approaches for microstructure characterization and has a deep impact on all subsequent stages of image processing, such as segmentation and 3D analysis. The enhancement of image perception, however, frequently involves observer-dependence, which reflects user-to-user dispersion and uncertainties in the calculated parameters. This work presents an objective quantitative method, which uses convolutional neural networks (CNN) for the quality assessment of the X-ray tomographic images. With only dozens of annotations, our method allows to evaluate directly and precisely the quality of tomographic images. Different metrics were employed to evaluate the correlation between our predicted scores and subjective human annotations. The evaluation results demonstrate that our method can be a direct tool to guide the enhancement process in order to produce reliable segmentation results. The processing of the tomographic image can thus evolve into a robust observer-independent procedure and advance towards the development of an efficient self-supervised approach.
Similar content being viewed by others
Introduction
X-ray computed tomography (XCT) is considered a powerful technique to study lithium-ion batteries (LIBs) since its nondestructive 3D imaging across multiple length scales provides quantitative and qualitative metrics for the characterization of their complex microstructure1. The effects of microstructural properties on the electrochemical performance of the battery can therefore be investigated, allowing the optimization of the electrode design. However, extracting reliable microstructural properties from 3D tomographic images is not straightforward and it usually follows a pre-processing step and a segmentation process2,3. The tomographic images contain many artifacts that have an impact on the 3D reconstruction and on the image quality as well, which affect the result of the analysis in evaluating the area and phases. Besides, it also causes ambiguity when different people process the same image. For instance, ring artifacts resulting from different sensitivity in detection, and emphasized after reconstruction, can be reduced using the flat-field correction method but the residual effect usually remained4. Center of rotation errors and cone beam errors affect the quality of the tomographic reconstruction and induce the appearance of a blurring effect in the image5. Several mechanisms can introduce different types of noise into the X-ray image acquisition process, such as statistical noise caused by the fluctuation of the raw x-ray signal, structural noise created by variations in the detector structure and in the differing response of elements, and scattering noise of scattered X-ray photons inducing a spurious signal and adding extra noise to the image6.
Hence, in X-ray computed tomography, image treatment is required to reduce the uncertainty in the 3D studied object. Image pre-processing is usually applied to improve the image quality, such as denoise, deblur and ring artifact removal, which involves the image feature enhancement (histogram equalization, normalization, brightness, and contrast adjustment) and distortion reduction. Segmentation is supposed to distribute pixels among certain groups based on pixel values, with the aim of assigning various regions of the image to different phases of the material.
In addition to the analysis, the pre-processing and the segmentation procedure are both non-trivial issues that have a significant impact on any subsequent image analyzes, such as the calculation of porosity, tortuosity, and the surface area of a specific phase. Due to the lack of a non-distorted reference image, the quality of the pre-processing is typically assessed by subjective visual inspection. However, image pre-processing has a profound impact on following segmentation performance. Schluter et al.7 presented that, with suitable image enhancement prior to segmentation, segmentation algorithms became more robust and were less prone to operator bias. He analyzed the segmentation accuracy of the images before and after pre-processing and pointed out that the distortion leads to poor segmentation. In addition, the absence of ground truth makes it difficult to assess the quality of the segmentation. Pietsch et al.8 proved that subjective judgment was not a reliable standard for the selection of binarization criteria in the segmentation procedure, leading to uncertainties in the results. Therefore, a numerical metric to assess the quality of images is needed to guide the pre-processing step (setting parameters, selecting filters) so that the next segmentation step can result in further highly reliable quantitative analysis.
Image quality assessment (IQA) aims to predict the perceptual quality of a distorted image. However, the human vision system (HVS)9 needs a reference to quantify the discrepancy by comparing the distorted image either directly with the original undistorted image or implicitly with a hallucinated scene in mind10. It is time-consuming and labor-intensive to assess image quality from a crowd of people. Moreover, due to different cultures and living environments, people sometimes give different views on the same picture. Especially for tomographic images, inexperienced and laymen would like to give totally different scores. Therefore, it is complicated to objectively assess the quality of tomographic images.
To avoid the distinction caused by cognitive bias and to provide robust professional estimation, some machine-assisted IQA methods have been proposed in recent decades. They are generally divided into three categories: (a) Full-reference image quality assessment (FR-IQA), which evaluates the distorted image by comparing it to the reference image and measuring the difference11,12. (b) Reduced-reference image quality assessment (RR-IQA) which measures image quality with part of the reference image13,14. (c) No-reference image quality assessment (NR-IQA), which requires little information about reference images and estimates image quality directly from distorted images15,16.
The conventional metrics used for FR-IQA and RR-IQA are peak signal-to-noise ratio (PSNR) and root mean square error (RMSE) which compare image intensity of distorted images to the reference images without considering HVS. By considering the luminance, contrast, and structural information, SSIM11 used average pooling to calculate a score from a similarity map. Based on SSIM, MS-SSIM17 compared the distorted image to the reference image at multiple scales. F-SIM18 leveraged phase congruency and gradient magnitude feature to derive a quality score, while GMSD19 only considered the image gradient as the criterial features. Besides the gradient, MDSI20 utilized chromaticity similarity and deviation pooling to imitate the HVS and achieved better results.
Although the above methods can serve as an indicator, reference images are not always available in real-world situations. Hence, NR-IQA methods have recently attracted extensive attention, which is also challenging due to the lack of reference information. Early NR-IQA methods mainly focused on specific types of distortions, such as noise21, contrast change22, blur23, and ring artifact24,25. Since the types of distortion of the images are unknown in real scenarios, these methods are impractical compared to the general methods26,27 which require no prior information about the distortion-types.
With the development of deep neural networks (DNNs), the deep learning methods have been exploited for NR-IQA28,29 without any prerequisites and have demonstrated superior prediction performance. Le et al.30 firstly proposed a shallow CNN to estimate the quality score for natural images. Ke et al.31 introduced a deep learning-based image quality index for blind image quality assessment, which was more efficient and robust. Instead of the multi-stage methods, Sebastian et al.32 presented an end-to-end neural network to regress the quality score by joint learning of local quality and local weights. Instead of considering the whole image in the network, Simone et al.33 cropped the image into patches, estimated the scores separately, and finally merged them, which was more suitable for cases of insufficient training data. However, the lack of training data was a crucial obstacle for the aforementioned methods. To overcome the limitation of data, Xialei et al.34 implemented data augmentation by generating artificial distorted images and then trained a Siamese network (RankIQA) to regress the quality scores. Kwan-Yee et al.10 combined the generative neural network to generate the reference images and the convolutional neural network to regress the quality score from the discrepancy. Hancheng et al.35 developed a meta-learning36 method to estimate the quality score of images with new distortion, which addressed the generalization problem of IQA.
Although many methods have been provided for IQA and achieved excellent results, most of them focus on natural images and require a huge number of annotated labels, which are not practical for X-ray tomography images. For example, the FR-IQA methods need a reference image for each estimation of a distorted image, which implies a high demand for annotations. The already developed NR-IQA methods require less data than the FR-IQA method but are still relatively large (hundreds of annotations) to avoid overfitting. Besides, the existing open-source datasets37,38,39 of battery electrodes tomographic images are not for IQA task, i.e., without various distortion-types and corresponding scores. Therefore, a light NR-IQA method, which requires less annotated data and is strong enough to transfer among different X-ray tomography images, is urgently demanded.
The main contributions of this work are summarized as follows:
-
A no-reference tomographic image quality assessment (TIQA) method is proposed for tomographic images, which requires only dozens of annotated images for training and achieves outperformed results.
-
A data generation method is developed by imitating the human observers to automatically label the distorted images for the purpose of addressing the insufficient data problem. Benefit from data generation, our TIQA method requires only one-fifth of the number of images compared to other NR-IQA methods.
-
The correlation between image quality score and segmentation results is studied to guide the pre-processing step.
The remainder of the paper is organized as follows: In section “Results”, we show the results of our data generation method and TIQA method. Moreover, the segmentation result and the link between quality score and segmentation performance are demonstrated in this section as well. In section “Discussion”, we summarize the results and emphasize the features of our method. We also propose several potential applications and future directions of our method. In section “Methods”, we introduce our dataset and the experiment details.
Results
Data generation results
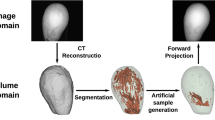
As shown in Fig. 1, the first step of our approach is to generate the data required for the subsequent training process of the score prediction network, whose purpose is to address the problem of insufficient data. The detailed workflow of the data generation process is illustrated in Fig. 2.
Firstly, the original image is resized and cropped into a fixed size, 224*224 pixels. Notably, to verify whether the resize operation affects the image quality scores, we compare the annotations on the images before and after this operation. The comparison results (Fig. S1) confirm that the pre-processing operations do not affect the image quality. Next, three types of distortion (ring artifact, blur, noise) that are commonly presented in X-ray tomographic images, are added to generate distorted images. (More generated images can be found in Fig. S2). Finally, the label projection step systematically produces the annotations of distorted images by comparing the HVS features of the original image and distorted image using different FR-IQA metrics (more details are in the Methods section).
To validate our method for data generation, we consider two criteria to quantify the correlation between generated results from the label projection step and corresponding labels from the survey, including Pearson’s linear correlation coefficient (PLCC) and Spearman’s rank-ordered correlation coefficient (SROCC). As presented in Fig. 3 and Fig. S3, for all types of distortions, the generated scores have a positive correlation with the annotations. Especially for the images with noise or blur, the correlation is high. As for the ring artifact, the results demonstrate that the existing general FR-IQA metrics cannot well handle this type of distortion.
It shows the data augmentation performance for three types of distortions. a, b Demonstrate the correlation between predicted scores and human annotated scores in three types of distorted images. c–e Illustrate the quantitative value of the predicted scores and human labels of images with blur, noise, and ring artifact. The red boxes represent the confident human annotations.
Score prediction results
In the procedure of image quality score prediction, as shown in Fig. 1, the network was first trained to rank the images according to their distortion levels. Then, based on the prior “ranking” knowledge, it was fine-tuned to regress the order information to a comprehensive quality score that represents the image quality in the range of 1 (worst) to 5 (best). In this work, we take the EfficientNet40 as the feature extractor instead of VGG41 used in RankIQA26 because it has less parameters (about 9 million parameters compared to VGG, about 138 million trainable parameters), which means easier to converge and less possibility for overfitting.
For the validation of the model, we predict the quality score of 56 images and compared the results with human annotations, as presented in Fig. 4(c–f). The results of images with different types of distortions were evaluated separately, which allows to observe the performance of the model towards different distortions. Taken together, these results indicate that there is a correlation between our predicted results and the human-labeled scores, which demonstrates that our method is able to imitate the HVS for the IQA. Interestingly, for blurred images, it performs excellently on both the relative order and the absolute score.
a Shows the box figure of the prediction results while (b) demonstrates the tested image volumes. They both are from the same material, but the volume Image Stack 01 has better quality than the volume Image Stack 02. The figure on the right shows the predicted quality score of the two volumes. The line in the box is the mean value of all scores. Quantitative comparison among different methods. c–e Show the results of assessing the images with ring artifact, noise, and blur distortion, respectively. The last figure (f) illustrates the results of different methods for all types of distortions.
We also apply our method to two X-ray tomographic image volumes to observe the consistency of the results. As demonstrated in Fig. 4a, b, we generate two image volumes with different quality and each of them contains 594 slices with a size of 720 × 720. The images with higher quality are generated by enhancing the boundary through a segmentation algorithm. In the box plot, we can see that the volume (purple) with high quality achieved a higher score while the one (cyan) with lower quality had a lower score. A more detailed comparison of different pre-processing methods can be found in Fig. S4. The results show that our method can be quantitatively compared with different pre-processing methods, allowing the selection of the most appropriate method. Moreover, from the variance of these two boxes, we can conclude that our method has stable performance because the difference among confident scores is small (less than 0.05) compared to human distinction. Besides selecting pre-processing methods, our method could also help to adjust filter parameters with the guidance of quality scores.
To demonstrate the advantage of our method, we compare it to other outstanding NR-IQA methods through two quantitative metrics (SROCC and PLCC) and the full table is shown in Table S5. Here we represent two of them, BRISQUE26 and RankIQA34 in Fig. 4f. Overall, it shows that our method excels in assessing the quality of tomography images since it yields the highest correlation score among these three methods. In terms of different types of distortion, our method outperforms BRISQUE for all three distortions. When compared with RankIQA, our method achieves better results for images with ring artifact and noise and on performance on the images with blur distortion. Besides, to avoid the shortcomings of correlation-based metrics, we adopt Krasula’s metric42 as well, and the results are shown in Fig. S6. The three analysis results show that the TIQA method achieves higher AUC than the others.
Segmentation evaluation method
The TIQA method provides us with an efficient tool to select the image with the best quality among pre-processing methods, and the clue of how the distortion affects the segmentation accuracy could suggest the pre-processing step. Therefore, extra experiments were conducted to inspect the relation between image quality and segmentation accuracy. We implemented a CNN based on D-linkNet43 to predict the semantic segmentation results and compared them with TIQA results to explore the influence of the distortions.
As presented in Fig. 5, a CNN network for segmentation is trained on X-ray tomography images and annotated segmentation ground truth before making predictions. The uncertainty map is generated by calculating the entropy44 of the possibility of each pixel belonging to different classes. It represents the uncertainty when the network assigns a phase (φi) to each pixel. High uncertainty is represented as a red pixel, while a low certainty is displayed as a white pixel. From the uncertainty map, we can see that a higher uncertainty exists at the interphases while a low one exists at the bulk, which proves that the network usually produces fuzzy boundaries. The segmentation results are obtained by binarizing the probability map. Here, only two classes are considered, but the segmentation process can be extended to multiple classes.
Relation between IQA results and segmentation accuracy
In addition to the uncertainty map, the F1 score, which is calculated from the confusion matrix, is also considered to quantify the segmentation accuracy. The correlation between the TIQA score and the segmentation accuracy is investigated. We select an original image and its corresponding images with different types of distortions as the data for both IQA and segmentation (see Fig. 6). From the results, we can clearly see that the distortion affects the image quality and the segmentation performance. With distortion, images have a lower quality score than the F1 score, which means lower segmentation accuracy. The uncertainty map clearly presents the influence of distortion on final segmentation results. Compared to these three types of distortion, the noise causes a large amount of incertitude points in the uncertainty map, shown as the red points in Fig. 6. Although it seems that the blur distortion causes little uncertainty, it leads to vague boundaries and misclassification as well as a huge reduction in HVS-based image quality score.
Moreover, the quantitative evaluation results of the TIQA and segmentation accuracy are shown in Table 1. From the SROCC and PLCC, we can see that the quality scores predicted by our approach are well correlated to the segmentation accuracy. The TIQA scores share a similar trend with the F1 scores, especially for the images with ring artifact and blur distortions.
To inspect the impact of distortion on classification results from a pixel perspective, we calculate the correlation point pixel by pixel between predicted segmentation and ground truth. As shown in Fig. 7, we can observe that the colorful lines (with distortion) have a positive correlation with the black line (without distortion). Nevertheless, they may have different sensitivity to specific types of distortion. For example, the correlation point line of the segmentation with noise do not converge at the reference line and the fluctuation indicates the serious impact of noise on segmentation results. Additionally, the third figure in Fig. 7 illustrates that, with the increase in distortion level, the IQA score decreases quickly, but the segmentation accuracy keeps stable, which implies that the network can tell very little difference in pixel values in the image and classify the pixels to different categories based on the distinction. Due to the limitation of HVS, people cannot distinguish the little variation of the pixel intensities, as the results of the blurred images shown in Fig. 7.
Figures a–c set out the correlation results from images with the ring, noise, and blur. The color bar shows the distortion at different levels, from little distortion to severe distortion. The solid line means the point correlation in X direction. The number labeled at the end of each line is the image quality score.
In summary, through the image quality score produced by our method, especially for images with blur and ring artifact, as described in Table 1, we can infer the corresponding segmentation performance without implementation. It greatly reduces the time of choosing an appropriate pre-processing algorithm to improve the image quality and achieve better segmentation accuracy.
Discussion
Tomography images are widely used for analyzing the battery microstructure. However, the essential pre-processing image procedure is, mostly, observer-dependent45. This observer-dependence can lead to dispersions and uncertainties in the segmentation process. The latter might produce unreliable results that deteriorate the subsequent quantitative analysis, especially when the segmentation involves the supervised training procedure (inaccurate ground truth). However, we believe that observer-dependence can be reduced or eliminated by the appropriate pre-processing step, that provides the image with good quality according to HVS. Hence, a trust-worthy metric, which can assess the image quality like human observers, to guide the pre-processing procedure helps with dependable post-processing workflow (segmentation and analysis).
In this paper, we propose a quantitative metric, denoted as TIQA, for X-ray tomographic image quality assessment. Moreover, we address the lack of data issues for X-ray tomographic images through the data generation process. Overall, our approach shows good performance and outperforms the other two IQA methods (BRISQUE & RankIQA) for X-ray tomographic images, given only a few annotations for training. It is worth noting that although we try to reduce the demand for training annotations, a small number of labels are still required so that it cannot be considered a totally blind IQA method.
The correlation between our metric and the segmentation performance has also been explored. The qualitative and quantitative evaluation results prove that the segmentation performance is associated with the predicted quality score, which is also related to subjective human annotations. This correlation gives us tips to reduce the uncertainties and variations of segmentation results by applying pre-processing algorithms to improve the image quality.
For the idea of using a neural network to evaluate the results of IQA, we use a similar method as Samuel et al.46, who investigated the effect of image quality on DNN results by applying differently distorted images on the same network, but we conducted more types of distortion. Instead of focusing on the image classification problem, which classifies an image into one category, we analyzed the impact of distortion on the image segmentation problem, that is concerned with pixels classification. Taking advantage of the uncertainty map and IoU map, the influence of distortion could be clearly visualized.
In conclusion, this work provides a quantitative IQA metric to guide the pre-processing step based on subjective human opinion so that the observer-dependence can be alleviated or removed from the pre-processing and the segmentation step. It greatly reduces the tedious work of selecting good images and facilitates the automation of analyzing X-ray tomography images. In addition, it provides a more reliable assessment of pre-processing image results, which avoids the conflicts of different human observers, and promises an outperformed segmentation analysis.
However, some limitations remain to be solved. The undistorted images are not well evaluated in our method due to the lack of images with excellent quality. Although our approach does not need hundreds of images for training, the estimation results of image quality can still be improved with the larger dataset. These limitations can be solved with the contribution of the community by sharing open-source X-ray tomographic data, such as Tomobank37,38,39.
Interestingly, thanks to the demand for automatically analyzing the tomography images, our TIQA method can be extended to improve the image quality by using different image processing methods. For example, by constructing a Teacher-Student model, our method (teacher) can teach a distortion removal network (student) to automatically eliminate the distortions. It will greatly release the burden of human observers and reduce the impact of distortion on segmentation. In addition, the image quality assessment can be extended to object-oriented assessment. For instance, through the learning of object information, the network can judge whether the materials inside of the battery are destroyed or not.
Methods
Dataset creation
We collected 40 8-bit images from 11 different types of batteries with different resolutions. All the images were rescaled to the same resolution 224 × 224. To avoid deformation, we resized the original image to the width or height equaling 255 while preserving the aspect ratio, then randomly cropped the region with a size of 224 × 224. We also maintained six original images for the analysis of the impact of the downsampling operation on the image quality score. To expand the dataset, we applied different algorithms with different parameters to generate images with different types of distortion. For example, we generated several rings with different radius and intensities based on original images and add them together to imitate the ring artifact distortion. For blur and noise, we used the methods implemented in scikit-image47. Similar to Hanne’s method48, we manually set the parameter values that control the distortion amount such that the visual quality of the distorted images varies, from an expected rating from 1 (terrible) to 5 (excellent). The distortion parameter values were chosen based on a small set of images and applied the same for the remaining images in our database.
We performed two surveys for subjective image quality scores and conveyed them to different people who included beginners and experts in this field for annotation among five levels: terrible, bad, average, good, and excellent. For each image, we collected annotations from 15 people and set the average number as its quality score.
Data generation
As illustrated in Fig. 2, the preprocessed images were regarded as reference images. Then several distortion filters, including noise, blur, and ring artifact, were applied to the reference image to generate the distorted images. The parameter values of the filters were set differently, as shown in Table S7, to create different distortion before adding them to the reference images to produce images at different levels of distortion. For label projection, we used five FR-IQA evaluators, mimicking the human observers, to calculate the difference between a reference image and a distorted image and pass a score for a distorted image. Due to the range of the score from each evaluator varies, we normalized and rescaled them to the same range. Finally, we averaged the produced scores and set it as the generated score.
Score prediction
As shown in Fig. 1, we took the EfficientNet network as the feature extractor and change the last three layers to output a score for each input image. Among the dense layers, we added dropout49 to avoid overfitting. Instead of training the network from scratch, we transferred the weights from the pre-trained model in ImageNet50 to reduce the time of convergence51. The input image size was fixed at 224 × 224 × 3 and the corresponding output was a score with a shape of 1 × 1.
We built the image by pair by picking an original image, generating the distorted images with distortions at different levels. The image with a lower level of distortion was regarded as a better image than the one with a higher level of distortion. Taking advantage of the generated ranking information, the network could order the images by quality. The corresponding rank loss52 function is
where \(\hat y_i - \hat y_j\) are the prediction results of a pair of images; m, set at 6 in our experiment, is a margin to control the minimum distance of the positive image pair.
After the image ordering process, the human annotations and the generated machine labels were inputted into the network to regress the output score to a fixed range by leveraging the Minor Square Error (MSE) loss function.
Training and testing parameters
In the score prediction module, we used 32 original images, which were expanded to 512 images after data generation but without labels for training the rank. The initial learning rate was set at 3e-5 and decayed after several iterations. The network was trained for 30 epochs, and on each epoch, it iterated on the whole dataset. The rate of the dropout was set at 0.5 to avoid overfitting. The Adam53 optimizer was applied for optimizing the rank loss.
After training the rank, the model was fine-tuned in the score regression step. The training dataset contains 29 images with the size of 224 × 224 × 3 and their corresponding labels, which are in the range from 1 to 5. The data generation method was also implemented to expand the training dataset to 464 images with generated annotations. Then, they were inputted into the network for regression with the MSE loss. The network iterated 20 epochs with the initial learning rate at 5e-5, which decayed every 4 epochs. The dropout rate was 0.5 in training. For the testing procedure, a total of 56 images were tested and evaluated with corresponding human annotations. All the experiments were conducted in python with the TensorFlow54 library. The computing hardware was Tesla K80.
Evaluation metrics
The PLCC (Pearson’s linear correlation coefficient) is the linear correlation coefficient between the predicted score and human-labeled score. It measures the prediction accuracy of an IQA metric, i.e., the capability of the metric to predict the subjective scores with low error. The PLCC is calculated as follows:
where \(\hat y_i\) and yi are the predicted score and the human-labeled score of the ith image in a dataset of size Md respectively, \(\hat y_{avg}\) and yavg are the average of the predicted scores and human-labeled scores, respectively.
The SROCC (Spearman’s rank-ordered correlation coefficient) is the rank correlation coefficient between the predicted score and labeled score, and it compares the monotonicity of the prediction performance, i.e., the limit to which the predicted scores agree with the relative magnitude of the labels. The SROCC can be calculated via the following equation:
where the di is the difference between the ith image’s rank in prediction results and labels.
Segmentation-based evaluation method
To inspect the effect of distortion on segmentation accuracy, we applied D-LinkNet43, which is an encoder-decoder network connected by dilated convolutions55, for tomography image segmentation. It segmented the image into two classes and produced the probability map, which indicated the possibility of each pixel belonging to a class. Finally, the classification result is generated by setting a threshold to binarize the probability map. The network ran for 200 epochs on 110 images with segmentation labels. The size of the input image and label was 1024 × 1024 and they were normalized to a range of 0 and 1 before inputting to the network. The initial learning rate was 1e-4 and decayed to one-fifth of the previous value after fixed steps. The optimizer was Adam and binary cross-entropy loss was used to measure the difference between prediction and ground truth.
In the testing procedure, the output of the network was utilized to generate the uncertainty map. We used the entropy function44 to calculate the uncertainty, which is described as follows,
where x is the test image, y is the predicted class, X and Y are the images and labels in the training process, c is the class index.
The IoU (intersection over union) and F1 scores were utilized to measure the segmentation performance. IoU means the area of overlap between the predicted segmentation and the ground truth divided by the area of union between them. It ranges from 0 to 1, with 0 signifying no overlapping and 1 indicating perfect overlapping. Different from IoU, the F1 score can be calculated by:
where the total pixels mean the number of pixels in both segmentation results and ground truth.
Data availability
Contact the corresponding author with requests to view raw data. Sample image sets are publicly available in the GitHub repository for this project (link provided below).
Code availability
The python code for IQA and segmentation evaluation of the project is available at https://github.com/kai-zhang-er/TomoIQA.
References
Nguyen, T.-T. et al. 3D quantification of microstructural properties of LiNi0.5Mn0.3Co0.2O2 high-energy density electrodes by X-Ray Holographic Nano-Tomography. Wiley Online Libr. https://doi.org/10.1002/aenm.202003529. (2021).
Chan, H., Cherukara, M., Loeffler, T. D., Narayanan, B. & Sankaranarayanan, S. K. R. S. Machine learning enabled autonomous microstructural characterization in 3D samples. npj Comput. Mater. 6, 1–9 (2020).
Su, Z. et al. Artificial neural network approach for multiphase segmentation of battery electrode nano-CT images. npj Comput. Mater. 8, 1–11 (2022).
Source, D. L., Science, H. & Campus, I. Superior techniques for eliminating ring artifacts in X-ray micro-tomography. 26, 28396–28412 (2018).
Davis, G. R. & Elliott, J. C. Artefacts in X-ray microtomography of materials. Mater. Sci. Technol. 22, 1011–1018 (2006).
Schofield, R. et al. Image reconstruction: Part 1 – understanding filtered back projection, noise and image acquisition. J. Cardiovasc. Comput. Tomogr. 14, 219–225 (2020).
Schlüter, S., Sheppard, A., Brown, K. & Wildenschild, D. Image processing of multiphase images obtained via X-ray microtomography: A review. Water Resour. Res. 50, 3615–3639 (2014).
Pietsch, P., Ebner, M., Marone, F., Stampanoni, M. & Wood, V. Determining the uncertainty in microstructural parameters extracted from tomographic data. Sustain. Energy Fuels 2, 598–605 (2018).
Gao, X., Lu, W., Tao, D. & Li, X. Image quality assessment and human visual system. In Visual Communications and Image Processing Vol. 7744, pp. 316–325. (SPIE, 2010).
Lin, K. Y. & Wang, G. Hallucinated-IQA: no-reference image quality assessment via adversarial learning. In Proc. IEEE Computer Society Conference on Computer Vision and Pattern Recognition 732–741 (IEEE Computer Society, 2018).
Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process 13, 600–612 (2004).
Zhang, L., Shen, Y. & Li, H. VSI: A visual saliency-induced index for perceptual image quality assessment. IEEE Trans. Image Process 23, 4270–4281 (2014).
Zhu, W., Zhai, G., Liu, Y., Lin, N. & Yang, X. Reduced-reference image quality assessment based on free-energy principle with multi-channel decomposition. In 2018 IEEE 20th International Workshop on Multimedia Signal Processing, MMSP 2018 (Institute of Electrical and Electronics Engineers Inc., 2018).
Golestaneh, S. & Karam, L. J. Reduced-reference quality assessment based on the entropy of DWT coefficients of locally weighted gradient magnitudes. IEEE Trans. Image Process 25, 5293–5303 (2016).
Geisler, W. S. Visual perception and the statistical properties of natural scenes. Annu. Rev. Psychol. 59, 167–192 (2008).
Leclaire, A. & Moisan, L. No-reference image quality assessment and blind deblurring with sharpness metrics exploiting Fourier phase information. J. Math. Imaging Vis. 52, 145–172 (2015).
Wang, Z., Simoncelli, E. P. & Bovik, A. C. Multi-scale structural similarity for image quality assessment. In The 37th Asilomar Conference on Signals, Systems and Computers 1398–1402 (IEEE, 2003).
Zhang, L., Zhang, L., Mou, X. & Zhang, D. FSIM: a feature similarity index for image quality assessment. IEEE Trans. Image Process 20, 2378–2386 (2011).
Xue, W., Zhang, L., Mou, X. & Bovik, A. C. Gradient magnitude similarity deviation: a highly efficient perceptual image quality index. IEEE Trans. Image Process 23, 668–695 (2014).
Nafchi, H. Z., Shahkolaei, A., Hedjam, R. & Cheriet, M. Mean deviation similarity index: efficient and reliable full-reference image quality evaluator. IEEE Access 4, 5579–5590 (2016).
Liu, M. et al. Blind image quality assessment for noise. In IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, BMSB (IEEE Computer Society, 2014).
Gu, K. et al. No-reference quality metric of contrast-distorted images based on information maximization. IEEE Trans. Cybern. 47, 4559–4565 (2017).
Yan, Q., Xu, Y. & Yang, X. No-reference image blur assessment based on gradient profile sharpness. In IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, BMSB (IEEE Computer Society, 2013).
Liu, H., Klomp, N. & Heynderickx, I. A no-reference metric for perceived ringing artifacts in images. IEEE Trans. Circuits Syst. Video Technol. 20, 529–539 (2010).
Vo, N. T., Atwood, R. C. & Drakopoulos, M. Superior techniques for eliminating ring artifacts in X-ray micro-tomography. Opt. Express 26, 28396 (2018).
Mittal, A., Moorthy, A. K. & Bovik, A. C. Blind/referenceless image spatial quality evaluator. In 2011 Conference Record of the 45th Asilomar Conference on Signals, Systems and Computers 723–727 (IEEE, 2011).
Manap, R. A. & Shao, L. Non-distortion-specific no-reference image quality assessment: a survey. Inf. Sci. 301, 141–160 (2015).
Ma, K., Liu, W., Liu, T., Wang, Z. & Tao, D. DipIQ: blind image quality assessment by learning-to-rank discriminable image pairs. IEEE Trans. Image Process 26, 3951–3964 (2017).
Ma, K. et al. End-To-end blind image quality assessment using deep neural networks. IEEE Trans. Image Process 27, 1202–1213 (2018).
Kang, L., Ye, P., Li, Y. & Doermann, D. Convolutional neural networks for no-reference image quality assessment. In Proc. IEEE Computer Society Conference on Computer Vision and Pattern Recognition 1733–1740 (IEEE Computer Society, 2014).
Gu, K., Zhai, G., Yang, X. & Zhang, W. Deep learning network for blind image quality assessment. In 2014 IEEE International Conference on Image Processing, ICIP 2014 511–515 (Institute of Electrical and Electronics Engineers Inc., 2014).
Bosse, S., Maniry, D., Müller, K. R., Wiegand, T. & Samek, W. Deep neural networks for no-reference and full-reference image quality assessment. IEEE Trans. Image Process 27, 206–219 (2018).
Bianco, S., Celona, L., Napoletano, P. & Schettini, R. On the use of deep learning for blind image quality assessment. Signal, Image Video Process. 12, 355–362 (2018).
Liu, X., Weijer, J. Van De & Bagdanov, A. D. RankIQA: learning from rankings for no-reference image quality assessment. In Proc. IEEE International Conference on Computer Vision 1040 (Institute of Electrical and Electronics Engineers Inc., 2017).
Zhu, H., Li, L., Wu, J., Dong, W. & Shi, G. MetaIQA: deep meta-learning for no-reference image quality assessment. Proc. IEEE Int. Conf. Comput. Vis. (IEEE, 2020).
Sun, Q., Liu, Y., Chua, T. S. & Schiele, B. Meta-transfer learning for few-shot learning. In Proc. IEEE Computer Society Conference on Computer Vision and Pattern Recognition (IEEE, 2019).
De Carlo, F. et al. TomoBank: a tomographic data repository for computational x-ray science. Meas. Sci. Technol. 29, 034004 (2018).
Usseglio-Viretta, F. L. E. et al. Resolving the discrepancy in tortuosity factor estimation for Li-Ion battery electrodes through micro-macro modeling and experiment. J. Electrochem. Soc. 165, A3403–A3426 (2018).
Ebner, M., Chung, D. W., García, R. E. & Wood, V. Tortuosity anisotropy in lithium-ion battery electrodes. Adv. Energy Mater. 4, 1301278 (2014).
Tan, M. & Le, Q. V. EfficientNet: rethinking model scaling for convolutional neural networks. 36th Int. Conf. Mach. Learn. ICML 2019 10691–10700 (2019).
Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. In 3rd International Conference on Learning Representation ICLR 2015, (eds Bengio, Y. & LeCun, Y.) (San Diego, CA, USA, 2015) http://arxiv.org/abs/1409.1556.
Krasula, L., Fliegel, K., Le Callet, P. & Klima, M. On the accuracy of objective image and video quality models: new methodology for performance evaluation. 2016 8th International Conference on Quality of Multimedia Experience. (IEEE, 2016).
Zhou, L., Zhang, C. & Wu, M. D-linknet: Linknet with pretrained encoder and dilated convolution for high resolution satellite imagery road extraction. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (IEEE, 2018).
Shannon, C. E. A mathematical theory of communication. In The Bell System Technical Journal (Nokia Bell Labs, 1948).
Baveye, P. C. et al. Observer-dependent variability of the thresholding step in the quantitative analysis of soil images and X-ray microtomography data. Geoderma 157, 51–63 (2010).
Dodge, S. & Karam, L. Understanding how image quality affects deep neural networks. In 2016 8th International Conference on Quality of Multimedia Experience, QoMEX 2016 7498955 (Institute of Electrical and Electronics Engineers Inc., 2016).
Van Der Walt, S. et al. Scikit-image: image processing in python. PeerJ 2014, e453 (2014).
Lin, H., Hosu, V. & Saupe, D. KADID-10k: A large-scale artificially distorted IQA database. In 2019 11th International Conference on Quality of Multimedia Experience, QoMEX 2019 (IEEE, 2019).
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958 (2014).
Deng, J. et al. ImageNet: a large-scale hierarchical image database. In 2009 IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2009).
He, K., Girshick, R. & Dollár, P. Rethinking ImageNet pre-training. 1–10 (2018).
Chen, W., Liu, T. Y., Lan, Y., Ma, Z. & Li, H. Ranking measures and loss functions in learning to rank. In Proc. 22nd International Conference On Neural Information Processing Systems (Curran Associates Inc., 2009).
Kingma, D. P. & Ba, J. L. Adam: a method for stochastic optimization. In 3rd International Conference on Learning Representations, ICLR 2015 (CLR, 2015).
Abadi, M. et al. TensorFlow: a system for large-scale machine learning. In Proc. 12th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2016 (USENIX Association, 2016).
Chen, L.-C., Papandreou, G., Schroff, F. & Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. Proc. IEEE Computer Society Conference on Computer Vision and Pattern Recognition (IEEE, 2017).
Acknowledgements
This research is supported by the French Ministry of Higher Education, Research and Innovation and ANR funding (ANR-19-CE42-0014). The authors are grateful to the researchers from the RS2E network (CNRS FR 3459) who participated in the survey about image quality assessment. The authors express gratitude to D. Boursier for the English proofreading.
Author information
Authors and Affiliations
Contributions
A.D., T.-T.N., and K.Z. have conceived the strategy for the investigation. This work was supervised by A.D. and T.-T.N. The datasets were acquired and reconstructed by T.-T.N. and Z.L.S. The algorithm was coded by K.Z. and partially contributed by T.-T.N. K.Z., T.-T.N., and A.D. wrote the paper. All authors participated in the discussion and revision of this paper and finally approved this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, K., Nguyen, TT., Su, Z. et al. Self-supervised image quality assessment for X-ray tomographic images of Li-ion battery. npj Comput Mater 8, 194 (2022). https://doi.org/10.1038/s41524-022-00870-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00870-z
This article is cited by
-
Capacitive tendency concept alongside supervised machine-learning toward classifying electrochemical behavior of battery and pseudocapacitor materials
Nature Communications (2024)
-
Detecting lithium plating dynamics in a solid-state battery with operando X-ray computed tomography using machine learning
npj Computational Materials (2023)
-
Grey wolf optimizer based IQA of mixed and multiple distorted images
International Journal of Information Technology (2023)