Abstract
We focus on gas sorption within metal-organic frameworks (MOFs) for energy applications and identify the minimal set of crystallographic descriptors underpinning the most important properties of MOFs for CO2 and H2O. A comprehensive comparison of several sequential learning algorithms for MOFs properties optimization is performed and the role played by those descriptors is clarified. In energy transformations, thermodynamic limits of important figures of merit crucially depend on equilibrium properties in a wide range of sorbate coverage values, which is often only partially accessible, hence possibly preventing the computation of desired objective functions. We propose a fast procedure for optimizing specific energy in a closed sorption energy storage system with only access to a single water Henry coefficient value and to the specific surface area. We are thus able to identify hypothetical candidate MOFs that are predicted to outperform state-of-the-art water-sorbent pairs for thermal energy storage applications.
Similar content being viewed by others
Introduction
Metal-organic frameworks (MOFs) are crystalline compounds consisting of metal ions and organic linkers, characterized by tunable porosity and incredibly high surface area1. Due to their properties, MOFs have recently attracted remarkable attention in a wide range of different fields, including gas/vapor separation2, reaction catalysis3, drug delivery4, energy storage, and heat transformations5,6. Given their nature as porous adsorbent materials, intensively active research is focused on the use of MOFs for CO2 capture, towards the development of effective technologies for mitigating greenhouse gas emissions7. Recently, MOFs have been also employed in adsorption-based atmospheric water harvesting driven by solar thermal energy8,9. In general, when dealing with applications of engineering relevance, different inlet gas streams, variable operating conditions, and target properties tailored per each specific case make it challenging to identify an ideal MOF crystal for all applications10, thus leading to a fragmented case-by-case optimization problem.
Hence, MOFs require proper and efficient methods for tailoring their features according to target properties of interest in each specific application. The latter is everything but an easy task. In fact, due to the myriad of degrees of freedom for MOFs structure and composition, more than 100 trillion compounds have been hypothesized11, while almost 100,000 have been synthesized so far12. High-throughput computational screening and machine learning have been recently adopted to analyse large MOF datasets13. Such computational tools allow us to identify significant correlations between nanoscale features and observable macroscale properties14,15, and to select the most suitable crystal for a given application case. A few representative examples are provided by gas-gas separation (D2/H216, O2/N217, CO/N218, CO2/H219, ethane/ethylene20, and other gas mixtures21), the enantioselectivity of chemical compounds22, gas adsorption (CO223, CH424, H225, thiol26, organosulfurs27, and acetylene28), and combinations thereof29,30. Several computational explorations of MOFs datasets have been carried out also for biomedical (drug delivery31), mechanical (CO2 Brayton cycle32 and osmotic heat engine33), and energy applications (heat pumps/chillers34,35 and thermal energy storage36).
In this context, modern sequential learning (SL) algorithms are emerging as particularly efficient tools for exploring the material high-dimensional (crystallographic) feature space. In particular, while evaluating an objective black-box function through demanding physical or numerical experiments, SL tools can provide a well-orchestrated procedure to rationally navigate the high-dimensional parameter (feature) space37,38. Thus, given an initial pool of evaluation points, one can sequentially choose the next experiment to carry out39,40, without relying on naive random guessing. Rather general techniques have been proposed in the area of material science holding the promise to accelerate materials discovery and research41, with a number of Authors reporting successful use of SL approaches in this field. Aggarwal et al.42, by means of optimal experimental design, successfully characterized a substrate under a thin film. Seko et al.43 found the compound with the highest melting temperature in a given ensemble of candidate materials with less attempts than a naive random choice. Kiyohara et al.44 accelerated the search of a stable interface structure with respect to a traditional brute force approach. Dehghannasiri et al.45 efficiently guided experiments to design the shape memory alloy with the lowest energy dissipation at a given temperature. Needless to say that the identification of the parameter space is a very important preliminary step when implementing SL algorithms. Here, we choose to specifically focus on MOFs properties as gas/vapor sorbent materials, since those are particularly relevant for energy applications.
The first important objective of this work is the identification of the minimal set of MOFs features (or descriptors) ruling critical adsorption properties in the low-coverage regime, i.e., the Henry solubility coefficients for both CO2-MOFs and, importantly, H2O-MOFs working pairs. The above minimal set represents the important crystallographic features underpinning a given adsorption property of interest. In this sense, each minimal set of descriptors can be regarded as the genetic code for a given property, and it is identified as described below.
First, we curate and enhance MOF data from a recently developed library made of 8206 compounds generated computationally46. Each Crystallographic Information File (CIF) representing a given material is first featurized by means of 1557 Classical Force-field Inspired Descriptors (CFID)47 taking into account both chemical and structural parameters. Subsequently, we train and validate regression models of target properties involved in heat storage applications, such as Henry coefficients and working capacity. These models are obtained by means of a Random Forest-based pipeline, with hyperparameter tuning in five fold cross-validation. The final ranking and selection of the minimal set of descriptors is performed by evaluating the importance of each feature on the models outputs by means of the Tree SHAP interpretation algorithm48.
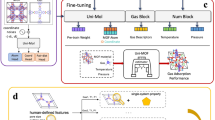
Upon identification of the above crystallographic genetic code of sorption properties in MOFs, we investigate its role when using SL algorithms. Therefore, we compare the performance of three different SL methodologies aiming at maximizing H2O and CO2 Henry coefficients, and CO2 working capacity: (a) random Forests with Uncertainty Estimates for Learning Sequentially (FUELS49); (b) kriging algorithm50; (c) COMmon Bayesian Optimization Library (COMBO)51. For each SL methodology, we compare several strategies for choosing the next material to test, combining the exploration of high-uncertainty regions with the exploitation of high-performing candidates. Importantly, we analyse the SL performance using both the minimal subset of features (from the pipeline and SHAP analysis) and a larger set of variables, to highlight how the identification of descriptors affects the minimum number of experiments needed to pick out a MOF with the highest value of the desired property. In Fig. 1 the above procedure is schematically represented.
Over 5000 hypothetical MOFs from ref. 46 are first featurized by CFID, with the corresponding full set of descriptors provided to a ML regression pipeline for a preliminary descriptor reduction and ML model training of sorption properties of interest. The Tree SHAP interpretation algorithm is thus used to finalize the identification and ranking of a reduced subset of ruling descriptors of the chosen property). Several sequential learning schemes are tested using both the full set of descriptors and the reduced one for a comprehensive comparison.
We highlight that sorption-based engineering applications rely upon sorbent material characterization in a wide coverage range. However, when a large number of hypothetical sorbents (here MOFs, but in principle also zeolites52,53 or other materials54) have to be evaluated as potential candidates, only low-coverage characterization (i.e. Henry coefficient) is often accessible thus making challenging any optimization of crucial figures of merits of engineering relevance. We thus formulate a procedure aiming at a fast evaluation of one of the most important figures of merit in closed water-sorption seasonal thermal energy storage applications, namely the material-based specific (stored) energy. Unlike traditional sensible or latent systems55, the above sorption-based energy storage technologies have the advantage to be loss-free. Our procedure can thus be used in SL-based (or other) optimization/screening processes of MOFs even under incomplete knowledge of the entire isosteric field of the candidate working pairs. Applied to the database of over 5000 computationally generated (hypothetical) compounds by ref. 46 (developed for different purposes), our procedure identifies MOFs that can possibly outperform state-of-the-art sorbent materials for thermal energy storage.
Results
In this work, a crucial source of data on MOFs stems from the dataset of Boyd et al.46, where important sorption properties (e.g., the Henry coefficients for CO2 and H2O, the working capacity for CO2, and the specific surface area) have been computed by DFT-based simulations for over 8000 potential MOFs. Capitalizing on the above comprehensive study, we construct machine learning (ML) models capable of accurately predicting MOFs solubility of both CO2 and H2O as well as CO2 working capacity and surface area. The above models enable us to achieve the first key result of this work, namely the identification of the minimal set of crystallographic-based descriptors56 ruling these sorption and geometric properties in MOFs.
Moreover, a systematic comparison of SL approaches on the above MOFs database reveals important conclusions on the performance of the different regression schemes adopted and, most importantly, the role played by the selection of the feature space to be explored. Those conclusions are also supported by results obtained on a highly-controllable synthetic dataset, as discussed in detail in Supplementary Note 1.
It is worth stressing that properties reported in ref. 46 only characterize MOFs in the Henry regime and are not sufficient to describe the equilibrium sorption properties in the high coverage regime. However, when targeting important engineering applications such as seasonal thermal energy storage, key figures of merits of the storage plant (e.g., the material-based specific energy) critically rely upon the access to the entire isosteric field of the chosen sorbent-sorbate pair or, equivalently, to the knowledge of equilibrium adsorption isotherms at several temperature values57,58. The latter isotherms describe the adsorption properties (at equilibrium) of sorbents in a wide range of coverage values, from the Henry regime up to the saturation pressure of the sorbate fluid.
Therefore, in this work, we also propose an approach enabling us to optimize one of the most important engineering figures of merit of MOFs for seasonal thermal energy storage applications (i.e., material-based specific energy in an ideal closed sorption cycle, see Methods, subsection Water-sorption thermal energy storage, and Results, subsection Optimization under incomplete access to the isosteric field of candidate MOFs-water working pairs), even if only an incomplete set of sorption properties are (experimentally or numerically) accessible. Based on the latter optimization procedure, we are finally able to identify potential MOFs candidates for seasonal thermal energy storage that can possibly outperform most of the current state-of-the-art sorbent materials.
Descriptors of sorption properties in MOFs and their use in SL algorithms
We constructed four MOFs datasets, each one with the same 1557 features and a different target property among Henry coefficient for CO2 (8194 data entries), working capacity for CO2 (8202 data entries), Henry coefficient for H2O (8202 data entries), and surface area (5028 data entries). The different number of data entries are due to missing values for some of the chosen properties in the available database by ref. 46.
The above database also reported, for all the compounds, both the crystallographic file (used to extract the 1557 CFID47 by means of Matminer56) and a list of DFT-computed properties, among which we have only considered the abovementioned adsorption properties of interest. More specifically, the computed 1557 explanatory variables (also referred to as descriptors) proposed by Choudhary et al.47 consist of a set of both chemical (e.g., average chemical properties over the elements in the cell, average atomic radial charge) and structural (e.g., distribution functions) quantities. More details on descriptor sub-categories are reported in Table 1.
We have trained four different ML models by means of a Random Forest-based pipeline with hyperparameter tuning in five fold cross-validation to predict the Henry coefficient for CO2, the working capacity for CO2, the Henry coefficient for H2O, and the surface area, achieving coefficients of determination of R2 = 0.785, R2 = 0.590, R2 = 0.874, and R2 = 0.924, respectively. We have used 80% of each dataset to train the models, and the remaining 20% to validate them. Since the Henry coefficient values span a few orders of magnitude, the corresponding ML models have been developed in terms of the natural logarithm of those properties. During the data preprocessing routines, each of the four trained pipelines (i.e., feature reduction and ML with hyperparameter tuning, see Supplementary Note 10 for details) already drops a significant number of the 1557 features, thus confirming that many of the initially selected descriptors do not significantly affect the chosen adsorption properties. More specifically, the final models include 237 descriptors for the CO2 Henry coefficient, 236 descriptors for CO2 working capacity, 177 descriptors for the H2O Henry coefficient, and 234 descriptors for surface area.
Then, the Tree SHAP routine48,59 allows to identify the most meaningful descriptors as those accounting for the 75% of the cumulative curve over the coefficients of importance. The SHAP routine identifies the most meaningful features for the trained models among the reduced set of descriptors retained by the trained pipelines after the preprocessing. In particular, the impact of a descriptor depends on the comparison between the output of a model trained with that feature and another model output, trained without that feature (see Methods, subsection Model training and choice of descriptors). The coefficients of importance are thus computed over the testing set, i.e., over samples the model has never encountered during the training.
Overall, starting from the original 1557 Classical Force-field Inspired Descriptors, 33 items for the CO2 Henry coefficient, 62 for the CO2 working capacity, 15 for the H2O Henry coefficient, and 14 for the surface area are found to explain 75% of the corresponding regression models. Furthermore, we have repeated an analogous procedure with AutoMatminer60, which allows us to automatically train and validate a complete pipeline—feature reduction, data cleaning, and machine learning—with automatic hyperparameter tuning, without cross-validation. Results are reported in Supplementary Note 2. Models performances with the corresponding cumulative importance curves of the ruling descriptors are reported in Fig. 2. The H2O Henry coefficient is key for the computation of the specific material energy in a MOF-based thermal energy storage plant (as discussed below in Results, Optimization under incomplete access to the isosteric field of candidate MOFs-water working pairs). Hence, for the H2O Henry coefficient only, we also report a few experimental values corresponding to real MOFs to compare with numerical predictions of hypothetical MOFs. In particular, numerical predictions happen to follow a good agreement with the experimental values. This aspect is key for material screening purposes and is further highlighted in the Discussion section below.
Results are reported for a Henry coefficient for CO2, b working capacity for CO2, c Henry coefficient for H2O (with experimental values for MIL-100(Fe)81,82, MIL-10181,83, MOF-801-SC68, MOF-80868, MOF-84168, Mg-MOF-7484,85), d surface area; model performances are shown in terms of coefficient of determination R2, mean absolute error (MAE), and root mean squared error (RMSE), with the size of training and testing sets Ntrain and Ntest, respectively.
Importantly, Fig. 3 shows the SHAP rankings of the five most meaningful descriptors for each of the properties of interest. Table 2 summarizes the physicochemical meaning of the identified descriptors, based on the complete list by Choudhary et al.47. The entire list of variables, together with their cumulative importance, the trained models, and the datasets on which they have been trained are publicly available online (see Data availability and Code availability).
Results are reported for a Henry coefficient for CO2, b working capacity for CO2, c Henry coefficient for H2O, d surface area. In each panel, for each feature (i.e., each line), 1639, 1641, 1641, and 1006 dots are shown respectively, representing the entire testing sets used for computing the related SHAP values (impacts on the model output, horizontal axes); the color represents the corresponding feature value, the features are sorted according to the mean over the absolute SHAP values.
As far as the four properties of MOF are concerned, the identification of those important descriptors represents per se an advancement of knowledge on sorption mechanism in MOFs and an important contribution to this work.
Focusing our attention on the top three descriptors in terms of importance, we notice that:
-
As far as the Henry coefficient for CO2 (see Fig. 3a) is concerned, such a property happens to be mainly ruled by the volume per atom, the nearest neighbor distribution, and an elastic constant. The former descriptor is the volume of a cell divided by the number of atoms in the cell, thus mainly representing a geometrical feature of the MOF crystal. The nearest neighbor distribution can also be regarded mainly as a geometry feature strictly related to the crystallographic structure. The elastic constant is one of the elements of an averaged 6 × 6 elastic tensor of the cell. In particular, for each of the chemical elements of a cell, the elastic tensor of the solid ground state structure at temperature 0 K is known. The weighted average of those tensor entries over the chemical elements of the cell are the elastic constants found by the featurizer. To our best interpretation, the latter two quantities effectively describe the chemical environment of the crystal thus underpinning the sorbent-sorbate interaction potential.
-
As far as the working capacity for CO2 (see Fig. 3b) is concerned, this quantity is mainly ruled by nearest neighbor distribution and volume per atom. Therefore, as expected, geometric features are playing a key role in determining the maximum CO2 uptake into the crystal.
-
As far as the Henry coefficient for H2O (see Fig. 3c) is concerned, we found that that quantity is mainly ruled by an elastic constant, radial distribution function, and nearest-neighbor distributions. As such, as opposed to the CO2 case above, we can observe that descriptors more related to the chemical environment are needed this time since a polar molecule is interacting with the MOFs structure.
-
Finally, for the surface area (see Fig. 3d), we found that it is mainly ruled by volume per atom, packing fraction, and nearest neighbor distribution, thus showing the prominence of geometrical features similar to the case of the above working capacity.
Upon the identification of the above lists of descriptors, we have compared the performance of SL algorithms for the sorption properties of interest using both the reduced set of important descriptors (i.e., those explaining the 75% of the models predicting CO2 Henry coefficient, CO2 working capacity, and H2O Henry coefficient, respectively) and a larger set of 100 descriptors composed by the previous and some additional (non-meaningful) ones.
In particular, for the aforementioned sorption properties, we have chosen the non-relevant features as the ones obtaining the least scores in the SHAP ranking. SL was adopted to find the maximum property value among a random subset of 500 samples from the original datasets (over 8000 MOFs), starting from a pool of 100 points with the lowest target property. Unexpectedly, SL optimization in the space of relevant descriptors does not ensure, in general, faster convergence of the procedure to the optimum property value (this is also confirmed by results in the synthetic case reported in Supplementary Note 1). Those six spaces (two domains for each of the three properties) are reported in Supplementary Note 9, as t-SNE projections over two components61. Furthermore, among the three methodologies examined, both Random Forest- and COMBO-based methods were able to provide always a faster convergence to the optimum value as compared to the random choice strategy. Results are shown in Fig. 4. As Ling et al. point out49, a pure exploitative strategy—RF-MEI, K-MEI, COMBO-PI—performs better when, already in the very first steps, the model is able to predict with high accuracy the value of the property of interest; conversely, a pure explorative strategy—RF-MU, K-MU—is more proper if the optimum is somehow very different with respect to all the other candidates, while the remaining strategies are a trade-off between those two extremes—RF-MLI, K-MLI, and COMBO-EI.
We notice that, over different regression methodologies—even with the same acquisition function—the performance ranking, in general, changes. For instance, in the case of the Henry coefficient for H2O in Fig. 4c, among the Random Forest-based strategies, RF-MLI is the top performer, followed by RF-MEI and RF-MU, for both 15- and 100-dimensional input spaces; the very same ranking applies for Kriging based acquisition functions, K-MLI, K-MEI, and K-MU. In the case of working capacity for CO2 in Fig. 4b, instead, among the Random Forest-based strategies, RF-MEI is the top performer, followed by RF-MU and RF-MLI; on the contrary, the same ranking does not apply for Kriging based strategies, since K-MEI is the top performer, followed by K-MLI and K-MU, for both 62- and 100-dimensional input spaces. An intermediate case is represented by the Henry coefficient for CO2 in Fig. 4a, where the ranking of Random Forest-based strategies (RF-MLI, RF-MEI, RF-MU, both 33- and 100-dimensional input spaces), is preserved over the Kriging methodology only for the 100-dimensional space (K-MLI, K-MEI, and K-MU), but not for the 33-dimensional (K-MEI, K-MLI, and K-MU). Among COMBO-based acquisition functions, COMBO-PI and COMBO-EI always require a similar number of evaluations, except in the 100-dimensional input space of Henry coefficient for CO2, and the 100-dimensional input space is consistently better performing than the corresponding low-dimensional one.
This brief comparison shows that no general rule is valid a priori for SL, neither in terms of regression methodology, nor in terms of acquisition function, nor in terms of dimensionality of the problem, albeit selecting relevant descriptors.
Optimization under incomplete access to the isosteric field of candidate MOFs-water working pairs
Without losing generality, here we aim at investigating the expected performance of hypothetical (i.e., computationally generated) MOFs for an important energy engineering application, namely water-sorption seasonal thermal energy storage (see also the Methods section, subsection Water-sorption thermal energy storage). The most challenging aspect of this task consists in the access to the entire isosteric field of each candidate MOF-water pair for estimating the engineering figure of merit of interest. Clearly, for a large number of MOFs candidates, this is challenging and time-consuming both computationally (typically, only the Henry low-coverage regime is reported in literature works62,63) and experimentally64. In this section, we specifically focus on such a challenging aspect. We envision an efficient optimization procedure that is capable of searching MOFs with the largest expected figure of merit of engineering relevance (either by SL, if materials are sequentially synthesized/computed, or by accessing readily available databases65). As far as seasonal thermal energy storage applications are concerned, here we focus on the highest specific energy of MOF-water working pairs among the compounds reported in ref. 46. An overview of the proposed methodology is schematically reported in Fig. 5.
By the knowledge of Henry coefficient for H2O at a certain temperature from literature data, an isotherm is obtained by Frumkin–Fawler–Guggenheim; the Polanyi potential is used for scaling to different temperatures. When two isotherms of interest are identified, upon the definition of the necessary environmental conditions and the use of an incomplete set of properties (e.g., solubility, uptake), the corresponding specific stored energy can be computed. SL algorithms can be employed for optimizing the desired figure of merit/properties in a discretized descriptor space.
As detailed in the Methods section (subsection Water-sorption thermal energy storage), the ideal thermodynamic cycle of a closed sorption thermal energy storage system is completely defined by four operating temperatures. In this study, we assume TA = 308 K (the minimum temperature on the user side), TC = 353 K (the maximum temperature on the source side), TE = 278 K (the average winter temperature), TF = 303 K (the average summer temperature). Those temperature values are reasonable for space heating applications in temperate climates64. Given the Antoine equation, the equilibrium water vapor pressures pE = 866.2 Pa at the evaporator and pF = 4231.6 Pa at the condenser are also uniquely defined considering the average winter and summer temperatures, respectively. We decided to evaluate and maximize over the database one of the most important engineering quantities in a thermal energy storage plant, namely the cycled heat per unit of material weight. While full details on the adopted models are given in the Methods section (subsection Water-sorption thermal energy storage), in the following we report and discuss the main simplifying assumptions in our approach:
-
A key quantity to be estimated is the H2O working capacity. That quantity is related to the available adsorption sites nTOT per unit of dry sorbent mass. Boyd et al.46 reported only the CO2 working capacity, while no data are available on the maximum H2O uptake. Nonetheless, we can rely on other related properties, such as the specific surface area of MOFs. To this end, we notice that Chaemchuen et al. have reported H2O working capacity for a pool of 66 MOFs5. A good correlation between the water uptake and the surface area (i.e., the available internal surface per gram of dry adsorbent) can be observed for typical MOFs used in the energy engineering field, and this is also in line with results found by Xu et al.66. In this work, on the basis of that correlation, we impose a linear regression for finding the constant of proportionality between water uptake and surface area (water uptake = η × surface area). This yields \(\eta =3.875\times 10^{-4}\,\rm{g}_{\rm{H}_{2}\rm{O}}\,\rm{m}^{-2}\). More details can be found in Supplementary Note 4. We also notice that, without a loss of generality, if more accurate values of the water uptake are available (e.g., from numerical simulations of adsorption experiments) the above assumption on the uptake-internal surface correlation can be fully relaxed.
-
Henry coefficients \(\widetilde{H}({T}_{0})\) for H2O are listed at the reference temperature T0 = 298 K with units of \({\rm{mol}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}{{{{\rm{kg}}}}}_{{{{\rm{MOF}}}}}^{-1}\,{{{{\rm{bar}}}}}^{-1}\), thus representing the moles of adsorbed H2O per kilogram of dry MOF per bar of H2O vapor. In our approach, we adopt the Frumkin–Fawler–Guggenheim (FFG) model to estimate the adsorption isotherm over the entire range of coverages only relying upon such Henry coefficient. However, as discussed in the Methods sections (subsection Water-sorption thermal energy storage), the FFG equation requires H(T0) in units of Pa−1: we have thus converted \(\widetilde{H}({T}_{0})\) (readily available from ref. 46) to H(T0). Let ns, mMOF and \({p}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\) be the number of adsorbed water moles, the mass of the hypothetical MOF, and the pressure of water in the vapor phase, respectively, it holds:
$$\widetilde{H}({T}_{0})=\frac{{n}_{{{{\rm{s}}}}}}{{m}_{{{{\rm{MOF}}}}}{p}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}}.$$(1)The approximation of the low-coverage regime yields the linear relationship between the coverage and pressure, namely \(\theta =H({T}_{0}){p}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\). Since the number of adsorbed water moles is related to the molar based total number of adsorption sites as ns = θnTOT, it follows:
$$H({T}_{0})=\widetilde{H}({T}_{0})\frac{{{{{\mathcal{M}}}}}_{{{{\rm{MOF}}}}}}{{n}_{{{{\rm{TOT}}}}}/{n}_{{{{\rm{MOF}}}}}},$$(2)with \({m}_{{{{\rm{MOF}}}}}={{{{\mathcal{M}}}}}_{{{{\rm{MOF}}}}}{n}_{{{{\rm{MOF}}}}}\), \({{{{\mathcal{M}}}}}_{{{{\rm{MOF}}}}}\) the molecular weight of the MOF, and nMOF the total number of moles. Furthermore, the molar based total number of adsorption sites nTOT corresponds to the maximum number of water moles \({n}_{{{{\rm{MAX}}}},{{{{\rm{H}}}}}_{{{{\rm{2}}}}}{{{\rm{O}}}}}\) that can be adsorbed, and the following relationship holds:
$$\frac{{n}_{{{{\rm{MAX}}}},{{{{\rm{H}}}}}_{{{{\rm{2}}}}}{{{\rm{O}}}}}}{{n}_{{{{\rm{MOF}}}}}}=\frac{{m}_{{{{\rm{MAX}}}},{{{{\rm{H}}}}}_{{{{\rm{2}}}}}{{{\rm{O}}}}}}{{m}_{{{{\rm{MOF}}}}}}\frac{{{{{\mathcal{M}}}}}_{{{{\rm{MOF}}}}}}{{{{{\mathcal{M}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}},$$(3)where \({{{{\mathcal{M}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\) is the molecular weight of water and \({m}_{{{{\rm{MAX}}}},{{{{\rm{H}}}}}_{{{{\rm{2}}}}}{{{\rm{O}}}}}\) denotes the maximum mass of water that can be adsorbed. The ratio \({m}_{{{{\rm{MAX}}}},{{{{\rm{H}}}}}_{{{{\rm{2}}}}}{{{\rm{O}}}}}/{m}_{{{{\rm{MOF}}}}}\) is related to the H2O working capacity of the MOF and it is equal to ηS, where η is the constant of proportionality between the uptake and the surface area S. A comparison of Equations (3) and (2) yields:
$$H({T}_{0})=\widetilde{H}({T}_{0})\frac{{{{{\mathcal{M}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}}{\eta S}\times 1{0}^{-8},$$(4)which is the final conversion formula of the Henry coefficient for H2O from measure units of \({{{{\rm{mol}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\,{{{{\rm{kg}}}}}_{{{{\rm{MOF}}}}}^{-1}\,{{{{\rm{bar}}}}}^{-1}\) into Pa−1. Here, the factor 10−8 appears because \([{{{{\mathcal{M}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}]=\,{{{{\rm{g}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\,{{{{\rm{mol}}}}}_{{{{\rm{H2O}}}}}^{-1}\), \([\eta ]=\,{{{{\rm{g}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\,{{{{\rm{m}}}}}^{-2}\), \([S]=\,{{{{\rm{m}}}}}^{2}{{{{\rm{g}}}}}_{{{{\rm{MOF}}}}}^{-1}\), and so \([\widetilde{H}({T}_{0}){{{{\mathcal{M}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}/(\eta S)]=\,{{{{\rm{g}}}}}_{{{{\rm{MOF}}}}}\,{{{{\rm{kg}}}}}_{{{{\rm{MOF}}}}}^{-1}\,{{{{\rm{bar}}}}}^{-1}\).
-
A crucial quantity for heat transformation is the isosteric heat of adsorption qst. Due to the Clausius–Clapeyron relationship (see Equation (7) in the Methods section, subsection Water-sorption thermal energy storage), at least two adsorption isotherm curves (at TA and at TC) are needed to estimate the corresponding qst. In our database, though, the Henry coefficients are only available at T0. In order to reconstruct a second adsorption isotherm for the same MOF-water working pair, we decided to resort to the potential theory of Polanyi, thus exploiting the basic notion that all adsorption isotherms are self-similar when rescaled with respect to the Polanyi potential function. Details are provided in the Supplementary Note 5. More specifically, the Polanyi potential is defined as:
$${{{\mathcal{A}}}}=-RT\ln \left(\frac{{p}_{{{{\rm{s}}}}}(T)}{p}\right),$$(5)where ps(T) is the saturation pressure of water at temperature T, while p is the pressure of the vapor phase on the adsorbent surface67. Since, at a given pressure p, the Polanyi potential is a constant of the sorption pair, we have computed \({{{\mathcal{A}}}}\) at T0 in a range from 10−4 Pa up to ps(T0) = 3157 Pa (Antoine equation for water); then, in the θ − p chart, we have rescaled the abscissa p of the isotherm obtained at the temperature T0 according to \(p={p}_{{{{\rm{s}}}}}(T)\exp \left({{{\mathcal{A}}}}/(RT)\right)\), for getting the new curves at TA and TC. We have finally computed the isosteric heat by means of the Clausius–Clapeyron relationship:
$${q}_{{{{\rm{st}}}}}=\frac{R}{3}\frac{{T}_{{{{\rm{C}}}}}{T}_{{{{\rm{A}}}}}}{{T}_{{{{\rm{C}}}}}-{T}_{{{{\rm{A}}}}}}\mathop{\sum }\limits_{i=1}^{3}\ln \frac{{p}_{2}({\theta }_{i})}{{p}_{1}({\theta }_{i})},$$(6)where the points 1 and 2 represent the intersections of an isosteric transformation with the two isotherms respectively at TA and TC. We have repeated the procedure for three coverage values (i.e., θ1 = 0.4, θ2 = 0.5, θ3 = 0.6) and averaged them.
-
Finally, upon determination of the low- and high-temperature adsorption isotherms curves at TA and TC, the coverage span Δθ during the discharge phase can be determined as detailed in the Methods section, subsection Water-sorption thermal energy storage. As for the estimate of the isosteric heat, this requires for all the compounds the rescaling of the horizontal axis in the θ − p chart of the isotherm obtained at temperature T0 according to the Polanyi potential theory.
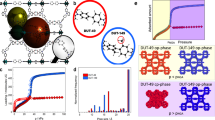
We have thus computed the following objective function SqstΔθ, which recovers the cycled heat up to a constant, over the entire list of 5028 potential MOFs with positive surface area in ref. 46. The MOF with the highest predicted specific energy turned out to be the compound with the chemical formula C96H48O28N8V4 and referred to as “str_m5_o18_o28_sra_sym.72” in the database (see also the molecular rendering in Fig. 6b), with Henry coefficient at 298 K of \(6110.54\,{{{{\rm{mol}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\,{{{{\rm{kg}}}}}_{{{{\rm{MOF}}}}}^{-1}\,{{{{\rm{bar}}}}}^{-1}\) (or equivalently, 6.89 × 10−4 Pa−1) and surface area \(S=4118.79\,{{{{\rm{m}}}}}^{2}\,{{{{\rm{g}}}}}_{{{{\rm{MOF}}}}}^{-1}\). Figure 7 shows also the ideal expected thermodynamic cycle related to this optimal potential MOF.
a 2D chart with the entire set of 5028 hypothetical MOFs in the database by Boyd et al.46, where the first two SHAP ranked descriptors for the H2O Henry coefficient are represented and the best four MOFs sorbents for the adsorption/desorption based thermal storage application are highlighted. b 3 × 3 × 13 replications of the respective crystallographic cells (C atoms: gray; H atoms: white; O atoms: red; N atoms: blue; V atoms: green).
The isotherms TA = 308 K and TC = 353 K are shown. Surface S, isosteric heat qst, and coverage span Δθ over the cycle are reported, giving an objective function \(S{q}_{{{{\rm{st}}}}}{{\Delta }}\theta =1.32\times 1{0}^{5}\,{{{\rm{kJ}}}}\,{{{{\rm{m}}}}}^{2}\,{{{{\rm{mol}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}^{-1}\,{{{{\rm{g}}}}}_{{{{\rm{MOF}}}}}^{-1}\) or equivalently \(2.83\times 1{0}^{-3}\,{{{\rm{GJ}}}}\,{{{{\rm{kg}}}}}_{{{{\rm{MOF}}}}}^{-1}\), which corresponds to 1.73 GJm−3.
We observe a coverage span Δθ = 0.653, an isosteric heat \({q}_{{{{\rm{st}}}}}=48.95\,{{{\rm{kJ}}}}\,{{{{\rm{mol}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}^{-1}\) with an objective function value of \(1.32\times 1{0}^{5}\,{{{\rm{kJ}}}}\,{{{{\rm{m}}}}}^{2}\,{{{{\rm{mol}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}^{-1}\,{{{{\rm{g}}}}}_{{{{\rm{MOF}}}}}^{-1}\). That quantity can be directly related to specific energy: upon multiplication by the constant \(\eta /{{{{\mathcal{M}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\) (\(\eta =3.875\times 1{0}^{-4}\,{{{{\rm{g}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\,{{{{\rm{m}}}}}^{-2}\), \({{{{\mathcal{M}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}=18.02\,{{{{\rm{g}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\,{{{{\rm{mol}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}^{-1}\)), we obtain a value of \(2.83\times 1{0}^{-3}\,{{{\rm{GJ}}}}\,{{{{\rm{kg}}}}}_{{{{\rm{MOF}}}}}^{-1}\). Furthermore, we can compute the theoretical density ρMOF of the crystal knowing the mass of the cell (1965.21 u = 3.263 × 10−21 gMOF, as from the database) and its volume (5.335 × 10−21 cm3, as from the CIF file), leading to ρMOF = 0.612 gMOFcm−3. As a result, the volume-based energy density turns out to be 1.73 GJm−3. For the sake of comparison, Fig. 6a shows a 2D map where the two axes represent the two most important descriptors according to the SHAP ranking for the Henry coefficient of H2O: the four top-performing potential MOFs are highlighted and the corresponding crystallographic cells are depicted in Fig. 6b. Moreover, Table 3 shows the ten most performing potential MOFs ranked in terms of specific energy. Interestingly, those compounds are all Vanadium-based, mostly due to values of the Henry coefficient for H2O in the optimal range, which produces a good coverage span Δθ over the thermodynamic cycle.
As depicted in Fig. 8 the four top-performing hypothetical MOFs are predicted to have (material-based) specific energy values among the highest available in the literature for sorption thermal energy storage under similar operating conditions. A more extensive comparison is shown in Supplementary Fig. 11, where estimates of the specific energy for real MOFs by means of the FFG model are also reported.
Specific energies are shown for different desorption temperatures TC both for the optimum MOFs identified in this work (either standard environmental conditions, i.e., evaporation temperature TE = 278 K and condensation temperature TF = 303 K, or with conditions of TE = 283 K and TF = 293 K, adsorption temperature TA = 308 K always) and for several water-sorbent materials in the literature6,64,86,87.
Discussion
Sequential learning (SL) algorithms can in principle dramatically reduce the number of evaluations needed for finding the optimum of an unknown function as compared with a naive random choice and, as such, they are emerging also as effective tools for material optimization and discovery. In this work, focusing on metal-organic frameworks (MOFs) and some of their crucial adsorption properties (both with H2O and CO2 as sorbate fluids), we have addressed a number of critical aspects related to the discovery of the minimal set of important crystallographic descriptors for SL-based optimization algorithms. We have shown that the general protocol for sorting out the minimal set of ruling descriptors for a given adsorption property is based on two steps: (i) construction and training of the machine learning (ML) model which identifies the number of ruling descriptors; (ii) evaluation of the relative importance of each explanatory variable on the chosen output by the SHAP analysis. We found that, as long as the set of such ruling descriptors (for a given property of interest) is included among the exploration space features, convergence performance is not affected, although the computational burden of an SL algorithm also depends on the dimension of the parameter space to be explored: taking into account only the most relevant features may be in fact beneficial in that respect. Furthermore, based on the several examples provided here (i.e., Henry coefficient for CO2, working capacity for CO2, and Henry coefficient for H2O as well as the synthetic example discussed in the Supplementary Note 1), we have consistently noticed that the COMBO algorithm always performs better than random guessing.
Furthermore, we recognize that full access to the adsorption properties of hypothetical MOFs in the entire coverage regime (as requested in important applications of engineering relevance) is very challenging both experimentally and computationally. This holds particularly for water-MOFs working pairs, that are promising for a number of energy applications. Hence, we formulate a general and efficient computational screening procedure of hypothetical MOFs which, only relying upon the adsorption properties reported in Fig. 2, is capable to estimate important figures of merit for sorption-based seasonal thermal energy storage. Remarkably, our procedure suggests that some of the MOFs hypothesized in the database by ref. 46 (developed for completely different purposes) can possibly outperform most of the state-of-the-art water-sorbent compounds. Interestingly, those compounds are all Vanadium-based, mostly due to values of the Henry coefficient for H2O in the optimal range, causing a good coverage span over the thermodynamic cycle. It is worth noticing that the above MOFs screening for thermal energy storage applications critically relies upon the prediction of the Henry coefficient for water.
Therefore, for the latter property only, we have also considered a number of real MOFs and their reported experimental values have been compared with the corresponding numerical values. It is worth stressing that finding both the experimentally evaluated property values and CIF file from the same publication is a non-trivial task, sometimes possibly leading to not necessarily consistent data. Furthermore, even for the three MOFs (i.e., MOF-801-SC, MOF-808, and MOF-841) considered in this study with experimental and computational data extracted from the same reference source, there is no guarantee that the tested material corresponds perfectly to the related CIF file, and discrepancies can always occur as demonstrated by the same Authors of ref. 68. Moreover, the CIF files needed to extract the descriptors are always very ideal if compared with the experimentally tested crystals. Possible defects in real compounds can be related to any chemical changes, leading to variation in the hydrophilic nature of the material69,70,71. Nonetheless, we observed that, while discrepancies can be found, the ML-based predictor of the Henry coefficient consistently shows a good agreement with the experimental values. Importantly, the numerical predictions based on the identified descriptors can selectively distinguish among MOFs with higher or lower values of the Henry coefficient. We believe that the above results represent an important step toward efficient MOFs screening and optimization, not only with respect to intrinsic materials properties but also (and importantly) with respect to figures of merit of engineering relevance for applications such as thermally driven water harvesting from the air, water-sorption thermal energy storage, and solar cooling.
Clearly, we are also aware that our approach is based on a number of approximations and it still requires additional research activities. First, we notice that a large set of hypothetical MOFs may be characterized by properties (e.g., Henry coefficients) whose values span several orders of magnitude. Hence a unique ML model, as used in this pipeline, may achieve a high coefficient of determination if its logarithm is considered. Nonetheless, the computation of the coverage span Δθ depends directly on the Henry coefficient, which may thus be affected by a relatively high error. Furthermore, additional simplifying assumptions that have been used in our approach include fixed parameters such as the constant of proportionality between the specific surface area and the water working capacity, as well as the steepness coefficient β in the FFG model. Without losing generality, those assumptions could be relaxed in the near future relying on more sophisticated models. One possible way to cope with those challenges (not necessarily the only possible strategy) may be a preliminary classification of the hypothetical MOFs based on properly trained ML classifiers, with the purpose of assigning a given compound of interest to a specific category (e.g., the set of MOFs with Henry coefficient of similar magnitude, similar β, etc.). Afterward, property predictions on each MOF category can be possibly performed with higher accuracy.
Methods
Water-sorption thermal energy storage
In this work, we focus on the use of potential MOFs for water-sorption-based thermal storage applications.
Physical adsorption processes are based on weak and reversible interactions between the (solid) sorbent material and the corresponding adsorbate, i.e., the fluid72. Those phenomena are relevant to thermal energy engineering as sorption/desorption in solid sorbents can be accompanied by a significant amount of energy exchange. In the following, the solid sorbents are MOFs, while water is the adsorbate.
To allow desorption of an infinitesimal number (dn) of moles of adsorbate from the adsorbent surface, a given amount of heat dQ = qst dn has to be provided to the system, where qst (with units of kJ/mol) denotes the isosteric heat. Since the process is reversible, the same amount of heat dQ is released by the dry sorbent when dn moles of fluid at a pressure p, initially in the vapor phase, are adsorbed. Furthermore, we define load X as the ratio between the mass of adsorbate and the mass of dry sorbent. A process characterized by constant load X is referred to as an isosteric transformation and the popular Clausius–Clapeyron relationship yields:
where T is the absolute temperature and R = 8.314 J mol−1K−1 denotes the gas constant73. Therefore, an isosteric transformation in the Clapeyron chart (\(\ln p\) vs − 1/T) is a curve with local slope qst/R. Similarly, the adsorbate isosteric curve has a slope ΔH(vap)/R, where ΔH(vap) is the molar enthalpy for liquid-vapor phase change of the adsorbate.
Closely related to load X, the coverage θ is defined as the ratio between the number of already occupied adsorption sites ns and the total available number of sites nTOT. At equilibrium and at a given temperature T, the coverage θ depends on the pressure p of the vapor phase according to an adsorption isotherm, whose shape depends on the sorbent/adsorbate pair. MOFs/water pairs are known to show typical S-shaped isotherms in the θ − p chart (i.e., type V of the IUPAC classification74). Thus, in this work, we make the assumption that the Frumkin–Fawler–Guggenheim (FFG) model can be used conveniently for describing analytically the MOFs-water adsorption isotherms:
where \(\beta =\frac{\overline{n}{E}_{{{{\rm{p}}}}}}{RT}\) rules the steepness of the S-shape, \(\overline{n}\) denotes the neighboring binding sites and Ep represents the additional binding energy due to lateral interactions67. We have used the FFG model to interpret eight experimental isotherms of real MOF-water pairs and achieve a proper choice of β. In particular, for each curve, we have identified the best value of β in terms of a least-squares approach; then, we have taken the mean over those eight values, ending up with β = 3.4. More details can be found in Supplementary Note 6. Finally, H(T) is the Henry coefficient for the specific sorbent/adsorbate pair (with units Pa−1) at a given absolute temperature T.
A schematic of a closed water-sorption thermal energy storage system is shown in Fig. 9. These systems are based on a reactor, containing the solid sorbent, connected with a condenser/evaporator by means of a valve57. Such chemical apparatus follows a seasonal closed-cycle completely defined by four temperatures: TA (the minimum temperature on the user side), TC (the maximum temperature on the source side), TE (the average winter temperature), and TF (the average summer temperature). The two pressures pE (evaporator) and pF (condenser) are related to the absolute temperatures TE and TF, respectively, through the Antoine equation for water saturation \({p}_{{{{\rm{E}}}},{{{\rm{F}}}}}=133.2\times 1{0}^{A-B/(C+{T}_{{{{\rm{E}}}},{{{\rm{F}}}}}-273)}\), where A = 8.07131, B = 1730.63, C = 233.42675. Hence, the ideal thermodynamic cycle of a closed thermal energy storage process (see Fig. 10) is based on the following four steps:
-
1.
The sorbent/adsorbate is heated isosterically up to a temperature TB, corresponding to a pressure pF in the condenser (line AB).
-
2.
Heating of the pair continues at constant pressure pF and desorbed vapor flows to the condenser through the opened valve. In the condenser, the adsorbate rejects the condensation heat into the environment while condensing until the maximum temperature of the heat source TC is reached (line BC). The condition of the minimum load is reached and the valve gets closed.
-
3.
Keeping the valve closed, the system in contact with the environmental temperature cools isosterically during the storage period (line CD) down to temperature TD, corresponding to the evaporator pressure pE.
-
4.
During the discharge phase of the heat storage system, the valve is opened to let the adsorbate evaporate and reach the reactor. During this isobaric transformation (line DA), the heat of adsorption QDA, also known as cycled heat, is released.
One of the most important figures of merit for energy storage systems is the specific stored energy, namely the maximum energy that can be stored per unit of mass of the plant or of the material76. Clearly, at fixed material (or plant) mass, the higher the cycled heat the higher the specific energy of the storage system. In this view, the choice of the solid sorbent material for a given adsorbate is key for maximizing the cycled heat in the ideal thermodynamic cycle. We thus perform below a material screening aiming at the maximum value of the following cycled heat (i.e., the released heat during the DA process in Fig. 10):
where we have used the definition of the heat of adsorption dQ = qst dns, coverage θ = ns/nTOT and the approximation \({q}_{{{{\rm{st}}}}}\approx {{{\rm{const}}}}\).
Sequential learning
Typical steps in any SL algorithm consist in (i) constructing a regression model over known data, (ii) using a strategy to suggest the best-unmeasured point to test, (iii) enlarging the known dataset with this tested point, and (iv) iterating up to the tested candidate meets the needed specification. Let \({{{\mathcal{D}}}}=\{({{{{\bf{x}}}}}_{1},{y}_{1}),\ldots ,({{{{\bf{x}}}}}_{n},{y}_{n})\}\) denote a set of n training data, where \({{{{\bf{x}}}}}_{i}\in {{\mathbb{R}}}^{d}\) and \({y}_{i}\in {\mathbb{R}}\) represent the i-th vector of descriptors and its known response, respectively. Let {xn+1, …, xm} denote the (m − n) d-dimensional arrays of descriptors with unknown responses {yn+1, …, ym}. To find the location x* of the maximum y*, we would need the exact model y = f(x). However, given the restricted set \({{{\mathcal{D}}}}\) of training data, only a surrogate model \(y=\hat{f}({{{\bf{x}}}}| {{{\mathcal{D}}}})\) can be constructed. Hence, for each unmeasured point i = n + 1, …, m, different regression methodologies (here FUELS-Random Forest, kriging and COMBO-Gaussian processes) can be used to estimate the response \(\hat{f}({{{{\bf{x}}}}}_{i})\) in terms of a mean value μ(xi) and the corresponding uncertainty σ(xi), indicating the robustness of the prediction. To measure the performance of any combination regression model/query strategy, we put ourselves in the practitioner’s perspective, who is interested in a unique sequence of points to be tested, and not in an average over more paths (as, for instance, shown in ref. 49). To achieve this, for those regression models not allowing a deterministic prediction (i.e., Random Forest and COMBO), at each step we have repeated 100 times the choice of the next point to query, picking the most preferred one. A comprehensive comparison of the above methodologies is reported in the Results (subsection Descriptors of sorption properties in MOFs and their use in SL algorithms), and the complete details on the adopted algorithms can be found in the Supplementary Notes 7 and 8.
Model training and choice of the descriptors
The first issue to be addressed when applying SL to material optimization is computation and selection of relevant features (or descriptors). The descriptor issue is critical in materials science77,78 as well as in other computational fields79. In this work, we first investigate to which extent the choice of a minimal set of relevant descriptors is critical for the fast convergence of SL algorithms.
To this end, before even implementing SL procedures, we decided to perform a preliminary feature pruning for discovering the most meaningful ones in terms of the target property. We use the entire dataset (both descriptors and target property) to train and validate a Random Forest-based pipeline—feature reduction and machine learning—for regression, with hyperparameter tuning in five fold cross-validation. More details can be found in Supplementary Note 10.
Upon model training and validation, we detect the most important features thanks to the Tree SHAP algorithm, which is optimized for tree-based models such as Random Forest48,59, thus quantifying to which extent a given feature impacts the output. The latter methodology is based on the classical Shapley value, which has in game theory its original field of application. There, the problem of assigning, in a cooperative game, a proportional reward to each player is addressed based on the real contribution provided to the common objective of the coalition. In a model, given F the set of all features and its generic subset S ⊆ F, the importance of the i-th descriptor depends on the comparison between the model fS∪{i} trained with that explanatory variable, and another model fS trained without that feature; then, the difference between the predictions fS∪{i}(xS∪{i}) − fS(xS) is computed, where xS∪{i} and xS represent respectively the values of the input feature over the subsets S ∪ {i} and S. This difference is weighted over all possible subsets S and the importance value of the i-th feature turns out to be
where ∣⋅∣ denotes the number of elements. Because of the huge number of possible descriptor subsets S of a set F, the classical Shapley values of Equation (10) are, in general, computationally challenging. Nonetheless, the Tree SHAP realization we have employed in this work is able to explain efficiently tree-based models, such as Random Forest.
Data availability
Datasets and trained models of this study are available in Zenodo (DOI:10.5281/zenodo.6351366)80.
Code availability
The codes used to obtain the results of this study are publicly available at https://github.com/giotre/MOFs.
References
Kitagawa, S. et al. Metal–organic frameworks (mofs). Chem. Soc. Rev. 43, 5415–5418 (2014).
Adil, K. et al. Gas/vapour separation using ultra-microporous metal–organic frameworks: insights into the structure/separation relationship. Chem. Soc. Rev. 46, 3402–3430 (2017).
Rogge, S. M. et al. Metal–organic and covalent organic frameworks as single-site catalysts. Chem. Soc. Rev. 46, 3134–3184 (2017).
Wuttke, S., Lismont, M., Escudero, A., Rungtaweevoranit, B. & Parak, W. J. Positioning metal-organic framework nanoparticles within the context of drug delivery–a comparison with mesoporous silica nanoparticles and dendrimers. Biomaterials 123, 172–183 (2017).
Chaemchuen, S., Xiao, X., Klomkliang, N., Yusubov, M. S. & Verpoort, F. Tunable metal–organic frameworks for heat transformation applications. Nanomaterials 8, 661 (2018).
de Lange, M. F., Verouden, K. J., Vlugt, T. J., Gascon, J. & Kapteijn, F. Adsorption-driven heat pumps: the potential of metal–organic frameworks. Chem. Rev. 115, 12205–12250 (2015).
Chen, S., Lucier, B. E., Boyle, P. D. & Huang, Y. Understanding the fascinating origins of co2 adsorption and dynamics in mofs. Chem. Mater. 28, 5829–5846 (2016).
Kim, H. et al. Adsorption-based atmospheric water harvesting device for arid climates. Nat. Commun. 9, 1–8 (2018).
Kalmutzki, M. J., Diercks, C. S. & Yaghi, O. M. Metal–organic frameworks for water harvesting from air. Adv. Mater. 30, 1704304 (2018).
Ejeian, M. & Wang, R. Adsorption-based atmospheric water harvesting. Joule 5, 1678–1703 (2021).
Lee, S. et al. Computational screening of trillions of metal–organic frameworks for high-performance methane storage. ACS Appl. Mater. Interfaces 13, 23647–23654 (2021).
Li, A., Bueno-Perez, R., Wiggin, S. & Fairen-Jimenez, D. Enabling efficient exploration of metal–organic frameworks in the cambridge structural database. CrystEngComm 22, 7152–7161 (2020).
Borboudakis, G. et al. Chemically intuited, large-scale screening of mofs by machine learning techniques. Npj Comput. Mater. 3, 1–7 (2017).
Anderson, R., Rodgers, J., Argueta, E., Biong, A. & Gómez-Gualdrón, D. A. Role of pore chemistry and topology in the co2 capture capabilities of mofs: from molecular simulation to machine learning. Chem. Mater. 30, 6325–6337 (2018).
Moghadam, P. Z. et al. Structure-mechanical stability relations of metal-organic frameworks via machine learning. Matter 1, 219–234 (2019).
Zhou, M., Vassallo, A. & Wu, J. Toward the inverse design of mof membranes for efficient d2/h2 separation by combination of physics-based and data-driven modeling. J. Membr. Sci. 598, 117675 (2020).
Yan, Y. et al. Machine learning and in-silico screening of metal–organic frameworks for o2/n2 dynamic adsorption and separation. Chem. Eng. J. 427, 131604 (2022).
Rampal, N. et al. The development of a comprehensive toolbox based on multi-level, high-throughput screening of mofs for co/n 2 separations. Chem. Sci. 12, 12068–12081 (2021).
Avci, G., Erucar, I. & Keskin, S. Do new mofs perform better for co2 capture and h2 purification? computational screening of the updated mof database. ACS Appl. Mater. Interfaces 12, 41567–41579 (2020).
Halder, P. & Singh, J. K. High-throughput screening of metal–organic frameworks for ethane–ethylene separation using the machine learning technique. Energy Fuels 34, 14591–14597 (2020).
Yang, W. et al. Computational screening of metal–organic framework membranes for the separation of 15 gas mixtures. Nanomaterials 9, 467 (2019).
Qiao, Z. et al. Molecular fingerprint and machine learning to accelerate design of high-performance homochiral metal–organic frameworks. AIChE J. 67, e17352 (2021).
Li, S., Chung, Y. G. & Snurr, R. Q. High-throughput screening of metal–organic frameworks for co2 capture in the presence of water. Langmuir 32, 10368–10376 (2016).
Pardakhti, M., Moharreri, E., Wanik, D., Suib, S. L. & Srivastava, R. Machine learning using combined structural and chemical descriptors for prediction of methane adsorption performance of metal organic frameworks (mofs). ACS Comb. Sci. 19, 640–645 (2017).
Bobbitt, N. S. & Snurr, R. Q. Molecular modelling and machine learning for high-throughput screening of metal-organic frameworks for hydrogen storage. Mol. Simul. 45, 1069–1081 (2019).
Qiao, Z., Xu, Q., Cheetham, A. K. & Jiang, J. High-throughput computational screening of metal–organic frameworks for thiol capture. J. Phys. Chem. C. 121, 22208–22215 (2017).
Liang, H. et al. Combining large-scale screening and machine learning to predict the metal-organic frameworks for organosulfurs removal from high-sour natural gas. APL Mater. 7, 091101 (2019).
Yang, P. et al. Analyzing acetylene adsorption of metal–organic frameworks based on machine learning. Green Energy Environ. https://doi.org/10.1016/j.gee.2021.01.006 (2021).
Dureckova, H., Krykunov, M., Aghaji, M. Z. & Woo, T. K. Robust machine learning models for predicting high co2 working capacity and co2/h2 selectivity of gas adsorption in metal organic frameworks for precombustion carbon capture. J. Phys. Chem. C. 123, 4133–4139 (2019).
Liu, Z. et al. Predicting adsorption and separation performance indicators of xe/kr in metal-organic frameworks via a precursor-based neural network model. Chem. Eng. Sci. 243, 116772 (2021).
Ma, P. et al. Computer-assisted design for stable and porous metal-organic framework (mof) as a carrier for curcumin delivery. LWT 120, 108949 (2020).
Du, Z. et al. A high-throughput computational screening of potential adsorbents for a thermal compression co2 brayton cycle. Sustain. Energy Fuels 5, 1415–1428 (2021).
Long, R. et al. Screening metal-organic frameworks for adsorption-driven osmotic heat engines via grand canonical monte carlo simulations and machine learning. iScience 24, 101914 (2021).
Shi, Z. et al. Machine learning and in silico discovery of metal-organic frameworks: Methanol as a working fluid in adsorption-driven heat pumps and chillers. Chem. Eng. Sci. 214, 115430 (2020).
Shi, Z. et al. Techno-economic analysis of metal–organic frameworks for adsorption heat pumps/chillers: from directional computational screening, machine learning to experiment. J. Mater. Chem. A 9, 7656–7666 (2021).
García, E. J., Bahamon, D. & Vega, L. F. Systematic search of suitable metal–organic frameworks for thermal energy-storage applications with low global warming potential refrigerants. ACS Sustain. Chem. Eng. 9, 3157–3171 (2021).
Liang, Q. et al. Benchmarking the performance of bayesian optimization across multiple experimental materials science domains. Npj Comput. Mater. 7, 1–10 (2021).
Kim, Y., Kim, E., Antono, E., Meredig, B. & Ling, J. Machine-learned metrics for predicting the likelihood of success in materials discovery. Npj Comput. Mater. 6, 1–9 (2020).
Brochu, E., Cora, V. M. & De Freitas, N. A tutorial on bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. Preprint at https://arxiv.org/abs/1012.2599 (2010).
Ahmadi, M., Vogt, M., Iyer, P., Bajorath, J. & Fröhlich, H. Predicting potent compounds via model-based global optimization. J. Chem. Inf. Model. 53, 553–559 (2013).
Rohr, B. et al. Benchmarking the acceleration of materials discovery by sequential learning. Chem. Sci. 11, 2696–2706 (2020).
Aggarwal, R., Demkowicz, M. & Marzouk, Y. in Information Science for Materials Discovery and Design (eds Alexander, F. J., Rajan, K. & Lookman, T.) Ch. 2 (Springer, 2016).
Seko, A., Maekawa, T., Tsuda, K. & Tanaka, I. Machine learning with systematic density-functional theory calculations: Application to melting temperatures of single-and binary-component solids. Phys. Rev. B 89, 054303 (2014).
Kiyohara, S., Oda, H., Tsuda, K. & Mizoguchi, T. Acceleration of stable interface structure searching using a kriging approach. Jpn. J. Appl. Phys. 55, 045502 (2016).
Dehghannasiri, R. et al. Optimal experimental design for materials discovery. Comput. Mater. Sci. 129, 311–322 (2017).
Boyd, P. G. et al. Data-driven design of metal–organic frameworks for wet flue gas co 2 capture. Nature 576, 253–256 (2019).
Choudhary, K., DeCost, B. & Tavazza, F. Machine learning with force-field-inspired descriptors for materials: Fast screening and mapping energy landscape. Phys. Rev. Mater. 2, 083801 (2018).
Lundberg, S. M. et al. From local explanations to global understanding with explainable ai for trees. Nat. Mach. Intell. 2, 2522–5839 (2020).
Ling, J., Hutchinson, M., Antono, E., Paradiso, S. & Meredig, B. High-dimensional materials and process optimization using data-driven experimental design with well-calibrated uncertainty estimates. Integr. Mater. Manuf. Innov. 6, 207–217 (2017).
Lophaven, S. N., Nielsen, H. B., Sondergaard, J. & Dace, A. A Matlab Kriging Toolbox. Report No. IMMTR-2002 12 (Technical University of Denmark, 2002).
Ueno, T., Rhone, T. D., Hou, Z., Mizoguchi, T. & Tsuda, K. Combo: an efficient bayesian optimization library for materials science. Mater. Discov. 4, 18–21 (2016).
Fasano, M. et al. Water/ethanol and 13x zeolite pairs for long-term thermal energy storage at ambient pressure. Front. Energy Res. 7, 148 (2019).
Fasano, M., Bevilacqua, A., Chiavazzo, E., Humplik, T. & Asinari, P. Mechanistic correlation between water infiltration and framework hydrophilicity in mfi zeolites. Sci. Rep. 9, 1–12 (2019).
Anstine, D. M., Tang, D., Sholl, D. S. & Colina, C. M. Adsorption space for microporous polymers with diverse adsorbate species. Npj Comput. Mater. 7, 1–9 (2021).
Neri, M., Chiavazzo, E. & Mongibello, L. Numerical simulation and validation of commercial hot water tanks integrated with phase change material-based storage units. J. Energy Storage 32, 101938 (2020).
Ward, L. et al. Matminer: An open source toolkit for materials data mining. Comput. Mater. Sci. 152, 60–69 (2018).
Fasano, M., Borri, D., Chiavazzo, E. & Asinari, P. Protocols for atomistic modeling of water uptake into zeolite crystals for thermal storage and other applications. Appl. Therm. Eng. 101, 762–769 (2016).
Fasano, M. et al. Atomistic modelling of water transport and adsorption mechanisms in silicoaluminophosphate for thermal energy storage. Appl. Therm. Eng. 160, 114075 (2019).
Lundberg, S. M. & Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 30, 4768–4777 (2017).
Dunn, A., Wang, Q., Ganose, A., Dopp, D. & Jain, A. Benchmarking materials property prediction methods: the matbench test set and automatminer reference algorithm. Npj Comput. Mater. 6, 1–10 (2020).
Van der Maaten, L. & Hinton, G. Visualizing data using t-sne.J. Mach. Learn. Res. 9, 2579−2605 (2008).
Wu, X., Xiang, S., Su, J. & Cai, W. Understanding quantitative relationship between methane storage capacities and characteristic properties of metal–organic frameworks based on machine learning. J. Phys. Chem. C. 123, 8550–8559 (2019).
Yu, X., Choi, S., Tang, D., Medford, A. J. & Sholl, D. S. Efficient models for predicting temperature-dependent henry’s constants and adsorption selectivities for diverse collections of molecules in metal–organic frameworks. J. Phys. Chem. C. 125, 18046–18057 (2021).
Lavagna, L. et al. Cementitious composite materials for thermal energy storage applications: a preliminary characterization and theoretical analysis. Sci. Rep. 10, 1–13 (2020).
Talirz, L. et al. Materials cloud, a platform for open computational science. Sci. Data 7, 1–12 (2020).
Xu, M., Liu, Z., Huai, X., Lou, L. & Guo, J. Screening of metal–organic frameworks for water adsorption heat transformation using structure–property relationships. RSC Adv. 10, 34621–34631 (2020).
Butt, H.-J., Graf, K. & Kappl, M. Physics and Chemistry of Interfaces (John Wiley & Sons, 2013).
Furukawa, H. et al. Water adsorption in porous metal–organic frameworks and related materials. J. Am. Chem. Soc. 136, 4369–4381 (2014).
Ni, L. et al. Defect-engineered uio-66-nh 2 modified thin film nanocomposite membrane with enhanced nanofiltration performance. Chem. Commun. 56, 8372–8375 (2020).
Huang, Y. et al. Tuning the wettability of metal–organic frameworks via defect engineering for efficient oil/water separation. ACS Appl. Mater. Interfaces 12, 34413–34422 (2020).
Xiang, W., Zhang, Y., Chen, Y., Liu, C.-j. & Tu, X. Synthesis, characterization and application of defective metal–organic frameworks: current status and perspectives. J. Mater. Chem. A 8, 21526–21546 (2020).
Ruthven, D. M. Principles of Adsorption and Adsorption Processes (John Wiley & Sons, 1984).
Schmidt, F. P. Optimizing Adsorbents for Heat Storage Applications: Estimation of Thermodynamic Limits and Monte Carlo Simulations of Water Adsorption in Nanopores. Ph.D. thesis, Fakultät für Mathematik und Physik, Universität Freiburg (2004).
Sing, K. S. Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (recommendations 1984). Pure Appl. Chem. 57, 603–619 (1985).
Speight, J. G. et al. Lange’s Handbook of Chemistry Vol. 1 (McGraw-Hill, 2005).
Dincer, I. & Rosen, M. A.Thermal Energy Storage Systems and Applications (John Wiley & Sons, 2021).
Ghiringhelli, L. M., Vybiral, J., Levchenko, S. V., Draxl, C. & Scheffler, M. Big data of materials science: critical role of the descriptor. Phys. Rev. Lett. 114, 105503 (2015).
Gomes, S. I. et al. Machine learning and materials modelling interpretation of in vivo toxicological response to tio 2 nanoparticles library (uv and non-uv exposure). Nanoscale 13, 14666–14678 (2021).
Chiavazzo, E. et al. Intrinsic map dynamics exploration for uncharted effective free-energy landscapes. Proc. Natl Acad. Sci. USA 114, E5494–E5503 (2017).
Trezza, G., Bergamasco, L., Fasano, M. & Chiavazzo, E. Models and datasets for “Minimal set of crystallographic descriptors for sorption properties in hypothetical Metal Organic Frameworks and their role in sequential learning optimization". Zenodo https://doi.org/10.5281/zenodo.6351366 (2022).
Küsgens, P. et al. Characterization of metal-organic frameworks by water adsorption. Microporous Mesoporous Mater. 120, 325–330 (2009).
Horcajada, P. et al. Synthesis and catalytic properties of mil-100 (fe), an iron (iii) carboxylate with large pores. Chem. Commun. 27, 2820–2822 (2007).
Lebedev, O., Millange, F., Serre, C., Van Tendeloo, G. & Férey, G. First direct imaging of giant pores of the metal- organic framework mil-101. Chem. Mater. 17, 6525–6527 (2005).
Yang, D.-A., Cho, H.-Y., Kim, J., Yang, S.-T. & Ahn, W.-S. Co2 capture and conversion using mg-mof-74 prepared by a sonochemical method. Energy Environ. Sci. 5, 6465–6473 (2012).
Henkelis, S. E. et al. A single crystal study of cpo-27 and utsa-74 for nitric oxide storage and release. CrystEngComm 21, 1857–1861 (2019).
Permyakova, A. et al. Synthesis optimization, shaping, and heat reallocation evaluation of the hydrophilic metal–organic framework mil-160 (al). ChemSusChem 10, 1419–1426 (2017).
Permyakova, A. et al. Design of salt–metal organic framework composites for seasonal heat storage applications. J. Mater. Chem. A 5, 12889–12898 (2017).
Acknowledgements
E.C. acknowledges financial support of the Italian National Project PRIN Heat transfer and Thermal Energy Storage Enhancement by Foams and Nanoparticles (2017F7KZWS) and of the research contract PTR 2019/21 ENEA (Sviluppo di modelli per la caratterizzazione delle proprietà di scambio termico di PCM in presenza di additivi per il miglioramento dello scambio termico) funded by the Italian Ministry of Economic Development (MiSE).
Author information
Authors and Affiliations
Contributions
E.C. conceived the idea and found financial support. G.T. performed all computations and wrote the first paper draft. E.C., M.F., and L.B. supervised the research activities. L.B. and M.F. helped with the result presentation and interpretation. M.F. suggested the synthetic dataset. All authors contributed to the final paper writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Trezza, G., Bergamasco, L., Fasano, M. et al. Minimal crystallographic descriptors of sorption properties in hypothetical MOFs and role in sequential learning optimization. npj Comput Mater 8, 123 (2022). https://doi.org/10.1038/s41524-022-00806-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00806-7
This article is cited by
-
Enhancing ReaxFF for molecular dynamics simulations of lithium-ion batteries: an interactive reparameterization protocol
Scientific Reports (2024)
-
Machine Learning and image analysis towards improved energy management in Industry 4.0: a practical case study on quality control
Energy Efficiency (2024)
-
The impact of physicochemical features of carbon electrodes on the capacitive performance of supercapacitors: a machine learning approach
Scientific Reports (2023)