Introduction

Rapid progress in batteries that shuttle cations has led to their widespread use. Although lithium–ion batteries dominate the market for high-energy-density batteries, there are considerable efforts to develop alternate cation shuttles, including magnesium, sodium, and zinc1. Here, we explore a divergent strategy for ion-shuttle batteries: the development of materials that conduct fluoride (F-)2. Comparatively, F- has a low atomic mass, large theoretical capacity, and high natural abundance3. Furthermore, because it is the most electronegative element, F- is stable against oxidation and could therefore yield batteries that operate at extreme voltages.

Despite these promising properties, fluoride-ion batteries (FIBs) have received little development. This is largely because the few existing fluoride-ion conductors have modest transport and low stability4,5,6. For example, the first reversible FIB, reported in 2011, achieved good fluoride-ion mobility only at 150 °C7. Since this initial breakthrough, improved conductors have been considered for FIBs, including BaSnF4, PbSnF4, Sm0.95Ca0.05F2.95, and Ce0.975Sr0.025 F2.975, which all achieve improved conductivity (>1 × 10−4 S cm−1 at 20 °C; ~300 meV energy barrier) but lack stability at extreme potentials8,9,10,11,12,13. This challenge with stability was especially notable with our development of Y2CF2 and Sc2CF2 as anodes, which operate at extreme potentials that fall outside the stability window of most fluoride–ion electrolytes3,14,15,16. Therefore, there is a strong need to identify fluoride-ion conductors.

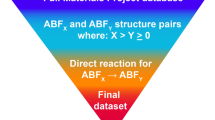
Because so few materials have been examined as possible fluoride-ion conductors, we suspected that there may be many high-performance materials that are yet undiscovered. While most studies on mobility have surveyed a limited number of structure types or systems17,18,19,20,21,22,23,24,25,26, large-scale analyses of ionic mobility27,28,29,30 used hierarchical calculations (Fig. 1a). In the hierarchical approach, simplified models are used to select candidates for more rigorous calculations, such as nudged elastic band (NEB) or molecular dynamics (MD). This is an efficient approach for generating ionic mobility databases and identifying promising materials, but it also has limitations. Most importantly, the existence of selection criteria requires a good understanding of the materials being studied, which was not the case for F- conduction. In addition, the removal of candidates at early stages does not allow one to assess whether the selection criteria are biased or incorrect; final candidates simply reinforce current models. These limitations of standard hierarchical studies led us to examine an alternate approach in our search for fluoride-ion conductors.

Fig. 1: Comparison of hierarchical27,28,29,30 and DDI (dynamic, decoupled, and iterative) search strategies.
figure 1

a Hierarchical searches perform successive calculations of increasing quality and computational cost, but low-quality predictors are used to remove most candidates. This strategy is possible only when heuristics are already known, and it does not allow selection criteria to change at later stages. b The DDI strategy used in this study creates a high-quality reference dataset, which is then used to create and iteratively refine rapid calculations. We used this approach to develop a rapid calculation for fluoride mobility and to predict barrier heights for a large pool of candidates.

Full size image

To this end, we employ a high-throughput search of fluoride-ion conductors using a decoupled, dynamic, and iterative (DDI) framework (Fig. 1b). In this framework, calculation stages are not hierarchical but are instead performed in any order (decoupled), predictive models are repeatedly updated during the search (iterative), and computational resources are reassigned as models change and materials are re-ranked (dynamic). A full account of the DDI framework will be presented elsewhere; instead, this manuscript describes the application of the DDI framework to the search for fluoride-ion conductors. In this search, we screened approximately 10,000 fluoride-containing structures, identified several crystal systems as promising conductors, and developed heuristics for quickly assessing ion transport in other materials. These materials will inspire future investigations of electrodes and electrolytes, while the heuristics will enable future high-throughput studies and provide a basic understanding of the factors that govern fluoride transport.

Results

Design strategy of the DDI framework

The typical strategy for high-throughput searches is to proceed from low-quality to high-quality calculations in distinct stages and with fixed cut-off criteria. However, when no preexisting models or heuristics exist, early-stage criteria cannot be accurately selected, and good candidates may be erroneously removed due to the larger error involved in the initial calculations. Moreover, the removal of candidates without subjecting them to high-quality calculations does not allow one to test the accuracy of the selection criteria. We, therefore, developed a framework where all workflows can be run independently, and low-quality calculations are not required prerequisites for intensive calculations. This allowed us to produce a constantly growing set of high-quality NEB calculations against which the low-quality calculations could be iteratively assessed. These assessments allowed us to refine our models and reallocate computational resources as the high-throughput search progressed. This strategy can be described as decoupled, dynamic, and iterative (DDI).

The DDI strategy is possible with workflow management software commonly used in the materials science community (such as AiiDA31, Atomate32,33, AFLOW34, and others35,36,37,38), but we utilize a custom framework in this study. While a technical discussion of the framework will be presented elsewhere, our source code has been made publicly available39, and we provide a high-level comparison to previous search strategies in the supporting information. Overall, computational resources are allocated via a centralized database server and asynchronous task executors. We define a task executor as a computational resource that requests and runs the candidates based on a priority ranking. For example, if the priority function of an NEB calculation is based solely on pathway length, the task executor will search the database for the shortest pathway yet to be calculated and run the NEB calculation. Task executors work through the database, and candidates may be deprioritized but are never removed. Thus, the DDI strategy creates an ongoing queue where uncompleted calculations are ranked according to priority.

Generating a pool of candidate pathways

The DDI framework requires a database of candidates, where dynamic priority ranking allows us to add new candidates even after the search has started. For our fluoride mobility calculations, individual candidates are not structures but instead pathways within a structure. This is because structures can contain multiple symmetrically unique diffusion pathways, where each unique pathway should be evaluated independently. A crystal’s cumulative diffusion network and long-range barrier for transport can then be evaluated using dimensional analysis, as described in our supporting information. Thus, we generated a starting pool of candidate pathways, built into the option to introduce new pathways, and identified promising candidates using the lowest-energy percolating pathway.

We used all fluoride-containing structures from the Materials Project database (version 2021-02-08)40, yielding 9747 structures. Symmetrically unique pathways – each represented by a unique combination of start and end crystallographic sites – were identified for each structure using pymatgen-diffusion’s distinct path finder41 with two criteria: (1) pathways were limited to 5 Å in length, and (2) only the five shortest symmetrically unique pathways per structure were considered. Although these choices limited our collection of candidate pathways, we examined whether these longer pathways were physically reasonable. Individual pathways longer than 5 Å required fluoride movement beyond its first- or second-nearest neighbor, leading to unfavorable interactions (Supplementary Fig. 3), and we also found that the shortest pathways within a structure yielded the lowest barriers (Supplementary Fig. 4). Thus, we concluded that loosening these criteria (leading to the addition of new candidate pathways) was unnecessary in the scope of this study. This produced 43,352 candidate pathways, and no other criteria were applied to limit or remove candidate pathways. These 40,000+ pathways establish a constant work-in-progress for the most computationally intensive calculations such as NEB, and we report on that progress herein.

Generating a high-accuracy reference dataset

The first step in our evaluation of candidates was the calculation of a high-quality reference dataset. Compared to standard hierarchical workflows, which perform high-quality calculations only on candidates selected by low-quality predictions, we instead selected a diverse subset of materials for these high-quality calculations. This provided reference values against which we could judge and iteratively refine our low-quality predictions. The DDI strategy allowed this dataset to cumulatively grow during our study (currently, N = 299), which further enabled iterative evaluation of low-quality predictions.

The most rigorous calculation used to assess fluoride transport was a midpoint-only NEB relaxation. Specifically, we calculated the diffusion barrier for pathways by fully relaxing the start, end, and midpoint supercell structures (R = 10 Å) via NEB, where the midpoint structure was prerelaxed by an image-dependent pair potential surface (IDPP) to improve our starting point42. Even though full relaxations were performed, the use of a single structure in NEB means that the predicted barrier is only the minimum possible barrier for the pathway. This is because the true transition state may lie off the midpoint, leading to a higher barrier than what is calculated here. Thus, this calculation can be viewed as an extension of Trottier et al.43 explicit-error approach combined with empirical pre-relaxations utilized by Smidstrup et al.42. This was selected over a full climbing image NEB44 analysis of promising pathways because the supercell relaxations required are extremely expensive, even with substantial efforts45,46,47,48 made in this area.

In building this reference dataset, various priority-ranking functions were utilized by our task executors, and these functions evolved throughout our search. Initial calculations were orchestrated by random selection of pathways. The reference dataset was then used to identify trends and establish heuristics, and these models prioritized future calculations for the reference dataset. Thus, as our reference dataset grew, we updated our models and their influence on priority queues (Fig. 1b). The flexibility of our priority functions also allowed us to focus on specific structure types or compositions in a subset of executors. This was particularly useful when we identified an interesting structure type and wanted to analyze similar candidates by NEB. Together, all these executors and various ranking functions worked to cumulatively produce the final dataset of NEB results.

At the time of publication, 299 pathways successfully converged for this midpoint-only NEB calculation, and all these pathways are listed in Supplementary Table 1. These reference calculations allowed us to evaluate the lower quality calculations described below.

Developing a rapid calculation within the DDI framework

Because the computational cost of NEB limited its use to fewer than 300 pathways out of >40,000 (<0.7% total), we sought to identify a faster calculation to estimate energy barriers. We therefore used small supercells (R = 7 Å) on the initial, final, and midpoint structures to calculate energy barriers, but these smaller supercells are still similar in size to those used in other high-throughput searches27,28,29,30. To further reduce the computational cost, the initial and final structures were not relaxed, while the midpoint image was relaxed using the IDPP method42. IDPP is an empirical method that uses bond lengths to produce a relaxed structure that is similar to that produced by NEB. With these steps to reduce computational cost, it became feasible to calculate thousands of pathways rather than hundreds. At present, we have calculated 8497 pathways via this method, and 6797 (80%) have been completed successfully.

We expected that these faster calculations would have a large error because of electrostatic repulsion among small supercells49, the absence of complete relaxation, and the possibility that the transition state was not located at the pathway’s midpoint43. To quantify the error in these calculations, we compared them to the more rigorous midpoint-only NEB calculations described above. We observed a moderate correlation between the approximated barriers (Eapprox) and the NEB barriers (ENEB) (Fig. 2, green), with a median error (Eapprox-ENEB) of +165 meV and a standard deviation of 427 meV. This is a large error distribution compared to typical DFT barrier predictions. Nevertheless, the approximation successfully isolates pathways with low-energy barriers. Specifically, 165 out of 167 (98.8%) pathways predicted to have Eapprox < 1.0 eV, in fact, have ENEB < 1.0 eV. Despite this agreement, our approximation also results in a large number of false negatives, where 6 out of 29 (20.7%) pathways with Eapprox > 1.5 eV actually have ENEB < 1.0 eV. The tendency to overestimate the barrier is consistent with the use of a small supercell, which can destabilize the transition state49. However, because this error is systematic, it can be corrected.

Fig. 2: Error distributions of approximated barrier heights relative to reference NEB barrier heights (R = 10 Å).
figure 2

The static pathway (green) as well as the partially relaxed pathway (red) used smaller supercells (R = 7 Å). Empirical corrections to barrier height were made for the static (blue) and partially relaxed (black) calculations using linear regression as described in the text. The partially relaxed calculations (red, black) were performed on a subset of pathways (N = 170). Gray regions are centered about the mean in (a) and the linear regression in (b), where the region width shows the standard deviation.

Full size image

To reduce the systematic error in Eapprox, we used a linear regression between our static approximation and fully relaxed NEB. The linear regression was updated as we collected NEB data, which allowed us to iteratively improve our empirical correction. At the time of publication, the empirical correction (in eV) is:

$$E_{{{{\mathrm{NEB}}}}} = 0.549E_{{{{\mathrm{approx}}}}} + 0.119$$
(1)

This correction greatly reduces the systematic error (Fig. 2, blue). The median error is reduced from +165 meV to −9 meV, and the standard deviation is reduced from 427 meV to 318 meV.

With the goal of further improving the approximation, we explored additional strategies to refine the trade-off between computational cost and error reduction. The DDI framework allowed us to explore alternative versions of the approximated calculation because we can initiate task executors that are independent of preexisting executors. We therefore examined how alternative relaxation convergence criteria would affect the calculation’s efficiency and accuracy. Start, midpoint (NEB), and end supercell structures (R = 7 Å) were relaxed to an ionic convergence of 0.5 meV, and all ionic steps were analyzed for convergence and CPU usage (Supplementary Fig. 5). This allowed us to understand how convergence criteria affect computational cost and calculation accuracy.

Our results show that as the convergence criteria are improved, the calculation accuracy also improves. However, decreasing the convergence criteria below 100 meV does not further improve the errors’ standard deviation, likely because the accuracy is not limited by convergence but rather by the use of a small supercell. Compared to a static-IDPP calculation, stopping the calculation at a 100 meV convergence increased the computation cost by 1.6x, decreased the median error from 165 to 92 meV, and reduced the standard deviation in the error from 427 to 330 meV (Fig. 2, red). We sought to further reduce the error using an empirical correction of the data, as we did above. We performed a linear regression on our data but added a second term that sought to account for the residual forces in the structure due to incomplete relaxation:

$$E_{{{{\mathrm{NEB}}}}} = 0.856E_{{{{\mathrm{approx}}}}} - 0.153F_{{{{\mathrm{rel}}}}} + 0.033$$
(2)

where Frel is a measure of the forces that remain on atoms in the incompletely relaxed structures. Frel is found by calculating the Euclidean vector norm of the force for all atomic sites in each of the start, end, and midpoint structures; Frel is the difference in the Euclidean vector norm between the midpoint and start (or end) structures, whichever is larger.

The Frel empirical coefficient of −0.153 implies that structures with higher Frel will often overestimate barriers. Although Frel has the primary purpose of correcting for incomplete relaxation, it also provides a partial correction for our use of small supercells49.

When linear regression is applied as an empirical correction, this fit yields an updated median error of −10 meV and a standard deviation of 286 meV. This is a drastic improvement from our original uncorrected static calculation that gave a median error of 165 and standard deviation of 427 meV. However, this is only a modest improvement in accuracy compared to the empirically corrected static calculation, which had a median error of −9 meV and standard deviation of 318 meV. Given that this small improvement in accuracy comes with a 60% increase in computational cost, we decided that our empirically corrected static approximation (described in the preceding section) would best balance computational costs with accuracy. Thus, by using this approximation, we were able to calculate 6797 barriers to identify promising materials. This overall strategy was enabled by our DDI framework, which simplified the process of testing different approximations and iteratively correcting errors without interrupting or restarting the search.

Identifying heuristics for fluoride-ion transport

At the time of publication, we completed 6797 empirically corrected static calculations. These calculations provide a high-quality dataset for fluoride-ion transport and provide us with the opportunity to identify heuristics. In fact, during the course of this study, we iteratively assessed the growing database for trends. This allowed us to use emerging trends to prioritize calculations on materials with promising characteristics.

Although heuristics for fluoride-ion transport have not been described previously, heuristics for cation transport have been developed30,45,50,51,52. For example, the size of free-volume networks, bond lengths, and pathway lengths were used to predict the ionic mobility of lithium, sodium, and zinc27,28,29,30. These heuristics were also applied to empirically predict fluoride transport in 1,500 materials53. Because of our recent discovery of a distinct transport mechanism in some anion conductors3, it is unlikely that heuristics for cation transport generally apply to anions. In the following section, we sought to use our ab-initio calculations to evaluate whether heuristics based on sterics, charge, and pathway length could be applied to fluoride diffusion.

We evaluated the sterics of the diffusing atom by treating atoms as hard spheres and measuring their overlap along the diffusion pathway. The overlap was quantified using the change in ionic radii overlap (ΔIRO), where ionic radii were obtained by using bond valence analysis. The ΔIRO descriptor uses the same underlying principles of sterics and charge as other software, such as SPSE27 and SoftBV50, which evaluate free volumes for cationic diffusion.

Initially, we hypothesized that ΔIRO would correlate strongly with barrier height because overlap between fluoride and neighboring atoms in the transition state would be unfavorable. Unexpectedly, we did not find a clear relationship between ΔIRO and barrier height. As we analyzed our data, however, we found that materials with a small ΔIRO and high barrier often had pathways where significant bond-breaking occurred. We also observed that increasing overlap between fluoride and anions (cations) resulted in larger (smaller) barriers. We, therefore, refined our model to incorporate both increasing overlap (positive ΔIRO) and bond breaking (negative ΔIRO) and distinguished between neighbors that were cations (ΔIROcation) and anions (ΔIROanion). For each type of ΔIRO, we used the maximum value for F- with each of its neighbors. The revision of our incorrect hypothesis highlights the value of the DDI strategy in contrast to traditional hierarchical searches. If this had been a hierarchical search, our incorrect hypothesis would have removed promising materials, and we might not have identified our error.

This updated model is presented in Fig. 3. The smallest barriers for fluoride transport occur when, in the transition state, the fluoride moves towards cations (positive ΔIROcation) and away from anions (negative ΔIROanion). Small barriers can also occur with a modest decrease in fluoride-anion distances or a modest increase in fluoride-cation distances. However, when fluoride-anion distances decrease more than ~0.5 Å or when fluoride-cation distances increase more than ~1.0 Å, barriers rapidly grow. Overall, the data show that anions in the vicinity of the diffusing fluoride have an especially profound influence on fluoride transport.

Fig. 3: Understanding the role of sterics and charge on barrier height based on 6797 pathways.
figure 3

The diffusing fluoride’s change in ionic radii overlap was separately evaluated for neighboring anions (ΔIROanion) and cations (ΔIROcation). All measurements were performed on the IDPP-relaxed path in R = 7 Å supercells, and the barrier corresponds to the static, midpoint-only approximation discussed in the main text. Each hexagon bin is colored using the average barrier of all pathways in that region.

Full size image

Even though this updated model considers the distinct roles of cations and anions, it does not consider the number of ions or the magnitude of their charge. To measure the change in electrostatic energy of the diffusing ion, we calculated the Ewald energy along the empirically relaxed pathway (ΔEEwald). Here, we expected that positive changes in Ewald energy (corresponding to more unfavorable electrostatic environments) would occur in higher energy pathways. This is corroborated by the positive trend of ΔEEwald with approximated DFT-calculated barriers (Fig. 4b). Nearly all pathways with an unfavorable change in ΔEEwald greater than 5 eV have a barrier greater than 1.5 eV, which indicates that ΔEEwald is a promising empirical predictor of high barrier pathways.

Fig. 4: Understanding fluoride transport using pathway length (left column, a, c, e) and the change in Ewald energy (ΔEEwald) (right column, b, d, f).
figure 4

Pathways for all structure types show moderate correlation with (a) pathway length and (b) ΔEEwald. When pathways were analyzed structure type-by-structure type (c–f), we observed much tighter distributions for barrier heights. However, many structure types display barrier heights that are independent of these predictors (Supplementary Fig. 6). Trendlines and error bars for each subplot depict the mean and standard deviation of barrier heights within binned regions, respectively.

Full size image

The final heuristic that we present is based on the hypothesis that longer pathways have higher barriers54. In Fig. 4a, we plot pathway length and barrier height and find that virtually all pathways shorter than 3.8 Å have barriers under 2.0 eV, but pathways longer than 3.8 Å often have much larger barriers. The radial distribution function in Supplementary Fig. 3 helps explain these observations: pathway lengths over 3.8 Å often require that fluoride moves not to a nearest-neighbor fluoride vacancy but to a second nearest-neighbor fluoride vacancy. Therefore, fluoride-ion conductors generally have lower barriers for shorter paths (Supplementary Fig. 4), which is consistent with heuristics for cation diffusion.

Up to this point, this section shows how heuristics can be applied to the entire population of fluoride-ion conductors. However, the large standard deviation for each of these relationships shows that these heuristics have limited explanatory or predictive value. We therefore sought to understand whether the standard deviation could be reduced by comparing only those structures that share the same structure type. Several exemplar structure types are presented in Fig. 3 and the SI (Supplementary Fig. 6). Interestingly, we find that these broad heuristics (e.g., barrier height increases with pathway length) describe a small number of structure types but that these heuristics are incorrect for most structure types. For example, we observe that the barrier height remains constant as the pathway length increases in many structure types. It therefore becomes clear that our general heuristics are often untrue for specific structure types, even if they are true for the overall population.

Although we find that general heuristics are poor predictors of ionic mobility, in specific structure types, our plots of barrier height vs. pathway length or ΔEEwald have very small standard deviations. These small standard deviations suggest that, when analyzed structure type-by-structure type, pathway length and Ewald energy are actually good predictors of barrier height. For example, given a specific structure type and pathway length, our dataset allows us to accurately predict the barrier height of a yet-unknown material. The fact that simple structural or electrostatic features can yield the barriers of unexplored compositions will be extremely useful in future explorations of other materials. Furthermore, we propose that our final dataset can be used to identify features beyond those found in this study. This can also extend to the development of complex descriptors via machine-learning and active-learning approaches, which may outperform the predictive capabilities of general heuristics.

Exploring the final dataset

By applying the DDI strategy to a large group of fluoride-containing crystals, we calculated 6797 approximate barriers and 299 NEB barriers. Because of the iterative refinement, the error in the approximate barriers is modest (std. deviation = 318 meV). While the magnitude of this error indicates that Eapprox should not be compared directly with experimental values, our results are sufficiently accurate to identify promising materials for further study. Moreover, although our calculations focused on single-vacancy diffusion in single crystals, many candidates may benefit from exploration at different stoichiometries and higher vacancy concentrations. To encourage follow-up studies on these materials, the full dataset is made available with common querying flags (e.g., hull energy) in the SI. To illustrate this dataset’s contents, we outline and apply three example use cases: (a) exploration of specific compositions, (b) identification of structure types for 2-D fluoride intercalation, and (c) identification of inexpensive solid-state electrolytes.

First, we sought to identify conductors in our dataset based on composition, and because our dataset is large and diverse, we hypothesized that we could explore families of chemically related materials. For example, lead is a common component of known fluoride-ion conductors, so we examined all Pb-containing systems in our dataset. This yielded 58 different structures, and a small sample of these structures (8 out of 58) is shown in Table 1.

Table 1 Subset of promising Pb-containing phases.
Full size table

Here, we can see Pb-F systems commonly used in FIBs, including PbF2, PbF4, and SnPbF413,55,56. We also find many common mixed fluorides, including BiPb2F7, that have been explored as fluoride conductors57. In addition to finding some of the previously known high-performing materials, our search also identified fluoride-ion conductors, such as Pb3IF5. This suggests that the strategy of incorporating a small amount of a larger halide may yield many high-performance materials.

Using other query flags, such as anonymous formulas, this approach can be extended to compositionally related systems as well. For example, searching for all structures that have an anonymous formula of AB3 results in 121 distinct structures. This includes all tysonite LaF3-type crystals (MF3), where each was predicted to have at least one low-barrier diffusion pathway (<1 eV). This therefore captured all known tysonite fluoride-ion conductors (M=La, Ce, Pr, Nd) and several additional conductors (M=Li, Cu, Y, Dy, Lu, Np, Pu)4. Likewise, searching for all AB2 structures results in 65 structures. These results include all known fluorite CaF2-type (MF2) conductors (M=Cd, Pb, Ba, Ca, Sr) as well as several additional conductors (M=Hg, Eu, Ti), which we list in order of increasing barrier4. The trend in barrier height among the known conductors agrees well with experimental measurements (Pb < Ba < Sr < Ca)58,59,60. These example searches illustrate the quality of our dataset and how it can assist the exploration of fluoride-ion conductors by composition.

As a second approach for identifying materials, we can explore our dataset by structure-type. For example, in cation shuttle batteries, intercalation electrodes have been used to improve cyclability relative to conversion electrodes. However, in FIBs, conversion-based electrodes are used in the majority of studies, and to our knowledge, only four intercalation structure types have been proposed: Ruddlesden–Popper (K2NiF4-type)61, Schafarzikite (MSb2O4)62, anion-deficient perovskite (y-AMO3)63, and layered rocksalts (MoS2-type)3. We therefore searched for layered structures that could facilitate intercalation.

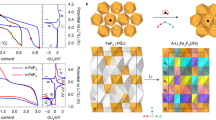
To identify intercalation structures, we searched for layered structure types that have (a) 2-D percolation networks for fluoride and (b) at least three stable structures with a pathway barrier height between 0 and 1 eV. Fig. 5 categorizes the resulting materials by structure type. None of these six structure types have been previously explored for fluoride intercalation. We emphasize that criterion (b) limited the number of structure types that we highlight here; in fact, our dataset includes a very large number of unexplored structures. For example, our search finds the promising material Ho2CF2 (MoS2-type, barrier = 258 meV) but fails to find three or more promising candidates because the Materials Project does not yet include Y2CF2 or Sc2CF2, which are even more promising as fluoride-intercalation electrodes3,14,15,16.

Fig. 5: Structure types for fluoride intercalation in layered materials.
figure 5

These six structure types contain at least three stable compositions (Ehull = 0 eV), each with a predicted pathway barrier between 0 and 1 eV. Each structure type shows an example crystal structure and its composition. The corresponding bar charts show barriers of compositions with the same structure. Compositions labeled by a green bar are thermodynamically stable, while gold is metastable according to the Material Project database40.

Full size image

A third and final strategy for identifying promising materials would consider the needs of specific applications. Here, we search our dataset for solid-state electrolytes that are stable, inexpensive, and fluoride-conducting. This is accomplished by filtering our dataset with the following conditions: (a) the structure is stable, (b) the bandgap is greater than 3.5 eV, (c) the barrier height is below 700 meV, (d) the raw element cost is less than $125 per kg and $125 per mole, (e) the material’s percolating network is 3-D, and (f) the material does not contain mobile cations. This results in 12 structures that are shown in Table 2.

Table 2 Candidate materials for cost-effective solid-state electrolytes.
Full size table

These 12 structures include a few well-known fluoride-ion conductors (PbF2, LaF3, InF3, and NdF3) but primarily consist of materials. The remaining results include promising but unexplored binary and ternary fluorides. The sole binary, GaF3, possesses a higher barrier and cost but still merits further exploration for fluoride conductivity as either a pure or mixed phase. The results also contain many promising ternary materials that have not been considered fluoride-ion conductors. Among these, we highlight ZnTiF6 and MgTiF6, which are isostructural to InF3. These two materials have the lowest barriers in this set of results (55 and 324 meV), and the oxidation states of Zn2+, Mg2+ and Ti4+ suggest that F− will be the only mobile ion. Moreover, the redox stability of Ti3+ would facilitate the formation of F- vacancies necessary for conduction.

Discussion

In this work, we introduced a high-throughput strategy to identify fluoride-ion conductors. An important component of our strategy was the development and validation of a low-cost, high-accuracy DFT method that yielded barrier heights for a large number of fluoride-containing materials. This dataset has allowed us to describe heuristics for the movement of fluoride and to identify many promising structure types for fluoride-ion conductors that have not been previously explored.

The development of FIBs has been limited by the few electrolytes and electrodes known, but our results now give many interesting materials to target for experimental exploration. In the context of electrolytes, some of the most exciting materials are the category M1M2F6 (e.g., ZnTiF6 and MgTiF6), for which there are many low-barrier conductors available from lightweight and inexpensive elements. From the standpoint of electrode development, many of the materials identified here may be suitable for either intercalation or conversion reactions as electrodes. These and many other applications may emerge from this dataset, which is available as an online database for download and searching (see SI).

As an alternative to hierarchical searches, our DDI strategy has demonstrated several advantages. Hierarchical searches must apply cutoff criteria based on initial understandings, but because no preexisting heuristics existed for F- transport, this approach was not possible. Thus, rather than removing candidates using unvalidated predictors, the DDI strategy allowed us to update the ranking of candidates as our understanding of F- transport improved. Our DDI strategy therefore enables the exploration of systems where there is little prior knowledge. This approach is certainly not limited to calculations of ionic conduction, and if adopted more widely, it could greatly improve our ability to explore material systems and properties.

Methods

All relevant methods are presented within our Results section, and additional details are available in the Supplementary Information.