Introduction

Two-dimensional (2D) materials with ultimate thinness are highly promising for applications in next-generation electronic, optoelectronic devices, and macroscopic assemblies, benefiting from their extreme structures and properties1,2,3,4,5,6,7. However, their rise begins only after high-quality monolayers being successfully isolated. Mechanical exfoliation is one of the most reliable techniques to obtain high-quality 2D materials8. A few 2D monolayers have been mechanically exfoliated from their parent layered solids8,9,10, in which the most canonical example is the exfoliation of graphene from graphite8. It should be noted that the method of mechanical exfoliation also has disadvantages in scalability and doping control. To overcome such limitations, several methods such as the liquid exfoliation11,12, chemical vapor deposition13,14, and wet-chemistry synthesis15, have been developed. These methods also play a significant role in the science of 2D materials. Regardless of different synthesis technologies, the existence of an exfoliable bulk precursor generally indicates a weak interlayer coupling and a relative stability of free-standing 2D monolayers. Therefore, measuring the exfoliability of 2D materials is crucial not only for discovering new 2D materials but also for assessing the stabilities of free-standing 2D materials.

Progress in this field would be accelerated if the family of 2D materials can be greatly extended. However, experimental identification of 2D materials out of their bulk counterparts is a trial-and-error and time-consuming approach, and hence, only a few 2D materials have been successfully exfoliated to date. For parent bulk crystals, the accumulated knowledge of structure-property has been collected in databases such as the Pauling file16, the Inorganic Crystal Structure Database (ICSD)17,18, the Crystallographic Open Database (COD)19, the Computational 2D Materials Database (C2DB)20, and Materials Project (MP)21. The growing crystal structure databases and computational methods have promoted the progress in powerful high-throughput techniques for screening materials before synthesizing them22,23. These techniques have been employed in mining 2D materials from three-dimensional crystal databases and remarkable achievements have been made24,25,26,27,28. Considering the characteristic of weak interlayer bonding of layered crystals, recent studies searched the ICSD for crystals with a large interlayer spacing24,25. They used packing fraction and interlayer gap criteria to successfully identify almost 100 layered solids. Furthermore, topology-scaling algorithms have been developed to search for layered materials, that is, the possible parents of 2D materials26,27. These structure-based algorithms and criteria are efficient for the identification of layered crystals. However, it depends on empirical parameters to determine whether two atoms are bonded, and it is noted that layered crystals are not equivalent to exfoliable bulk crystals for 2D materials for the following reasons: (i) Not all exfoliable crystals are layered crystals. For example, if the interlayer of a crystal is loosely or weakly bonded, it can be an exfoliable crystal although it is a non-layered crystal (Fig. 1). (ii) Not all layered crystals are exfoliable crystals. For example, if the in-plane strength of a layered crystal is not strong enough to resist the interlayer interaction, the material’s plane will be fractured during the mechanical exfoliation, and hence this layered crystal is not an exfoliable crystal (Fig. 1). Briefly, both layered crystals and non-layered crystals are potentially exfoliable or non-exfoliable, which significantly depends on their interlayer interactions and in-plane resistance.

Fig. 1: Illustration of different types of crystals.
figure 1

The exfoliable layered crystal, non-exfoliable layered crystal, non-exfoliable non-layered crystal, and exfoliable non-layered crystal are illustrated.

Full size image

To assess the exfoliability of bulk crystals (the feasibility of exfoliating 2D materials from their parent bulk crystals), several measures have been proposed from the views of energy and mechanical force, where the interlayer binding energy is a widely used parameter. Intuitively, the lower the binding energy is, the easier the 2D materials can be exfoliated from the bulk counterparts29. Yet, this intuition may break down since it does not consider the in-plane mechanical resistance of 2D materials (Fig. 1, the non-exfoliable layered crystal)30. Considering the requirement of a high in-plane strength and a weak interlayer interaction for mechanically exfoliable 2D materials, Gao et al.30 derived a dimensionless measure σs/γ based on an exfoliation mechanics model, where σs and γ are the in-plane 2D strength (the fracture force divided by the width of 2D sheet) and the interlayer binding energy, respectively. Despite that this measure shows a great reliability for measuring the exfoliability of 2D materials30, the costly calculations of the in-plane strength and interlayer binding energy limit its uses in high-throughput computational identification of exfoliable 2D materials. Therefore, based on the literature survey, a proper measure of exfoliability which has (i) a clear physical meaning, (ii) a universal applicability, and (iii) is simple and efficient for high-throughput calculations is still missing for 2D materials.

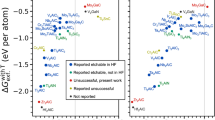
Herein, we derived an elasticity-based-exfoliability measure based on an exfoliation mechanics model, i.e., the maximum ratio of the minimum in-plane Young’s modulus to the out-of-plane Young’s modulus of crystals over all possible exfoliable planes. This measure has a clear physical meaning and is universally applicable to all material systems. More importantly, it can be efficiently determined from experiments or first-principles calculations, making it attractive for high-throughput identification of exfoliable 2D materials. Using this measure, we evaluated the exfoliability of 10,812 screened crystals having a first-principles calculated elastic tensor from MP crystal structure database. Based on the minimum and median values of elasticity-based-exfoliability measure for 34 already-exfoliated crystals from literature survey, we screened out 58 easily and 90 potentially exfoliable bulk crystals for 2D materials, which have an elasticity-based-exfoliability measure larger than the median value (25.9), and between the minimum (10.5) and median values of already-exfoliated crystals, respectively. Afterward, an extended topology-scaling algorithm shows that 138 (93%) of these exfoliable bulk crystals are layered solids, and the analysis on packing ratios shows that 147 (99%) predicted exfoliable bulk crystals exhibit a relatively low packing ratio value ranging between 0.1 and 0.8, providing further supports to our prediction. Finally, the characteristics of these predicted 2D materials were discussed for practical applications.

Results and discussion

Elasticity-based-exfoliability measure based on an exfoliation mechanics model

The mechanical exfoliation of 2D materials can be rationalized into a forced peeling model as illustrated in Fig. 2a (see ref. 30 for details). Based on the Rivlin model31, the peeling force F can be written as F(1-cosα) = γw, where α and w are the peeling angle and peeling sheet width (Fig. 2a), respectively, and γ is the cleavage energy density. Then, we define a 2D peeling stress which is the applied peeling force divided by the width of the 2D sheet, that is, σ2D = F/w = γ/(1-cosα). To ensure the in-plane mechanical integrity during mechanical exfoliation, σ2D should be lower than the intrinsic 2D strength of the material (σs), that is σ2D = γ/(1-cosα) < σs, since the real strength of 2D materials that usually contain defects can be much lower than σs32,33,34,35. Consequently, a fracture-based-exfoliability measure σs/γ > C can be derived, where C is an exfoliable threshold. First-principles calculations for some already-exfoliated 2D materials show that the values of σs/γ for graphene, h-BN, MoS2, and black phosphorus are 104.4, 191.6, 50.3, and 42.9, respectively, indicating their high exfoliability. This measure considers both in-plane and out-of-plane mechanical properties of 2D materials and shows great reliability30. However, both computational and experimental determinations of in-plane strength and cleavage energy density for bulk crystals are costly, which prevents the fracture-based-exfoliability measure from being widely used for high-throughput identification of exfoliable 2D materials.

Fig. 2: Mechanical exfoliation model and elastic modulus distribution for an exfoliable crystal.
figure 2

a Model of mechanical exfoliation of 2D materials. b Spatial dependence of the Young’s moduli for graphite.

Full size image

As an alternative, elasticity-based techniques have been widely used to characterize the properties of materials, engineering structures, and biological tissues. These techniques are non-destructive and efficient, as the elastic deformation can be fully recovered after mechanically unloading. A canonical example is ultrasonic testing that utilizes elastic waves to detect cracks and defects in parts and materials. Inspired by the elasticity-based techniques, we extended the aforementioned fracture-based-exfoliability measure (σs/γ) into an elasticity-based-exfoliability measure for high-throughput computational identification of exfoliable 2D materials. Under a linear elasticity assumption, the 2D uniaxial tensile strength of a 2D material can be written as σs = Yinεind, where Yin, εin, and d are the in-plane Young’s modulus, strain-to-failure, and interlayer distance, respectively. The cleavage energy density is γ = Youtεout2d/2, where Yout and εout are the out-of-plane Young’s modulus and strain-to-failure, respectively. Hence, the fracture-based-exfoliability measure can be written as

$$\sigma _s/\gamma = (2\varepsilon_{{{{\mathrm{in}}}}}/\varepsilon_{{{{\mathrm{out}}}}}^2)\left( {Y_{{{{\mathrm{in}}}}}/Y_{{{{\mathrm{out}}}}}} \right).$$
(1)

As most single crystals would break at a certain strain32,36, a constant pre-factor f = 2εin/εout2 can be assumed. The justification of this assumption is made as follows. Since the tensile strength and cleavage energy are much more complex than the linear-elastic moduli, it is challenging to screen these properties over all possible exfoliable planes (or directions) by using first-principles calculations for anisotropic materials. As an alternative, the tensile strength and cleavage energy of crystals were correlated with the elastic moduli based on the above-mentioned assumptions for an ideal crystal, Frenkel’s model37 indicates that the tensile strength is about 1/10 of the Young’s modulus, that is σth ≈ Y/10. This is generally consistent with more recent results38,39,40, which predict that crystals can break at the stress of Y/15-Y/8. In addition, we calculated the in-plane and out-of-plane mechanical properties for two typical exfoliable crystals (graphite and h-BN, see “Methods” for calculation details). It can be seen that the in-plane and out-of-plane strain-to-failure are 19% and 18% for graphite, and 18% and 16% for h-BN, respectively, resulting in the corresponding pre-factor values of 11.73 and 14.06, respectively. These results indicate a relatively narrow range of pre-factor values. Considering that the elasticity-based-exfoliability measure values for exfoliable crystals are orders of magnitude larger than that of non-exfoliable crystals as discussed below, it is expected that the assumption of constant pre-factor would have relatively insignificant effects on the prediction of exfoliability. Therefore, the ratio of the in-plane Young’s modulus to the out-of-plane Young’s modulus of crystals is proportional to the fracture-based-exfoliability measure (σs/γ)

$$Y_{{{{\mathrm{in}}}}}/Y_{{{{\mathrm{out}}}}} \propto \sigma _{{{\mathrm{s}}}}/\gamma .$$
(2)

Notably, this formula is derived for in-plane isotropic sheet crystals that has a definite exfoliable plane. However, for most bulk crystals, the exfoliable plane is unknown and the in-plane property is anisotropic. It is expected that for any plane of a generally anisotropic bulk crystal (xy-plane), there is a minimum in-plane Young’s modulus [minxy(Yin)], and the most possible exfoliable plane of a bulk crystal is the plane having the maximum value of [minxy(Yin)]/Yout. Hence, the maximum ratio of the minimum in-plane Young’s modulus to the out-of-plane Young’s modulus over all possible exfoliable planes of an unknown bulk crystal can be used to define a measure of exfoliability as

$$E = \mathop {{\max }}\limits_z \left[ {\frac{{\mathop{\min}\nolimits_{xy}(Y_{{{{\mathrm{in}}}}})}}{{Y_{{{{\mathrm{out}}}}}}}} \right],$$
(3)

where z is the out-of-plane directional vector of an arbitrarily possible exfoliable plane xy. The xy-plane for obtaining E can be seen as the most possible exfoliable plane of the crystal. Notably, the minimum in-plane Young’s modulus was adopted for calculating the exfoliability of anisotropic crystals (Eq. (3)). Considering that some materials might be exfoliated along a higher in-plane modulus direction, our measure would provide a conservative prediction on the exfoliability of such materials. The larger of E for a specific crystal is, the easier the 2D material can be mechanically exfoliated from the crystal. Overall, E satisfies all three criteria for a proper measure of exfoliability as specified above: (i) It has a clear physical meaning from an exfoliation mechanics model. (ii) It is universally applicable to all material systems. Although empirical assumptions and threshold values have been adopted in the derivation of this measure, no empirical parameters are needed when calculating the measure from the elastic tensors of crystals by using Eq. (3). Meanwhile, it can correctly filtrate out the crystals having low in-plane mechanical resistance that cannot resist the exfoliating loads by considering the in-plane and out-of-plane mechanical properties of bulk crystals. (iii) It can be calculated from the elastic tensors of crystals that can be conveniently obtained by first-principles calculations or experimental measurements. Since the elastic tensors have been calculated and collected for a large number of crystals in the MP database, this measure can be directly used for high-throughput computational exfoliation of 2D materials.

High-throughput computational identification

The elasticity-based-exfoliability measure can be extracted from the elastic tensor of crystals. We first calculated the Young’s moduli of all directions for a crystal (see “Methods” for details). Typical Young’s moduli distribution of graphite is shown in Fig. 2b. Afterward, the elasticity-based-exfoliability measure can be obtained based on Eq. (3).

Following the above-mentioned procedures, we calculated the elasticity-based-exfoliability measure for crystals having a first-principles calculated elastic tensor from MP database to identify exfoliable 2D materials. It should be noted that our prediction of the exfoliability depends on the accuracy of calculated data in MP database. Although some data in MP database are found to be incorrectly presented due to the possible processing or calculating errors41, our previous work41 indicated that most of the data in the MP database are reliable. By October 1, 2021, MP crystal structure database organizes 144,595 inorganic crystal materials, in which 13,176 crystals have structural information and first-principles calculated elastic tensors. As shown in Fig. 3a, we first extracted these 13,176 crystals from MP database. Before calculating the elasticity-based-exfoliability measure of these crystals, we cleaned the database by filtering out crystals having non-positive definite stiffness tensor (in the processing, the crystals have the minimum eigenvalue of the elastic tensor λmin ≤ 0.1 GPa were filtrated out). Thus, 11,503 crystals that satisfy the Born criteria of elastic stability were retained. Furthermore, 691 crystals containing radioactive elements were also filtered out. Finally, the elasticity-based-exfoliability measures and the corresponding exfoliable planes of all 10,812 retained crystals were automatically calculated using a developed batch program.

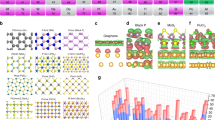
Fig. 3: High-throughput computational identification of exfoliable 2D materials.
figure 3

a Tiered screening pipeline for discovery of easily and potentially exfoliable crystals. Tier 1: Filter out the crystals having non-positive definite stiffness tensor. Tier 2: Filter out the crystals which contain radioactive elements. Tier 3: Filter out the crystals with a measure less than Emin. Tier 4: Filter out the duplicate crystals. b Distribution of the minimum in-plane Young’s modulus [minxy(Yin)] and the out-of-plane Young’s modulus (Yout) for the most possible exfoliated plane of all 10,812 crystals. c Top 10 crystals with the largest elasticity-based-exfoliability measure.

Full size image

The minimum in-plane Young’s modulus [minxy(Yin)] and the out-of-plane Young’s modulus (Yout) for the most possible exfoliated plane of each crystal were calculated as distributed in Fig. 3b. Approximately 3% (293 crystals), 2% (190 crystals), and 1% (106 crystals) of the total crystals have E values above 5, 10, and 20, respectively. To filtrate out the duplicate crystals, we determined the crystal topologies using a topological approach42, and then identified duplicate crystal structures based on their topologies. After filtering out the duplicate crystals, the crystals having the top 10 values of E were sorted in Fig. 3c, which contains 6 experimentally exfoliated 2D materials, including graphene8, VS243, WS244, BN45, MoS246, and ReS247. Table 1 presents the related information of these 10 materials. Furthermore, we did a literature survey on already-exfoliated 2D crystals and calculated their values of E, and found 34 already-exfoliated 2D crystals with E ≥ 10 in experiments. The already-exfoliated 2D crystals in experiments have E ranging from 10.5 to 1156.3 (Supplementary Table 1). Herein, the median value and the minimum value of E of already-exfoliated 2D crystals (Emed = 25.9, Emin = 10.5) are defined as two exfoliable thresholds for easy and potential exfoliation, there are 58 crystals exhibiting E ≥ Emed and 90 crystals having Emed > E ≥ Emin (Supplementary Table 1), which are expected to be easily exfoliable 2D crystals and potentially exfoliable 2D crystals, respectively. The typical atomistic views of predicted top 10 exfoliable 2D crystals are shown in Fig. 4a.

Table 1 Information of top 10 crystals with the largest elasticity-based-exfoliability measure.
Full size table
Fig. 4: Structures of typical predicted promising exfoliable crystals.
figure 4

a Crystal structure prototypes of the top 10 crystals with the largest elasticity-based-exfoliability measure. b Two typical non-layered crystals with an elasticity-based-exfoliability measure above Emin. The xy-plane shown in the top view of crystals corresponds to the exfoliation plane.

Full size image

Supports for the prediction

We then checked whether the predicted exfoliable bulk crystal is a layered crystal and where the cleaved plane locates. To this end, we first extended the topology-scaling algorithm proposed by Ashton et al.26 to identify layered crystals and the normal vectors of cleaved planes therein. In this algorithm, the bonded clusters of atoms in a crystal cell are first determined, where a bond is formed if the distance between two neighboring atoms is <1.3 times of the sum of their covalent radii (the adopted covalent radii are from refs. 26,48). Afterward, the original crystal cell is extended into a n × n × n supercell, in which the maximum number of atoms in an isolated bonded cluster (m) is counted. If m scales as n2, it is identified as a layered crystal. Then, a least square method is used for fitting the atoms coordinates in the cluster to obtain the normal vector of the cleaved plane (a) for the identified layered crystal. The results show that 55 (95%) of the predicted 58 easily exfoliable crystals and 83 (92%) of the 90 potentially exfoliable crystals are layered crystals, and all predicted exfoliable planes are the out-of-planes of these layered crystals, which supports the prediction of exfoliable 2D materials from our measure. Notably, the exfoliable crystals are not equivalent to layered crystals. If a crystal contains material planes that are loosely interlayer bonded, it might be exfoliable, such as LiC6 and Ca2Cu(ClO)2 (Fig. 4b). Recent experiments provided supports on that non-layered materials can be exfoliated into 2D materials, such as WO349, PbS50, Bi51, and Te52. Among these materials, Bi and Te are prepared by hot-pressing their bulk agglomerates, indicating the potential of breaking interfacial bonds by mechanical methods. Furthermore, we found that the percentage of layered crystals increases for crystals having larger E (Fig. 5a), which falls within our expectation. These results support our prediction on exfoliable crystals and suggest that non-layered crystals are possible to be exfoliated.

Fig. 5: Supports from topological and structural analysis of a large number of crystals.
figure 5

a Percentage of layered crystals, and b box plots and distributions of packing ratios for 10,812 crystals having different ranges of E. The dots represent the packing ratio value for each crystal. On each box, the central mark indicates the median, and the bottom and top edges indicate the 25th and 75th percentiles of packing ratio values, respectively.

Full size image

In addition, we calculated the packing ratio of each crystal (Fig. 5b), which is defined as the covalent volume of all atoms divided by the total volume of the crystal cell. Most (99%) predicted exfoliable bulk crystals have packing ratios ranging between 0.1 and 0.8. Figure 5b also shows that the mean value of packing ratio will increase for crystals having smaller E. This indicates that our predicted exfoliable crystals generally have a relatively low packing ratio and thus a loosely packed structure, which is consistent with the conclusions in references25,29 and further supports the prediction of exfoliable 2D crystals from our elasticity-based-exfoliability measure.

Characteristics of exfoliable crystals

Finally, we extracted the characteristics for 148 promising exfoliable crystals (Fig. 6). We first showed the distributions of crystal systems in all crystals from MP database, compared to that of our identified 149 exfoliable crystals (Fig. 6a). The notable difference exists in cubic crystal system, in which there is no promising exfoliable crystals. The results also show that crystals of trigonal crystal system are most promising for mechanical exfoliation. Figure 6b compares the distribution of compositional complexity of identified exfoliable crystals, from which we can find that binary (85) and ternary (54) compounds comprise 94% of all 148 crystals. Furthermore, the stability is significant for using such exfoliable crystals, which can be measured by the value of energy-above-hull41. Figure 6c shows the values of energy-above-hull for all 10,812 crystals. The distribution range of energy-above-hull values for crystals with larger E values becomes narrow. These results might be attributed to that the number of crystals is rapidly reduced as E values increase (Fig. 6c).

Fig. 6: Characteristics of 149 easily and potentially exfoliable crystals.
figure 6

a Distributions of crystal systems for all 10,812 crystals from MP database and 148 crystals with an elasticity-based-exfoliability measure above 10.5. b Distributions of the compositional complexity among 10,812 crystals and 148 exfoliable crystals. c Distributions of energy-above-hull values for all 10,812 crystals.

Full size image

In summary, we theoretically derived a simple and universal elasticity-based-exfoliability measure for high-throughput computational identification of exfoliable 2D materials. Based on this measure, we evaluated the feasibility of exfoliating 2D materials from bulk crystals in MP database. By roughly setting the median (25.9) and minimum (10.5) values of the elasticity-based-exfoliability measure for already-exfoliated 2D materials as threshold values for easily and potentially exfoliable materials, respectively, the search yields 58 easily and 90 potentially exfoliable 2D materials. Our predictions are supported by topological and structural analysis of 10,812 crystals, and literature survey of already-exfoliated crystals. In addition, characteristics of predicted exfoliable crystals were discussed. This work not only provides a fundamental measure of exfoliability for the high-throughput computational identification of exfoliable 2D materials, but also extends the scope of potential 2D materials to be explored.

Methods

First-principles calculations

The density functional theory calculations were conducted via the Vienna ab initio simulation package (VASP)53. The Perdew–Burke–Ernzerhof parameterization of the generalized gradient approximation was used for the exchange and correlation interactions54,55. The cut-off energy was set as 520 eV in all calculations to ensure the accuracy. To avoid the interaction from periodically repeated images, the vacuum layer of 40 Å was adopted. A Monkhorst-Pack k-mesh with densities about 40 Å (the product of each lattice constant and the corresponding number of k-points) was adopted. For all calculations, the convergence criteria for energy and force on each atom were 0.1 meV and 0.001 eV/Å, respectively.

Computation of Young’s moduli in all directions

The generalized Hooke’s law describes the relation between the stress (σ) and strain (ε) for a material, that is, σij = Cijklεkl or εij = Sijklσkl, where Cijkl is the stiffness tensor and Sijkl is the compliance tensor. For anisotropic materials, the stiffness and compliance tensors are orientation-dependent. With Einstein’s summation rule, the transformation for the fourth-order tensor can be described as \(S_{\alpha \beta \gamma \delta }^\prime = r_{\alpha i}r_{\beta j}r_{\gamma k}r_{\delta l}S_{ijkl}\), where rαi is the direction cosine between the new (α) and reference (i) coordinates. By defining two angles (θ and φ) in spherical coordinates, a single unit vector a can be used to represent the Young’s modulus along a certain direction, that is56:

$${{{\boldsymbol{a}}}} = \left( {\begin{array}{*{20}{c}} {\sin \theta \cos \varphi } \\ {\sin \theta \sin \varphi } \\ {\cos \theta } \end{array}} \right),\,(0 \le \theta \le {\uppi},0 \le \varphi \le 2{\uppi}).$$
(4)

With the above equation, the Young’s modulus in an arbitrary direction is derived as

$$Y = \frac{1}{{S_{1111}^\prime }} = \frac{1}{{r_{1i}r_{1j}r_{1k}r_{1l}S_{ijkl}}} = \frac{1}{{a_ia_ja_ka_lS_{ijkl}}}.$$
(5)