Abstract
The optimal design of shape memory alloys (SMAs) with specific properties is crucial for the innovative application in advanced technologies. Herein, inspired by the recently proposed design concept of concentration modulation, we explore martensitic transformation (MT) in and design the mechanical properties of Ti-Nb nanocomposites by combining high-throughput phase-field simulations and machine learning (ML) approaches. Systematic phase-field simulations generate data of the mechanical properties for various nanocomposites constructed by four macroscopic degrees of freedom. An ML-assisted strategy is adopted to perform multiobjective optimization of the mechanical properties, through which promising nanocomposite configurations are prescreened for the next set of phase-field simulations. The ML-guided simulations discover an optimized nanocomposite, composed of Nb-rich matrix and Nb-lean nanofillers, that exhibits a combination of mechanical properties, including ultralow modulus, linear super-elasticity, and near-hysteresis-free in a loading-unloading cycle. The exceptional mechanical properties in the nanocomposite originate from optimized continuous MT rather than a sharp first-order transition, which is common in typical SMAs. This work demonstrates the great potential of ML-guided phase-field simulations in the design of advanced materials with extraordinary properties.
Similar content being viewed by others
Introduction
Titanium-based shape memory alloys (SMAs), such as Ti-Nb alloys, are an important class of smart materials that possess shape memory effect (SME) and pseudoelasticity (PE)1, as well as high specific strength, excellent corrosion resistance, superior biocompatibility2,3, etc. These fascinating merits are widely exploited for industrial4 and biomedicine applications5. In general, the SME and PE originate from temperature- or/and stress-induced reversible first-order martensitic transformation (MT)6,7,8. The common PE stress-strain curve during loading consists of an initial true elasticity stage with a high Young’s modulus (>80 GPa) of austenite phase until MT occurring, following by the stress-plateau associated with the structural transition, and final true elastic deformation of martensitic phase, while during unloading the stress lever causing the reverse MT is lower than that causing MT during loading, thereby exhibiting a large stress-strain hysteresis. Due to the stress-strain hysteresis, low efficiency and poor position control of the SMA actuators are generally observed due to the large hysteresis and strong nonlinearity9. Moreover, as potential metallic biomaterials, a low Young’s modulus comparable with those of natural human bones (~20 GPa10) is essential for Ti-Nb alloys to avoid the “stress-shielding effect”11 and the resulting bone degradation. Although several efforts have been made to optimize the mechanical responses of metallic alloys, e.g., modulation of the components and concentrations12,13, defect engineering14,15, introduction of elastic-inelastic strain matching16,17, and grain refinement18,19, the deliberate design and control of MTs for a combination of specific properties, such as low modulus, linear super-elasticity, and free-hysteresis is still highly desired for various advanced biomedical and engineering applications.
Recently, Zhu et al.20,21,22,23,24. have conducted comprehensive investigations via phase-field simulations on the design of how to make apparently linear-superelastic alloys with ultralow modulus and high strength in SMAs. The pioneer works illustrate that concentration modulation, which can be obtained by spinodal decomposition20,21,22, multilayer deposition23, and precipitation of nanoprecipitates24, is able to convert the first-order MT to pseudo-high-order MT and result in purely apparent elastic deformation with low Young’s modulus and high strength. From the perspective of the Landau thermodynamic theory, such manipulation of the mechanic properties essentially derives from the flattening the average thermodynamic energy density profile of the structures, since many physical quantities of ferroic materials are associated with free-energy derivatives with respect to certain thermodynamic variables. More specifically, elastic constants of ferroelastics such as SMAs are determined by second derivatives of the Gibbs free-energy density with respect to strain25,26, i.e., the curvature of the thermodynamic energy profile. This design concept has also been widely used in ferroelectrics to optimize corresponding properties, such as ultrahigh piezoelectricity27,28 and ultrahigh energy density dielectrics29 achieved by deliberately introducing nanoscale structural heterogeneity or nanodomain.
On the other hand, the rational design of these concentration modulations or nanoscale structural heterogeneity usually requires synergistic control of various structural attributes (such as concentration gradient, distribution, and morphology, etc) and chemical features, which poses a great challenge for the conventional time-consuming experimental or computational searches by the trial-and-error process. The emerging data-driven material design approach through the combination of high-throughput (HTP) calculations and machine learning (ML) has been recognized as a powerful tool in the search for new materials or structures with tailored properties and novel functionalities30. There have been many inspirational HTP first-principles works, from which direct links between atomic-scale information and macroscopic functionalities are established. These approaches have shown many successes in the discovery of new piezoelectric and dielectric materials31, thermoelectric materials32, magnetic materials33, and so on. Nevertheless, the origin of material properties resides in not only chemical constituent itself but also mesoscale morphological and microstructure evolutions34. Mesoscale phase-field simulations in a high-throughput manner that allow for the investigation of microstructure effects are rather limited35,36,37. The development of HTP mesoscale calculations is not only indispensable for the accelerated characterization of microstructure evolutions but also a boost for data- and modeling-driven discovery of new materials and structures.
In this work, we propose an alternative concentration modulation approach, i.e., nanocomposite engineering, meanwhile developing an integrated framework of HTP phase-field simulations and ML, to achieve the extraordinary mechanical properties in the Ti-Nb SMAs. A HTP phase-field simulations procedure is designed to optimize the mechanical response of various Ti-Nb SMA nanocomposites constructed by four structural feature variables and to seek the optimal microstructure with desired properties. Guided by the ML, a nanocomposite with a perfect combination of ultralow modulus, quasi-linear elasticity, and near-zero hysteresis is screened out, which shows great potential for biomedical material applications. The developed computational approach is also applicable to the design of a wide range of advanced materials.
Results
Workflow of high-throughput phase-field simulations
We design a series of Ti-Nb square-array nanocomposite structures38 consisting of different Nb-lean nanofillers that are uniformly and coherently embedded in a Nb-rich Ti-Nb alloy matrix (Fig. 1b). In the simulations of uniaxial tension tests, the displacement of the lower-left corner and the x-direction displacement of the left side of the nanocomposite are fixed at zero to prevent the rigid body translation and rotation (see Fig. 1b). The motivation for the choice of such a nanostructure is the advancements in fabrication techniques of composites and their various associated phenomena39,40,41. The Ti-Nb nanocomposite has four structural feature variables (macroscopic degrees of freedom) related to the macroscopic mechanical properties, namely the Nb concentration (CNb) of the matrix (MNb) and nanofillers (FNb), volume fraction of nanofillers (VF), and the number of nanofillers (NF). Following the novel approach of concentration modulation and concentration gradient layer structure developed by Zhu et al.20,21,22,23, MNb and FNb are set with 15–20 at.% and 5–10 at.%, respectively, with a 1% interval, to facilitate the stress-induced MT during loading and inverse MT during unloading. To systematically study the effect of VF, a series of nanofillers with the total areas of 82 nm2, 162 nm2, 242 nm2, 322 nm2, and 402 nm2 are adopted in the simulations, which correspond to the variation of VF from 1.56% to 39.06%. Correspondingly, three groups of NF are defined: 4, 16, and 64. The detail of four structural feature variables are also summarized in Supplementary Table 1 in the Supplementary information. The computational framework for the design of the Ti-Nb nanocomposite is represented schematically in Fig. 1c. A computing script framework is developed to concurrently handle multiple calculation tasks. With a multi-core workstation, more than 10 tasks are concurrently calculated. We start by specifying the above four features (MNb, FNb, VF, and NF) with automatic nanocomposite modeling, which yields 540 candidates from a combinatorial point of view. Although the nanofillers could be randomly distributed in the matrix, we restrict the nanofillers to a square nanocomposite structure38, a typical Archimedean lattice structure, to reduce the computational complexity. We then carry out HTP phase-field simulations for the established nanocomposite models and compute their microstructure evolutions and stress-strain (SS) curves under mechanical stress along the [100] direction as shown in Fig. 1b. The quantitative analyses of the SS curves are subsequently conducted, and the main mechanical properties are extracted, including the apparent incipient Young’s modulus (EI), the apparent elastic stress limit (σL), and the hysteresis area (AH). In the present study, the apparent elastic limit is defined as the critical point of the apparent elastic stage on a stress-strain curve obtained by the “backward convex splitting method”, as schematically explained in Figure S7 in the Supplementary information, where εL and σL denote the apparent elastic strain limit and associated stress, respectively. The apparent Young’s modulus is defined by EI=σL/εL. The hysteresis area of AH measures the size of the hysteresis area encircled by the whole SS curve. Based on the data sets from HTP phase-field simulations, we employ ML strategy to perform multiobjective optimization of the mechanical properties for the nanocomposites. The recommended candidates are further verified by the phase-field simulations and the underlying mechanisms are also clarified.
Overview of high-throughput phase-field results
Based on the HTP phase-field simulations, we plot the obtained four features dependence of the mechanical properties of the nanocomposites in Fig. 2, in which VF increases from 1.56 to 39.06% on each row and NF decreases from 64 to 4 on each column. It can be seen that EI and εL of the nanocomposites are widely distributed within 10–35 GPa and 0–3%, respectively. This tunable and variable modulus indicates that engineering the chemical composition and geometry of the nanocomposite offers great flexibility to tune the mechanical properties of the materials. According to the map shown in Fig. 2a, there is a rough trend that nanocomposites with larger VF exhibit lower EI, although the Nb-lean nanofillers are assumed to have the same elastic constants as that of the matrix. It is also interesting that FNb dramatically reduces EI at a lower FNb (FNb < 8%) (see Fig. 2a) and higher VF (VF > 14.06%), while MNb and NF are negligible on EI for the whole VF range. These results suggest that coupling between nanofillers and matrix with different CNb gives rise to EI superior to their inherent ones. As displayed in Fig. 2b, σL also decreases with increasing VF, which is consistent with the conclusion of EI. In comparison, σL increases with increasing MNb, indicating that the Nb-rich matrix effectively maintains the linear elasticity of the nanocomposites. The opposite variation tendencies are observed for EI and σL with FNb and MNb, manifesting that FNb and MNb play different roles in regulating the mechanical properties of the nanocomposites. Moreover, the calculated AH of the nanocomposites spans a large range from 0 MJ m−3 to 3 MJ m−3 for different features (Fig. 2c), and thus the embedding of nanofillers greatly reduces the energy loss during the loading-unloading cycle. Although the regulated effect of NF is not as obvious as other features, it can be seen from Fig. 2a to c that NF is also of great significance in fine-tuning mechanical properties of nanocomposites. All these results indicate that the mechanical properties of nanocomposites are nonlinearly affected by all four features.
Effect of the coherent nanocomposite
The widely tunable and variable mechanical responses of the nanocomposites could be attributed to the change in the MT nucleation critical stress and the local stress fields associated with the inserted nanofillers. Figure 3a plots the Landau free-energy density curves as a function of the order parameter for the Ti-Nb alloys with different CNb at 300 K, in which the martensitic phase gradually transformed from an unstable state to a stable state with decreasing CNb. It is evident that the martensitic phase is stable in the Nb-lean cases (CNb < 8%), while in the Nb-rich cases (CNb ≥ 8%), the martensitic phase could not nucleate without the aid of external loads. The critical stress for the stress-induced martensitic nucleation versus CNb is further calculated (see Fig. 3b) and the results demonstrate that the critical stress increases exponentially with increasing CNb. For the heterogeneous nanocomposites, martensite thus preferentially nucleates in Nb-lean nanofillers and generates local stress fields associated with the CNb-dependent stress-free transformation strain (SFTS) tensors (see Fig. 3b) to promote the growth of martensite into the matrix, while the high critical stress in the Nb-rich matrix will confine the extent of growth. The critical stress for the nucleation (or growth) of martensite is the minimum stress for the nucleation (or growth) of martensite transformed from austenite in a homogeneous system. To qualitatively investigate and clarify the mechanism for the modulation of mechanical properties, we adopt a simplified 2-dimensional model with the nonperiodic condition and stress-free condition to explore the competitive relationship between the Landau energy and the elastic energy. It consists of 8 nm2 martensite particle with Nb concentration of fNb (denoted as the green square) and the adjacent 8 nm2 austenitic matrix with Nb concentration of mNb (denoted as the orange square), corresponding to the martensite volume fraction of 0.5. After relaxation, the interface between martensite and austenite moves toward the particle or matrix depending on fNb and mNb. Different combinations of fNb and mNb will generate various martensite volume fractions as shown in Fig. 3c. The heatmap of martensite volume fraction after relaxation is divided by a dashed line into the suppressed and non-suppressed region, which is highlighted in blue and red colors, respectively. These results thus indicate that FNb (fNb) and MNb (mNb) significantly mediate the Landau free-energy and SFTS, and further regulate the MT nucleation critical stress and spread of martensite in the nanocomposites.
a Landau free-energy curves with different CNb, b SFTS tensors component, and MT critical stress with different CNb, and c the ability that Nb-rich matrix inhibits the spread of martensite in fillers into matrix determined by FNb and MNb. d–r Local stress field on the [100] direction of Ti-Nb nanocomposites of different VF and different NF and s–u local stress field probability distribution with VF = 1.56, 6.28, 14.06, 25.00, and 39.06% for different NF.
Furthermore, the geometric features (i.e., NF and VF) modulate the strength and distribution of the generated stress field. We perform simplified simulations to investigate the local stress field σ11 (Fig. 3d–r) generated by the lattice mismatch between the embedded martensitic fillers (V3 with FNb = 7%) and the matrix with different NF and VF. The local stress field probability distribution is further summarized in Fig. 3s-u. We observe that an increase in VF resulted in the gradual expansion of the local stress distribution range, such that VF greater than 25% produces a second stress distribution peak around 400 MPa. In addition, the increase of VF not only increases the maximum value of the local stress field (represented by the red dashed line) but also significantly increases the probability that the local stress is greater than the critical stress of martensite spread into the matrix, as indicated by the blue dashed line in Fig. 3s–u for the median value (i.e., 600 MPa). Moreover, NF also regulates the distribution and probability density of the local stress field. Contrary to VF, a smaller NF increases the maximum value of the local stress field and the probability of σ11 ≥ 600 MPa. Hence, VF and NF effectively affect the magnitude and extent of the local stress field. The shear component σ12 also contributes to the nucleation and growth of the MT process. The high shear stress region in the nanocomposite beyond the critical shear stress is very small and highly localized, as shown in Figure S5 in the Supplementary information. Therefore, all four features regulate the nucleation and spread of the MT process by altering the MT nucleation critical stress and the local stress field distribution.
Machine learning guided optimization of the nanocomposites
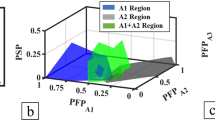
As previously discussed, reducing the Young’s modulus while maintaining a large εL is critical for the ideal orthopedic implant. Through the HTP phase-field simulations of the initial hundreds of nanocomposites, we have obtained the structures with widely tunable mechanical properties. However, an exhaustive search for the optimal one is intractable and computationally expensive. To remedy this, we apply the Artificial Neural Network (ANN) method to achieve the highly efficient multiobjective optimization of the nanocomposites. Since the AH of training samples is tiny (minimum and average values are 0 MJ m−3 and 0.51 MJ m−3, respectively) compared with other SMAs, such as TiNi (~10 MJ m−3)42, we select the other two mechanical properties (i.e., EI and σL) for the multiobjective optimization based on the Pareto front43. On the Pareto front, we use a selection strategy to find the three “best” configurations as the candidate and verify them by the phase-field simulation. Our selection strategy transforms the two-objective optimization problem into a single-objective optimization problem by calculating the normalized distance δ from a point in search space to the target (EIt = 10 GPa, σLt = 500 MPa), and the normalized Euclidean distance δ is given by
In order to avoid samples with poor performance dominating the construction of the ML model, we classify the calculated configurations from the HTP phase-field simulations by performing K-Means clustering using the mechanical properties (i.e., EI and σL) as the input variable. As illustrated in Fig. 4a, the calculated configurations are grouped into three data sets, in which Cluster 1 shows poor mechanical performance in terms of its large EI and low σL. We thus select Cluster 0 and Cluster 2 (324 samples) as training data for the construction of ANN model. As shown in Supplementary Figure 8, all four features are independent of each other and have certain correlations with the mechanical properties. Moreover, since the chemical features (i.e., FNb and MNb) are sampled linearly while the geometric features (i.e. NF and VF) are sampled squarely in the HTP phase-field simulations, we treat the geometric features by square root transformation as \(N_{{{\mathrm{F}}}}^{{{\mathrm{L}}}} = \sqrt {N_{{{\mathrm{F}}}}}\) and \(V_{{{\mathrm{F}}}}^{{{\mathrm{L}}}} = 64 \times \sqrt {V_{{{\mathrm{F}}}}}\) to eliminate the influence of the numerical differences on the prediction performance of the ML model. In order to predict new configurations with better properties, a large unexplored search space is created by increasing the resolution of four structural features: We allow FNb to vary from 5.0 to 10.0% with an interval of 0.2% and MNb to vary from 15.0 to 20.0% with an interval of 0.2%. For geometric features, we set \(N_{{{\mathrm{F}}}}^{{{\mathrm{L}}}}\) from 2 to 8 in steps of 2 and \(V_{{{\mathrm{F}}}}^{{{\mathrm{L}}}}\) from 8 to 40 in steps of 4. Overall, 42588 virtual samples (\(C_{26}^1C_{26}^1C_7^1C_9^1\)) are formed out of which only 324 are computationally studied.
a The ML training data is selected according to the K-Means algorithm. Scattering plots of cross-validation performance presented by comparing the results of the ML and the training data of b EI; c σL. d The distribution of calculated optimized configurations and training data from HTP phase-field simulations.
Figure 4b-c show the ten-fold cross-validation performance of EI and σL obtained by the ANN algorithm. As we can see, the ANN model has a great cross-validation performance for EI (R = 0.9889) and σL (R = 0.9536). According to the hyperparameters determined by the cross-validation, we use all 324 training data samples to train two new ANN models to predict the EI and σL of samples in the unexplored search space. According to our selection strategy, three new configurations with improved properties are screened out in the search space, which are selected as promising nanocomposite configurations for the next set of phase-field simulations. Their predicted and calculated mechanical properties are shown in Table 1. The predicted EI is higher than the calculated value with an average prediction error of 1.86%, while the predicted σL is higher than the calculated value with an average prediction error of 9.46%, indicating that the ML model yield accurate predictions for the unexplored nanocomposites. The calculated properties of the three recommended configurations (denoted as red pentagons) are compared with those from HTP phase-field simulations (denoted as blue dots) in Fig. 4d. Improvements can be observed for the recommended configurations and the red pentagon sample with the most obvious performance improvement is selected as the configuration of the ideal orthopedic implant. Compared with the result of HTP phase-field simulations, the normalized Euclidean distance δ is reduced from 0.231 to 0.200, decreasing by 13.4%. Thus, we could locate the configuration with the best compromise of low EI and large σL with the aid of ANN. The optimized configuration (as shown in Fig. 5b) is composed of Nb-rich TiNb matrix (MNb = 18.4%) and 25.0% volume fraction of Nb-lean TiNb square fillers (FNb = 7.2%) with NF = 16, which will be discussed in detail below. It is also worth to mention that the application of the proposed data-driven approach based on the HTP phase-field simulations is not confined to the design of the present orthopedic implant with low EI and large σL, but applies to a wide range of materials and structures with target mechanical and other functional properties.
Ideal orthopedic implant design strategy
The comparison of EI and εL of the constructed nanocomposites designed from the ML-aided simulation with those of Ti2448 (Ti-24Nb-4Zr-8Sn in wt.%)44, a typical metallic biomaterial, and other state-of-the-art systems proposed in the literature45, are shown in Fig. 5a. It is readily seen that the candidate nanocomposite for the ideal orthopedic implant exhibits an ultralow EI relative to other reported systems, which is essential for metallic biomaterials. The nanocomposite also outperforms Ti2448 in terms of the relatively large elastic strain limit and small hysteresis area. The SS curve of the designed nanocomposite during the loading-unloading cycle together with that of uniform bulk Ti2448 is shown in Fig. 5c with the red curve and gray curve, respectively. The SS curve of Ti2448 features a typical characteristic of a large stress hysteresis with an obvious stress plateau, which is consistent with the experimental observations. By contrast, the stress plateau completely disappears in the SS curve of an ideal orthopedic implant, and exhibits a quasi-linear elasticity and almost hysteresis-free mechanical behavior. As shown in Fig. 5a, compared with the state-of-the-art functional material16, such as Ti2448 (Ti-24Nb-4Zr-8Sn in wt.%), NICSMA (nanowire in situ composite with SMA), Gum metals et al., the nanocomposite designed by HTP calculations and ML are superior in mechanical properties in terms of their linear super-elasticity, ultralow Young’s modulus, large apparent elastic stress limits, and near-hysteresis-free. These properties in the nanocomposites designed by ML-assisted HTP calculations are comparable with the recently reported phase-field simulation results via concentration modulation and concentration gradient film designs20,21,22,23.
a Comparison of the modulus and elastic strain limit between prediction from this study with those reported in the literature. b The configuration of the ideal orthopedic implant obtained from the ML-guided HTP phase-field simulations. c SS curves of ideal orthopedic implant (red curve) and Ti2448 (gray curve). d Microstructure evolution during MT in ideal orthopedic implant during loading e-h, and unloading i-k process.
To gain a thorough understanding of the exceptional mechanical properties, the microstructure evolutions corresponding to the marked points of the loading-unloading SS curve are analyzed, and the results are displayed in Fig. 5d. As shown Fig. 5e, abundant martensitic particles are observed in the nanofillers, while the matrix still presents an austenite phase when the nanocomposite is quenched to 300 K in a stress-free configuration. These observations are because the martensitic phase is more stable in the Nb-lean fillers (FNb = 7.2%), as illustrated in Fig. 3a. The emerged temperature-induced martensitic particles are composed of multivariants in self-accommodating domain patterns. These martensitic particles behave as seeding beds of martensite, eliminating the nucleation barriers for MT. Upon loading, the stress-induced martensite re-orientation occurs, and the favored variants (such that V2, V3, and V4) dominate and gradually fill the fillers. These martensitic variants gradually and continuously grow into the matrix, which is significantly different from the common avalanche-like discontinuous MT. With increasing stress (Fig. 5g and h), the existing martensitic variants continue to expand in the matrix, which is also accompanied by the formation and merging of new martensitic configurations in the matrix. At the end of the loading (600 MPa), the martensitic domains spread almost over the entire area of the nanocomposite with a volume fraction of 94.4%, as illustrated in Fig. 5i, in which the remaining parent phase mainly originates from the martensitic variant interfaces. In the process of unloading, these remaining parent phases initiate the inverse martensite to austenitic transition in the matrix, and the austenite gradually spread from the matrix towards the interfaces of the nanocomposite (Fig. 5j). The martensite completely disappears in the matrix when the applied stress is reduced to 75 MPa (Fig. 5k). In addition, the Nb-lean fillers also transform back to the initial self-accommodating multivariants martensite configurations after unloading, which contributes to the zero-residual strain in a loading-unloading cycle. Therefore, the nanocomposite experiences macroscopically continuous MT throughout the loading and unloading procedure rather than a sharp first-order transition as that in typical SMAs, which thus exhibits linear super-elasticity and ultralow EI (Fig. 5d). The continuous characteristics of the forward and backward MTs originate from the embedded nanofillers with local heterogeneity that induce nonuniform local stress field associated with the geometrical structure and the variation of MT critical stress due to the change of CNb as discussed above. For a given nanocomposite, nonuniform stress field appears under a certain applied load, as shown in Supplementary Figure 6. The variation in local stresses tailors the total free-energy landscape with multiple local minima and facilitates the pseudo-high-order MT in the nanocomposite.
These results thus suggest a new route for achieving desirable mechanical properties to meet the requirement of different applications by nanocomposite engineering. In particular, the designed Ti-Nb nanocomposite realizes a perfect combination of ultralow modulus, linear super-elasticity, and near-hysteresis-free, which cannot be obtained in common materials and will enable many new advanced applications. For instance, the achieved ultralow EI in the current Ti-Nb-based alloys without compromising their good biocompatibility and superior corrosion resistance is of particular importance for biomedical applications. The mismatch in the Young’s modulus between the common implant materials (~110 GPa) and human bone usually causes stress shielding, leading to bone degradation and implant loosening originated from inhomogeneous stress distribution between the implant and the adjacent bone. The elastic modulus of 16.13 GPa in the designed nanocomposite match closely to that of human bones and thus is promising in overcoming this stress-shielding issue completely. To verify the functional stability of the designed nanocomposite, the repeated loading-unloading cycles are performed for the ideal orthopedic implant. The second SS curve and the corresponding evolution of microstructures are illustrated in Supplementary Figure 1 in the Supplementary information, which coincide with those in the first one, indicating the mechanical stability of the designed ideal orthopedic implant. In addition, we perform calculations of nanocomposites with organized (triangular and honeycomb-array) and random arrays of nanofillers. Supplementary Figure 2 in the Supplementary information shows the simulation results, viz., the SS curves, corresponding microstructures and their evolutions. The SS curves indicate that the mechanical behavior of the nanocomposite is also insensitive to the nanofiller distribution profile. Moreover, we investigate the effect of different shapes of nanofillers on the mechanical properties of the designed nanocomposite. As shown in Supplementary Figure 3 in the Supplementary information, the SS curves of the nanocomposites with square, hexagonal, and spherical nanofillers are almost coincide, indicating that the mechanical properties of the nanocomposite are insensitive to the shape of nanofillers. Last but not least, we also verify that the results remain almost unchanged within the loading rate range of 20 MPa s−1 – 500 MPa s−1, as shown in Supplementary Figure 4 in the Supplementary information. Experimental preparation of the proposed fine nanocomposite is a great challenge currently; yet, recent fabrications of size and composition-controlled nanocomposites using colloidal synthesis method, replacement reaction, and accumulative roll bonding (ARB) suggest the promising strategies to pursue40,46,47. The combination of HTP phase-field simulations and the ML approach thus provides an efficient paradigm for designing target properties of shape memory alloys, which will also be beneficial to a wide range of functional materials.
Discussion
In conclusion, we have developed a HTP phase-field simulations to accelerate the design of microstructures with desired mechanical properties. HTP phase-field simulations are performed for various Ti-Nb nanocomposites designed by four structural feature variables and it is found that the mechanical responses of the nanocomposites are widely tunable and variable. Based on the combination of HTP phase-field simulations and ML techniques, we design a Ti-Nb alloy nanocomposite with ultralow modulus, linear super-elasticity, and nearly free hysteresis, which is promising for biomaterial applications. These superior mechanical properties attribute to the nonuniform stress distribution and the modulation of the critical stress that facilitates continuous MT. The present approach developed by the combination of phase-field simulations and ML is thus an important extension to the previous method of concentration modulations to regulate the MTs, jointly to provide theoretical guidance for the experiments.
Methods
Phase-field model
The Ti-Nb-based alloys undergo diffusionless and reversible MT between the cubic β-austenite (point group \(m\bar 3m\)) and orthorhombic α”-martensite (point group mmm) phases48 during the thermomechanical loading, as shown in Fig. 1a. This cubic-to-orthorhombic MT is associated with six variants49,50. Since ML demands a large amount of simulation results, two-dimensional phase-field simulations within the plane stress condition are conducted in the present work to illustrate the developed methodology of phase-field simulations integrated with ML. As a result, there are four possible variants (V1–V4) corresponded to four different SFTS tensors after dropping the out-of-plane strain. All the SFTSs can be found in the Supplementary information. In the phase-field model, a continuous structure order parameter ηi (i = 1 − 4) is employed to characterize the MT, with ηi = 0 and ηi = ±1 representing austenitic and i-th martensitic variant, respectively. The total free-energy of the system F consists of the Landau free-energy fch, the gradient energy fgr, and the elastic energy fel: 51
The microstructure evolution of the MT is governed by the time-dependent Ginzburg-Landau (TDGL) equation:52
where L is the kinetic parameter, and ζi (r,t) is the Stochastic-Langevin noise term accounting for the effect of thermal fluctuations53. All the phase-field simulation parameters employed in the present work are from Ref. 20 and listed in Supplementary Table 2 in the Supplementary information.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The codes that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Lexcellent, C. Shape-memory Alloys Handbook, (John Wiley & Sons, Inc, Hoboken, NJ, USA, 2013).
Huang, W. M. et al. Shape memory materials. Mater. Today 13, 54–61 (2010).
Jani, M. J., Leary, M., Subic, A. & Gibson, M. A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 56, 1078–1113 (2014).
Lagoudas, D. C. Shape Memory Alloys: Modeling and Engineering Applications (Springer, 2008).
Yonemaya, T., Miyazaki, S. Shape Memory Alloys for Biomedical Applications, (Woodhead Publishing, Cambridge, 2009).
Kim, H. Y., Ikehara, Y., Kim, J. I., Hosoda, H. & Miyazaki, S. Martensitic transformation, shape memory effect and superelasticity of Ti-Nb binary alloys. Acta Mater. 54, 2419–2429 (2006).
Xie, X., Kang, G. Z., Kan, Q. H., Yu, C. & Peng, Q. Phase field modeling for cyclic phase transition of NiTi shape memory alloy single crystal with super-elasticity. Comp. Mater. Sci. 143, 212–224 (2018).
Christian, J. W. The Theory of Transformations in Metals and Alloys, (Elsevier, Oxford, UK, 2002).
Villoslada, A., Flores, A., Copaci, D., Blanco, D. & Moreno, L. High-displacement flexible Shape Memory Alloy actuator for soft wearable robots. Robot. Auton. Syst. 73, 91–101 (2015).
Turner, C. H., Rho, J., Takano, Y., Tsui, T. Y. & Pharr, G. M. The elastic properties of trabecular and cortical bone tissues are similar: results from two microscopic measurement techniques. J. Biomech. 32, 437–441 (1999).
Kennady, M. C., Tucker, M. R., Lester, G. E. & Buckley, M. J. Stress shielding effect of rigid internal fixation plates on mandibular bone grafts. a photon absorption densitometry and quantitative computerized tomographic evaluation. Int. J. Oral. Max. Surg. 18, 307–310 (1989).
Wang, Q. Z., Lin, Y. G., Zhou, F. & Kong, J. Z. The influence of Ni concentration on the structure, mechanical and tribological properties of Ni–CrSiN coatings in seawater. J. Alloy. Compd. 819, 152998 (2020).
Besse, M., Castany, P. & Gloriant, T. Mechanisms of deformation in gum metal TNTZ-O and TNTZ titanium alloys: A comparative study on the oxygen influence. Acta Mater. 59, 5982–5988 (2011).
Rajasekaran, G., Narayanan, P. & Parashar, A. Effect of Point and Line Defects on Mechanical and Thermal Properties of Graphene: A Review. Crit. Rev. Solid. State 41, 47–71 (2016).
Wang, D., Wang, Y. Z., Zhang, Z. & Ren, X. B. Modeling Abnormal Strain States in Ferroelastic Systems: The Role of Point Defects. Phys. Rev. Lett. 105, 205702 (2010).
Hao, S. J. et al. A Transforming Metal Nanocomposite with Large Elastic Strain, Low Modulus, and High Strength. Science 339, 1191 (2013).
Hamilton, R. F., Sehitoglu, H., Efstathiou, C. & Maier, H. J. Mechanical response of NiFeGa alloys containing second-phase particles. Scr. Mater. 57, 497–499 (2007).
Nasiri, Z., Ghaemifar, S., Naghizadeh, M. & Mirzadeh, H. Thermal mechanisms of grain refinement in steels: a review. Met. Mater. Int. 27, 2078–2094 (2021).
Murty, B. S., Kori, S. A. & Chakraborty, M. Grain refinement of aluminium and its alloys by heterogeneous nucleation and alloying. Int. Mater. Rev. 47, 3–29 (2002).
Zhu, J. M., Gao, Y. P., Wang, D., Zhang, T. Y. & Wang, Y. Z. Timing martensitic transformation via concentration modulation at nanoscale. Acta Mater. 130, 196–207 (2017).
Zhu, J. M. et al. Making metals linear super-elastic with ultralow modulus and nearly zero hysteresis. Mater. Horiz. 6, 515–523 (2019).
Zhu, J. M. et al. Dissecting the influence of nanoscale concentration modulation on martensitic transformation in multifunctional alloys. Acta Mater. 181, 99–109 (2019).
Zhu, J. M., Wang, D., Gao, Y. P., Zhang, T. Y. & Wang, Y. Z. Linear-superelastic metals by controlled strain release via nanoscale concentration-gradient engineering. Mater. Today 33, 17–23 (2020).
Zhu, J. M. et al. Influence of Ni4Ti3 precipitation on martensitic transformations in NiTi shape memory alloy: R phase transformation. Acta Mater. 207, 116665 (2021).
Mamivand, M., Zaeem, M. A. & Kadiri, H. E. A review on phase field modeling of martensitic phase transformation. Comp. Mater. Sci. 77, 304–311 (2013).
Levitas, V. I. & Preston, D. L. Three-dimensional Landau theory for multivariant stress-induced martensitic phase transformation. I. Austenite ↔ Martensite. Phys. Rev. B. 66, 134206 (2002).
Fu, H. X. & Cohen, R. E. Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature 403, 281–283 (2000).
Li, F. et al. Ultrahigh piezoelectricity in ferroelectric ceramics by design. Nat. Mater. 17, 349–354 (2018).
Park, S. E. & Shrout, T. R. Ultrahigh strain and piezoelectric behavior in relaxor based ferroelectric single crystals. J. Appl. Phys. 82, 1804 (1997).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Choudhary, K. et al. High-throughput density functional perturbation theory and machine learning predictions of infrared, piezoelectric, and dielectric responses. npj Comput. Mater. 6, 64 (2020).
Li, R. X. et al. High-Throughput Screening for Advanced Thermoelectric Materials: Diamond-Like ABX2 Compounds. ACS Appl. Mater. Inter 11, 24859–24886 (2019).
Choudhary, K., Garrity, K. F., Jiang, J., Pachter, R. & Tavazza, F. Computational search for magnetic and non-magnetic 2D topological materials using unified spin-orbit spillage screening. npj Comput. Mater. 6, 49 (2020).
Lich, L. V. et al. Colossal magnetoelectric effect in 3-1 multiferroic nanocomposites originating from ultrafine nanodomain structures. Appl. Phys. Lett. 107, 232904 (2015).
Shen, Z. H. et al. High-Throughput Phase-Field Design of High-Energy-Density Polymer Nanocomposites. Adv. Mater. 30, 1704380 (2018).
Shen, Z. H. et al. High-throughput data-driven interface design of high-energy-density polymer nanocomposites. J. Materiomics 6, 573–581 (2020).
Zhang, K. N. et al. High-throughput phase-field simulations and machine learning of resistive switching in resistive random-access memory. npj Comput. Mater. 6, 198 (2020).
Shimada, T., Lich, L., Nagano, K., Wang, J. & Kitamura, T. Hierarchical ferroelectric and ferrotoroidic polarizations coexistent in nano-metamaterials. Sci. Rep.-UK 5, 14653 (2015).
Guo, S. et al. Deformation behavior of a novel sandwich-like TiNb/NiTi composite with good biocompatibility and superelasticity. Mat. Sci. Eng. A-Struct. 794, 139784 (2020).
Jiang, D. Q. et al. High performance Nb/TiNi nanocomposites produced by packaged accumulative roll bonding. Compos. Part. B-Eng. 202, 108403 (2020).
Zhang, X. D. et al. Origin of high strength, low modulus superelasticity in nanowire-shape memory alloy composites. Sci. Rep.-UK 7, 46360 (2017).
Wang, D. et al. Phase field simulation of martensitic transformation in pre-strained nanocomposite shape memory alloys. Acta Mater. 164, 99–109 (2019).
You, J. Y., Ampomah, W. & Sun, Q. Development and application of a machine learning based multi-objective optimization workflow for CO2-EOR projects. Fuel 264, 116758 (2020).
Zhang, Y. W. et al. Elastic properties of Ti-24Nb-4Zr-8Sn single crystals with bcc crystal structure. Acta Mater. 59, 3081–3090 (2011).
Zhou, M. Exceptional Properties by Design. Science 339, 1161–1162 (2013).
Clarysse, J., Moser, A., Yarema, O., Wood, V. & Yarema, M. Size- and composition-controlled intermetallic nanocrystals via amalgamation seeded growth. Sci. Adv. 7, 1934 (2021).
Zhang, Q. B., Lee, J. Y., Yang, J., Boothroyd, C. & Zhang, J. X. Size and composition tunable Ag-Au alloy nanoparticles by replacement reactions. Nanotechnology 18, 245605 (2007).
Liu, J. P. et al. New intrinsic mechanism on gum-like superelasticity of multifunctional alloys. Sci. Rep.-UK 3, 2156 (2013).
Gao, Y. P., Shi, R. P., Nie, J. F., Dregia, S. A. & Wang, Y. Z. Group theory description of transformation pathway degeneracy in structural phase transformations. Acta Mater. 109, 353–363 (2016).
Zheng, Y. F. et al. The effect of alloy composition on instabilities in the β phase of titanium alloys. Scr. Mater. 116, 49–52 (2016).
Chen, L. Q. Phase-Field Models for Microstructure Evolution. Annu. Rev. Mater. Res. 32, 113–140 (2002).
Cahn, J. W. & Allen, S. M. A Microscopic Theory for Domain Wall Motion and Its Experimental Verification in Fe-Al Alloy Domain Growth Kinetics. J. Phys. Colloq. 38, 51–54 (1977).
Wang, Y. & Khachaturyan, A. G. Three-Dimensional Field Model and Computer Modeling of Martensitic Transformations. Acta Mater. 45, 759–773 (1997).
Acknowledgements
The work is supported by the National Key R&D Program of China (No. 2018YFB0704404) and the National Natural Science Foundation of China (Grant Nos. 11802169 and 12172370).
Author information
Authors and Affiliations
Contributions
Y.Q.Z. and T.X. equally contributed to this work. T.Y.Z. and T.X. supervised and conceived the project. T.X. designed the simulation model. Y.Q.Z. conducted the simulations with J.W.M. and the machine learning with Q.H.W., H.X.Y., H.R.Z., T.S., and T.K. discussed the results. Y.Q.Z., T.X., and T.Y.Z. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhu, Y., Xu, T., Wei, Q. et al. Linear-superelastic Ti-Nb nanocomposite alloys with ultralow modulus via high-throughput phase-field design and machine learning. npj Comput Mater 7, 205 (2021). https://doi.org/10.1038/s41524-021-00674-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00674-7
This article is cited by
-
Unravelling Role of the Microwave Sintering Effects on Microstructure, Density, and Corrosion Behaviour of Porous Ti-13.3at.% Nb Shape Memory Alloys
Metallography, Microstructure, and Analysis (2024)
-
Understanding and design of metallic alloys guided by phase-field simulations
npj Computational Materials (2023)
-
Recent Computational Approaches for Accelerating Dendrite Growth Prediction: A Short Review
Multiscale Science and Engineering (2023)
-
Application of phase-field modeling in solid-state phase transformation of steels
Journal of Iron and Steel Research International (2022)