Introduction

Ferroelectric materials with spontaneous electric dipole moments switchable by an external electric field offer a broad range of technological applications, such as non-volatile memories, field-effect transistors, and active elements in electromechanical and electro-optical devices1,2. The ability to switch electric polarization is a key ingredient in modern nanotechnology, where the need for further reduction of individually polarized domains towards the atomic scale, as well as for the ease of their switchability has been constantly growing.

Thinning down ferroelectrics is one promising direction to miniaturize electronic devices, and several ferroelectric materials have been found to maintain macroscopic polarization in ultrathin films3,4,5,6,7. Furthermore, the development of van der Waals assembly has enabled heterostructure engineering8,9; where physical properties are tuned to the desired functionality by combining different individual layers, which can be used to design two-dimensional ferroelectrics from non-ferroelectric parent compounds.10,11 Other venues to overcome the challenges can be found in van der Waals layered materials that possess properties favourable for tailoring ferroelectricity, such as durability against strain and surface functionalization.12 Robust polarization in these systems was shown to sustain down to atomic thicknesses and can provide improved building blocks for functional heterostructures.13,14,15,16

Following the immense growth of activity in two-dimensional systems, layered transition metal dichalcogenides (TMDs) have recently drawn great attention due to their diverse physical properties, ranging from extremely large magnetoresistance17 and superconductivity18 to the topological electronic states.19,20 Recent studies have demonstrated that the out-of-plane switchable polarization originating from interlayer sliding exists in polar Weyl semimetals MoTe2 and WTe2.21,22 Although the value of spontaneous polarization is small and can be partially screened by metallic states, its rigidity upon interlayer sliding and importance for potential applications as a ferroelectric memory have prompted the urge to search for vertical ferroelectrics. Despite rising research activity in this field dubbed slidetronics, only a few materials have been discovered so far, such as MoTe2, WTe2, CuInP2S6,23 In2Se3,24,25, and VS2.26 Exploration of layered ferroelectrics elucidating the microscopic origin of electric polarization and their intrinsic properties, such as domain walls, are in high demand for further development of slidetronics.

In this work, we report on the first-principles evidence of robust vertical ferroelectricity in layered ZrI2, a semiconducting counterpart of isostructural semimetal TMDs MoTe2 and WTe2. Being several orders of magnitude smaller than in conventional ferroelectrics, the out-of-plane polarization in ZrI2 is found to be rigid upon interlayer sliding, and the low energy barrier for its ferroelectric switching combined with a small bandgap can hold out the prospect for slidetronics applications. Our theoretical study reveals that the ferroelectric activity in ZrI2 stems from a subtle interplay of charge redistribution and ionic displacements, providing important insights on the origin of vertical ferroelectricity in layered materials and justifying its persistence in the ultrathin limit. We investigate the complexity of domain boundaries in multidomain structures of ZrI2 that arise due to the breaking of stacking sequences. Our results demonstrate the formation of stable charged domain walls with a quasi-two-dimensional electron gas and a high built-in electric field that can be put to good use in multifunctional devices.

Results

Ferroelectric activity in ZrI2

Historically, there have been identified three polymorph forms of ZrI2 studied by Guthrie and Corbett: α (P21/m)27, β (Pmn21)28, and γ (\(R\bar{3}\))29 phases. The γ-phase is comprised of the antiprism clusters formed by six Zr atoms which are surrounded by twelve iodine atoms, whereas the α- and β-phases have layered structures and are reported to be isostructural, respectively, to the 1T\(^{\prime}\) and Td phases of MoTe2 and WTe2. The latter phases consist of the buckled I–Zr–I trilayers coupled by weak van der Waals interactions, where the Zr atoms form the zigzag chains in each layer, as shown in Fig.1a. Among the three polymorphs, only the β-phase has a polar structure and can be expected to reveal ferroelectric properties.

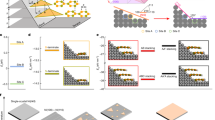
Fig. 1: Relation of the T0, Td and 1T\(^{\prime}\)phases of ZrI2.
figure 1

a Crystal structures: 1T\(^{\prime}\), designed T0, and Td phases. Side and top views presented to the right show the interlayer zigzag I–I bonds (black dotted lines) and the intralayer zigzag Zr–Zr chains (blue solid lines). Trilayers with the clockwise and counterclockwise rotated ZrI6 octahedra are denoted as M (Minus) and P (Plus), respectively. The ± signs stand for positive and negative displacements of the interlayer zigzag I–I bonds (with respect to the lower trilayer). The \({{{\Gamma }}}_{2}^{-}\) and \({{{\Gamma }}}_{4}^{+}\) modes relate the Pnma structure to the Pmn21 (Td) and P21/m (1T\(^{\prime}\)) phases, respectively. b Band structure of the designed T0 phase and partial charge densities. The Zr d and I p states are highlighted with blue and pink colours, respectively. c Energy profile obtained from the devised T0 phase as a function of interlayer displacement and the monoclinic a–c angle. d Enlarged phonon spectrum of the T0 phase of ZrI2.

Full size image

Similar to its sister compounds MoTe2 and WTe2, the α- and β-phases of ZrI2 (hereafter referred to as 1T\(^{\prime}\) and Td, respectively) can be derived from the devised parent T0 phase with the Pnma structure by distorting the orthorhombic a − c angle or by sliding adjacent trilayers, respectively (Fig. 1a). All three phases are found to be semiconducting with an indirect energy bandgap Eg ~0.20 eV (see Supplementary Fig. 1). As shown in Fig. 1b, the states near the Fermi level correspond to the Zr d states that form strong metal-metal bonding along the zigzag chains, and the bands below represent the I p states. In contrast to semimetals MoTe2 and WTe2 which demonstrate a sizeable mixing of the anionic p and metal d states at the Fermi level that alongside with spin-orbit coupling stabilizes the Weyl points,19 the I p states in ZrI2 are pushed way below the Fermi level due to much longer intralayer I–I bonds, without affecting a small gap opened in the Zr d states.

In Fig. 1c, we computed the energy landscape as a function of the monoclinic distortion and interlayer sliding starting from the devised T0 structure and fixing the unit cell volume and atomic arrangement in each trilayer. For both types of displacement, a double-well structure is clearly seen in the calculated energy profile, where the center with higher energy corresponds to the parent T0 phase. By this means, interlayer sliding leads to two local minima at Δ ~ ± 0.71 Å representing two polar Td structures, whereas rotating the monoclinic a–c angle stabilizes two ferroelastic 1T\(^{\prime}\)-I and 1T\(^{\prime}\)-II phases at 84.5∘ and 95.5∘, respectively. The corresponding energy barrier connecting the twin structures via direct pathways through the T0 phase is ~ 5.3 meV/u.c for both the Td and 1T\(^{\prime}\) phases, and the energy difference between the 1T\(^{\prime}\) and Td phases is found to be small, less than 0.05 meV/u.c. (\({E}_{{T}_{{{{\rm{d}}}}}}-{E}_{1T^{\prime} }=-0.17\)meV/u.c. for the fully optimized structures).

The calculated phonon spectra of the T0 phase presented in Fig. 1d clearly indicate two types of lattice instabilities: an optical zone-centered mode \({{{\Gamma }}}_{2}^{-}\) and a linear phonon mode \({{{\Gamma }}}_{4}^{+}\) along the Γ-X direction carrying an elastic instability. From group-theoretical analysis (see Supplementary Table 3), it follows that the two modes with irreducible representations \({{{\Gamma }}}_{2}^{-}\) and \({{{\Gamma }}}_{4}^{+}\) transform the Pnma phase to the Pmn21 and P21/m structures, respectively. Indeed, the atomic displacement corresponding to the \({{{\Gamma }}}_{2}^{-}\) instability includes an in-plane sliding displacement of the alternating trilayers, while the \({{{\Gamma }}}_{4}^{+}\) mode amounts to a shear distortion of the unit cell, resulting in a ferroelastic structure.

The T0, 1T\(^{\prime}\) and Td phases can be characterized by the way the trilayer sequences are stacked in a layered structure. In the T0 phase with the D2h symmetry, the I–Zr–I trilayers are invariant under the mirror reflection with respect to the b axis accompanied by a half-lattice vector translation, \(\{{M}_{b}| \frac{{{{\boldsymbol{b}}}}}{2}\}\), and the adjacent trilayers can be transformed by \(\{{M}_{a}| \frac{{{{\boldsymbol{a}}}}}{2}+\frac{{{{\boldsymbol{b}}}}}{2}\}\) or \(\{{M}_{c}| \frac{{{{\boldsymbol{a}}}}}{2}\}\). Consequently, the trilayers are stacked with two alternating orientations where the ZrI6 octahedra twist either clockwise or counterclockwise, denoted by taking notations of Ref. 21 as M (Minus) and P (Plus), respectively. In the Td phase, the interlayer sliding along the a axis breaks inversion symmetry reducing the point symmetry to C2v, so that the adjacent trilayers are invariant under \(\{{M}_{b}| \frac{{{{\boldsymbol{b}}}}}{2}\}\) and can be connected by \(\{{M}_{a}| {{\Delta }}+\frac{{{{\boldsymbol{a}}}}}{2}+\frac{{{{\boldsymbol{b}}}}}{2}\}\). On the other hand, the monoclinic distortion along the a axis in the 1T\(^{\prime}\) phase preserves inversion symmetry but lowers the symmetry to C2h with the mirror plane along the b axis. The twin structures in both phases driven by the \({{{\Gamma }}}_{2}^{-}\) and \({{{\Gamma }}}_{4}^{+}\) modes can be further classified by the way the I ions in adjacent trilayers move relative to each other: in a positive (+) or negative (−) direction, if seen with respect to the lower layer, as shown in Fig. 1a. Then, if going up from the bottom trilayer, the patterns M+ P+ and M− P− will correspond to the ferroelastic 1T\(^{\prime}\)-I and 1T\(^{\prime}\)-II structures, while the patterns M − P+ and M+ P− will stand for the polar Td↑ and Td↓ phases, respectively. With that said, the 1T\(^{\prime}\) phase has only one type of interlayer displacement, whereas the Td phase contains both ± types that break inversion symmetry.

To investigate the ferroelectric activity of the Td phase, we considered the devised T0 phase modulated along the \({{{\Gamma }}}_{2}^{-}\) mode while keeping fixed the unit cell volume and atomic arrangement in each trilayer. Electric polarization calculated from the Berry phase theory as a function of interlayer sliding is presented in Fig. 2 and shows that a net dipole moment appears strictly along the vertical axis and changes its direction when going between positive and negative sliding displacements. Since interlayer sliding amounts to rigid ionic translations, electric polarization is purely of electronic origin. The absolute value of Pel corresponding to the energy minimum of the constrained Td structure is 0.22 μC cm−2 (0.24 μC cm−2 for the fully optimized Td phase). Despite being a few orders of magnitude smaller compared to conventional ferroelectrics, electric polarization in ZrI2 is caused solely by interlayer sliding and is switchable without vertical ionic displacements. Importantly, the switching barrier between two ferroelectric Td structures of ZrI2 is much lower than in conventional ferroelectrics (34 meV/atom for BaTiO3 and 67 meV/atom for PbTiO3).30

Fig. 2: Ferroelectric polarization in the Td phase of ZrI2.
figure 2

a Td↑ and Td↓ structures obtained from the devised T0 phase by interlayer sliding. The M trilayers are denoted with blue rectangles, and the P trilayers with positive and negative sliding displacements are highlighted with orange and yellow rectangles, respectively. b Double-well energy profile and electric polarization along the c axis calculated from the Berry phase theory as a function of interlayer sliding in the devised T0 phase.

Full size image

Given the rigidity of a single trilayer, intralayer antiferroelectric structures are found to be highly unstable relaxing to the non-polar T0 phase and confirming the robustness of ferroelectric properties in the Td phase. From molecular dynamics simulations, the lower bound for the Curie temperature of the Td phase can be estimated as ~ 400 K.

It is worth noting that interlayer sliding alone is not sufficient to explain the appearance of the net dipole moment in the Td phase. Several previous studies attributed the ferroelectric activity in WTe2 to the vertical charge transfer between adjacent trilayers that occurs upon interlayer sliding.31,32 While the Berry phase analysis presented above shows that the ferroelectric activity in ZrI2 is purely of electronic origin, the calculated change in the charge density demonstrates that the P and M trilayers are rigid in the sense that a sheer ionic displacement is accompanied by the same intralayer shift of the electronic charges, and the corresponding change in the interlayer charge density, representing interlayer bonding, indicates that interlayer sliding results solely in the charge density redistribution between the trilayers (see Supplementary Fig. 2).

The microscopic origin of the uncompensated dipole moment in the Td phase of ZrI2 can be elaborated by examining displacements of the electronic charges driven by interlayer sliding. The electronic contribution to the net dipole moment can be expressed as a sum of the centers of the Wannier functions, rn, as del = − 2e∑nrn (e is a positive electron charge). As shown in Fig. 3a, the Wannier functions of the I p states are well localized in the vicinity of the I ions, whereas the Wannier functions corresponding to the Zr d states are not centered at the Zr sites and are, instead, located at the Zr triangles, reflecting strong metallic bonding in the zigzag chains. Due to the hybridization effects, the Wannier functions move off the atomic sites, and their vertical displacements can be described by the shift of the Wannier centers relative to their symmetry specified positions, δd and δI, as depicted in Fig. 3b. As a result of the intralayer hybridization, the p-orbital Wannier functions at the top and bottom I sites tend to shift inwards the trilayer, which is accompanied by the shift of the d orbital Wannier functions at the corresponding Zr triangles. The intralayer hybridization is strong and determines an overall displacement of electronic charge centers. However, the charge density distribution is also affected by interlayer bonding, in particular by steric I–I interactions. In the centrosymmetric phase, the top and bottom I1 and I2 sites are equivalent in each trilayer resulting in symmetric shifts of the Wannier centers, so that all corresponding δ’s are equal giving zero del. The calculated charge centers shifts for the centrosymmetric T0 phase are δd = 0.0712 Å, δI1 = 0.1660 Å, and δI2 = 0.2197 Å (for δI is an average over three p orbitals). When sliding adjacent trilayers, inversion symmetry is broken, and the top and bottom I sites in each trilayer become non-equivalent. Notably, interlayer sliding modifies steric bonding in the interlayer zigzag I–I chains leading to the alternating shorter and longer I–I bonds that change depending on the sliding direction (Fig. 3b). These bonds reverse their order between adjacent trilayers, so that the top and bottom I ions in each trilayer experience an asymmetric bonding environment giving rise to non-equivalent shifts of their charge centers. The shorter the bond length, the more the electronic charge density is pulled outwards the trilayer reducing its vertical shift. Since interlayer bonding is weak, the resulting shifts and the net dipole moment are small. The calculated shifts in the Td↑ phase are δd1 = − 0.0756 Å, δd2 = 0.0687 Å, δI1 = 0.1661 Å, δI2 = 0.2176 Å, δI3 = −0.2201 Å, δI4 = − 0.1662 Å, and the net dipole moment is 0.0585 e Å, in perfect agreement with the value of 0.0579 e Å (0.243 μC cm−2) obtained from the Berry phase theory. It should be noted that in the 1T\(^{\prime}\) phase, the interlayer zigzag I–I chains also alternate between the trilayers, but the corresponding top and bottom I ions are always connected by the same type of the I–I bonds and have symmetric shifts of their charge centers (see Supplementary Fig. 3).

Fig. 3: Schematics of electronic charge displacements in ZrI2.
figure 3

a Wannier functions (top and side views) constructed for the occupied I p (left) and Zr d (middle and right) states. The Wannier functions are presented for one trilayer, and only one p Wannier function at each I site is shown for clarity. Centers of the d orbital Wannier functions are denoted with red circles. b Electronic charge displacements in the centrosymmetric and non-centrosymmetric phases due to interlayer sliding. Vertical shifts of the Wannier centers off their specified atomic positions are schematically shown with arrows. Centers of the d orbital Wannier functions are denoted with green circles. The alternating longer dL and shorter dS zigzag I–I bonds are shown with blue and pink colours, respectively. The inversion center is marked with the black cross.

Full size image

The hybridization also causes the in-plane shifts of the charge centers within a trilayer. Since the interlayer zigzag I–I chains alternate periodically in the bulk structure, the in-plane shifts will sum up to zero. Nevertheless, in the case of only two trilayers, such cancellation will not be perfect giving rise to the in-plane electric polarization (see Supplementary Fig. 9).33

Domain walls

When cooled down below the transition temperature, ferroelectric materials tend to form complex multidomain structures with different orientations of macroscopic polarization, and nanometric-scale domain walls (DW) develop at the domain boundaries. Structural and functional properties of DWs, such as width and energy barrier across the DW, substantially impact the polarization switching process and the DW mobility.34

As follows from the results of first-principles calculations, the energy difference between the Td and 1T\(^{\prime}\) phases of ZrI2 is small, and both forms can coexist in a sample producing different types of DW structures. Following the symmetry analysis reported in Ref. 21, a stacking sequence \({({{{{\rm{T}}}}}_{{{{\rm{d}}}}})}_{n}/{(1{{{\rm{T}}}}^{\prime} )}_{m}\) has the Pm space symmetry (C1h point group) that can be derived from both the P21/m and Pmn21 space groups by taking the corresponding \({{{\Gamma }}}_{2}^{-}\) and Γ3 modes, respectively, which represent the breaking of the ± patterns. Owing to the rigidity of a single trilayer, there exist several possible ways of vertical stacking at the boundaries, which adopt the patterns of the Td and 1T\(^{\prime}\) stacking sequences. For example, when two ferroelectric Td↑ and Td↓ domains are stacked along the c axis (. . . M− P+/M+ P− . . . ), the 1T\(^{\prime}\)-I pattern will be formed at the boundary. Or, similarly, for a 1T\(^{\prime}\)-I/1T\(^{\prime}\)-II stacking (. . . M+ P+/M− P− . . . ) the DW will have the Td↑ pattern. Because the Pm space group is polar, there are two possibilities for vertical DWs in ZrI2: a (polar) DW with the Td pattern at the 1T\(^{\prime}\)/1T\(^{\prime}\) stacking will exhibit ferroelectric properties due to the local inversion symmetry breaking at the boundary, whereas the Td/Td and Td/1T\(^{\prime}\) arrangements will form a (non-polar) charged DW with the 1T\(^{\prime}\) pattern arising from polarization discontinuity.

When a normal component of electric polarization changes across the domain boundary as in the latter case of the Td/Td and Td/1T\(^{\prime}\) arrangements, the interface will accommodate a high density of bound charges that give rise to large depolarizing fields suppressing ferroelectricity. If these charges are compensated by free carriers or electron-hole transfer across the gap, a stable charged DW can form as a movable ultrathin conductive layer. Taking a nominal value of Pel in the Td phase of ZrI2 and assuming a DW width w of several nanometers, the bound charge concentration can be estimated as 2Pel/ew ~ 3 × 1019 cm−3, which is an appreciable value for a small bandgap semiconductor.35

The results obtained for the Td/Td arrangement are summarized in Fig. 4, where the P+ M+ and P− M− patterns at the boundaries form, respectively, the 180∘ head-to-head (Td↑/Td↓) and tail-to-tail (Td↓/Td↑) charged DWs. Due the presence of bound charges at the interfaces, the bottom of the conduction states and the top of the valence states approach the Fermi level, thus providing electrons and holes for screening at the head-to-head and tail-to-tail DWs, respectively (Fig. 4b). This band bending driven by electron-hole transfer across the gap further leads to a potential difference. The calculated potential profile across the heterostructure reveals a small barrier of  ~ 0.24 eV with the minimum and maximum corresponding to the head-to-head and tail-to-tail DWs (Fig. 4c). Assuming that a domain width can be varied up to tens of nanometers, the induced potential will give rise to a large built-in electric field of hundreds kV cm−1 across the domain. Combined with a strong dielectric anisotropy (see Supplementary Table 4), the dielectric and piezoelectric responses in ZrI2 can be greatly enhanced and controlled by changing the density of charged DWs.36 The calculated formation energy of the charged DWs well converges to the estimation EDW = 2PelEg/e ~ 1.0 mJ m−2 as a function of the supercell size (see Supplementary Figure 11). This value is significantly smaller than in conventional ferroelectrics (35 mJ m−2 for the 90∘ DWs and 132 mJ m−2 for the 180∘ DWs in PbTiO3,37 71 mJ m−2 for the 180∘ DW in BiFeO338, ~ 70 mJ m−2 for anti-phase DWs in SmFeO339), allowing for the ease to control the DW motion (see Supplementary Fig. 12).

Fig. 4: First-principles calculations of the charged DWs in β-ZrI2.
figure 4

a a 1 × 1 × 8 supercell with the Td/Td arrangement containing the head-to-head (HH) and tail-to-tail (TT) DWs at the center and boundaries, respectively. The M trilayers are denoted with blue rectangles, and the P trilayers with positive and negative sliding displacements are highlighted with orange and yellow rectangles, respectively. b Electronic band structure and charge densities corresponding to the valence band maximum (VBM) and conduction band minimum (CBM1 and CBM2). The isosurfaces correspond to 0.01 e Å−3. c Planar and macroscopic average electrostatic potentials across the supercell and planar average charge densities of VBM and CBM.

Full size image

As a direct consequence of strong charge compensation, the charged DWs exhibit metallic behaviour and can feature noticeable inwall conductivity.40 The tail-to-tail DW at the Td↓/Td↑ interface is found to be less pronounced slowly decaying over several layers beyond its core, because the band bending by the valence states is rather weak (Fig. 4c). On the contrary, the head-to-head DW at the Td↑/Td↓ stacking demonstrates a much higher concentration of bound charges that are strongly localised at the potential cavity of the interfacial trilayers forming a quasi-two-dimensional electron gas. Since the bound charges at the interface are proportional to the normal component of electric polarization, varying conductivities are expected for different types of DWs at the Td/Td and Td/1T\(^{\prime}\) boundaries. Thus, the electron confinement can be modulated by interlayer sliding, that allows to controlling both the conductivity and carrier mobility at the interfaces.41

Taking the estimated charge density at the DW boundary, one can calculate the Debye length to be ~0.5 nm at room temperature. The value is rather small, but this estimate should be taken with care. As shown in Fig. 4, the charged DWs of ZrI2 reveal a generic quantum structure where the electron motion perpendicular to the DW is quantized. Since the number of subbands corresponding to the electron’s inwall propagation is small, the semiclassical approximations for screening effects can be violated. This feature is different from DWs in typical oxide ferroelectrics, where the number of subbands is much larger and the Thomas-Fermi approximation holds true.42

An example of the polar DW structure is presented in Fig. 5 for the 1T\(^{\prime}\)/1T\(^{\prime}\) arrangement. The Td pattern formed at the boundary breaks inversion symmetry, and the ± stacking discontinuity gives rise to the uncompensated dipole moment at the interfacial trilayer. Since the 1T\(^{\prime}\) phase in the bulk is non-polar, there are no boundary charges, and the 1T\(^{\prime}\)/1T\(^{\prime}\) stacking remains semiconducting with the ferroelectric interface.

Fig. 5: Polar DWs in ZrI2.
figure 5

Electronic band structure and planar average electrostatic potential for a 1 × 1 × 8 supercell with the 1T\(^{\prime}\)-II/1T\(^{\prime}\)-I arrangement. The M and P trilayers are denoted with blue and grey rectangles. The yellow and orange rectangles denote the Td↑ and Td↓ boundaries, respectively.

Full size image

We have considered the variety of DW structures in ZrI2 that can be promising for various slidetronics applications. The presented analysis is limited to the vertical arrangements and is based on the breaking of stacking sequences. However, it is worth noting that the DW structures have also been reported for the in-plane boundaries in MoTe2.21 While our calculations show that the antiferroelectric arrangements in a single trilayer are highly unstable (see Supplementary Fig. 14), the formation of neutral DWs at the Td/Td structures in ZrI2 is also possible by introducing a minimal strain mismatch between adjacent domains.

Discussions

Based on extensive first-principles calculations, we have established that vertical ferroelectricity in β-ZrI2 is a robust consequence of lattice instability resolved by interlayer sliding between the adjacent trilayers. The microscopic origin of electric polarization in ZrI2 is attributed to a subtle interplay of ionic displacements and charge redistribution, leading to asymmetric shifts of the electronic charge centers within each trilayer and thus refuting the previously proposed scenario of interlayer charge transfer. While the out-of-plane polarization in ZrI2 is found to be several orders of magnitude smaller than in conventional ferroelectrics, the low energy barrier for its ferroelectric switching combined with a small bandgap can provide opportunities for further developments in the field of ferroelectric semiconductors, such as ferroelectric tunnel junctions.43

Our study can shed light on some aspects of the ferroelectric activity in isostructural TMDs MoTe2 and WTe2, whose properties are summarized in Table 1.44,45,46 The essential difference between these polar semimetals and semiconducting ZrI2 is that electric polarization of the latter is not screened by metallic states, and β-ZrI2 itself can be regarded as another alternative to the layered TMDs, thus enriching the family of slidetronics ferroelectrics. The presented analysis of ferroelectric activity applies to semimetallic TMDs, explaining the persistence of electric polarization down to the ultrathin limit, and, in principle, can be extended to other vertical ferroelectrics.

Table 1 Experimental lattice parameters and theoretically predicted electric polarization for the Td phase of ZrI2, MoTe2, and WTe2.
Full size table

We have established the complexity and variability of domain boundaries in multidomain structures of ZrI2. Importantly, the same types of DWs and superlattice-like arrangements were previously reported experimentally in MoTe221 between the Weyl semimetal Td and higher-order topological 1T\(^{\prime}\) phases,19,20 which can provide a proving ground for exploring interfacial topological states and related quantum phenomena. Given their semimetallic behaviour, no static charge accumulation is expected at the domain boundaries in TMDs. In contrast, the DWs in semiconducting ZrI2 offer another diversity related to the breaking of stacking sequences and polarization discontinuity, which greatly adds up to multifunctional aspects of vertical ferroelectrics. In particular, we have predicted a stable charged DW at the phase boundaries with a pronounced metallic behavior and a high built-in electric field that can be used to enhance dielectric and piezoelectric properties. A head-to-head charged DW was shown to form a high-density quasi-two-dimensional electron gas confined at the interfacial trilayers. Such DWs can be manipulated in a controllable way and allow to creating ultrathin conductive layers embedded in a semiconducting matter and to increase electron mobility in electronic devices, which can bring advanced functionalities for future slidetronics applications.

Methods

Structural parameters of the Pmn21 and P21/m phases of ZrI2 were adopted from previous experimental studies,27,28 and the Pnma phase was devised by symmetrising the Pmn21 structure. One should bear in mind that notations of the Pnma and Pmn21 structures have different orders of the lattice vectors, which are related as (a, b, c) and (b, a, c), respectively.

Group-theoretical analysis was performed using the Bilbao Crystallographic Server (see Supplementary Table 3).47,48 The crystal structures were visualized with VESTA.49

Electronic structure

First-principles calculations were performed using the Vienna ab-initio simulation package (VASP)50 within the framework of projected augmented waves51 and Quantum-ESPRESSO (QE) realized in the basis of plane waves.52 The calculations were carried out using local density approximation (LDA)53 and generalized gradient approximation (Perdew-Burke-Ernzerhof, PBE,54 and Perdew-Burke-Ernzerhof revised for solids, PBEsol55) for the exchange-correlation potential. The calculations in QE were performed with ultrasoft and norm-conserving pseudopotentials.56 For all calculations, the valence state configurations were taken as 4s24p65s24d2 for Zr and 5s25p5 for I. The plane wave cutoff was set to 500 eV and 900 eV for VASP and QE, respectively. The Brillouin zone was sampled by a Monkhorst-Pack k-point mesh,57 6 × 10 × 3 for the T0 and 1T\(^{\prime}\) phases and 10 × 6 × 3 for the Td phase. The convergence criteria for the total energy calculations was set to 10−8 eV, and all structures were optimized with the total force convergence criteria of 10−8 eV Å−1. The optimized crystal structures used in the main text are given in Supplementary Table 1. Electronic band structures of the T0, Td, and 1T\(^{\prime}\) phases calculated with LDA, PBE, and PBEsol are shown in Supplementary Fig. 1. The effect of spin-orbit coupling was shown to give minor changes (see Supplementary Fig. 4a).

To investigate the effect of van der Waals interactions on the structural and ferroelectric properties of ZrI2, we performed a comparative analysis using the DFT-D2 correction method of Grimme,58 the DFT-D3 method with Becke-Jonson damping,59,60 the vdW-DF and vdW-DF2 functionals,61,62,63, and the optimized vdW functionals (optPBE, optB88, and optB86b).64,65 The optimized structure parameters for the Td phase are shown in Supplementary Table 2, and the corresponding band structures are presented in Supplementary Fig. 5. One can see that most of the functionals show a reasonable agreement with the experimental crystal structure parameters28 and with the bandgap of ~ 0.1 eV27 (available for the 1T\(^{\prime}\) phase only). Significant deviations were obtained for the PBE and vdW-DF functionals that give larger values of the c axis and band gaps with smaller values of electric polarization compared to the other functionals.

The effect of electronic correlations in the Zr d shell was checked within the LDA + U method66 and shown to give minor changes (see Supplementary Fig. 4b). We have also considered the effect of long-range Coulomb interactions using the GW method67 as implemented in VASP:68 a single shot G0W0 approach with 150-200 unoccupied bands and 100-150 frequencies. The results are presented in Supplementary Fig. 5. While the GW method may seem applicable owing to the large spatial extension of the Zr 4d orbitals, one can see that the bandgap is largely overestimated compared to the experimental estimates, which could be related to the implementation or other known issues of the GW method in polar materials.69

Given its computational flexibility, PBEsol without spin-orbit coupling was used for all the results presented in the main text, including the analysis of ferroelectric properties and DW structures.

High-symmetry k-points used for the band structure and phonon dispersion calculations are \({{{\rm{X}}}}=(\frac{1}{2},0,0)\), \({{{\rm{S}}}}=(\frac{1}{2},\frac{1}{2},0)\), \({{{\rm{Y}}}}=(0,\frac{1}{2},0)\), \({{{\rm{Z}}}}=(0,0,\frac{1}{2})\), \({{{\rm{U}}}}=(\frac{1}{2},0,\frac{1}{2})\), \({{{\rm{R}}}}=(\frac{1}{2},\frac{1}{2},\frac{1}{2})\), \({{{\rm{T}}}}=(0,\frac{1}{2},\frac{1}{2})\) for the Pnma (#62) and Pmn21 (#31) structures; \({{{\rm{Z}}}}=(0,\frac{1}{2},0)\), \({{{\rm{B}}}}=(0,0,\frac{1}{2})\), \({{{\rm{Y}}}}=(\frac{1}{2},0,0)\), \({{{\rm{C}}}}=(\frac{1}{2},\frac{1}{2},0)\), \({{{\rm{D}}}}=(0,\frac{1}{2},\frac{1}{2})\), \({{{\rm{A}}}}=(-\frac{1}{2},0,\frac{1}{2})\), \({{{\rm{E}}}}=(-\frac{1}{2},\frac{1}{2},\frac{1}{2})\) for the P21/m (#11) structure.

Phonon spectra

The phonon spectra for the T0 phase of ZrI2 were calculated using the method of frozen phonons as implemented in VASP and Phonopy70 and density functional perturbation theory71 (DFPT) as implemented in QE. The calculations within frozen phonons were carried out for a 2 × 4 × 1 supercell on a 3 × 3 × 3 k-point mesh. The calculations within DFPT were performed on a 3 × 6 × 2 k-point mesh. The calculated phonon spectra are summarized in Supplementary Fig. 6.

The Born effective charges and the dielectric matrix with and without local field effects were calculated using DFPT as implemented in VASP.72

Electric polarization

Electric polarization was calculated within the Berry phase theory.73,74 For the results shown in Fig. 2, we have considered the T0 phase modulated along the \({{{\Gamma }}}_{2}^{-}\) mode while keeping fixed the unit cell volume and atomic arrangement in each trilayer. Electric polarization of the fully optimized Td phase obtained within different approximations for the exchange-correlation potential is summarized in Supplementary Table 2 and Supplementary Fig. 7.

The analysis of electronic charge centers was carried out using maximally localized Wannier functions as implemented in the Wannier90 package.75 The resulting Wannier functions are obtained by projecting the states below the Fermi level onto the Zr d and I p atomic orbitals. Contributions from all sites to the net dipole moment can also be seen in the non-diagonal components of the Born effective charge tensors (see Supplementary Fig. 8).

Molecular dynamics

Ab-initio molecular dynamics simulations were performed on a 2 × 2 × 1 supercell for the structure optimized with PBEsol. The NVT ensemble with the Nosé-Hoover thermostat76 was chosen to simulate the effects of temperature, and the calculations were run up to 2000 fs with a time step of 2 fs.

In order to estimate the Curie temperature of ZrI2 while taking into account the energetic proximity of the Td and 1T\(^{\prime}\) phases, one has to consider large supercells and allow for elastic changes in the unit cell’s shape and volume. In this study, molecular dynamics was performed with the fixed volume of the supercell, and possible structural instability of the Td phase was associated with the deviation of the interlayer I-I distances from their values at 0 K. The results are summarized in Supplementary Fig. 10. At low temperatures, the interlayer I-I bonds between the middle and upper/lower trilayers evolve on average around their equilibrium 0 K values. At temperatures higher than 400 K, the middle trilayer starts to float alternately between the upper and lower trilayers (the values of the interlayer I-I bonds with the upper and lower trilayers decrease and increase by turns). While this behaviour does not unambiguously imply the transition to the paraelectric T0 phase, it can be associated with the onset of structural instability. We believe that such an approach allows us to consider 400 K as an effective lower bound for the Curie temperature in the Td phase of ZrI2.

Domain walls

Calculations for the Td↑/Td↓ heterostructure were performed on a 1 × 1 × 8, 1 × 1 × 10, and 1 × 1 × 12 supercells in the Pmn21 notation. Calculations for the 1T\(^{\prime}\)/1T\(^{\prime}\) heterostructure were carried out for a 1 × 1 × 8 supercell in the Pnma notation. The Brillouin zone was sampled by a 10 × 5 × 1 Monkhorst-Pack k-point mesh, and the heterostructures were optimized with the total force convergence criteria of 10−5 eV/Å. The DW energy is calculated as EDW = (EMD − ESD)/2A, where EMD is the energy of a supercell containing the DW, ESD is the corresponding single domain energy, and A is the DW cross-sectional area. To reduce systematic errors, the single domain structures were optimized within the same supercell. Since the \({({{{{\rm{T}}}}}_{{{{\rm{d}}}}})}_{n}{(1{{{\rm{T}}}}^{\prime} )}_{m}\) heterostructure has the Pm symmetry, there may be a tendency towards monoclinic distortions during structural optimization. We have compared our results for the fully optimized structures and the constrained structures with a fixed shape and found only minor changes in the calculated DW energies and electrostatic potentials. The results obtained with PBEsol are summarized in Supplementary Fig. 11, showing the convergence of the DW energy and electrostatic potentials with the respect to the supercell size.

The formation of charged DWs largely depends on the values of the bandgap and electric polarization, which specify the degree of the band bending. Electronic spectra of the Td↑/Td↓ heterostructure obtained for a variety of exchange-correlation functionals considered in our study are compared in Supplementary Fig. 13. One can see that the band bending by the conduction states and the formation of the head-to-head DWs are well defined and pronounced for most of the functionals. In contrast, the band bending from the valence states is rather weak, and the formation of the tail-to-tail DWs is less definite and may be unfavourable. The optPBE and vdW-D2 functionals only reveal the head-to-head DW, which can be attributed to the reduced value of electric polarization compared to the other functionals. The calculations with PBE and vdW-DF do not show the formation of any charged DWs, which can be related to the fact that these functionals largely overestimate the c axis and give larger band gaps with smaller values of electric polarization compared to the other functionals.

The Debye length was estimated using the Debye-Hückel model:77

$$\lambda =\sqrt{\frac{{\epsilon }_{{{{\rm{r}}}}}{\epsilon }_{0}{k}_{{{{\rm{B}}}}}T}{n{e}^{2}}},$$
(1)

where ϵr is the static dielectric constant along the c axis, ϵ0 is the vacuum permittivity, kB is the Boltzmann constant, T is temperature, n is the carrier charge density at the DW, and e is the elementary charge.