Abstract
Understanding the quantum dynamics of spin defects and their coherence properties requires an accurate modeling of spin-spin interaction in solids and molecules, for example by using spin Hamiltonians with parameters obtained from first principles calculations. We present a real-space approach based on density functional theory for the calculation of spin-Hamiltonian parameters, where only selected atoms are treated at the all-electron level, while the rest of the system is described with the pseudopotential approximation. Our approach permits calculations for systems containing more than 1000 atoms, as demonstrated for defects in diamond and silicon carbide. We show that only a small number of atoms surrounding the defect needs to be treated at the all-electron level, in order to obtain an overall all-electron accuracy for hyperfine and zero-field splitting tensors. We also present results for coherence times, computed with the cluster correlation expansion method, highlighting the importance of accurate spin-Hamiltonian parameters for quantitative predictions of spin dynamics.
Similar content being viewed by others
Introduction
Spin defects in semiconductors are promising quantum bits (qubits) for quantum information technologies including quantum computation, communication and sensing1,2. A prime example of spin defects is the nitrogen-vacancy (NV) center in diamond3,4,5,6,7, which can be optically initialized and read-out, and possesses millisecond coherence time even at room temperature. In recent years, much effort has been devoted to realizing spin defects in industrially mature host materials with properties similar or superior to those of diamond NV centers. For instance, several promising spin defects have been identified in silicon carbide, including the divacancy (VV)8,9, Cr10,11,12, and V impurities13. There is also a growing interest in discovering and designing spin qubits in piezo-electric materials such as aluminum nitride14,15, in oxides16, and in 2D materials17,18.
First-principles calculations based on density functional theory (DFT) have played an important role in the discovery and identification of spin defects, in particular in understanding their electronic and thermodynamical properties19,20. DFT results have been instrumental in interpreting optical and magnetic measurements, and in predicting atomistic and electronic structures of defects yet to be realized experimentally. In addition, specific spin dynamical properties may be investigated with the aid of DFT calculations, using spin Hamiltonians (SH) with parameters obtained from first principles. For systems with a single effective electron spin, e.g., a spin defect in a semiconductor, the leading terms in the SH are21,22,23:
where μB is Bohr magneton; S is the effective electron spin; B is the external magnetic field; IN and γN are the spin and gyromagnetic ratio of the Nth nucleus; g, A, D, and P are rank-2 tensors that characterize the strength of electron Zeeman interaction, hyperfine interaction, zero-field splitting and nuclear quadrupole interaction, respectively. Nuclear spin–spin interactions and the chemical shielding effect in nuclear Zeeman interactions are neglected in Eq. (1).
The SH parameters g, A, D, and P can be determined from first principles electronic structure calculations24,25,26,27,28,29,30,31,32,33,34,35,36, the majority of which are based on plane-wave pseudopotential (PW-PP) approaches. DFT calculations of SH parameters using basis sets different from PW have been proposed (e.g., numerical atomic orbitals37, linearized augmented plane-wave38, linear muffin-tin orbitals26,39, and Gaussian orbitals40), but they are often limited to smaller systems than those accessible to PW calculations. In the PW-PP method, PP are used to describe the interaction between valence and core electrons, and single-particle wavefunctions of core electrons in the solid are not explicitly evaluated. All-electron (AE) wavefunctions may be reconstructed, for example using the projected augmented wave (PAW) procedure41, and then used to compute the parameters of the SH. Recently, we proposed and benchmarked a real-space AE DFT framework42 using a finite-element (FE) basis set43 for accurate predictions of SH parameters in molecules and solids, which does not require any reconstruction of core-wavefunctions. This framework allows one to systematically convergence the results of SH parameters with respect to the basis set size and hence to establish robust results to compare with experiments for a chosen level of first principles theory. However, the method is computationally rather demanding and it only permitted the investigation of systems with tens of atoms.
Here we propose a computational scheme where only selected atoms are treated at the AE level, while the rest of the system is described within the PP approximation. We show that in order to obtain accurate SH parameters for spin defects, only a small number of atoms surrounding the defect (of the order of 10) needs to be treated at the AE level. Our approach permits calculations for cells with hundreds of atoms, as shown for the NV center in diamond and the VV in 4H–SiC, for which we used cells with up to 1022 atoms. In addition, using the cluster correlation expansion (CCE)44 method, we demonstrate the importance of accurate SH parameters for precise predictions of coherence times of spin defects in semiconductors.
Results
We carried out mixed AE-PP DFT calculations of hyperfine constants and zero-field splitting tensors using a finite-element (FE) basis and we compared the results to those obtained with PP calculations using plane waves (PW). A brief discussion on the FE basis is provided in the Supplementary Notes along with systematic convergence trends (Supplementary Table 1). In this work, we applied the mixed AE-PP approach to the negatively-charged NV center in diamond and neutral VV in 4H–SiC (see Fig. 1). Both defects have spin-triplet ground states. For VV we considered the axial kk configuration, where both the carbon and silicon vacancies are located at quasi-cubic sites. In addition, for coherence time calculations we also reported results for VV in 4H–SiC in the basal kh configuration, which exhibits avoided crossing of spin levels due to the lack of axial symmetry. We modeled the diamond and 4H–SiC using cubic and hexagonal supercells, respectively, except for kh VV in 4H–SiC, which we modeled using a orthorhombic supercell. For consistency, both PW and FE calculations were performed using structures relaxed with PW DFT. All calculations were performed with the Perdew–Burke–Ernzerhof exchange-correlational functional45. The use of the FE basis sets for SH parameter calculations permits an increase in resolution in the core regions of atoms, where wavefunctions exhibit a highly oscillatory behavior, while a coarser resolution suffices in the valence region. Due to its spatial adaptivity, the FE basis set is perfectly suited to carry out mixed AE-PP calculations. We briefly summarize below our strategy to evaluate hyperfine and zero-field splitting tensors, before presenting our results.
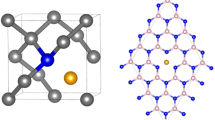
a, b Structures and spin densities of the negatively-charged nitrogen-vacancy center in diamond (a) and the axial kk-divacancy in 4H–SiC (b). In both systems, the spin density is localized around the carbon atoms with dangling bonds. By only treating a few atoms at the all-electron (AE) level, and the remaining using the pseudopotential (PP) approximation, an accurate prediction of spin Hamiltonian parameters can be achieved.
Computational framework for hyperfine and zero-field splitting tensors
For each nuclear spin, the hyperfine AN-tensor is composed of an isotropic part Afc originating from the Fermi contact of electrons at the nuclei, and an anisotropic part Asd originating from spin dipolar interactions. Afc and Asd can be evaluated using the electron spin density of the system as:
where ns(r) is the electronic spin density in real space, rN is the position of the nucleus of interest, and \({({{{\boldsymbol{r}}}}\,-\,{{{{\boldsymbol{r}}}}}_{N})}_{a}\) is the a-direction component of r − rN. S is the spin quantum number of the system (S = 0 for a singlet, \(\frac{1}{2}\) for a doublet, etc.), γe and γN are gyromagnetic ratios for electron and nuclei, respectively. We note that, while the Fermi contact term requires an accurate value of the electronic spin density exactly at the nucleus, the spin-dipole term requires an accurate description of the spin density in a region surrounding the nucleus, with the size of the region determined by the compact support of the spin density (i.e., the region where the spin density is non negligible) and by the decay of the kernel in Eq. (3). The spatial adaptivity of the FE basis is important for accurate descriptions of the spin density both in the core and valence regions, thus providing an efficient and systematic means of obtaining converged results, as described in the “Methods” section.
The spin–spin component of the zero-field splitting tensor D is evaluated as the expectation value of the magnetic dipole–dipole operator, \(\frac{{\tilde{r}}^{2}{\delta }_{ab}\,-\,3{\tilde{r}}_{a}{\tilde{r}}_{b}}{{r}^{5}}\), using a Slater determinant built from Kohn–Sham orbitals28,42. The operator is essentially the ab element of the Hessian of the Green’s function, \(G({{{\bf{r}}}},{{{{\bf{r}}}}}^{\prime})\,=\,\frac{1}{| {{{\bf{r}}}}\,-\,{{{{\bf{r}}}}}^{\prime}| }\); \(\tilde{r}\) is a scalar representing \(| {{{\bf{r}}}}\,-\,{{{{\bf{r}}}}}^{\prime}|\); \({\tilde{r}}_{a}\) is the a-th component of the vector \({{{\bf{r}}}}\,-\,{{{{\bf{r}}}}}^{\prime}\). A straightforward evaluation of the D-tensor in real-space involves computing double integrals that are computationally very demanding. In our recent work42, we reformulated the evaluation of the D-tensor in real-space by solving a series of Poisson equations, as detailed in the “Methods” section.
Numerical accuracy of the mixed pseudopotential, all-electron approach
In order to validate our approach for the calculation of the SH parameters using a mixed AE-PP approach, we first consider the Fermi contact term of the A-tensor for a NV center in a 3 × 3 × 3 diamond supercell containing 215 atoms, computed using the Γ-point for Brillouin zone sampling. Starting from a case where only the nitrogen atom is treated with an AE description, we gradually increase the number of atoms treated using AE calculations by considering eight cases (or levels), with 1, 4, 7, 13, 16, 19, 22, and 25 atoms near the defect treated at the AE level. As shown in Supplementary Fig. 2, when 16 neighbor atoms are treated at the AE level, which includes all the C atoms with dangling bonds around the N atom, the value of the Fermi contact is converged (see Supplementary Table 2). In fact, even considering only the nitrogen atom and the three dangling bond carbon atoms at the AE level yields a value of the Fermi contact of −2.125 MHz, which is in very close agreement with the value of −2.096 MHz obtained by a full AE calculation. Our results suggest that by only treating a few atoms at the AE level, the mixed AE-PP calculation, henceforth denoted as FE-mixed, is adequate and accurate to obtain the Fermi contact term. Next, we increased the system size to a 4 × 4 × 4 supercell containing 511 atoms, and found that a mixed calculation with the same number of atoms treated at the AE level as in the 215 atom cell, accurately reproduces the Fermi contact term. This indicates that the number of atoms requiring an AE description in a FE-mixed calculation is independent of the system size. We also found that the spin-dipolar term of the A-tensor (cf. Supplementary Fig. 2) is much less sensitive to the number of atoms treated with an AE approach than the Fermi contact.
As previously noted, the evaluation of the D-tensor is computationally more demanding than that of the A-tensor, and a complete AE description becomes intractable even for a system with a few hundred atoms. Thus, to validate our mixed approach, we consider NV center in a 2 × 2 × 2 diamond supercell containing 63 atoms. We performed the mixed calculation with an AE description of the four atoms including the nitrogen atom and the three carbon atoms with dangling bonds. We obtained an excellent agreement for the values of the D-tensor obtained using FE-mixed and FE-AE calculations. Due to the C3v symmetry of the system, the eigenvalues of the D-tensor Di (i ∈ [1, 3]) follow the relation \({D}_{1}\,=\,{D}_{2}\,=\,-\frac{1}{2}{D}_{3}\). We report \(\frac{3}{2}| {D}_{3}|\) throughout this manuscript. We obtained a value of 2928.31 MHz in a mixed calculation, to be compared to 2939.47 MHz obtained from a full AE description. Thus, we conclude that the SH parameters obtained for the NV center in diamond by using a FE-mixed approach, where only the nitrogen atom and the three carbon atoms with dangling bonds are described at the AE level, are as accurate as those obtained with a calculation where all atoms are treated with an AE approach.
We consider next the VV in 4H–SiC in the kk configuration (referred to as VV-SiC)46,47. As in the case of NV-diamond, the VV-SiC has 3 carbon atoms adjacent to a silicon vacancy that contribute to the spin density of the system. Further, VV-SiC also has a silicon atom with 3 dangling bonds, adjacent to the carbon vacancy that give rise to mid-gap states. Based on our results for NV-diamond, we only treat these 6 atoms with an AE description. For validation purposes, we first considered a 4 × 4 × 1 supercell of VV-SiC containing 126 atoms, and we carried out two separate calculations, one using a complete AE description (FE-AE) and the other one using AE descriptions only for the atoms with dangling bonds. We found good agreement for the A-tensors computed with the two methods. Similar to the case of NV-diamond, we conclude that also for VV-SiC, treating a small number of atoms at the AE level (the three carbon and three silicon atoms with dangling bonds) suffices to obtain accurate results. In the case of VV-SiC, a full AE calculation of the D-tensor is not feasible with reasonable computational resources, and we limited our study to mixed calculations only.
Large scale calculations
We now turn to present results for A and D obtained with large supercells, using the FE-mixed method. The importance of large supercells to obtain accurate results of spin defects has been emphasized in several recent papers9,48. For the NV in diamond, we consider cubic cells ranging from 2 × 2 × 2 to 4 × 4 × 4 in size, containing 63 to 511 atoms. In the case of VV-SiC, we consider hexagonal cells ranging from 4 × 4 × 1 to 8 × 8 × 2 in size, containing 126 atoms to 1022 atoms.
The A-tensor and D-tensor for the various cell-sizes are shown in Figs. 2, 3, for NV-diamond and VV-SiC, respectively. For comparison, we also report the same parameters obtained using PW-PP DFT calculations. We found notable differences between the results obtained with the PW-PP method and with the FE-mixed approach, which does yield an overall AE accuracy, as shown above. In the case of VV-SiC (cf. Fig. 3), the errors associated to PW-PP values are as large as ~20% for the value of the Fermi contact term of the A-tensor. In the case of the D-tensor, we performed PW calculations using pseudowavefunctions obtained with two PPs: GIPAW49 and ONCV50, and found results that agree closely, but differ significantly from those obtained using FE-mixed calculations.
a The values of Fermi contact and spin dipolar terms for the nitrogen atom, (b) The values of Fermi contact and spin dipolar terms for the dangling bond carbon atoms. For both types of atoms, the spin dipolar terms are reported in terms of the largest eigenvalue of the 3 × 3 tensor. (c) The zero-field splitting, D-tensor, where the quantity reported is \(\frac{3}{2}| {D}_{3}|\) with D3 being the eigenvalue with largest absolute magnitude. Calculations are performed with finite-element (FE) and plane-wave (PW) basis. In the case of FE calculations, we used the proposed mixed all-electron and pseudopotential scheme (FE-mixed), and for select cases we also performed pure all-electron (FE-AE) calculations. All calculations used Γ-point sampling of the Brillouin zone. Results for higher Brillouin zone sampling are provided in the Supplementary Data (cf. Supplementary Table 3).
a The values of Fermi contact and spin dipolar terms for the dangling bond silicon atoms, (b) The values of Fermi contact and spin dipolar terms for the dangling bond carbon atoms. For both types of atoms, the spin dipolar terms are reported in terms of the largest eigenvalue of the 3 × 3 tensor. (c) The zero-field splitting, D-tensor, where the quantity reported is axial splitting \(\frac{3}{2}| {D}_{3}|\) with D3 being the eigenvalue with largest absolute magnitude. Calculations are performed with finite element (FE) and plane-wave (PW) basis. PW calculations are carried out using ONCV50 and PAW pseudopotentials. In the case of FE calculations, we used the mixed all-electron and pseudopotential scheme (FE-mixed), and for select cases we also performed pure all-electron (FE-AE) calculations. All calculations used Γ-point sampling of the Brillouin zone. Results for different Brillouin zone sampling are provided in the Supplementary Data (cf. Supplementary Table 4).
The ability to compute SH parameters for cells of different sizes provides important insights into the cell-size dependence of the results (see Supplementary Tables 3, 4). In order to understand the role of defect-defect interactions, we consider the A-tensor of the dangling bond carbon in NV-diamond computed using 2 × 2 × 2 supercells and 3 × 3 × 3 k-point sampling with that computed using 3 × 3 × 3 supercells and 2 × 2 × 2 k-point sampling. These calculations correspond to the same periodic boundary conditions (Born-von Karman boundary condition) for wavefunctions and thus, any change in the A-tensor is solely due to cell-size effects arising from defect interactions. The Fermi contact value obtained in the two ways changes from 104.77 to 123.36 MHz. Similar cell-size effects arising from the defect-defect interaction are also evident in the case of VV-SiC (Supplementary Table 4). In the case of the D-tensor, while the cell-size effects are only marginal in NV-diamond, they are substantial for the VV-SiC (cf. Fig. 3). Our results underscore the importance of carrying out large scale calculations with AE accuracy to obtain accurate SH parameters.
Coherence time in weakly coupled nuclear-spin baths: the need for all-electron descriptions
Having established an efficient approach to compute SH parameters, we now use the SH to compute dynamical properties of spin defects, in particular coherence times, for which we adopted the CCE method51. In CCE calculations, the coherence function \(L\,=\,\frac{{{{\rm{Tr}}}}\{\hat{\rho }(t){\hat{S}}^{+}\}}{{{{\rm{Tr}}}}\{\hat{\rho }(0){\hat{S}}^{+}\}}\) (\(\hat{\rho }\) is the density matrix of the qubit and \({\hat{S}}^{+}\) is the spin raising operator) is approximated as a product of contributions from different nuclear-spin clusters. The coherence time is obtained by fitting the coherence function to a compressed exponential function, \(L\,\approx\, \exp -{(t/{T}_{2})}^{n}\). The convergence of the results is checked against the size of the spin bath, the number of clusters, and the maximum size of the cluster. Here, the ensemble-averaged coherence function is computed for configurations without nuclear spins with high hyperfine constants (A∣∣ > 1 MHz). In our CCE calculations, we used hyperfine tensors predicted from DFT calculations for nuclear spins included in the DFT supercell and adopted the point dipole approximation for nuclear spins at distances larger than those included in the supercell.
In general, there are two ways to control nuclear spins in defect systems. The strongly-coupled nuclear spins (with hyperfine coupling of order ~1 MHz) can be directly accessed via radio frequency radiation. Here we define nuclear spins as strongly coupled when their hyperfine parameter is larger than the linewidth of the optically detected magnetic resonance46 and separate oscillations in the Ramsey sequence due to the nuclear spin are observed52. These nuclear spins can be controlled with short gate times but they are highly susceptible to electron spin induced noise.
The second type of nuclear spins, weakly coupled to the electron spin (A ≪ 1 MHz) are controlled by dynamical decoupling schemes53. Applying refocusing pulses to the central spin may be used to not only increase the coherence time of the defect but also to isolate and control weakly coupled nuclear spins. These spins provide significantly longer coherence times than strongly-coupled spins, and the number of weakly coupled nuclear spins is not limited by the short distance to the central spin which is required for strong coupling.
The strength of the nuclear-spin induced dephasing mechanism, limiting coherence time \({T}_{2}^{* }\) in spin defects is directly related to the A-tensor54, which therefore requires accurate calculations. Here, we first estimate the sensitivity of the inhomogeneous dephasing time \({T}_{2}^{* }\) and the Hahn-echo coherence time T2 on the values of the A-tensor by carrying out CCE calculations (Fig. 4); T2 determines the stability of the qubit under dynamical decoupling schemes. We used two sets of hyperfine coupling computed for 4 × 4 × 4 supercell of the NV center in diamond: one set for which the A-tensor is calculated using the PAW reconstructed spin densities, and a second one based on the A-tensor calculated using FE-AE calculations. Figure 4b shows a histogram of the calculated A∣∣ (Azz in the defect reference frame) obtained using the two methods. We found that for large hyperfine coupling values, the relative difference is rather minor compared to the one for the smaller coupling terms. In order to see the impact of these differences on the dephasing of the electron spin, first we compute the ensemble-averaged dephasing time, \({T}_{2}^{* }\), by considering the decay of the coherence function averaged over a set of nuclear-spin configurations. The difference in the ensemble averages dephasing time was found not to be significant (1.35 (FE-AE) μs vs. 1.37 (PAW) μs). We note that the predicted value is close to the generally accepted value of nuclear-spin-limited \({T}_{2}^{* }\) in diamond of ~1 μs55. The dynamical decoupling changes the sensitivity of the qubit to the static noise, and the resulting Hahn-echo coherence time T2 is found to be insensitive to the choice of hyperfine couplings and equal to 0.89 ms, in agreement with previously reported CCE predictions14.
a Structure of the NV center in diamond (b) Histogram of A∣∣ (see text) for carbon atoms in a 4 × 4 × 4 NV-diamond supercell calculated using PAW and FE-AE methods. c Comparison of coherence times \({T}_{2}^{* }\) and T2 induced by weakly coupled nuclear-spin baths, predicted with hyperfine values from PAW (T2 PAW) and FE-AE (T2 FE) calculations. d Structure of the basal kh-VV in 4H–SiC. e Histogram of A∣∣ (see text) for silicon and carbon atoms in a 6 × 3 × 2 4H–SiC supercell with kh-VV in the middle calculated using PAW and FE-AE methods. f Comparison of coherence times \({T}_{2}^{* }\) and T2 of the basal divacancy at clock transition.
Next, we focus on the single-defect dephasing time in the weakly coupled nuclear-spin bath considering the example to NV center in diamond (Fig. 4a). We select nuclear configurations whose Fourier transform of the free induction decay contains only one peak. This procedure ensures that the coherence function of the defects in the chosen subset of nuclear configurations does not contain any oscillations due to the nuclear spins with high hyperfine coupling. Hence the procedure guarantees that the nuclear baths contain only weakly coupled nuclear spins and we can thus use an exponential decay fit to obtain the value of \({T}_{2}^{* }\). Figure 4c shows the \({T}_{2}^{* }\) for the chosen subset of nuclear configurations. In these systems, the difference between PAW and FE-AE results is significant as the dephasing time differs by a factor of 2 for certain nuclear configurations. We note that in general for weakly coupled spins, the hyperfine coupling computed with PAW are higher (as can be seen in Fig. 4b compared to their FE-AE counterpart, leading to significant differences in the predictions of the dephasing time. At the same time the Hahn-echo coherence time (Fig. 4c, right pane) does not depend on the choice of hyperfine couplings, as the main dephasing mechanism under dynamical decoupling is pairwise spin flip of distant spin pairs14.
However, in the emerging qubit systems based on the clock transitions at avoided crossings of spin levels56,57,58, the sensitivity of the coherence time to the magnetic noise from the nearby nuclear spins is different. As an example, we consider the basal kh divacancy in 4H–SiC (Fig. 4d). Compared to kk-VV, the basal divacancy has a lower symmetry and ZFS tensor contains both axial splitting D3 and basal splitting E = D2 − D1 = 18.4 MHz59, leading to emergence of avoided crossing in spin levels at zero magnetic field. Using hyperfine couplings computed with PAW and FE-AE in 6 × 3 × 2 orthorhombic supercell containing 574 atoms (Fig. 4e) we predict the ensemble average \({T}_{2\ \,{{\mbox{PAW}}}\,}^{* }\,=\,0.13\) ms, \({T}_{2\ \,{{\mbox{FE}}}\,}^{* }\,=\,0.14\) ms and T2 PAW = 1.04 ms, \({T}_{2\ \,{{\mbox{FE}}}\,}^{* }\,=\,1.11\) ms using generalization of CCE method60. The PW-PAW results consistently overestimate the hyperfine couplings of the weakly coupled nuclear spins, which leads to notable differences even in the ensemble-averaged coherence times of this system. Both values are smaller than the ones, reported in the previous work (\({T}_{2}^{* }\,=\,0.16\) ms, T2 = 1.15 ms)60 where we used larger 9 × 5 × 2 orthorhombic supercell containing 1438 atoms to compute hyperfines with PW-PAW approach, which confirms the importance of larger supercell for precise calculations of hyperfine couplings. Finally, we analyze the coherence times of basal divacancy at clock transition in the single nuclear-spin spatial configurations (Fig. 4f). We find that both \({T}_{2}^{* }\) and T2 depend significantly on the approximation used to obtain hyperfine couplings of the nearby nuclear spins, leading to significant differences in predicted coherence times.
Discussion
In summary, we presented an efficient approach based on real-space DFT to compute SH parameters. Our approach treats a few selected atoms close to a defect of interest with AE accuracy and uses the PP approximation for the remaining atoms; the method uses a FE basis set and is systematically convergent with respect to the basis set size. We presented results demonstrating that the accuracy obtained in the computation of the SH parameters using the mixed AE-PP approach is commensurate with that of full AE calculations. The mixed approach in conjunction with the spatial adaptivity of the FE basis enabled the computation of hyperfine and zero-field splitting tensors for large systems, containing ~1000 atoms, with AE accuracy. Our results revealed significant cell-size effects in the calculations of both the hyperfine and the zero-field splitting interaction, indicating that finite size scaling is important in determining accurate values for these tensors.
We computed hyperfine constants for both strongly and weakly coupled nuclei spins from AE calculations in two systems, NV in diamond and kh-VV in SiC, followed by coherence times estimation in those two systems. This shows that the relative difference between AE and PP predictions of hyperfine tensors for strongly-coupled nuclear spins (those for which A ≥ 1 MHz) is small. However, absolute differences in hyperfine tensors predicted with PW-PP and AE methods for weakly coupled spins (A ≪ 1 MHz), even when similar in magnitude to those found for strongly-coupled spins, may dramatically impact the prediction of \({T}_{2}^{* }\) of the NV center, with differences up to a factor of 2 for certain nuclear-spin configurations. In the case of the clock transitions of the basal kh-VV in SiC, the variance in the predictions is even more drastic, with relative difference up to a factor of 4. In this case, the choice of the approximation affects both T2 and \({T}_{2}^{* }\) coherence times. We note that, in addition to coherence time calculations, accurate predictions of zero-field splitting and hyperfine tensors for strongly-coupled nuclear spins are important to identify the atomistic structure of spin defects19; furthermore, accurate predictions of hyperfine tensors for weakly coupled nuclear spins are key for the spatial mapping of experimental multinuclear registers61 and the prediction of plausible memory units in spin centers52.
Finally we note that here we focused on hyperfine coupling and work is in progress to address the accuracy of other parameters entering the definition of the SH. For example, it has been recently shown that the addition of quadrupole splitting for nuclei with spin ≥1 both three- and two-dimensional materials can significantly impact the coherence time of the spin qubits62. The calculations of D tensors including spin-orbit interaction are usually computed using AE GTO basis sets for clusters of atoms, rather than conducting calculations in the condensed phase63, but recently a PAW formalism has been proposed64 which would be interesting to compare with FE calculations.
The method introduced here, which may be applied also to the calculations of SH parameters in addition to the hyperfine coupling, represents a substantial progress towards accurate computations of SH parameters of spin defects in large scale condensed and molecular systems, paving the way to high-throughput screening of spin defects for quantum information technologies.
Methods
PAW calculations of SH parameters
PW based DFT calculations are performed with the Quantum ESPRESSO code65 with a kinetic energy cutoff of 75 Ry. GIPAW PP developed by Ceresoli49 were used for the calculation of the A- and D-tensor. Moreover, the D-tensor calculations were also carried out using ONCV PP50. After solving the Kohn–Sham equations, the A-tensor is evaluated by PAW reconstruction using the GIPAW code27, while the D-tensor calculations are performed with the PyZFS code66 using normalized pseudowavefunctions9,15,67,68. In A-tensor calculations, we considered nuclear isotopes 13C, 14N, and 29Si for C, N, and Si, respectively.
FE based calculations of SH parameters
FE based DFT calculations are carried out using the DFT-FE code43. The convergence of the SH parameters with respect to the FE mesh discretization parameters is studied on the smallest supercell for each system considered here. Our convergence study was carried out with respect to the FE polynomial order and the FE mesh element size in the vicinity of the AE atoms (cf. Supplementary Table 1 for convergence of A-tensor of nitrogen atom in NV center of a 2 × 2 diamond supercell). Both the polynomial and mesh size requirements are more stringent for the A-tensor calculations compared to the D-tensor ones, as the former depends on the cusps of the spin density at the nucleus. More details related to convergence properties can be found in our previous work42.
Computational specifics of FE based A-tensor calculation
The computation of the A-tensor uses the self-consistent spin density obtained from the DFT calculation in the following manner. The spin density is evaluated at the FE quadrature points during a self-consistent DFT calculation (as quadrature values are directly used in the ensuing evaluation of integrals), while the Kohn–Sham wavefunctions are computed at the FE nodal points (cf.43 for details; also see Supplementary Information for a brief discussion on FE discretization). The Fermi contact term, which requires the value of the spin density at the FE nodes (where the atoms of interest are located), is computed by reevaluating the spin-density at these relevant FE nodes from the Kohn–Sham wavefunctions. The available quadrature point values of the spin density are used for the evaluation of the spin dipolar term, which involves an integral over the spin density (cf. Eq (3)). However, instead of directly carrying out the integral in Eq. (3), we evaluate the integral as the Hessian of the potential (Φs(r)) resulting from the spin density, where Φs(r) is computed as a solution of the partial differential equation (PDE), ∇2Φs(r) = − 4πns(r) with periodic boundary conditions. This reformulation accounts for the contributions of periodic images, which otherwise would have to be explicitly computed in the direct evaluation of the integral in Eq. (3). We note that in order to ensure spin neutrality in the solution of the Poisson equation with periodic boundary conditions, a uniform and opposite background with spin density (−M/Ω, where M is the net magnetization of the system, and Ω is the volume of the supercell) is added to ns(r). It is straightforward to show that the contribution of such a uniform background on the Hessian of Φs(r) is exactly zero.
Computational specifics of FE based D-tensor calculation
The calculation of the D-tensor in real-space is cast into the solution of a series of Poisson equations as described below.
with
where ϕi(r) is the ith single electron wavefunction obtained from DFT, and \({{{\Lambda }}}_{b}^{ij}({{{\bf{r}}}})\) is the solution of the Poisson equation \({\nabla }^{2}{{{\Lambda }}}_{b}^{ij}\,=\,-4\pi \frac{\partial ({\phi }_{i}^{* }({{{\bf{r}}}}){\phi }_{j}({{{\bf{r}}}}))}{\partial {r}_{b}}\). The superscript D and E represent the terms corresponding to direct and exchange interactions. χij = ± 1 for ith and jth wavefunctions having parallel and antiparallel spins, respectively. The most expensive part of the calculation of the D-tensor is the solution of the \(\frac{N(N\,+\,1)}{2}\) Poisson equations, where N is the number of electrons in the system. These Poisson equations are solved using the same FE discretization used to obtain the Kohn–Sham wavefunctions. Hence the reduction in the degrees of freedom achieved via a spatially adaptive FE discretization also aids in improving the computational efficiency of solving the Poisson equations. In addition, Poisson equations corresponding to different pairs of wavefunctions may be solved in parallel since they are independent from each other. The PDE involved in the D-tensor calculation takes the form \({\nabla }^{2}{{{\Lambda }}}_{b}^{ij}\,=\,-4\pi \frac{\partial ({\phi }_{i}^{* }({{{\bf{r}}}}){\phi }_{j}({{{\bf{r}}}}))}{\partial {r}_{b}}\). Here, the right hand side of the PDE is computed by first evaluating \({\phi }_{i}^{* }({{{\bf{r}}}}){\phi }_{j}({{{\bf{r}}}})\) on the FE nodes and then interpolating the gradient to the quadrature points that are subsequently used in the ensuing integrals of the weak formulation of the FE method. The PDEs are solved using the framework for the Poisson problem in the self-consistent cycle of DFT. The potential fields (\({{{\Lambda }}}_{b}^{ij,D}({{{\bf{r}}}})\) and \({{{\Lambda }}}_{b}^{ij,E}({{{\bf{r}}}})\)) obtained from the PDE are defined on the FE nodes and are interpolated to quadrature points before carrying out the integrations in Eq. (5). The interpolation errors systematically decrease with increasing FE polynomial order and decreasing FE mesh size.
Computational cost benefit of the mixed framework
As we showed above, the number of relevant atoms that need to be treated at the AE level is much smaller (<10) than the total number of atoms in the system, and does not scale with the system size. We note that for systematically convergent calculations, the FE basis functions in AE calculations are ~10-fold larger than in PP calculations for the elements considered here. For the benchmark calculations presented in this work, mixed AE-PP calculations reduce the number of basis functions by ~80% compared to full AE calculations. This advantage of mixed calculations becomes increasingly important for heavier atoms. Importantly, the DFT-FE code has the ability to treat both AE and PP calculations in the same framework. In DFT-FE, the solution to the Kohn–Sham equations is obtained via the Chebyshev polynomial filtered subspace iteration (ChFSI) procedure69,70. The various computational steps in the ChFSI procedure scales as \({{{\mathcal{O}}}}(MN)\), \({{{\mathcal{O}}}}(M{N}^{2})\), and \({{{\mathcal{O}}}}({N}^{3})\), where M denotes the number of basis functions, and N is the number of electrons. The computational complexity of solving a Poisson equation is \({{{\mathcal{O}}}}(Mlog(M))\). As the computation of the D-tensor requires the solution of \(\frac{N(N\,+\,1)}{2}\) Poisson equations, the computational complexity of the D-tensor calculations scales as \({{{\mathcal{O}}}}(Mlog(M){N}^{2})\). Thus the computational cost of both the DFT calculation and the evaluation of the D-tensor are substantially reduced in mixed AE-PP calculations, given significantly smaller M and N.
Data availability
Most of the data generated or analysed during this study are included in this published article and in the Supplementary Data. Full dataset is available at University of Chicago Qresp node at: https://paperstack.uchicago.edu/paperdetails/60dcb1b0057dbbfb35b05d4f?server=https://paperstack.uchicago.edu.
Code availability
The mixed AE-PP approach is implemented in an in-house version of the open source code DFT-FE (https://sites.google.com/umich.edu/dftfe).
Change history
11 August 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41524-021-00604-7
References
Weber, J. R. et al. Quantum computing with defects. Proc. Natl. Acad. Sci. USA. 107, 8513–8518 (2010).
Anderson, C. P. et al. Electrical and optical control of single spins integrated in scalable semiconductor devices. Science 366, 1225–1230 (2019).
Davies, G. & Hamer, M. F. Optical studies of the 1.945 eV vibronic band in diamond. Proc. R. Soc. A 348, 285–298 (1976).
Rogers, L. J., Armstrong, S., Sellars, M. J. & Manson, N. B. Infrared emission of the NV centre in diamond: Zeeman and uniaxial stress studies. New J. Phys. 10, 103024 (2008).
Doherty, M. W., Manson, N. B., Delaney, P. & Hollenberg, L. C. L. The negatively charged nitrogen-vacancy centre in diamond: the electronic solution. New J. Phys. 13, 025019 (2011).
Maze, J. R. et al. Properties of nitrogen-vacancy centers in diamond: the group theoretic approach. New J. Phys. 13, 025025 (2011).
Goldman, M. L. et al. State-selective intersystem crossing in nitrogen-vacancy centers. Phys. Rev. B 91, 165201 (2015).
Koehl, W. F., Buckley, B. B., Heremans, F. J., Calusine, G. & Awschalom, D. D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 479, 84–87 (2011).
Whiteley, S. J. et al. Spin-phonon interactions in silicon carbide addressed by Gaussian acoustics. Nat. Phys. 15, 490–495 (2019).
Son, N. T. et al. Photoluminescence and zeeman effect in chromium-doped 4h and 6h SiC. J. Appl. Phys. 86, 4348–4353 (1999).
Koehl, W. F. et al. Resonant optical spectroscopy and coherent control of Cr4+ spin ensembles in sic and gan. Phys. Rev. B 95, 035207 (2017).
Diler, B. et al. Coherent control and high-fidelity readout of chromium ions in commercial silicon carbide. npj Quantum Inform. 6, 1–6 (2020).
Wolfowicz, G. et al. Vanadium spin qubits as telecom quantum emitters in silicon carbide. Sci. Adv. 6, eaaz1192 (2020).
Seo, H., Govoni, M. & Galli, G. Design of defect spins in piezoelectric aluminum nitride for solid-state hybrid quantum technologies. Sci. Rep. 6, 20803 (2016).
Seo, H., Ma, H., Govoni, M. & Galli, G. Designing defect-based qubit candidates in wide-gap binary semiconductors for solid-state quantum technologies. Phys. Rev. Mater. 1, 075002 (2017).
Morfa, A. J. et al. Single-photon emission and quantum characterization of zinc oxide defects. Nano Lett. 12, 949–954 (2012).
Ye, M., Seo, H. & Galli, G. Spin coherence in two-dimensional materials. npj Comput. Mater. 5, 1–6 (2019).
Yim, D., Yu, M., Noh, G., Lee, J. & Seo, H. Polarization and localization of single-photon emitters in hexagonal boron nitride wrinkles. ACS Appl. Mater. Interfaces 12, 36362–36369 (2020).
Ivády, V., Abrikosov, I. A. & Gali, A. First principles calculation of spin-related quantities for point defect qubit research. npj Comput. Mater. 4, 1–13 (2018).
Dreyer, C. E., Alkauskas, A., Lyons, J. L., Janotti, A. & Van de Walle, C. G. First-principles calculations of point defects for quantum technologies. Annu. Rev. Mater. Res. 48, 1–26 (2018).
Schweiger, A. & Jeschke, G. Principles of Pulse Electron Paramagnetic Resonance (Oxford University Press, 2001).
Harriman, J. E. Theoretical Foundations of Electron Spin Resonance (Academic press, 2013).
Abragam, A. & Bleaney, B. Electron Paramagnetic Resonance of Transition Ions (Oxford University Press, 2013).
Van de Walle, C. G. & Blöchl, P. E. First-principles calculations of hyperfine parameters. Phys. Rev. B 47, 4244–4255 (1993).
Blügel, S., Akai, H., Zeller, R. & Dederichs, P. H. Hyperfine fields of 3d and 4d impurities in nickel. Phys. Rev. B 35, 3271–3283 (1987).
Overhof, H. & Gerstmann, U. Ab initio calculation of hyperfine and superhyperfine interactions for shallow donors in semiconductors. Phys. Rev. Lett. 92, 087602 (2004).
Bahramy, M. S., Sluiter, M. H. & Kawazoe, Y. Pseudopotential hyperfine calculations through perturbative core-level polarization. Phys. Rev. B 76, 035124 (2007).
Rayson, M. & Briddon, P. First principles method for the calculation of zero-field splitting tensors in periodic systems. Phys. Rev. B 77, 035119 (2008).
Bodrog, Z. & Gali, A. The spin–spin zero-field splitting tensor in the projector-augmented-wave method. J. Phys.: Condens. Matter 26, 015305 (2013).
Biktagirov, T., Schmidt, W. G. & Gerstmann, U. Calculation of spin-spin zero-field splitting within periodic boundary conditions: Towards all-electron accuracy. Phys. Rev. B 97, 115135 (2018).
Olsen, L., Christiansen, O., Hemmingsen, L., Sauer, S. P. & Mikkelsen, K. V. Electric field gradients of water: A systematic investigation of basis set, electron correlation, and rovibrational effects. J. Chem. Phys. 116, 1424–1434 (2002).
Sinnecker, S. & Neese, F. Spin- spin contributions to the zero-field splitting tensor in organic triplets, carbenes and biradicals a density functional and ab initio study. J. Phys. Chem. A 110, 12267–12275 (2006).
Neese, F. Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations. J. Chem. Phys. 122, 034107 (2005).
Reviakine, R. et al. Calculation of zero-field splitting parameters: Comparison of a two-component noncolinear spin-density-functional method and a one-component perturbational approach. J. Chem. Phys. 125, 054110 (2006).
Kossmann, S., Kirchner, B. & Neese, F. Performance of modern density functional theory for the prediction of hyperfine structure: meta-GGA and double hybrid functionals. Mol. Phys. 105, 2049–2071 (2007).
Neese, F. Calculation of the zero-field splitting tensor on the basis of hybrid density functional and Hartree-Fock theory. J. Chem. Phys. 127, 164112 (2007).
Kadantsev, E. S. & Ziegler, T. Implementation of a density functional theory-based method for the calculation of the hyperfine a-tensor in periodic systems with the use of numerical and Slater type atomic orbitals: Application to paramagnetic defects. J. Phys. Chem. A 112, 4521–4526 (2008).
Schwarz, K. & Blaha, P. Solid state calculations using WIEN2k. Comput. Mater. Sci. 28, 259 – 273 (2003).
Daalderop, G. H. O., Kelly, P. J. & Schuurmans, M. F. H. Magnetocrystalline anisotropy of yco5 and related reco5 compounds. Phys. Rev. B 53, 14415–14433 (1996).
Dovesi, R. et al. Quantum-mechanical condensed matter simulations with crystal. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8, e1360 (2018).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Ghosh, K., Ma, H., Gavini, V. & Galli, G. All-electron density functional calculations for electron and nuclear spin interactions in molecules and solids. Phys. Rev. Mater. 3, 043801 (2019).
Motamarri, P. et al. DFT-FE–a massively parallel adaptive finite-element code for large-scale density functional theory calculations. Comput. Phys. Commun. 246, 106853 (2020).
Yang, W. & Liu, R.-B. Quantum many-body theory of qubit decoherence in a finite-size spin bath. Phys. Rev. B 78, 085315 (2008).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Christle, D. J. et al. Isolated electron spins in silicon carbide with millisecond coherence times. Nat. Mater. 14, 160–163 (2015).
Seo, H. et al. Quantum decoherence dynamics of divacancy spins in silicon carbide. Nat. Commun. 7, 1–9 (2016).
Davidsson, J. et al. First principles predictions of magneto-optical data for semiconductor point defect identification: the case of divacancy defects in 4h–sic. New J. Phys. 20, 023035 (2018).
Ceresoli, D. GIPAW pseudopotentials. https://sites.google.com/site/dceresoli/pseudopotentials (2021).
Schlipf, M. & Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Comput. Phys. Commun. 196, 36–44 (2015).
Yang, W. & Liu, R.-B. Quantum many-body theory of qubit decoherence in a finite-size spin bath. Phys. Rev. B 78, 085315 (2008).
Bourassa, A. et al. Entanglement and control of single nuclear spins in isotopically engineered silicon carbide. Nat. Mater. 19, 1319–1325 (2020).
Taminiau, T. H., Cramer, J., van der Sar, T., Dobrovitski, V. V. & Hanson, R. Universal control and error correction in multi-qubit spin registers in diamond. Nat. Nanotechnol. 9, 171 (2014).
Merkulov, I., Efros, A. L. & Rosen, M. Electron spin relaxation by nuclei in semiconductor quantum dots. Phys. Rev. B 65, 205309 (2002).
Barry, J. F. et al. Sensitivity optimization for nv-diamond magnetometry. Rev. Mod. Phys 92, 015004 (2020).
Wolfowicz, G. et al. Atomic clock transitions in silicon-based spin qubits. Nat. Nanotechnol. 8, 561–564 (2013).
Zadrozny, J. M., Gallagher, A. T., Harris, T. D. & Freedman, D. E. A porous array of clock qubits. J. Am. Chem. Soc 139, 7089–7094 (2017).
Miao, K. C. et al. Universal coherence protection in a solid-state spin qubit. Science 369, 1493–1497 (2020).
Miao, K. C. et al. Electrically driven optical interferometry with spins in silicon carbide. Science Advances 5, eaay0527 (2019).
Onizhuk, M. et al. Probing the coherence of solid-state qubits at avoided crossings. PRX Quantum 2, 010311 (2021).
Abobeih, M. H. et al. Atomic-scale imaging of a 27-nuclear-spin cluster using a quantum sensor. Nature 576, 411–415 (2019).
Onizhuk, M. & Galli, G. Substrate-controlled dynamics of spin qubits in low dimensional van der waals materials. Appl. Phys. Lett. 118, 154003 (2021).
Bhandari, C., Wysocki, A. L., Economou, S. E., Dev, P. & Park, K. Multiconfigurational study of the negatively charged nitrogen-vacancy center in diamond. Phys. Rev. B 103, 014115 (2021).
Biktagirov, T. & Gerstmann, U. Spin-orbit driven electrical manipulation of the zero-field splitting in high-spin centers in solids. Phys. Rev. Res. 2, 023071 (2020).
Giannozzi, P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Condens. Matter Phys. 21, 395502 (2009).
Ma, H., Govoni, M. & Galli, G. Pyzfs: A python package for first-principles calculations of zero-field splitting tensors. J. Open Source Softw. 5, 2160 (2020).
Ivády, V., Simon, T., Maze, J. R., Abrikosov, I. A. & Gali, A. Pressure and temperature dependence of the zero-field splitting in the ground state of nv centers in diamond: a first-principles study. Phys. Rev. B 90, 235205 (2014).
Falk, A. L. et al. Electrically and mechanically tunable electron spins in silicon carbide color centers. Phys. Rev. Lett. 112, 187601 (2014).
Zhou, Y., Saad, Y., Tiago, M. L. & Chelikowsky, J. R. Parallel self-consistent-field calculations via Chebyshev-filtered subspace acceleration. Phys. Rev. E 74, 066704 (2006).
Motamarri, P., Nowak, M. R., Leiter, K., Knap, J. & Gavini, V. Higher-order adaptive finite-element methods for Kohn-Sham density functional theory. J. Comput. Phys. 253, 308–343 (2013).
Acknowledgements
K.G. and V.G. are grateful for the support of the Department of Energy, Office of Basic Energy Science, through grant number DE-SC0017380, under the auspices of which the computational framework for FE based AE DFT calculations was developed. M.O. and G.G. are grateful for the support from AFOSR FA9550-19-1-0358 under which applications to spin defects were developed and H.M. and G.G. are grateful for the support from MICCoM, under which code development was supported. MICCoM is part of the Computational Materials Sciences Program funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division through Argonne National Laboratory, under contract number DE-AC02-06CH11357. This work used computational resources from the University of Michigan through the Greatlakes computing platform, resources from the Research Computing Center at the University of Chicago through UChicago MRSEC (NSF DMR-1420709), and resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
K.G. developed the mixed AE-PP approach and performed FE calculations. H.M. performed plane-wave calculations. M.O. performed CCE simulations. V.G. and G.G. supervised the project. All authors wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghosh, K., Ma, H., Onizhuk, M. et al. Spin–spin interactions in defects in solids from mixed all-electron and pseudopotential first-principles calculations. npj Comput Mater 7, 123 (2021). https://doi.org/10.1038/s41524-021-00590-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00590-w
This article is cited by
-
Author Correction: Ab-initio calculations of shallow dopant qubits in silicon from pseudopotential and all-electron mixed approach
Communications Physics (2022)
-
Ab-initio calculations of shallow dopant qubits in silicon from pseudopotential and all-electron mixed approach
Communications Physics (2022)