Introduction

Density functional theory (DFT) is one of the most successful methods for simulating condensed matter thanks to a reasonable accuracy for a wide range of systems. Ab initio molecular dynamics (AIMD) offers a way to simulate the atomic motion using forces computed at the DFT level. Unfortunately, computational requirements limit the timescale and size of AIMD simulations to a few hundred atoms for a few hundred picoseconds of time, precluding investigation of phase transitions and heterogeneous reactions. Such large-scale molecular dynamics (MD) simulation must resort to empirically derived analytical interatomic force fields with fixed functional form1,2,3,4, trading accuracy and transferability for larger length and timescales. Classical analytical force fields often do not match the accuracy of ab initio results, limiting simulations to describing results qualitatively at best or, at worst, deviating from the correct behavior. In order to broaden the reach of computational simulations, it would be desirable to compute forces with ab initio accuracy at the same cost of classical interatomic force fields.

In recent years, machine learning (ML) algorithms emerged as powerful tools in regression and classification problems. This interest has inspired several works to develop ML algorithms for interatomic force fields, for example neural networks (NNs)5,6,7,8,9,10,11,12, MTP13,14,15, FLARE16,17, GAP18,19,20,21, SNAP22, SchNet23,24,25, DeePMD26,27,28, among others. All these ML potentials can make predictions at near ab initio accuracy, while greatly reducing the computational cost compared to DFT.

However, most ML models have no predictive distributions, which provide uncertainty for energy/force predictions. Without uncertainty, the training data are generally selected from ab initio calculations via a manual or random scheme. Determining the reliability of the force fields then becomes difficult, which could result in untrustworthy configurations in the MD simulations. Therefore, uncertainty quantification is a highly desirable capability29,30. NN potentials, e.g., ANI11,31 uses ensemble disagreement as an uncertainty measure. This statistical approach is, however, not guaranteed to yield reliable calibrated uncertainty. In addition, NN approaches usually require tens of thousands of data for training, and are a few orders of magnitude slower than analytical force fields. Bayesian models are promising for uncertainty quantification in atomistic simulations since they have an internal principled uncertainty quantification mechanism, the variance of the posterior prediction distribution, which can be used to keep track of the error on forces during a MD run. For instance, Jinnouchi et al.32,33 used high-dimensional SOAP descriptors with Bayesian linear regression19. Gaussian process (GP) regression18,19,34,35,36 is a Bayesian method that has been shown to learn accurate forces with relatively small training data sets. Bartok et al.21 used GP uncertainty with the GAP/SOAP framework to obtain only qualitative estimates of the force field’s accuracy. Recently Vandermause et al.16 demonstrated a GP-based Bayesian active learning (BAL) scheme in the FLARE framework, utilizing rigorously principled and quantitatively calibrated uncertainty, applying it to a variety of multi-component materials.

In the most common form, however, GP models require using the whole training data set for prediction of both the force and uncertainty, meaning that the computational cost of prediction grows linearly with the size of the training set, and so accuracy increases together with computational cost. In complex multi-component structures, more than O(102) training structures or O(103) local environments are typically required to construct an accurate GP model, which makes predictions slow37,38. Because of the linear scaling of GP, the on-the-fly training becomes slower as more data are collected. This precludes the active learning of GP on larger system sizes, which may be needed due to finite size effects, as well as longer timescales needed to explore phase space more thoroughly. To accelerate the on-the-fly training, fast and lossless mappings as approximations of both the force and uncertainty are desired, such that the mappings can replace GP to make predictions during the BAL.

The force mapping has been addressed by Glielmo et al.34,34,35,36 and Vandermause et al.16. They noted that, for a suitable choice of the n-body kernel function, it is possible to decompose GP force/energy prediction into a summation of low-dimensional functions of atomic positions. As a result, one can construct a parametric mapping of the n-body kernel function combined with a fixed training set. This approach reaches a constant scaling, which increases the speed of the GP model without accuracy loss. We also present the formalism of the force mapping in “Methods”.

Since the uncertainty plays a central role in the on-the-fly training16 and also suffers from the linear-scaling complexity with respect to the training set size, it is desirable to have a similar mapping of the uncertainty as that of the force. However, this was not attempted in refs. 16,34,35,36, since the mathematical form of the predictive variance results in decomposition with twice the dimension of the corresponding mean function, dramatically increasing the computational cost of their evaluation with spline interpolation. Thus, to date there is no method that combines high accuracy, modest training data requirement and fast prediction of both forces and their principled Bayesian uncertainty. In this work, we introduce a dimensionality reduction technique for the uncertainty mapping, such that the interpolation can be done on the same dimensionality as the force mapping, enabling development and application of efficient Bayesian force field (BFF) models for complex materials. The mathematical formalism of the uncertainty mapping is presented in “Methods”.

In this article, we present an accurate mapping of both force (mean) and uncertainty (variance) implemented as the mapped Gaussian process (MGP) method. As a result, the MGP method benefits from the capability of quantifying uncertainty, while at the same time retaining cost independent of training size. The original BAL with GP can then be accelerated by the fast evaluation of forces and uncertainties of MGP. The training can also be extended to larger system sizes and longer timescales that are challenging for the full GP. To illustrate the performance for large-scale dynamics simulations, we incorporate the MGP force field with mean-only mapping in the parallel MD simulation code LAMMPS39, and apply it to the investigation of phase transformation dynamics. The MGP force field is shown to be efficient for large-scale (million atom) simulations, achieving speeds comparable to classical analytical force fields, several orders of magnitude faster than available NN or full GP approaches.

As a test application, we focus on stanene, a 2D material that has recently gathered attention as a quantum spin Hall insulator40. Moreover, the only published force field for stanene is, to the best of our knowledge, the bond-order potential by Cherukara et al.41, which is fitted to capture stanene’s low-temperature crystalline characteristics but, as common to many empirical interatomic potentials, suffers in accuracy near the melting temperature. In particular, we show that MGP is capable of rapidly learning to describe a wide range of temperatures, below and around the melting temperature, and that we can efficiently monitor the uncertainty on forces at each time step of the MD, and use this capability to iteratively increase the accuracy of the force field by hierarchical active training. Using parallel simulations of large-scale structures, we characterize the unusual phase transition, where the 2D monolayer transforms to bcc bulk Sn at the temperature of 200 K, and melts to ultimately form a 3D liquid phase at the temperature of 500 K.

Results

Accelerated Bayesian active learning with MGP

In a MD simulation, it is likely that the system will evolve to atomic configurations unseen before, and are far from those in the training set. In this situation, the uncertainties of the predictions will grow to large values, which may be considered unsatisfactory. Therefore, it is desirable to obtain an accurate estimate of the forces for such configurations using a relatively expensive first principles calculation, and add this new information to the training set of the GP regression model.

This procedure is referred to as BAL, where training examples are added on the fly as more information is obtained about the problem. Bayesian ML models such as GP are particularly well-suited to such uncertainty-based active learning approaches, as they provide a well-defined probability distribution over model outputs, which can be used to extract rigorous estimates of model uncertainty for any test point42,43.

Here we adopt BAL to achieve automatic training of models for atomic forces, expanding on our earlier workflow16. This way the accuracy of the GP model increases with time, particularly in the configuration regions that are less explored and likely to be inaccurate.

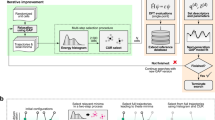
As mentioned above, GP regression cost scales linearly with the training set size, so the prediction of forces and uncertainties becomes more expensive as the BAL algorithm keeps adding data to the training set, hindering simulations of complex materials systems. The MGP approach is an essentially exact mapping of both mean and variance of the predicted forces from a full GP model for a fixed training set to a low-dimensional spline model. This approach has the ability to accelerate prediction of not only the mean, but also GP’s internal uncertainty without loss of accuracy. MGP is incorporated into the BAL workflow as depicted in Fig. 1. In this scheme, the mapping is constructed every time the GP model is updated. Atomic forces and their uncertainties for MD are produced by MGP, reducing the computational cost of the full original GP prediction by orders of magnitude. We stress that not only is the MGP BFF faster than the original GP, but also its speedup is more pronounced as the training data set size NT increases. This is especially critical in complex systems with multiple atomic and molecular species and phases, where more training configurations are needed.

Fig. 1: Bayesian active learning (BAL) workflow with MGP.
figure 1

Iterations of BAL can be run for different system sizes to refine the force field.

Full size image

In addition, fast evaluation of forces and their variances enables training the force field model on larger system sizes. Therefore, we can train the BFF using a hierarchical scheme, i.e., for different system sizes, we can run several iterations of active learning. First, a small system size is used to train the BFF using the BAL workflow. Then, we perform BAL on a larger system size, where DFT calculations are more expensive but are needed less frequently, in order to capture potentially new unexplored configurations such as defects that are automatically identified as high uncertainty by the model of the previous step. We note that DFT calculations scale as the 3rd power of the number of electrons in the system, so it is efficient to perform most of the training at smaller sizes, and to only require re-training on fewer large-scale structures. This way the hierarchical training scheme helps to overcome finite size effects and explore phenomena that cannot be captured with small system sizes, such as phase transformations.

Case study: 2D to 3D transformation of stanene

To illustrate our method, we apply the mapped on-the-fly workflow (Fig. 1) to study the phase transformation of stanene, a two-dimensional slightly buckled honeycomb lattice of tin. This structure has received much attention recently due to its unique topological electronic properties. Stanene can be synthesized by molecular beam epitaxy44 and has been shown to have topologically protected states in the band gap45. Moreover, tri-layer stanene is a superconductor46. As a demonstration of our methodology, here we want to focus on the less-studied aspects of thermodynamic stability and phase transition mechanisms of free-standing stanene. We note that a substrate is currently always used in the growth of stanene monolayers, and the interaction between the monolayer and the substrate will be investigated in a future work. By studying the intrinsic thermodynamics properties of the free-standing stanene, we are able to examine its stability and decomposition timescales as a function of temperature, which are relevant for device engineering.

Despite the intense interest, capability is still lacking for accurate modeling of thermodynamic properties and phase stability of stanene, and most other 2D materials, for which ~nm scale supercells are required. Such simulations are beyond the ability of DFT, and to the best of our knowledge, the only published classical force field for stanene is a bond-order potential (BOP)41. Our focus is on developing an accurate potential to model the 2D melting process, which is a notoriously difficult problem to tackle with existing classical force fields. In fact, describing the melting mechanism of a 2D material is a highly nontrivial problem, since it can be characterized by specific behaviors such as defect formation and nucleation. For example, the melting of graphene is thought to occur in a temperature range between 4000 and 6000 K47,48,49, and seems to be characterized by the formation of defects, while above 6000 K, the structure melts directly into a totally disordered configuration. Since bulk tin melts at a much lower temperature (~500 K) than graphite (~4300 K), we expect that stanene will transform at a relatively low temperature. However, little is known about its melting mechanism and transition temperature. The MGP method is uniquely suited to describe the transformation processes, as it is scalable to large systems and capable of accurately describing any configuration that is sufficiently close to the training data.

To train the force field for stanene, we start by training the MGP BFF using the BAL loop on a small system size, and gradually increase the size of the simulation, iteratively improving upon the force field developed for the smaller size.

The DFT settings and the hyperparameters of GP are shown in Supplementary Table 1. The parameters of MGP model are shown in Supplementary Table 2. The atomic configurations are plotted by OVITO50.

The first iteration of training is started with a 4 × 4 × 1 supercell of stanene (32 atoms in total) and a 20-ps long MD simulation at a temperature of 50 K. Subsequently, we increase the temperature of the system at 300, 500, and 800 K by velocity rescaling, and let the system evolve for 20, 30, and 30 ps, respectively. This way we efficiently augment the training set with relevant configurations. During the simulation, DFT was called whenever the uncertainty on any single force component exceeded the current optimized noise parameter of the GP, after which the N = 1 atomic environment with the highest force uncertainty was added to the training set. Figure 2b shows the mean square displacement of atoms during the on-the-fly BAL training. As one would expect, the DFT is called multiple times at the beginning of the MD simulation, since the model needs to build an initial training data set to make force predictions. In addition, the DFT is called whenever temperature is increased, as the trajectory explores new configurations that have not been visited before. Clearly, the variance increases rapidly when temperature is increased.

Fig. 2: Bayesian active learning of stanene.
figure 2

a Pristine stanene, top view and front view. b Atomic mean square displacement (MSD) of the on-the-fly training trajectory. The solid black line shows the MSD of the 32 atoms, the color blocks indicate time intervals corresponding to different temperatures, and the red dots represent events when DFT calculations are called as the uncertainty predictions exceed the data acquisition decision threshold and new data are added to the training set.

Full size image

In this small simulation, the stanene monolayer decomposes at 800 K, where Sn atoms start moving around the simulation cell. This allows us to augment the training set with such disordered configurations. However, the small size of the simulation cell does not yet allow us to draw conclusions about the melting process of stanene: for this, we need a larger simulation cell.

We continue with our hierarchical active learning scheme to refine the force field, but retaining the training data from the previous smaller MD run. We now increase the number of atoms in the simulation, which allows us to explore additional atomic configurations and improve the quality of the model. Since the system becomes larger and more computationally expensive, instead of updating the model at each learning step, we update it at the end of each MD simulation. This “batching” approach is one of many possible training schemes and is chosen for reasons of efficiency. The procedure is as below:

  1. (1)

    Run MD simulation on a system of a given size with MGP;

  2. (2)

    Predict mapped uncertainties for the frames from the MD trajectory;

  3. (3)

    Select frames of highest uncertainties in different structures (crystal, transition state, and disordered phase) for additional DFT calculations;

  4. (4)

    Add atomic environments from those frames based on uncertainty to the training set of GP;

  5. (5)

    Construct a new MGP BFF using the updated GP;

  6. (6)

    Repeat the process for same or larger simulation using the new BFF.

The above steps form one iteration, and can be run several times to refine the force field. In our force field training for stanene, we performed one iteration of 32 atoms as described before, and two iterations all on the system size of 200 atoms at 500 K, a relatively high temperature to explore diverse structures in the configuration phase space. We denote the MGP BFF from the on-the-fly training of 32 atoms as MGP-1, the ones from the two iterations of training on 200 atoms as MGP-2 and MGP-3. MD are simulated by MGP-1, 2, 3, and the predicted uncertainties of the frames from the three MD trajectories predicted by MGP BFF are shown in Fig. 3a. First, there is a drastic increase of uncertainty within each trajectory at a certain time. This increase corresponds to the transition from crystal lattice to a disordered phase, so the uncertainty acts as an automatic indicator of the structural change. Next, the uncertainties of MGP-1, 2, 3 decrease iteration by iteration, indicating our model becomes more confident as it collects more data. The mean absolute error of force predictions of MGP BFF against DFT is investigated, as presented in Fig. 3b, showing that MGP BFF becomes also more accurate with each subsequent training iterations. The accuracy of force prediction from MGP force field is also much higher than BOP41 for different phases of stanene, as shown in Supplementary Table 4.

Fig. 3: Uncertainty and accuracy in the Bayesian active learning.
figure 3

a Uncertainty of the force predictions in the whole MD trajectory decreases in three iterations. b Mean absolute errors (MAE) of MGP forces against DFT in three iterations, validated on atomic structures of different phases. c Upper: a snapshot of 2048 atoms from MD simulation at 500 K, colored by MGP uncertainty. The outlined area has highest predicted uncertainty, since it contains a defect and a compact region not known to the first MGP model. Lower-left: zoomed-in structure of the region of high uncertainty, colored by atomic heights (z-coordinate) to show the bilayer structure of the defect. Lower-right: the same snapshot colored by coordination number, which shows strong correlation with the uncertainty measure.

Full size image

It is worth noting that in the transition process of the simulation by MGP-1, there appear a bilayer stacked defect and a specific compact triangular lattice around the defect. It is a visibly new ordered structure different from the hexagonal stanene, and is thus missing in the initial training set, as shown in Fig. 3c. The uncertainty is low in honeycomb lattice, as expected, and becomes high around the bilayer defect, exhibiting also a strong correlation with the coordination number. Thus, the mapped uncertainty is an accurate automatic indicator of the novelty of the new configurations. We note that after iterative model refinement by the hierarchical training scheme, the triangular lattice no longer appears in the simulation. This example illustrates how the hierarchical active learning scheme helps avoid qualitatively incorrect results that arise due to the a priori unknown relevant configurations. In contrast, a single-pass training of a force field based on manually chosen configurations is very likely to result in nonphysical predictions.

To investigate the full phase transition mehanism of stanene, we consider low temperature (below 200 K) and high temperature (above 500 K) values, corresponding to the crystal and liquid phase for bulk tin. In studying the graphite–diamond transition, Khaliullin et al.51 identified that nucleation and growth of the disordered phase play key roles in the phase transition process. We also find that in stanene, the phase transition begins with the appearance of defects and the consequent nucleation and growth of the disordered phase that eventually transforms the structure.

From DFT ab initio calculations, the ground state energy of honeycomb monolayer is ~0.38 eV/atom higher than the bulk, so the 2D monolayer structure is expected to be meta-stable. The full transformation described below is therefore a sequence of 2D melting, followed by a kinetically controlled transition to the bulk phase of lower free energy. We set up the simulation of stanene monolayer of size 15.6 × 18.1 nm (3000 atoms), and run MD in the NPT ensemble for 3 ns at the temperature of 200 K. We discover that the ordered honeycomb monolayer loses long-range order and undergoes densification, and finally rearranges into the bcc bulk structure spontaneously, following three transformation steps. At first, the atoms vibrate around the honeycomb lattice sites, and the monolayer remains in its ordered 2D phase (Fig. 4a—0.3 ns). The main deviation from the ideal lattice is the out-of-plane rippling due to membrane fluctuations. The fluctuating ripples are similar to what was reported in simulations of graphene47,48,49. Next, double-layer stacking defects appear due to buckling and densification. These defect regions grow and quickly expand to the whole system, indicative of a first order phase transition in 2D. The atomic configuration appears to be a “disordered” phase (Fig. 4a—0.8 ns). In this stage, the structure becomes denser and increasingly three-dimensional driven by energetic gains from increasing Sn atom coordination, with the unit cell dimensions shrinking. Finally, patches of bcc lattice nucleate during the atomic rearrangement (Fig. 4a—1.6 ns), and those patches grow until the whole system forms the crystal bcc slab and atoms start vibrating around the lattice sites (Fig. 4a—2 ns).

Fig. 4: Large-scale molecular dynamics simulation of the inter-dimensional transformation of stanene.
figure 4

a The monolayer–bulk transition at ~200 K. Using common neighbor analysis, the orange atoms are identified as bcc sites, and atoms of other colors are identified as other sites. b Frames from ~500 K NPT simulation with 10,000 atoms (39.4 × 22.7 nm) at 100, 200, 400, and 600 ps, showing the melting process of the monolayer.

Full size image

The stable phase of bulk tin below 286.35 K is expected to be the α-phase with the diamond structure, which is different from what we observe here. The reason for the formation of the bcc phase is kinetic rather than thermodynamic, caused by a lower free energy barrier separating the 3D disordered structure from the bcc phase than the α-phase, making the former phase more kinetically accessible. One well-known example is the graphite–diamond transition, in which the meta-stable hexagonal diamond (HD) is obtained from hexagonal graphite (HG) in most laboratory synthesis, instead of the more thermodynamically stable cubic diamond (CD)52,53,54,55,56. Computational study51 reveals that the higher in-layer distortions result in higher energy barrier for HG–CD than HG–HD transformation, under most of the experimental conditions. We observe that the 2D stacking order-disorder and the 3D crystallization transformation steps proceed via nucleation and growth, where the defect nuclei grow and turn the whole system into the intermediate disordered dense phase, while in the second step the bcc nuclei appear from the disordered configuration and grow, turning the system into the bcc crystal phase. Our simulation result implies the meta-stability of the free-standing stanene monolayer. The evidences provided by the MD simulation are consistent with the experimental fact that all the existing growths of the stanene monolayer are achieved on substrates3,44,45,46,57,58,59. The role that the substrate plays in stabilizing the two-dimensional stanene monolayer is thus of great interests and realistic significance, and will be investigated in our future work.

To investigate the melting behavior at higher temperature, we focus on a 600 ps long MD run that starts from a pristine sample of stanene with size 39.4 × 22.7 nm (10,000 atoms) at ~500 K. A few frames of this simulations are shown in Fig. 4b. The melting process can also be identified as three stages. The first stage is the development of large out-of-plane ripples in the free-standing 2D lattice. In the second stage, at around 100 ps, double-layer defects in the monolayer form and agglomerate, causing densification. After 200 ps, densification due to large patches of disordered structures lead to the formation of holes, and a large void area grows. We observe breaking of the two-dimensionality of the crystal and formation of stacked configurations where atoms climb over other atoms of 2D stanene. In the third stage, the disordered stacked configurations shrink into spherical liquid droplets connected by a neck (400 ps). Subsequently the droplets merge to form a large sphere, minimizing the surface energy (600 ps). In Supplementary Fig. 3, we include more discussions and animations of the transition processes.

Performance

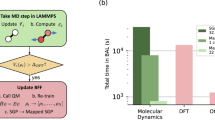
In this section, we discuss the computational cost of the MGP model in application to large-scale MD simulations, and its advantages and limitations. Timing results are shown in Fig. 5a, comparing different models including DFT, full GP (without mapping; implemented in Python), MGP (with mapped force and uncertainty; Python), MGP-F (MGP with force prediction only; Python), MGP (force only; implemented in LAMMPS), and BOP (LAMMPS force field). For DFT, we tested prediction time for system sizes of 32 and 200 atoms, where computational cost grows as the cube of the system size. The other algorithms’ cost scales linearly with system size, since they rely on local environments with finite cutoff radius, we measure the same per atom computational cost for both system sizes.

Fig. 5: Computational cost and scaling.
figure 5

a The comparison of prediction time (s × processors/atom) between DFT, full GP, MGP (Python, with force and uncertainty), MGP-F (Python, with force only), MGP (LAMMPS, with force only), and BOP (LAMMPS). b The scaling of MGP in LAMMPS with respect to different system sizes, in different phases. Green: 2D honeycomb lattice. Blue: 3D dense liquid.

Full size image

It is important to highlight the acceleration of the MGP relative to the original full GP. We present the timings of GP and MGP built from different training set sizes (100 and 400 training data) in Fig. 5, where the GP scales linearly. MGP-F (without uncertainty) and MGP (with uncertainty, fixed rank) are independent of the training set size. In the stanene system, MGP BFF is two orders of magnitude faster than GP with O(102) training data points when both force and variance are predicted, and the speedup becomes more significant as the GP collects more training data, as reported in Supplementary Fig. 4. We also note that although the prediction of MGP gets rid of the linear scaling with training set size, the construction of the mappings does scale linearly with training set size, since it requires GP to make prediction on each grid point.

The cost of the MGP force field implemented in LAMMPS (force only) is comparable to that of empirical interatomic BOP force field, since both BOP and MGP models consider interatomic distances within the local environment of a central atom and thus have similar computational cost at the same cutoff radius. For accurate simulations, however, the MGP uses a larger cutoff radius (7.2 Å) than what is used by the BOP (6 Å), and thus a simulation with our MGP force field for stanene is slower by a factor of 4–7 approximately, see our test of 1 million atoms in Table 1. The computational cost of the MGP force field in LAMMPS as a function of the system size is shown in Fig. 5b. The prefactor of the linear dependence depends on the number of pairs and triplets within a local environment. The scaling factor for the 2D honeycomb lattice structure is lower than for the dense 3D liquid, because each atom in the 3D liquid has more neighbors than the honeycomb lattice within the same cutoff radius.

Table 1 Performance in LAMMPS.
Full size table

The hierarchical active learning scheme adopted here is an efficient path to systematically improve the force field. However, it must be noted that the training is still limited by the system sizes that can be tackled with a DFT calculation. In fact, DFT calculations with thousands of atoms are unaffordable. To circumvent this problem, regions of high uncertainties may be cropped out of the large simulation cell, in order to perform DFT calculation on a smaller subset of atoms with a relevant structure. In this direction, we note that uncertainty is a local predicted property in MGP BFF, indicating how each atom contributes to the total uncertainty. In Fig. 3c, we show that the largest uncertainty in an MD frame of 2048 atoms comes from regions close to defects, since these configurations are missing in the training set for that particular model. Therefore, one may use the uncertainty to automatically select a section of the crystal close to the high-uncertainty region, and use a DFT simulation to add a training data point to the MGP. Automatically constructing such structures remains an open challenge in complex materials. However, access to the local uncertainty for each force prediction already allows for assessment of reliability of simulations, and is central to the paradigm of BFFs.

Finally, we mention that the descriptive power of our current BFF is limited due to the lack of full many-body interactions in GP kernel, since the n-body kernel only uses low-dimensional functions of crystal coordinates. In this work, we have implemented the MGP for 2- and 3-body interactions, which, for the mapping problem, translate to interpolation problems in three dimensions. The approach may be extended to higher interaction orders at the expense of computational efficiency, but it becomes expensive in terms of both computation and storage requirements for splines on uniform grids to reach a satisfactory accuracy. Many-body descriptors can be taken into account to increase the descriptive power. To map it in the same way as the methodology we introduced, it is necessary to have a descriptor such that it can be decomposed into low-dimensional functions. For example, the SOAP approach of refs. 32,33 cannot be mapped using the methodology followed in this work, since it relies on a high-dimensional descriptor. In particular, the interpolation procedure may be too computationally expensive to be a viable solution.

Discussion

In conclusion, we present an extended method for mapping the GP regression model with many-body kernels, where we accurately parameterize both the force and its variance obtained from the original Bayesian model as functions of atomic configurations. The mapped forces and their variance are then utilized in an active learning workflow to obtain a machine-learned force field that includes its own uncertainty, the first realization of a fast BFF. The resulting model has near-quantum accuracy and computational cost comparable to empirical analytical interatomic potentials. Large-scale simulations are used as a demonstration to investigate the microscopic details of inter-dimensional transformation behavior of 2D stanene into 3D tin. We discover that the transformation proceeds by nucleation of bilayer defects, densification due to continued disordered multilayer stacking, and finally conversion into either crystalline or molten bulk tin, depending on temperature. This application shows that we can actively monitor the uncertainties of force predictions during MD simulations and iteratively improve the model as the material undergoes reorganization, exploring diverse structures in the configuration phase space. The ability to reach simulation sizes of over 1 million atoms is promising for application of ML force fields to study phase diagrams and transformation dynamics of complex systems, while automated active learning of force fields opens a way to accelerate wide-range material design and discovery.

Methods

Background: Gaussian process force field

In this section, we summarize the GP model introduced in ref. 16. From here on, we use bold letters to denote matrices/vectors and regular letters for scalars/numbers.

An atomic configuration is defined by atomic coordinates Rα, a vector of dimension equal to the number of atoms Natoms, where α labels the three Cartesian directions α = x, y, z. While in general the crystal may contain atoms of different species, we here consider only a single species case for the sake of simplicity. The results can be extended to the multi-component case, which is discussed in Supplementary Method 1.

The objective of the GP regression model is to predict the forces Fα for a given atomic configuration Rα. To this aim, we associate the forces of an atom i, Fi, α, to the local environment around this atom ρi. Fi, α can then be computed by comparing its environment with a training data set of atomic environments with known forces, which is quantified by distance d between the target environment and the training set.

The atomic environment ρi of the atom i is defined as all the atoms that are within a sphere of a cutoff radius rcut centered at the atom i. We proceed by partitioning this atomic environment ρi into a set of n-atom subsets, denoted by \({\rho }_{i}^{(n)}\). A distance d(n) can be defined to quantify the difference between environments. We show examples of n = 2 and n = 3 on the construction of \({\rho }_{i}^{(n)}\) and d(n). For n = 2, \({\rho }_{i}^{(2)}\) is a set of pairs p, between central atom i and another atom \(i^{\prime}\) in ρi,

$${\rho }_{i}^{(2)}=\{p=(i,\,i^{\prime} );\,i^{\prime} \in {\rho }_{i},\,i^{\prime}\, \ne \,i\};$$
(1)

To each atomic pair p we associate an interatomic distance rp between the two atoms. The distance metric between two pairs p and q is then defined as \({({r}_{p}-{r}_{q})}^{2}\). And the distance metric between two atomic environments \({\rho }_{i}^{(2)}\) and \({\rho }_{j}^{(2)}\) is defined as:

$${({d}_{ij}^{(2)})}^{2}=\mathop{\sum }\limits_{p\in {\rho }_{i}^{(2)},q\in {\rho }_{j}^{(2)}}{({r}_{p}-{r}_{q})}^{2}.$$
(2)

This distance d(2) will be used to determine the two-body contribution to the atomic forces, for the purposes of constructing the kernel function.

This construction can be extended to higher-order interatomic interactions. In this work, we also include three-body interactions, corresponding to n = 3. Similar to the two-body case, the set \({\rho }_{i}^{(3)}\) of triplets p between the central atom i and two other atoms \(i^{\prime}\) and i″ in ρi is defined as:

$${\rho }_{i}^{(3)}=\{p=(i,\,i^{\prime} ,\,i^{\prime\prime} );\,i^{\prime} ,\,i^{\prime\prime} \in {\rho }_{i},\,i^{\prime}\, \ne \,i,\,i^{\prime\prime}\, \ne \,i,\,i^{\prime}\, \ne \,i^{\prime\prime} \}.$$
(3)

This time, each triplet p is characterized by a vector rp = {rp,1, rp,2, rp,3}, which represents the three interatomic distances of this atomic triplet p. Including permutation, the distance metric between two triplets p and q can be defined as \({\sum }_{u,v}{({r}_{p,u}-{r}_{q,v})}^{2}\). And the 3-body distance metric between two atomic environments \({\rho }_{i}^{(3)}\) and \({\rho }_{j}^{(3)}\) is

$${({d}_{ij}^{(3)})}^{2}=\mathop{\sum }\limits_{p\in {\rho }_{i}^{(3)},q\in {\rho }_{j}^{(3)}}\sum _{u,v}{({r}_{p,u}-{r}_{q,v})}^{2}\ .$$
(4)

Having now defined a distance between atomic environments, we can build a GP regression model for atomic forces. We define the equivariant force–force kernel function to compare two atomic environments as:

$${k}_{\alpha \beta }({\rho }_{i},{\rho }_{j})=\mathop{\sum }\limits_{n}{k}_{\alpha \beta }^{(n)}({\rho }_{i}^{(n)},{\rho }_{j}^{(n)})=\mathop{\sum }\limits_{n}\frac{{\partial }^{2}{k}^{(n)}({\rho }_{i}^{(n)},{\rho }_{j}^{(n)})}{\partial {R}_{i\alpha }\partial {R}_{i\beta }}\ ,$$
(5)

where α and β label Cartesian coordinates, and \(\frac{\partial }{\partial {R}_{i\alpha }}\) indicates the partial derivative of the kernel with respect to the position of atom i. The n-body energy kernel function \({k}^{(n)}({\rho }_{i}^{(n)},{\rho }_{j}^{(n)})\) is first expressed in terms of the partitions of n atoms of the two atomic environments ρi and ρj, and is defined as:

$${k}^{(n)}({\rho }_{i}^{(n)},{\rho }_{j}^{(n)})=\mathop{\sum }\limits_{\begin{array}{l}p\in {\rho }_{i}^{(n)}\\ q\in {\rho }_{j}^{(n)}\end{array}}{\tilde{k}}^{(n)}(p,q)=\mathop{\sum }\limits_{\begin{array}{l}p\in {\rho }_{i}^{(n)}\\ q\in {\rho }_{j}^{(n)}\end{array}}{\sigma }_{{\rm{sig}}}^{(n)}\exp \left[-\frac{{({d}_{ij}^{(n)})}^{2}}{2{({l}^{(n)})}^{2}}\right]{\varphi }_{{\rm{cut}}}^{(n)}\ ,$$
(6)

where \({\tilde{k}}^{(n)}(p,q)\) is a Gaussian kernel function, built using the definition of distance between n-atoms subsets as described before. The \({\sigma }_{{\rm{sig}}}^{(n)}\) and l(n) are hyperparameters independent of p and q, that set the signal variance related to the maximum uncertainty and the length scale, respectively. The smooth cutoff function \({\varphi }_{{\rm{cut}}}^{(n)}\) dampens the kernel to zero as interatomic distances approach rcut. In this work, we chose a quadratic form for the cutoff function

$${\varphi }_{{\rm{cut}}}^{(2)}(p,q)={({r}_{q}-{r}_{{\rm{cut}}})}^{2}{({r}_{p}-{r}_{{\rm{cut}}})}^{2},$$
(7)
$${\varphi }_{{\rm{cut}}}^{(3)}(p,q)=\prod _{s}{({r}_{p}^{s}-{r}_{{\rm{cut}}})}^{2}\prod _{t}{({r}_{q}^{t}-{r}_{{\rm{cut}}})}^{2}.$$
(8)

The GP regression model uses training data as a reference set of NT atomic environments. In particular, predictions of force values and variances require a 3NT × 3NT covariance matrix

$${\boldsymbol{\Sigma }}=\Sigma_{i\alpha ,j\beta }={k}_{\alpha \beta }({\rho }_{i},{\rho }_{j})+{\sigma }_{n}^{2}{\delta }_{ij}{\delta }_{\alpha \beta }$$
(9)

where σn is a noise parameter (indices iα and jβ are grouped together). We define an auxiliary 3NT dimensional vector η with components

$${\eta }_{i\alpha }:= {({{{\Sigma }}}^{-1})}_{i\alpha ,j\beta }{F}_{j\beta }\ .$$
(10)

In order to make a prediction of forces and their errors on a target structure ρi, we compute the Gaussian kernel vector \({\bar{{\boldsymbol{k}}}}_{i\alpha }\) for atom i and a direction α (α = x, y, z), where the components of the vector are kernel distances \({({\bar{k}}_{i\alpha })}_{j\beta }:= {k}_{\alpha \beta }({\rho }_{i},{\rho }_{j})\) between the prediction iα and the training set points jβ, j = 1, ..., NT, β = x, y, z. Finally, the predictions of the mean value of the Cartesian component α of the force Fiα acting on the atom at the center of the atomic environment ρi and its variance Viα are given by ref. 60:

$${F}_{i\alpha }={\bar{{\boldsymbol{k}}}}_{i\alpha }^{\top }{\boldsymbol{\eta }}\ ,$$
(11)
$${V}_{i\alpha }={k}_{\alpha \alpha }({\rho }_{i},{\rho }_{i})-{\bar{{\boldsymbol{k}}}}_{i\alpha }^{\top }{{\boldsymbol{\Sigma }}}^{-1}{\bar{{\boldsymbol{k}}}}_{i\alpha }.$$
(12)

We notice that this formulation has two major computational bottlenecks, that we intend to address in this work. First, the vector \({\bar{{\boldsymbol{k}}}}_{i\alpha }\) needs to be constructed for every force prediction; for each atom, the evaluation of \({\bar{{\boldsymbol{k}}}}_{i\alpha }\) requires the evaluation of the kernel between the atomic environment and the entire training data set, i.e., NT calls to the Gaussian kernel. We discuss an approach to speed up the evaluation of \({\bar{{\boldsymbol{k}}}}_{i\alpha }\). Second, every variance calculation requires a matrix-vector multiplication that is computationally expensive, and thus will be further discussed in “Methods”.

Mapped force field

In GP regression, a kernel function is used to build weights that depend on the distance from training data: training data that are similar to the test data contribute with a larger weight, and vice versa, dissimilar training data contribute less. To make a prediction on a data point (force on an atom in its local environment), the GP regression model requires the evaluation of the kernel between such point and all the NT training set data points. The GP mean prediction is a weighted average of the training labels, using the distances as measured by the kernel function as weights. In Eq. (11), we notice that the predictive mean requires the evaluation of a 3NT-dimensional vector \({\bar{{\boldsymbol{k}}}}_{i\alpha }\), which quantitatively weighs the contribution to the test atomic environment ρi coming from the training atomic environments ρj.

In the following discussion, we consider a specific subset size n, capturing n-body atomic structure information, i.e., \({({\bar{k}}_{i\alpha }^{(n)})}_{j\beta }={k}_{\alpha \beta }^{(n)}({\rho }_{i}^{(n)},{\rho }_{j}^{(n)})\) without loss of generality. The same treatment below can be implemented on each n and summed over the mappings of all “n”s to get the final prediction if we are using a kernel function of the form of Eq. (5).

Starting with the idea introduced in ref. 34, the kernel definition (Eq. (6)) allows us to decompose the force prediction into contributions from n-atom subsets, and to decompose the variance into contributions from pairs of n-atom subsets.

To see this, we first note that the kernel vector of atomic environments ρi can be decomposed into the kernel of all the n-atom subsets in ρi, and the kernel of an n-atom subset p can be further decomposed into the contributions from all the n − 1 neighbor atoms (except for the center atom i). We denote \({{\bf{r}}}_{p}^{s}:= {{\bf{R}}}^{s}-{{\bf{R}}}^{i}\) as a bond in p, where s labels the remaining n − 1 neighbor atoms, and introduce the unit vector \({\hat{r}}_{p}^{s}:= {{\bf{r}}}_{p}^{s}/{r}_{p}^{s}\) denoting the direction of the bond. Then the force kernel has decomposition

$${\bar{{\boldsymbol{k}}}}_{i\alpha }^{(n)}=\mathop{\sum }\limits_{p\in {\rho }_{i}}{\tilde{{\boldsymbol{k}}}}_{i\alpha }^{(n)}(p)=\mathop{\sum }\limits_{p}\mathop{\sum }\limits_{s}{{\boldsymbol{\mu }}}_{s}^{(n)}(p){\hat{r}}_{p,\alpha }^{s}\ ,$$
(13)

where

$${\left[{\tilde{k}}_{i\alpha }^{(n)}(p)\right]}_{j\beta }:= \frac{{\partial }^{2}{\tilde{k}}^{(n)}(p,q)}{\partial {R}_{\alpha }^{i}\partial {R}_{\beta }^{j}}$$
(14)

and

$${\left[{\mu }_{s}^{(n)}(p)\right]}_{j\beta }:= \mathop{\sum }\limits_{q\in {\rho }_{j}}\mathop{\sum }\limits_{t}\frac{{\partial }^{2}{\tilde{k}}^{(n)}(p,q)}{\partial {r}_{p}^{s}\partial {r}_{q}^{t}}{\hat{r}}_{q,\beta }^{t}$$
(15)

are vectors in \({{\mathbb{R}}}^{3{N}_{\text{T}}}\) space. In the first equality of Eq. (13), we used the decomposition of Eq. (6), and in the second equality we first convert the derivative from atomic coordinates to the relative distances of the n-atom subset, then take advantage of the fact that the kernel only depends on relative distances between atoms, i.e., \({r}_{p}^{s}=\parallel {{\bf{r}}}_{p}^{s}\parallel\).

Therefore, forces may be written as

$${F}_{i\alpha }^{(n)}=\mathop{\sum }\limits_{p\in {\rho }_{i}}\mathop{\sum }\limits_{s}{f}_{s}^{(n)}(p){\hat{r}}_{p,\alpha }^{s}\ .$$
(16)

where

$${f}_{s}^{(n)}(p):= {{{\boldsymbol{\mu }}}_{s}^{(n)}}^{\top }(p){\boldsymbol{\eta }}$$
(17)

and η is defined in Eq. (10).

As noted in ref. 34, we can achieve a better scaling by a computationally efficient parametric method, i.e., an approximate way for constructing such functions f. In fact, a parametric function can quickly yield the value without evaluating kernel distances from all the GP training points, making the cost independent of the size of the training set, thus remove a computational bottleneck of the full GP implementation.

In order to achieve an effective parametrization of these weight functions, we use a cubic spline interpolation on a uniform grid of points, which benefits from having an analytic form and a continuous second derivative. By increasing the number of points in the uniform grid, the MGP BFF prediction can be made arbitrarily close to the original functions.

The construction of the mapped force field includes the following steps:

Step 1: Define a uniform grid of points \(\{{x}_{k}\in {[a,b]}^{({{n} \atop {2}})}\}\) in the space of distances given by the vectors rp. The lower bound a ≥ 0 is chosen to be smaller than the minimal interatomic distance, and the upper bound b can be set to the cutoff radius of atomic neighborhoods, above which the prediction vanishes (using the zero prior of GP), and \(\left(\begin{array}{l}n\\ 2\end{array}\right)=\frac{n(n-1)}{2}\) is the number of interatomic distances in the n-atom subset.

Step 2: A GP model with a fixed training set yields the values \(\{{f}_{s}^{(n)}({x}_{k})\}\) for each grid point xk using Eq. (17).

Step 3: Interpolate with a cubic spline function \({\hat{f}}_{s}^{(n)}\) through the points \(\{({x}_{k}^{(n)},{f}_{s}^{(n)}({x}_{k}))\}\).

In prediction, contributions from all n-bodies are added up, so the force of local environment ρ is predicted as:

$${\hat{F}}_{\alpha }(\rho )=\mathop{\sum }\limits_{n}\mathop{\sum }\limits_{p\in {\rho }^{(n)}}\mathop{\sum }\limits_{s}{\hat{f}}_{s}^{(n)}(p){\hat{r}}_{p,\alpha }^{s}.$$

Mapped variance field

Using a derivation similar to that of the force decomposition (Eq. (16)), we derive the decomposition of the variance

$${V}_{i\alpha }=\mathop{\sum }\limits_{n,n^{\prime} }\mathop{\sum }\limits_{\begin{array}{c}p\in {\rho }^{(n)}\\ q\in {\rho }^{(n^{\prime} )}\end{array}}\mathop{\sum }\limits_{\begin{array}{c}s,t\end{array}}{v}_{s,t}^{(n,n^{\prime} )}(p,q){\hat{r}}_{p,\alpha }^{s}{\hat{r}}_{q,\alpha }^{t}\ ,$$
(18)

where

$${v}_{s,t}^{(n,n^{\prime} )}(p,q):= {\delta }_{nn^{\prime} }{\tilde{k}}_{\alpha \alpha }^{(n)}(p,q)-{{\boldsymbol{\mu }}}_{s}^{(n)}{(p)}^{\top }{{\mathbf{\Sigma }}}^{-1}{{\boldsymbol{\mu }}}_{t}^{(n^{\prime} )}(q)\ .$$
(19)

with the covariance matrix Σ defined in Eq. (9).

We note that the domain of the variance function v has dimensionality twice that of f, so that when the interaction order n > 3, the number of grid points becomes prohibitively large to efficiently map v. Even for a 3-body kernel, when v is a 6-D function, we find that the evaluation of the variance, both in terms of computational time and memory footprint, limits its usage to simple benchmarks.

An efficient evaluation of the variance is critical for adopting BAL. We now discuss a key result of this work and introduce an accurate yet efficient approximate mapping field for the variance. In particular, we focus on simplifying the vector \({{\boldsymbol{\mu }}}_{s}^{(n)}(p)\), which, from our tests, is the most computationally expensive term for predicting variance. In particular, since \({{\boldsymbol{\mu }}}_{s}^{(n)}(p)\) evaluates the kernel function between the test point p and all the training points, it scales linearly with the training set size. By implementing a mapping of the variance weight field, the cost of variance prediction depends only on the rank of our dimension reduction approach, and is independent of the training data set size.

To this aim, we first define the vector \({{\boldsymbol{\psi }}}_{s}^{(n)}(p):= {{\bf{L}}}^{-1}{{\boldsymbol{\mu }}}_{s}^{(n)}(p)\in {{\mathbb{R}}}^{3{N}_{\text{T}}}\), where L is the Cholesky decomposition of Σ, i.e., Σ = LL⊤, so that Eq. (19) can be written as:

$${v}_{s,t}^{(n,n^{\prime} )}(p,q)={\delta }_{nn^{\prime} }{\tilde{k}}_{\alpha ,\alpha }^{(n)}(p,q)-{{\boldsymbol{\psi }}}_{s}^{(n)}{(p)}^{\top }{{\boldsymbol{\psi }}}_{t}^{(n^{\prime} )}(q)\ .$$
(20)

The domain of vector function \({{\boldsymbol{\psi }}}_{s}^{(n)}(p)\) is half the dimensionality of that of \({v}_{s,t}^{(n,n^{\prime} )}(p,q)\).

As a first idea, since each component of ψ(n) has domain of lower dimensionality, one may think of building 3NT spline functions to interpolate the 3NT components separately, which means the number of spline functions needed grows with the training set size.

To achieve a more efficient mapping of \({{\boldsymbol{\psi }}}_{s}^{(n)}\), we take advantage of the principal component analysis (PCA), a common dimensionality reduction method. The construction of the mapped variance field includes the following steps:

Step 1: We start by evaluating the function values on the uniform grid \(\{{x}_{k}\in {[a,b]}^{\left({{n} \atop {2}}\right)},k=1,\ldots ,G\}\) as introduced in the section above. At each grid point xk, we evaluate the vectors \({{\boldsymbol{\psi }}}_{s}^{(n)}({x}_{k})\) and use them to build the matrix \({{\bf{M}}}_{s}^{(n)}:= {({{\boldsymbol{\psi }}}_{s}^{(n)}({x}_{1}),{{\boldsymbol{\psi }}}_{s}^{(n)}({x}_{2}),...,{{\boldsymbol{\psi }}}_{s}^{(n)}({x}_{G}))}^{\top }\in {{\mathbb{R}}}^{G\times 3{N}_{\text{T}}}\).

Step 2: In PCA, we perform singular value decomposition on \({{\bf{M}}}_{s}^{(n)}\), such that \({{\bf{M}}}_{s}^{(n)}={{\bf{U}}}_{s}^{(n)}{{\mathbf{\Lambda }}}_{s}^{(n)}{({{\bf{V}}}_{s}^{(n)})}^{\top }\), where \({{\bf{U}}}_{s}^{(n)}\in {{\mathbb{R}}}^{G\times 3{N}_{\text{T}}}\) and \({{\bf{V}}}_{s}^{(n)}\in {{\mathbb{R}}}^{3{N}_{\text{T}}\times 3{N}_{\text{T}}}\) have orthogonal columns, and \({{\mathbf{\Lambda }}}_{s}^{(n)}\in {{\mathbb{R}}}^{3{N}_{\text{T}}\times 3{N}_{\text{T}}}\) is diagonal.

Step 3: We reduce the dimensionality by picking the m largest eigenvalues of \({{\mathbf{\Lambda }}}_{s}^{(n)}\) and their corresponding eigenvectors from \({{\bf{U}}}_{s}^{(n)}\) and \({{\bf{V}}}_{s}^{(n)}\) (here we assume that eigenvalues are ordered). Then, we readily obtain a low-rank approximation as:

$${{\bf{M}}}_{s}^{(n)}\approx {\bar{{\bf{M}}}}_{s}^{(n)}={\bar{{\bf{U}}}}_{s}^{(n)}{\bar{{\mathbf{\Lambda }}}}_{s}^{(n)}{({\bar{{\bf{V}}}}_{s}^{(n)})}^{\top }\ ,$$
(21)

with \({\bar{{\mathbf{\Lambda }}}}_{s}^{(n)}\in {{\mathbb{R}}}^{m\times m}\), \({\bar{{\bf{U}}}}_{s}^{(n)}\in {{\mathbb{R}}}^{G\times m}\), and \({\bar{{\bf{V}}}}_{s}^{(n)}\in {{\mathbb{R}}}^{3{N}_{\text{T}}\times m}\).

Step 4: Define \({\boldsymbol{\phi} }_{s}^{(n)}=({\mathbf{\bar{V}}}_{s}^{(n)})^\top \boldsymbol{\psi}_s^{(n)}\), which is a vector in \({{\mathbb{R}}}^{m}\), and interpolate this vector between its values at the grid points {xk} (in detail, \({\phi }_{s,i}^{(n)}({x}_{k})={\bar{U}}_{s,ki}^{(n)}{\bar{{{\Lambda }}}}_{s,ii}^{(n)}\), for i = 1, ..., m). As done previously for the force mapping, spline interpolation \(\hat{{\boldsymbol{\phi }}}\) can now be used for approximating the \({{\boldsymbol{\phi }}}_{s}^{(n)}\) vector as well.

Therefore, the MGP prediction of the variance is given by:

$${\hat{v}}_{s,t}^{(n,n^{\prime} )}(p,q):= {\delta }_{nn^{\prime} }{\tilde{k}}_{\alpha ,\alpha }^{(n)}(p,q)-{\hat{{\boldsymbol{\phi }}}}_{s}^{(n)}{(p)}^{\top }{({\bar{{\bf{V}}}}_{s}^{(n)})}^{\top }{\bar{{\bf{V}}}}_{t}^{(n^{\prime} )}{\hat{{\boldsymbol{\phi }}}}_{t}^{(n^{\prime} )}(q)\ .$$
(22)

In this form, the variance would still require a multiplication between two matrices of size m × 3NT. However, we note that the computational cost of total variance can be reduced

$${\hat{V}}_{\alpha }(\rho )={k}_{\alpha ,\alpha }(\rho ,\rho )-{\left(\mathop{\sum }\limits_{n}\mathop{\sum }\limits_{p\in {\rho }^{(n)}}\mathop{\sum }\limits_{s}{\bar{{\bf{V}}}}_{s}^{(n)}{\hat{{\boldsymbol{\phi }}}}_{s}^{(n)}(p){\hat{r}}_{p,\alpha }^{s}\right)}^{2}\ .$$
(23)

Nominally, the calculation of the second term in the variance still scales with the data set size NT, since the size of \({\bar{{\bf{V}}}}^{(n)}\) depends on NT. However, we find the cost of the vector-matrix multiplication negligible compared to evaluations of the self-kernel function (the 1st term in Eq. (22)). Therefore, we have formulated a way to significantly speed up the calculation of the variance, which only weakly depends on the training set size. In addition, by tuning the PCA rank m, we can optimize the balance between accuracy and efficiency, increasing the flexibility of this model.

The convergence of the accuracy of mapped forces and uncertainty with different grid numbers G and ranks m is discussed in Supplementary Fig. 2.