Introduction

Machine learning interatomic force fields have recently emerged as powerful tools in modeling interatomic interactions. They are capable of reaching near-quantum accuracy while being orders of magnitude faster than ab initio methods1,2,3,4,5,6,7,8,9.

Recently, efficient active learning schemes have been demonstrated for high-efficiency data collection, where molecular dynamics (MD) is driven by the machine learning force field, and only configurations satisfying certain acquisition criteria6,10,11,12,13,14,15 are computed with accurate but expensive DFT calculations and added to the training set. Among them, the FLARE6 framework utilizes principled Gaussian process (GP) uncertainties to construct a Bayesian force field (BFF), a force field equipped with internal uncertainty quantification from Bayesian inference, enabling a fully autonomous active learning workflow.

The cost of prediction of conventional GP models scales linearly with the training set size, making it computationally expensive for large data sets. The sparse Gaussian process (SGP) approach selects a set of representative atomic environments from the entire training set to build an approximate model, which can scale to a larger training data set, but still suffers from the linear scaling of the inference cost with respect to the sparse set size. To address this issue, it was noticed that for the particular structure of the squared exponential 2+3-body kernel, it is possible to map the mean prediction of a trained model onto an equivalent low-dimensional parametric model6,16,17 without any loss of accuracy. It was subsequently shown that the evaluation of the variance can also be mapped onto a low-dimensional model, achieving a dramatically accelerated uncertainty-aware BFF18. While the 2-body and 3-body descriptions used in the previous work6,18 approach the computational speed of classical empirical potentials, they are limited in accuracy. To systematically increase the descriptive power of that approach, it is possible to extend the formalism to include higher body order interactions. However, inclusion of e.g. 4-body interactions requires summing contributions of all quadruplets of atoms in each neighborhood, which adds significant computational expense. Therefore, in a more recent work19 we used the atomic cluster expansion20 to construct local structure descriptors that scale linearly with the number of neighbors, enabling efficient inclusion of higher body order correlations. An inner product kernel is then constructed based on the rotationally invariant ACE descriptors, forming a basis for a sparse Gaussian Process (GP) regression model for energies, forces and stresses. Crucially, it was shown in general that in the case of inner-product kernels with high dimensional many-body descriptors, the prediction of the mean can also be mapped exactly onto a constant-cost model via reorganization of the summation in the SGP mean calculation19. This allows for efficient evaluation of the model forces, energies and stresses, but does not address the cost of evaluating uncertainties. In this work, we present a method to map the variance of SGP models with inner product kernels. This advance enables large-scale uncertainty aware MD and overcome the linear scaling issue of SGPs. Building on this approach, we achieve a significant acceleration of the Bayesian active learning (BAL) workflow and integrate it with Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)21. Bayesian force fields are implemented within the LAMMPS MD engine, such that both forces and uncertainties for each atomic configuration are quantified at computational cost independent of the training set size.

As a demonstration of the accelerated autonomous workflow, we train an uncertainty-aware many-body BFF for silicon carbide (SiC) on its several polymorphs and phases. SiC is a wide-gap semiconductor with diverse applications ranging from efficient power electronics to nuclear physics and astronomy. With the discovery of a large number of extrasolar planets22, the compositions and processes under extreme conditions have led to a wide range of studies. In particular, SiC has been identified from the adsorption spectroscopy of carbon-rich extrasolar planets23,24, which has motivated numerous experimental and computational studies of its high temperature high pressure behavior. The phase transition of SiC from the zinc blende (3C) to the rock salt (RS) phase is observed at high pressure in experiments25,26,27,28,29,30,31 and ab initio calculations32,33,34,35,36,37,38,39. Empirical potentials such as Tersoff40,41, Vashishta42,43, MEAM44, and Gao-Weber45 have been developed and applied in large-scale simulations for different purposes. However, empirical analytical potentials are limited in descriptive complexity, and hence accuracy, and require intensive human effort to select training configurations and to train. Machine learning approaches have allowed for highly over-parameterized or non-parametric models to be trained on a wide range of structures and phases7,46,47,48,49,50. Recently, neural network potentials were trained for SiC to study dielectric spectra51 and thermal transport properties52, but they do not capture high-pressure phase transitions.

In the present work, we deploy the accelerated autonomous BAL workflow to the high-pressure phase transition of SiC, and demonstrate that the transition process can be captured by the uncertainty quantification of the BFF. Then the BFF is used to perform large-scale MD simulations, and compute vibrational and thermal transport properties of different phases. The FLARE BFF shows good agreement with ab-initio calculations53 and experimental measurements, and significantly outperforms available empirical potentials in terms of accuracy, while retaining comparable computational efficiency.

Results

Accelerated bayesian active learning workflow

Directly using ab initio MD to generate a sufficiently diverse training set for machine learning force fields is expensive and time consuming, and may still miss higher-energy configurations important for rare transformation phenomena. Here, we develop an active learning workflow, where MD is instead driven by the much faster surrogate FLARE many-body BFF. During the MD simulation, the model uses its internal uncertainty quantification, deciding to call DFT only when the model encounters atomic configurations with uncertainty above a chosen threshold. Within this framework, a much smaller number of DFT calls are needed, which greatly reduces the training time and increases the efficiency of phase space exploration.

In this work, we extend the formalism of efficient lossless mapping to include uncertainty of ACE-based many-body SGP models. Specifically, we implement mapped SGP variance to enable efficient uncertainty quantification and achieve large-scale MD simulations by interfacing the Bayesian active learning algorithm with LAMMPS. The mappings of the forces and uncertainty overcome the scaling with the training set size of the computational cost of SGP regression, resulting in a significant acceleration of the training process in comparison with using the full SGP19.

We illustrate our active learning workflow in Fig. 1a. Starting from a SGP model with a small initial training set, we map both prediction mean and variance into quadratic models to obtain an efficient BFF (details are discussed in Methods). With the mapped SGP force field, MD simulation runs in LAMMPS with uncertainty associated with the local energy assigned to each atom in a configuration at each time step. The MD simulation is interrupted once there are atoms whose uncertainties are above the threshold. Then DFT is used to compute energy, forces and stress for the high-uncertainty configurations. The training set is augmented with the newly acquired DFT data, the SGP model is retrained and mapped, and the MD simulation continues with the updated model.

Fig. 1: Workflow and performance.
figure 1

a Bayesian active learning (BAL) workflow with LAMMPS. It closely follows our previous work19, with the key addition that the SGP uncertainties are now mapped and therefore much cheaper, and the MD part of the training can be done within LAMMPS. b Time profiling of the BAL workflow with a system of 72 atoms and 100,000 MD time steps. The SGP BAL workflow collected 14 frames with 72 atoms each, with 10 representative sparse environments selected per frame. The MD is greatly accelerated using mapped forces and uncertainty compared to sparse GP. “Others” includes time consumed outside of MD and DFT, e.g. adding training data to SGP and optimizing hyperparameters.

Full size image

To illustrate the acceleration of active learning workflow with mapped forces and variance compared to that with the SGP model, we deploy a single active learning run of bulk 4H-SiC system and show the performance of each part of the workflow in Fig. 1b. If the model is not mapped, the computational cost of MD with the SGP dominates the BAL procedure. When the mapped force field and variances are used, the computational cost is significantly reduced. The FLARE BFF achieves 0.76 ms ⋅ CPU/step/atom in LAMMPS MD, which includes uncertainty quantification, and is comparable in speed to empirical interatomic potentials such as ReaxFF54. With mapped uncertainties, the DFT calculations become the dominant part from Fig. 1b, i.e. the computational time for BAL is determined by the number of DFT calls. We also note that the SGP model used for timing here has a small training set of 14 frames, and the computational cost of prediction grows linearly with sparse set size. It is worth emphasizing that after mapping, the prediction of model forces, energies, and stresses, and their variances is independent of the sparse set size. Therefore, the speedup versus the SGP model is more pronounced as more training data are collected and sparse representatives are added.

Bayesian force field for SiC high pressure phase transition

In this work, we demonstrate the accelerated BAL procedure by training a mapped uncertainty-aware Bayesian force field to describe the phase transition of SiC at high pressure. We set up compressive and decompressive MD simulations at temperatures of 300 K and 2000 K for on-the-fly training simultaneously, where each SGP model is initialized with an empty training set. The parameters set for the on-the-fly training workflow is in the Supplementary Table 1, and the complete training set information is in the Supplementary Table 2.

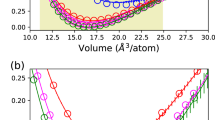
The compressive MD starts with the 2H, 4H, 6H, and 3C polytypes that are stable at low pressure, and the pressure is increased by 30 GPa every 50 ps. The decompressive MD starts with the RS phase at 200 GPa, and the pressure is decreased by 20 GPa every 50 ps. The training data are collected by the BAL workflow shown in Fig. 1. Fig. 2a shows the system volume and relative uncertainty, i.e. the ratio between the uncertainty of the current frame and the average uncertainty of the training data set (see details in Supplementary Method 155). In the compressive (decompressive) MD, when the transition happens, the volume decreases (increases) rapidly and the uncertainty spikes, since the model has never seen the transition state or the RS (3C) phase before. The post-transition high-pressure structure of the compression run has 6-fold (4-fold) coordination corresponding to the RS (3C) phase, and the transition is observed at 300 GPa (0 GPa) at room temperature. The difference of the transition pressures between the compressive and decompressive simulations is caused by nucleation-driven hysteresis. After the on-the-fly training is done, the training data from compressive and decompressive MD are combined to train a master force field for SiC, such that different phases at different pressures are covered by our force field. In Supplementary Fig. 2 and Supplementary Table 355, we demonstrate the accuracy of our force field on cohesive energy and elastic constants in comparison with DFT.

Fig. 2: Phase transition simulation with FLARE BFF and enthalpy calculations.
figure 2

a A 5 ps segment of the whole training trajectory where the 3C-RS phase transition is captured during the compressive (decompressive) on-the-fly active learning, the volume decreases (increases), and the model uncertainty spikes in the transition state. The uncertainty threshold is shown as the blue dashed line. DFT is called, and new training data is added to the model when the relative uncertainty exceeds the threshold. b Enthalpy difference predictions from DFT (PBE, PBEsol34), FLARE BFF and existing empirical potentials40,42,44,54,56 at pressures from 0 to 150 GPa. The crossing with the dotted zero line gives the transition pressure predicted by enthalpy.

Full size image

Using the mapped master force field, the phase transition pressure (at zero temperature) can be obtained from the enthalpy H = Etotal + PV of the different phases. At low pressure, the RS phase has higher enthalpy than 3C. With the pressure increased above 65 GPa, the enthalpy of RS phase becomes lower than 3C. As shown in Fig. 2, empirical potentials such as ReaxFF54, MEAM44, Tersoff40 and EDIP56 produce qualitatively incorrect enthalpy curves, likely because they are trained only at low pressures. The Vashishta potential is the only one trained on the high pressure 3C-RS phase transition42 and presents a consistent scaling of enthalpy with pressures qualitatively, but it significantly overestimates the transition pressure at 90 GPa compared to DFT. FLARE BFF achieves a good agreement with the ab initio (DFT-PBE) enthalpy predictions, with both methods yielding 65 GPa. We note that our PBE value is consistent with previous first-principles calculations such as 66.6(LDA)32 and 58(PBEsol)34.

Next we run a large-scale MD simulation with 1000 atoms for 500 ps at the temperature of 300 K. The NPT ensemble is used, and the pressure is increased by 30 GPa every 50 ps. At 300 GPa, the phase transition is observed from 4-fold coordination to 6-fold, as shown in Fig. 3b. The final 6-fold coordinated structure has radial distribution function as shown in Fig. 3c. The highest C-C, C-Si, Si-Si peaks match the perfect RS structure, confirming that the final structure is in the rock salt phase.

Fig. 3: Large-scale simulation of phase transition and analysis.
figure 3

a Large-scale MD with 1000 atoms for the 3C-RS phase transition after the training of FLARE BFF is finished. The transition is observed at 300 GPa at room temperature in MD. b The radial distribution function of the final structure after transition in the MD, compared with the perfect RS crystal lattice, indicating the final configuration is in the RS phase. c The fraction of simple cubic (RS) and cubic diamond (3C, zinc-blende) atomic environments from the phase boundary evolution at different pressures.

Full size image

As in the smaller training simulations, the nucleation-controlled hysteresis caused the transition pressure (300 GPa) to be much higher than in experimental measurements (50–150 GPa)25,26,28. To eliminate the nucleation barrier, we start our simulation with a configuration where the 3C and RS phases coexist, separated by a phase boundary, and evolve differently as a function of pressures. It is worth noting that such large scale two-phase simulations are enabled by the efficient force field and would not be possible to perform with DFT. To recognize simple cubic (RS) and cubic diamond (3C, zinc-blende) environments, we use polyhedral template matching57 in OVITO58. The time evolution of the fractions of simple cubic and cubic diamond atomic environments is shown in Fig. 3c. The phase boundary evolves quickly within 10 fs. When pressure is greater than 160 GPa, the phase boundary evolves to RS phase, while below 155 GPa it evolves to 3C phase, which indicates the phase transition pressure is located between 155–160 GPa at the temperature of 300 K.

A number of experiments have measured the density-pressure relations of zinc blende (3C) and rock salt at room temperature25,26,27,28,29. As shown in Fig. 4, the equation of state shows two parallel density-pressure curves, where the one with lower density is associated with the zinc-blende phase, and the other one with the rock salt phase. The pressures and corresponding densities at room temperature are extracted from the MD trajectories, and the equation of state is plotted to compare with the experimental measurements. FLARE BFF accurately agrees with the experimental measurements for both phases. For the transition state, there are not many experimental data points available, and the measurements can be affected by the quality of the sample, but the FLARE BFF still shows good agreement with the measured data points.

Fig. 4: The density-pressure relation from experimental measurements25,26,27,28,29 and MD simulations from FLARE BFF.
figure 4

Zinc blende and rock salt phases correspond to two different curves of equation of state. Our FLARE BFF shows close agreement with experiments.

Full size image

Vibrational and thermal transport properties

To validate that the FLARE BFF gives accurate predictions of thermal properties, we investigate the phonon dispersions and thermal conductivities of the different polytypes and phases of SiC. The phonon dispersions are computed using Phonopy59. As shown in Fig. 5, FLARE BFF produces phonon dispersions in close agreement with both DFT and experiments60,61,62,63 for both the low pressure polytypes and the high pressure rock salt phase at 200 GPa. While in the optical branches the FLARE BFF prediction shows minor discrepancies with DFT at the highest frequencies, the phonon density of states (DOS) presents good agreement. In particular, FLARE BFF captures the peak at 23 THz corresponding to a number of degenerate optical branches. In Supplementary Fig. 3, we show that the optical branches can be improved by increasing the cutoff of BFF. Existing empirical potentials are much less accurate than FLARE BFF by comparing the phonon DOS in Fig. 5. We note that the SiC crystals are polarized by atomic displacements and the generated macroscopic field induces an LO-TO splitting near Γ point. The contribution from the polarization should be included through non-analytical correction (NAC)59,64, and the first principle calculation with NAC is discussed in ref. 65. However, since FLARE BFF model does not contain charges and polarization, the NAC term is not considered. Thus, our comparison is made between the FLARE BFF and DFT without NAC. The lack of NAC accounts for the disagreement in the high frequencies of the optical bands of 2H DFT phonon (Fig. 5) with experimental measurements near Γ point.

Fig. 5: Phonon dispersions and phonon density of states of different polytypes from experimental measurements60,61,62,63, FLARE BFF and DFT calculations.
figure 5

Lower right: Thermal conductivity of 3C-SiC at 0 GPa and RS phase at 200 GPa with temperatures from 100 to 1000 K, from DFT and FLARE BFF calculations, and the experimental measurements69,70,71,72 are for 3C-SiC.

Full size image

Having confirmed the accuracy of the 2nd order force constants by the phonon dispersion calculations, we then compute the thermal conductivity within the Boltzmann transport equation (BTE) formalism. The 2nd and 3rd order force constants are computed using the Phono3py66 code, and then used in the Phoebe67 transport code to evaluate thermal conductivity with the iterative BTE solver68. In Supplementary Fig. 455, we verify that the exclusion of the non-analytic correction does not have a significant effect on the thermal conductivity values. Fig. 5 presents the thermal conductivities of the zinc blende phase at 0 GPa and the rock salt phase at 200 GPa as a function of temperature. The FLARE BFF results are in good agreement with the DFT-derived thermal conductivity for both zinc blende and rock salt phases. The thermal conductivity of zinc blende phase computed from DFT and FLARE BFF is also in good agreement with experimental measurements69,70,71,72. For the high-pressure rock salt phase, the thermal conductivity has not been previously computed or measured to the best of our knowledge. Therefore, our calculation provides a prediction that awaits experimental verification in the future.

Discussion

In this work we develop a BFF that maps both the mean predictions and uncertainties of SGP models for many-body interatomic force fields. The mapping procedure overcomes the linear scaling issue of SGPs and results in near-quantum accuracy, while retaining computational cost comparable to empirical interatomic potentials such as ReaxFF. The efficient uncertainty-aware BFF model forms the basis for the construction of an accelerated autonomous BAL workflow that is coupled with the LAMMPS MD engine and enables large-scale parallel MD simulations. The key improvement with respect to previous methods is the ability of the many-body model to efficiently calculate forces and uncertainties at comparable computational cost.

As a demonstration of the ability of this method to capture and learn subtle interactions driving phase transformations on-the-fly, we use the BAL workflow to train a BFF for SiC on several common polytypes and phases. The zinc-blende to rock-salt transition is captured in both the active learning and the large-scale simulation, facilitated by the model uncertainty. FLARE BFF is shown to have good agreement with DFT for the enthalpy prediction in a wide range of pressure values. The BFF model is readily employed to perform a large-scale MD of the phase boundary evolution, which allows for reliable identification of the transition pressure at room temperature to be located at 155–160 GPa. The density-pressure relation predicted by FLARE BFF agrees very well with experimental measurements. We also find close agreement for phonon dispersions and thermal conductivities of several SiC phases, as compared with DFT calculations and experiments, outperforming existing empirical potentials.

The high-performance implementation of BFFs, combining accuracy with autonomous uncertainty-driven active learning, opens numerous possibilities to explicitly study dynamics and microscopic mechanisms of phase transformations and non-equilibrium properties such as thermal and ionic transport. The presented unified approach can be extended to a wide range of complex systems and phenomena, where interatomic interactions are difficult to capture with classical approaches while time- and length-scales are out of reach of first-principles computational methods. Uncertainty quantification in MD simulations allows for systematic monitoring of the model confidence and detection of rare and unanticipated phenomena, such as reactions or nucleation of phases. Such events are statistically unlikely to occur in smaller simulations and become increasingly likely and relevant as the simulation sizes increase, as may be needed to study complex and heterogeneous materials systems.

Methods

In this section, we use bold letters such as α and Λ to denote a vector or a matrix, and use indices such as αi and Λij to denote the components of the vector and matrix respectively. In addition, we use F to represent all the collected configurations with all atomic environments (the “full” data set), and use S for a subset atomic environments selected from those configurations (the “sparse” data set).

Gaussian process regression

The local atomic environment ρi of an atom i consists of all the neighbor atoms within a cutoff radius, and is associated with a label yi that can be the force Fi on atom i or a local energy εi. The local energy labels are usually not available in practice, but total energies, stresses and atomic forces are. A kernel function k(ρi, ρj) quantifies the similarity between two atomic environments, which is also the covariance between local energies. Gaussian process regression (GP) assumes a Gaussian joint distribution of all the training data {(ρi, yi)} and test data (ρ, y). The posterior distribution for test data is also Gaussian with the mean and variance

$$\varepsilon (\rho )={{{{\bf{k}}}}}_{\varepsilon F}{\left({{{{\bf{K}}}}}_{FF}+{{{\mathrm{\Lambda }}}}\right)}^{-1}{{{\bf{y}}}}$$
(1)
$$V(\rho )={k}_{\varepsilon \varepsilon }-{{{{\bf{k}}}}}_{\varepsilon F}{\left({{{{\bf{K}}}}}_{FF}+{{{\mathrm{\Lambda }}}}\right)}^{-1}{{{{\bf{k}}}}}_{F\varepsilon }$$
(2)

Here, ε is the local energy of ρ, kεF is the kernel vector describing covariances between the test data and all the training data, with element k(ρ, ρi), kεε = k(ρ, ρ) is the kernel between test data ρ and itself, KFF is the kernel matrix with element k(ρi, ρj), Λ is a diagonal matrix describing noise, and y is the vector of all training labels.

Since the full GP evaluates the kernel between all configurations in the whole training set, it becomes computationally inefficient for large data sets. A sparse approximation is needed such that the computational cost can be reduced while keeping the information as complete as possible. Following our recent work19 we consider the mean prediction from Deterministic Training Conditional (DTC) Approximation73, and the variance on local energies

$$\varepsilon (\rho )={{{{\bf{k}}}}}_{\varepsilon S}{\left({{{{\bf{K}}}}}_{SF}{{{{\mathrm{\Lambda }}}}}^{-1}{{{{\bf{K}}}}}_{FS}+{{{{\bf{K}}}}}_{SS}\right)}^{-1}{{{{\bf{K}}}}}_{SF}{{{\bf{y}}}}$$
(3)
$$V(\rho )={k}_{\varepsilon \varepsilon }-{{{{\bf{k}}}}}_{\varepsilon S}{K}_{SS}^{-1}{{{{\bf{k}}}}}_{S\varepsilon }$$
(4)

where the kεS is the kernel vector between the test data ρ and the sparse training set S, KSF is the kernel matrix between the sparse subset S and the complete training set F, and KSS is the kernel matrix between S and itself. The energy, forces and stress tensor of a test configuration are given by the mean prediction, and their corresponding uncertainties are given by the square root of the predictive variance.

ACE descriptors with inner product kernel

In the FLARE SGP formalism19 we use the atomic cluster expansion20 (ACE) descriptors to represent the features of a local environment. The total energy is constructed from atomic clusters, represented by the expansion coefficients of an atomic density function using spherical harmonics. We refer the readers to ref. 19,20 for more details. To build up the SGP model for interatomic Bayesian force field, or BFF, we use the inner product kernel defined as

$$k({\rho }_{1},{\rho }_{2})={\sigma }^{2}{\left(\frac{{{{{\bf{d}}}}}_{1}\cdot {{{{\bf{d}}}}}_{2}}{{d}_{1}{d}_{2}}\right)}^{\xi }$$
(5)

where d1 and d2 are ACE descriptors of environments ρ1 and ρ2, σ is the signal variance which is optimized by maximizing the log likelihood of SGP, and ξ is the power of the inner product kernel which is selected a priori. We also normalize the kernel by the L2 norm of the descriptors. For simplicity of notations and without loss of generality, we ignore the normalization and only showcase the kernel without derivative associated with energy.

With inner product kernels, a highly efficient but lossless approximation is available via reorganization of the summation in the mathematical expression19. Defining \({{{\boldsymbol{\alpha }}}}:\,= {\left({{{{\bf{K}}}}}_{SF}{{{{\boldsymbol{\Lambda }}}}}^{-1}{{{{\bf{K}}}}}_{FS}+{{{{\bf{K}}}}}_{SS}\right)}^{-1}{{{{\bf{K}}}}}_{SF}{{{\bf{y}}}}\) and \({\tilde{{{{\boldsymbol{d}}}}}}_{i}={{{{\bf{d}}}}}_{i}/{d}_{i}\), the mean prediction of test data ρi (Eq. (3)) from sparse training set S = {ρs} can be written as19

$$\begin{array}{lll}\varepsilon ({\rho }_{i})={\sigma }^{2}\mathop{\sum}\limits_{t}{\left({\tilde{{{{\boldsymbol{d}}}}}}_{i}\cdot {\tilde{{{{\boldsymbol{d}}}}}}_{t}\right)}^{\xi }{\alpha }_{t}\\ \qquad\;\, ={\sigma }^{2}\mathop{\sum}\limits_{t,{m}_{1},...,{m}_{\xi }}{\tilde{d}}_{i{m}_{1}}{\tilde{d}}_{t{m}_{1}}\cdot \cdot \cdot {\tilde{d}}_{i{m}_{\xi }}{\tilde{d}}_{t{m}_{\xi }}{\alpha }_{t}\\ \qquad\;\,={\sigma }^{2}\mathop{\sum}\limits_{{m}_{1},...,{m}_{\xi }}{\tilde{d}}_{i{m}_{1}}\cdot \cdot \cdot {\tilde{d}}_{i{m}_{\xi }}\left(\mathop{\sum}\limits_{t}{\tilde{d}}_{t{m}_{1}}\cdot \cdot \cdot {\tilde{d}}_{t{m}_{\xi }}{\alpha }_{t}\right)\\ \qquad\;\,=\mathop{\sum}\limits_{{m}_{1},...,{m}_{\xi }}{\tilde{d}}_{i{m}_{1}}\cdot \cdot \cdot {\tilde{d}}_{i{m}_{\xi }}{\beta }_{{m}_{1},...,{m}_{\xi }},\end{array}$$
(6)

The β tensor can be computed from the training data descriptors. Thus, we can store the β tensor, and during the prediction we directly evaluate Eq. (6) without the need to sum over all training data t.

Crucially, the variance Eq. (4) has the similar reorganization as the mean prediction of Eq. (6)

$$V({\rho }_{i})={\sigma }^{2}{\left({\tilde{{{{\boldsymbol{d}}}}}}_{i}\cdot {\tilde{{{{\boldsymbol{d}}}}}}_{i}\right)}^{\xi }-{\sigma }^{4}\mathop{\sum}\limits_{s,t}{\left({\tilde{{{{\boldsymbol{d}}}}}}_{i}\cdot {\tilde{{{{\boldsymbol{d}}}}}}_{s}\right)}^{\xi }{\left({K}_{SS}^{-1}\right)}_{st}{\left({\tilde{{{{\boldsymbol{d}}}}}}_{t}\cdot {\tilde{{{{\boldsymbol{d}}}}}}_{i}\right)}^{\xi }$$
(7)
$$=\mathop{\sum}\limits_{\begin{array}{c}{m}_{1},...,{m}_{\xi }\\ {n}_{1},...,{n}_{\xi }\end{array}}({\tilde{d}}_{i{m}_{1}}\cdot \cdot \cdot {\tilde{d}}_{i{m}_{\xi }}){\gamma }_{\begin{array}{c}{m}_{1},...,{m}_{\xi }\\ {n}_{1},...,{n}_{\xi }\end{array}}({\tilde{d}}_{i{n}_{1}}\cdot \cdot \cdot {\tilde{d}}_{i{n}_{\xi }})$$
(8)

where γ is a tensor that can be calculated and stored once the training data is collected, and used in inference without explicit summation over training data i.

The reorganization indicates that the SGP regression with inner product kernel essentially gives a polynomial model of the descriptors. Denote nd as the descriptor dimension. The reorganized mean prediction has both the β size and the computational cost as \(O({n}_{d}^{\xi })\). While the reorganized variance prediction has both the γ size and the computational cost as \(O({n}_{d}^{2\xi })\). By the reorganization, both the mean and variance predictions become independent of the training set and get rid of the linear scaling with respect to training size. Here, we choose ξ = 2 for the mean prediction, because (1) it is shown19 that ξ = 2 has a significant improvement of likelihood compared to ξ = 1, while the improvement of ξ > 2 is marginal; and (2) higher order requires a much larger memory for β tensor, and the evaluation of Eq. (6) is much costlier than ξ = 2.

From Eq. (8) we see that the variance has twice the polynomial degree of that for the mean prediction. For example, when ξ = 2, the mean prediction is a quadratic model while the variance is a quartic model of descriptors. For computational efficiency, in this work we use Vξ=1 for variance prediction. Vξ=1 is not the exact variance of our mean prediction εξ=2, but an approximation using the same hyperparameters as Vξ=2. It has a strong correlation with the exact variance Vξ=2 as shown in Supplementary Fig. 155. Especially, the correlation coefficients between Vξ=1 and higher powers are close to 1.0, the perfect linear relation, even with a training size of 200 frames. This indicates that uncertainty quantification with Vξ=1 is able to recognize discrepancies between different configurations as well as Vξ=2. Specifically, atomic environments with higher Vξ=2 uncertainties will also be assigned higher Vξ=1 uncertainties than others. It is then justified that Vξ=1 can be used as a strongly correlated but much cheaper approximation of Vξ=2.

To summarize, we use εξ=2 and Vξ=1 for mean and variance predictions respectively, where both are quadratic models with respect to the descriptors. During the on-the-fly active learning, every time the training set is updated by the new DFT data, the β and γ matrices are computed from training data descriptors and stored as coefficient files. In LAMMPS MD, the quadratic models are evaluated to make predictions for energy, forces, stress and uncertainty of the configurations.