Introduction

High entropy alloys (HEAs), or compositionally complex alloys (CCAs), have inspired a new era in alloy design1,2. Particularly the body-centered cubic (bcc) HEAs composed of refractory elements from the groups 4, 5, and 6 in the periodic table reveal excellent materials properties such as high strength and high melting points and are thus potential alternatives to Ni-based superalloys3. The unique mechanical strength of HEAs is ascribed to local lattice distortions (LLDs) that are driven by chemical disorder. For example, solid solution strengthening has often been rationalized by the degree of LLDs4. However, specifically for refractory HEAs, a critical drawback is their low ductility, as also more generally known from bcc metals and alloys. To overcome this deficiency, it has recently been suggested5,6 to make use of transition-induced plasticity (TRIP) that relies on the structural transformation from the bcc to the hexagonal close-packed (hcp) phase. Experiments have shown that a transformation from bcc to hcp-based phases can be achieved for non-equiatomic compositions of the refractory Ti–Zr–Nb–Hf–Ta alloy family (Ti35Zr27.5Hf27.5Nb5Ta55 and Ti29.4Zr29.4Hf29.4Ta11.86) and ductility can be improved as compared to the equiatomic TiZrHfTa alloy6. A bcc TRIP-HEA design route thus seems indeed very promising.

Parameter-free ab initio calculations can be employed to compute LLDs7,8,9,10 as well as phase stabilities11,12, i.e., the key driving force for structural transformations. LLDs have been investigated from various ab initio perspectives. In fcc HEAs, interatomic distances were shown to be strongly affected by local chemical environments13, and this clearly reveals the importance of local chemistry for determining LLDs. Reversely, LLDs can also modify the local and global chemistry by their impact on short-range and long-range order14. Correlations between LLDs and local atomic properties (atomic charges and volumes) could be established for various 3d-transition-element HEAs9 and refractory HEAs15. Furthermore, relaxation energies due to LLDs were shown to substantially affect phase stabilities of HEAs16,17. Therefore, in view of an accurate prediction of phase stabilities for the design of TRIP HEAs, a careful treatment of LLDs is indispensable.

For bcc refractory HEAs containing a significant fraction of group 4 elements (Ti, Zr, Hf) the situation is, however, seriously complicated because of the imminent dynamical instability of these alloys at low temperatures. Complications can indeed be expected by considering the intrinsic low-temperature dynamical instability of the individual group 4 elements in the bcc structure, which is reflected by imaginary phonon modes in ab initio calculations at 0 K18,19,20,21. Dynamical instability is also signified for the bcc HEAs, e.g., TiZrNbHf22, ZrNbHf22,23, and TiZrMoHfTa23 by ab initio-computed phonon dispersions. In general, dynamical instability indicates the tendency of the system to transform spontaneously to another, low-temperature stable structure. As a consequence, chemically induced LLDs cannot be determined by merely utilizing the standard atomic relaxation procedure, because the latter unavoidably intermixes LLDs and atomic displacements due to the structural transformation.

Previous molecular-dynamics (MD) simulations21,24 revealed that, at low temperatures and under cell-shape-constraints, bcc Ti transforms to a hexagonal ω phase. The ω phase was also observed in Zr25 and Hf26,27, and in Ti-based alloys like Ti–Nb28. Recent experiments reported the ω phase for some bcc HEAs as well. For example, Ti31.25Zr31.25Hf31.25Nb6.2529, Sc10Ti30Zr30Hf25Re5, and Sc7Ti30Zr30Hf25Re812 exhibit ω nanoprecipitates in the as-cast state. Homogenized and recrystallized equiatomic TiZrNbHfTa features the ω phase at bcc twin boundaries when deformed at 77 K30. From an experimental perspective, control over the ω phase is of high importance, because ω precipitates can cause embrittlement12,31,32.

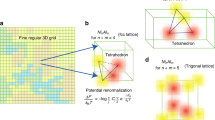
To distinguish the atomic displacements caused by the bcc–ω structural transformation (which could cause embrittlement) from those induced by chemically induced LLDs (which are often beneficial for improving the materials’ strength10) it is essential to systematically distinguish the bcc and the ω structures. For pure metals (Fig. 1a), this is immediately possible due to the apparent symmetry differences between the two structures. For a typical relaxed configuration of a disordered alloy (Fig. 1b), however, a distinction of the two structures is much less straightforward due to the chemical disorder, which breaks the ideal crystallographic symmetries in both structures. This becomes even more challenging if the relaxed ω structures show line defects21,24.

Fig. 1: Schematics of the bcc and ω structures.
figure 1

a Pure metals. b Disordered alloys. Spheres with different colors represent different chemical elements. Visualization was performed using VESTA55.

Full size image

In this study, we tackle the challenge and develop a robust method for bcc-disordered alloys to distinguish the bcc–ω transformation from chemically induced LLDs. Using this method, in combination with ab initio calculations, we evaluate the phase stabilities of Ti–Zr–Hf–Ta and Ti–Zr–Nb–Hf–Ta refractory HEAs and reveal the critical importance of relaxation energies on the bcc–hcp phase stability. Our results agree well with recent experiments and give guidance to the design of novel bcc–hcp TRIP HEAs.

Results

Perfect and defective ω structures

The ω phase is particularly known from Ti and Zr alloys33, in which it can be stabilized by alloying with bcc-stabilizing elements such as V, Cr, Nb, and Mo28,33. In experiments, it can be likewise stabilized for the unary crystals of the group 4 elements Ti25, Zr25, and Hf26,27 by application of high pressure. In DFT calculations at 0 K, the ω phase is found to be the most stable phase for Ti even at zero pressure, i.e., it is lower in energy than bcc and hcp34,35. Conventionally, the ω phase is represented by the perfect ω crystal structure.

The perfect ω structure belongs to the hexagonal crystal system and, in particular, obeys the symmetries of the P6/mmm space group (No. 191). The primitive cell of the perfect ω structure consists of three atoms, one atom located on a 1a Wyckoff site and the other two atoms on 2d Wyckoff sites. The ω structure can be obtained by a martensitic transformation starting from the bcc structure via atomic displacements along one of the 〈111〉bcc directions without significant cell deformation. The relation between the lattice parameters of the coherent bcc and ω structures is

$${a}_{\omega }=\sqrt{2}{a}_{{\rm{bcc}}},$$
(1)
$${c}_{\omega }=\frac{\sqrt{3}}{2}{a}_{{\rm{bcc}}},$$
(2)

where abcc is the lattice parameter of the bcc structure, and aω and cω are the lattice parameters of the ω structure perpendicular and parallel to the sixfold rotation axis, respectively. Specifically, the ω structure is obtained from the bcc structure by displacing one-third of the atoms by cω/6 into a positive 〈111〉bcc direction and another one-third of the atoms into the corresponding negative direction as sketched in Fig. 2a.

Fig. 2: Schematics of the bcc–ω transformation.
figure 2

Black and red circles represent the bcc and the ω lattice sites, respectively. a Perfect ω structure. b Defective ω structure. c Twin variant of the original bcc structure, obtained from the twice larger displacements for the perfect ω structure. Orange circles represent the twin-variant bcc lattice sites.

Full size image

In MD simulations, the perfect ω structure is rarely observed21,24. Instead, defective ω structures are mostly found. These structures can be constructed from the perfect ω structure by introducing linear-chain defects along the symmetry-broken 〈111〉bcc direction as illustrated in Fig. 2b. Korbmacher et al.21,24 reported such defective ω structures for MD simulations in pure Ti. The authors found that the density of linear-chain defects becomes higher for larger supercell models and that the arrangement of these defects is random if not constrained by periodic images21,24. The specific arrangement of the 〈111〉bcc line defects depends on the supercell geometry. As discussed below, the HEAs in the focus of the present work, Ti–Zr–Hf–Ta and Ti–Zr–Nb–Hf–Ta, display defective ω structures in the same manner as pure Ti.

Korbmacher et al.21,24 proposed an approach to effectively distinguish between the perfect ω structure, any possible defective ω structure, and the bcc structure which, with slight modifications, reads:

  1. 1.

    Compute atomic displacements according to

    $${{\bf{d}}}_{i}={{\bf{r}}}_{i}-{{\bf{r}}}_{i}^{{\rm{bcc}}},$$
    (3)

    where \({{\bf{r}}}_{i}^{{\rm{bcc}}}\) and ri denote the internal atomic coordinates of the ith atom on the ideal bcc lattice site and after relaxation. In addition to the original bcc lattice sites, the four possible twin variants obtained according to Fig. 2c should be considered as candidates for \({{\bf{r}}}_{i}^{{\rm{bcc}}}\). Among the five possible candidates, the relevant \({{\bf{r}}}_{i}^{{\rm{bcc}}}\) coordinates can be selected by considering the smallest value of the average of \({p}_{{\langle 111\rangle }_{\,}{\rm{bcc}}}\) as defined in the next step. The reference values \({{\bf{r}}}_{i}^{{\rm{bcc}}}\) are adjusted to satisfy

    $$\sum _{i}{{\bf{d}}}_{i}=\sum _{i}({{\bf{r}}}_{i}-{{\bf{r}}}_{i}^{{\rm{bcc}}})={\bf{0}},$$
    (4)

    which ensures that all atomic displacements are exactly zero in the ideal case, i.e., when all atoms are on their bcc lattice sites. For MD simulations, the relaxed positions ri should be understood to correspond to the MD time-averaged positions \({\overline{{\bf{r}}}}_{i}\) over a sufficient number of MD steps.

  2. 2.

    Calculate the following projection amplitude for each of the four 〈111〉bcc directions:

    $${p}_{{\langle 111\rangle }_{{\rm{bcc}}}}\equiv \langle | {{\bf{d}}}_{i}\cdot {{\bf{e}}}_{{\langle 111\rangle }_{{\rm{bcc}}}}| \rangle =\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}| {{\bf{d}}}_{i}\cdot {{\bf{e}}}_{{\langle 111\rangle }_{{\rm{bcc}}}}| ,$$
    (5)

    where n is the number of atoms, \({{\bf{e}}}_{{\langle 111\rangle }_{{\rm{bcc}}}}\) the unit vector along the considered 〈111〉bcc direction, and \({{\bf{d}}}_{i}\cdot {{\bf{e}}}_{{\langle 111\rangle }_{{\rm{bcc}}}}\) the projected displacement of the ith atom along the 〈111〉bcc direction. The explicit formulae for the four 〈111〉bcc directions are as follows:

    $${p}_{{[111]}_{{\rm{bcc}}}}=\langle | {{\bf{d}}}_{i}\cdot {{\bf{e}}}_{{[111]}_{{\rm{bcc}}}}| \rangle ,$$
    (6)
    $${p}_{{[1\bar{1}\bar{1}]}_{{\rm{bcc}}}}=\langle | {{\bf{d}}}_{i}\cdot {{\bf{e}}}_{{[1\bar{1}\bar{1}]}_{{\rm{bcc}}}}| \rangle ,$$
    (7)
    $${p}_{{[\bar{1}1\bar{1}]}_{{\rm{bcc}}}}=\langle | {{\bf{d}}}_{i}\cdot {{\bf{e}}}_{{[\bar{1}1\bar{1}]}_{{\rm{bcc}}}}| \rangle ,$$
    (8)
    $${p}_{{[\bar{1}\bar{1}1]}_{{\rm{bcc}}}}=\langle | {{\bf{d}}}_{i}\cdot {{\bf{e}}}_{{[\bar{1}\bar{1}1]}_{{\rm{bcc}}}}| \rangle .$$
    (9)
  3. 3.

    Sort the projections according to their values:

    $${p}_{{[111]}_{{\rm{bcc}}}},{p}_{{[1\bar{1}\bar{1}]}_{{\rm{bcc}}}},{p}_{{[\bar{1}1\bar{1}]}_{{\rm{bcc}}}},{p}_{{[\bar{1}\bar{1}1]}_{{\rm{bcc}}}}\Rightarrow {p}_{1},{p}_{2},{p}_{3},{p}_{4},$$
    (10)

    where p1 is the largest, followed by p2, p3, and p4.

  4. 4.

    Pick up p1, corresponding to the direction showing the largest amplitude, as the structure descriptor. This direction is the one along which the symmetry is broken and which is therefore representative of the bcc–ω transformation. Then classify the investigated structure according to p1 into the different possible classes of structures. Specifically, if the structure is bcc, p1 should be close to zero. If the structure is pefect or defective ω, in contrast, p1 should be close to the values corresponding to the displacements visualized in Fig. 2. Table 1 shows the values of p1 for the ideal cases.

    Table 1 {p1, p2, p3, p4} values for several ideal cases in units of cω (cf. Eq. (2)).
    Full size table

In the following, we will take the approach above for pure metals as our starting point and extend it to disordered alloys.

Detection of the bcc–ω transformation for disordered alloys

The approach described above is well suited to detect the bcc–ω transformation in pure metals21,24. For disordered alloys, however, this approach is not sufficient, because the atomic displacements are induced not only by the structural transformation but also by chemical disorder, i.e., chemically induced LLDs. Consequently, regardless of whether the bcc structure is dynamically stable or not, the relaxed atomic positions can feature significant deviations from the ideal bcc lattice sites due to the different local chemical environments. This means that a nonzero p1 cannot be uniquely connected to the bcc–ω transformation.

The key to solve this issue is to consider the symmetry breaking due to the bcc–ω transformation. Specifically, when a transformation to an ω-like structure occurs, the atomic displacements should be substantially larger for the symmetry-broken 〈111〉bcc direction than for the other directions, i.e., p1 ≫ p2. If the relaxed structure is bcc, in contrast, there should be no substantial preference towards a certain 〈111〉bcc direction.

We thus modify the approach as follows to distinguish the bcc–ω transformation from chemically induced LLDs for disordered alloys:

  1. 1.

    Same as for unary systems.

  2. 2.

    Same as for unary systems.

  3. 3.

    Same as for unary systems.

  4. 4.

    Classify into bcc-like and ω-like structures according to

    $${\rm{bcc}}:\quad {\rm{if}}\quad{{\Delta }}p={p}_{1}-{p}_{2}\,<\,{{{\Delta }}}_{{\rm{bcc}} \to \omega},$$
    (11)
    $$\omega {\hbox{-}}{\rm{like}}:\quad {\rm{if}}\quad{{\Delta }}p={p}_{1}-{p}_{2}\,>\,{{{\Delta }}}_{{\rm{bcc}}\to \omega },$$
    (12)

    where Δbcc → ω is a given criterion to distinguish the bcc and the ω-like structures.

The proper critical value for Δbcc → ω will likely show some dependence on the considered system. For our present system, as shown below and in Supplementary Discussion, we found that a value of Δbcc→ω ≈ 0.04cω distinguishes well the bcc and the ω-like structures.

For the structures detected as bcc, the atomic displacements ∣di∣ are in general not zero for disordered alloys, unlike for pure metals. These “remaining” displacements can be now unambiguously identified with chemically induced LLDs.

Relaxation of atomic positions at zero temperature

Figure 3 shows the values (marked by the black crosses) of Δp = p1 − p2 for a pseudobinary section of the quaternary Ti–Zr–Hf–Ta alloy after atomic relaxation starting from the ideal bcc lattice sites. It should be emphasized that for each of the investigated compositions many different calculations have been performed representing various chemical arrangements. This variety in the chemical arrangements leads to a spread of the Δp values for a fixed composition, as can be observed by the many vertically stacked crosses in each of the columns.

Fig. 3: Values of Δp = p1 − p2 to distinguish bcc and ω-like structures for the pseudobinary Ti(1−x)/3Zr(1−x)/3Hf(1−x)/3Tax alloys relaxed from the ideal bcc lattice sites at 0 K.
figure 3

For each composition, the results from all the SQS models and from all the volumes are shown.

Full size image

For the alloys enriched by group 4 elements (left side of the plot), many calculations show p1 to be substantially larger than p2, indicating the preference of the atomic displacements to occur along one of the 〈111〉bcc directions. As detailed above, this reveals the dynamical instability of the bcc phase and the transformation towards the ω phase. Note, however, that at each of the shown concentrations in Fig. 3, there are always calculations that give Δp values in the lower region. In fact, it is possible to classify the results of all these calculations into two distinct groups, i.e., a group that shows larger and a group that shows smaller Δp values. The critical value that serves best to separate the two groups is Δbcc→ω ≈ 0.04cω. This choice for Δbcc→ω is corroborated by inspecting other composition regimes and different initial structures (see Supplementary Discussion).

We therefore choose this value as the criterion to distinguish bcc and ω-like structures within the approach for disordered alloys introduced above. As a result, we can now quantify that among the whole set of calculations contributing to Fig. 3 (including all SQS models and all volumes) there are 65%, 68%, 26%, 3%, and 6% of ω-like structures for a Ta content of x = 0%, 5.6%, 11.1%, 16.7%, and 22.2%, respectively. For alloys with a Ta content of more than 25 at.%, none of the calculations shows a Δp larger than Δbcc→ω. This means that these alloys do not show any preference for atomic displacements along one of the four possible 〈111〉bcc directions, indicating that the bcc phase is dynamically stable at 0 K and that the corresponding atomic displacements represent pure chemically induced LLDs.

It is worth stressing with emphasis the fact that even for the alloy composition containing exclusively group 4 elements (x = 0%), there is still a substantial amount of relaxed structures that are detected as bcc. This is likely due to the complex potential energy hypersurface of these chemically disordered alloys, on which the structure can relax at 0 K to a local minimum in the vicinity of the ideal bcc sites rather than the positions corresponding to the ω phase. From a technical perspective, this finding highlights that such derived atomic positions sensitively depend on the specific computational conditions for the relaxation procedure. It is therefore practically essential to compute a sufficient number of configurations to derive reliable conclusions.

Atomic trajectories at finite temperatures

An important feature of low-temperature dynamically unstable phases is the fact that they may be stabilized at higher temperatures. We have therefore also conducted ab initio MD simulations for TiZrHf to analyze the temperature-driven stabilization. Figure 4 shows a representative set of atomic trajectories (Fig. 4a–c) and respective averaged atomic positions (Fig. 4d–f) at different temperatures.

Fig. 4: Atomic positions for a 54-atom model of TiZrHf at the bcc lattice parameter of ≈3.469 Å from ab initio MD simulations.
figure 4

The thin gray grids correspond to the boundaries of the 2-atom conventional bcc unit cells. a–c Two-dimensional histograms of the atomic positions projected onto the {001}bcc plane at the corresponding temperature. The histograms are normalized into one and color-coded in a log scale. d–f Mean atomic positions at the corresponding temperatures.

Full size image

At 1500 K, the average atomic positions are close to the ideal bcc lattice sites, with the MD trajectories fluctuating around these average positions (Fig. 4c, f). This observation matches the behavior of the constituting group 4 elements (Ti, Zr, Hf), all of which show a thermodynamically stable bcc phase at elevated temperatures. In contrast, at lower temperatures (300 and 900 K) the trajectories and more clearly the average atomic positions show a preference to be shifted along a particular direction indicating the structural transition from the bcc to the ω phase. In order to quantify the transformation behavior, we utilize the averaged atomic positions as the key input to our detection method. This enables us to separate the impact of atomic vibrations from the transformation and from the chemically induced LLDs.

Figure 5 shows the absolute values of the projections (p1–p4) obtained from the average atomic positions. At temperatures less than ≈1000 K, p1 (blue symbols) is clearly larger than the other p’s (i.e., Δp > Δbcc→ω), which demonstrates that for TiZrHf ω-like structures are more favorable as compared to the bcc structure. From the representation of the absolute values of the projections it is possible to directly classify the average structures obtained at 300 and 600 K as defective ω structures (cf. Table 1). For 900 K the averaged MD geometries correspond to the defective ω structure as well, but the values of the projections can occasionally be higher due to the possibility of transforming into the twin-variant bcc structure (cf. Fig. 2c). This observation is consistent with results obtained for pure Ti21,24 and indicates that the simulations at 900 K are close to the bcc–ω transformation.

Fig. 5: Projected displacements of the average MD positions of TiZrHf at the bcc lattice parameter of ≈ 3.469 Å.
figure 5

The projection directions are distinguished by the orientation of the triangular markers. The solid and dashed horizontal lines indicate the projection amplitudes for the ideal (perfect and defective ω) cases provided in Table 1.

Full size image

At temperatures higher than ≈1000 K, all projections show similar values (i.e., Δp < Δbcc→ω) confirming the thermodynamic and dynamical stability of the bcc phase at high temperatures. The projections are however non-zero as it would be the case for the ideal bcc structure, and these non-zero values indicate the impact of chemically induced LLDs even at these high temperatures. For TiZrHf at 1500 K, the such obtained chemical-disorder-induced mean displacement is ≈0.16 Å (cf. Supplementary Discussion C). This value is similar to the chemical-disorder-induced atomic displacements for other bcc refractory alloys with 60–70 at.% of group 4 elements, namely, ZrNbHf, TiZrNbHfTa, and TiZrMoHfTa, reported previously15.

Note that the here-employed 54-atom 3 × 3 × 3 supercell of the 2-atom conventional bcc unit cell may not provide a quantitative bcc–ω transition temperature, as previously found for pure Ti21,24. Calculations with larger supercells are beyond the scope of the present work.

Phase stabilities and TRIP behavior

Based on the foregoing analysis that allows us to properly distinguish between bcc and ω structures, we are now in a position to derive well-quantified phase stabilities including atomic relaxations also for refractory HEAs enriched by group 4 elements. We thus analyze in the following the phase stabilities for the quaternary Ti–Zr–Hf–Ta and quinary Ti–Zr–Nb–Hf–Ta alloys and show the connection to the experimentally observed TRIP behavior. We start the discussion by considering unrelaxed, i.e., ideal-lattice, phase stabilities to clarify the impact of relaxations.

Figure 6a shows the ideal-lattice ab initio energies of the bcc, hcp, and ω phases for the same pseudobinary section of Ti–Zr–Hf–Ta as in Fig. 3. While the hcp and the ω phase are close in energy over the whole composition range, there is a strong destabilization of the bcc phase with respect to the other two phases when the Ta concentration is decreased. When the Ta content becomes less than ≈30 at.%, bcc becomes energetically destabilized as compared with the other two phases. These results are largely inconsistent with the experimental findings; in ref. 6 a bcc phase was observed for Ta concentrations down to 12 at.%. This contradiction can be resolved by taking the impact of LLDs into account. Figure 6b shows the corresponding phase stabilities and reveals that the stability of bcc with respect to hcp and ω is strongly affected by LLDs. Note that, as discussed above, a bcc-initialized structure can relax into an ω phase and vice versa, which can be detected by our proposed approach. The bcc phase is now the energetically preferred phase even down to a Ta concentration of ≈14 at.%, which is in close agreement with experiments6. The strong change in the bcc stability is due to the much larger impact of LLDs in the bcc phase than in the hcp and the ω phases (see Supplementary Fig. 6). Note that the bcc phase may be further stabilized by temperature effects as demonstrated by the MD results above.

Fig. 6: Phase stabilities with respect to the bcc phase for the pseudobinary section Ti(1−x)/3Zr(1−x)/3Hf(1−x)/3Tax.
figure 6

a Atoms fixed to the ideal lattice sites. b Atoms allowed to relax. The energies shown for ω correspond to the defect-free ω structure. The bcc–hcp TRIP composition confirmed by experiments (≈12 at.%6) is shown by the thick gray vertical line.

Full size image

As highlighted in Fig. 6b by the thick gray line, the ab initio-computed phase stabilities are in good consistency with the experimentally reported occurrence of the bcc–hcp TRIP behavior reported in ref. 6. To make TRIP possible, the bcc–hcp energy difference must be close to zero, which is reflected in Fig. 6b. Turning this argument around, we can say that the ab initio-computed phase stabilities—properly containing the impact of LLDs—can be utilized as a guiding descriptor in the design of TRIP-supported bcc HEAs.

To scrutinize this design hypothesis we extend our analysis to the quinary Ti–Zr–Nb–Hf–Ta system. Figure 7 shows the energy difference between bcc and hcp for a ternary subsection. The lower right corner corresponds to Nb0.5Ta0.5 and this is the composition where the bcc phase is the most stable, by ≈140 meV/atom over the hcp phase. Moving away from this composition into the triangle increases the concentration of the group 4 elements (Ti, Zr, Hf), and we observe that the bcc phase is quickly destabilized with respect to the hcp phase.

Fig. 7: Ab initio-computed relaxed energy differences between bcc and hcp for the pseudoternary Tix(Zr0.5Hf0.5)y(Nb0.5Ta0.5)1−x−y alloys.
figure 7

Compositions investigated experimentally in ref. 5 are shown by the circles. The thin gray dotted line shows the bcc–hcp equilibrium composition when the atoms are fixed to the ideal lattice sites (cf. Supplementary Fig. 8a). The two arrows highlight the impact of the relaxations. Visualization was performed using MPLTERN56.

Full size image

Similarly as for the quaternary alloy system, the ab initio energies for the quinary Ti–Zr–Nb–Hf–Ta alloy system are in good consistency with experiments if atomic relaxations are taken into account. In ref. 5 various compositions were experimentally investigated for Ti–Zr–Nb–Hf–Ta as indicated by the circles in Fig. 7. TRIP behavior was observed for the composition of Ti35Zr27.5Hf27.5Nb5Ta5 (pink circle) which is located close to the contour of the bcc–hcp equilibrium compositions, but not for the other compositions (orange circles). This strengthens the argument that the ab inito predicted bcc–hcp equilibrium compositions provide a good descriptor for selecting candidates for TRIP alloys, if LLDs are properly included. Inclusion of LLDs is indeed necessary as it modifies the bcc–hcp energy difference qualitatively and quantitatively (see also dotted vs. thick lines in Fig. 7 as well as Supplementary Fig. 8a).

We note that in general for a high-accuracy prediction of phase stabilities other contributions such as chemical short-range order may be of relevance36. Such effects could be assessed with Monte Carlo simulations14,37 also in combination with MD simulations7,38,39,40,41,42,43,44,45.

Valence electron concentration (VEC)

Ab initio simulations of phase stabilities are computationally expensive, and it would be useful to have a more efficient descriptor for the search of TRIP HEAs available. In this respect, we have analyzed the VEC, which was previously reported to correlate well with HEA phase stabilities46,47,48. Our results for Ti–Zr–Nb–Hf–Ta (Supplementary Fig. 8b) show that the VEC indeed correlates well; however, only with the ideal-lattice energy differences (Supplementary Fig. 8a). Since, as mentioned above, LLDs change the dependence qualitatively and quantitatively, the correlation with the VEC is impaired for the relaxed energy differences. The quantitative shift can be accounted for by “calibrating” the VEC with our explicit ab initio data. The qualitative changes cannot be easily accounted for, and they reveal the approximative nature of the VEC descriptor. The best estimate extracted from our data is that the VEC for finding bcc–hcp TRIP HEAs should lie in the range of 4.1–4.2.

Discussion

For disordered alloys, it is a non-trivial task to rigorously separate atomic displacements caused by a structural transformation from those induced by chemical disorder. We have therefore introduced and applied a method to solve this challenge. In our method, the symmetry breaking due to the structural transformation is analyzed by utilizing projected atomic displacements. We have applied the developed method to a large set of bcc refractory HEAs including group 4 elements (Ti, Zr, Hf) to analyze their dynamical and thermodynamic phase stability.

A crucial finding of our study is that the—properly determined—chemically induced LLDs significantly shift the bcc–hcp equilibrium compositions towards larger contents of group 4 elements. The such obtained bcc–hcp equilibrium compositions are in good agreement with those for which experimental studies reported a beneficial bcc–hcp TRIP effect. By calibration to our ab initio data, we could device a VEC range of 4.1–4.2 as the most promising one for the search of bcc–hcp TRIP HEAs.

The results in the present study highlight the strong coupling between bcc–hcp TRIP, LLDs, and ω precipitates, all of which are key factors of mechanical properties of refractory alloys. We have demonstrated that, by carefully analyzing the atomic displacements, the relations among these key factors can be discussed in a rigorous way. The approach introduced in the present study will promote the understanding of mechanical properties of refractory alloys on the basis of ab initio calculations and will help designing of novel bcc–hcp TRIP HEAs.

Methods

Supercell models

In this study, we considered two sets of alloys, namely, Ti(1−x)/3Zr(1−x)/3Hf(1−x)/3Tax pseudobinary alloys and Tix(Zr0.5Hf0.5)y(Nb0.5Ta0.5)1−x−y pseudoternary alloys. For Ti(1−x)/3Zr(1−x)/3Hf(1−x)/3Tax, we considered seven x from 0 up to 1/3. For Tix(Zr0.5Hf0.5)y(Nb0.5Ta0.5)1−x−y, we considered 16 compositions.

All the considered refractory alloys were modeled based on the supercell approach. 54-atom supercells based on a 3 × 3 × 3 expansion of the 2-atom unit cells of the bcc and the hcp phases were considered. Chemical disorder was mimicked using special quasirandom structures (SQSs)49, where the pair probabilities of the first few nearest-neighbor shells were optimized to be close to those in the ideal-mixing state. To achieve better energy convergence, we computed several SQS-based configurations with similarly optimized pair correlation functions and by permuting the elements. Further details can be found in Supplementary Methods A.

As discussed in the “Results” section, the bcc structure is dynamically unstable for alloys consisting mainly of group 4 elements and hence transforms to the ω-like structures. We therefore also computed the energies of the perfect ω structure to discuss this structural transformation and also the stability with respect to the hcp phase. The supercell models of the perfect ω structure were made by displacing the atoms in the bcc-phase supercell models according to the way described in Fig. 2a.

Electronic-structure calculations

The plane-wave basis projector-augmented wave (PAW) method50 was employed in the framework of density functional theory (DFT) within the GGA of the Perdew–Burke–Ernzerhof (PBE) form51 as implemented in the VASP code52,53,54. Internal atomic positions were initialized on the ideal lattice sites. For each fixed volume, ionic relaxations were performed until the residual forces became <5 × 10−2 eV/Å with keeping the cell shape fixed. Further details can be found in Supplementary Methods B.

Ab initio molecular dynamics (MD)

To analyze the structural stability of the bcc phase we also evaluated the averaged atomic positions at finite temperatures employing ab initio MD simulations. For this purpose we considered the prototypical bcc TiZrHf alloy, which reveals strong dynamical instabilities at low temperatures. We utilized two 54-atom bcc SQS models with a lattice parameter of ≈3.469 Å, which is close to the equilibrium lattice parameter at 0 K taking relaxations into account. For the MD runs, the NVT-ensemble was employed, where the temperature was controlled by the Langevin thermostat. Further details can be found in Supplementary Methods C.