Abstract
The functionality of many materials is critically dependent on the integration of dissimilar components and on the interfaces that arise between them. The description of such heterogeneous components requires the development and deployment of first principles methods, coupled to appropriate dynamical descriptions of matter and advanced sampling techniques, in order to capture all the relevant length and time scales of importance to the materials’ performance. It is thus essential to build simple, streamlined computational schemes for the prediction and design of multiple properties of broad classes of materials, by developing interoperable codes which can be efficiently coupled to each other to perform complex tasks. We discuss the use of interoperable codes to simulate the structural and spectroscopic characterization of materials, including chemical reactions for catalysis, the description of defects for quantum information science, and heat and charge transport.
Similar content being viewed by others
Introduction
The understanding and prediction of materials properties and their de novo design are widespread research activities in science and engineering, contributing to the development of new technologies, with impacts in quantum information science, energy, health and national security. Computational materials science is now recognized as an integral part of the innovative process leading to materials discovery and design, and the developments of predictive, simulation frameworks at various length scales, as well as of databases for materials1,2,3,4,5,6,7,8,9 have flourished in the last two decades.
The use of software to engineer materials and molecules is not a new activity. There has been widespread use of simulations in the semiconductor and pharmaceutical industries, where simulation codes have traditionally been used as end-of-the-line engineering tools. An example is the use of numerical simulations in the design process of new chips which were previously planned based on specific materials chosen through experimentation. The objective of modern materials’ theories, codes and software is to be predictive and to eventually lead to strategies to design materials that have not yet been made, have not yet been fully planned based on experiments, and perhaps do not even result from conventional synthetic and fabrication routes. First-principles codes have a broad potential and they may be used to produce the necessary data to machine learn properties of vast classes of materials, such as those required for the development of quantum information science and technology10,11. Computationally generated data, ideally made searchable through the definition of metadata and available to the community12,13, may then be used to design strategies that include innovative feedback loops with experiments.
There are many requirements that materials design should satisfy. It is critical to predict functionalities of systems with complex, heterogeneous morphologies and to simulate and enable engineering of basic mass, charge and energy transport processes. In most cases it is also essential to understand and predict the interaction of matter with external stimuli, e.g., light, used to probe materials properties or to design specific functionalities. A number of phenomena involved in the spectroscopic characterization of materials or in fundamental transport processes, are inherently quantum-mechanical and thus require a quantum-mechanical treatment of interatomic interactions, at the atomistic scale. Likewise, chemical reactions occurring during many processes of interest in materials science, e.g., catalysis or corrosion, or in processes related to material synthesis, often require an atomistic, quantum mechanical description.
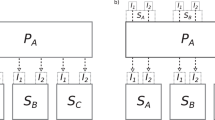
Here we discuss codes that simulate the properties of materials at the quantum mechanical level and specifically ways of enabling modular simulations of multiple properties for prediction and design purposes. In recent years, an emerging trend in computational materials science has been the development of codes that singly carry out specific tasks and cooperatively perform complex simulations. The interface between codes is critical for maintainability, re‐usability, and extensibility of simulation software. In particular we describe in the following the coupling of several codes for the simulations of materials at the atomistic, quantum mechanical level: a first principles molecular dynamics (FPMD) code, Qbox14 (http://qboxcode.org/), coupled with advanced sampling software, SSAGES15 (https://ssagesproject.github.io/), and with software that simulates spectroscopic properties, WEST16 (http://west-code.org/). The objective is to tackle a widespread problem in processes of interest in materials science, i.e., rare events and long time-scales, while building, at the same time a computational strategy for advanced characterization of materials, through the use of various type of computational spectroscopies (see Fig. 1). We also discuss coupling of a classical molecular dynamics code, LAMMPS17, with FPMD to facilitate the simulation of thermal transport processes, and the use of FPMD in the presence of external potentials to describe electronic charge transport, PyCDFT18. Although we focus on specific codes, the strategy presented below is general and the chosen examples, including molecular and condensed systems, chemical reactions at surfaces, and liquids under various thermodynamic conditions, are representative of the heterogeneous systems that can be tackled today with quantum simulations.
Basic physical quantities (in blue) exchanged between first principles molecular dynamics simulations, advanced sampling techniques and calculations of spectroscopic properties. The codes used here (Qbox14; SSAGES15; WEST16) are coupled using a driver-engine approach, where data-exchange operations are regulated by the client-server protocol.
We now turn to the description of coupling software strategies followed by specific examples.
Results
Coupling interoperable software
Methods for the calculations of a variety of materials properties from first principles have been actively developed in the last few decades. Their implementation and release in, for instance, electronic structure codes, is a challenging task due to the rapidly increasing complexity of parallel simulation codes on changing architectures. This problem may be solved or alleviated by adopting a modular computational strategy where an entire simulation is obtained either through in vivo or ex vivo coupling of interoperable codes, i.e., by executing multiple codes concurrently or sequentially19. In this way the scope of each code is limited to a portion of the entire calculation workflow, with reduced software dependencies; hence each code can grow vertically and independently, while maintaining interoperability through inter-process communication. Devising interoperable codes is challenging because of the lack of standardized procedures for sharing information between the codes: each code may use different data structures, file formats, units and coding language. One further complication arises when the codes are required to communicate frequently, in this case in vivo coupling is necessary to achieve efficient interoperability, and synchronization schemes are required to manage the concurrent execution of codes. Deploying seamlessly coupled codes rests on important technical developments and decisions.
We describe an in vivo interoperability strategy that enables the calculation of materials properties encompassing free energies and electronic properties using a driver-engine approach (see Fig. 1). In this context, a driver code controls the execution flow of one or more engine codes, with inter-process communication between the driver and the engines regulated by a client-server interface20. In the following we describe the client-server protocol adopted to couple codes, which uses a markup language to document exchanged data between codes.
Within the client-server model, the driver program acts as a client and sends a set of instructions to an engine code acting as a server. Multiple servers may be used to distribute computationally intensive workloads. In the current approach, all operations occur through interaction via the file system. Hence, the client and the servers may be located in separate machines and either share the same filesystem or allow for fast data movements, such as via gridFTP21. Although using the file system for inter-process communication is admittedly a primitive protocol, the overhead of exchanging files is negligible relative to the cost of quantum-mechanical calculations in all applications reported below, involving FPMD.
The modularity of the client-server protocol minimizes software dependencies between the driver and the engine programs. Ensuring backward compatibility of syntax for the coupling is the only requirement to maintain code interoperability, and the remaining details of the implementation of each code are not restricted. Two kinds of files are shared between the client and the server: (i) a file that contains a set of instructions to be performed by the server, (ii) datasets that are used as input/output by the server. Specifically, the driver writes the set of instructions to a file. The server opens the file, executes all the sequence of commands line-by-line in a predefined way, and closes the file. The server may be instructed to read or write auxiliary data sets, in this case a markup language is used to impose integrity constrains. This process can repeatedly occur, e.g., at every integration step of a FPMD simulation.
The synchronization between the client and server is implemented through the construction and destruction of a lock file that signals when the server is idle or is executing the set of instructions decided by the driver, respectively. In particular, at the beginning of the calculation both the client and the servers are instantiated, with the latter being placed in lock mode by creating a lock file for each server; whenever the client needs to offload the calculation to one of the servers, the driver generates the necessary files and removes the lock file associated to the requested server. The driver will then wait for the lock file to appear again, which indicates that the operations assigned to the server are completed and the driver can read the output generated by the server.
Since the only required feature by the client-server protocol is the ability to exchange text files, any language may be adopted. In the examples discussed below, the server is the FPMD code Qbox, written in C + + , while the clients are written in C + + , Fortran, or Python. The command line interpreter that Qbox uses to read commands represents an added flexibility to the client-server interface. Qbox keeps information in memory between sessions, which facilitates the execution of multiple runs of similar sets of tasks.
In order to ensure interoperability, data exchanged by each code are rigorously documented using a markup language (see Supplementary Methods). The examples reported in this work use the www.quantum-simulation.org (QSO) format to exchange datasets, which is based on the XML markup language, thus ensuring portability and facilitating extensibility, i.e., the addition of new information into the data format. Binary formats are avoided in order to ensure portability of QSO documents. The base64 binary-to-text encoding is used to represent array data structures, and a little-endian byte ordering is enforced on all platforms. In addition, we have packaged together codes and dependencies into containers, thus facilitating multi-site computation using interoperable software.
The client-server strategy for coupling codes is general and may be deployed by several software packages within the computational materials science community. We now turn to discussing applications that are enabled by such in vivo interoperability scheme.
Advanced sampling using first principles molecular dynamics
One of the most widely used methods to investigate a wide spectrum of materials properties is molecular dynamics (MD), a technique22,23 that generates trajectories of collections of atoms obeying classical dynamics. MD simulations with empirical potentials (i.e., force fields parameterized using experimental data) are routinely used to investigate physical phenomena ranging from protein folding24,25 to glass formation26,27 and from self-assembly28 and nucleation29,30,31 to aqueous solutions and electrolytes32 and the structural properties of complex materials33. In many instances, relevant processes may be rare events, where a property of interest occurs within a time scale that is not accessible within a reasonable amount of simulation time due to the presence of large free energy barriers that separate local minima along a rough free energy landscape.
As previous studies showed34,35,36, challenges associated with rugged free energy landscapes may be overcome with advanced sampling methods. A wide range of these methods has been developed to accelerate the exploration of a system and generate free energy profiles along known reaction coordinates, to find transition pathways, and to compute transition rates37,38,39,40,41. These techniques have been majorly applied in conjunction with empirical classical force fields, parametrized using a combination of results from quantum mechanical calculations and experimental data42,43,44,45,46. However, for a number of problems of interest in materials science, especially those involving chemical reactions, adsorption, or isomerization or just rearrangement of bonds, accurate interatomic potentials are not easily available or simply not transferable from the conditions under which they were fitted to other thermodynamic conditions of interest42,43,47,48.
Advanced sampling has been recently coupled with FPMD15,32,33,49, where interatomic forces are computed on-the-fly from quantum mechanical calculations using density functional theory (DFT) thus overcoming the transferability issues present in classical interatomic potentials and avoiding the need to parametrize a force field. The accuracy of FPMD depends on the accuracy of the chosen density functional. Although much experience has been gained for numerous classes of systems and problems regarding the accuracy of certain functionals, there are no established rules yet on how to choose the best functional for a given problem, without going through a number of validation procedures50,51,52,53,54,55,56,57. Nevertheless, FPMD has many advantages23: it does not require experimental input; it allows for the description of bond breaking and formation and, in principle, chemical reactions, and it is of wide applicability. Unfortunately, FPMD remains much more computationally demanding than MD with empirical potentials and it is thus limited to shorter time scales and smaller systems.
A few examples of advanced sampling simulations coupled with FPMD include the use of blue moon sampling58,59,60,61, metadynamics38,62,63 and umbrella sampling64 to address problems involving chemical reactions, phase transitions, and ionic or molecular dissociation65,66,67,68,69,70. The level of theory used in these calculations has been limited to DFT within the Local Density Approximation (LDA) or Generalized Gradient Approximation (GGA), which are among the simplest approximations to the exchange correlation energy71,72. Using the client-server interface between the FPMD code Qbox14 and the SSAGES15 suite of advanced sampling methods, we recently showed how to hierarchically transfer free energy estimates from one level of approximation to another, enabling free energy calculations using FPMD at a hybrid DFT level of theory49. We significantly decreased the time required to obtain a free energy surface (FES) using a hybrid functional71,73 for a simple peptide, by initializing hybrid functional simulations from those based on GGA (PBE74) free energy calculations (see Fig. 2), which are computationally less demanding. We found that FES obtained from classical force fields and FPMD are qualitatively similar, but they exhibit important quantitative differences: the minimum pathway that connects the main free energy minima is different and force fields yield higher free energy barriers. This difference is due to an overestimate of the internal energy contribution imposed by the force field fitting process, and an accompanying underestimate of the entropy of the system in classical simulations (see Fig. 2). Interestingly, FPMD results for selected configurations are consistent with those of high-level quantum chemistry methods, thus validating the accuracy of the chosen density functionals.
Representation of the three metastable minima, β, C7eq, and C7ax of the alanine dipeptide together with the two angles (φ, θ) used as bias (panel a). Entropic (b, c, d panels) and potential energy (e, f, g panels) contributions to the free energy surface of the alanine di-peptide as a function of the illustrated torsion angles49. Free energies are obtained with the force field Amber99sb43,147 and with first principles calculations with semi-local (PBE74) and hybrid (PBE071,73) functionals. The arrows in panel a indicate the minimum free energy path. The circled region in panel e shows significant overestimation of repulsive forces in the classical model. Adapted with permission from ref. 49, copyright (American Chemical Society, 2018).
The in vivo coupling between Qbox and SSAGES is achieved using the client-server model described in the previous section (additional information on the XML files exchanged is included in the Supplementary Methods). In particular, Qbox initially performs a wavefunction optimization to compute the electronic ground state of the system, initializes velocities at the correct temperature, and performs one molecular dynamics integration step. All other integration steps are performed in the following way: SSAGES reads the information needed for the enhanced sampling calculation, e.g., velocities and atomic positions, computes the external bias by specifying new atomic positions, forces and/or velocities, and triggers Qbox to perform a new wavefunction optimization or instructs Qbox to exit after saving a checkpoint. A key feature of this coupling strategy is its efficiency, enabled by the fact that both processes remain active throughout the simulation and current electronic wavefunctions are kept in memory between ionic moves during the FPMD simulation. FPMD dominates the computational time for typical simulations, resulting in minimal overhead on a per-timestep basis.
The Qbox-SSAGES coupled software was used to investigate the dissociation of aqueous solutions under pressure, which represents a much more complex application than the peptide discussed before. In ref. 32 we considered sodium chloride in water at high temperature at pressure, namely at conditions (11 GPa, 1000 K) relevant to geochemical problems. Consistent with the decrease of the water dielectric constant at these conditions75,76, we found that the stability of contact ion pairs increases under pressure, relative to ambient conditions, although much more moderately than anticipated. The relative stability of the different ionic configurations is affected by water self-dissociation, which is properly described by FPMD simulations. Interestingly, we found that the dissociation path of the salt at extreme conditions differs from that observed at ambient conditions, with no intermediate states corresponding to different solvation structures.
In another case involving a chemical reaction at a solid surface33, the free energy landscape of a heterogeneous catalytic reaction was computed. The dissociation of a nitrogen molecule on a ruthenium surface—a classic reaction in catalysis—was simulated using FPMD coupled to a neural-network assisted enhanced sampling algorithm, referred to as the Combined Frequency Force (CFF) method77, implemented in the SSAGES15 software. Figure 3 shows representative results for the underlying FES, where the two basins correspond to the reactants and the product. This approach allowed for an improved evaluation of the dissociation free energy barrier compared to the harmonic approximation used in previous calculations. Importantly, it does not require a priori knowledge of the reaction pathway, thereby providing an important advantage over traditional methods based on DFT calculations of the potential energy.
Free energy surface (FES) for nitrogen dissociation on ruthenium computed from CFF77—FPMD simulations using 16 walkers33. The axes correspond to the distance Z from the surface and the separation r between the nitrogen atoms, in Angstrom. The converged FES shown here corresponds to the stage reached after 33 ps of FPMD. The mean free energy path between N2* (square) and 2 N* (circle) is represented by a white dashed line. Adapted with permission from ref. 33 under the Creative Commons Attribution License CC BY 4.0.
Although simulations such as those reported in ref. 32,33 remain computationally demanding, they are clearly reaching the stage of addressing important problems, way beyond proof-of-principle demonstrations.
Spectroscopy from first principles
Techniques enabling the calculation of spectroscopic properties of materials and molecules are critical components of a predictive simulation framework of complex systems. Through the calculation of response functions and electronically excited states, these tools may be used as computational probes of the atomic structure simulated with FPMD, or FPMD coupled with advanced sampling. Numerous excited state properties and spectroscopic signatures may not be accurately obtained from the solution of the Kohn-Sham equations78,79, i.e., the basic equations of DFT used for the predictions of ground state properties80. Recent developments of hybrid functionals have led to improved simulations of charged excitations for certain classes of materials81,82,83,84, while the time-dependent formulation of DFT (TDDFT)85 has provided a computationally tractable method to compute neutral excitations86. However, most hybrid functionals are not yet able to reliably treat broad classes of heterogeneous systems where materials with different dielectric properties are combined87; on the other end, TDDFT within the adiabatic approximation to the exchange−correlation functional may not be sufficiently accurate to describe certain types of excited states where charge transfer and excitonic effects are relevant88.
Many-body perturbation theory (MBPT)89 provides a way of predicting excited state properties of molecules and materials, and holds the promise of overcoming the limitations, at least for certain materials, of hybrid DFT and TDDFT. Within MBPT, one can obtain charge excitation energies corresponding to photoemission and inverse photoemission spectra by evaluating16,90,91 so called self-energies (e.g., electron-electron92 or electron-phonon93 self-energies); furthermore, one can obtain90,91,94 neutral excitation energies corresponding to optical spectra by solving the Bethe−Salpeter equation (BSE)89,95,96,97,98. Several methodological advances have been proposed to improve the efficiency of MBPT calculations16,94,99,100,101,102,103,104, which have enabled the simulations of relatively large and complex systems, e.g., heterogeneous solids and liquids and nanoparticles with thousands of electrons. In particular, electronic structure calculations based on MBPT can be performed using a low-rank representation of density response functions16,104, whose spectral decomposition is obtained through iterative diagonalization16,105,106, thus avoiding the inversion and storage of large dielectric matrices. Such a diagonalization can be carried out without explicitly computing empty electronic states using density functional perturbation theory (DFPT)107. An implementation based on this strategy is at the core of the WEST code16 interfaced with the Quantum Espresso108 code, and it has been successfully applied to investigate the quasi-particle energies of numerous systems109 including defects in semiconductors52,110,111,112, nanoparticles16,83,99, aqueous solutions50,55, and solid/liquid interfaces16,52.
We have recently reformulated MBPT calculations of charged113 and neutral94 excitations by performing DFT calculations in finite electric fields, instead of using DFPT. The formulation has been implemented by coupling the Qbox14 and WEST16 codes using the client-server protocol. In particular, the variation of the charge density δn in response to the applied perturbation δV is computed by Qbox performing two self-consistent calculations: \(\left( {H \pm \delta V} \right)\left| {\psi _i^ \pm } \right\rangle = \varepsilon _i^ \pm \left| {\psi _i^ \pm } \right\rangle\), where H is the Kohn-Sham Hamiltonian. The variation of the charge difference may be obtained as \(\delta n = \frac{1}{2}(n^ + - n^ - )\), where \(n^ \pm = \mathop {\sum }\nolimits_i \left| {\psi _i^ \pm } \right|^2\). The finite-field approach allows for the straightforward calculation of response functions beyond the so called random phase approximation (RPA), which neglects the response of the perturbation arising from the exchange-correlation term; in addition the approach can be readily combined to DFT calculations using hybrid functionals for which analytical expressions of the functional derivative of the exchange correlation potential with respect to the charge density are not available113. In our implementation, WEST is the driver program of multiple Qbox instances, which initially perform a wavefunction optimization step to compute the electronic ground state of the system. WEST generates the perturbation δV, and the self-consistent calculations are solved by Qbox, which returns the linear variation of the charge density δn. Data for both δV and δn are exchanged by the two codes using an XML file that conforms to the annotated function3d.xsd XML schema (see Supplementary Methods). Analogously to the case described in the previous section, the in vivo coupling between WEST and Qbox facilitates the execution of response commands by keeping in memory the electronic structure of the system.
Using the WEST-Qbox coupling, we have computed exciton binding energies of several molecules and absorption spectra of condensed systems, including water samples with hundreds of atoms94. We emphasize that the coupling allows one to solve the BSE bypassing altogether the calculation of dielectric matrices and virtual states. In addition, the formulation implemented in ref. 94 uses linear combinations of Bloch orbitals that are localized in appropriate regions of real space using the recursive bisection method, thus leading to substantial computational savings. We note that calculations beyond the random-phase approximation become straightforward in finite field, and the complexity and scaling of solving the BSE is the same when using local or hybrid-DFT calculations as starting points. The same finite field approach can also be used to perform GW calculations113,114 and obtain quasi-particle orbitals, through the evaluation of the eigenvectors of the irreducible density-density response function. Recently, a method based on machine learning was introduced to speed-up MBPT calculations115. In particular, the data sets exchanged by WEST and Qbox for the calculation of absorption spectra were used to train a surrogate model of the dielectric screening computed in finite field. Interoperability between WEST and Tensorflow (https://www.tensorflow.org/) enabled computational gains of up to two orders of magnitude for the calculation of absorption spectra of molecules and materials at finite temperature.
The ability to obtain the screened Coulomb interaction by solving DFT in finite electric field has made possible quantum embedding calculations116,117. In the presence of specific localized electronic states, e.g., those associated with spin defects in semiconductors or insulators, one may obtain geometries and energies of excited states by performing DFT calculations with constrained occupation numbers. In addition, the effect of the environment around the defect may be incorporated in the calculation through the definition of an effective Hamiltonian including a screened Coulomb interaction. Using these two concepts, and computing the screened Coulomb interaction inclusive of exchange-correlation interactions through the WEST-Qbox coupling, we have built a quantum embedding theory116,117 (Fig. 4) that goes beyond the constrained random phase approximation118,119,120. The accuracy and effectiveness of this approach was demonstrated by investigating several spin defects in semiconductors that are of interest for quantum information technologies116. Importantly, the proposed quantum embedding theory is able to capture strongly-correlated electronic states of active regions (defined by the localized electronic states of the defects), with the rest of the system described within DFT. An important consequence of the quantum embedding theory, as demonstrated in ref. 116,117, is that an effective Hamiltonian describing strong correlations within the active site may be defined and solved on classical as well as on quantum computers using ex vivo interoperability schemes with quantum chemistry and quantum computing software packages, e.g., PySCF121 and Qiskit (https://qiskit.org/). Quantum computers promise, in principle, a much more favorable scaling as a function of system size than classical architectures although noise and quantum correction issues are still affecting the accuracy of results obtained on near-term quantum computers and substantial progress is needed before complex materials science simulations may be carried out on quantum computers122.
In vivo coupling of the Qbox14 and WEST16 codes was used to build an embedding theory to study strongly correlated defects in semiconductors and insulators116,117. Single particle wavefunctions and eigenvalues obtained from DFT calculations are used to compute the screening of the environment on a chosen active region of the material (defined, e.g., by the localized single particle states of a defect). The screening enters the definition of a second quantized Hamiltonian that may be diagonalized using configuration interaction techniques to obtain many body states of the defect.
Transport from first principles
Similar to the computation of free-energy surfaces and spectroscopic properties, coupled interoperable codes may be used to compute transport properties, in particular, to evaluate quantities relevant to the description of electronic transport in the hopping regime, and to simulate heat transport in insulators.
The hopping regime of charge transfer between localized states in molecules and solids is the dominant charge transfer mechanism in many organic crystals, conducting polymers, in several metal oxides in the solid state, and in nanoparticle solids123,124,125,126. In many instances, charge transfer in the hopping regime may be described using Marcus theory127,128,129 which predicts the charge transfer rate in terms of diabatic electronic coupling and reorganization energies, in addition to free-energy differences. Constrained density functional theory (CDFT)130 provides a robust framework for constructing diabatic states from first principles and for predicting their electronic coupling in molecules and solids (see Fig. 5): constraint potentials are added to the Kohn‐Sham Hamiltonian, and their strengths are optimized so as to obtain a desired localized charge on a given site. By using the client-server functionality of Qbox as described in the previous section, we recently implemented a Python package (PyCDFT18) to perform single‐point self‐consistent‐field and geometry optimization calculations using CDFT. The operations specific to PyCDFT are decoupled from those carried out by Qbox, again presenting important advantages for the maintainability and reusability of the package.
Charge transfer excitation processes in assemblies of hydrogenated Si nanoparticles148 (panel a) and in the bulk and at the surface of crystalline BiVO4149,150 (panel b), investigated using constrained density functional theory18. Panel b is reproduced with permission from ref. 150, copyright (American Chemical Society, 2020).
As a last example, we describe the simulation of heat transport, in particular the calculation of the ionic thermal conductivity. As in the case of advanced sampling, most calculations of the thermal conductivity, especially those for large systems, have been carried out using empirical interatomic potentials. However, first principles methods have been proposed in the recent literature, based on approximate solutions of the Boltzmann transport equation (BTE)131,132, on Green-Kubo (GK) formulations133,134, and using nonequilibrium molecular dynamics (NEMD)135,136. Approximate solutions of the BTE can only be applied to solids. The method proposed in ref. 133 is the only one available to perform first principles simulations based on GK. This elegant approach involves repeated solutions of the Sternheimer equation to calculate the heat current within DFPT107. Addressing the need for an efficient and general quantum simulation framework for thermal properties of materials, we developed a method to simulate heat transport from first principles based on approach to equilibrium simulations (SAEMD)137. The method can be used for homogeneous and heterogeneous solids, and in the latest generalization also to liquids138; it has the important advantage of requiring only the computation of MD trajectories and atomic forces, with no additional calculation of energy derivatives or direct calculations of currents. Recently, we carried out FPMD simulations of the thermal conductivity of a representative oxide, MgO, by using Qbox to compute DFT forces on atoms and LAMMPS17 to integrate the equation of motion and to apply the local thermostats required in the application of SAEMD. We successfully simulated systems with ~1000 atoms and using extrapolation techniques we obtained the thermal conductivity of MgO from first principles. However, our calculations highlighted the need of much larger simulation cells to obtain robustly converged results. Hence, a direction we are exploring is the use of deepMD139 to simulate thermal properties and work is in progress to apply this technique to liquid water.
Discussion
We described a strategy to couple interoperable software for quantum simulations of materials and we presented examples of calculations of properties of heterogeneous systems, including molecules, solids, liquids and surfaces. Interoperable software elements can be independently modified and maintained, thus facilitating rapid developments and release of new ideas and new features. Although we described specific codes in this article, the strategy presented here is general. It does not require the definition of universal format standards, and it is generalizable to include properties and systems beyond the examples we have discussed. For example, work is in progress to couple FPMD and calculation of excited state properties with machine learning techniques of dielectric screening115, and to couple FPMD with quantum thermostats and calculations of excited state properties beyond DFT to evaluate electron phonon interaction in clusters, solids and amorphous systems containing light atoms. Additional work is in progress to evaluate activation energies in reactive systems and morphology changes in metallic clusters by coupling Qbox and SSAGES, and to evaluate coherence times of spin defects in solids by coupling DFT and spin Hamiltonian calculations140,141,142,143.
Finally, we note that the ability to carry out coupled calculations will serve as a stepping stone to build hybrid strategies to use classical and quantum computers, especially near-term quantum computers116. Different properties or different parts of a calculation may be performed on different architectures, depending on the scaling of the algorithm used.
We expect that the development of extensible codes that can be interfaced with each other to perform complex tasks will enable modular simulations of multiple properties of materials, thus accelerating the development of design strategies applicable to broad classes of systems and effectively broadening the scope of quantum simulations.
Methods
The interoperable codes discussed in this work are Qbox, WEST, SSAGES and PyCDFT
Qbox14 is a first principles molecular dynamics code based on the plane-wave, pseudopotential formalism. The electronic structure is obtained using density functional theory (DFT) or hybrid-DFT. In addition to the simulation of thermodynamic and structural properties of materials, Qbox allows for the calculations of vibrational spectra144,145, ionic conductivity146, and heat transport coefficients137.
WEST16 performs large-scale, many-body perturbation theory (MBPT) calculations providing electronic and optical spectroscopic characterization of complex materials. WEST uses the plane-wave, pseudopotential formalism109 and is interfaced with the Quantum Espresso code108 and with Qbox in client-server mode94,113. In addition to the calculation of electron-electron16,99,101,109,113, electron-phonon100 and electron-hole interactions94, WEST enables calculations based on a quantum embedding theory116.
SSAGES15 provides a unified, extensible framework to calculate reaction coordinates and reactive pathways, and free energies within molecular simulations. SSAGES offers a comprehensive suite of advanced methods for phase space sampling organized into a unified framework that can function as a wrapper, adding functionality to first-principles and classical molecular dynamics and Monte Carlo engines.
PyCDFT18 is a Python package to compute diabatic states using constrained density functional theory (CDFT)130. PyCDFT allows for both single‐point self‐consistent‐field calculations and geometry optimizations. PyCDFT is designed to interface with existing DFT codes to perform CDFT calculations where constraint potentials are added to the Kohn–Sham Hamiltonian.
Data availability
The examples reported in this work use the www.quantum-simulation.org (QSO) format to exchange datasets, which is based on the XML markup language. Data that support the findings discussed in this study are available through the Qresp12 portal (http://qresp.org).
Code availability
The examples reported in this work use open-source codes: Qbox (http://qboxcode.org), WEST (http://west-code.org), SSAGES (https://ssagesproject.github.io/).
Change history
01 March 2021
The link to the open-source code Qbox in the Code availability section was updated shortly after publication, changing from "Qbox (http://qbox-code.org)" to "Qbox (http://qboxcode.org)".
References
Curtarolo, S. et al. AFLOWLIB.ORG: a distributed materials properties repository from high-throughput ab initio calculations. Comput. Mater. Sci. 58, 227–235 (2012).
Jain, A. et al. Commentary: The Materials Project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B. & Wolverton, C. Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD). J. Mater. 65, 1501–1509 (2013).
Bhat, T. N., Bartolo, L. M., Kattner, U. R., Campbell, C. E. & Elliott, J. T. Strategy for extensible, evolving terminology for the materials genome initiative efforts. J. Mater. 67, 1866–1875 (2015).
Kalidindi, S. R. & De Graef, M. Materials data science: current status and future outlook. Ann. Rev. Mater. Res. 45, 171–193 (2015).
Rajan, K. Materials informatics: the materials “Gene” and big data. Ann. Rev. Mater. Res. 45, 153–169 (2015).
Blaiszik, B. et al. The materials data facility: data services to advance materials science research. J. Mater. 68, 2045–2052 (2016).
Jain, A., Persson, K. A. & Ceder, G. Research update: the materials genome initiative: data sharing and the impact of collaborative ab initio databases. APL Mater. 4, 053102 (2016).
Thygesen, K. S. & Jacobsen, K. W. Making the most of materials computations. Science 354, 180 (2016).
Bennett, C. H. & DiVincenzo, D. P. Quantum information and computation. Nature 404, 247–255 (2000).
Koehl, W. F., Seo, H., Galli, G. & Awschalom, D. D. Designing defect spins for wafer-scale quantum technologies. MRS Bull. 40, 1146–1153 (2015).
Govoni, M. et al. Qresp, a tool for curating, discovering and exploring reproducible scientific papers. Sci. Data 6, 190002 (2019).
Talirz, L. et al. Materials Cloud, a platform for open computational science. Sci. Data 7, 299 (2020).
Gygi, F. Architecture of Qbox: a scalable first-principles molecular dynamics code. IBM J. Res. Dev. 52, 137–144 (2008).
Sidky, H. et al. SSAGES: Software suite for advanced general ensemble simulations. J. Chem. Phys. 148, 044104 (2018).
Govoni, M. & Galli, G. Large scale GW calculations. J. Chem. Theory Comput. 11, 2680–2696 (2015).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).
Ma, H. et al. PyCDFT: A Python package for constrained density functional theory. J. Comput. Chem. 41, 1859–1867 (2020).
Barnes, T. A., Marin-Rimoldi, E., Ellis, S. & Crawford, T. D. The MolSSI Driver Interface Project: a framework for standardized, on-the-fly interoperability between computational molecular sciences codes. Comput. Phys. Commun. 261, 107688 (2021).
Gygi, F., Duchemin, I., Donadio, D. & Galli, G. Practical algorithms to facilitate large-scale first-principles molecular dynamics. J. Phys. Conf. Ser. 180, 012074 (2009).
Foster, I. Globus online: accelerating and democratizing science through cloud-based services. IEEE Internet Comput. 15, 70–73 (2011).
Car, R. & Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55, 2471–2474 (1985).
Marx, D. & Hutter, J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods. (Cambridge University Press, 2009).
Chodera, J. D. & Noé, F. Markov state models of biomolecular conformational dynamics.Curr. Opin. Struct. Biol. 25, 135–144 (2014).
Miao, Y., Feixas, F., Eun, C. & McCammon, J. A. Accelerated molecular dynamics simulations of protein folding. J. Comput. Chem. 36, 1536–1549 (2015).
Helfferich, J., Lyubimov, I., Reid, D. & de Pablo, J. J. Inherent structure energy is a good indicator of molecular mobility in glasses. Soft Matter 12, 5898–5904 (2016).
Reid, D. R., Lyubimov, I., Ediger, M. D. & de Pablo, J. J. Age and structure of a model vapour-deposited glass. Nat. Commun. 7, 13062 (2016).
Perilla, J. R. et al. Molecular dynamics simulations of large macromolecular complexes. Curr. Opin Struct. Biol. 31, 64–74 (2015).
Cheng, B. & Ceriotti, M. Bridging the gap between atomistic and macroscopic models of homogeneous nucleation. J. Chem. Phys. 146, 034106 (2017).
Giberti, F., Salvalaglio, M. & Parrinello, M. Metadynamics studies of crystal nucleation. IUCrJ 2, 256–266 (2015).
Giberti, F., Salvalaglio, M., Mazzotti, M. & Parrinello, M. 1,3,5-tris(4-bromophenyl)-benzene nucleation: from dimers to needle-like clusters. Cryst. Growth Des. 17, 4137–4143 (2017).
Zhang, C. et al. Dissociation of salts in water under pressure. Nat. Commun. 11, 3037 (2020).
Lee, E. et al. Neural network sampling of the free energy landscape for nitrogen dissociation on ruthenium. ChemRxiv, (2020).
Singh, S., Chopra, M. & Pablo, J. J. D. Density of states–based molecular simulations. Annu. Rev. Chem. Biomol. Eng. 3, 369–394 (2012).
Fu, H., Shao, X., Cai, W. & Chipot, C. Taming rugged free energy landscapes using an average force. Acc. Chem. Res. 52, 3254–3264 (2019).
Bussi, G. & Laio, A. Using metadynamics to explore complex free-energy landscapes. Nat. Rev. Phys. 2, 200–212 (2020).
Torrie, G. M. & Valleau, J. P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 23, 187 (1977).
Laio, A. & Parrinello, M. Escaping free-energy minima. Proc. Natl Acad. Sci. USA 99, 12562 (2002).
Dellago, C., Bolhuis, P. & Geissler, P. L. Transition path sampling. Adv. Chem. Phys. 123, 1 (2003).
Darve, E., Rodríguez-Gómez, D. & Pohorille, A. Adaptive biasing force method for scalar and vector free energy calculations. J. Chem. Phys. 128, 144120 (2008).
Barducci, A., Bussi, G. & Parrinello, M. Well-tempered metadynamics: a smoothly converging and tunable free-energy method. Phys. Rev. Lett. 100, 020603 (2008).
Jorgensen, W. L., Maxwell, D. S. & Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225 (1996).
Hornak, V. et al. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins Struct. Funct. Genet. 65, 712 (2006).
Marrink, S. J., Risselada, H. J., Yefimov, S., Tieleman, D. P. & De Vries, A. H. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B 111, 7812 (2007).
Babin, V., Leforestier, C. & Paesani, F. Development of a “first principles” water potential with flexible monomers: Dimer potential energy surface, VRT spectrum, and second virial coefficient. J. Chem. Theory Comput. 9, 5395 (2013).
Chen, C., Arntsen, C. & Voth, G. A. Development of reactive force fields using ab initio molecular dynamics simulation minimally biased to experimental data. J. Chem. Phys. 147, 161719 (2017).
Henriques, J. & Skepö, M. Molecular dynamics simulations of intrinsically disordered proteins: on the accuracy of the TIP4P-D water model and the representativeness of protein disorder models. J. Chem. Theory Comput. 12, 3407 (2016).
Lyubartsev, A. P. & Rabinovich, A. L. Force field development for lipid membrane simulations. Biochim. Biophys. Acta Biomembr. 1858, 2483 (2016).
Sevgen, E. et al. Hierarchical coupling of first-principles molecular dynamics with advanced sampling methods. J. Chem. Theory Comput. 14, 2881–2888 (2018).
Gaiduk, A. P. et al. Photoelectron spectra of aqueous solutions from first principles. J. Am. Chem. Soc. 138, 6912–6915 (2016).
Pham, T. A. et al. Electronic structure of aqueous solutions: Bridging the gap between theory and experiments. Sci. Adv. 3, e1603210 (2017).
Gerosa, M., Gygi, F., Govoni, M. & Galli, G. The role of defects and excess surface charges at finite temperature for optimizing oxide photoabsorbers. Nat. Mater. 17, 1122–1127 (2018).
Gaiduk, A. P., Gustafson, J., Gygi, F. & Galli, G. First-principles simulations of liquid water using a dielectric-dependent hybrid functional. J. Phys. Chem. Lett. 9, 3068–3073 (2018).
Dawson, W. & Gygi, F. Equilibration and analysis of first-principles molecular dynamics simulations of water. J. Chem. Phys. 148, 124501 (2018).
Gaiduk, A. P., Pham, T. A., Govoni, M., Paesani, F. & Galli, G. Electron affinity of liquid water. Nat. Commun. 9, 247 (2018).
LaCount, M. D. & Gygi, F. Ensemble first-principles molecular dynamics simulations of water using the SCAN meta-GGA density functional. J. Chem. Phys. 151, 164101 (2019).
Harmon, K. J. et al. Validating first-principles molecular dynamics calculations of oxide/water interfaces with x-ray reflectivity data. Phys. Rev. Mater. 4, 113805 (2020).
Carter, E. A., Ciccotti, G., Hynes, J. T. & Kapral, R. Constrained reaction coordinate dynamics for the simulation of rare events. Chem. Phys. Lett. 156, 472–477 (1989).
Sprik, M. & Ciccotti, G. Free energy from constrained molecular dynamics. J. Chem. Phys. 109, 7737–7744 (1998).
Ciccotti, G. & Ferrario, M. Blue moon approach to rare events. Mol. Simula. 30, 787–793 (2004).
Ciccotti, G., Kapral, R. & Vanden-Eijnden, E. Blue moon sampling, vectorial reaction coordinates, and unbiased constrained dynamics. Chem. Phys. Chem. 6, 1809–1814 (2005).
Barducci, A., Bonomi, M. & Parrinello, M. Metadynamics. WIREs Comput. Mol. Sci. 1, 826–843 (2011).
Sutto, L., Marsili, S. & Gervasio, F. L. New advances in metadynamics. WIREs Comput. Mol. Sci. 2, 771–779 (2012).
Kästner, J. Umbrella sampling. WIREs Comput. Mol. Sci. 1, 932–942 (2011).
Martoňák, R., Donadio, D., Oganov, A. R. & Parrinello, M. Crystal structure transformations in SiO2 from classical and ab initio metadynamics. Nat. Mater. 5, 623 (2006).
Ensing, B., De Vivo, M., Liu, Z., Moore, P. & Klein, M. L. Metadynamics as a tool for exploring free energy landscapes of chemical reactions. Acc. Chem. Res. 39, 73 (2006).
Guido, C. A., Pietrucci, F., Gallet, G. A. & Andreoni, W. The fate of a zwitterion in water from ab initio molecular dynamics: Monoethanolamine (MEA)-CO2. J. Chem. Theory Comput. 9, 28 (2013).
Pietrucci, F. & Saitta, A. M. Formamide reaction network in gas phase and solution via a unified theoretical approach: Toward a reconciliation of different prebiotic scenarios. Proc. Natl Acad. Sci. USA 112, 15030 (2015).
Herron, J. A., Morikawa, Y. & Mavrikakis, M. Ab initio molecular dynamics of solvation effects on reactivity at electrified interfaces. Proc. Natl Acad. Sci. USA 113, 201604590 (2016).
Kubota, Y., Ohnuma, T. & Bučko, T. Carbon dioxide capture in 2-aminoethanol aqueous solution from ab initio molecular dynamics simulations. J. Chem. Phys. 146, 094303 (2017).
Perdew, J. P., Ernzerhof, M. & Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 105, 9982–9985 (1996).
Martin, R. M. Electronic Structure: Basic Theory and Practical Methods. (Cambridge University Press, 2004).
Adamo, C. & Barone, V. Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Pan, D., Spanu, L., Harrison, B., Sverjensky, D. A. & Galli, G. Dielectric properties of water under extreme conditions and transport of carbonates in the deep Earth. Proc. Natl Acad. Sci. USA 110, 6646 (2013).
Pan, D., Govoni, M. & Galli, G. Communication: dielectric properties of condensed systems composed of fragments. J. Chem. Phys. 149, 051101 (2018).
Sevgen, E., Guo, A. Z., Sidky, H., Whitmer, J. K. & de Pablo, J. J. Combined force-frequency sampling for simulation of systems having rugged free energy landscapes. J. Chem. Theory Comput. 16, 1448–1455 (2020).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Becke, A. D. Perspective: fifty years of density-functional theory in chemical physics. J. Chem. Phys. 140, 18A301 (2014).
Skone, J. H., Govoni, M. & Galli, G. Self-consistent hybrid functional for condensed systems. Phys. Rev. B 89, 195112 (2014).
Skone, J. H., Govoni, M. & Galli, G. Nonempirical range-separated hybrid functionals for solids and molecules. Phys. Rev. B 93, 235106 (2016).
Brawand, N. P., Vörös, M., Govoni, M. & Galli, G. Generalization of dielectric-dependent hybrid functionals to finite systems. Phys. Rev. X 6, 041002 (2016).
Brawand, N. P., Govoni, M., Vörös, M. & Galli, G. Performance and self-consistency of the generalized dielectric dependent hybrid functional. J. Chem. Theory Comput. 13, 3318–3325 (2017).
Runge, E. & Gross, E. K. U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 52, 997–1000 (1984).
Casida, M. E. in Recent Advances in Density Functional Methods Vol. Volume 1 Recent Advances in Computational Chemistry 155-192 (WORLD SCIENTIFIC, 1995).
Zheng, H., Govoni, M. & Galli, G. Dielectric-dependent hybrid functionals for heterogeneous materials. Phys. Rev. Mater. 3, 073803 (2019).
Casida, M. E. & Huix-Rotllant, M. Progress in time-dependent density-functional theory. Annu. Rev. Phys. Chem. 63, 287–323 (2012).
Onida, G., Reining, L. & Rubio, A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601–659 (2002).
Deslippe, J. et al. BerkeleyGW: a massively parallel computer package for the calculation of the quasiparticle and optical properties of materials and nanostructures. Comput. Phys. Commun. 183, 1269–1289 (2012).
Sangalli, D. et al. Many-body perturbation theory calculations using the yambo code. J. Phys. Condens. Matter 31, 325902 (2019).
Golze, D., Dvorak, M. & Rinke, P. The GW compendium: a practical guide to theoretical photoemission spectroscopy. Front. Chem. 7, (2019).
Giustino, F. Electron-phonon interactions from first principles. Rev. Mod. Phys. 89, 015003 (2017).
Nguyen, N. L., Ma, H., Govoni, M., Gygi, F. & Galli, G. Finite-field approach to solving the Bethe-Salpeter equation. Phys. Rev. Lett. 122, 237402 (2019).
Salpeter, E. E. & Bethe, H. A. A relativistic equation for bound-state problems. Phys. Rev. 84, 1232–1242 (1951).
Albrecht, S., Reining, L., Del Sole, R. & Onida, G. Ab initio calculation of excitonic effects in the optical spectra of semiconductors. Phys. Rev. Lett. 80, 4510–4513 (1998).
Benedict, L. X., Shirley, E. L. & Bohn, R. B. Optical absorption of insulators and the electron-hole interaction: an ab initio calculation. Phys. Rev. Lett. 80, 4514–4517 (1998).
Rohlfing, M. & Louie, S. G. Electron-hole excitations in semiconductors and insulators. Phys. Rev. Lett. 81, 2312–2315 (1998).
Scherpelz, P., Govoni, M., Hamada, I. & Galli, G. Implementation and validation of fully relativistic GW calculations: spin–orbit coupling in molecules, nanocrystals and solids. J. Chem. Theory Comput. 12, 3523–3544 (2016).
McAvoy, R. L., Govoni, M. & Galli, G. Coupling first-principles calculations of electron–electron and electron–phonon scattering, and applications to carbon-based nanostructures. J. Chem. Theory Comput. 14, 6269–6275 (2018).
Yang, H., Govoni, M. & Galli, G. Improving the efficiency of G0W0 calculations with approximate spectral decompositions of dielectric matrices. J. Chem. Phys. 151, 224102 (2019).
Umari, P., Stenuit, G. & Baroni, S. GW quasiparticle spectra from occupied states only. Phys. Rev. B 81, 115104 (2010).
Giustino, F., Cohen, M. L. & Louie, S. G. GW method with the self-consistent Sternheimer equation. Phys. Rev. B 81, 115105 (2010).
Nguyen, H. V., Pham, T. A., Rocca, D. & Galli, G. Improving accuracy and efficiency of calculations of photoemission spectra within the many-body perturbation theory. Phys. Rev. B 85, 081101 (2012).
Wilson, H. F., Gygi, F. & Galli, G. Efficient iterative method for calculations of dielectric matrices. Phys. Rev. B 78, 113303 (2008).
Wilson, H. F., Lu, D., Gygi, F. & Galli, G. Iterative calculations of dielectric eigenvalue spectra. Phys. Rev. B 79, 245106 (2009).
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Govoni, M. & Galli, G. GW100: comparison of methods and accuracy of results obtained with the WEST code. J. Chem. Theory Comput. 14, 1895–1909 (2018).
Seo, H., Govoni, M. & Galli, G. Design of defect spins in piezoelectric aluminum nitride for solid-state hybrid quantum technologies. Sci. Rep. 6, 20803 (2016).
Seo, H., Ma, H., Govoni, M. & Galli, G. Designing defect-based qubit candidates in wide-gap binary semiconductors for solid-state quantum technologies. Phys. Rev. Mater. 1, 075002 (2017).
Smart, T. J., Wu, F., Govoni, M. & Ping, Y. Fundamental principles for calculating charged defect ionization energies in ultrathin two-dimensional materials. Phys. Rev. Mater. 2, 124002 (2018).
Ma, H., Govoni, M., Gygi, F. & Galli, G. A finite-field approach for GW calculations beyond the random phase approximation. J. Chem. Theory Comput. 15, 154–164 (2019).
Ma, H., Govoni, M., Gygi, F. & Galli, G. Correction to a finite-field approach for GW calculations beyond the random phase approximation. J. Chem. Theory Comput. 16, 2877–2879 (2020).
Dong, S., Govoni, M. & Galli, G. Machine learning dielectric screening for the simulation of excited state properties of molecules and materials. arXiv 2012, 12244 (2020).
Ma, H., Govoni, M. & Galli, G. Quantum simulations of materials on near-term quantum computers. npj Comput. Mater. 6, 85 (2020).
Ma, H., Sheng, N., Govoni, M. & Galli, G. First-principles studies of strongly correlated states in defect spin qubits in diamond. Phys. Chem. Chem. Phys. (2020).
Aryasetiawan, F. et al. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 70, 195104 (2004).
Miyake, T. & Aryasetiawan, F. Screened Coulomb interaction in the maximally localized Wannier basis. Phys. Rev. B 77, 085122 (2008).
Vaugier, L., Jiang, H., Biermann, S. & Hubbard, U. and Hund exchange J in transition metal oxides: Screening versus localization trends from constrained random phase approximation. Phys. Rev. B 86, 165105 (2012).
Sun, Q. et al. PySCF: the Python-based simulations of chemistry framework. WIREs Comput. Mol. Sci. 8, e1340 (2018).
Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567, 491–495 (2019).
Yu, D., Wang, C., Wehrenberg, B. L. & Guyot-Sionnest, P. Variable range hopping conduction in semiconductor nanocrystal solids. Phys. Rev. Lett. 92, 216802 (2004).
Talapin, D. V., Lee, J.-S., Kovalenko, M. V. & Shevchenko, E. V. Prospects of colloidal nanocrystals for electronic and optoelectronic applications. Chem. Rev. 110, 389–458 (2010).
Guyot-Sionnest, P. Electrical transport in colloidal quantum dot films. J. Phys. Chem. Lett. 3, 1169–1175 (2012).
Lan, X. et al. Quantum dot solids showing state-resolved band-like transport. Nat. Mater. 19, 323–329 (2020).
Marcus, R. A. On the theory of oxidation‐reduction reactions involving electron transfer. I. J. Chem. Phys. 24, 966–978 (1956).
Marcus, R. A. Electron transfer reactions in chemistry. Theory Exp. Rev. Mod. Phys. 65, 599–610 (1993).
Nan, G., Yang, X., Wang, L., Shuai, Z. & Zhao, Y. Nuclear tunneling effects of charge transport in rubrene, tetracene, and pentacene. Phys. Rev. B 79, 115203 (2009).
Kaduk, B., Kowalczyk, T. & Van Voorhis, T. Constrained density functional theory. Chem. Rev. 112, 321–370 (2012).
Broido, D. A., Malorny, M., Birner, G., Mingo, N. & Stewart, D. A. Intrinsic lattice thermal conductivity of semiconductors from first principles. Appl. Phys. Lett. 91, 231922 (2007).
Garg, J., Bonini, N., Kozinsky, B. & Marzari, N. Role of disorder and anharmonicity in the thermal conductivity of silicon-germanium alloys: a first-principles study. Phys. Rev. Lett. 106, 045901 (2011).
Marcolongo, A., Umari, P. & Baroni, S. Microscopic theory and quantum simulation of atomic heat transport. Nat. Phys. 12, 80–84 (2016).
Carbogno, C., Ramprasad, R. & Scheffler, M. Ab initio Green-Kubo approach for the thermal conductivity of solids. Phys. Rev. Lett. 118, 175901 (2017).
Stackhouse, S., Stixrude, L. & Karki, B. B. Thermal conductivity of periclase (MgO) from first principles. Phys. Rev. Lett. 104, 208501 (2010).
Zhou, F., Nielson, W., Xia, Y. & Ozoliņš, V. Lattice anharmonicity and thermal conductivity from compressive sensing of first-principles calculations. Phys. Rev. Lett. 113, 185501 (2014).
Puligheddu, M., Gygi, F. & Galli, G. First-principles simulations of heat transport. Phys. Rev. Mater. 1, 060802 (2017).
Puligheddu, M. & Galli, G. Atomistic simulations of the thermal conductivity of liquids. Phys. Rev. Mater. 4, 053801 (2020).
Zhang, L., Han, J., Wang, H., Car, R. & E, W. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics. Phys. Rev. Lett. 120, 143001 (2018).
Seo, H. et al. Quantum decoherence dynamics of divacancy spins in silicon carbide. Nat. Commun. 7, 12935 (2016).
Bourassa, A. et al. Entanglement and control of single nuclear spins in isotopically engineered silicon carbide. Nat. Mater., (2020).
Ghosh, K., Ma, H., Gavini, V. & Galli, G. All-electron density functional calculations for electron and nuclear spin interactions in molecules and solids. Phys. Rev. Mater. 3, 043801 (2019).
Ma, H. G. Marco; Galli, Giulia. PyZFS: a Python package for first-principles calculations of zero-field splitting tensors. J. Open Source Softw. 5, 2160 (2020).
Wan, Q. & Galli, G. First-principles framework to compute sum-frequency generation vibrational spectra of semiconductors and insulators. Phys. Rev. Lett. 115, 246404 (2015).
Wan, Q., Spanu, L., Galli, G. A. & Gygi, F. Raman spectra of liquid water from ab initio molecular dynamics: vibrational signatures of charge fluctuations in the hydrogen bond network. J. Chem. Theory Comput. 9, 4124–4130 (2013).
Rozsa, V., Pan, D., Giberti, F. & Galli, G. Ab initio spectroscopy and ionic conductivity of water under Earth mantle conditions. Proc. Natl Acad. Sci. USA 115, 6952 (2018).
Wickstrom, L., Okur, A. & Simmerling, C. Evaluating the performance of the ff99SB force field based on NMR scalar coupling data. Biophys. J. 97, 853–856 (2009).
Goldey, M. B., Brawand, N. P., Vörös, M. & Galli, G. Charge transport in nanostructured materials: implementation and verification of constrained density functional theory. J. Chem. Theory Comput. 13, 2581–2590 (2017).
Seo, H., Ping, Y. & Galli, G. Role of point defects in enhancing the conductivity of BiVO4. Chem. Mater. 30, 7793–7802 (2018).
Wang, W. et al. The role of surface oxygen vacancies in BiVO4. Chem. Mater. 32, 2899–2909 (2020).
Acknowledgements
We thank S. Dong, E. Lee, H. Ma, M. Puligheddu, and W. Wang for fruitful discussions. This work was supported by MICCoM, as part of the Computational Materials Sciences Program funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences, and Engineering Division through Argonne National Laboratory. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231, resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357, and resources of the University of Chicago Research Computing Center.
Author information
Authors and Affiliations
Contributions
M.G. and G.G. designed the research. The various concepts discussed in the paper were developed and implemented by all authors. All authors contributed to the writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Govoni, M., Whitmer, J., de Pablo, J. et al. Code interoperability extends the scope of quantum simulations. npj Comput Mater 7, 32 (2021). https://doi.org/10.1038/s41524-021-00501-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00501-z
This article is cited by
-
Quantum embedding theories to simulate condensed systems on quantum computers
Nature Computational Science (2022)