Introduction

Advanced materials with high performance are increasingly being pursued to achieve enhanced operating efficiency and reduced environmental pollution. Fortunately, the discovery of new materials has been accelerated by replacing traditional trial-and-error design strategies with high-throughput materials design, aided by machine-learning (ML) techniques1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17. As promising new class of structural materials with potential excellent mechanical, functional, and environmental properties18,19,20, high-entropy alloys (HEAs) were proposed 15 years ago as a way to unlock the unlimited potential within materials design. Research has intensified in the intervening years21,22,23,24,25,26 as more resources have been brought to bear. However, one of the more central issues in the HEA design is how to effectively and efficiently identify new HEA compositions with high reliability in an almost unlimited and unexplored compositional space. Although the formation of solid solutions can be determined from Gibbs free energies of the multicomponent alloys and their subsystems in theory, accurately computing the latter using only first-principle calculations is impractical for these compositionally complex alloys over wide ranges of temperature and composition in a high throughput manner. Therefore, approximations, or empirical rules, have been proposed for specific cases.

More than six decades before the term of HEA was coined, Hume-Rothery proposed a set of rules to predict the formation potential of solid solutions of binary alloys27,28,29. His original rules included four basic requirements. Recently, as a result of the emergence of HEAs, new empirical rules have been proposed to predict solid–solution HEAs30,31,32,33,34,35,36,37,38. These rules were constructed using very limited data sets of experimental information. Therefore, it is not surprising that the predictability of these rules is generally problematical.

In this study, an unbiased and complete ML screening of all available physical properties has been performed for each constituent element of an alloy. It is additionally assumed that these properties play equally important roles in forming solid–solution alloys. The ML exercise undertaken herein identifies the most important physical properties. Of these physical properties, molar volume, bulk modulus, and melting point (temperature) are considered to be among the most important quantities for the formation of solid solutions, in addition to Hume-Rothery rules. For example, bulk modulus is a measure of the resistance of a solid against compression and is defined as the volume times the negative derivative of pressure with respect to volume. Its importance to solid–solution formation is surprising, since it was not considered previously by Hume-Rothery or by others as a critical physical property for empirical rule development. In this study, these elemental properties have been evaluated with a new parameter proposed to more accurately predict the formation of solid–solution alloys.

Generally, empirical rules applied to HEAs use some variants of Gibbs free energy or fit the available experimental data in some manner. These rules can be grouped into two classes: (i) rules that use computationally expensive quantities from density functional theory (DFT)39,40; and (ii) rules that use only concentration-weighted elemental properties. One of the major driving forces for the rules in group (i) is the development of more efficient and accurate algorithms within the DFT approach and the increasing availability of powerful supercomputers. A main objective of this study was to identify additional parameters/relations beyond Hume-Rothery rules by taking advantage of the simplicity and high efficiency of component-weighted elemental properties. One very interesting and important open question to be answered is: How accurate can empirical rules (in the spirit of Hume-Rothery rules, not the rules themselves) be if only the elemental properties are used? The approach herein is to use ML to evaluate the correlation of individual elemental properties pertaining to solid–solution formation, based on a much more extensive set of alloys (i.e., 1252, see ref. 35 and Supplementary Information), in contrast to previous work that utilized smaller, more limited data sets. The results of the new rule show predictability of 73% and over 80% if applied jointly with the atomic size misfit rule31.

The present paper consists of two major parts: (i) performing a ML study based on unprecedented large dataset (1252) and their 85 × N elemental properties of N-component alloys, which gives insights into the “upper boundary” of predictability of empirical models and identifies physical properties that are critical for solid solution formations; (ii) constructing a new empirical rule using the critical physical properties (bulk modulus, melting temperature, etc.) identified by ML.

Results

ML solution

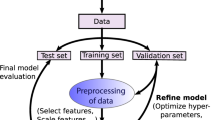
The input dataset for the ML exercise consists of 1252 observations with 625 single-phase and 627 multi-phase alloys, covering binaries and multi-component systems. The features under consideration for these alloys are their elemental properties. The flow chart for the ML exercise is shown in Fig. 1. The available elemental properties for each element (or component), i.e., 85, were collected from ref. 41. There are 170–425 features for a single N-component alloy (where N = 2, 3, 4, 5). Applying as many features as this in a ML training exercise is not only computationally expensive but also diminishes possible physical insight into the problem.

Fig. 1: The flow chart of data processing for machine-learning exercise (Gaussian process classification).
figure 1

Three key physical properties considered for the construction of new rules are melting point (temperature), bulk modulus, and volume. In the present study, N-component alloys are considered with N = 2, 3, 4, 5.

Full size image

This occurs because the features belonging to each element are correlated and it is problematic to assess which feature is more important relative to the others. To address this problem, a weight-average of properties for each alloy based on its constituent elements and corresponding concentration is used. As an exploratory analysis, the pair correlation of properties and alloy phases has been plotted and is shown in Fig. 2a. For example, properties such as bulk modulus, valence, vaporization heat, etc., have relatively strong correlation (<0.6). However, since those elemental properties are also strongly correlated with each other, it is not possible to build a general linear model to best predict alloy phases due to collinearity. Simple pair correlation is not sufficient in capturing the mapping from elemental properties to alloy phases and a form of nonlinear modeling is needed.

Fig. 2: The machine-learning results for the prediction of solid solutions.
figure 2

a The correlation matrix of elemental properties and alloy phase. The matrix shows that simple pair correlation is not enough to well capture the mapping from elemental properties to alloy phases. b Gaussian process classification receiver operating characteristic (ROC) with confidence band for single-phase versus multi-phase (top) and face-centered cubic (FCC) versus body-centered cubic (BCC) versus hexagonal closest packed (HCP) single-phase (bottom) classification, respectively. c The area under curve (AUC) is calculated for each ROC curve. d Gaussian process classification (GPC) probability as a single-phase alloy versus atomic size difference. The symbols (triangle, square, hexagon, and circle) represent the experimentally measured phase states.

Full size image

Gaussian processes are a powerful learning method for both regression and classification tasks. It finds a distribution over the possible covariance functions (also known as kernels) that are consistent (quantified by marginal likelihood p(y|x, M), a condition probability of observing y on given data x and model M) with the observed data, where the kernels measure the similarities between a pair of data points (x, x′) assuming data points close to the observed data (HEAs with similar elemental properties, in our case) produce similar outputs (single-phase or multi-phase). Without embedding physics knowledge (e.g., the function form governing (x, x′) is not clear), the selection of kernels is usually determined by the goodness of fit on the data. One common choice is the so-called radial basis function (RBF), \((x,x^\prime )\sim {\mathrm {exp}}\left( { - \mathop {\sum }\nolimits_i \frac{{(x_i - x_i^\prime )^2}}{{2l_i^2}}} \right)\), where the length scale li indicates the importance of feature xi. Gaussian processes are well suited for moderate-sized (computational complexity O(N3), N is the number of data points) structural input data where features are well defined. Due to its Bayesian nature, the prediction is probabilistic, and the resulting model is generally interpretable.

To build a Gaussian process classification (GPC) model, a procedure as outlined for a Mg alloy model8 was followed, i.e., (1) down-select the physical properties to obtain a smaller feature set (~10) based on various metrics that measure the relevance of features in making the prediction, such as chi-square (a statistics test on whether the input is independent of the output), mutual information (how much information the presence of a feature contributes to making the classification), etc.; (2) iterate through all feature combinations and train a GPC model with RBF as the kernel for each combination, then select the top performers based on model’s marginal likelihood, i.e., a metric for model goodness; and (3) cross-validate the candidate models and identify the best one.

There are 1252 HEAs in the dataset, and the model accuracy is evaluated via the standard 10-fold cross-validation procedure, in which the dataset is randomly split into 10 smaller sets (folds) and for each of the 10 folds, a model is trained on the 9 folds and validated on the remaining 1 fold. The entire procedure is repeated for different random splits, and the resulted model accuracy 93(2)% is the average of validation accuracies. In fact, the model prediction is quite robust and five-fold cross-validation produces consistent results. The model performance is also consistent with respect to several choices of kernel functions, i.e., RBF, Mart’ern covariance kernel (a generalization of RBF), and rational quadratic kernel (equivalent to combining RBF with different length scales) for GPC. Features of interest in descending order of importance (based on length scale parameter) were molar volume, bulk modulus, electronegativity, melting temperature, valence, vaporization heat, and thermal conductivity. The corresponding length scales for RBF are shown in Table 1. The receiver operating characteristic (ROC) is a more descriptive metric than accuracy for classification. The ROC curves are plotted in Fig. 2b, c for both single versus multi-phase and FCC versus BCC versus HCP within single-phase classification. Similar cross-validation procedure has been applied to the evaluation of ROC curves in order to obtain confidence bands (gray areas in the plot). The only difference is for the case of single phases (Fig. 2c), a stratified sampling is used to split training and validation data in order to preserve the percentage of samples for each class. The area under the ROC curve (AUC), which is a measure of the goodness-of-fit for the model, is above 0.95 in all cases. This demonstrates the high predictability of the ML models.

Table 1 Features and corresponding length scales (normalized) for radial basis function (RBF) kernel of the Gaussian process classification (GPC).
Full size table

The atomic size difference δ provides a well-recognized upper bound (6%) for single-phase solid solution, which results from a summary and evaluation of experimental data. The GPC probability of an alloy is plotted in terms of single-phase against δ in Fig. 2d. It is natural to consider a probability of 0.5 as the dividing line with alloys probability >0.5 as solid solutions and otherwise multi-phases. By this criterion our GPC method correctly separates almost all solid–solution and multi-phase alloys42.

New thermodynamics-based rule to predict the single phase of HEA

To ensure accurate ML predictability, obtaining high-affinity dataset is crucial. The ML knowledge can provide deeper insight into the problem. Consequently, the most significant features derived from the ML exercise will be used to construct a new thermodynamics-based rule for predicting the formation of single-phase solid solution alloys.

The rules can have many mathematical forms, such as the ones defined in Zhang et al. 31 and Troparevsky et al. 34. It is natural to take a variant of Gibbs free energy, which allows the important entropic contributions to be considered. The important role of entropies in phase stability has been previously recognized and recently confirmed by Manzoor et al. 43 using DFT calculations. In the following, the details of the newly developed methods to calculate the enthalpy and entropy are provided, using only the key features (bulk modulus, volume, melting temperature, and constitutions) identified by the ML exercise.

Configurational entropy

A number of previous studies have demonstrated that the ideal configurational entropy is not an accurate approximation43,44,45,46,47,48. The configurational entropy in real materials is only a fraction of the ideal one, i.e., \(S_{\mathrm {{conf.}}} = - R\mathop {\sum}\nolimits_i^N {c_i} {\mathrm{ln}}(c_i)\) for N-component alloys with concentrations. Mathematically, the real configurational entropy can be expressed by Sre = α1Sconf, for 0 < α1 ≤ 1, for an N-component system. The value of parameter α1 is system specific. For some systems, α1 can be much smaller than 1.

A solid solution phase starts to form at solidus temperature and will decompose as the temperature decreases. A wider temperature range signifies greater stability of the solid solution phase. The term α2Tm with 0 < α2 < 1 is used to represent the temperature at which the solid solution phase is stable. Based on the arguments above, the Gibbs free energy for a system can be written as

$${\mathrm{\Delta }}G = {\mathrm{\Delta }}H - \alpha _2T_{\mathrm {m}}\alpha _1S_{\mathrm {{conf.}}} = {\mathrm{\Delta }}H - \alpha T_{\mathrm {m}}S_{\mathrm {{conf.}}},\alpha = \alpha _1\alpha _2.$$
(1)

For an alloy, the melting temperature is taken as the average of all melting temperatures of its constituent elements weighted by the concentrations, i.e., \(T_{\mathrm {m}} = \bar T_{\mathrm {m}} = \mathop {\sum}\nolimits_i^N {c_i} T_{{\mathrm {m}},i}\). The introduction of the empirical parameter α is an important contribution of the model. A value of 0.2−0.25 gives satisfactory consistency (i.e., ∼73%) with experiment, and >80% if applied jointly with the δ parameter (see subsequent discussion).

Enthalpy

The formation enthalpy is calculated based on the Lennard-Jones potential, \(V_{\mathrm {{L - J}}}\left( r \right) = - {\it{\epsilon }}\left( {\left( {\frac{{r_{\mathrm {e}}}}{r}} \right)^6 - \left( {\frac{{r_{\mathrm {e}}}}{r}} \right)^{12}} \right)\), where \({\it{\epsilon }}\) is the depth of the potential well and re is the equilibrium distance between atoms, corresponding to the lowest point of the potential well. From a different perspective, \({\it{\epsilon }}\) can be considered as the energy cost in bringing two atoms from infinite distance to re. Typically, \({\it{\epsilon }}\) is considered to be the energy of one bond. For example, for a BCC crystal, the total energy of formation per atom within the nearest-neighbor approximation is: \(E\left( {\left\{ {r_{ij}} \right\}} \right) = \frac{1}{{2N}}\mathop {\sum}\nolimits_{i = 1}^N {\mathop {\sum}\nolimits_{j = 1}^N {V_{\mathrm {{L - J}}}} } (r_{ij})\delta _{ij}^\prime\), where \(\delta _{ij}^\prime = 1\) when j is the nearest neighbor of i, and \(\delta _{ij}^\prime = 0\) otherwise. At equilibrium, \(E_{\mathrm {{coh}}} = E\left( {\left\{ {r_{ij} = r_0} \right\}} \right) = - z{\it{\epsilon }}/2\), where z is the number of nearest neighbor and r0 is the equilibrium atomic distance. The values for these parameters are given in Table 2 for the common structures. In order to calculate the parameter \({\it{\epsilon }}\), the bulk modulus B and the equilibrium volume V0 must be considered.

Table 2 The parameters for the four different crystal structures considered in this study.
Full size table

The definitions of pressure P and bulk modulus B allow the determination of unknown parameters re and \({\it{\epsilon }}\):

$$P = - \frac{{\partial E}}{{\partial V}} = - \frac{{\partial E}}{{\partial r}}\frac{{\partial r}}{{\partial V}},$$
(2)
$$B = - \frac{{\partial P}}{{\partial \ln \left( V \right)}} = - V\frac{{\partial ^2E}}{{\partial r^2}}\left( {\frac{{\partial r}}{{\partial V}}} \right)^2 - V\frac{{\partial E}}{{\partial r}}\frac{{\partial ^2r}}{{\partial V^2}}.$$
(3)

When P = 0, the equilibrium distance is connected with volume: \(V_0 = \left( {\frac{{r_{\mathrm {e}}}}{c}} \right)^3\), the constant \(c = f^{ - 1}(V_0)/V^{1/3}\). The second equation connects bulk modulus with the energy parameter \({\it{\epsilon }}\): \(B = - 8V_0^{ - 1}{\it{\epsilon }}\), or \({\it{\epsilon }} = - BV_0/8\). The parameters can be found in Table 2. Therefore, the cohesive energy, or the formation energy, of a pure metal without local distortion is

$$E_{\mathrm {{coh}}} = - zBV_0/16.$$
(4)

For a N-component alloy, the formation energy can be calculated by taking the cohesive energies of each constituting component as energy reference,

$$E_{\mathrm {{fi}}} = - z\langle B\rangle \langle V\rangle/16 + z\langle BV\rangle/16,$$
(5)

where \(\langle B\rangle = \mathop {\sum}\nolimits_i^N {c_i} B_i\), \(\langle V\rangle = \mathop {\sum}\nolimits_i^N {c_i} V_i\), \(\langle BV\rangle = \mathop {\sum}\nolimits_i^N {c_i} B_iV_i\).

Efi represents the amount of energy needed to bring atoms from infinite distance to ideal lattice sites with the same spacing, r0. It is only one part of the total formation energy. Since different species can have different atomic sizes, the energy can be further lowered by releasing the strain energy. When the strain is not large, the strain energy can be calculated by the Kanzaki force49. Here the harmonic approximation and oscillator model are adopted to calculate the contribution to the strain-induced energy of species i:

$$E_{{\mathrm {si}},i} = - \int_{\langle V\rangle}^{V_i} \langle B\rangle\frac{{V - \langle V\rangle}}{\langle V\rangle}{\mathrm {d}}V = - \frac{\langle B\rangle}{{2\langle V\rangle}}\left( {V_i - \langle V\rangle} \right)^2.$$
(6)

The total strain energy \(E_{\mathrm {{si}}} = \mathop {\sum}\nolimits_i^N {c_i} E_{{\mathrm {si}},i}\), having the following explicit form:

$$E_{{\mathrm {si}}} = - \frac{\langle B\rangle}{{2\langle V\rangle}}\left( {\langle V^{2}\rangle - \langle V\rangle^2} \right).$$
(7)

Combining the unrelaxed cohesive energy and strain-induced energy can describe the total enthalpy of formation described as follows:

$$\Delta H = E_{\mathrm {{fi}}} + E_{\mathrm {{si}}}.$$
(8)

These two constituent contributions of the total formation enthalpy for the alloys considered in this work are plotted in Fig. 3. A 45◦ dashed line is used as a guide through the data. As is shown in the figure, most of the data points are situated close to the dashed line, indicating that both contributions are almost equally important to the formation enthalpy.

Fig. 3: The formation energy in ideal lattice (without relaxation) Efi and the local strain-induced energy reduction (by relaxation) Esi.
figure 3

Both contributions are almost equally important for the formation enthalpy ΔH.

Full size image

The above procedure is employed to calculate the formation enthalpy for the same alloy (with same components and concentrations). There are three viable crystal structures for structural metals/alloys (i.e., FCC, BCC, and HCP). The simple cubic crystal structure can also be considered. Subsequently, the formation enthalpy with respect to the four crystal structures can be minimized (see Table 2):

$$\Delta H = {\mathrm{min}}\left\{ {\Delta H(z)} \right\}.$$
(9)

The minimum formation enthalpy can be used in Eq. (1) to calculate the Gibbs free energy.

Model predictability

The procedure described above allows ΔGN to be calculated for any N-component system and ΔG2 for its binaries. The values of ΔG can be compared to find the lowest one. If ΔGN is the lowest, the system is considered as a single-phase alloy. Otherwise, the system is considered as a multi-phase alloy. For convenience, an equivalent new parameter γ is defined to replace ΔGN:

$$\gamma : = \left\{ {\begin{array}{*{20}{l}} {{\mathrm{\Delta }}G_N/\min \left( {\Delta G_2} \right){\mathrm{if}}\,{\mathrm{min}}({\mathrm{\Delta }}G_2)\,<\, 0;} \hfill \\ { - {\mathrm{\Delta }}G_N/\min \left( {\Delta G_2} \right)\,{\mathrm{if}}\,{\mathrm{\Delta }}G_N\, <\, 0\,{\mathrm{and}}\,{\mathrm{min}}({\mathrm{\Delta }}G_2)\, >\, 0} \hfill \end{array}} \right.$$
(10)

The criterion now becomes γ ≥ 1 for forming a single-phase solid solution.

The parameter γ for all multicomponent alloys has been calculated. The results are shown in Fig. 4 and Tables 3 and 4. The new criterion gives much better predictability than do previous criteria. It correctly predicts not only the majority of single-phase alloys but also correctly predicts the majority of multi-phase ones. More specifically, the new model correctly predicts 88% of FCC, 80% of BCC, and 100% of HCP single-phase alloys. The average consistency of the model is 64%.

Fig. 4: The predictability of the new rule.
figure 4

The upper subfigure: New rule gives an accuracy of 64%, but together with the lattice misfit rule, slightly increases to 75%. The lower subfigure: If we tune the parameter α down to 0.2 from 0.25, the new rule alone gives an accuracy of 73%, but together with the lattice misfit rule, slightly increases to 81%. For better visualization the values of γ ≥ 3 are changed to 3.

Full size image
Table 3 The predictability of our new rule γ ≥ 1 with α = 0.25 only (a) and jointly with the emprical rule of lattice misfit δ ≤ 6% (b).
Full size table
Table 4 The predictability of our new rule γ ≥ 1 with α = 0.2 only (a) and jointly with the emprical rule of lattice misfit δ ≤ 6% (b).
Full size table

Among the proposed rules so far, a frequently used one is based on lattice misfit δ, i.e., δ ≤ ~6%. The criterion is necessary but not sufficient for single phase HEAs to form since many multi-phase alloys also meet the requirement. If the δ parameter is combined with the one developed herein, i.e., γ ≥ 1, then 75% of the alloys are correctly predicted to be consistent with experiment.

In the methodology part, an empirical parameter, α, was used to tune the contribution of the configurational entropy and melting temperature. The optimal value of α is alloy specific. For simplicity, α equal to 0.25 was used for the predictions previously presented. This value gave good separation between single-phase (i.e., solid solutions) and multi-phase alloys. If α is varied (i.e., tuned), a small change can give significantly better division between single-phase and multi-phase alloys. Based on the specific dataset in this study, α = 0.2 is optimum. With this value for α, the new rule gives a consistency of 73%, but when used with the atomic size misfit rule (δ ≤ 6%), the consistency increases to 81%.

Prediction and validation of new solid solution HEAs

To test the predictability of the new rule, γ ≥ 1 (α = 0.2), three 9-element blocks in the periodic table are tested (see Fig. 5). Each 9-element block is selected to be stable in FCC, BCC, or HCP structure. The elements are assumed to form solid-solution HEAs of the same structure as the major components. Only single-phase HEAs are considered, i.e., equimolar HEAs with 4–9 components, respectively, totaling 382 combinations/compositions for each block. The predicted single-phase solid solutions are summarized in Table 5 and shown in Fig. 5. Of these HEAs, 47 are FCC, 74 are BCC and the remaining 145 are HCP. Applying an additional criterion, i.e., δ ≤ ~6%, does not significantly alter these results. In all cases, the solid solution HEAs are the absolute minority, which is consistent with existing knowledge that it is more difficult to form solid solutions than alloys with multiple phases. With increasing the number of components of the alloy system, there will be more intermetallic compound phases competing against the solid solution HEA phase for thermodynamic stability, and hence the ratio of solid solution alloys over multi-phase ones decreases. The similar trend was predicted by the model of Troparevsky et al. 34.

Fig. 5: Application of the new rule to predict the possible single-phase HEAs for the FCC, BCC, and HCP groups.
figure 5

Here all combinations of ≥4 elements are considered. As shown by these figures, the ratio of single-phase alloys over multi-phase ones decreases with increasing number of components. The more components, the stronger competition between the HEA with its subsystem, and thus the lower possibility for the HEA being the most stable.

Full size image
Table 5 Summarization of predicting single-phase HEAs for the FCC, BCC, and HCP groups.
Full size table

CALculations of PHAse Diagram (CALPHAD) calculations are carried out using TCNI8 thermodynamic database provided by ThermoCalcTM50. The database covers the entire composition ranges of the constituent binaries and limited ternaries. The TCNI8 database does not contain elements Os, Tc, Rh, Ir, Au, and Ag, and hence, only HEA compositions that do not contain these six elements are considered. This limits validation to 77 equimolar solid solution HEAs, comprised of 4, 5, or 6 elements. Among these 77 HEAs, 72 are successfully validated by CALPHAD calculations comprising 5 FCC and 67 BCC HEAs, with consistency as high as 94% (see Table 6). While some are validated by experiment, among these 72 HEAs, others are new alloys previously unreported in the literature. A detailed list of results is supplied in the Supplementary Information. The high consistency between CALPHAD and the rule developed herein indicates that the new rule can act as a guide to experiment and the predicted HEAs are worth being synthesized.

Table 6 Validation of the γ ≥ 1 (a = 0.2) rule by CALPHAD method.
Full size table

Discussion

Troparevsky et al. proposed a successful model to screen for high-entropy solid solutions based on enthalpies of formation of binary alloys from DFT data and a limited experimental dataset34. Although their model has a similar form for the entropy term with the present study, the arguments are different. In their model, the total ideal entropy of mixing was used for the calculations, while in our model only a fraction of the entropy (α2Sconf.) is considered to play a role. The latter argument is more realistic, considering that the configurational entropy is a continuous function of temperature for a real system. Theoretically, the parameter α is material specific and varies in different ranges for different materials. Fortunately, as a reduced parameter (product of the percentages of the melting temperature and configurational entropy), most of the alloys have overlaps in certain ranges of the parameter. This is the underlying reason that both models identified respective empirical values for α, based on different datasets with our data size being orders of magnitude larger. Compared with previous models or parameters30,31,32,33,35,36, the present model has much improved predictability and is tested on a more extensive data set. The prediction of multi-phase alloys is usually even more difficult31, but is also much improved by the present model and the γ parameter (71–82%).

The present model is ML informed, which is its most significant feature. ML effectively helps extract the most important elemental properties for the construction of this model. The key elemental properties lay the foundation for its high predictability. In addition, the high predictability of our ML model (93%) can be deemed as the likely upper boundary of empirical parameters/models for the same data used here. Therefore, it serves as a guide for the best possible predictability of our model. The ML model itself can also be used to predict the formation of solute solution, albeit less transparent than the γ parameter.

In constructing the new rule, only the easily accessible elemental properties are adopted. By doing so, the efficiency in predicting single-phase HEAs is maximized. This work aims at addressing a long-standing open question of broad interest: What is the role of the empirical rule (based on only elemental properties) with increasingly accessible first-principles calculations? This work shows that new rules with good accuracy can be indeed devised based on a better understanding of the physical nature of the problem utilizing ML solutions. This study is an example to show how ML contributes to understand physics in materials science, different from most previous studies that use ML only as a black box to obtain mathematical solutions.

Previously proposed rules to predict single-phase, HEAs using very small datasets with very limited predictability were not encouraging. As such this ML study used 1252 alloys, including substantial number of HEAs, and explored the upper boundary of empirical rules’ predictability. Using a large training dataset of multicomponent alloys, single-phase alloys could be accurately predicted (i.e., 93%) by ML methods. The high predictability of the ML results is surprising, considering that of the previous studies. The ML results also identify the most important features (such as the bulk modulus), some of which are not considered in the Hume-Rothery rules. This ML insight and its high predictability lead to a new thermodynamics-based rule for predicting solid–solution alloys. The new rule is nonetheless slightly less accurate (73%) but has roots in the physical nature of the problem. The new rule is further employed to predict solid solutions for three 9-element blocks, and the predictions are of 94% consistency with Calphad calculations. Since the new thermodynamics-based rule employs only elemental properties, which is in line with the spirit of the Hume-Rothery rule, these results will encourage researchers to use our rule to search for new high-entropy solid–solution alloys. Our study also demonstrates a pathway to find more predictive rules that maximize simplicity and efficiency in application.