Automated calculation and convergence of defect transport tensors

Abstract

Defect diffusion is a key process in materials science and catalysis, but as migration mechanisms are often too complex to enumerate a priori, calculation of transport tensors typically have no measure of convergence and require significant end-user intervention. These two bottlenecks prevent high-throughput implementations essential to propagate model-form uncertainty from interatomic interactions to predictive simulations. In order to address these issues, we extend a massively parallel accelerated sampling scheme, autonomously controlled by Bayesian estimators of statewide sampling completeness, to build atomistic kinetic Monte Carlo models on a state-space irreducible under exchange and space group symmetries. Focusing on isolated defects, we derive analytic expressions for drift and diffusion coefficients, providing a convergence metric by calculating the Kullback–Leibler divergence across the ensemble of diffusion processes consistent with the sampling uncertainty. The autonomy and efficacy of the method is demonstrated on surface trimers in tungsten and Hexa-interstitials in magnesium oxide, both of which exhibit complex, correlated migration mechanisms.

Introduction

The migration and transformation of intrinsic and extrinsic crystal defects play a central role in numerous materials science and chemistry phenomena, such as postirradiation annealing^1,2, plasma surface interactions³, or active site formation for heterogeneous catalysis^4,5. The atomistic mechanisms by which defects migrate are generally impossible to divine a priori due to the routine presence of complex multiatom transformations^{6,7,8,9,10,11,12}. While these mechanisms self-average with increasing defect size, allowing the use of suitably parametrized coarse-grained models^13,14,15, the smallest defects are both the least predictable and most mobile¹², with the greatest influence on transport behavior.

In the general case, atomistic mechanisms must be discovered through unbiased dynamic^{10,16,17,18,19,20} or static^11,21,22 sampling approaches. When the true dynamics can be characterized as rare transitions between metastable basins on the energy landscape²³, the basin-to-basin dynamics can be mapped to a continuous-time Markov chain^24,25, which forms the theoretical foundation of atomistic kinetic Monte Carlo (akMC) methods²⁶. The resulting model can then be stochastically or in some cases (such as that presented here) analytically integrated to extract observables of interest.

A well-recognized problem is that an akMC model will in general have an incomplete catalog of available mechanisms due to a finite amount of sampling, and this can produce catastrophically erroneous predictions if important mechanisms are omitted^19,20,27,28. Sampling adequacy is often assessed qualitatively using the domain expertise of simulation practitioners. Whilst this approach has undoubtedly yielded significant successes, it requires significant end-user analysis for each system under study. This has a punitive impact on the feasibility of automating complex materials simulations on massively parallel computational resources, where the required decision frequency rapidly exceeds practical human limits. Further, in absence of quantitative uncertainty quantification approaches, assessing the reliability of mesoscale or macroscale predictions is extremely challenging.

For example, the system sizes required even for small defect clusters render ab initio calculation unfeasible. As a result, interatomic potential models must be used which induces an additional model form uncertainty. The development of interatomic potentials has been revolutionized in recent years through the use of linear-in-descriptor or neural network regression techniques^29,30,31. These approaches offer a natural encoding of model form uncertainty through isosurfaces of the cost function used for potential parametrization. High-throughput calculations are essential in this context to enable the systematic propagation of this uncertainty on interatomic interactions to the observables of scientific interest, without prohibitive hours of end-user analysis.

In this contribution, we present an autonomous, highly scalable sampling scheme to efficiently calculate defect diffusion tensors with quantified uncertainty on the sampling completeness. We demonstrate the ability to discover complex migration behaviors of defects in tungsten and magnesium oxide and show how the quantified uncertainty can be used to rapidly yield well-defined convergence measures. Our approach enables high-throughput workflows to rapidly discover, converge, and analyze complex kinetic properties of defect structures in surrogate energy landscapes, with minimal end-user involvement.

Results

Isomorphic compression of state-space

In previous work²⁸ we introduced TAMMBER, a massively parallel accelerated sampling scheme whose formal objective is to exhaustively sample the set of all metastable minima ${\mathcal{M}}$ and all inter-minima transitions ${\mathcal{T}}$ for a given system. TAMMBER builds a matrix K_ji of j ← i rates in the known state space and a vector ${{\rm{k}}}_{i}^{u}$, which estimates the “unknown” (as yet undiscovered) escape rate from each state i, encoded as transitions to an absorbing sink^{19,20,28,32,33} (Methods). States are identified by constructing a connectivity graph from a minimized configuration, which is then hashed to produce a pseudo-unique integer label for each configuration^11,34. The presence of nonzero k^u causes trajectories to leave the known state space, giving a natural measure of model validity, the expected residence time²⁸ in the known state space

$$\langle {\tau }_{res}\rangle ={\bf{1}}{\left[{{\bf{K}}}^{tot}-{\bf{K}}\right]}^{-1}{{\bf{P}}}_{0},$$

(1)

where ${{\bf{K}}}_{ji}^{tot}={\delta }_{ji}\left[{{\rm{k}}}_{i}^{u}+{\sum }_{l}{{\rm{K}}}_{li}\right]$, P₀ is the initial distribution, and 1 is a row vector of ones. In practice, truly comprehensive sampling of ${\mathcal{M}}$ and ${\mathcal{T}}$ is often impractical as their size grows exponentially with the number of atoms in the system. However, ${\mathcal{M}}$ and ${\mathcal{T}}$ are both highly reducible under exchanges of indistinguishable atoms ${\mathcal{R}}$, lattice vector translations ${\mathcal{S}}$ and space group symmetries ${\mathcal{G}}$, especially in the case of quasi-zero-dimensional defects. It is known that configurations that are degenerate (in the periodic minimum image sense) under these operations will have isomorphic connectivity graphs^11,34, with isomorphisms that can be efficiently calculated³⁵. We exploit this reducibility to make a partition of ${\mathcal{M}},{\mathcal{T}}$ into equally sized subsets

$${\mathcal{M}}=\mathop{\bigcup }\limits_{p\in [1,P]}{{\mathcal{M}}}_{p},\quad \quad {\mathcal{T}}=\mathop{\bigcup }\limits_{p,q\in {[1,P]}^{2}}{{\mathcal{T}}}_{pq},$$

(2)

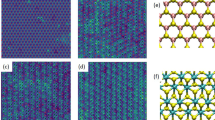
where all states in ${{\mathcal{M}}}_{p}$ are identical to all others up to a translation ${\bf{t}}\in {\mathcal{S}}$ and reindexing ${\mathcal{R}}$. For a given set of primitive lattice vectors, ${{\mathcal{M}}}_{p}$ is thus completely determined by a single local minimum, meaning we can focus all sampling effort on a single state per subset. All of the distinct exit pathways from the chosen ${{\mathcal{M}}}_{p}$ state that end in ${{\mathcal{M}}}_{q}$, or vice versa, are sufficient to fully determine ${{\mathcal{T}}}_{pq}$. This already produces a space of P states irreducible under translation that will be used to generate transport coefficients, as illustrated in Fig. 1.

Fig. 1: Compressed sampling methodology applied to trimer migration on W(110).

a Cartoon of the full akMC state space and those irreducible under space and translation symmetries. Isomorphic states have the same color. b One primitive unit cell with self transitions (closed loops) is sufficient to build a Markov model for transport. c A set of states irreducible under all space group symmetries is optimal for discovering new states and transitions through accelerated sampling. d Atomic structure of the lowest energy irreducible states and found transition mechanisms. Atoms colored by centrosymmetry⁵¹. e Diffusion tensor eigenvalues D₁, D₂, as determined by (5), over a range of temperatures. The Monte Carlo bounds ${{\rm{D}}}_{1\pm }^{MC}$, ${{\rm{D}}}_{2\pm }^{MC}$ are described in the main text. Effective Arrhenius slopes at low temperature are given. Inset: 〈τ_res〉 with temperature.

To exploit space group symmetries, consider transforming every member of some subset ${{\mathcal{M}}}_{p}$ with a symmetry operation ${\bf{G}}\in {\mathcal{G}}$ of the host crystal, producing a new subset of states ${{\mathcal{M}}}_{q}={\bf{G}}{{\mathcal{M}}}_{p}$. There are two possible outcomes—if q = p we have identified operations ${\bf{G}}\in {{\mathcal{G}}}_{p}$ of that subset’s symmetry group ${{{\boldsymbol{\mathcal G}}}}_{p}$, which contains at least the identity operation. As all members of ${{{\boldsymbol{\mathcal M}}}}_{p}$ are related by translation, they share the same space group symmetries. If q ≠ p we have further reduced the size of our state space to P_G ≤ P, as we can generate all members of the subset ${{\mathcal{M}}}_{q}$ from the subset ${{\mathcal{M}}}_{p}$ through the action of G.

However, ${{\mathcal{M}}}_{p}$ is left unchanged under the action of any operation ${{\bf{G}}_p\in{\mathcal{G}}}_{p}$, i.e., ${{\bf{G}}}_{p}{{\mathcal{M}}}_{p}={{\mathcal{M}}}_{p}$. This means the symmetry operation which takes ${{\mathcal{M}}}_{p}$ to ${{\mathcal{M}}}_{q}$ is not unique. To resolve this ambiguity we generate the left cosets³⁶ with respect to ${{\mathcal{G}}}_{p}$, defined for any operation ${\bf{G}}$ as $\{{\bf{G}}{{\bf{G}}}_{p}:{{\bf{G}}}_{p}\in {{\mathcal{G}}}_{p}\}$, i.e., the set of operations formed by postmultplying G with every operation in ${{\mathcal{G}}}_{p}$. It can be shown that each operation in ${\mathcal{G}}$ appears in exactly one coset³⁶.

Acting on ${{\mathcal{M}}}_{p}$ with any operation from a given coset will give the same result. For example, the subset’s symmetry group ${{{\mathcal{G}}}_{p}}$ forms a coset, whose action is the identity operation. We can then index the nonequivalent partitions $\{{{\mathcal{M}}}_{q}\}$ which can be generated from ${{\mathcal{M}}}_{p}$ by the coset which generates them; drawing some operation G_qp from each coset we can thus make the further compression ${\mathcal{M}}=\mathop{\bigcup }\nolimits_{p = 1}^{{P}_{G}}{\bigcup }_{q}{{\bf{G}}}_{qp}{{\mathcal{M}}}_{p}$, with analogous partitioning of ${{\mathcal{T}}}_{pq}$. This maximally compressed representation is used for sampling, as illustrated in Fig. 1, and we then partially “decompress” into the partitioning (2) of P distinct states irreducible under translation for the calculation of transport tensors.

We, therefore, only need to sample the exit transitions from a maximum of P_G configurations, as all others can be generated by the known symmetric relations. By focusing sampling resources on a much smaller number of possible states, the unknown rates decrease at a much faster rate, with a subsequent increase in the validity timescales for the constructed Markov chain. As in TAMMBER the unknown rates at low temperatures decrease as an inverse power of the MD time invested at high temperatures, state-space compression can yield extremely large benefits in practice. As an example of the efficiencies this approach affords, in previous work we investigated the breakup of two interstitial defects in bcc iron²⁸, obtaining a Markov model on the uncompressed (reducible) state-space with 〈τ_res〉 ~ 80 s at 300 K, an insufficient duration to make confident predictions on the breakup mechanism. Despite the relatively low symmetry of this defect system, we show in the Supplementary Information that the compressed sampling scheme described above yields a Markov model with 〈τ_res〉 ~5 × 10⁶ s with only 75% of the computational effort, allowing convergence in the model predictions. The isolated point defects we consider in this work are typical of even higher symmetry, giving correspondingly greater efficiencies.

Evaluation of transport tensors

To define the drift and diffusion tensors, we first require a defect position in the supercell for each configuration. To remove ambiguities from periodic boundary conditions, we carve out a defective region of some configuration in each partition by thresholding some structural descriptor, here the centrosymmetry, then take a descriptor-weighted center of mass. As we allocate sampling to increase the residence time, the threshold value can be freely determined in post-processing; typically a single value is suitable for the same material system.

A periodic minimum image displacement vector d_lm for any $l\in {{\mathcal{M}}}_{p}\to m\in {{\mathcal{M}}}_{q}$ transition is found through the application of the known rigid transformation from the sampled configurations. Importantly, transitions between states within the same space group partition are then represented as self transitions $l\in {{\mathcal{M}}}_{p}\to m\in {{\mathcal{M}}}_{p}$ (closed loops in Fig. 1) and d_lm is a lattice vector.

We are then able to construct an irreducible group of states from the space group partitioning of Eq. (2), with one state indexed by p ∈ [1, P] for each set ${{\mathcal{M}}}_{p}$. All the transitions from a state p to states q in the uncompressed model are mapped to their compressed states, forming a (possibly empty) set ${{\mathcal{C}}}_{qp}=\{{{\rm{k}}}_{l},{{\bf{d}}}_{l}\}$ of transitions and displacement vectors. The compressed rate matrix is then defined as ${{\rm{K}}}_{qp}^{c}={\sum }_{l\in {{\mathcal{C}}}_{qp}}{{\rm{k}}}_{l}$, with a statewise total escape rate matrix ${{\rm{K}}}_{qp}^{tot,c}={\delta }_{qp}({{\rm{k}}}_{p}^{u,c}+{\sum }_{r}{{\rm{K}}}_{rp}^{c})$, where the superscript c indicates we consider rates in the compressed model. The unknown rates ${{\rm{k}}}_{p}^{u,c}$ are taken from the maximally compressed representation, with the same unknown rate for symmetrically equivalent partitions. One could then generate akMC trajectories³⁷ with a matrix and vector of branching probabilities ${{\bf{B}}}^{c}\equiv {{\bf{K}}}^{c}{[{{\bf{K}}}^{tot,c}]}^{-1}$ and ${{\bf{B}}}^{u,c}\equiv {{\bf{k}}}^{u,c}{[{{\bf{K}}}^{tot,c}]}^{-1}$, accumulating a total displacement x = ∑d_l in a residence time τ_res = ∑δτ_l before absorption. In the Supplementary Information we show that the drift and diffusion coefficients μ, D can then be extracted from the relations 〈x〉 = 〈τ_res〉μ and $\langle {\bf{x}}\otimes {\bf{x}}\rangle =2\langle {\tau }_{\rm{res}}\rangle {\bf{D}}+\langle {\tau }_{\rm{res}}^{2}\rangle {\boldsymbol{\mu }}\otimes {\boldsymbol{\mu }}$ for large 〈τ_res〉. However, it is also possible to analytically evaluate averages over all possible pathways using a “displacement generating function”

$$Z({\boldsymbol{\lambda }},{{\bf{P}}}_{0})={{\bf{B}}}^{u,c}{{\bf{G}}}^{c}({\boldsymbol{\lambda }}){{\bf{P}}}_{0},\quad {\left[{{\bf{B}}}^{c}({\boldsymbol{\lambda }})\right]}_{qp}\equiv \mathop {\sum}\limits_{l\in {{\mathcal{C}}}_{qp}}\frac{{{\rm{k}}}_{l}{e}^{-{\boldsymbol{\lambda }}\cdot {{\bf{d}}}_{l}}}{{{\rm{K}}}_{pp}^{tot,c}},$$

(3)

where ${{\bf{G}}}^{c}({\boldsymbol{\lambda }})=\mathop{\sum }\nolimits_{n = 0}^{\infty }{\left[{{\bf{B}}}^{c}({\boldsymbol{\lambda }})\right]}^{n}={\left[{{\mathbb{I}}}-{{\bf{B}}}^{c}({\boldsymbol{\lambda }})\right]}^{-1}$. Moments of the total displacement can then be written 〈x〉 = − ∂_λZ(λ, P₀)∣_λ=0 and 〈x ⊗ x〉 = ∂_λ ⊗ ∂_λZ(λ, P₀)∣_λ=0 (Supplementary Information). While (3) could be used for any choice of the initial condition, we note that in the well-sampled limit ${{\rm{k}}}_{p}^{u,c}\ll {\sum }_{r}{{\rm{K}}}_{rp}^{c}$, which is necessary but not sufficient for global convergence, the matrix $\left[{{\bf{K}}}^{tot,c}-{{\bf{K}}}^{c}\right]$ will have a spectral gap, with one eigenvalue 0 < ν₀ ≪ ν₁ < ν₂. . . much smaller than all others²⁴. The right eigenvector for ν₀ is the quasistationary distribution (QSD) π^QSD in the known state space²⁴, the limiting distribution conditional on not absorbing for an arbitrarily long time, which as k^u,c → 0 becomes the Boltzmann distribution, ${{\boldsymbol{\pi }}}^{\rm{QSD}}\to \hat{{\boldsymbol{\pi }}}$. As the QSD is the longest-lived mode and transport coefficients are defined as the limit of infinitely long trajectories, it is natural to set ${{\bf{P}}}_{0}={\hat{{\boldsymbol{\pi }}}}^{\rm{QSD}}={{\boldsymbol{\pi }}}^{\rm{QSD}}/({\bf{1}}{{\boldsymbol{\pi }}}^{\rm{QSD}})$ to eliminate the influence of initial conditions. With this choice, it is simple to show that $\langle {\tau }_{\rm{res}}^{n}\rangle =n!/{\nu }_{0}^{n}$ and the expected drift and diffusion coefficients emerge as (Supplementary Information)

$${\boldsymbol{\mu }}({{\bf{k}}}^{u,c})\equiv {\langle {\tau }_{\rm{res}}\rangle }^{-1}{\partial }_{{\boldsymbol{\lambda }}}{\left.\left[1/Z({\boldsymbol{\lambda }},{\hat{{\boldsymbol{\pi }}}}^{\rm{QSD}})\right]\right|}_{{\boldsymbol{\lambda }} = {\bf{0}}},$$

(4)

$${\bf{D}}({{\bf{k}}}^{u,c})\equiv \frac{1}{2}{\langle {\tau }_{\rm{res}}\rangle }^{-1}{\partial }_{{\boldsymbol{\lambda }}}\otimes {\partial }_{{\boldsymbol{\lambda }}}{\left.\left[1/Z({\boldsymbol{\lambda }},{\hat{{\boldsymbol{\pi }}}}^{\rm{QSD}})\right]\right|}_{{\boldsymbol{\lambda }} = {\bf{0}}}.$$

(5)

Equations (4) and (5) are a central result of this contribution, expressions for the drift and diffusion tensors of an arbitrarily complex diffusion process in a periodic system, autonomously constructed in a massively parallel sampling scheme, which crucially are dependent on ‘unknown’ rates k^u,c that robustly quantify sampling incompleteness. In the Supplementary Information we show the limiting expressions ${\boldsymbol{\mu }}\equiv {\mathrm{lim}\,}_{{{\bf{k}}}^{u,c}\to {\bf{0}}}{\boldsymbol{\mu }}({{\bf{k}}}^{u,c})$ and ${\bf{D}}\equiv {\mathrm{lim}\,}_{{{\bf{k}}}^{u,c}\to {\bf{0}}}{\bf{D}}({{\bf{k}}}^{u,c})$ reduce to expressions obtained in previous derivations on multistate diffusion in periodic media^38,39, with all uncorrelated and correlated contributions that are essential to capture complex diffusion pathways. We also show that the error in our estimators scales inversely with 〈τ_res〉, and we confirm that for systems obeying detailed balance, which we focus on in the remainder, μ = 0 and the correlated contribution to the diffusivity is always nonpositive⁴⁰.

The convergence of the diffusivity

The key feature of (5) is that D(k^u,c) estimates the diffusion tensor over all possible trajectories in the known state-space before exit due to the unknown rates. Possible changes to the diffusivity under the discovery of additional transition rates between known states can then be bounded; the rate matrix K^c can be modified by an additional rates matrix δK^c, which must satisfy detailed balance and not increase the total exit rate from each known state p by more than the unknown rate ${{\rm{k}}}_{p}^{u,c}$, meaning ${\left[{\bf{1}}\delta {{\bf{K}}}^{c}\right]}_{p}\le {{\rm{k}}}_{p}^{u,c}$¹. We have designed a Monte Carlo procedure to sample the space of permissible δK^c (see Supplementary Information) which typically requires less than a core-minute for the systems studied here and is trivially parallelizable. We discuss the sensitivity to the discovery of additional states at the end of this section.

Anisotropic diffusion is most conveniently expressed using the eigenvalues and eigenvectors {D_l, v_l}, l ∈ [1, 3] of the symmetric 3 × 3 diffusion matrix. In the limit of comprehensive sampling, we have found that the ensemble of diffusion tensors produced in our Monte Carlo procedure can be simultaneously diagonalized to high accuracy, allowing a direct measure of convergence by comparing the spread D_l+ − D_l− in eigenvalues, where D_l± are the maximum and minimum values obtained by Monte Carlo, as can be seen in figure 1. However, in the general case, the eigenbasis can vary significantly over the ensemble of diffusion tensors, requiring a more robust measure of convergence.

As diffusive processes are characterized by a probability distribution that broadens with time, we build a convergence measure by comparing the Kullback–Leibler divergence⁴¹${{\mathcal{R}}}_{\pm }\equiv \int {\rm{d}}{\bf{x}}\rho \,{\mathrm{ln}}\,\rho /{\rho }_{\pm }$ between fundamental solutions ρ(x, t), ρ_±(x, t) to the three-dimensional diffusion equation with a diffusion tensor D, D_±, where ${{\mathcal{R}}}_{\pm }=0$ if and only if ρ = ρ_±. The matrices D_± are chosen such that ${{\mathcal{R}}}_{\pm }$ are the maximum and minimum values obtained during Monte Carlo. It can be shown that, for this choice of distribution, ${{\mathcal{R}}}_{\pm }$ is time-independent for identical initial conditions (Supplementary Information). For our convergence measure we take the spread $\delta {\mathcal{R}}\equiv {{\mathcal{R}}}_{+}-{{\mathcal{R}}}_{-}\ge 0$, reading

$$\delta {\mathcal{R}}=\frac{1}{2}{\rm{Tr}}\left({{\bf{D}}}^{-1}\left[{{\bf{D}}}_{+}-{{\bf{D}}}_{-}\right]\right)+\mathrm{ln}\,\sqrt{{\rm{Det}}\left({{\bf{D}}}_{-}^{-1}{{\bf{D}}}_{+}\right)}.$$

(6)

In the limit of comprehensive sampling is is simple to show that $\delta {\mathcal{R}}\to {\sum }_{l}({{\rm{D}}}_{l+}-{{\rm{D}}}_{l-})/2{{\rm{D}}}_{l}$, meaning that $\delta {\mathcal{R}}$ reduces to the above convergence definition, the relative spread in eigenvalues. We thus identify $\delta {\mathcal{R}}$ as a well defined dimensionless convergence metric ideal for autonomous implementation, which has an informative limit, namely the relative spread in eigenvalues consistent with the sampling uncertainty. In the Supplementary Information, we show how $\delta {\mathcal{R}}$ monotonically decays with sampling effort, with asymptotic rate 1/〈τ_res〉, even when starting from poorly converged samples.

It is clear that the diffusivity cannot be globally bounded against the discovery of some new set of states which are free to possess arbitrary transport properties. However, as transition rates to such a set of states are bounded by the k^u, the Monte Carlo procedure outlined above does characterizes transport behavior in the known state-space over timescales of order 〈τ_res〉. Convergence to the large 〈τ_res〉 limit can be accelerated by seeding the TAMMBER procedure with as many states as possible, which are free to be completely disconnected (in this case we have independent QSDs ${{\boldsymbol{\pi }}}_{s}^{\rm{QSD}}$ for each connected sub-network s). The integration of automated structural search algorithms^23,42 into the present workflow will be the subject of future work. Of course, as TAMMBER generates thousands of high-temperature molecular dynamics trajectories across the known state space, it is an automated global minimum search method, with 〈τ_res〉 acting as a quantitative measure of sampling quality when the system is ergodic. As a result, whilst in common with all theoretical studies on high dimensional landscapes, we cannot provide bounds on global minima, we can provide a key uncertainty quantification on the validity of our findings, namely a rigorous prediction timescale from an arbitrary distribution on the known state space with a corresponding bound on transport coefficients. We emphasize that the inability to assign bounds on global minima searches applies equally to human-guided sampling or the present approach. The convergence metrics we provide is thus a valuable analytical tool that removes ambiguities inherent to traditional methods in addition to enabling a fully automated workflow suitable for high-throughput computation.

Application to trimer diffusion on W(110)

The diffusion of adatom clusters is a fundamental process in surface science and has recently been conjectured to play a crucial role in the formation of complex “fuzzy” surface morphologies during plasma exposure in nuclear fusion reactors⁴³. We focus here on the trimer defect a demonstrative case study; comprehensive high-throughput investigations for which the present approach is designed will be presented elsewhere. In the present case, TAMMBER was initialized with state A₁ in Fig. 1, then run for 8 h on 144 cores using the EAM4 embedded atom method potential by Marinica et al.⁴⁴, covering a temperature range of 400–1400 K. The corresponding values of 〈τ_res〉 as a function of temperature are also shown in Fig. 1.

The resultant diffusion behavior is highly correlated, with many A₁ ↔ A₂ and D₁ ↔ D₂ transitions in particular. However, the overall system does not exhibit a clear “superbasin-to-superbasin” diffusion mechanism, meaning access to the full highly correlated trajectory ensemble is essential to extract accurate transport coefficients. As shown in Fig. 1, the eigenvalues D₁, D₂ (D₃ → 0 for surface diffusion) show a high degree of convergence under the Monte Carlo sensitivity procedure, with $\delta {\mathcal{R}}\le 2$ at all temperatures. The eigenvectors for D₁ and D₂ were found to be v₁ = [001] and ${{\bf{v}}}_{2}=[1\bar{1}0]$. To look for dominant pathways, we form a weighted graph from the connectivity of four primitive unit cells, where the graph edges are weighted by the corresponding saddle point energy^23,28. Dijkstra’s shortest path algorithm⁴⁵ was then used to identify the dominant pathways. In agreement with the found Arrhenius slopes, migration along v₂ is dominated by A₁ → D₁ → C₁ → D₂ → A₅ paths, with a well-defined activation energy of ΔE₁ = 1.32 eV at the lower temperatures. Migration along v₁ is similarly dominated by A₁ → A₄ paths at lower temperatures, but A₁ → A₃ paths have a growing contribution with temperature, giving a weak nonlinearity to the Arrhenius gradient $\Delta E(\beta )=-{\partial }_{\beta }\mathrm{ln}\,| D|$. An in-depth study of this procedure, and its role in a fully automated workflow, will be the subject of future work. We note that a recent study⁴³ of surface island diffusion on W(110) at 1000K using a different interatomic potential⁴⁶ reported trimer migration via A₁ → A₃, which is accounted for in the present study but is not found to be the dominant mechanism. The ability to efficiently resolve such ambiguities, without prohibitive person-hours, is a key advantage of the methodology presented here.

Application to Hexa-interstitial in bulk MgO

To conclude this contribution, we investigate the diffusion of a stochiometric Hexa-interstitial in MgO, whose lattice has a space group $Fm\bar{3}m$ with point group ${{\mathcal{O}}}_{h}$. In a cubic supercell with axes aligned with 〈100〉 directions, we thus retain the full symmetry of the host lattice before the introduction of any defective structures. Connectivity graphs are constructed with vertices colored to indicate specie. Due to the high degree of symmetry, the maximally reduced state space contained only four states, while the state space irreducible under translation contained 56 states. TAMMBER was initialized in a relatively high energy state (red circle) that was found by Uberuaga et al.^7,8 to possess very low migration barriers; a much lower energy state was rapidly found, upon which sampling was subsequently concentrated, demonstrating the ability of TAMMBER to act as a massively parallel global minimum search routine. Using the same modified Buckingham potential as in that work, TAMMBER was run for 8 h on 144 cores targeting a temperature range of 500–1000 K. While we find the very low migration barriers (<0.1 eV) in agreement with^7,8, the full diffusion tensor was found to be isotropic D₁ = D₂ = D₃, with characteristic activation energy that converged to 0.887 eV at the lower temperatures, which slowly increases at higher temperatures, as found for the above trimer example. Analyzing the dominant pathways with temperature reveals that this activation barrier corresponds to self-migration of the lowest energy state, with little effect of correlation on the diffusion paths; analyzing the state-by-state contribution to the uncorrelated diffusivity, shown in Fig. 2, we see that at higher temperatures the self-migration of other states have an increasingly large contribution. 〈τ_res〉 as a function of temperature are also shown in Fig. 2. The Monte Carlo procedure indicated a high degree of convergence, with $\delta {\mathcal{R}}\,<\,0.001$ over all temperatures considered.

Fig. 2: Sampling of Hexa-interstitial in MgO.

a Connectivity graph²³ between states irreducible under translation. The very low diffusion barriers (<0.1 eV) observed in previous work^7,8 can be seen. b Nonequivalent positions in the primitive unit cell for the four irreducible states. c Cross-section of the lowest energy state. Atoms colored by centrosymmetry⁵¹. d Atomic structure of the four lowest energy irreducible states. e Single eigenvalue of the diffusion tensor at various temperatures. Error bounds, calculated through the Monte Carlo procedure detailed in the main text, are not visible on the presented scale. Insets show 〈τ_res〉 at various temperatures and the contribution to the overall diffusivity from self transitions within each state. The fast diffusing states have increasing contribution at high temperatures as they are occupied more frequently.

Discussion

We have presented a fully automatable and efficient method to evaluate the transport tensors resulting from the arbitrarily complex diffusion processes of crystal defects, with well-defined convergence criteria based on quantitative measures of sampling uncertainty combined with a Monte Carlo procedure to sample the admissible diffusion tensors consistent with sampling uncertainty and a detailed balance. The method was demonstrated on a surface trimer in tungsten and a hex-interstitial in magnesium oxide. By effectively eliminating user input beyond the seeding of some initial state(s), the presented approach demonstrates sufficient computational and critically end-user efficiencies to extend the phenomenological reach of high throughput computations to point defect kinetics. Future work will exploit these efficiencies to analyze defect transport over a wide range of material systems, and the influence of breaking detailed balance through external driving forces, giving nonzero limits for the drift vector μ.

Methods

Massively parallel sampling routine

Through the use of NEB calculations⁴⁷ and transition, state theory⁴⁸TAMMBER constructs a transition matrix K of rank equal to the number of discovered states, giving a continuous-time Markov chain $\dot{{\bf{P}}}(t)=\left[{\bf{K}}-{{\bf{K}}}^{tot}\right]{\bf{P}}(t)$. Exploiting the known Poissonian distribution of exit times from a suitably thermalized basin²⁴, a Bayesian likelihood (and thus posterior distribution) for the $\{{{\rm{k}}}_{i}^{u}\}$ was derived using parallel trajectory data obtained through a modified temperature accelerated dynamics method¹⁸. Continuous self-optimization was achieved by calculating the derivative of each ${{\rm{k}}}_{i}^{u}$ with respect to additional computational work, allowing the degree of temperature acceleration to be statewide optimized and the massively parallel sampling effort distributed across states to differentially maximize a key measure of model validity, the expected residence time before absorption²⁸, Eq. (1). Typically, a simulation starts with one state then the rank of P, K, and K^tot increases as states are discovered. If P₀ is fixed to be unity for the initial state and zero otherwise, i.e., ${[{{\bf{P}}}_{0}]}_{j}={\delta }_{ij}$ for initial state i, $\langle {\tau }_{{\rm{res}}}\rangle$ is monotonically increasing with sampling effort, a key consequence of the estimation procedure for $\{{{\rm{k}}}_{i}^{u}\}$. An implementation of this method is available as an open-source code at https://github.com/tomswinburne/tammber, whose near-ideal parallel efficiency has been demonstrated on massively parallel resources employing 1000 to more than 80,000 cores.

Isomorphically compressed representation

Isomorphic configurations are identified in two ways—the connectivity graph for every state is duplicated and reindexed into McKay’s pseudo unique canonical order³⁵, which is identical for isomorphic states. Alternatively, the VF2 graph matching routine⁴⁹ is applied to a single state to find self-isomorphisms. To determine a given reindexing ${{\mathcal{R}}}_{ij}$ between two isomorphic states i, j we first find the mappings ${{\mathcal{R}}}_{ic}$ and ${{\mathcal{R}}}_{jc}$ to the McKay canonical order then obtain ${{\mathcal{R}}}_{ij}={{\mathcal{R}}}_{ic}{{\mathcal{R}}}_{cj}^{-1}$.

As isomorphisms will be with respect to the simulation supercell, not the host crystal structure, the relevant point group is $\bar{{\mathcal{G}}}={\mathcal{W}}\cap {\mathcal{G}}\in {{\mathcal{O}}}_{h}$, the intersection of the point group of ${\mathcal{G}}$ and the supercell point group ${\mathcal{W}}$, where ${\mathcal{W}}$ is a subgroup of the cubic group ${{\mathcal{O}}}_{h}$. Unlike an arbitrary element of ${\mathcal{G}}$ or ${\mathcal{W}}$, any element of $\bar{{\mathcal{G}}}$ is guaranteed to leave both the perfect lattice and supercell unchanged up to a translation and reindexing. We then iterate through all members of $\bar{{\mathcal{G}}}$, applying the point transform, aligning the first indexed atom then checking for minimum image coincidence atom-by-atom, rejecting the candidate member of $\bar{{\mathcal{G}}}$ at the first failure.