Introduction

The use of austenitic stainless steels such as 304 and 316 is ubiquitous across applications that demand strength and corrosion resistance at moderate cost. Advanced austenitic steels are undeniably among the most important materials of the modern age, spanning automotive, aerospace, nuclear, and consumer household applications. Recently, advances in nonequilibrium additive manufacturing methods such as selective laser melting (SLM) have revitalized scientific inquiry into processing and microstructural properties of such steels. Specifically, the formation of complex 3D dislocation networks and chemical ordering has been observed, leading to novel deformation behavior without the traditional tradeoff between strength and ductility1,2,3,4. The phenomena that affect material responses and properties span multiple length scales. The modeling of such defect structures is an inherently multiscale problem5,6, and balancing accuracy and applicability becomes increasingly important. The behavior of individual dislocations, microstructure-scale mechanisms, and collective dislocation interactions must be bridged to enable predictive simulation of dislocation plasticity. Discrete dislocation dynamics (DDD) is one such method that seeks to describe mesoscale phenomena by evolving microstructures using a set of physics-based heuristic rules6,7,8. Continued advancements in the implementation of such rules has equipped DDD with the ability to describe mechanisms such as dislocation glide, climb, and cross slip, which contribute to development of three-dimensional dislocation structures9,10. A fundamental driver in all such extensions is the mapping of the local resolved shear stress to the dislocation glide velocity on specific slip systems, described by the mobility law11,12,13,14,15. While difficult to ascertain experimentally, mobilities have been readily computed via molecular dynamics (MD) simulations for pure metals and binary alloys for both face-centered-cubic (fcc) and body-centered-cubic (bcc) crystals12,13,14,15,16,17,18. To date, the lack of mobility data for more complex alloys has limited the application of DDD simulations to the SLM austenitic stainless steels of interest, with some authors19,20 opting to take single bulk handbook values for the mobility despite clear evidence of temperature and composition dependence12,16,21. Furthermore, the temperature ranges simulated in typical mobility calculations must be extended to capture the high temperatures induced by the laser path traversal and subsequent cooling during SLM. Moreover, austenitic stainless steels are often employed in elevated temperature applications and these ranges are simultaneously captured. Lastly, an examination of composition effects on dislocation mobility is key to understanding the effects of alloying on the strengthening behavior. In this work, we conduct an extensive MD study on screw dislocation mobility in the austenitic Fe0.7NixCr1−x stainless steels in an extended temperature and composition regime.

The dislocation mobility can be generally divided into thermally activated17,21 regime, a linear drag-dominated16,22 regime which at higher strain rates represents phonon drag, and an asymptotic shear wave-limited relativistic regime12,23,24. In pure fcc metals, where the Peierls stress (i.e., minimum stress to move the dislocation at 0 K) is negligible, only the phonon and relativistic regimes are observed. Mobility functions relate the resolved shear stress τ to the dislocation velocity v, and typically reflect a piecewise phenomenological form, i.e.,

$$\tau b = \left\{ {\begin{array}{*{20}{c}} {{\mathrm{\it{ATv}}}} & {v \, < \, v_0} \\ {{\mathrm{\it{ATv}}} + D(v - v_0)^{3/2}} & {v \, > \, v_0} \end{array}} \right.$$
(1)

Here, fitting parameters A and D are linear and nonlinear drag coefficients, respectively, b is the Burgers vector length, and v0 a minimum critical velocity for radiative dispersion. It is also common to define a friction coefficient that incorporates temperature effects as AT = B(T), though this term is often interchangeable with drag coefficient17,25,26. The power law exponent of 3/2, as originally suggested by Eshelby for the dispersive term23, is commonly cited in the literature; however, recent studies have sought to render more accurate fits as a function of character angle and stress state13,14,27. Moreover, various interpolations between screw and edge character drag coefficients are typically used in the absence of this data during conventional DDD simulations28. In the low stress regime at zero temperature, a threshold stress may be required to initiate dislocation glide in the fully linear drag-dominated regime. For a pure metal this is governed by the Peierls stress. In random solid solutions, the presence of solute–dislocation and solute–solute interactions21 induces elastic misfit strain fields29,30, presenting non-negligible pinning barriers16 that must be overcome to initiate dislocation glide. This threshold stress controls the material’s resistance to dislocation glide at low temperatures, where the kinetics of thermally activated obstacle bypass is slow. Recently, efforts to predict this in the context of concentrated solid solutions have been proposed30 and will be discussed later in this work. However, most DDD simulations in the literature consider only the regions described by Eq. (1), applying the linear drag fit through the regime of lower effective stress range14,19,28,31,32. On the other hand, the threshold for the onset of dislocation glide becomes increasingly negligible at elevated temperatures33 at which thermally-assisted dislocation migration is more pronounced. In this work, we focus primarily on the linear drag region while characterizing variations in the threshold stress. Furthermore, for the range of applied resolved shear stress explored here we omit dispersive (high velocity) effects34.

In order to describe temperature and composition effects on linear drag induced by the solute fluctuation in a binary alloy, Marian and Caro12 proposed an additional term in the drag coefficient A, i.e.,

$$A(T,x)\,=\,A^ \ast + x\beta (T),$$
(2)

where x is the solute concentration. This suggests a linear dependence on composition. However, this form was derived and validated against a binary alloy within a limited temperature range; the presence of multiple solute atoms may require additional terms or an alternate form altogether, particularly if their relative misfit volumes differ30. In most previous work seeking to define DDD mobility functions, explicit values for drag coefficient have been calculated and used at a few select temperatures and compositions of interest. To the best of our knowledge, the current work offers the most comprehensive analysis to date across both temperature and composition variables in the Fe0.7NixCr0.3−x austenitic stainless-steel alloy system.

Results and discussion

Fitting procedure for dislocation velocity data

Dislocation velocities are extracted from MD simulations run for fcc Fe0.7NixCr0.3−x at seven compositions (xNi = 0.00, 0.05, 0.10, 0.15, 0.20, 0.25, and 0.30), eight stresses (τ = 30, 40, 60, 80, 90, 100, 120, and 140 MPa), and seven temperatures (T = 100, 300, 500, 700, 900, 1100, and 1300 K). The standard deviation of velocity across replicate simulations diminishes with increasing stress (maximum of 3% at 100 MPa); therefore, only one simulation was performed for each case when τ ≥ 120 MPa. Dislocation velocities obtained at different stresses for a fixed Ni composition of xNi = 0.15 are shown in Fig. 1a for temperature = 100 K and Fig. 1b for temperature = 500 K. Two linear fits to each set of MD data points are presented: the green line indicates a linear fit excluding velocities below 0.1 Å/ps, while the red line indicates the linear fit through all data points. For subsequent analysis we fit to the truncated mobility data defined here.

Fig. 1: Temperature effect on linear fit determination.
figure 1

Dislocation velocity as a function of stress for Ni concentration of xNi = 0.15 at a T = 100 K and b T = 500 K. Comparison of the truncated and full linear fits to the MD data are shown.

Full size image

The R-squared value (inset, Fig. 1) of these fits decreases with increasing temperature. This can be attributed to the non-negligible threshold stress from the thermally-activated regime to the onset of drag-dominated dislocation glide, as discussed in “Methods” section. Significant threshold stresses at low temperature are observed across all compositions. When temperature is increased to 500 K, it is observed that this threshold stress is diminished, and a linear approximation through the entire stress range is increasingly valid at higher temperatures. We do not enforce a fit through the origin; the regression is allowed to compute a nonzero stress intercept that would correspond to the transition to the thermally-activated regime at lower stress levels. A detailed discussion regarding the use of least squares regression in determining drag coefficient can be found in the ref. 22.

Dislocation mobility curves

Average dislocation velocities (over the five replicas) are calculated as a function of shear stress for all compositions and temperatures simulated, and results are summarized in Fig. 2a–g. The more significant nonlinearity at low temperatures (100 and 300 K) and the nonzero stresses for the onset of dislocation motion in the linear solute drag regime seen in Fig. 1a, b, can be observed across all compositions. It is also apparent that the slopes of the mobility curves decrease with increasing temperature at all compositions, consistent with drag-controlled dynamic behavior. In other words, the drag coefficient increases with temperature once the initial threshold stress is overcome; this is discussed further in the following sections.

Fig. 2: Dislocation mobility curves.
figure 2

Dislocation velocity as a function of resolved shear stress for different Ni compositions at temperatures a 100 K, b 300 K, c 500 K, d 700 K, e 900 K, f 1100 K, and g 1300 K. Lines plotted here serve as a visual guide to demarcate data and do not reflect any fitting procedure.

Full size image

Qualitatively, Fig. 2 shows no evidence of a plateaued relativistic or dispersive regime for the stress range tested. Indeed, the critical velocity v0 for crossover into this regime is comparable to the lowest shear wave speed in the solid12, and was determined for various other systems to be at least double that of our highest observed velocity of ~8 Å/ps13,16,22,32,35. Taken together, these two observations indicate that a linear mobility law with nonzero stress at zero velocity suffices in the viscous damping region.

To examine solute effects, we plot the average velocity as a function of Ni composition for different stresses and temperatures, shown in Fig. 3. It is evident that the average velocity decreases monotonically with increasing Ni content, suggesting a stronger pinning contribution from Ni relative to Cr. Note, we also considered binary Fe1−xNix alloys and a similar decrease in velocity was observed as the alloy concentration increased (see Supplementary Fig. 3).

Fig. 3: Composition dependent dislocation velocity.
figure 3

Averaged velocity in the ternary alloy as a function of Ni composition. Lines plotted here serve as a visual guide to demarcate data and do not reflect any fitting procedure.

Full size image

Local environment effect on dislocation mobility

The dislocation mobility in random alloys is controlled primarily by solute–dislocation interactions. Local environment heterogeneity resulting from fluctuations in swelling volume and elastic constant differences are important to capture in executing MD simulations of this nature. To expand on this, average atom simulations are executed for a fixed composition and temperature of xNi = 0.15, T = 300 K for comparison. The simulation cell and parameters follow those outlined in “Methods” section. The dislocation position is plotted as a function of timestep for a single simulated stress τ = 60 MPa in Fig. 4a, and the full mobility curve for these parameters is shown in Fig. 4b. It is evident here that the stress required to initiate dislocation motion is much lower for the average atom results, resembling a pure FCC crystal. In addition, the glide velocity of the dislocation is also significantly higher for a given applied shear stress when using a purely average atom representation. In fact, many solute-strengthening theories like the one explored later in this work, among others21,24,29, derive from the interaction between solute and dislocation stress fields during glide. While an average-atom potential may very well capture the static energetics and bulk properties of alloys, these direct comparisons show it does not adequately capture glide in random alloys. This fact was pointed out in36, though a mixed average atom potential wherein true solutes interact with average atom types may address this. A detailed comparison of the lattice distortion effect stemming from random solute distributions for a different system can be found in the ref. 37.

Fig. 4: Comparison of average-atom and true random alloy simulations.
figure 4

a Dislocation position vs. time for a fixed composition of xNi = 0.15 at T = 300 K and τ = 60 MPa, b dislocation mobility curve for a fixed composition of xNi = 0.15 at T = 300 K.

Full size image

Drag coefficient

Based on Eq. (2), drag coefficient is defined as B in \(v = \frac{{\tau b}}{{B\left( T \right)}} + c\) where c is introduced to represent the intercept computed by the fit. Here, by applying the regression through the truncated mobility data as described in Fig. 1, and the drag coefficient at each simulated temperature and composition can be extracted. Figure 5a, b show the computed drag coefficients as a function of temperature and Ni content and vice versa. The drag coefficient increases significantly with increasing temperature and Ni composition. Figure 5a shows that the dependence of the drag coefficient on temperature can be reasonably well approximated as linear. The fitting parameters for Fig. 5a are reported in Table 1.

Fig. 5: Fitted drag coefficient for all parameters.
figure 5

Drag coefficient as a function of a temperature for various Ni contents and b Ni content for various temperatures. Parameters for linear regressions in a are given in Table 1.

Full size image
Table 1 Parameters for drag coefficient as a function of temperature: B(T) = mT + B0.
Full size table

Threshold stress

In solid solutions, dislocations are pinned at obstacles and must be overcome by the applied stress in order to initiate glide. This threshold stress τth is sometimes referred to as the static friction stress12,16,30; we define this threshold as the resolved shear stress at which the dislocation velocity exceeds 0.25 Å/ps, which is approximately the smallest velocity which could be obtained from the MD data38. As emphasized previously, the mobility curve does not remain linear for the entire stress and temperature range, in particular at the lower temperatures considered; therefore, the stress corresponding to 0.25 Å/ps is determined by interpolation of the MD data. At elevated temperature, where the mobility curve is linear, we estimate the threshold stress as the x-axis intercept value from the linear fit to the MD data. A comparison of intercept and interpolated threshold stress is shown as a function of temperature in Fig. 6a–g for different Ni compositions. The friction stresses are fit to an exponential function of temperature of the form τth = A0 exp(−δT); the fits are shown in red in Fig. 7. Note that the interpolated stresses are used for the fit where possible. We can thereby estimate the friction stresses at 0 K, τth0, by extrapolating the exponential fit. Fitting parameters for each composition are listed in Table 2.

Fig. 6: Threshold stress as a function of temperature from MD.
figure 6

a xNi = 0.0, b xNi = 0.05, c xNi = 0.1, d xNi = 0.15, e xNi = 0.2, f xNi = 0.25, and g xNi = 0.3.

Full size image
Fig. 7: Temperature dependent drag coefficient function.
figure 7

Drag coefficient rate of increase with composition as a function of temperature from Fig. 5b. Linear fit is included in the inset, as defined by Marian and Caro12.

Full size image
Table 2 Fitting parameters for threshold stress as a function of temperature:τth = A0 exp(−δT).
Full size table

Solute effect on drag coefficient

In simulations of complex alloy systems, dislocation glide is sensitive to the random seed used to generate the alloys21. To address this, the dislocation velocities were averaged and large simulation cells were used. Additionally, our calculations (Supplementary Fig. 2) and previous work38 indicate that there exists a critical dislocation line length below, which dislocation mobility is sensitive to the simulation cell size due to the pinning-depinning characteristics of dislocation motion in alloys, especially at lower stresses (see refs. 21,35,38 for a more detailed discussion of this phenomena). In this work, the dislocation line length is ~400 nm, almost ten times longer than that used in ref. 21, and five times larger than that used in ref. 12. Together, these improvements lend confidence to the composition-dependent results acquired here. Moreover, the drag coefficient dependence on solute concentration has been clearly identified by various MD simulations in binary alloys12,16,21. In previous work on pure elements, it has been observed that the drag coefficient is nearly independent of temperature, when calculated as A = B/T in Eq. (1)16; however, when our drag coefficient calculations are normalized by temperature this is not observed, particularly at lower temperatures. A similar behavior was observed in38, where a power–law dependence of the drag coefficient on temperature was necessary to fit the MD data. A possible explanation for this is the additional variation in energetic barriers introduced by solute atom interactions with the dislocation. This temperature dependence can become more complex with an increasing number of components, since multiple solute types can have interacting stress fields. The drag coefficient expression, Eq. (2), derived by Marian and Caro13 was initially based on narrow ranges of concentration and temperature for binary systems. In this equation, the composition and temperature effects are coupled into a single multiplicative term, so that the intercept parameter A* reduces to a temperature-independent and composition-independent value for the pure system. In contrast, we cannot fit our data to Eq. (2) because the system explored here is a ternary alloy, resulting in multiple values for the intercept; therefore, we point to Table 1 for a more easily interpreted form of the mobility function. We may still estimate the derivative dB/dx of the drag coefficient with respect to concentration x at each temperature and obtain β(T), as defined in Eq. (2), from the linear regressions shown in Fig. 5b. Note that since we are simultaneously varying xNi and xCr, dB/dx = dB/dxNi = −dB/dxCr and our fit to β(T) is only strictly valid for the case of xNi + xCr = 0.3 considered here. The result is shown with its linear fit in Fig. 7.

The above analysis suggests that Eq. (2) is difficult to apply to ternary alloy systems and other complex alloys (e.g., high-entropy alloys). Figure 5 reveals that the drag coefficient remains fairly linear as a function of both variables; therefore, we explore a multiple regression approach:

$$B(T,x) = B_0 + \omega T + \gamma x$$
(3)

Here, ω and γ are linear fitting constants. Equation (3) decouples the temperature and composition dependence but enables a single compact drag coefficient function to be implemented into DDD simulations for alloys with a wide range of temperature and composition. Its linear nature does not conflict with the existing theory, regarding temperature and composition, on dislocation mobility.

Table 3 Parameters for drag coefficient as a function of temperature and composition: B(T, x) = B0 + ωT + γx.
Full size table

Parameters of Eq. (3) are fit to our MD data and are listed in Table 3. Using the fitted parameters, the estimated drag coefficient is shown as a function of temperature and composition in Fig. 8a. The absolute percent error of the fitted expression is shown in Fig. 8b. We can see that the functional form in Eq. (3) results in a good fit for the entire domain. (maximum error of 10% at low temperature and an average error below 3%). This confirms that the temperature and composition effects are not strongly nonlinearly coupled in the ranges investigated and separation of these two variables is a good approximation.

Fig. 8: Characteristics of fitted drag coefficient.
figure 8

a Full drag coefficient surface from MD data and bivariate linear fit (wireframe grid) as a function of temperature and composition, b error of the fitted expression as a function of temperature and composition.

Full size image

Theoretical predictions of zero temperature threshold stress

The 0 K friction stress calculated above is the purely static contribution of the solute atoms to material strengthening in the absence of kinetic contributions at finite temperature. Conceptually, it is analogous to the zero-temperature flow stress τth0 recently derived by Leyson et al.39 for solid solutions and applied to high entropy alloys by Varvenne et al.30. Based on the purely elastic interactions between the solute and dislocation’s hydrostatic stress field, Varvenne et al. derived an analytical expression for τth0 as

$$\tau _{{\mathrm{th}}0} = 0.051\alpha ^{ - \frac{1}{3}}\mu \left( {\frac{{1 + \nu }}{{1 - \nu }}} \right)^{\frac{4}{3}}f_1\left( {w_{\mathrm{c}}} \right) \times \left[ {\frac{{\mathop {\sum }\nolimits_{\mathrm{n}} x_{\mathrm{n}}\left( {\overline {{\mathrm{{\Delta}}}V} _{\mathrm{n}}^2 + \sigma _{{\mathrm{{\Delta}}}V_{\mathrm{n}}}^2} \right)}}{{b^6}}} \right]^{2/3}.$$
(4)

Here, xn is the concentration of solute species n, α is the dislocation line tension parameter, μ is the alloy shear modulus, ν is the Poisson’s ratio, f1(wc) is a factor describing the bowing geometry, b is the magnitude of the composition-weighted Burgers vector component in the glide (edge) direction, and \(\overline {{\mathrm{{\Delta}}}V} _{\mathrm{n}}\) and σΔVn are the mean misfit swelling volume and associated standard deviation, respectively. f1 is referred to as the minimized core coefficient and was derived by Varvenne et al.30 to be a constant 0.35 for the fcc edge dislocation case in Fe0.70NixCr0.3-x. In general, the partial spacing is reduced for pure screw dislocations30, and therefore the value of f1 must be recalculated for screw dislocations. Following the approach of Varvenne et al.30, we recalculate f1 = 0.059 (see Supplementary Figs. 4, 5). The line tension parameter is α = 0.492 for screw dislocations based on MD calculations of screw and edge line tension in Al40. Elastic constants μ and ν are determined by molecular statics at 0 K for each solute concentration in the ternary alloy using five random alloy configurations for each concentration with 4000 atoms in the simulation cell. We calculate the “isotropic average” elastic constants by rotating the Voigt elastic tensor through all orientations normal to the dislocation Burgers vector (\(\left[ {1\bar 10} \right]\) direction)41. To illustrate, Fig. 9a shows Poisson’s ratio as a function of the rotation angle and Fig. 9b shows the averaged Poisson’s ratio and shear modulus μ as a function of Ni composition.

Fig. 9: Composition-dependent average elastic properties.
figure 9

Calculated Poisson’s ratio and shear modulus: a Poisson’s ratio as a function of rotation angle (shaded region represents standard deviation across five random alloy initializations), and b averaged “isotropic” Poisson’s ratio and shear modulus as a function of Ni composition.

Full size image

In order to calculate τth0 using Eq. (4), \(\overline {{\mathrm{{\Delta}}}V} _{\mathrm{n}}\) and σΔVn are needed. Following the previous approach38, molecular statics simulations with 868 atoms are performed to calculate \(\overline {{\mathrm{{\Delta}}}V} _{\mathrm{n}}\) and σΔVn associated with substitution of a single solute atom for every lattice site in the system. We loop over all lattice sites in a random ternary solid solution at each target composition for both Cr and Ni solutes. When the site is occupied by Fe, it is switched to the desired solute atom. When the site is occupied by the solute atom, it is switched to Fe. The average volume change ΔVn due to the insertion of the solute atom to a random Fe0.7NixCr0.3−x alloy can thus be determined. The resulting \(\overline {{\mathrm{{\Delta}}}V} _{{\mathrm{Cr}}}\), \(\overline {{\mathrm{{\Delta}}}V} _{{\mathrm{Ni}}}\), \(\overline {{\mathrm{{\Delta}}}V} _{{\mathrm{Fe}}}\) values and their standard deviations are shown in Fig. 10 as a function of xNi. Using \(\overline {{\mathrm{{\Delta}}}V} _{\mathrm{n}}\) and σΔVn, the 0 K friction stress is calculated using the theoretical expression Eq. (4).

Fig. 10: Solute insertion swelling volumes.
figure 10

a Swelling volume (ΔVn) and b its standard deviation as a function of Ni, Cr, and Fe insertions in the ternary alloy.

Full size image

The results of τth0 obtained from the theory and MD are compared in Fig. 11. The molecular statics results indicate large standard deviation σΔVn, in some cases exceeding the computed mean value \(\overline {{\mathrm{{\Delta}}}V} _{\mathrm{n}}\). This observation is unsurprising due to the highly variable local solute environment in the alloy system. The friction stress predictions shown in ref. 30 neglected the influence of σΔVn for each solute, whereas our computations here explicitly include it. We similarly calculate μ and ν at each composition rather than taking an averaged value, and the elastic constant terms introduce another degree of composition dependence that is reflected in the analytical model results (Fig. 11).

Fig. 11: Zero temperature friction stress comparison from theory.
figure 11

Comparison of the theoretical30 and MD results for the 0 K friction stress as a function of xNi.

Full size image

We note that the predictions presented in Varvenne et al.30 below a temperature of 200 K also deviate from the available experimental results by over 50 MPa for the alloys investigated, and Varvenne et al.30 noted that the predictions become increasingly dependent on the line tension parameter α at low temperatures. In addition, while we rederived the core parameters for the dissociated screw dislocation, the edge components cancel beyond the core region, and the long-range stress fields for the screw dislocation do not interact with the purely hydrostatic solute misfit stress. The Varvenne et al. theory accounts for solute interactions at both short and long ranges; however, so we do not expect this to affect the applicability of the theory for screw dislocations.

The final point is that this theory was developed and validated against equiatomic multicomponent alloys, whereas the present work considers a relatively dilute solid solution in comparison. As such, the use of averaged values in the analytical expression may be sufficient for high entropy alloys; however, in our case we notice that the Varvenne et al.30 expression predicts a stronger dependence on composition which is not reflected in the MD results. One interesting feature that is captured by both models is the non-monotonic behavior at xNi = 0.25, which emphasizes again that the fluctuations in solute interaction with the dilatational stress field of the screw dislocation is a major contributor to strengthening.

Extensive MD simulations carried out in this work have allowed us to obtain reliable mobility data for the Fe0.7NixCr0.3−x alloy. We find the following:

  1. 1.

    The dislocation drag coefficient follows a consistent trend with temperature and composition in the linear solute drag regime. In particular, Ni has a more pronounced dragging effect than Cr on screw dislocations. This effect is slightly stronger at higher temperatures (Fig. 4).

  2. 2.

    The conventional drag coefficient B(T) has been computed as a function of temperature at each composition for ternary Fe0.7NixCr0.3−x alloys representative of austenitic stainless steels. This is useful to inform DDD simulations at a fixed alloy composition.

  3. 3.

    We have proposed a bivariate linear fit of the drag coefficient applicable to temperature, stress, and composition range. The error of the fit is low for applied stress between 10 and 140 MPa, suggesting weak nonlinear coupling between composition and temperature effects in this range.

  4. 4.

    Our results are compared to a recently developed analytical model for strengthening in concentrated solid solutions which we extend to the screw dislocation case, suggesting predictive limitations for low temperature behavior, notably the 0 K friction stress.

As a direct outcome of this work, the functional form for the drag coefficient as a function of temperature and solute composition in austenitic stainless steels may be implemented directly in mesoscale models. This is an important advancement in the development of a physically informed mobility model for enabling accurate DDD simulations of 3XX austenitic stainless-steel. In particular, it is applicable to elevated temperatures and a range of composition typical in applications of interest or associated with composition gradients resulting from additive manufacturing processes. The high cost of simulating such large systems and parameter spaces at full atomic resolution may motivate the use of coarse-graining techniques such as the concurrent-atomistic-continuum (CAC) method42 or other multiscale methods5 in future studies, particularly for considering extended defect-defect or defect-interface reactions.

Methods

Interatomic potential

Herein we employ a recently developed Fe–Ni–Cr embedded atom method (EAM) potential43 as a surrogate for austenitic stainless steel. This potential was selected because: (1) it enables stable MD simulations of the fcc structure; (2) it captures the correct unstable stacking and stable stacking fault energies (SFE); (3) it accurately reproduces elastic constants; (4) it gives reasonable trends of various energies and volumes for a range of compositions; and (5) it predicts that solutes remain in solution for the composition range of interest here. The latter two points are particularly relevant when considering the overall effect of alloying. Together, these five features are pertinent to studying the mechanical behavior of stainless steels. In the context of dislocation behavior, the correct SFE trend with composition is especially important, as the SFE controls equilibrium Shockley partial spacing. The potential selected matches closely the trend observed in both DFT and experiments44,45,46 (see Supplementary Figs. 6, 7). Phonon characteristics for this potential can be found in the ref. 38 and are important in controlling phonon drag behavior. One thing to note is that that while varying the composition in Fe0.7NixCr0.3−x, the alloy is not strictly austenitic at xNi = 0.0 but remains fcc at all temperatures considered here. This does not affect the interpretation of composition-dependent results obtained. Average-atom EAM potentials36 have also recently been proposed as an efficient way to represent random alloy characteristics. We generate average-atom potentials for each target composition studied here to compare with the true random alloy results reported.

Molecular dynamics simulation

Our simulation cells embedded with a single screw dislocation contain 11,108,370 atoms with dimensions of approximately 4000 Å in x, 160 Å in y, and 200 Å in z. This large dimension in the dislocation line direction allows for additional sampling of a wide range of solute environments, giving a more accurate dislocation line response and size-independent velocities38. Using different random number seeds, five replica simulations were performed for each stress and temperature condition to reduce any effect of the particular initialization method.

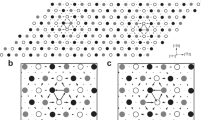
As shown in Fig. 12, a displacement field is applied to the atoms to create a perfect screw dislocation with both its line direction and Burgers vector \({\it{\mathop{b}\limits^{\rightharpoonup} }} = [1\bar 10]{\mathrm{a}}/2\) parallel to x. The initially perfect dislocation is allowed to relax, resulting in its dissociation into two Shockley partials on the expected (111) slip plane.

Fig. 12: MD simulation cell geometry.
figure 12

MD simulation cell geometry for dislocation mobility simulations. The initial position of the inserted screw dislocation is indicated by the black arrow. Atoms in green are fcc coordination while white atoms indicate the free surface in the y direction.

Full size image

Our simulations employ periodic boundary conditions in x and z, and a free boundary condition in y. Note that for this fcc geometry, the stacking period in z is 6(11\(\bar 2\)) planes as in the ABCDEFABCDEF… sequence. Our nominal size (dislocation line direction) is set as large as possible to circumvent the dislocation length-dependent regime for most simulated conditions (stress and temperature)38. Weinberger et al.22 have previously investigated the effect of nonperiodic line length; however, this introduces the effects of pinning at the free surfaces, which we avoid here by using fully periodic boundaries in both the glide(z) and line(x) directions. The effects of y and z (nonline direction) dimensions were not explicitly studied previously38 and are included in Supplementary Fig. 1; we found that the y and z dimensions do not affect the velocity in an appreciable way. Moreover, no cross slip along the screw dislocation was observed for any of the configurations simulated.

During the MD simulations, the upper and lower 2(111) planes of surface atoms are subject to constant opposing forces parallel to the Burgers vector (i.e., parallel to x) to obtain the intended resolved shear stress is τ. The initial velocities of atoms in these two surface layers are set to zero, and initial velocities of other atoms are assigned based on a Boltzmann distribution and the simulated temperature. Atom trajectories are then solved using an NVE (constant volume and energy) ensemble for the surface atoms and a 1 atm pressure NPT (constant pressure and temperature) ensemble for the other atoms. All MD simulations are performed for a total of 4 ns using LAMMPS47, and dislocation position as a function of time is calculated from total relative displacement of the crystal above and below the dislocation glide plane following the previous approach38. We employ standard thermostat/barostat damping parameters of 100 * dt and 1000 * dt, respectively, with a timestep size of dt = 0.004 ps. To ensure that the results were not sensitive to the choice of damping parameter, mobility calculations were also run for a fixed configuration with three different values for each. There was negligible variation between the velocities calculated.