Abstract
Many quantum emitters have been measured close or near the grain boundaries of the two-dimensional hexagonal boron nitride where various Stone–Wales defects appear. We show by means of first principles density functional theory calculations that the pentagon–heptagon Stone–Wales defect is an ultraviolet emitter and its optical properties closely follow the characteristics of a 4.08-eV quantum emitter, often observed in polycrystalline hexagonal boron nitride. We also show that the square–octagon Stone–Wales line defects are optically active in the ultraviolet region with varying gaps depending on their density in hexagonal boron nitride. Our results may introduce a paradigm shift in the identification of fluorescent centres in this material.
Similar content being viewed by others
Introduction
Two-dimensional (2D) materials are rich in novel phenomena in phyics. Hexagonal boron nitride (h-BN) is one of the key 2D materials in the field, which consists of boron–nitrogen bonds in a honeycomb lattice. Because of the strong polarization of the covalent bond between boron and nitrogen, it exhibits a large gap of about 6 eV1 unlike the semimetallic graphite or graphene. Recently, room temperature quantum emitters have been found in h-BN2,3. These findings have attracted large interest as they may serve as a basis to realize room temperature photon quantum blockade or very sensitive quantum sensors4. In particular, the first quantum emitters were found to emit in the visible2 and one in the ultraviolet (UV) region3. The origin of these emitters is unknown but assumed to come from point defects with states in the fundamental band gap of h-BN2. It can be envisioned in 2D materials that these quantum emitters may be created in a well-controlled fashion because the composition of the top layer can be directly manipulated with different techniques (e.g., ref. 5), but first, the nature of these quantum emitters should be identified, in order to further develop quantum optics measurements on these quantum emitters and their deterministic creation.
We focus our attention to the UV quantum emitter3 that has a zero-phonon line (ZPL) energy at around 4.08 eV with prominent phonon sideband peaks3,6 (see Fig. 1). We note that Huang–Rhys factor (S) of 1.3 was deduced in ref. 6 but S = 1 − 2 was estimated in ref. 7 for the PL spectrum. By integrating the area of ZPL emission and the total emission as plotted in Fig. 1c in ref. 6, its ratio, i.e. the Debye–Waller factor (DW), is ≈0.14 which corresponds to S ≈ 2. The optical lifetime of the emitter was observed at 1.15 ± 0.05 ns6. We note that this colour centre is distinct from similar UV emitters8,9 that have ZPL emission at around 4.1 eV but less pronounced phonon sideband with S ≈ 1 (see “Results and discussion” and Supplementary Note 1 for further discussion).
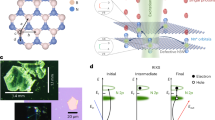
a Structure of the pentagon–heptagon Stone–Wales defect in hexagonal boron nitride as optimized by HSE DFT (see “Methods”). The arrows represent the change in the atomic positions going from the optimized ground state to the optimized electronic excited state. b The experimental (excitation by 4.5-eV laser as reported in ref. 6) (black curve) and calculated PL spectrum by HSE (red curve) and PBE (blue curve). The ZPL position of HSE was aligned by +0.02 eV whereas that of PBE was aligned by +0.65 eV, in order to directly compare the features in the phonon sideband, and Gaussian broadening of 20 meV was applied for the ZPL peak and the phonon sideband. The first prominent feature in the PL sideband nearest to ZPL contains two overlapping phonon modes that are shown with vertical lines with the corresponding phonon energies. S is the calculated Huang–Rhys factor.
Here, we computed the optical properties of the pentagon–heptagon Stone–Wales defect by Kohn–Sham hybrid density functional theory (DFT) in h-BN. We find that the calculated ZPL energy, the phonon modes participating in the fluorescence spectrum (see Fig. 1), and the optical lifetime agree with the observed data on the 4.08-eV quantum emitter. The metastable triplet state has characteristic zero-field splitting due to the low symmetry of the defect where the corresponding spin states may be selectively addressed under illumination. Our study implies that abundant emitters may exist with relatively high formation energies near or inside grain boundaries of h-BN, and extended defects could be the origin of other colour centres in this material.
Results and discussion
Electronic structure and formation energy
We apply first principles plane-wave DFT calculations on the pentagon–heptagon rings Stone–Wales defect in monolayer h-BN (see “Methods”). The pentagon–heptagon structure in h-BN can be created by rotating one boron–nitrogen pair by 90° in the hexagonal lattice about the axis perpendicular to the h-BN sheet which automatically introduces a nitrogen antisite and a boron antisite with creating a nitrogen–nitrogen bond and a boron–boron bond, respectively [see Fig. 1a]. We find that the nitrogen-nitrogen bond creates a level at Ev + 0.44 eV whereas the boron–boron bond creates a level at Ec − 0.40 eV in the fundamental band gap, where Ev and Ec are the valence band maximum and conduction band minimum, respectively (see Fig. 2). This structural defect is isovalent with the perfect lattice, thus the lower energy level is fully occupied whereas the upper level is empty with constituting a closed shell singlet electronic configuration. This is an electrically and optically active defect as the defect may be ionized and optical transition can occur between the occupied and empty defect levels in the gap. Indeed, previous scanning electron microscope measurements associated a 2.5-eV energy gap with the pentagon–heptagon Stone–Wales defect in h-BN10, but the calculated levels do not confirm this interpretation because the electronic gap rather remains in the UV region (≈5.2 eV).
The formation energy (Eform(SWq)) and adiabatic ionization energies of the defect can be calculated by the thermodynamic equation developed by Zhang and Northrup11 with using a charge correction energy (Δq) with a charge q of the defect from refs 12,13 as follows:
where Etot(SWq) and Etot(BN) are the total energy of the defect in the charge state q and the perfect supercell, respectively, whereas EF is the Fermi level between Ev and Ec. The calculated formation energy of the neutral defect is 7.2 eV, which is relatively high and it is basically in accord with a previous DFT PBE study14. The calculated donor and acceptor levels in the single sheet of h-BN are resonant with Ev and Ec, respectively.
Optical properties
In the neutral defect, the optical transition may occur between the occupied and unoccupied defect states in the gap in the UV region. In the Franck–Condon approximation, the strength of optical transition does not change as a function of the coordinate of the ions and the participation of the phonons in the optical transition, i.e. the phonon sideband in the luminescence spectrum, can be calculated as the overlap between the phonon modes in the adiabatic potential energy surface (APES) of the electronic ground state and of the electronic excited state. We apply this theory to characterize the optical transition of this defect. We further simplify this picture by assuming that the APES in the electronic ground state and excited state is very similar, and thus the corresponding phonons are equivalent, i.e., we apply Huang–Rhys approximation. In the Huang–Rhys approximation, the calculated Huang–Rhys factor (S) has a direct relation to the observed Debye–Waller factor, DW as \({\mathrm {DW}}=\exp (-S)\).
As a consequence, the calculation of the luminescence spectrum requires several steps: (i) computing the electronic excited state with geometry optimization, (ii) computing the phonons in the electronic ground state, (iii) computing the overlap between the phonon modes in the electronic ground and excited states. We go through these steps one-by-one, with providing analysis on the results.
Electronic excited state
Before computing the electronic excited state, it is intriguing to analyse the electronic structure by group theory. The pentagon–heptagon Stone–Wales defect has a single mirror plane symmetry, C1h. Both the lower energy and upper energy defect states show a″ symmetry because they are basically pz orbitals localized on the nitrogen and boron atoms around the nitrogen–nitrogen and boron–boron bonds, respectively. The closed shell singlet state is an \({\,}^{1}{A}^{\prime}\)(g) state. Excited states can be constructed by promoting an electron from the lower defect level to the upper defect level in the gap. This can produce a \({\,}^{3}{A}^{\prime}\) triplet and a \({\,}^{1}{A}^{\prime}\)(e) singlet excited state. The \({\,}^{3}{A}^{\prime}\) state is dark, and it is lower in energy than the \({\,}^{1}{A}^{\prime}\)(e) because of the exchange interaction of the two electrons. The many-body \({\,}^{1}{A}^{\prime}\)(e) is a correlated state that can be only described by two Slater-determinants. The spinpolarized hybrid DFT method might not be able to produce an accurate charge density of this interacting many-electron system; therefore, the ΔSCF method has larger inaccuracy than anticipated (e.g., ≈0.1 eV in energy, see ref. 15) for less severe excited states. This can affect the optimized geometry in the excited state and the total energy of the \({\,}^{1}{A}^{\prime}\)(e) state. The latter can be corrected by estimating the exchange energy by the calculated DFT total energies of the singlet and triplet excited states similarly to a previous work16. At the ground state geometry, the corrected excitation energy is 4.53 eV, which is reduced by 0.47 eV in the geometry optimization procedure. The final calculated ZPL energy is 4.06 eV, which perfectly agrees with the ZPL energy of the 4.08-eV emitter.
Phonon density of states
The calculated phonon densities of states for the perfect and defective supercells are shown in Fig. 3a. As can be seen, the defect introduces new phonon modes at about 206 meV slightly above the phonon bands, and two other ones at 149 and 54 meV, respectively. The two highest energy phonon modes asymmetrically stretch the boron–boron and nitrogen–nitrogen bonds, as reported in Fig. 3b, c. In the optical excitation, these bonds are indeed stretched [see Fig. 1a]; therefore, they should appear in the corresponding optical excitation spectrum.
a Calculated phonon density of states for the pristine (red curve) and defective (black curve) hexagonal boron nitride. The phonons were calculated in the Γ-point of the applied supercell. The position of the (quasi)local phonon modes are highlighted by circles and arrows. The motion of ions in the highest energy (quasi)local phonon modes at b 206 meV and c 149 meV. The length of the arrows represents the relative amplitude of the motion of the ions where larger scale was applied for c for the sake of visibility.
Computed photoluminescence spectrum and optical lifetime
Next, we turn to the contribution of phonons to the optical transition. The computed luminescence spectrum is shown in Fig. 1b. The calculated phonon prominent peaks in the phonon sideband occurs exactly at those energies that were observed in the experiment, and their corresponding replica can be also well recognized. The first intense peak near the ZPL line consists of predominantly two broad phonon modes at 149 and 206 meV that were analysed above. On the other hand, the present calculational approach seems to overestimate the intensity of the phonon sideband and the calculated S ≈ 3 is larger than the observed one at ~2 for the 4.08-eV emitter6. Since the optimized geometry of the \({\,}^{1}{A}^{\prime}\)(e) state directly enters the calculation of the luminescence phonon sideband and the Huang–Rhys factor that suffers from an error due to the spin contamination it can cause a larger inaccuracy in the calculated intensity of the phonon sideband than anticipated for other defects (e.g., refs 17,18). We note that our PBE (Perdew, Burke, and Ernzerhof) calculations predict S ≈ 2 for this defect, which may be due to a fortuituous cancellation of errors in the PBE functional for this particular state that finally provides a good optimized geometry for the electronic excited state. As a consequence, the calculated phonon sideband based on the PBE geometries provide excellent agreement with the observed PL phonon sideband. The main point of these findings is that the peak positions in the phonon sideband of the 4.1-eV emitter can be well-explained by the (quasi)localized phonon modes associated by the Stone–Wales defect. Our analysis emphasizes the importance of the local or quasilocal phonon modes in understanding the PL spectrum. The prominent phonon modes either coincide or are very close to the corresponding bulk phonon modes in energy, e.g., 200-meV Raman mode of bulk h-BN, but they are rather localized on the defect with producing relatively sharp phonon replicas in the luminescence spectrum.
Finally, we address the optical lifetime of the defect which depends on the radiative and non-radiative rates. The non-radiative decay from the \({\,}^{1}{A}^{\prime}\)(e) may occur via the intersystem crossing (ISC) towards the \({\,}^{3}{A}^{\prime}\) state. The \({\,}^{3}{A}^{\prime}\) triplet state splits via dipolar electron spin–spin interaction where the calculated zero-field splitting falls in the GHz region (see Fig. 4). Group theory analysis implies that the ISC towards the ms = 0 state is faster than that towards ms = {x, y} states. The ISC rate can be calculated as (refs 18,19,20),
where λz = 0.31 GHz is the calculated spin–orbit coupling between \({\,}^{1}{A}^{\prime}\)(e) and \({\,}^{3}{A}^{\prime}\), whereas F is the phonon overlap spectral function between \({\,}^{1}{A}^{\prime}\)(e) and \({\,}^{3}{A}^{\prime}\) separated by Δ = 0.3 eV, which yields very small value because S ≈ 0.1 between the two states. As a consequence, Γnr ∝ 0.1 kHz. Thus, the non-radiative decay rate can be neglected in the optical lifetime, which can be then calculated from the radiative lifetime as
where n = 2.5 is the refractive index of h-BN at \(\hbar\)ω = 4.08 eV ZPL energy (see ref. 21), μ is the optical transition dipole moment as derived from the calculated imaginary part of the dielectric function between the corresponding Kohn–Sham wave functions representing the ground and excited states at the ground state geometry, ϵ0 is the vacuum permittivity, c is the speed of light. We obtain τ = 2.4 ns, which broadly agrees to the observed one. We again assumed Franck–Condon theory in applying the ZPL energy in Eq. (3). We note that the radiative lifetime of another UV emitter in h-BN, the carbon-dimer defect (see below), was derived similarly in ref. 16.
For the sake of clarity, the energies are not scaled. The zero-field splitting is depicted for the triplet state. Intersystem crossing can occur between \({\,}^{1}{A}^{\prime}\)(e) and the ms = 0 of \({\,}^{3}{A}^{\prime}\) state by spin-orbit interaction (solid line) whereas electron–phonon coupling weakly enables it towards the ms = {x, y} states.
We conclude from the calculated ZPL energy, characteristic phonon replica in the phonon sideband, and the optical lifetime that the 4.08-eV quantum emitter can be associated with the pentagon–heptagon Stone–Wales defect in h-BN.
Comparison to other models
UV emission with the ZPL energy at around 4.1 eV was often found in polycrystalline h-BN; therefore, these emitters were erroneously associated with the free exciton of h-BN in the past22. Other early experimental and theoretical studies assumed23,24 that the UV emitters are associated with the presence of carbon defects because carbon is a common impurity during the growth of h-BN. Later, it was proposed based on some analogue with the donor–acceptor pair emission in GaN and related materials, that the UV emission may include two types of defects with donor and acceptor nature involving a carbon-related defect25,26. However, the observed fast optical lifetime goes strongly against this argument and rather indicates a defect with localized electronic ground and excited states as alluded in ref. 16. Recently, a carbon-dimer defect has been proposed as the origin for the 4.1-eV emitters based on first principles calculations16.
The confusion about the origin of the UV emitters may be caused by the fact that these UV emitters could have very similar ZPL energies at around 4.1 eV but they belong to different colour centres. In a recent work9, a series of UV emitters with ZPL energies at around 4.1 eV has been detected, including emitters with S ≈ 1 phonon sideband8. They prepared 13C doped h-BN too and observed the same series of UV emitters, but no isotope shift was found in the corresponding PL spectra9 (see Supplementary Note 1). Furthermore, one UV emitter with ZPL energy at 4.08 eV always appeared in the sample whereas the PL intensity of the other UV emitters with blueshift compared to the 4.08-eV emitter exhibited some correlation with the carbon content of h-BN. Our study focuses on the single UV emitter3 with ZPL emission at 4.08 eV, which has a broad prominent peak shifted from the ZPL energy between 150 and 200 meV, and it has a Huang–Rhys factor at S ≈ 2. This type of UV emitter was previously measured as ensembles in polycrystalline h-BN6.
We realized that the 4.08-eV emitter may be situated near or inside the grain boundaries of polycrystalline h-BN. In the grain boundary regions, pentagon–heptagon structural defects have been observed in the hexagonal lattice27, a very well known type of defects in carbon nanotubes or graphene sheets called Stone–Wales defect. The Stone–Wales defect contains boron and nitrogen antisites in h-BN [see Fig. 1a]; therefore, it has relatively high formation energy14,28. However, the large strain at the grain boundaries mediates the formation of Stone–Wales defects29. We note that the series of pentagon–heptagon structural defects were often observed in lines in the core of grain boundaries27. Simulations showed30 that those arrangements can decrease the strain in the h-BN sheet. The Stone–Wales defect is a pair of pentagon–heptagon defects which introduces a small strain to the lattice and is commensurate with the periodicity of the host h-BN lattice. Previous studies already confirmed10,14,31 that pentagon–heptagon Stone–Wales defects may introduce levels into the band gap but the feasible optical signature has not yet been explored. We find here that they produce the commonly observed UV emission.
4.08-eV optical centre as a quantum bit
We note that the calculated very slow ISC rate implies that the high-spin triplet state cannot be effectively pumped optically from the ground state. Continuous wave photo-excitation might drive the system very slowly to the triplet state but absorption of the UV photon in the triplet state would immediately photo-ionize the pentagon–heptagon Stone–Wales defect into a dark state, thus the lifetime of the triplet state under continuous UV illumination would be short. On the other hand, injection of holes and electrons into h-BN can result in trapping the exciton into the triplet state by pentagon–heptagon Stone–Wales defects which should have a long lifetime in dark. We tentatively propose that the triplet state plays a role in the ~100 ns antibunching signal in the cathodoluminescence measurements of the 4.08-eV emitter32. The relatively long lifetime of the triplet state would make possible to induce quantum bit operation with alternating magnetic fields in the microwave region when the mobile Wannier–Mott exciton is trapped into this state of the pentagon–heptagon Stone–Wales defect.
Structural defects and quantum emitters
Beside pentagon–heptagon Stone–Wales defect, square-octagon Stone–Wales defects can occur in h-BN at the grain boundaries31. Among the different types of square-octagon Stone–Wales defects10,31,33, scanning tunneling microscope studies clearly identified those structures that have N–N and B–B bonds (see Fig. 5) which often forms line defects33. Here we only consider this type of square–octagon Stone–Wales defect.
a Structure of square–octagon Stone–Wales line defect (see ref. 33). The density of the defect was varied by adding pristine h-BN units in the b direction with increasing the distance between the defects which releases the strain induced by the defect. The nitrogen atoms from the neighbour unit cell is depicted along a direction for showing the square defect. b HSE band structure for b = 12 defective lattice. Red curves are the valence band maximum (VBM) and conduction band minimum (CBM) of the pristine h-BN, whereas the other coloured bands are the defect related bands near the VBM and CBM. c Shift of the electronic band gap as a function of the distance between the line defects and self-induced stress between the defects as obtained by HSE. We plot the isotropic planar stress (1/2 [pxx + pyy]) with a vacuum size of 2.5 nm between the h-BN sheets.
The square-octagon Stone–Wales line defect with N–N and B–B bonds create bands: the N–N occupied bands (blue curves) appear above and near the valence band maximum of the pristine h-BN whereas the B–B empty band (green curve) appears below the conduction band minimum of the pristine h-BN (see Fig. 5). The line defect related band structure is direct at the Γ-point in which the band gap strongly varies by the distance between the line defects because the strain field induced by them in a rigid environment forced by the grain boundaries (see Fig. 5c). We note that the modelling of strain field acting on the line defects caused by the grain boundaries is oversimplified by the picture of self-interaction of line defects but the physical trends of strain can be well recognized by this model. The band gap of isolated square-octagon Stone–Wales line defect approaches 4.6 eV. These line defects could also reside relatively close to each other33, and then the band gap can reduce substantially in the order of 100 meV in a rigid environment. Thanks to the direct gap nature, the line defect is optically active and may also contribute to the ultraviolet emission in h-BN.
In summary, we have reported the results of hybrid functional calculations for the pentagon–hexagon Stone–Wales defect in h-BN. The calculated optical properties of this Stone–Wales defect, in particular, the phonon modes participating in the optical transitions, reproduce all the known features of a 4.08-eV quantum emitter. Our study shows that polycrystalline h-BN may contain such defects that have relatively high formation energy but still abundant and optically active. Our findings complement previous plausible models based on phenomenological approaches34 and recent first principles calculations16 on the origin of 4.1-eV emitters which are all based on extrinsic point defects.
Our results imply that intrinsic structural defects may affect the overall optical properties of h-BN. The extended Stone–Wales line defects introduces occupied and empty bands in the fundamental band gap of pristine h-BN which effectively reduces the band gap for proximate point defects. As a consequence, the ionization energies of these point defects are reduced that can affect their photo-stability as found for divacancy defects inside stacking faults in 4H SiC35. Moreover, some common defects in h-BN, like carbon substitutional defects28, have optical transition between the in-gap defect level and band edges. Since the effective band edges shift closer to the in-gap defect level for defects near the Stone–Wales line defect the corresponding optical signal will change with showing generally longer wavelength emission. Stone–Wales line defects also generate a strain field that can act on the optical transition of point defects, in which the optical transition occurs between in-gap defects states but sensitive to the strain field, e.g., vacancy complexes36.
As many optical centres and quantum emitters were found near or inside the grain boundaries or cracks of h-BN, this study may turn the direction of research towards exploring the magneto-optical properties of structural defects and the interaction between point defects and structural defects for identification of the observed colour centres in h-BN.
Methods
First principles methodology
First principles calculations are performed using Kohn–Sham spinpolarized DFT with the VASP package37. We use the screened hybrid functional of Heyd, Scuseria, and Ernzerhof (HSE)38. In this approach, the short-range exchange potential is calculated by mixing a fraction of nonlocal Hartree-Fock exchange with the generalized gradient approximation of PBE39. The screening parameter is set to 0.2 Å−1 and the mixing parameter to α = 0.32. These parameters closely reproduce the experimental band gap and structural parameters of h-BN, similarly to GaN and AlN materials40. The valence electrons are separated from the core electrons by projector augmented wave potentials41. An energy cutoff of 500 eV is used for the plane-wave basis set. We model the pentagon–heptagon Stone–Wales (SW) defect in a 162-atom h-BN supercell in which Γ-point calculation for mapping the Brillouin-zone suffices. The vacuum size is set to 25 Å. In the geometry optimization procedures, the force criterion is set to 0.001 eV/Å. The phonons in the Γ-point of the applied supercell are determined by calculating the numerical derivatives of the forces for creating the Hessian matrix in the ground state electronic configuration within PBE. The spin–orbit coupling is calculated in non-collinear approximation with the spin axis set perpendicular to the h-BN sheet within HSE. The square-octagon line defect was calculated by the same parameters but modelled in a rectangular unit cell of h-BN using 4 × 1 × 1 k-point mesh. We note that previous calculations on well-localized defect states showed that monolayer and bulk models of h-BN produce very similar ZPL energies for the same defect, also as a function of strain36. We expect here the same behaviour for the considered defects.
The magneto-optical properties are calculated with employing the ab initio toolkit developed in our group18. Briefly, the excited state is calculated by the ΔSCF method15 where the correction for the total energy of the open-shell singlet excited state is applied, similarly to a previous work16. The phonon sideband in the calculated luminescence spectrum is calculated within the Huang–Rhys approximation using our home-built implementation17 in the spirit of ref. 42. The dipolar electron spin–spin interaction part of the zero-field splitting is calculated as implemented by Martijn Marsman (see also ref. 43).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The codes that were used in this study are available upon request to the corresponding author.
References
Cassabois, G., Valvin, P. & Gil, B. Hexagonal boron nitride is an indirect bandgap semiconductor. Nat. Photonics 10, 262–266 (2016).
Tran, T. T., Bray, K., Ford, M. J., Toth, M. & Aharonovich, I. Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 11, 37–41 (2016).
Bourrellier, R. et al. Bright UV single photon emission at point defects in h-BN. Nano Lett. 16, 4317–4321 (2016).
Abdi, M. & Plenio, M. B. Quantum effects in a mechanically modulated single-photon emitter. Phys. Rev. Lett. 122, 023602 (2019).
Krivanek, O. L. et al. Atom-by-atom structural and chemical analysis by annular dark-field electron microscopy. Nature 464, 571–574 (2010).
Museur, L., Feldbach, E. & Kanaev, A. Defect-related photoluminescence of hexagonal boron nitride. Phys. Rev. B 78, 155204 (2008).
Vokhmintsev, A., Weinstein, I. & Zamyatin, D. Electron-phonon interactions in subband excited photoluminescence of hexagonal boron nitride. J. Lumin. 208, 363–370 (2019).
Vuong, T. et al. Phonon-photon mapping in a color center in hexagonal boron nitride. Phys. Rev. Lett. 117, 097402 (2016).
Pelini, T. et al. Shallow and deep levels in carbon-doped hexagonal boron nitride crystals. Phys. Rev. Mater. 3, 094001 (2019).
Li, Q. et al. Grain boundary structures and electronic properties of hexagonal boron nitride on Cu(111). Nano Lett. 15, 5804–5810 (2015).
Zhang, S. B. & Northrup, J. E. Chemical potential dependence of defect formation energies in GaAs: application to Ga self-diffusion. Phys. Rev. Lett. 67, 2339–2342 (1991).
Freysoldt, C., Neugebauer, J. & Van de Walle, C. G. Fully ab initio finite-size corrections for charged-defect supercell calculations. Phys. Rev. Lett. 102, 016402 (2009).
Freysoldt, C. & Neugebauer, J. First-principles calculations for charged defects at surfaces, interfaces, and two-dimensional materials in the presence of electric fields. Phys. Rev. B 97, 205425 (2018).
Wang, R., Yang, J., Wu, X. & Wang, S. Local charge states in hexagonal boron nitride with Stone-Wales defects. Nanoscale 8, 8210–8219 (2016).
Gali, A., Janzén, E., Deák, P., Kresse, G. & Kaxiras, E. Theory of spin-conserving excitation of the N −V− center in diamond. Phys. Rev. Lett. 103, 186404 (2009).
Mackoit-Sinkevičiené, M., Maciaszek, M., Van de Walle, C. G. & Alkauskas, A. Carbon dimer defect as a source of the 4.1 eV luminescence in hexagonal boron nitride. Appl. Phys. Lett. 115, 212101 (2019).
Thiering, G. & Gali, A. Ab initio calculation of spin-orbit coupling for an NV center in diamond exhibiting dynamic Jahn-Teller effect. Phys. Rev. B 96, 081115 (2017).
Gali, A. Ab initio theory of the nitrogen-vacancy center in diamond. Nanophotonics 8, 1907–1943 (2019).
Goldman, M. et al. Phonon-induced population dynamics and intersystem crossing in nitrogen-vacancy centers. Phys. Rev. Lett. 114, 145502 (2015).
Thiering, G. & Gali, A. Theory of the optical spin-polarization loop of the nitrogen-vacancy center in diamond. Phys. Rev. B 98, 085207 (2018).
Cappellini, G., Satta, G., Palummo, M. & Onida, G. Optical properties of BN in cubic and layered hexagonal phases. Phys. Rev. B 64, 035104 (2001).
Solozhenko, V. L., Lazarenko, A. G., Petitet, J. P. & Kanaev, A. V. Bandgap energy of graphite-like hexagonal boron nitride. J. Phys. Chem. Solids 62, 1331–1334 (2001).
Katzir, A., Suss, J. T., Zunger, A. & Halperin, A. Point defects in hexagonal boron nitride. I. EPR, thermoluminescence, and thermally-stimulated-current measurements. Phys. Rev. B 11, 2370–2377 (1975).
Era, K., Minami, F. & Kuzuba, T. Fast luminescence from carbon-related defects of hexagonal boron nitride. J. Lumin. 24-25, 71–74 (1981).
Du, X. Z., Li, J., Lin, J. Y. & Jiang, H. X. The origin of deep-level impurity transitions in hexagonal boron nitride. Appl. Phys. Lett. 106, 021110 (2015).
Uddin, M. R., Li, J., Lin, J. Y. & Jiang, H. X. Probing carbon impurities in hexagonal boron nitride epilayers. Appl. Phys. Lett. 110, 182107 (2017).
Gibb, A. L. et al. Atomic resolution imaging of grain boundary defects in monolayer chemical vapor deposition-grown hexagonal boron nitride. J. Am. Chem. Soc. 135, 6758–6761 (2013).
Weston, L., Wickramaratne, D., Mackoit, M., Alkauskas, A. & Van de Walle, C. G. Native point defects and impurities in hexagonal boron nitride. Phys. Rev. B 97, 214104 (2018).
Mortazavi, B. & Cuniberti, G. Mechanical properties of polycrystalline boron-nitride nanosheets. RSC Adv. 4, 19137–19143 (2014).
Abadi, R., Uma, R. P., Izadifar, M. & Rabczuk, T. The effect of temperature and topological defects on fracture strength of grain boundaries in single-layer polycrystalline boron-nitride nanosheet. Comput. Mater. Sci. 123, 277–286 (2016).
Liu, Y., Zou, X. & Yakobson, B. I. Dislocations and grain boundaries in two-dimensional boron nitride. ACS Nano 6, 7053–7058 (2012).
Meuret, S. et al. Photon bunching in cathodoluminescence. Phys. Rev. Lett. 114, 197401 (2015).
Cretu, O., Lin, Y.-C. & Suenaga, K. Evidence for active atomic defects in monolayer hexagonal boron nitride: a new mechanism of plasticity in two-dimensional materials. Nano Lett. 14, 1064–1068 (2014).
Vokhmintsev, A. S. & Weinstein, I. A. Temperature effects in luminescence of associated oxygen-carbon pairs in hexagonal boron nitride under direct optical excitation within 7-1100 K range. Preprint at https://arxiv.org/ftp/arxiv/papers/2003/2003.02789.pdf (2020).
Ivády, V. et al. Stabilization of point-defect spin qubits by quantum wells. Nat. Commun. 10, 1–8 (2019).
Li, S. et al. Giant shift upon strain on the fluorescence spectrum of VNNB color centers in h-BN. npj Quantum Inf. 6, 85 (2020).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Erratum: Hybrid functionals based on a screened coulomb potential [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys. 124, 219906 (2006).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Moses, P. G., Miao, M., Yan, Q. & Van de Walle, C. G. Hybrid functional investigations of band gaps and band alignments for AlN, GaN, InN, and InGAn. J. Chem. Phys. 134, 084703 (2011).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Alkauskas, A., Buckley, B. B., Awschalom, D. D. & Van de Walle, C. G. First-principles theory of the luminescence lineshape for the triplet transition in diamond NV centres. N. J. Phys. 16, 073026 (2014).
Bodrog, Z. & Gali, A. The spin–spin zero-field splitting tensor in the projector-augmented-wave method. J. Phys. Condens. Matter 26, 015305 (2013).
Acknowledgements
A.G. acknowledges the support from the National Research, Development and Innovation Office in Hungary for Quantum Technology Program (Grant No. 2017-1.2.1-NKP-2017-00001), National Excellence Program (Grant No. KKP129866), the Ministry of Innovation and Technology and the National Research, Development and Innovation Office within the Quantum Information National Laboratory of Hungary, and the European Commission for the EU H2020 Asteriqs project (Grant No. 820394). V.I. acknowledges the MTA Premium Postdoctoral Research Program and the support from the Knut and Alice Wallenberg Foundation through WBSQD2 project (Grant No. 2018.0071). G.T. was supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences and the ÚNKP-20-5 New National Excellence Program for Ministry Innovation and Technology from the source of the National Research, Development and Innovation Fund. We acknowledge the fruitful discussions from Guillaume Cassabois and technical help from Joel Davidsson and Bálint Somogyi.
Author information
Authors and Affiliations
Contributions
All authors contributed to the discussion and writing the manuscript. A.G. conceived and led the entire scientific project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hamdi, H., Thiering, G., Bodrog, Z. et al. Stone–Wales defects in hexagonal boron nitride as ultraviolet emitters. npj Comput Mater 6, 178 (2020). https://doi.org/10.1038/s41524-020-00451-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00451-y
This article is cited by
-
Exceptionally strong coupling of defect emission in hexagonal boron nitride to stacking sequences
npj 2D Materials and Applications (2024)
-
Pure and Stone-Wales Defect Armchair Boron Nitride Graphene Nanoribbons as Anticancer Drug Delivery Vehicles: A Theoretical Investigation
Journal of Cluster Science (2024)
-
Tuning colour centres at a twisted hexagonal boron nitride interface
Nature Materials (2022)
-
Computational design of quantum defects in two-dimensional materials
Nature Computational Science (2021)