Introduction

In recent years, there has been an intense research effort surrounding the conversion of solar energy into electric power through photovoltaic cells1,2,3. Hybrid organic-inorganic perovskites (HOIPs) with composition ABX3 (A = organic cation, such as [CH3NH3]+; B = divalent metal cation, such as Sn2+, Pb2+; X = halogen anion) are proposed as a next generation of materials for solar cells and light-emitting diodes4,5,6,7,8. The increase in structural degrees of freedom from the inclusion of organic cations into a BX3 inorganic framework enables structural distortions and columnar shifts which are otherwise forbidden in standard inorganic perovskites. Furthermore, ferroelectricity (FE) originating from structural symmetry breaking is a potentially critical phenomenon in such soft and flexible photovoltaic materials, where the electric field plays an important role in promoting electron–hole pair separation and suppressing charge recombination, inherently breaking the Shockley–Queisser limit9,10,11,12,13. Therefore the FE properties of perovskites have attracted broad attention, though their presence and influence in perovskite solar cells are still a matter of debate14,15,16,17,18,19.

A strong spin–orbit coupling (SOC) involving the heavy Pb atom and its surrounding halogens, combined with the absence of inversion symmetry in the crystal structure, can lead to a Rashba effect which, in turn, can impact photovoltaic performance20,21,22,23,24. Non-centrosymmetry provides a spin-degenerate band with the possibility to split two reversely spin-polarized states described by the equation:

$$\begin{array}{*{20}{c}} {E_ \pm \left( k \right) = \frac{{\hbar ^2k^2}}{{2m}} \pm \alpha _R\left| k \right|} \end{array}$$
(1)

which can be used to clarify the dispersion relation of electrons (or/and holes), where αR is the Rashba splitting parameter25,26,27. The coexistence of FE and a Rashba effect is believed to mediate interesting effects, such as the switching of spin-texture chirality with an electric-polarization reversal28,29. These effects are mainly studied in the context of inorganic materials; only a few hybrid-material examples have been explored so far25,30,31.

Very recently, Sum et al. demonstrated the presence of both FE and a Rashba effect in a layered Dion–Jacobson (DJ) phase HOIP with formula (AMP)PbI4, where AMP is the divalent 4-aminomethyl-piperidinium cation (Fig. 1, FE state)32. Its measured value of spontaneous polarization (Ps) is 9.8 μC cm−2, which is very high among HOIPs33,34, and more comparable to those of conventional inorganic perovskites such as BaTiO3 (15–26 μC cm−2)35,36. A measured Rashba splitting energy (ER) of 85 meV and Rashba coefficient (αR) of 2.60 eV Å suggest real promise for spintronic applications30,31. This exciting experimental evidence now motivates a theoretical investigation into the microscopic mechanism of FE and its interplay with SOC in the HOIPs.

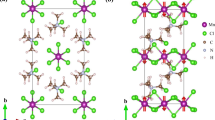
Fig. 1: The structures of AFE and FE (+P) phases.
figure 1

Top (a) and side (b, c) views with purple Pb, gray I, brown C, and blue N. AMP-cation hydrogen atoms are omitted for clarity. The black dot or cross in the yellow circle of (a) represent the AMP-cation orientation as having the aminomethyl group of the molecule along with the up (+a) or down (−a) axis, respectively.

Full size image

Starting with this aim in mind, we perform a detailed density functional theory (DFT) analysis of (AMP)PbI4, focusing on estimates of the ferroelectric and spin–orbit properties of the band structure. While the estimate of the Rashba splitting is now routine work, we focus here on the corresponding anisotropy, which is far much less studied. Our estimate of Ps and αR are 10.72 μC cm−2 and 2.39 eV Å, in excellent agreement with the experimental 9.80 μC cm−2 and 2.60 eV Å. In addition, the ER of spin-polarized bands is calculated to be 16 meV, which is of the same order of magnitude as the experimental 85 meV value. In addition to a spin-texture that can be switched via ferroelectric polarization reversal, we further observe a sizeable anisotropy in the Rashba spin splitting. Remarkably, we show that the axis of major anisotropy can be switched between two orthogonal directions by reversing the ferroelectric polarization from +P to −P. Reversing the FE polarization induces an apparent 90° “rotation” of the anisotropy ellipse, i.e., a pseudo-rotation. This effect has never been highlighted in the context of usual spin-texture tunability under polarization reversal and may suggest interesting avenues for spin-optoelectronic devices based on HOIPs.

Results and discussion

Structural analysis

We start our simulations with the experimental ferroelectric phase of (AMP)PbI4 refined at T = 298 K having space group Pc (#7, \(C_s^2\)) with monoclinic b-axis in ref. 32. Two nearby AMP2+ cations located in the space between [PbI4]2− layers have alternating orientations when they are adjacent along the b or c axes, but common orientations when adjacent along with diagonal b + c or b − c directions, as shown in Fig. 1 (FE state), so that the structure lacks a center of inversion, thus paving the way for the existence of ferroelectric polarization in the system. It is interesting to note that the cation’s center of mass is displaced somewhat from the ideal midpoint between two adjacent [PbI4]2− layers so as to be slightly closer to one layer or the other. We perform quantum chemical analyses of the isolated AMP2+ cation using both the Hirshfield37 and Natural population methods38 implemented in the Gaussian16 software39. Both methods define an electric dipole moment of the molecule pointing approximately towards the aminomethyl group from the center of the AMP cation, as shown in Supplementary Fig. 2. Although the long-range ordering of AMP-cation orientations should be associated with a strong FE polarization along the a-axis at the first glance, this alone is not sufficient for understanding the overall polarization of a hybrid system, which typically has several different contributions to the polarization, as explained in details in ref. 32. According to the modern theory of polarization40, we introduce a centrosymmetric anti-ferroelectric (AFE) phase by enforcing the existence of an inversion point and define a suitable path connecting the AFE and FE state via atomic rotations or/and displacements in order to estimate the polarization by first-principles calculations. The AFE model is built from the FE model by simultaneously rotating two AMP2+ cations adjacent along the b-axis by 180° so that the diagonal AMP cations are related by inversion symmetry. The [PbI4]2− the framework is also properly centrosymmetric to ensure that the AFE structure (both framework and AMP cations) possesses an inversion symmetry point at (0.5, 0.5, 0.5), as shown in Fig. 1 (AFE state). The resulting space group symmetry is P2/m (#10, \(C_{2h}^1\)) with a monoclinic b-axis in the same unit cell.

Ferroelectric properties

We introduce the normalized variable λ to simultaneously parameterize both the rotations of the AMP cations and the atomic displacements of the [PbI4]2− framework from AFE (λ = 0) to FE (λ = 1) states. Therefore λ represents the amplitude of the combined roto-displacive distortions connecting the prototype AFE-phase structure and the real FE-phase structure. The intermediate structures along the path (0 ≤ λ ≤ 1) are only introduced in order to monitor the accidental introduction of a quantum of polarization and to ensure a continuous variation of the polarization along the path itself. In practice, λ has been varied infinite increments, so that stepwise AMP-cation rotations are approximated by 18 steps of 10° each from 0° (AFE state) to 180° (FE state), together with incremental linear displacements of the [PbI4]2− framework.

In order to understand the origin of the polarization, the separate contributions of the organic AMP2+ cations and the inorganic [PbI4]2− a framework to the total polarization are considered in three different ways. Firstly, we rotate AMP cations while keeping the [PbI4]2− framework centrosymmetric. In this way, we obtain the contribution coming from the organic groups (Pcation), i.e., a rotational contribution to the polarization. Secondly, the displacive distortions of [PbI4]2− framework are considered while fixing AMP cations in a centrosymmetric configuration. In this way, the polarization only originates from the inorganic framework (Pframe), i.e., a displacive contribution to the total polarization. Finally, both AMP-cation rotations and [PbI4]2− layer displacements are simultaneously activated in order to recover the total polarization (Ptotal), i.e., the full roto-displacive contribution to the polarization. In this way, we are able to disentangle the different contributions to the polarization and to observe the couplings between them. For each case, we consider the contribution from the ionic and electronic subsystems to the resulting polarization.

The results of the polarization calculations are presented in Fig. 2. In the AFE state, the net polarization is exactly zero, as expected. As λ gradually increases toward 1, the asymmetry with respect to the centric phase and the magnitude of the total polarization both increase steadily along the a-axis but remain near zero for the b- and c-axis components. For (λ = 1), we extract the estimated value of Ptotal, which is equal to 10.72 μC cm−2, in very good agreement with the experimental value of 9.80 μC cm−2. From our analysis, the contributions from organic cations and inorganic frameworks are 10.34 μC cm−2 and 0.59 μC cm−2, respectively. Clearly, the AMP cations dominate the total polarization, so that the framework contribution appears negligible in comparison. An applied electric field then mainly rotates the AMP cations while displacing the [PbI4]2− framework only a little. Because the switchable FE polarization is primarily due to the long-range orientational order of the organic cations, the true AFE state lying between the +P and −P states could be consistent with either ordered or disordered but balanced arrangements of AMP-cation orientations, thus supporting a null electric polarization. Indeed, the AFE ordered state of the crystal represents only a computational reference phase to evaluate the final polarization, and in principle may be not exclusively defined. In the present case, we have fixed a possible AFE ordering, but, according to the modern theory of polarization, the final polarization does not depend on the particular path considered for 0 ≤ λ ≤ 141.

Fig. 2: The FE polarization along the a-, b-, and c-axes of (AMP)PbI4 as a function of the parameter λ, which represents the normalized AMP2+ cation rotations and [PbI4]2− framework displacements.
figure 2

a The total FE polarization. b, c The polarization contribution of the cation and framework, respectively.

Full size image

Electronic structure and Rashba SOC effect

We now examine the electronic structure and Rashba SOC effect of ferroelectric (AMP)PbI4. The Brillouin zone (BZ) and corresponding Rashba spin-polarized bands of the FE structure are shown in Fig. 3a, b. The valence band maximum (VBM), conduction band minimum (CBM), and related bandgap are localized in k-space around the high-symmetry B point. The VBM and CBM are strongly spin-split due to the spin–orbit interaction and are also shifted away from the B point in k-space. As usual, the “momentum offset” (kR) corresponds to the distance between the apex of the splitting band and the high-symmetry point in k-space, while ER corresponds to the energy difference between them. In our case, kR and ER are estimated as 0.0133 Å−1 and 16 meV for the VBM and as 0.0132 Å−1 and 12 meV for the CBM, which shows rather fairly good agreement with the respective experimental values of 0.067 Å−1 and 85 meV. Indeed, according to the definition

$$\begin{array}{*{20}{c}} {\alpha _{R} = \frac{{2E_R}}{{k_R}}} \end{array},$$
(2)

αR is calculated to be 2.39 eV Å for the VBM, which agrees with the experimental 2.60 eV Å very well. It must be noted that the kR values for the VBM and CBM are very similar, indicating that they are located essentially at the same point in k-space to form a “direct” bandgap, which is beneficial for electronic transitions in photovoltaic-cell applications.

Fig. 3: The band structure of FE state.
figure 3

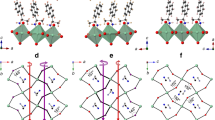
a The high-symmetry points of BZ. b Dispersed band structures along the whole BZ; the spin-split bands of the VBM (bottom) and CBM (top) were magnified in the red frames for emphasis. c 3D plot of band dispersion for valence bands (VBs) around B point. The color evolution from blue to yellow represents the VB eigenvalues. d, e The spin-textures projected on the 2D plane perpendicular to the FE polarization (P). The color code represents the sx spin component.

Full size image

We show the band dispersion of the spin-split bands, i.e., a 3D plot of the VBs around the high-symmetry B point, in Fig. 3c. The corresponding spin-textures of the spin-split bands are projected onto the 2D plane perpendicular to the FE polarization (P) in Fig. 3d. In the inner and outer bands, the sense of rotation (left-handed or right-handed) of the spin-textures are opposite due to the spin–orbit interaction. As reported in refs. 42,43, the polarization reversal resulting from the application of an external electric field should be able to switch the spin textures. Indeed, we also observe that the spin textures completely switch from left- to a right-handed sense of rotation as the polarization goes from −P to +P, as shown in Fig. 3d, e.

While most studies on spin-orbit related properties estimate the Rashba parameter for a given direction (in the plane perpendicular to the polarization) and visualize the spin-texture and its switching properties, in addition here we focus on the anisotropy of the Rashba parameter and its relationship to the switching of the ferroelectric polarization. To probe this anisotropy, the band structure was calculated on a fine grid of points in the vicinity of the reciprocal-space B point within the 2D plane perpendicular to the FE polarization (the yellow kykz plane in Fig. 3a). The calculated αR parameters are summarized in Fig. 4a, where we use a polar plot indicating the blue curves corresponding to the αR obtained from the VBs and the green curves corresponding to those from the CBs. It can be seen that αR parameters show a marked anisotropy, both at VBs and CBs. The maximum αR of the VB at the B point (the blue curve in Fig. 4a) is 2.39 eV Å, located on the kz-axis, whereas the minimum is 0.94 eV Å, located on the ky-axis, which indicates that αR is not a constant but rather a function of the angle θ with respect to the negative kz-axis (in the yellow plane in Fig. 3a).

Fig. 4: Polar plots of variable αR for Rashba spin-split bands obtained along with different directions in the plane perpendicular to the FE polarization.
figure 4

The plots of a–c are acquired at the B point while those of d, e are at the G point. The blue curves correspond to the αR obtained from the VBs while the green curve corresponds to those from the CBs. The red arrows indicate the direction of the polarization, and −P′ indicates an alternative −P structure wherein each AMP molecule rotates 180° relative to the +P structure around the axis perpendicular to its maximum-electron-density plane rather than around the b axis. However, this −P′ is energetically unfavorable as discussed in the text.

Full size image

Remarkably, we find that when the FE polarization is switched from +P to −P, the major and minor axis of the Rashba anisotropy are exchanged as shown in Fig. 4b, so that the maximum αR value of the VB (2.22 eV Å) shifts from the kz-axis (b-axis) to the ky-axis (c-axis), and the minimum αR value (0.87 eV Å) shifts the opposite way. In other words, while the polarization switches from +P to −P, the major axis αR value decreases, while the minor axis αR value increases. If we compare the +P and −P anisotropy ellipses, the net effect is an apparent 90° rotation of the anisotropy ellipse, i.e., a pseudo-rotation. To the best of our knowledge, this is the first time that a polarization-switchable Rashba anisotropy has been observed, which is also connected to a very large anisotropy.

We propose a structural mechanism for this highly unusual polarization-switchable pseudo rotation of the Rashba anisotropy. As the AMP-cation orientations evolve between the +P and −P states, the roughly 180° rotation (approximately around the b-axis) of each cation not only switches the aminomethyl group between the +a and −a sides of the cation but also rotates its maximum-electron-density plane (MEDP) by about 90° in the bc plane, which is dual to the kykz plane of the BZ (can be seen in Supplementary Fig. 3). To verify our hypothesis that this polarization-reversal-induced 90° rotation of the AMP cation’s MEDP is responsible for the rotation of the Rashba-anisotropy, we construct an alternative −P′ structure from the +P structure by rotating each AMP cations by 180° around the axis perpendicular to its MEDP, so that its aminomethyl group is still moved between the +a and −a sides, but without allowing the MEDP to rotate in the bc plane. When the structure is thus evolved, we see no rotation of the Rashba anisotropy in its band structures (Fig. 4c, f). Furthermore, compared to the isoenergetic +P and normal −P structures, the alternative −P′ structure has a 0.48 eV higher energy than −P and is separated from +P by an energy barrier of greater than 1.20 eV, demonstrating that the −P′ structure would be very difficult to obtain at room temperature.

To understand the Rashba anisotropy and spin texture under polarization switching, we construct the effective k·p model near the B point. The little group of the B point is Cs with only mirror symmetry operator My. Under the mirror transformation \(My:\left( {x,y,z} \right) \to \left( {x, - y,z} \right),(k_x,k_y,k_z) \to (k_x, - k_y,k_z)\) and \((\sigma _x,\sigma _y,\sigma _z) \to ( - \sigma _x,\sigma _y, - \sigma _z)\). Then the two-band Hamiltonian for the VBM or CBM at kx = 0 near the B point can be written as

$$\begin{array}{*{20}{c}} {H\left( {k_y,k_z} \right) = {\upvarepsilon}_0 + \frac{{\hbar ^2k_y^2}}{{2m_y}} + \frac{{\hbar ^2k_z^2}}{{2m_z}} + \alpha _1k_z\sigma _y + \alpha _2k_y\sigma _z + \alpha _3k_y\sigma _x}{.} \end{array}$$
(3)

Here my and mz are the effective masses along the ky and kz directions near the B point, and σx, σy, and σz are Pauli matrices. α1, α2, and α3 are three Rashba parameters. The last three terms are SOC terms that include the Rashba and Dresselhaus SOC effects, which can be rewritten in the form

$$\begin{array}{*{20}{c}} {H_{so} = \lambda _D\left( {k_z\sigma _y + k_y\sigma _z} \right) + \lambda _R\left( {k_z\sigma _y - k_y\sigma _z} \right) + \alpha _3k_y\sigma _x}, \end{array}$$
(4)

where

$$\begin{array}{*{20}{c}} {\lambda _D = \left( {\alpha _1 + a_2} \right)/2}, \end{array}$$
(5)

and

$$\begin{array}{*{20}{c}} {\lambda _R = \left( {\alpha _1 - a_2} \right)/2}, \end{array}$$
(6)

are the Dresselhaus and Rashba parameters, respectively44,45. The last term kyσx leads to the emergence of the sx spin component on the kykz plane which is consistent with our first-principles calculation of the spin textures. The eigenvalues of the two-band Hamiltonian reads as

$$\begin{array}{*{20}{c}} {E\left( {k_y,k_z} \right) = {\upvarepsilon}_0 + \frac{{\hbar ^2k_y^2}}{{2m_y}} + \frac{{\hbar ^2k_z^2}}{{2m_z}} \pm \sqrt {\alpha _1^2k_z^2 + \alpha _2^2k_y^2 + \alpha _3^2k_y^2} } \end{array}.$$
(7)

To understand the Rashba anisotropy under polarization switching, the eigenvalues can be written as

$$\begin{array}{*{20}{c}} {E\left( {k_r,\theta } \right) = {\upvarepsilon}_0 + \left( {\frac{{\hbar ^2}}{{2m_y}}{\mathrm{sin}}^2\theta + \frac{{\hbar ^2}}{{2m_z}}{\mathrm{cos}}^2\theta } \right)k_r^2 \pm \sqrt {\alpha _1^2{\mathrm{cos}}^2\theta + \left( {\alpha _2^2 + \alpha _3^2} \right){\mathrm{sin}}^2\theta } \left| {k_r} \right|} \end{array},$$
(8)

in polar coordinates. Here kr is defined as the distance of k from the B point in the kykz plane, and θ is the angle between \(\vec k_r\) and \(\vec k_z\). One can define the general “Rashba parameter” with different directions on the kykz plane in polar coordinates as

$$\begin{array}{*{20}{c}} {\alpha ^ \uparrow \left( \theta \right) = \sqrt {\alpha _1^2{\mathrm{cos}}^2\theta + \left( {\alpha _2^2 + \alpha _3^2} \right){\mathrm{sin}}^2\theta } } \end{array},$$
(9)

where the arrow ↑ means the polarization along with the +x direction corresponding to the +P state. The reorientation of the AMP cation, which involves the combination of a Mx mirror operation and a C4x rotation operation, effects a 90° rotation of the crystal fields at the cation site such that \((x,y,z) \to ( - x,z,y)\) and \(\left( {k_x,k_y,k_z} \right) \to ( - k_x,k_z,k_y)\). The eigenvalue of effective Hamiltonian of the −P state should then be

$$\begin{array}{*{20}{c}} {E^ \downarrow \left( {k_r,\theta } \right) = {\upvarepsilon}_0 + \left( {\frac{{\hbar ^2}}{{2m_y}}{\mathrm{cos}}^2\theta + \frac{{\hbar ^2}}{{2m_z}}{\mathrm{sin}}^2\theta } \right)k_r^2 \pm \sqrt {\alpha _1^2{\mathrm{sin}}^2\theta + \left( {\alpha _2^2 + \alpha _3^2} \right){\mathrm{cos}}^2\theta } \left| {k_r} \right|} \end{array},$$
(10)

in polar coordinates. So the anisotropy of the Rashba parameter of the −P state is

$$\begin{array}{*{20}{c}} {\alpha ^ \downarrow \left( \theta \right) = \sqrt {\alpha _1^2{\mathrm{sin}}^2\theta + \left( {\alpha _2^2 + \alpha _3^2} \right){\mathrm{cos}}^2\theta } } \end{array},$$
(11)

where the arrow ↓ means the polarization along the −x direction. It is easy to see that

$$\begin{array}{*{20}{c}} {\alpha ^ \uparrow \left( \theta \right) = \alpha ^ \downarrow \left( {\theta + \frac{\pi }{2}} \right)} \end{array},$$
(12)

which means the anisotropy of the Rashba parameter is rotated by 90° under polarization switching, which is equivalent to a 180° rotation of polarization. The proposed k·p model is thus nicely consistent with our DFT results in terms of a 90° pseudo-rotation.

We introduce parameter

$$\begin{array}{*{20}{c}} {\mu = \left| {\frac{{\alpha _R\left( {k_z} \right) - \alpha _R\left( {k_y} \right)}}{{\alpha _R\left( {k_y} \right)}}} \right| = \left| {\frac{{\alpha _R\left( {k_z} \right)}}{{\alpha _R\left( {k_y} \right)}} - 1} \right|} \end{array},$$
(13)

to quantify the strength of the anisotropy where αR(kz) and αR(ky) are the numerical values of the Rashba parameter along the kz and ky axes of the BZ, respectively. The larger the value of µ, the more pronounced the anisotropy of αR is. In the case of the −P and +P polarizations, µ has quite similar values of 1.7 and 1.6, respectively, reflecting the robustness of the Rashba anisotropy in this system.

It is interesting to note that the pseudo-rotation of the Rashba anisotropy induced by polarization reversal occurs not only at a single point in k-space, but at several points where the Rashba splitting is effective. Our observations of the Rashba anisotropy in the VB and CB near both the B and G points of the BZ are all qualitatively consistent with the description and explanation of Fig. 4d–f above. At both of these points, the pseudo-rotation of the anisotropy ellipse occurs when reversing the polarization perpendicular to the framework layers.

Symmetry mode analysis

The +P and −P FE structures can be viewed as distorted “children” of an idealized “parent” structure, which allows us to characterize their symmetry-breaking structural variables (i.e., symmetry modes) in terms of the irreducible representations (irreps) of the parent space-group symmetry. We construct this idealized parent from the centrosymmetric AFE structure in the left panel of Fig. 1a by regularizing the PbI6 octahedra and zeroing the PbI6 octahedral rotations in order to straighten out the framework, and by replacing each AMP cation with a polar vector (attached to a dummy atom at the molecular centroid location) that points along the appropriate ±a direction, resulting in centrosymmetric space group Pcmm (#51, \(D_{2h}^5\)) on an orthorhombic (a, b/2, c) unit-cell basis with zero origin shift relative to the child. We also idealize the FE children by replacing each AMP cation with an appropriate polar vector in order to apply the symmetry mode analysis consistently.

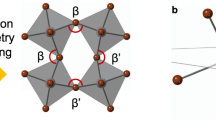
The key order parameters of the idealized parent structure that characterize our FE child structures are (1) the PbI6 octahedral framework rotation around the a-axis, which belongs to parent irrep \(Y_3^ + \), (2) the ferroelectric displacements along the a-axis, which belong to FE parent irrep \({{\Gamma }}_2^ - \), and (3) the large AMP-cation rotations around the b-axis, which are achieved through the cooperative action of two-parent irreps, ferrorotational (FR) irrep \({{\Gamma }}_4^ + \) and anti-FR (AFR) irrep \(Y_1^ - \), as shown in Fig. 5. Using the INVARIANTS software package, we find that these four primary order parameters provide a quadrilinear invariant term in the free energy expansion, so that simultaneously invoking the framework (\(Y_3^ + \)) and the cation (\({{\Gamma }}_4^ + \), \(Y_1^ - \)) rotational modes breaks the inversion symmetry of parent, thus allowing them to couple to a secondary (i.e., improper) ferroelectric moment (\({{\Gamma }}_2^ - \)).

Fig. 5: Molecular rotation modes. Short (90°) and long (180°) red arrows indicate right-handed molecular rotations relative to the AFE configuration.
figure 5

Summing the ferrorotational (FR) (a) and anti-ferrorotational (AFR) (b) patterns of 90° rotations cause only two of four molecules to rotate by 180° (c), which is precisely the FE structure (d).

Full size image

Because the PbI4 framework is only slightly disturbed in switching between the +P and −P states, it is convenient to treat the \(Y_3^ + \) framework rotation as a large preexisting structural feature in a slightly less-symmetric parent structure with space group Pnmm (#59, \(D_{2h}^{13}\)) and unit-cell basis and origin identical to those of the child. For this less-symmetric parent structure, the FR and AFR cation rotations form a simple trilinear invariant with the ferroelectric moment.

The +P cation arrangement is obtained from the parent via the superposition of a 90° FR motion \(({\Gamma}_4^ + )\) and a 90° AFR motion \((Y_1^ - )\), so that two of the AMP cations are rotated by a full 180° while the other two remain stationary (as shown in Fig. 1). The −P cation arrangement is achieved instead by merely reversing the sense of the AFR contribution. Due to the unfavorable energy at the 90° midpoint of rotation, it makes no sense to view the FR and AFR rotations as separate processes; they must occur simultaneously and cooperatively so that the \(\Gamma _4^ + \) and \(Y_1^ - \) order parameters are tightly coupled to have equal amplitudes. The product of two such large order parameters facilitates a strong trilinear coupling to the FE polarization. It remarkable that two centric modes, i.e., \(\Gamma _4^ + \) and \(Y_1^ - \), combine together to give rise a hybrid mode, which in turn, breaks inversion symmetry and allows the polarization to arise in this system. Moreover, the coherent switching of both of them, i.e., the switching of the hybrid model, allows switching the polarization giving rise to a hidden pseudo-rotation in k-space, as highlighted in this work with the switchable Rashba anisotropy ellipse. It is intriguing that the switchable Rashba anisotropy occurs coherently at different relevant points in the k-space.

In summary, HOIPs are emerging as a class of photovoltaic materials. In this work, DFT methods have been used to study the ferroelectric properties and Rashba spin–orbit effect as well as the coupling between the FE polarization (Ps) and the anisotropy of the Rashba parameter (αR) for a layered HOIP, (AMP)PbI4, where AMP is 4-(aminomethyl)piperidinium. We calculate Ps and αR to be 10.72 μC cm−2 and 2.39 eV Å, respectively, which are nicely consistent with the experimentally reported values of 9.8 μC cm−2 and 2.60 eV Å. To gain insight into the origin of the polarization, the contributions of the organic AMP2+ cations (10.34 μC cm−2) and inorganic [PbI4]2− framework (0.59 μC cm−2) have been disentangled, demonstrating that the AMP cations contribute almost all of the total polarization. This clearly suggests that a proper choice of organic cations could possibly enhance the ferroelectric polarization, by exploiting both the molecular dipole moment and their relative tilting, giving rise to an uncompensated electric polarization.

As previously reported for Rashba ferroelectrics, the sense of rotation of the spin-texture can be reversed by a switching of the FE polarization direction along the polar axis40. However, in (AMP)PbI4, we calculate a large and robust anisotropy in the Rashba parameter. Remarkably, we find that the major and minor axes of the ellipse can be exchanged under reversal of the electric polarization, causing a 90° pseudo-rotation of the Rashba anisotropy, which we have also been confirmed from a theoretical k·p model. The same effect is observed in both the VBs and CBs at multiple points in the BZ where the Rashba splitting is significant. A structural mechanism for this effect is presented and explained in terms of a quadrilinear coupling of order parameters involving two large-amplitude AMP-cation rotation modes, a large octahedral framework rotation, and the ferroelectric polarization. To the best of our knowledge, this is the first report of a coupling of ferroelectric polarization and switchable highly anisotropic Rashba spin-split bands and it may be possible that the same property can be found in other layered hybrid perovskites. This deserves further investigation. Indeed, spin-optoelectronic devices based on hybrid organic–inorganic trihalide perovskites like spin-LEDs have been recently discussed for the parent compound MAPbBr346, circularly polarized light detections have been considered for chiral hybrid perovskite47, spin-FETs. This strong coupling may provide a potential probe of the spin degrees of freedom in photovoltaic materials and a different avenue for developing spin-optoelectronic devices based on HOIPs materials.

Methods

Computational details

The starting point for our calculations is the experimental crystallographic data reported in ref. 33, where we relax all of the atoms of the ferroelectric structure until the Hellmann–Feynman forces are smaller than 0.001 eV Å−1. The projector augmented wave (PAW)48 method is used to solve Kohn–Shan equations with the PBE exchange-correlation functional49, as implemented in the Vienna ab initio simulation package. The energy cutoff for the plane wave expansion is set to 550 eV, and a 2 × 2 × 2 Monkhorst–Pack grid of k-point is used after systematic convergence tests. The van der Waals interactions are taken into account in calculations using the DFT-D3 method50. The Berry phase approach is used to evaluate the ferroelectric polarization by constructing a properly AFE reference state and a suitable path connecting FE with AFE states40,51,52. Details of this approach are discussed in the results section. Spin–orbit interaction is self-consistently considered in all band structure calculations, but not in the calculations of polarization. Van der Waals interactions are included in all calculations53.