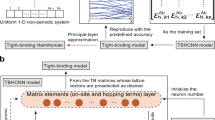
Introduction

Density functional theory (DFT) is the work horse of electronic structure simulations. In particular, semi-local exchange-correlation functionals, such as the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE)1,2 are widely used for high-throughput materials discovery efforts3,4,5. However, due to the self-interaction error (SIE), local and semi-local functionals systematically underestimate band gaps, occasionally to the extent that semiconductors are erroneously predicted to be metallic6,7. One way to mitigate SIE is including a fraction of excact (Fock) exchange in a hybrid functional8,9, such as the Heyd-Scuseria-Ernzerhof (HSE) functional10,11. Hybrid functionals produce improved band gaps; However, their relatively high computational cost may be prohibitive for large systems, such as interface models containing several hundred atoms, and/or for screening a large number of materials.

The DFT+U method is an alternative approach, first introduced by Anisimov et al.12 and further developed by Dudarev et al.7 A Hubbard-like model is adopted to correct the self-interaction error as follows:

$${E}_{{\mathrm{tot}}}={E}_{{\mathrm{DFT}}}+\frac{U-J}{2}\mathop{\sum }\limits_{\sigma}{n}_{m,\sigma }-{n}_{m,\sigma }^{2},$$
(1)

where n is the atomic-orbital occupation number, m is the orbital momentum, σ is a spin index, U represents the on-site Coulomb repulsion, and J represents the exchange interaction. The exchange interaction may be incorporated into the Coulomb term to define the effective Hubbard U as Ueff = U − J7. The accuracy of DFT+U calculations hinges on the choice of the system dependent parameter, Ueff.

Often, Ueff is determined empirically by searching for values that reproduce experimental results, such as the band gap of a given material. The empirical approach will inevitably fail if no experimental data are available, which is frequently the case in materials discovery efforts. Several approaches have been proposed for determining the U parameter from first principles13. One popular approach is the linear response (LR) method, based on constrained DFT (CDFT) proposed by Cococcioni and de Gironcoli14. In this approach, linear behavior of the total energy with respect to the occupation number is imposed to correct the unphysical curvature of local and semi-local functionals. The effective U parameter is then given by the difference between the inverse non-interacting density response, \({\chi }_{0}^{-1}\), and the inverse interacting density response, χ−1, which correspond, respectively, to the second derivatives of the non-charge-self-consistent DFT energy, E, and the charge-self-consistent DFT energy, EKS, with respect to the localized occupation of a single site, qI:

$${U}_{{\mathrm{eff}}}=\frac{{\partial }^{2}E[\{{q}_{I}\}]}{\partial {q}_{I}^{2}}-\frac{{\partial }^{2}{E}^{{\mathrm{KS}}}[\{{q}_{I}\}]}{\partial {q}_{I}^{2}}={({\chi }_{0}^{-1}-{\chi }^{-1})}_{II}$$
(2)

To simulate the variation of occupations in an infinite crystal, a super-cell is constructed. The size of the super-cell is increased until the value of Ueff converges, which may result in a significant computational cost. A modified self-consistent formulation of LR has been proposed by Kulik et al.15. Another method for determining the Hubbard U parameter from first principles is the unrestricted Hartree-Fock (UHF) approach proposed by Mosey et al.16,17. Within this approach, UHF calculations are performed for an electrostatically embedded finite-sized cluster to simulate the bulk material. Similar to the super-cell size in the LR method, the U parameters have to be converged with increasing cluster size. A third approach is the constrained random-phase approximation (cRPA)18,19,20, which is significantly more computationally expensive.

Here, we propose an approach for determining Ueff based on Bayesian optimization (BO). To demonstrate the performance of our approach, we have chosen three classes of materials, for which semi-local functionals are known to perform poorly: transition metal monoxides, europium chalcogenides, and narrow-gap semiconductors. The results and the computational cost of GGA+UBO are also compared to the LR method for determining Ueff. We show that for materials of all three classes, BO with a well-designed objective function produces band structures of comparable quality to a hybrid functional. The band structures obtained using GGA+UBO are either similar to or better than those obtained with GGA+ULR. In all cases BO is more computationally efficient than LR.

Results and discussion

Bayesian optimization

BO21 is a machine learning algorithm that performs global optimization of a black box function by guessing the shape of the function and then iteratively improving it by sequentially sampling points that are promising and/or have high information content. A Bayesian statistical model is used to emulate the objective function. Gaussian process (see additional information in the Supplementary Discussion) is a common choice for BO algorithms22 because it also quantifies the uncertainty associated with each prediction. Future function evaluations are decided by an acquisition function23. BO is superior to grid search because it utilizes acquired data to make informed sampling decisions, thus requiring fewer expensive function evaluations (e.g., DFT calculations). The successful application of Bayesian optimization requires an appropriate objective function. Here, the surrogate objective function, \(f(\overrightarrow{U})\), is formulated such that its maximum corresponds to the Ueff values that best reproduce the band gap, Eg, and the band structure obtained from HSE:

$$f(\overrightarrow{U})=-{\alpha }_{1}{({{\rm{E}}}_{{\rm{g}}}^{{\rm{HSE}}}-{{\rm{E}}}_{{\rm{g}}}^{{\rm{PBE+U}}})}^{2}-{\alpha }_{2}{\left(\Delta {\rm{Band}}\right)}^{2}$$
(3)

Here, \(\overrightarrow{U}=[{U}^{1},{U}^{2},\ldots ,{U}^{n}]\) is the vector of Ueff values applied to different atomic species and Ui ∈ [−10, 10] eV. ΔBand is defined similarly to ref. 24 as the mean squared error of the PBE+U band structure with respect to HSE:

$$\Delta {\rm{Band}}=\sqrt{\frac{1}{{N}_{{\mathrm{E}}}}\mathop{\sum }\limits_{i = 1}^{{N}_{k}}\mathop{\sum }\limits_{j = 1}^{{N}_{b}}{({\epsilon }_{{\mathrm{HSE}}}^{j}[{k}_{i}]-{\epsilon }_{{\mathrm{PBE}}+U}^{j}[{k}_{i}])}^{2}}$$
(4)

NE represents the total number of eigenvalues, ϵ, included in the comparison, Nk is the number of k-points, and Nb is the number of bands selected for comparison. To avoid double counting the band gap difference in the calculation of ΔBand, the valence band maximum (VBM) and conduction band minimum (CBM) are shifted to zero for both the PBE+U and HSE band structures. Hence, ΔBand captures differences in the qualitative features of the band structures produced by PBE+U vs. HSE, independently of the difference in the band gap. Hybrid functionals have been used in the past as a reference for DFT+U25. Here, the HSE functional has been chosen as the reference thanks to its well-established accuracy for various materials26,27,28. The method can be easily adapted to use any other reference band structure, including different hybrid functionals or many-body perturbation theory. The coefficients α1 and α2 may be used to assign different weights to the band gap vs. the band structure. We set α1 = 0.25 and α2 = 0.75 as default. Additional analysis of the sensitivity of the U parameters and the resulting band structures to the choice of α1 and α2 is provided in the Supplementary Discussion.

BO is applied to maximize the objective function, as illustrated in Fig. 1. To initialize the calculation, the geometry information and input settings of VASP are required. Gaussian process with the radial basis function kernel (see additional information in the Supplementary Discussion) is used as the statistical model to fit the objective function29. The Gaussian process defines a mean, μ, and a standard deviation, σ, for every point, \(\overrightarrow{U}\), and updates those parameters from the training data in each iteration29. The upper confidence bound (UCB)29 acquisition function is used to predict the value that would be generated by evaluation of the objective function at a new point and decide what value of \(\overrightarrow{U}\) to sample in the nth iteration:

$${\vec U _n} = \mathop {\arg \max }\limits_{\vec U } \,\mu (\vec U ) + \kappa \sigma (\vec U )$$
(5)
Fig. 1: Bayesian optimization.
figure 1

Workflow of the algorithm for determining Ueff.

Full size image

The hyperparameter κ controls the trade-off between exploration and exploitation. Here, we set κ = 1. In each iteration VASP is called to evaluate \(f(\overrightarrow{{U}_{n}})\). The posterior probability distribution and acquisition function are updated until the maximal number of iterations, N, is reached. Then, the code outputs the value of \(\overrightarrow{U}\) that maximizes \(f(\overrightarrow{U})\). The reference HSE calculation is performed only once. The total computational cost of BO amounts to performing one HSE calculation and N PBE+U calculations. The computational cost of updating the BO posterior probability distribution and acquisition function in each iteration is negligible compared to the cost of DFT calculations. Because N is typically small and all calculations are performed for one unit cell (as opposed to a supercell or a large cluster), the computational cost of determining Ueff by BO is often lower than that of determining Ueff by the aforementioned first principles methods. Below, we demonstrate the performance of PBE+UBO for NiO, EuTe, and InAs. In the Supplementary Discussion, we provide additional examples for EuS, InP, InSb, GaSb, Ge, NiO, MnO, FeO, and CoO. The LR method of determining Ueff is used for comparison. We note that all DFT+U results presented here are based on the implementation of the Dudarev formalism in VASP. Different DFT+U implementations may yield different results30.

Transition metal oxide: NiO

Transition metal oxides are among the materials most often studied with DFT+U15. In particular, NiO and other transition metal monoxides have been shown to be poorly described by the PBE functional because of their strongly correlated d electrons31,32,33,34. Our PBE result shown in Fig. 2a is no exception. The PBE band gap of 0.73 eV is considerably underestimated compared to the HSE result of 4.26 eV shown in Fig. 2b. The latter is close to the experimental band gap of 4.0–4.3 eV35,36. For both PBE and HSE, the valence band maximum (VBM) is located at point T. However, there are qualitative differences in the structure of the valence band and the location of the conduction band minimum (CBM). The contribution of different states to the PBE band structure, shown in Fig. 2a, suggests that the reason could be that the Ni 3d bands are located below the Ni 4s bands leading to an inverted band ordering at the Γ point, which should have been the CBM. Thus, we start by applying the Hubbard U correction to the Ni d states. Based on the HSE band structure, we included the top 10 valence bands and the bottom 4 conduction bands in the optimization. As shown in Fig. 3, the BO algorithm converges within 13 iterations and finds the optimum at \({U}_{{\mathrm{eff}}}^{{\mathrm{Ni}},d}\)= 6.8 eV. This leads to rearrangement of the top valence bands and moves the first two conduction bands upward, as shown in Fig. 2c. These changes increase the gap to 3.36 eV and correct the position of the CBM. In comparison, the LR method produces a \({U}_{{\mathrm{eff}}}^{{\mathrm{Ni}},d}\) value of 5.4 eV, which yields a similar band structure with a somewhat smaller gap of 3.20 eV and the CBM incorrectly located between T and K, as shown in Fig. 2d.

Fig. 2: Band structures of NiO obtained using different methods.
figure 2

a PBE with the projected contributions of Ni d states, Ni s states, and O p states colored in green, yellow, and red, respectively; b HSE; c PBE+U with one-parameter BO; d PBE+U with one-parameter LR; e PBE+U with two-parameter BO; and f PBE+U with two-parameter LR. The VBM is referenced to 0 eV.

Full size image
Fig. 3: 1D BO for NiO.
figure 3

a The Gaussian process predicted mean values and b the acquisition function after 13 BO steps.

Full size image

Although applying a Hubbard U correction to the Ni d states leads to a significant improvement over pure PBE, some residual differences between the PBE+U and HSE results may be attributed to the non-negligible contribution of the oxygen 2p states, as shown in Fig. 2a37. Therefore, a two-dimensional (2D) BO was performed. As illustrated in Fig. 4a, it results in Hubbard U values of \({U}_{{\mathrm{eff}}}^{{\mathrm{Ni}},d}\)= 5.9 eV and \({U}_{{\mathrm{eff}}}^{O,p}\)= 9.4 eV after 55 iterations. This yields a gap of 3.70 eV and a band structure in closer agreement with HSE, as shown in Fig. 2e. Another indication for the closer agreement with HSE is an increase of the objective function from −0.37 to −0.11 eV2. In comparison, LR produces a Hubbard U value of \({U}_{{\mathrm{eff}}}^{O,p}\)= 8.3 eV for the O 2p states. With the two-parameter LR, the band gap increases to 3.53 eV and the CBM is in the right position, as shown in Fig. 2f. For NiO, the accuracy of the BO and LR methods for determining U is similar, however the BO method is more efficient. For one-parameter optimization on the same number of CPU cores, LR with a 3 × 3 × 3 super-cell takes about 4.5 times longer than BO, as detailed in Supplementary Table 3. When two parameters are considered, LR is more computationally expensive than BO by a factor of eight.

Fig. 4: 2D BO for NiO.
figure 4

a The Gaussian process predicted mean values, and b the acquisition function after 55 BO steps.

Full size image

Europium chalcogenide: EuTe

In addition to the d-block transition metals, f-block elements are considered as strongly correlated and are often treated with DFT+U38,39. EuTe, a ferromagnetic semiconductor with a gap of 2.0 eV (refs. 40,41), is a representative example. As shown in Fig. 5a, the PBE functional erroneously predicts EuTe to be metallic. Analysis of the contributions of different orbitals shows that the conduction bands are mostly formed by the d and s states of Eu. The 7 valence bands closest to the Fermi level are formed by the f states of Eu. The p states of Te are found in a separate manifold below the Eu-4f derived bands42,43,44. The vanishing gap can be attributed to the overlap between bands dominated by the 4f and 5d states of Eu. The HSE calculation, shown in Fig. 5b, produces an indirect band gap of 1.24 eV with the VBM located at the Γ point.

Fig. 5: Band structures of EuTe obtained using different methods.
figure 5

a PBE with the projected contributions of Eu f states, Eu d states, and Te p states colored in green, red, and yellow, respectively; b HSE; c PBE+U with \({U}_{{\mathrm{eff}}}^{{\mathrm{Eu}},f}\) from BO; and d PBE+U with \({U}_{{\mathrm{eff}}}^{{\mathrm{Eu}},f}\) from LR. The VBM is referenced to 0 eV.

Full size image

BO was performed with the Hubbard U correction applied to the 4f orbitals of Eu. 20 eigenvalues around the Fermi level (10 above and 10 below) were included in the optimization. The resulting band structure with \({U}_{{\mathrm{eff}}}^{{\mathrm{Eu}},f}\) = 7.1 eV is plotted in Fig. 5c. The Hubbard U correction pushes the Eu 4f bands away from the Fermi level and opens a band gap of 0.71 eV. The PBE+UBO calculation reproduces the qualitative features of HSE band structure. In comparison, the LR method produces a value of \({U}_{{\mathrm{eff}}}^{{\mathrm{Eu}},f}\) = 5.5 eV. As shown in Fig. 5d, this results in a somewhat smaller band gap of 0.56 eV. In this case, BO also produces similar results to LR at a fraction of the computational cost. The total amount of CPU time required for LR with a 3 × 3 × 3 super-cell is higher than BO by a factor of 9, as shown in Supplementary Table 3. Based on Fig. 5a, the d states of Eu contribute significantly to the bottom conduction bands. Therefore, it may possible to further reduce the difference between the HSE and PBE+U results by considering the d orbital of Eu (refs. 45,46) in 2D BO. However, applying U corrections to two orbitals of the same element is not implemented in VASP.

Narrow gap semiconductor: InAs

Although all the examples discussed so far involve strongly correlated electrons, SIE also manifests in PBE calculations of narrow-gap semiconductors47,48,49. The band structure of InAs, shown in Fig. 6a, is a representative example, where PBE produces no band gap50. HSE, shown in Fig 6b, gives a band gap of 0.37 eV, which is comparable to the experimental gap of 0.417 eV51,52. We find that conducting BO with a single Ueff applied to the p orbitals of either In or As yields no band gap. Therefore, 2D BO is performed to optimize \({U}_{{\mathrm{eff}}}^{{\mathrm{In}},5p}\) and \({U}_{{\mathrm{eff}}}^{{\mathrm{As}},4p}\) simultaneously. The resulting band structure with \({U}_{{\mathrm{eff}}}^{{\mathrm{In}},5p}\) = −0.5 eV and \({U}_{{\mathrm{eff}}}^{{\mathrm{As}},4p}\) = −7.5 eV is shown in Fig. 6c. PBE+UBO produces a band gap of 0.31 eV and a band structure in good agreement with HSE. Negative Ueff values are theoretically permissible when the exchange term, J, is larger than the on-site Coulomb repulsion, U, as suggested in refs. 53,54,55,56,57. It has been argued that negative values of Ueff are appropriate for delocalized states, such as the In s and As p states, where the exchange-correlation hole is overestimated by GGA. In comparison, the LR method, which does not permit negative values of Ueff, yields \({U}_{{\mathrm{eff}}}^{{\mathrm{In}},5p}\) = 0.7 eV and \({U}_{{\mathrm{eff}}}^{{\mathrm{As}},4p}\) = 3.3 eV. This produces a band structure with no gap, as shown in Fig. 6d. Thus, for InAs BO is not only more efficient, but also more accurate than LR. In the Supplementary Discussion, we further demonstrate the transferability of the U values found by BO for bulk InAs to a slab of InAs with 11 atomic layers.

Fig. 6: Band structures of InAs obtained using different methods.
figure 6

a PBE with the projected contributions of In p states, In s states, and As p states colored in green, red, and yellow, respectively; b HSE; c PBE+U with \({U}_{{\mathrm{eff}}}^{{\mathrm{In}},p}\) and \({U}_{{\mathrm{eff}}}^{{\mathrm{As}},p}\) from BO; d PBE+U with \({U}_{{\mathrm{eff}}}^{{\mathrm{In}},p}\) and \({U}_{{\mathrm{eff}}}^{{\mathrm{As}},p}\) from LR. The VBM is referenced to 0 eV.

Full size image

In summary, we have developed a method of determining the optimal Hubbard U parameter in DFT+U by using the Bayesian optimization machine learning algorithm. The objective function was formulated to reproduce as closely as possible the band gap and the qualitative features of the band structure obtained with a hybrid functional. We have demonstrated robust performance for several materials, including transition metal oxides, Eu chalcogenides, and narrow-gap semiconductors. PBE+UBO consistently produces band structures comparable to HSE. Furthermore, BO is more efficient than the linear response method and performs better, particularly in cases that call for negative values of Ueff. Based on this, we conclude that PBE+UBO can provide the accuracy of a hybrid functional at the computational cost of a semi-local functional. This may enable conducting simulations for larger systems, such as surfaces and interfaces, which would be unfeasible with a hybrid functional.

Methods

Computational details

All DFT calculations were performed using the Vienna Ab Initio Simulation Package (VASP) code with the projector augmented wave (PAW) method58,59,60. Spin-orbit coupling (SOC) was included in the calculations of transition metal oxides, Eu chalcogenides, and narrow-gap semiconductors61. Details of the lattice parameter and energy cutoff used for each compound are provided in Supplementary Table 1. The Brillouin zone was sampled using an 8 × 8 × 8 k-point grid for PBE and PBE+U calculations and 6 × 6 × 6 for HSE calculations. The coordinates of the high-symmetry k-points used for plotting the band structures are provided in Supplementary Table 2.

Linear response calculations

For LR calculations, a small potential was applied to the target state of a single site. Non-charge-self-consistent and charge-self-consistent calculations of the state occupation were performed as the potential was varied from −0.04 eV to 0.04 eV in increments of 0.02 eV. The derivatives of the occupation with respect to the potential give the non-interacting and interacting response matrices, used in Eq. 2 to calculate Ueff (see also Yang et al.62). To avoid interactions between periodic images of the perturbed atom, a 3 × 3 × 3 super-cell was constructed.