Introduction

The properties of polycrystalline ceramics for applications such as solid oxide fuel cells, actuators, sensors, capacitors, and rechargeable batteries are dictated by the underlying point defects and their interactions with the grain boundaries that develop during processing. The extent of these interactions varies with grain size, crystallographic orientation, and misorientation distributions, as well as applied fields, such as stress and electric fields. The resultant microstructure and interfacial character defines the macroscopic properties of these solids1. Therefore, understanding the mechanisms that control the grain growth dynamics is a necessary step to enhance the development of energy efficient and environmentally friendly storage systems.

Experimental studies in ionic solids reveal that point defect–grain boundary interactions fundamentally alter the macroscopic behavior of materials2,3. The defect interactions result in structural, chemical, and electrical transitions4,5,6,7,8. These transitions impact the transport properties along and across the interface due to space-charge and chemical inhomogeneities at grain boundaries6,9,10. Based on the transport of mass and charge across the interface, experimentalists have tried to control densification and coarsening mechanisms to obtain desirable microstructure and properties11,12, which has led to new processing technologies like solid-state-activated sintering, liquid phase sintering, and field-assisted sintering13,14,15. Specifically, the addition of doping elements in ionic ceramics favors its interfacial segregation16, which, in turn, affects its microstructural evolution. The motion of grain boundaries, in particular, is suppressed by the drag effect that the solute imposes17,18,19, requiring large driving forces to overcome the solute pinning effect11,17,18,19,20,21.

The first quantitative atomistic theory of grain boundary motion that includes the solute drag effects in single phase material was pioneered by Lucke and Detert22. The theory introduced a binding energy on solute atoms at the grain boundary. However, the theory falls short in explaining experimental results23. In contrast, Cahn successfully described the effects of driving forces on the solute profiles in the vicinity of a grain boundary and its impact on the grain boundary motion24. He demonstrated the drag effect on grain boundary motion imposed by the segregated solute for electrically neutral alloys. Hillert and Sundman developed an alternative theory for high solute content metallic systems and showed that their approach is identical to Cahn’s in the dilute limit25,26. Mendelev and Srolovitz included mixing non-idealities by using a regular solution model27.

Variational and phase field formulations employed to resolve the solute drag effect on grain boundary motion include the work of Fan et al.28 and Cha et al.29, who described the solute drag effect on grain growth of single phase polycrystals. Ma and co-workers introduced a gradient energy penalty in a regular solution model to predict the abrupt transition of solute concentration and grain boundary mobility as a function of temperature30. Grönhagen and Ågren introduced a concentration-dependent double-well migration barrier height in a free energy formulation31. Suwa et al.32 and Kim et al.33 used a precipitation-based multiphase field method to simulate abnormal grain growth in alloys. Kim et al. extended Grönhagen and Ågren’s model to a multiphase field formulation to understand abnormal grain growth34. Ko et al. introduced anisotropic low-angle grain boundaries to simulate solid-state wetting abnormal grain growth35. Heo and coauthors introduced elastic strain interactions in solid solutions using a regular solution parameter36. Overall, all of the solute drag theories and phase field descriptions focus on the thermochemistry of metallic systems and miss to incorporate the structural and electrochemical contributions to describe grain boundary coarsening kinetics, including the effect of drag in ionic solids that would allow an accurate rationalization of sintering and grain growth of ionic ceramic materials37.

In this paper, a thermodynamically consistent variational theory is proposed to comprehensively consider the effect of the electrically charged grain boundary core and its adjacent space charge layers on grain boundary motion in ionic ceramics. Specifically, the developed model provides a rational basis to understand the drag effects of solute and point defects on the grain boundary motion in ionic solids. The theory is demonstrated on Fe-doped SrTiO3.

Results

Theoretical framework

Consider an ionic ceramic comprising of N chemical species, \(\{[{V}_{i}^{{Z}_{i}}]\}=\{[{V}_{1}^{{Z}_{1}}],\ldots ,[{V}_{N}^{{Z}_{N}}]\}\), and η, a coarse-grained order parameter measuring the degree of crystallinity, so that η = 1 for a structurally ordered/crystalline region, and η = 0 for a structurally disordered region (see Supplementary Summary of Symbols). \([{V}_{i}^{{Z}_{i}}]\) represents the concentration of ith ionic defect. The volumetric structural and chemical free energy density due to solute and chemical defect interactions is38,39:

$$\begin{array}{lll}f(\eta ,\{[{V}_{i}^{{Z}_{i}}]\},T)\,=\,\frac{1}{\omega }\left(\mathop{\sum }\limits_{i=1}^{N}({f}_{i}(\eta ,T)[{V}_{i}^{{Z}_{i}}]+{k}_{b}T[{V}_{i}^{{Z}_{i}}]{\mathrm{ln}}\,[{V}_{i}^{{Z}_{i}}])\right.\\ \qquad\qquad\qquad\qquad+{k}_{b}T \left(1-\mathop{\sum }\limits_{i=1}^{N}[{V}_{i}^{{Z}_{i}}]\right) {\mathrm{ln}}\, \left[1-\mathop{\sum }\limits_{i=1}^{N}[{V}_{i}^{{Z}_{i}}]\right]\\ \qquad\qquad\qquad\qquad\left.+\mathop{\sum }\limits_{j = 1,i\ne j}^{N}{\Omega }_{ij}[{V}_{i}^{{Z}_{i}}][{V}_{j}^{{Z}_{j}}]\right)\\ \qquad\qquad\qquad\qquad+\frac{{a}^{2}}{2}{\eta }^{2}{(1-\eta )}^{2}+\Delta H\frac{\Delta T}{{T}_{m}}p(\eta ),\end{array}$$
(1)

where \({f}_{i}(\eta ,T)={f}_{i}^{X}(T)p(\eta )+{f}_{i}^{S}(T)(1-p(\eta ))\), is the free energy contribution from the ith chemical component. In agreement with Hart40, García and coauthors41, and recent work42,43,44, each of the ith chemical species has a valence, Zi, and contributes to the electrostatic energy density, ρϕ, and the dipolar moment density, \(\frac{1}{2}\overrightarrow{D}\cdot \overrightarrow{E}\), to define the free energy of the system, f∘:

$${f}_{\circ }\left(\eta ,\{[{V}_{i}^{{Z}_{i}}]\},\rho ,\overrightarrow{D},T\right)=f\left(\eta ,\{[{V}_{i}^{{Z}_{i}}]\},T\right)+\rho \phi +\frac{1}{2}\overrightarrow{D}\cdot \overrightarrow{E}$$
(2)

The Legendre transform, \({f}_{ec}(\eta ,\{[{V}_{i}^{{Z}_{i}}]\},\overrightarrow{E},T)={f}_{\circ }(\eta ,\{[{V}_{i}^{{Z}_{i}}]\},\overrightarrow{D},T)-\overrightarrow{D}\cdot \overrightarrow{E}\), defines the electrochemical free energy density38,45. The local electric field, \(\overrightarrow{E}\), is a solution of Faraday’s Law, \(\nabla \times \overrightarrow{E}=\overrightarrow{0}\), for a constant magnetic field, so that \(\overrightarrow{E}=-\nabla \phi\), where ϕ is the electrostatic potential. Further, the electric displacement field, \(\overrightarrow{D}\), and the position-dependent electric field, \(\overrightarrow{E}\), are related through the constitutive equation, \(\overrightarrow{D}=\epsilon \overrightarrow{E}=-\epsilon \nabla \phi\), for ionic ceramics in the absence of ferroelectric effects. Additionally, the local charge density, ρ, in Eq. (2) is coupled to the concentration of ith species through physical constraint, \(\rho =\mathop{\sum }\nolimits_{i=1}^{N}e{Z}_{i}[{V}_{i}^{{Z}_{i}}]\)41,42,43,44,46,47.

In a two-dimensional polycrystalline ionic ceramic, each single-crystal grain is described by the local crystallographic orientation, θ, of a crystal with respect to a fixed laboratory reference frame48. The interfacial grain boundary energy of the two adjoining grains is, s1g(η)∣∇θ∣, a function of local crystallographic misorientation, ∣∇θ∣, and the degree of crystallinity, η, coupled through g(η) = η2. The grain boundary energy formulation reduces to the classical Read–Shockley energy for low angle tilt grain boundaries composed of an array of edge dislocations in the limit of crystallographically small-angle misorientations, as demonstrated by ref. 48. Other physical, spatially resolved interactions, such as hydrostatic stresses and dislocation arrays for small-angle grain boundaries are currently not included in the present formulation. \(\frac{{s}_{2}}{2}g(\eta )| \nabla \theta {| }^{2}\), which contributes to the energy penalty due to curvature48. α, s1, and s2 directly correlate to physical quantities such as equilibrium grain boundary thickness and interfacial energy, as reported by Lobkovsky and Warren,49,50. The sum of chemical, structural, and electrical contributions to the total free energy functional is defined as:

$$\begin{array}{lll}F[\eta ,\theta ,\{[{V}_{i}^{{Z}_{i}}]\},\rho ,\phi ;T]\,=\,{\int_{\Omega }}\left[f(\eta ,\{[{V}_{i}^{{Z}_{i}}]\},T)\right.\\ \qquad\qquad\qquad\qquad\qquad+\frac{{\alpha }^{2}}{2}{\left(\nabla \eta \right)}^{2}+{s}_{1}g(\eta )| \nabla \theta | +\frac{{s}_{2}}{2}g(\eta )| \nabla \theta {| }^{2}\\ \qquad\qquad\qquad\qquad\qquad\left.+\rho \phi -\frac{\epsilon }{2}{\left(\nabla \phi \right)}^{2}\right]{\rm{d}}\Omega. \end{array}$$
(3)

The general conditions of electrochemical and structural equilibrium of an ionic ceramic are defined through the variational derivatives of Eq. (3) with respect to the controlling variables, \(\{[{V}_{i}^{{Z}_{i}}]\},\eta ,\theta ,\phi\):

$$\begin{array}{lll}\frac{\delta F}{\delta \theta }\,=\,{\mu }_{\theta }=-{s}_{1}g(\eta )\nabla \cdot [\frac{\nabla \theta }{| \nabla \theta | }]-{s}_{2}g(\eta ){\nabla }^{2}\theta; \\ \frac{\delta F}{\delta \eta }\,=\,{\mu }_{\eta }=\frac{\partial f}{\partial \eta }-{\alpha }^{2}{\nabla }^{2}\eta +{s}_{1}\frac{\partial g}{\partial \eta }| \nabla \theta | +\frac{{s}_{2}}{2}\frac{\partial g}{\partial \eta }{(\nabla \theta )}^{2};\\ \frac{\delta F}{\delta [{V}_{i}^{{Z}_{i}}]}\,=\,{\mu }_{i}=\frac{\partial f}{\partial [{V}_{i}^{{Z}_{i}}]}+{Z}_{i}e\phi; \\ \frac{\delta F}{\delta \phi }\,=\,{\mu }_{\phi }=\nabla \cdot \epsilon \nabla \phi +\rho =0.\end{array}$$
(4)

In agreement with Kobayashi et al.48, and Tang et al.51, the first and second rows of Eq. (4) define the equilibrium orientation potential, μθ, and structural potential, μη, of the grain boundary. The third row of Eq. (4) represents the structural–electrochemical potential of the ith species, μi. In the absence of structural disorder in a grain boundary, the structural–electrochemical potential reduces to electrochemical potential, in agreement with several authors41,46,47, and to the chemical potential in the absence of electrical and structural interactions. In addition, local gradients in the structural–electrochemical potential drive charge and solute segregation to the interfaces. In this formulation, gradients of structural disorder, chemical potential, or electrostatic potential alike will favor microstructural evolution. Finally, the fourth row of Eq. (4) corresponds to Coulomb’s equation, in agreement with several authors41,42,43,44,46,47.

The kinetic equations for microstructural evolution obtained from the driving forces in Eq. (4) are:

$$\begin{array}{lll}\frac{\partial \theta }{\partial t}\,=\,-{M}_{\theta }{\mu }_{\theta }=-{M}_{\theta }\left[g(\eta )(-{s}_{1}\nabla \cdot \frac{\nabla \theta }{| \nabla \theta | }-{s}_{2}{\nabla }^{2}\theta )\right];\\ \frac{\partial \eta }{\partial t}\,=\,-{M}_{\eta }{\mu }_{\eta }=-{M}_{\eta }\left[\frac{\partial f}{\partial \eta }-{\alpha }^{2}{\nabla }^{2}\eta +\frac{\partial g}{\partial \eta }({s}_{1}| \nabla \theta | +\frac{{s}_{2}}{2}| \nabla \theta {| }^{2})\right];\\ \frac{\partial [{V}_{i}^{{Z}_{i}}]}{\partial t}\,=\,\nabla \cdot {M}_{i}\nabla {\mu }_{i}=\nabla \cdot {M}_{i}\nabla \left[\frac{\partial f}{\partial [{V}_{i}^{{Z}_{i}}]}+{Z}_{i}e\phi \right].\end{array}$$
(5)

Specifically, the local crystallographic orientation and the structural order parameters are non-conserved order quantities and follow Allen–Cahn kinetics48,51. The first and second rows of Eq. (5) represent the dynamics of microstructural evolution via grain boundary migration and grain rotation. The third row of Eq. (5) corresponds to the mass conservation equation of the ith component in agreement with several authors41,46.

For a flat grain boundary moving in the x direction at a constant velocity, v, Eq. (5) is rewritten as:

$$\begin{array}{lll}-v\frac{\partial \theta }{\partial x}\,=\,-{M}_{\theta }{\mu }_{\theta };\\ -v\frac{\partial \eta }{\partial x}\,=\,-{M}_{\eta }{\mu }_{\eta };\\ -v\frac{\partial [{V}_{i}^{{Z}_{i}}]}{\partial x}\,=\,\frac{\partial }{\partial x}\left[{M}_{i}\frac{\partial {\mu }_{i}}{\partial x}\right].\end{array}$$
(6)

The first and second rows of Eq. (6) predict the orientation and structural change of a moving grain boundary with constant velocity. The third row of Eq. (6) describes the composition profile of the ith ionic species in the vicinity of a moving grain boundary. Overall, the velocity of grain boundary, v, is dependent on the transport kinetic parameters of the ionic solid, i.e., the grain boundary mobility for structural order/disorder, Mη, the grain boundary mobility for crystallographic orientation, Mθ, and the chemical mobility of ith species, Mi. The velocity of the interface is given by11:

$$v={\mathcal{M}}{F}_{T}.$$
(7)

Following Cahn24, and in agreement with Eq. (3), the change in free energy as a result of grain boundary motion is expressed as:

$${d}{F}_{T}(\eta ,\theta ,\{[{V}_{i}^{{Z}_{i}}]\},\phi )={\mu }_{\eta }{d}\eta +{\mu }_{\theta }{d}\theta +\mathop{\sum }\limits_{i=1}^{N}{\mu }_{i}{d}[{V}_{i}^{{Z}_{i}}]+{\mu }_{\phi }{d}\phi.$$
(8)

By using, \({\mu }_{\eta }=\frac{v}{{M}_{\eta }}\frac{\partial \eta }{\partial x}\), \({\mu }_{\theta }=\frac{v}{{M}_{\theta }}\frac{\partial \theta }{\partial x}\) from the first and second rows of Eq. (6), and μϕ = 0 from the last row of Eq. (4), it follows:

$${d}{F}_{T}=\frac{v}{{M}_{\eta }}\frac{\partial \eta }{\partial x}d\eta +\frac{v}{{M}_{\theta }}\frac{\partial \theta }{\partial x}{d}\theta +\mathop{\sum }\limits_{i=1}^{N}{\mu }_{i}{d}[{V}_{i}^{{Z}_{i}}].$$
(9)

The total driving force for motion of a grain boundary is obtained by integrating Eq. (9):

$${F}_{T}={\int\nolimits_{-\infty }^{\infty }}\frac{v}{{M}_{\eta }}{\left(\frac{\partial \eta }{\partial x}\right)}^{2}{d}x+{\int\nolimits_{-\infty }^{\infty }}\frac{v}{{M}_{\theta }}{\left(\frac{\partial \theta }{\partial x}\right)}^{2}{d}x+{\int\nolimits_{-\infty }^{\infty }}\mathop{\sum }\limits_{i=1}^{N}{\mu }_{i}\frac{\partial [{V}_{i}^{{Z}_{i}}]}{\partial x}{d}x.$$
(10)

The first and second terms on the right hand side of Eq. (10) contributes to the intrinsic drag on a grain boundary due to grain boundary migration and rotation. Here the intrinsic grain boundary mobility, \({\mathcal{M}}\), is identified as:

$$\frac{1}{{\mathcal{M}}}={\int\nolimits_{-\infty }^{\infty }}\left[\frac{1}{{M}_{\eta }}{\left(\frac{\partial \eta }{\partial x}\right)}^{2}+\frac{1}{{M}_{\theta }}{\left(\frac{\partial \theta }{\partial x}\right)}^{2}\right]{d}x,$$
(11)

in agreement with Lobkovsky and Warren50. The third term on the right-hand side of Eq. (10) corresponds to the electrochemical drag force, \({F}_{{ecd}}={\int\nolimits_{-\infty }^{\infty }}\mathop{\sum }\nolimits_{i=1}^{N}{\mu }_{i}\frac{\partial [{V}_{i}^{{Z}_{i}}]}{\partial x}{d}x\), due to N species on a grain boundary. Integration by parts leads to \({\int\nolimits_{-\infty }^{\infty }}\mathop{\sum }\nolimits_{i=1}^{N}{\mu }_{i}\frac{\partial [{V}_{i}^{{Z}_{i}}]}{\partial x}{d}x=\mathop{\sum }\nolimits_{i=1}^{N}{\mu }_{i}[{V}_{i}^{{Z}_{i}}]{| }_{-\infty }^{\infty }-\mathop{\sum }\nolimits_{i=1}^{N}{\int\nolimits_{-\infty }^{\infty }}([{V}_{i}^{{Z}_{i}}]-{[{V}_{i}^{{Z}_{i}}]}_{\infty })\frac{\partial {\mu }_{i}}{\partial x}{d}x\), where \(\mathop{\sum }\nolimits_{i=1}^{N}{\mu }_{i}[{V}_{i}^{{Z}_{i}}]{\left|\right.}_{-\infty }^{\infty }=0\). Substituting Eq. (4) results in the expression:

$${F}_{{ecd}}=-\mathop{\sum }\limits_{i=1}^{N}{\int\nolimits_{-\infty }^{\infty }}\frac{1}{\omega }([{V}_{i}^{{Z}_{i}}]-{[{V}_{i}^{{Z}_{i}}]}_{\infty })\left[\Delta {f}_{i}^{S\to X}{p}^{\prime}(\eta )\frac{\partial \eta }{\partial x}+{Z}_{i}e\frac{\partial \phi }{\partial x}+\mathop{\sum }\limits_{j=1,i\ne j}^{N}{\Omega }_{ij}\frac{\partial [{V}_{j}^{{Z}_{j}}]}{\partial x}\right]{\rm{d}}x.$$
(12)

Equation (12) shows that local gradients of structural disorder, electrostatic potential, and chemical wind exert a force on the moving grain boundary, which can suppress (or enhance) grain boundary migration or grain rotation. The current formulation reduces to Cahn’s description in the binary dilute limit, in the absence of electrostatic potential gradients and chemical wind24. In the absence of grain rotation and electrical contributions, Eq. (10) reduces to existing drag models for metallic systems27,28,29.

Application to Fe-doped SrTiO3

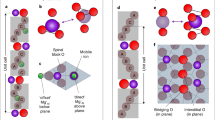
Equations (2)–(12) were applied to describe the grain boundary motion of Fe-doped SrTiO3 under an isobaric or constant stress of 1 atm. The annealing temperature was set to 1350 °C, to relax any possible local chemical or thermal stress localization in the system. Two defects, oxygen vacancies, \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\), and iron defects, \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\), are considered. At equilibrium, results demonstrate that the amount of Fe that segregates at grain boundaries is dependent on the crystallographic grain boundary misorientation. The equilibrium spatial distribution of Fe and point defects in the neighborhood of a grain boundary of SrTiO3, for a small misorientation, Δθ = 10°, is summarized in Fig. 1a. Here the atomically sharp interface is a Debye-type (D) layer and has a thickness of δ ~ 0.8 nm. The interface is rich in oxygen vacancies and iron defects that formed a depletion space charge layer of ~1.5-nm thick, adjacent to the grain boundary.

Fig. 1: Equilibrium defect distribution in the vicinity of a flat grain boundary.
figure 1

For 2 at% Fe-doped SrTiO3 for selected misorientations: Δθ = 10° (a), Δθ = 20° (b), and Δθ = 30° (c), the grain boundary is located at x = 0. The grain boundary core, highlighted by two dashed lines, is positively charged as a result of \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) being chemically attracted to the interface, depleting the point defects in the vicinity of the surrounding grains. As a result, a positive electrostatic interfacial potential develops at the grain boundary, which in turn attracts \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) due to its opposite charge polarity. A depletion zone of \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) develops in the vicinity of the grain boundary.

Full size image

For intermediate angle grain boundary misorientations, e.g., Δθ = 20° (see Fig. 1b), the degree of crystallinity decreases with the crystallographic misorientation, forming a thick interface allowing more oxygen vacancies to segregate at the core. The core, which is rich in oxygen vacancies, forms an electrostatically positive interface that further extends the space charge depletion layers of \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) and \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) in front of the homointerface. The thick, structurally disordered grain boundary core is of a Mott–Schottky-type interface52,53, (MS), and is surrounded by two wide diffuse charge layers43.

For large-angle grain boundaries, e.g., Δθ = 30°, the equilibrium thickness of the interface increases to δ ~ 2.1nm, further allowing more \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) in the grain boundary core and extending the \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) depletion zone thickness to ~7 nm, in front of the grain boundary (see Fig. 1c). The increase in amount of Fe segregation at the grain boundary creates a large depletion zone in the immediate neighborhood of the interface.

The corresponding effect of misorientation on the spatial distribution of charge density in the vicinity of the grain boundary is shown in Fig. 2a. The grain boundary core charge density increases by a factor of five as the misorientation increases from 10° to 30°, in agreement with reports in the scientific literature on low angle grain boundaries of ionic ceramic systems54,55,56. This increases the equilibrium structural thickness of the grain boundary from ~0.8 to ~2.1 nm, which further extends the space charge region in front of the grain boundary from ~1.5 to ~7 nm. Here the grain boundary space charge is negative (n) while the grain boundary core charge is positive (p), defining an n–p–n-type charge distribution, reminiscent of the space charge in a bipolar transistor57. Fig. 2b shows that the interfacial electrostatic potential increases from 0.035 to 0.26 V with misorientation as a result of an excess amount of oxygen vacancies chemically attracted to the interface. The increase in interfacial voltage extends the space charge layers, from ~1.5 to ~7 nm to minimize the total free energy of the system consisting of structural, chemical, and electrical free energy densities.

Fig. 2: Equilibrium electrical state of a flat grain boundary.
figure 2

The charge density (a) and electrostatic potential (b) distribution in the vicinity of the grain boundary for 2 at% Fe-doped SrTiO3, for selected misorientations in gray: Δθ = 10° (darkest), Δθ = 20°, and Δθ = 30° (lightest). The grain boundary core is positively charged as a result of excess \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) being chemically attracted to the interface, surrounded by a negative space charge layer. The increase in the positive core charge with misorientation increases the interfacial electrostatic potential, which, in turn, extends the electrostatic potential gradients in front of the grain boundary.

Full size image

For small deviations away from equilibrium, Fig. 3 summarizes the effect of grain boundary velocity on the spatial distribution of point defects, charge density, and electrostatic potential in the vicinity of a flat grain boundary for a misorientation of Δθ = 30°. Here, the degree of disorder and the grain boundary structural thickness is insensitive to the velocity of the interface. For small grain boundary velocities, e.g., v = 0.1 nm/s (see Fig. 3a), \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) and \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) in the grain boundary core slightly decreases from the equilibrium concentration. Also, the depletion zone of \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) in front of the grain boundary is smaller than that in the back of the grain boundary, resulting in an asymmetric \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) profile. The \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) depletion zone in front of the grain boundary slightly decreases, as compared to behind the grain boundary, due to its high diffusivity value. The corresponding charge density distribution (see Fig. 3b) demonstrates that the grain boundary core is positively charged due to a \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) excess. Also, the depth of the negatively charged layer in front of the grain boundary is higher than the back of the grain boundary due to an asymmetric \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) distribution. Here, the positively charged grain boundary core induces a positive interfacial electrostatic potential, see Fig. 3c. Additionally, the asymmetric charge density profile in the vicinity of the grain boundary induces a slightly positive potential in the left side crystal, compared to the right side crystal.

Fig. 3: Electrochemical state of a moving grain boundary.
figure 3

Defect distribution, charge density, and electrostatic potential in the vicinity of a moving grain boundary of misorientation, Δθ = 30°, for a 2 at% Fe-doped SrTiO3. The grain boundary velocities, a–c 0.1, d–f 1, g–i 50, and j–l 100 nm/s are shown.

Full size image

For an intermediate grain boundary velocity, e.g., v = 1 nm/s (see Fig. 3d), the slow Fe defects cannot keep up with the moving interface resulting in a drastic decrease of \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) in the grain boundary core, followed by the appearance of a small depletion zone thickness of \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) in the back of the grain boundary. The drastic decrease in \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) in the grain boundary core increases the grain boundary core charge density (see Fig. 3e) and the interfacial electrostatic potential (see Fig. 3f). Also, a potential difference of 0.11 V is generated between left and right side crystals.

For a large grain boundary velocity, e.g., v = 50 nm/s (see Fig. 3g), neither the Fe defects nor the oxygen vacancies can keep up with the moving boundary, resulting in a charge distribution that is reminiscent of a p–n junction57. Similarly, the grain boundary core charge density (see Fig. 3h) and the interfacial electrostatic potential (see Fig. 3i) decrease due to a decrease in oxygen vacancies. The moving interface creates a potential difference of 0.2 V between left and right side crystals and the electrostatic potential gradient extends ~50 nm in front of the moving boundary. At a grain boundary velocity of v = 100 nm/s (see Fig. 3j), there is no segregation of oxygen vacancies at the grain boundary core, displaying no charge (see Fig. 3k) and zero Schottky potential (see Fig. 3l).

The effect of misorientation on the grain boundary velocity as a function of driving force for a 2 at% Fe-doped SrTiO3 is shown in Fig. 4. Results demonstrate that, with the increase in misorientation, the grain boundary velocity decreases. At large driving forces, grain boundary core segregation and space charge layers adjacent to the grain boundary are negligible, thus the velocity of the interface increases linearly with the driving force. Here, the intrinsic mobility of grain boundaries decreases with structural disorder and misorientation, which facilitates small-angle grain boundaries to move faster than large-angle grain boundaries.

Fig. 4: Grain boundary velocity as a function of driving force.
figure 4

The shade of gray changes from dark to light with misorientation, Δθ = 10° (darkest), Δθ = 15°, Δθ = 20°, Δθ = 30°, and Δθ = 40° (lightest) for a 2 at% Fe-doped SrTiO3.

Full size image

The increase in misorientation increases the structural disorder of the grain boundary, which in turn induces enhanced grain boundary core segregation and thick depletion space charge layers. The resultant structural, chemical, and electrostatic interfacial potential leads to a stronger drag force that reduces the velocity of the interface for any given driving force. The critical driving force for a grain boundary to break away from its space charge increases from 107 to 7 × 108 N/m2 when the misorientation increases from Δθ = 10° to 40°. The corresponding critical velocity of the interface is 0.45 nm/s and is insensitive to crystallographic misorientation. For driving forces >7 × 108 N/m2, grain boundary motion is insensitive to misorientation.

The effect of Fe dopant on the grain boundary velocity as a function of driving force is shown in Fig. 5. Results demonstrate that, when the added Fe increases from 0.2 to 5 at% in SrTiO3, the velocity of grain boundary decreases for any given driving force, in agreement with experimental results12,37,58,59,60. For small-angle misorientations, e.g., Δθ = 10° (see Fig. 5a), it was observed that the critical driving force for a grain boundary to break away from its space charge increases from 2 × 106 to 1.2 × 107 N/m2, and the corresponding critical velocity of the interface increases from 0.31 to 0.58 nm/s. For driving forces greater than 1.2 × 107 N/m2, Fe does not impose any drag force on grain boundary motion. For large-angle grain boundaries, e.g., Δθ = 30° (see Fig. 5b), an increase in Fe from 0.2 to 5 at% impedes the grain boundary motion by exerting large drag forces and shifts the critical driving force for grain boundary motion from 0.9 × 108 to 4 × 108 N/m2. The corresponding critical velocity of the interface increases from 0.39 to 0.84 nm/s. Overall, results demonstrate that the critical driving force for a grain boundary to break away from its space charge increases due to large local structural disorder, chemical, and electrostatic potential.

Fig. 5: Effect of Fe substitution on grain boundary velocity as a function of driving force.
figure 5

For a specific misorientations of Δθ = 10° (a) and Δθ = 30° (b), the shade of gray changes from dark to light with Fe concentration, 0.2 at% (darkest), 2 at%, and 5 at% (lightest).

Full size image

Discussion

A continuum thermodynamic framework was developed to investigate the structural and electrochemical character of moving grain boundaries in ionic solids. Chemical segregation and space charge was demonstrated to contribute to the drag forces opposing grain boundary motion. The study on grain boundary motion of Fe-doped SrTiO3 performed herein demonstrates that: (1) at low velocities or small driving forces, the defect profiles of \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) and \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) defects are symmetrically distributed about the structural grain boundary core; (2) at intermediate velocities, a larger number of oxygen vacancies accumulate on one side of the grain boundary and the iron defects are unable to keep up, enabling the interface to completely break away from the localized space charge; and (3) above the critical driving force or high velocities, the grain boundaries have no effective charge and exhibit zero Schottky potential. Small-angle misorientations induce thin, structurally ordered grain boundaries and experience a low electrochemical drag force due to negligible space charge, while large-angle misorientations favor structurally thick, disordered interfaces with large grain boundary core segregation followed by a broad space charge layer. These interfaces experience a large electrochemical drag force. Overall, for the generality of ionic solids, the developed theory provides the ideal basis to control the microstructure and material properties for a wide variety of applications, multiphysical properties, as well as existing and emerging processing techniques.

Methods

The effects of misorientation, solute, and point defects on the motion of an isolated grain boundary were modeled by solving Eqs. (1)–(12) and placing the interface at the origin of the laboratory reference frame and the normal in x-axis direction. The initial \([{\,\text{V}}_{\text{O}\,}^{\cdot \cdot }]\) and \([{\,\text{Fe}}_{\text{Ti}\,}^{\prime}]\) were set to its experimental equilibrium values based on Fe dopant concentration in SrTiO3. See Fe-doped SrTiO3 properties in Supplementary Table 1. Electrically, the right edge of the simulation domain was grounded and a no-polarization boundary condition was set on the left edge. A no-flux boundary condition was set on all the edges for solute and other point defect concentration, structural, and orientation order parameters. Equation set (6), Eq. (9), and Coulomb’s equation were solved across a 1-μm simulation domain and discretized into a 1000-elements mesh. Simulations were carried out on a 2.6-GHz, 16-core, Ubuntu 16.04 workstation with 128 GB of RAM. The relative tolerance for convergence was set to 1 × 10−8. Each one-dimensional calculation took on the order of 1 h of wall time to complete.