Abstract
Two-dimensional (2D) crystals are attracting growing interest in various research fields such as engineering, physics, chemistry, pharmacy, and biology owing to their low dimensionality and dramatic change of properties compared to the bulk counter parts. Among the various techniques used to manufacture 2D crystals, mechanical exfoliation has been essential to practical applications and fundamental research. However, mechanically exfoliated crystals on substrates contain relatively thick flakes that must be found and removed manually, limiting high-throughput manufacturing of atomic 2D crystals and van der Waals heterostructures. Here, we present a deep-learning-based method to segment and identify the thickness of atomic layer flakes from optical microscopy images. Through carefully designing a neural network based on U-Net, we found that our neural network based on U-net trained only with the data based on realistically small number of images successfully distinguish monolayer and bilayer MoS2 and graphene with a success rate of 70–80%, which is a practical value in the first screening process for choosing monolayer and bilayer flakes of all flakes on substrates without human eye. The remarkable results highlight the possibility that a large fraction of manual laboratory work can be replaced by AI-based systems, boosting productivity.
Similar content being viewed by others
Introduction
Two-dimensional (2D) crystals,1 such as graphene, transition metal dichalcogenides, and van der Waals heterostructures2 have been intensively studied in a wide range of research fields since they show significant properties that has not been observed in their bulk counter parts. Examples include materials engineering, such as electronics and optoelectronics devices,3,4,5,6,7 solid state physics including superconductors8 and magnets,9,10 chemistry,11,12 and biomedical applications.13 To manufacture such 2D crystals with atomic layer thickness, especially monolayer or a few-layers samples, mechanical exfoliation, chemical exfoliation, chemical vapor deposition and molecular beam epitaxy have been introduced.11 Among them, mechanical exfoliation has been instrumental to 2D materials research because it enables us to obtain highly crystalline and atomically-thin 2D layers as is exemplified by ultraclean and high-mobility devices based on exfoliated 2D materials combined with the encapsulation by h-BN. Recently, high-throughput identification of various unexplored 2D materials via machine learning and the development of a machine for mechanically exfoliated 2D atomic crystals to autonomously build van der Waals superlattices14 have been reported. These advancements are suggestive of a new research direction for 2D materials that is aimed to explore efficiently enormous materials’ properties in large scale using robotics and machine learning. In such a situation, a rapid and versatile method for layer number identification of mechanically exfoliated atomic-layer crystals on substrates is highly desirable in their fundamental research and practical applications.
However, the bottleneck of using mechanical exfoliation is that, through the process, not only do we produce desirable atomic layers (mostly monolayer or bilayer) but also many impractical thicker flakes making it tough to quickly separate the useful layers from the unwanted. To identify the thickness of 2D crystals, several methods such as atomic force microscopy (AFM),15 Raman spectroscopy,16,17 and optical microscopy (OM)18,19 are used. AFM is one of the most versatile methods to measure the thickness of various 2D materials, but it takes a relatively long time to measure one region. In addition, the measured value strongly depends on the offset conditions15 due to, for example, bubbles beneath the sample. OM is nowadays a widely utilized technique to measure the thickness of 2D crystals based on the optical contrast between atomic layers and the substrate.20 In fact, we can determine the thickness of 2D atomic layers using the contrast difference between the flakes and substrate obtained from the brightness profile of color or grayscale images.18 The methods explained above, however, need manual work and take a relatively long time to identify atomic-layer thickness, and are therefore inappropriate for studying various kinds of materials.
Recently emerged deep learning, a machine-learning technique via deep-neural networks, has shown immense potential for regression and classification tasks in a variety of research fields.20,21,22,23,24,25 In particular, deep-neural networks have been very successful in image recognition tasks such as distinguishing images of cats and dogs with high accuracy, and also several physical problems in theoretical physics, for example, detection of phase transitions26,27 and searching for exotic particles in high-energy physics.28 Given this, deep-neural networks provide an alternative pathway to quickly identifying layer thicknesses of 2D crystals from OM images.
Results
Here, we introduce a versatile technique to autonomously segment and identify the thickness of 2D crystals via a deep-neural network. Using a deep-neural network architecture, we reproduced the images of 2D crystals from the augmented data based on 24 and 30 OM images of MoS2 and graphene, respectively, used as training data and found that both the cross-validation score and accuracy rate for the test images through deep-neural networks is surprisingly around 70–80%, which means that our model can distinguish monolayer and bilayer with a practical success rate for initial screening process. The present results suggest the deep-neural network can become another promising way to quickly identify the thickness of various 2D crystals in an autonomous way, suggesting a large fraction of manual laboratory work can be dramatic decreased by replacing AI-based systems.
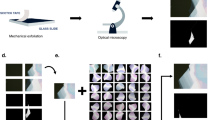
Figure 1 shows an overview of data collection using the OM and the training architecture of the deep-neural network. First, we prepared the OM images of thin flakes. Bulk single crystals of MoS2 crystals and graphite were employed for the preparation of mechanically exfoliated 2D atomic layers, which were then transferred onto the 300-nm-thick SiO2/Si substrates in the air. The bright-field OM (BX 51, Olympus) was used to locate and take pictures (optical microscope images) of the thin flakes on the Si/SiO2 substrate with one-hundred magnification. Each OM image includes different number of flakes with various thicknesses under the different light intensity conditions, we then confirmed the thickness and layer number of each samples using AFM and contrast based on OM images, which were randomly divided into the training data set (24 images for MoS2 and 30 images for graphite) and test images (11 images for MoS2 and 14 images for graphene), the latter of which were prepared to compare prediction with a non-expert human as discussed below, by dividing into three regions of monolayer (blue), bilayer (green), and others (black). It is noted that as we mention below, we used 960 images which are augmented from 24 images as a training data set of MoS2, for example.
First, we mechanically exfoliate MoS2 crystals on a SiO2/Si substrate and take images using optical microscope. After recording data, we train deep-neural networks to generate images from optical microscope images using segmented images. Here, our targets are monolayer and bilayer crystals. For training, we prepared segmented data, which is divided into monolayer (blue), bilayer (green) and other parts (black).
In the present study, we used the augmented data based on 24 original OM images and corresponding segmentation maps to train the network and use 11 images to evaluate the performance for MoS2 classification (See Supplementary Information Section III for details of results of graphene/graphite) via the deep-neural network architectures, U-Net, which is based on the fully convolutional encoder–decoder network29 (see Methods for the construction). Here, we particularly choose the classification of MoS2 and graphene monolayer and bilayer because the number of training data set is limited to expand the classifications to thicker multilayer. We employed the data argumentation technique, which is one of learning techniques widely used for deep-neural networks to improve learning accuracy and prevent overfitting.20,30,31,32,33 By augmentation with randomly cropping, flipping, rotating and changing the color of the original images,34 we increased the training data up to 960 data points. The rotation range was a value in degree (−90 to 90). We randomly shifted a value of Hue (within ±10) on the converted image in the HSV (Hue, Saturation, Value) color mode, and randomly normalized contrast by a factor of 0.7 to 1.3. Indeed, this kind of random manipulation and augmentation of the original data is useful for averaging the difference of contrast and number of flakes in each original image. For the color changing augmentation, we converted images to grayscale or adjusted the contrast of the image. With this augmentation, we increased the data to 960 points. Finally, we normalized all pixels between 0 and 1 as preprocessing before training. We then used cross entropy as a loss function of the multi-class classification and also used a weighted cross entropy in order to balance the frequency of each class. The normal cross entropy E is computed as
Here, xi is the output of the softmax activation of the U-Net at pixel i, yi, and yik are the one hot vector of the label at pixel i and k-th element (scalar quantity) of yi, respectively, such that only the element at the position of the true label is 1 and the others are 0, K is the number of labels, and N is the number of pixels in the image. Similarly, weighted cross entropy Ew is computed as
where wk is the weight of the class k. To compute the weight wk, we use median frequency balancing,35 where the weight assigned to a class is the ratio of the median of class frequencies computed on the entire training set divided by the class frequency. This implies that smaller classes in the training data get heavier weights. In the training, we employed mini-batch Adam,36 a variant of mini-batch SGD37,38 solver. We performed hyperparameter selection based on threefold cross-validation within the following ranges: learning rate of Adam in 10−5, 10−4, and 10−3, batch size in 1, 5, 10, 50, and 100, and epoch number in 10, 30, 50, 100, and 500, respectively.
Figure 2 shows four examples of the original OM images, the segmented images and generated images using U-Net with weighted loss. The blue, green, and black regimes show monolayer, bilayer, and other parts, including thicker flakes and substrate, respectively. It seems that the training neural network can pick up the information of color contrast (against background color of substrate), as well as the edge thickness/sharpness, which is indeed useful information for the real-screening process. We calculated receiver operating characteristic (ROC) and precision-recall (precision-true-positive rate) curves of two-class classifications for the monolayer/others (blue) and bilayer/others (red) identification and confirmed the learning performance in Fig. 3a, b. The ROC curve shows sharply below the false-positive rate of 0.1 and then saturates to 1.0 and precision-recall curve show the high-precision value (>90%) below recalls of 0.76 and 0.94 for monolayer and bilayer, respectively, both of which show the high performance of the U-Net with weighted loss.
a ROC curve for the monolayer and bilayer identification. Blue and red curve show the ROC for two-class classifications of monolayer/others and bilayer/others, respectively. This ROC curve shows the high performance of the U-Net with weighted loss because the ROC curve rises sharply below the false-positive rate of 0.1 and then saturates to 1.0. b Precision-recall (true-positive rate) curves for the monolayer and bilayer identification.
To perform further evaluations, we investigated and compared the difference of the cross-validation score and accuracy rate for the test images by changing the learning process using the grayscale images and/or contrast adjusted images. To evaluate the performance of the trained U-Net, we used both cross-validation score and an accuracy score on the test images. In the cross-validation, we performed threefold cross-validation, in which a mean of the pixel-wise accuracy in each class was used as an evaluation metric. We also calculated mean of pixel-wise precision in each class (macro-average precision) as an evaluation metric in the cross-validation. On the other hand, in the test images, we prepared the test images, each of which has problem region to be answered. To check whether the U-Net can predict the test image correctly or not, we predict the class of each pixel of the image by using U-Net and define the class whose pixel is most in the problem region as the predicted class of that region, then compare it with the true class.
Discussion
We summarize the cross-validation scores for each learning process in Table 1. The U-Net with weighted loss using contrast adjusted augmentation shows the highest score of all, 0.789, which is much higher than that of a normal U-Net without any options. The value of 0.789 is surprisingly high, considering that while a deep-neural network needs thousand or even more training points, our case used the data based on 24 training data points for MoS2. We also listed the macro-average precisions by the U-Net approaches in Supplementary Table S2. This remarkable result allows us to generate a practical number of training sets, which can initially be prepared by lab works using OM. This result also suggests that once we prepare training data sets and perform leaning for a 2D material, we can obtain a tool that can quickly identify atomic-layer thickness, monolayer/bilayer/other thicker parts, with an accuracy rate of almost 80%, which is practically value that can be helpful for the initial screening process. We also performed the classification of monolayer/bilayer/other thicker parts of graphene/graphite (See Supplementary Information Section III) and got similar accuracy rate, which suggests the present network is highly transferable. It is noted that the U-net have a tendency that it can mistakenly recognize the background (wafer) as a monolayer flake. This might be because the number of the training data is limited and the network learn all the features in the entire images. The problem above might be negligible if the number of training data increases and thus the network can distinguish the background color and monolayer/bilayer flakes.
More importantly, in practice, it is not necessary to check and distinguish of all monolayer or bilayer candidates on the substrate, but just needed to pick up some amount of monolayer or bilayer with a high accuracy. According to the precision-recall curve in Fig. 2d, at miss rates of 24% and 6.0% (1-true-positive rate), which means that the U-net miss the flakes with a target layer number (monolayer or bilayer), it can distinguish monolayer and bilayer with an accuracy of 90%. This value is practically high for the real experiments. These high success rates of the identifications mean that the present technique based on the U-net potentially can apply other 2D materials on various wafers because it is very rigid against external conditions (e.g., the number of flakes surrounding the target flakes and the light intensity of optical microscope.), and can detect sensitively the color contrast of the surface against background color and edge thickness from the optical microscope images.
We compared the identification performance of the U-net with traditional CV approaches based on a bag-of-visual-words (BoVW)39 technique using a hand-crafted image descriptor and based on convolutional neural networks (CNNs)21 named as pixel-wise CNN (see Supplementary Information Section V for details). We show prediction examples by pixel-wise CNN in Fig. 2m–p. From Fig. 2, pixel-wise CNN failed to predict layers as a whole compared to U-net based predictions (i–l). The contours of flakes in (a–d) and ones of the predicted layers in (m–p) did not match precisely, because pixel-wise CNN predicted the layer independently for each pixel. On the other hand, U-net achieved highly accurate prediction reflecting flake shapes due to its network architecture using skip connections and upsamplings. We also summarize the cross-validation scores for these traditional approaches in Supplementary Table 3. From these results in Supplementary Table 3 and Fig. 2, it was confirmed that the U-net base approach achieves higher accuracy compared to the traditional CV approaches. Finally, to compare the accuracy rate between U-Net and non-expert humans, we calculated the accuracy rate using 11 randomly selected test images of MoS2 flakes (see Supplementary Information Section I). We found that the accuracy score of U-Net with weighted loss model is 0.733 in all cases, which is higher than the that of a normal U-Net model. Such a tendency is observed in cross-validation score, which indicates that the U-Net with weighted loss is better than the normal U-Net for both segmentation and layer number identification tasks. We then compared the accuracy score with that of twelve researchers who were not familiar with 2D materials (non-expert human). The researchers were given three minutes to learn the training data set (see Supplementary Information Section I for details) and were then asked to respond with the layer numbers (mono- and bilayer) for each segment of new images, which were the same as the test images used in determining the accuracy score for the deep-neural network. The accuracy score for humans was 0.67 ± 0.11, which was comparable value to that of a U-Net with weighted loss. The present results suggest that the deep-neural network based on U-Net with weighted loss is a new tool to rapidly and autonomously segment and identify number of layers of 2D crystals with an accuracy rate comparable to non-expert humans, indicating it can be an essential tool to significantly decrease manual work in the laboratory by boosting the first screening process, which has been usually done by human eyes.
In conclusion, we introduce a versatile technique to autonomously segment and identify the thickness of 2D crystals via a deep-neural network. Constructing an architecture consisting of convolutions, U-Net, we reproduced the images of 2D crystals from the less than 24 and 30 OM images of MoS2 and graphene, respectively, and found that both the cross-validation score and the accuracy rate of generated data through U-Net is around 70–80 percent, which is comparable with non-expert human level. This means that our neural network can distinguish monolayer, bilayer and other thicker flakes of MoS2 and graphene on Si/SiO2 substrates with the practical accuracy in the first screening process for searching desirable before further transport/optical experiments. The present study highlights that deep-neural networks have great potential to become a new tool for quickly and autonomously segmenting and identifying atomic-layer thickness of various 2D crystals and opening a new way for AI-based quick exploration for manufacturing 2D materials and van der Waals heterostructures in large scale.
Methods
Construction of the convolutional encoder–decoder network
The encoder that we used for the fully convolutional encoder–decoder network extracts the small feature map from the input image by convolution and pooling layers, and decoder expands it to the original image size by convolution and upsampling layers. Figure 4 shows an overview of our network. The encoder and decoder are composed of 14 and 18 layers, respectively. The encoder consists of four repeated layers set which consist of 3 × 3 convolutions, each followed by a rectified linear unit (ReLU) activation and 2 × 2 max pooling with stride 2 for downsampling. At each downsampling step, the number of the feature map is doubled. The decoder consists of four repeated layers set which consist of 2 × 2 upsampling convolution and 3 × 3 convolution followed by ReLU. We added 50% dropout layers after each of the first three upsampling convolution layers. At the final layer of the decoder, a 1 × 1 convolution converts the feature map to the desired number of classes and softmax activation is then applied. To transmit high-resolution information in the input images, the network has skip connections between each convolutional layer of the encoder and the corresponding upsampling layer of the decoder. Each skip connection simply concatenates all channels at the layer of the encoder with one of the decoders. The dimension, width × height × channels, of the input image is 512 × 512 × 3 and it changes to 256 × 256 × 64, 128 × 128 × 128, 64 × 64 × 256, 32 × 32 × 512, and 16 × 16 × 1024 at each downsampling step in the encoder, respectively, and changes in reverse order through the upsampling steps in the decoder.
The encoder of U-Net extracts the small feature map from the input image by convolution and pooling layers, and decoder expands it to the original image size by convolution and upsampling layers. Skip connections are added between each layer of the encoder and the corresponding layer of the decoder in order to transmit a high-resolution information to the decoder. In the architecture, the encoder and decoder are composed of 14 and 18 layers, respectively. The dimension, width × height × channels, of the input image is 512 × 512 × 3 and it changes to 256 × 256 × 64, 128 × 128 × 128, 64 × 64 × 256, 32 × 32 × 512, and 16 × 16 × 1024 at each downsampling step in the encoder, respectively, and changes in reverse order through the upsampling steps in the decoder.
Data availability
The data used to train and test the models is available along with the source code at https://github.com/xinkent/mos2_segmentation
Code availability
Our code is available at https://github.com/xinkent/mos2_segmentation
References
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. U. S. A. 102, 10451–10453 (2005).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Castro Neto, A. H. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Xia, F., Wang, H., Xiao, D., Dubey, M. & Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photonics 8, 899–907 (2014).
Jariwala, D., Sangwan, V. & Lauhon, L. Emerging device applications for semiconducting two-dimensional transition metal dichalcogenides. ACS Nano 8, 1102–1120 (2014).
Fiori, G. et al. Electronics based on two-dimensional materials. Nat. Nanotechnol. 9, 768–779 (2014).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216–226 (2016).
Saito, Y., Nojima, T. & Iwasa, Y. Highly crystalline 2D superconductors. Nat. Rev. Mater. 2, 16094 (2016).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013).
Wang, H., Yuan, H., Sae Hong, S., Li, Y. & Cui, Y. Physical and chemical tuning of two-dimensional transition metal dichalcogenides. Chem. Soc. Rev. 44, 2664–2680 (2015).
Chimene, D., Alge, D. L. & Gaharwar, A. K. Two-dimensional nanomaterials for biomedical applications: emerging trends and future prospects. Adv. Mater. 27, 7261–7284 (2015).
Masubuchi, S. et al. Autonomous robotic searching and assembly of two-dimensional crystals to build van der Waals superlattices. Nat. Commun. 9, 1413 (2018).
Ni, Z. H. et al. Graphene thickness determination using reflection and contrast spectroscopy. Nano Lett. 7, 2758–2763 (2007).
Lee, C. et al. Anomalous lattice vibrations of single-and few-layer MoS2. ACS Nano 4, 2695–2700 (2010).
Li, H. et al. Optical identification of single- and few-layer MoS2 sheets. Small 8, 682–686 (2012).
Li, H. et al. Rapid and reliable thickness identifi cation of two-dimensional nanosheets using optical microscopy. ACS Nano 7, 10344–10353 (2013).
Li, Y. et al. Optical identification of layered MoS2via the characteristic matrix method. Nanoscale 8, 1210–1215 (2016).
Krizhevsky, A. & Hinton, G. E. Imagenet classification with deep convolutional neural networks. Proc. Adv. Neural Inf. Process. Syst. 25, 1097–1105 (2012).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Silver, D. et al. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484–489 (2016).
Fauw, J. De et al. Clinically applicable deep learning for diagnosis and referral in retinal disease. Nat. Med. 24, 1342–1350 (2018).
Poplin, R. et al. Prediction of cardiovascular risk factors from retinal fundus photographs via deep learning. Nat. Biomed. Eng. 2, 158–164 (2018).
Ryan, K., Lengyel, J. & Shatruk, M. Crystal structure prediction via deep learning. J. Am. Chem. Soc. 140, 10158–10168 (2018).
Van Nieuwenburg, E. P. L., Liu, Y. H. & Huber, S. D. Learning phase transitions by confusion. Nat. Phys. 13, 435–439 (2017).
Carrasquilla, J. & Melko, R. G. Machine learning phases of matter. Nat. Phys. 13, 431–434 (2017).
Baldi, P., Sadowski, P. & Whiteson, D. Searching for exotic particles in high-energy physics with deep learning. Nat. Commun. 5, 4308 (2014).
Ronneberger, O., Fischer, P. & Brox, T. U-Net: convolutional networks for biomedical image segmentation. Springer International Publishing, In Proc. International Conference on Medical Image Computing and Computer Assisted Intervention. 234–241 (2015).
Szegedy, C. et al. Going deeper with convolutions. IEEE Computer Society, In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition. 1–9 (2015).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. IEEE Computer Society, In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition. 770–778 (2016).
Kim, E., Huang, K., Jegelka, S. & Olivetti, E. Virtual screening of inorganic materials synthesis parameters with deep learning. NPJ Comput. Mater. 3, 53 (2017).
Perol, T., Gharbi, M. & Denolle, M. Convolutional neural network for earthquake detection and location. Sci. Adv. 4, e1700578 (2018).
Dosovitskiy, A., Fischer, P., Springenberg, J. T., Riedmiller, M. & Brox, T. Discriminative unsupervised feature learning with exemplar convolutional neural networks. IEEE Trans. Pattern. Anal. Mach. Intell. 1734–1747 (2016).
Eigen, D. & Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proc. IEEE International Conference on Computer Vision. 2650–2658 (2015).
Kingma, D. P. & Ba, J. L. ADAM: a method for stochastic optimization. In Proc. International Conference on Learning Representations. arXiv preprint arXiv:1412.6980 (2015).
Dekel, O. & Xiao, L. Optimal distributed online prediction using mini-batches. J. Mach. Learn. Res. 13, 165–202 (2012).
Li, M., Zhang, T., Chen, Y. & Smola, A. J. Efficient mini-batch training for stochastic optimization. ACM, In Proc. 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 661–670 (2014).
Csurka, G. et al. Visual categorization with bags of keypoints. ACM, In Proc. Workshop on Statistical Learning in Computer Vision, European Conference on Computer Vision. 1–22 (2004).
Acknowledgements
This work was supported by the “Materials research by Information Integration” Initiative (MI2I) project and Core Research for Evolutional Science and Technology (CREST) (JSPS KAKENHI Grant Numbers JPMJCR1502 and JPMJCR17J2) from Japan Science and Technology Agency (JST). It was also supported by Grant-in-Aid for Scientific Research on Innovative Areas “Nano Informatics” (JSPS KAKENHI Grant Number JP25106005) and Grant-in-Aid for Specially Promoted Research (JSPS KAKENHI Grant Number JP25000003) from JSPS. M.O. and Y.M.I. were supported by Advanced Leading Graduate Course for Photon Science (ALPS). Y.S. was supported by Elings Prize Fellowship. Y.N. was supported by Materials Education program for the future leaders in Research, Industry, and Technology (MERIT). M.O. and Y.N. were supported by the Japan Society for the Promotion of Science (JSPS) through a research fellowship for young scientists (Grant-in-Aid for JSPS Research Fellow, JSPS KAKENHI Grant Numbers JP17J09152 and JP17J08941, respectively). M.Y. was supported by JST PRESTO (Precursory Research for Embryonic Science and Technology) program JPMJPR165A.
Author information
Authors and Affiliations
Contributions
Y.S., K. Terayama, M.Y., and K. Tsuda conceived the idea, designed, and supervised the experiment. Y.S., K.S., K. Terayama implemented the proposed method and analyzed the experimental results. Y.S. collected images of atomic layers with the help of M.O., Y.N., and Y.M.I. All authors discussed the results. Y.S., K.S., K. Terayama, and K. Tsuda wrote the manuscript with contributions from all other co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Saito, Y., Shin, K., Terayama, K. et al. Deep-learning-based quality filtering of mechanically exfoliated 2D crystals. npj Comput Mater 5, 124 (2019). https://doi.org/10.1038/s41524-019-0262-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-019-0262-4
This article is cited by
-
Prediction of electrode microstructure evolutions with physically constrained unsupervised image-to-image translation networks
npj Computational Materials (2024)
-
Deep learning in two-dimensional materials: Characterization, prediction, and design
Frontiers of Physics (2024)
-
Physically informed machine-learning algorithms for the identification of two-dimensional atomic crystals
Scientific Reports (2023)
-
A reusable neural network pipeline for unidirectional fiber segmentation
Scientific Data (2022)
-
Reaching the Full Potential of Machine Learning in Mitigating Environmental Impacts of Functional Materials
Reviews of Environmental Contamination and Toxicology (2022)